Etude prévisionnelle de la consommation nationale du gaz en Algérie

^{Etude prÈvisionnelle de la consommation}

nationale du gaz naturel

Faouzi Chaibi & Maher Guennoun

FacultÈ de MathÈmatiques,

UniversitÈ des Sciences et de la Technologie Houari Boumediene,

U. S. T. H. B..

i

Table de MatiËres

Chapitre 1 : PrÈsentation gÈnÈrale 1

1.1. PrÈsentation de la SONELGAZ 1

1.2. Origine et caractÈristiques du gaz 4

Chapitre 2 : problÈmatique 6

2.1. Introduction 6

2.2. MÈthodologie 6

Chapitre 3 : Processus stochastiques et SÈries chronologiques 8

3.1. Introduction 8

3.2. DÈÖnitions 9

3.3. ClassiÖcation des processus stochastiques 9

3.4. CaractÈristiques díun processus stochastique 10

3.5. Les processus stationnaires 10

3.6 Fonction díautocovariance 12

3.7. Fonction díautocorÈlation 12

3.8. Fonction díautocorÈlation partielle 13

3.9. SÈries chronologiques 14

Chapitre 4 : MÈthodologie de Box & Jenkins 38

4.1. IdentiÖcation du modËle 39

4.2. Estimation 49

4.3. Validation 40

ii

4.4. PrÈvision 46

Chapitre 5 : Application de la mÈthodologie de Box & Jenkins 48

5.1. Etude de la sÈrie consommation des distributeurs publics (7C ) 49

5.2. Etude de la SÈrie consommation des centrales Èlectriques (6 8) 67

5.3. Etude de la sÈrie consommation industrielle (6 < ) 79

Chapitre 6 : ModËle VAR 91

6.1. Introduction 91

6.2. ModËles multivariÈs 92

6.2.1. Fonction díautocovariance 92

6.2.8. ModËle autoregressif I 4E']( 95

Chapitre 7 : Application de la modËlisation multivariÈe 106

7.1. Etude des sÈries de consommation '6 8F4/ 7?7C F4/ 6 8F4( 106

7.1.1 IdentiÖcation du modËle 106

7.1.2. Estimation du modËle 106

7.1.3 Validation 119

7.1.4. PrÈvision 126

7.2. Conclusion 130

Chapitre 8 : Conclusion gÈnÈrale 133

ANNEXE [A] MÈthodes díestimation 136

ANNEXE [B] Tableaux statistiques 136

ANNEXE [C] PrÈsentation du logicel EVIEWS 4.0

iii

ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó ó

4YYN 5N_NXNaV 8? ?NUV

Chapitre 1

PrÈsentation gÈnÈrale

1.1 PrÈsentation de la SONELGAZ

1.1.1 Historique

1947 : CrÈation de "ElectricitÈ et Gaz díALGERIE " : EGA

1969 : CrÈation de la SociÈtÈ Nationale de líElectricitÈ et du Gaz : Sonelgaz

Par ordonnance n^!6959 du ,6 juillet 1969 parue dans le journal ocents ciel du 1er ao°t 1969,

la Societe Nationale de líElectricite et du Gaz (Sonelgaz) est creee en substitution ‡ EGA (19.1 1969) dissout par ce même decret. Líordonnance lui assigne pour mission generale de síintegrer de faÁon harmonieuse dans la politique energetique interieure du pays. Le mono- pole de la production, du transport, de la distribution, de líimportation et de líexportation

de líenergie electrique attribue ‡ Sonelgaz a ete renforcee. De même, Sonelgaz síest vue at-

tribuer le monopole de la commercialisation du gaz naturel ‡ líinterieur du pays, et ce pour tous les types de clients (industries, centrales de production de líenergie electrique, clients domestiques). Pour ce faire, elle realise et gËre des canalisations de transport et un reseau

de distribution.

1983 : Restructuration de Sonelgaz

Toutes les unites de travaux et de fabrication de materiels, crees pour palier au manque

de capacites nationales se sont transformees en 1983 en entreprise autonome.cíest ainsi que

KAHRIF : Travaux díelectriÖcation.

1

KAHRAKIB : Montage des infrastructures et installations électriques.

KANAGAZ : Réalisation des canalisations de transport et de distribution du gaz.

INERGA : Travaux de génie civil.

ETTERKIB : Montage industriel.

AMO : Fabrication des compteurs et des appareils de mesure et de contrOle. Ont été crées.

1991 : Nouveau statut de Sonelgaz

Sonelgaz : Société Nationale díElectricité et du Gaz change de nature juridique et devient

un établissement Public ‡ CaractËre Industriel et Commercial (décret exécutif n^!91-475 du

14 décembre 1991).

1995 : Sonelgaz (EPIC)

Le décret exécutif n^!95-280 du 17 septembre 1995 conÖrme la nature de Sonelgaz en tant quíétablissement public ‡ caractËre industriel et commercial. Sonelgaz est placé sous tutelle

du Ministre chargé de líénergie, est doté de la personnalité morale et jouit de líautonomie ÖnanciËre, est régie par les rËgles de droit public dans ses relations avec líétat. et est réputé commerÁant dans ses rapports avec les tiers

Le même décret déÖnit (en son article 6( les missions de Sonelgaz :

ñAssurer la production, le transport et la distribution de líénergie électrique, ñAssurer la distribution publique du gaz,

dans le respect des conditions de qualité, de sécurité et au moindre co°t, dans le cadre

de sa mission de service public.

2002 : Sonelgaz.Spa

le décret présidentiel N^! 02-195 du 1 juin ,* * , Öxe les statuts de la société algérienne de líélectricité et du gaz Sonelgaz.spa, ayant pour missions :

1- La production, le transport, la distribution et la commercialisation de líélectricité, tant en Algérie quí‡ líétranger,

2- Le transport du gaz pour les besoins du marché national,

3- La distribution et la commercialisation du gaz par canalisations tant en Algérie quí‡ líétranger,

4- Le développement et la fourniture de toutes prestations en matiËre de service énergétiques,

5- Líétude, la promotion et la valorisation de toutes formes et sources díénergie

6- Le développement par tout moyen de toute activité ayant un lien direct ou indirect avec les industries électriques et gaziËres et de toute activité pouvant engendrer

un intérêt pour "Sonelgaz.Spa" et généralement toute opération de quelque nature quíelle soit pouvant se rattacher directement ou indirectement ‡ son objet social, notamment la recherche, líexploration, la production et la distribution

díhydrocarbures,

7- Le développement de toute forme díactivités conjointes en Algérie et hors díAlgérie avec des sociétés algériennes ou étrangËres,

8- La création de Öliales, les prises de participation et la détention de tous porte feuilles díactions et autres valeurs mobiliËres dans toute société existante ou ‡ créer en Algérie et ‡ líétranger.

Le même décret consacre la mission de service public conÖée ‡ Sonelgaz.Spa.

2004 : Un groupe síannonce

En application de la loi sur líélectricité et la distribution du gaz par canalisations, Sonel- gaz a transformé les directions de production, de transport électrique et de transport gaz en trois nouvelles Öliales sous formes de sociétés par actions : SPE (Sonelgaz Production Elec- tricité), GRTE (Gestionnaire du Réseau Transport Electricité) et GRTG (Gestionnaire du Réseau Transport Gaz). Préparant la transformation du métier de la distribution en quatre Öliales di§érentes, Sonelgaz a mis en place quatre directions générales pour la région díAlger,

la région Centre, la région Est et la région Ouest. Ces directions générales sont chargées de

réunir toutes les conditions pour réussir ce passage dés janvier ,* * 6.

1.2 Origine et caractÈristiques du gaz

Le gaz naturel a été découvert au Moyen-Orient au cours de líantiquité. Il y a de cela quelques milliers díannées. Líapparition soudaine de gaz naturel síenáammant brutalement était assimilé ‡ des sources ardentes. En Perse, en GrËce ou en Inde, les Hommes ont érigé

des temples autour de ces feux pour leurs pratiques religieuses. Cependant ils níévaluËrent pas immédiatement líimportance de leur découverte. Cíest la Chine qui autour de 9* * avant Jésus-Christ, comprit líimportance de ce produit et fora le premier puits aux alentours de

,11 avant Jésus Christ. En Europe, il fallut attendre jusquíen 16/ 9 pour que la Grande- Bretagne découvre le gaz naturel et le commercialise ‡ partir de 119* . En 12 ,1, ‡ Fredonia (Etats-Unis), les habitants ont découvert le gaz naturel dans une crique par líobservation de bulles de gaz qui remontaient jusquí‡ la surface. William Hart est considéré comme le "pËre

du gaz naturel". Cíest lui qui creusa le premier puits nord-américain.

1.2.1 CaractÈristiques techniques

Le gaz naturel est incolore, inodore, insipide, sans forme particuliËre et plus léger que líair. Il se présente sous sa forme gazeuse au-dessus de -161^!Celssus. Pour des raisons de sécurité, un parfum chimique, le mercaptan, qui lui donne une odeur díúufs pourris, lui est souvent ajouté de sorte quíune fuite de gaz puisse ainsi être détectée.

Le gaz naturel est un mélange díhydrocarbures comprenant du méthane, de líéthane,

du propane, des butanes et des pentanes. Díautres composants tels que le CO2, líhélium,

le sulfure díhydrogËne et líazote peuvent également y être trouvés. La composition du gaz naturel níest jamais la même. Cependant, on peut dire que son composant principal est le méthane (au moins 9* & ). Il possËde une structure díhydrocarbure simple, composée díun atome de carbone et de quatre atomes díhydrogËne '6 ; .(. Le méthane est extrêmement ináammable. Il br°le facilement et presque totalement et níémet quíune faible pollution. Le gaz naturel níest ni corrosif ni toxique. . En outre, en raison de sa densité * .6* , inférieure ‡ celle de líair (1.** ), le gaz naturel a tendance ‡ síélever et peut, par conséquent, disparaÓtre facilement du site ocents il se trouve par níimporte quelle Össure.

1.2.2 Evolution du gaz naturel en tant quíÈnergie

Le gaz naturel est la source díénergie fossile qui a connu la plus forte progression depuis

les années 1* . En e§et, elle représente le cinquiËme de la consommation énergétique mondiale.

En raison de ses avantages économiques et écologiques, le gaz naturel devient chaque jour plus attractif pour beaucoup de pays. Les propriétés de ce produit, comme par exemple

le faible intervalle de combustion le caractérisant, en font líune des sources díénergie les plus Öables connue a ce jour. Actuellement, il représente la deuxiËme source díénergie la plus utilisée aprËs le pétrole. DíaprËs líEIA, du département américain de líénergie, la part du gaz naturel dans la production énergétique mondiale était de ,- & en 1999 et les perspectives de développement de la demande sont excellentes. Il est considéré comme le combustible fossile

du siËcle, comme le pétrole líétait lors du siËcle précédent et le charbon il y a deux siËcles.

Le gaz naturel présente un avantage concurrentiel par rapport aux autres sources díénergie car, seuls 1* & (environ) du gaz naturel produit sont perdus avant díarriver chez le consom- mateur Önal. En outre, les progrËs technologiques améliorent constamment líecents cacité des techniques díextraction, de transport et de stockage ainsi que le rendement énergétique des équipements fonctionnant ‡ base de gaz naturel.

1.2.3 Les rÈserves du gaz naturel

Ces réserves sont trËs importantes et les estimations concernant leur taille continuent de progresser ‡ mesure que de nouvelles techniques díexploration ou díextraction sont décou- vertes. Les ressources de gaz naturel sont abondantes et trËs largement distribuées ‡ travers

le monde. On estime quíune quantité signiÖcative de gaz naturel reste encore ‡ découvrir.

Chapitre 2

ProblÈmatique

Introduction

étant donné que líAlgérie est en plein développement social, culturel et économique, ce qui ináue sur la consommation nationale du gaz naturel, il est intéressant pour la SONELGAZ

de faire une étude scientiÖque et rigoureuse sur líévolution dans le temps de cette matiËre stratégique dans ses di§érents aspects, et ce tant pour des prises de décisions que pour les planiÖcations futures.

Cíest dans ce but que la compagnie nous chargé díélaborer un modËle prévisionnel sur la consommation nationale du gaz naturel.

Cette derniËre se présente sous trois aspects : la consommation publique, la consommation industrielle et la consommation des producteurs díélectricité.

MÈthodologie

Pour líobjectif assigné, il existe un axe important dans les séries chronologiques, de l‡ nous modélisons la consommation publique, la consommation industrielle et la consommation des producteurs díélectricité comme des séries temporelles.

Les modËles de séries chronologiques identiÖées, estimés et diagnostiqués adéquats aux séries

de consommation publique, industrielle et les producteurs díélectricité, seront par la suite exploités pour établir la prévision ‡ court et ‡ moyen terme. AÖn díétablir une relation tendancielle entre les di§érentes séries de consommation ‡ moyen et ‡ long terme, une étude

du vecteur multivarié, dont les composantes sont des séries chronologiques des trois types de consommation sera envisagée. La relation tendancielle éventuelle entre les trois séries de est aussi envisagé.

6

CHAPITRE 2. PROBL...MATIQUE 7

Cette étude fait appel ‡ des concepts en analyse des séries temporelles, ‡ savoir les modËles

I 4E et la méthodologie de Box & Jenkins.

Chapitre 3

Processus stochastiques et sÈries chronologiques

3.1 Introduction

Les processus aléatoires décrivent líévolution díune grandeur aléatoire en fonction du temps (ou líespace). Il existe de nombreuses applications des processus aléatoires notam- ment en physique statistique, en biologie et bien entendu dans les sciences de líingénieur et

les domaines économiques et Önanciers.

Líétude des processus stochastiques síinsËre dans la théorie des probabilités dont elle consti-

tue líun des objectifs les plus profonds, elle soulËve des problËmes mathématiques intéres- sants et souvent trËs dicents ciles. Ce chapitre présente quelques notions et aspects des processus aléatoires utiles ‡ la statistique chronologique.

8

CHAPITRE 3. PROOESSUS STOOHASTIQUES ET S...RIES OHRONOLOGIQUES 9

3.2 DeÖnitions

Soit '2 , A , F ) un espace probabilisé et ¹2 , A un espace probabilisable

DeÖnition 1

On appelle une variable aleatoire notee K toute application mesurable, telle que

K : '2 , A ) ' '2 , A ), tel que / 5 E A ) K ^%'5) E A

DeÖnition 2

Un processus aleatoire ou encore stochastique note 3 KK, a E G 4 est une famille

de variables aleatoires indicees par a, deÖnies sur un mÍme espace probabilise

'2 , A , F ) et a valeurs dans ¹2 , A ocents ¹2 , A est appele "espace díetats du pro- cessus aleatoire"

3.3 ClassiÖcation des processus stochastiques

Nous distinguons les processus suivants :

ó 1. Si G est dénombrable, alors le processus 3 KK, a E G 4 est dit ‡ temps discret, sinon

il est dit ‡ temps continu .

ó ,. Si 2 est dénombrable, alors le processus 3 KK, a E G 4 est ‡ espace díétats discret, sinon il est ‡ espace díétats continu.

ó - . Si 2 6 R^F alors le processus est dit multivarié.

Remarques

ó 1. Une réalisation díun processus est appelée trajectoire. Donc, cíest une suite des réalisations des variables aléatoires KK. Les réalisations díune même variable aléatoire pouvant être di§érentes, les réalisations díun même processus peuvent donner des

trajectoires di§érentes.

ó ,.Dans ce qui suit on síintéresse aux processus aléatoires ‡ temps discret, autrement dit G 6 Z.

3.4 Caracteristiques díun processus stochastique

Soit le processus aléatoire3 Xt, a E Z4 , alors la moyenne (espérance mathématique), la variance et la covariance de ce processus Xt sont données respectivement par :

^{1) E (X}t^{) 6 %} t ^{(moyenne de X}t^),

& "

^{2) I N_ (Xt) 6 E ! (Xt %} t⁾

^{(variance de Xt)}

^{et la covariance entre X}t ^{et X}s ^{est déÖnie comme suit :}

- ) 6 \b (Xt, Xs) 6 E 8 (Xt % t) (Xs % s)] (covariance entre Xt et Xs),

3.5 Les processus stationnaires

La notion de stationnarité joue un rOle central dans la théorie des processus. Deux types

de stationnarité sont généralement considérées. Et dans ce qui suit nous passons en revue

les déÖnitions de bases liées ‡ ces deux types de processus stationnaires.

3.5.1 Processus strictement stationnaire (la stationnarite forte)

Soit un processus stochastique3 Xt, a E Z4 , le processus est dit strictement (ou forte-

ment) stationnaire si : / (a%, a& *..., aF) E Z^F et / U E Z, alors la suite (Xt # @, ..., Xt

# @) a la

1 "

même loi de probabilité que la suite (Xt1 , ..., Xt" ), autrement dit :

^{F (X}t1 ^{$ c} %^{, ..., X}t" ^{$ c} F^{) 6 F (X}t1 # @ ^{$ c} %^{, ..., X}t" # @ ^{$ c} F^{) ,}

/ (a%, a& *..., aF) E Z^F, / (c %, c & *..., c F) E R^F et / U E Z.

De cette déÖnition découle que tous les moments díordre (síils existent), díun processus stochastique strictement stationnaire sont invariants pour toute translation dans le temps,

or cette déÖnition est rarement vériÖée en pratique, cíest ainsi que nous proposerons un autre

type de stationnarité, dite stationnarité du second ordre.

3.5.2 Processus faiblement stationnaire (second ordre)

Le processus 3 xt, t E Z4 est dit faiblement stationnaire si :

ó 1. E (xt) 6 % (constante), / t E Z,

M

ó 2. I N_ (xt) 6 ) ^&

6 ! $

(constante), / t E Z,

ó - . 6 \ b (xt, xt# @) 6 E 8 (xt % t)(xt# @ % t] 6 ! M (U), / t, U E Z,

! M (U) est la fonction díautocovariance du processus3 xt, t E Z4 .

Remarques

ó 1. La covariance dun processus faiblement stationnaire depend seulement de la di§erence entre les instants.

ó 2. Dans les processus stochastiques du second ordre, la stationnarite stricte implique

la stationnarite faible (la reciproque est fausse sauf pour les processus gaussiens).

ó - . Desormais, le terme stationnaire renverra au concept de stationnarite du second ordre, sauf mention contraire

Implication de la stationnarite

La stationnarite signiÖe que le degre de relation entre deux termes díune serie depend uni- quement de líintervalle temporel entre eux et non du temps. Cela signiÖe que la fonction de generation du processus ne change pas au cours du temps. Ainsi, si par exemple xt est genere

^{par líequation x}t ^{6 -} t ^{) b (t)-} t 1 ^{et que le paramétre b (t) áuctue avec le temps, alors la serie}

níest pas stationnaire. Cette deÖnition de la stationnarite implique aussi que la variance de

la serie est invariante avec le temps.

3.5.3 Processus bruit blanc (white noise process)

Un bruit blanc3 - t, t E Z4 est une suite de variables aleatoires non correlees de moyenne nulle et de variance Önie constante. Un processus bruit blanc veriÖe les proprietes suivantes :

^* E (- t) 6 * ,

I (- t) 6 E (- & ) 6 ) & . ^{/ E}

t Z

t (

Et en consequence sa fonction díautocovariance est donnee par :

^* ) & , U 6 * ,

^{! (U) 6 E (-} t ^- t# @^{) 6}

* , U 6 * .

Remarques

ó 1. Les bruits blancs sont des processus stationnaires particuliers sans "memoire". Le niveau de la serie consideree aujourdíhui nía aucune incidence sur son niveau de demain, tout comme le niveau díhier nía aucune incidence sur le niveau díaujour- díhui.

ó 2. Le terme bruit blanc provient de líanalogie dans le domaine des frequences entre la

densite spectrale díune variable i.i.d (constante) et le spectre de la lumiére blanche dans le spectre des couleurs.

ó - . Par rapport ‡ un processus bruit blanc, un processus stationnaire peut se caracte-

1

riser par une certaine non correlation de ses termes. Quand le processus est un bruit blanc, le coecents cient díautocorrelation est nul des le premier decalage. Dans un pro- cessus stationnaire, la moyenne níest pas forcement nulle.

3.6 Fonction díautocovariance

La fonction díautocovariance du processus 3 Xt, t E Z4 notee 7 (h) est deÖnie par :

7 (h) 6 6 \b (Xt, Xt h) 6 E 8 (Xt E (Xt)) (Xt h E(Xt h))] , V h, t E Z.

On remarque que pour h 6 * ; I N_(Xt) 6 7 (* )

Proprietes

7 ( h) 6 7 (h) , V h E Z, (la fonction díautocovariance est symetrique)

5 7 (h)5 $ 7 (* ) 6 I (Xt) , V h, t E Z,

Estimateur

^{Considerons (X}1^{, ...., X}: ^{), líestimateur de la fonction díautocovariance est donne par :}

1

: h

: ( (

7 (h) 6

^>

^{T h} tl 1

^Xt ^X t

1

^Xt# h ^X t# h ^,

: h :

:

^{avec X} t h ⁶

^{T h} tl 1

^Xt ^{et X} t ⁶

^: Xt

^T tl 1

3.7 Fonction díautocorrelation

La fonction díautocorélation de h, (h E Z), díun processus stationnaire du second ordre

^{de moyenne E (X}t^{) 6 % , notée p (h) est déÖnie par :}

p (h) 6

6 \b (Xt, Xt h)

^{C 6}

^{I N_ (X}t^{) B I N_(X}t h⁾

7 (h)

^{V E}

, h Z,

^{7 (* )}

avec p (h) E 8 1, 1]

Proprietes

p (* ) 6 1, V h E Z,

5 p (h)5 < 1, V h E ZI

Estimateur

7 (h)

p (h) 6 ^>

^> 7 (* )

^>

Remarques

ó 1I La représentation graphique de p (h) est appelée îcorrelogrammeî

ó 2I Si la fonction díautocorélation p (h) décroÓt rapidement quand le nombre de retards augmente, cela signiÖe que la série est stationnaire.

3.8 Fonction díautocorrelation partielle

La fonction díautocorrélation partielle mesure la corrélation entre Xt et Xt h, líináuence

des variables Xt h i (pour i < h) ayant été retirée. Notons p (h) et + hh les fonctions respecti- vement díautocorrélations et díautocorrélation partielle de XtI Soit p h la matrice symétrique

^{formée des (h 1) premieres autocorrélations de X}t ^:

⁰

I I

^I

p 6 ^I

^{h I}

^I

⁶

¹

1

I

2 I I

' I I I I

I

I

I

^ph

⁷

1	^p1	^p2	I	I	^ph
^p1	1	I	I	I	^ph
^p2	^p1	1	I	I	^ph
I	I	I	I	I
I	I	I	I	I

I

^p h 1 ^p h 2

^{% %}

^{% %}

^% p ^%

h

La fonction díautocorrélation partielle est donnée par : + hh 6 ^%

^% , ocents ^% p

^% est le déterminant

^{% % %} h ^%

% p h%

^{% %}

de la matrice p

^h

et p

^h

est donnée par :

⁰

I I

^I

p 6 ^I

^{h I}

^I

I

I

I

1

⁶

¹

I I I I I I

⁷

1	^p1	^p2	I	I	^p1
^p1	1	I	I	I	^p2
^p2	^p1	1	I	I	^p'
I	I	I	I	I	I
I	I	I	I	I	I

^p h 1 ^p h 2

p est la matrice p

^{h h}

^{dans laquelle on a remplacé la derniere colonne par le vecteur 8 p} 1^{, IIIIII, p} h^{] # ,}

la fonction díautocorrélation partielle síécrit :

^{2 +} 11^{, ` i i 6 1,}

⁾⁵ Pi ^: + i 1*a p i a

⁺ ii ⁶

⁵3

i 1

1 ^:

a l 1

⁺ i 1*a ^p a

, ` i i 6 2, >

Cet algorithme est connu sous le nom díalgorithme de Durbin (196* ). Il est basé sur les

équations de Yulle-Walker.

3.9 Series chronologiques

Líapproche de modélisation par les séries chronologiques est utilisée pour faire des prévi- sions, elle consiste ‡ exploiter líinformation contenue dans les valeurs passées díune variable

et des perturbations aléatoires (on aura besoin de collecter des informations sur une assez longue période pour avoir des prévisions Öables), de faÁon ‡ déterminer les caractéristiques intrinseques et la nature de líévolution dans le temps de la série ; nous pourrons alors pré- voir les valeurs futures de la variable. A titre díexemple, nous citerons quelques domaines díapplication :

ó 1I Líéconométrie (prédiction de quantités économiques, les prix de ventes et díachats..)

ó 2I La Önance (évaluation des cours de la bourse au cours díune séance.....)

ó - I La météorologie (analyse des données climatiques, prévision ......)

DeÖnitions

Une serie chronologique dite aussi chronique ou serie temporelle (time series en terminologie anglaise) est une suite díobservations 3 c t, t E T 4 indexees par un ensemble ordonnee T .

Suivant líensemble des indices T nous distinguons deux types de chroniques, ‡ savoir :

Serie continue : une série est continue lorsque líensemble des valeurs possibles de t est non dénombrable. Nous pourrons rencontrer ce genre de séries en physique quantique.

Serie discrËte : une série est discrete lorsque líensemble des valeurs possibles de t est

un ensemble dénombrable .Nous distinguons deux types de variables constituant une série discrete.

ó Les variables de áux : elles représentent le mouvement intervenu durant un certain intervalle de temps (le nombre díaccidents durant líannée en cour, le traÖc aérien - quotidien).

ó Les variables de niveau : elles représentent un état ‡ un moment donné.(taux de - chOmage, température ‡ un lieu Öxe...).

Une série chronologique peut être représentée graphiquement en plaÁant les instants (ti , 1 <

i < [ ) en abscisses et les observations (d i , 1 < i < [ ) en ordonnées.

3.9.1 Operateurs sur les chroniques

Operateur retard et avance

Pour formaliser le déplacement dans le temps de la série temporelle, nous déÖnissons une application, quí‡ partir díune observation prise ‡ une date donnée nous permet díexprimer

les observations passées ou futures.

Ainsi, nous introduisons líopérateur retard (Backward) noté B comme líapplication

Xt ' BXt 6 Xt 1

Nous pourrons alors établir une relation de récurrence selon :

^{B2 X}t ^{6 X}t 2 ^{5 IIIIIIIIII5 BFX}t

^{6 X}t F

De maniere analogue, nous déÖnissons líopérateur avance (Forward) noté F tel que :

9 Xt 6 Xt# 1. IIIIIIII5 9 ^FXt 6 Xt# F.

Líavantage de ces opérateurs est de permettre une expression formelle plus simple des modeles

de séries chronologiques et de líétude de leurs propriétés.

Ainsi nous pourrons écrire Yt 6

H

H

^:

i l $

ai Xt i selon Yt 6

⁽ H

^:

i l $

⁾

ai Bⁱ

Xt ce qui déÖnit une

nouvelle application 4

^:

i l $

^ai ^{Bi , qui síapplique aux séries temporelles. Cette application met}

en évidence les propriétés suivantes :

ó 1. B^$ Xt 6 Xt,

ó 2. Bⁱ B^a Xt 6 B^{i # a} Xt 6 Xt i a ,

ó - . B ⁱ Xt 6 Xt# i V i E e , B ¹ 6 F ,

ó .. B^{i # a} Xt 6 Bi Xt ) Ba Xt.

Notons que ces propriétés síappliquent également ‡ líopérateur F .

Operateur de di§erence ordinaire

Líopérateur de di§érence ordinaire noté V, associé au processus 3 Xt, t E Z4 est tel que :

V t E Z, VXt 6 (1 B) Xt 6 Xt Xt 1.

Et par construction, nous obtiendrons líopérateur de la d^{? E ?} di§érence noté V^> tel que :

V t E Z, V^> Xt 6 (1 B)^> Xt

Operateur de di§erence saisonniËre

Líopérateur de di§érence saisonniere díordre ` , noté Vs associé au processus3 Xt, t E Z4 est

tel que : V t E Z, VsXt 6 (1 B^s) Xt et par construction nous obtiendrons líopérateur de la

s

d^{? E ?} di§érence díordre ` , noté V^>

s

V t E Z, V^> Xt 6 (1 B^s)^> Xt.

telle que :

3.9.2 Analyse des series chronologiques

Líanalyse des séries chronologiques a pour objectif de décrire les principales caractéris- tiques du processus générateur de la série, líajustement du modele adéquat, la prévision et

le contrOle.

Les composantes díune serie chronologique

Les premieres études sur les séries chronologiques ont amené ‡ considérer que la chronique

peut se mettre sous la forme fonctionnelle suivante : L t 6 S (Tt, Ft, 6t, - t) ocents

Tt : représente la tendance de la chronique

Ft : représente la saisonnalité,

6t : représente le cycle conjoncturel,

- t : représente les áuctuations irrégulieres(erreurs)

Donnons pour chacune de ces composantes, quelques déÖnitions.

- La tendance(Trend en terminologie anglaise) notée T décrit le mouvement ‡ long terme

de la série, ce mouvement est traditionnellement représenté par des formes : polynomial, logarithmique, exponentielle ..., elle est en fonction du temps et marque líallure générale du phénomene.

- Le cycle conjoncturel regroupe les variations autour de la tendance avec des alternances díépoques ou des phases díexpansion et de contraction.

- Les variations saisonniËres ;beaucoup de séries chronologiques díorigine économique comportement une composante saisonniere, cela se manifeste par la répétition díun proÖl particulier avec une certaine périodicité. Parmi les causes de la saisonnalité, nous retrouvons

les variations météorologiques qui accompagnent le rythme des saisons, les habitudes (fêtes

de Ön díannée, le ramadan, les congés annuels...

- Les variations accidentelles ou erreurs, rassemblent tout ce que les autres composantes níont pas pu expliquer du phénomene observé, elles contiennent donc de nombreuses áuc- tuations, en particulier accidentelles dont le caractere est exponentiel et imprévisible.

Ces di§érents composantes peuvent être combinées selon un des trois modeles suivants :

modËle additif :

L 6 Tt ) Ft ) - t

Pour bien séparer la tendance de la composante saisonniere et pour des raisons díunicité

G

dans la décomposition proposée, on impose ^:

a l 1

` a 6 *

modËle multiplicatif :

L 6 Tt(1 ) Ft)(1 ) - t)

L‡ encore on impose

modËle mixte :

G

^:

a l 1

` a 6 * ,

Il síagit l‡ de modeles, ocents addition et multiplication sont utilisés. Nous pouvons supposer par

exemple que la composante saisonniere agit de faÁon multiplicative alors que les áuctuations irrégulieres soient additives :

L 6 Tt(1 ) Ft) ) - t

(toutes les autres combinaisons sont également possibles).

3.9.3 Modelisation des series chronologiques

Líobjectif de la modélisation est de construire des modeles permettant de décrire le comportement díune chronique, et de ce fait résoudre les problemes liés ‡ la prévision.

Decomposition de wold

Le théoreme de Wold (19-2 ) est le théoreme fondamentale de líanalyse des séries chrono- logiques.

TheorËme

Tout processus stochastique du second ordre 3 Xt, t E M 4 , possËde une decompo- sition unique donnee par Xt 6 H t ) It tel que :

ó 1 ces deux processus (H t, It) sont orthogonaux de plus H t est purement déterminable

et It est purement indéterminable (aléatoire)

ó 2 le processus 3 It, t E M 4 peut être représenté sous forme díune combinaison linéaire inÖnie du présent et du passé du processus bruit blanc 3 - t, t E M 4 .

Cette expression devait être convergente en moyenne quadratique cela veut dire que I a_(It)

doit être Önie cíest ‡ dire

²

^{) I}t ⁶

^:$

a l 1

^a! ^- $ !

^{3 I a_(I}t^{) 0 +}

ModËle autoregressif moyenne mobile & / , & (: , ; )

Les modeles 4E@ 4 (Auto Regressive Moving Average) ont été introduits par Box et Jen-

kins (191* ). Líobjet est de modéliser une série temporelle en fonction de ses valeurs passées, mais aussi en fonction des valeurs présentes et passées díun bruit.

ModËle autoregressif & / (: )

DeÖnition :

Le processus stationnaire 3 Xt, t E Z4 satisfait une representation & / díordre : , note & / (: ), síil est solution de líequation aux di§erences stochastique suivante :

- t 6 Xt

p

^z

j l 1

+ j Xt j

^Xt ^{6 +} 1^Xt 1 ^{) +} 2 ^Xt 2 ^{) ......... ) +} p ^Xt p ^{) -} t

- t 6 Xt + 1Xt 1 + 2 Xt 2 ......... + p Xt p

p

^- t ^{6 X}t ⁺ 1 ^Xt ⁺ 2 ^{2 X}t ^{......... +} p ^Xt

p

^- t ^{6 (1 +} 1 ⁺ 2 ^{2 ......... +} j

)Xt

- t 6 # ( )Xt avec # ( ) 6

6

j

^{z +} j

j l $

V W 0 ], + j

E R, + $ 6 1

^{et +} p ^{E R oü # ( ) représente le polynOme de retard et -} t ^{est un bruit blanc de moyenne}

(

nulle et de variance ) ² .

^Remarque

Le modele autoregressif díordre(]) explique la valeur de la chronique ‡ líinstant t comme une combinaison linéaire de ] observations antérieurs. Il apparaÓt aussi comme une régression multiple oü líon explique les valeurs de la série chronologique aux instants t 1, t 2, .......t ], cíest pour cela que nous líappelions autoregressif díordre (]).

ModËle moyenne mobile @ 4(^ )

DeÖnition :

Le processus stationnaire 3 Xt, t E Z4 satisfait une representation moyenne mobile díordre ; , note , & (; ), síil est solution de líequation aux di§erences stochastique

suivante :

Xt 6 - t

H

^z

j l 1

^# j ^- t j

En introduisant le polynOme de retard on obtient :

^Xt ^{6 ! ( )-} t

oü ! ( ) 6

H

^z

j l $

# j ^j , # j E R , oü # $ 6 1 et # H E R , V W 0 q ,

(

^- t ^{est un bruit blanc de moyenne nulle et de variance ) 2 .}

Remarque

Le modele moyenne mobile díordre q , @ 4(q ) explique la valeur de la série ‡ líinstant t

par une moyenne pondérée díaléas - t jusquí‡ la q ^{? E ?} période qui sont supposés générés par

un processus de type bruit blanc.

ModËle mixte 4R@ 4

Le processus stationnaire 3 Xt, t E Z4 satisfait une representation & / , & díordre :

et ; , note & / , & (: , ; ), síil est solution de líequation aux di§erences stochastiques suivante :

Xt

ou encore :

p

^z

j l 1

+ j Xt j 6 - t

H

^z

j l 1

^# j ^- t j

# ( )Xt 6 ! ( )- t.

Remarque

ó 1 Le modele 4R@ 4 est une composition díun modeles autoregressif 4R et díun modeles moyenne mobile @ 4.

Causalite et Inversibilite

DeÖnition

Un modËle de serie chronologique (lineaire ou non lineaire) de la forme :

Xt 6 T (Xt 1, Xt 2 , ... Xt p 5 - t, - t 1, - t 2 , ... - t H ) ,

ocents - t est un bruit blanc, est dit causal si, et seulement si, on peut exprimer

le processus stochastique Xt sous forme combinaison lineaire (Önie ou inÖnie)

convergente, en moyenne quadratique, du present et du passe du bruit blanc - t.

ConnaÓtre la causalité díun modele níest pas une tche facile, une raison pour laquelle

on doit imposer une condition de causalité, qui nous permet díacents rmer ou díinÖrmer sa

causalité.

TheorËme :

Soit 3 Xt, t E Z4 un modËle 4R@ 4 (], q ) deÖni par

# (B) Xt 6 ! (B) - t.

tel que les polynÙmes # (.) et ! (.) díordres respectifs ] et q níont pas de racines communes. Alors, le modËle est causale si et seulement si les racines de # sont

de module strictement superieure a líunite, i.e : # (e ) 6 * , V e E M , 5 e 5 < 1.

Remarque

La causalité est une notion qui ne concerne pas le processus 3 Xt, t E Z4 seul, mais la relation

qui lie 3 Xt4 et 3 - t4 ..

DeÖnition

Un modËle de serie chronologique (lineaire ou non lineaire) de la forme

Xt 6 T (Xt 1, Xt 2 , ... Xt p 5 - t, - t 1, - t 2 , ... - t H ) ,

ocents 3 - t4 est un bruit blanc, est dit inversible si, et seulement si, on peut exprimer

le processus 3 - t4 comme combinaison lineaire (Önie ou inÖnie) convergente, en moyenne quadratique, du present et du passe du processus stochastique 3 Xt4 .

Le théoreme suivant établi une condition nécessaire et sucents sante pour quíun modele moyenne mobile díordre q , soit inversible.

TheorËme

Soit 3 Xt, t E Z4 un modËle & / , & (: , ; ) deÖni par # ( )Xt 6 ! ( )- t tel que les polynÙmes # (.) et ! (.) díordres : et ; respectivement, níont pas de racines com- munes. Alors, 3 t est inversible si et seulement si les racines de ! sont de module strictement superieur a líunite.

Remarque

Un processus 3 Xt, t E Z4 satisfait une représentation 4R(]), est toujours inversible.

3.9.4 Fonction díautocorrelation

Fonction díautocorrelation díun & / (: )

Soit le modele autoregressif díordre ] vériÖant líéquation 1

Xt 6 2 1Xt 1 ) 2 2 Xt 2 ) ......... ) 2 p Xt p ) 6 t V t E Z.........(1)

avec :

1) E(Xt) 6 0 (processus centré) ,

2) E(Xt h6 t) 6 0 (comme 6 t est indépendant de 6 t 1, 6 t 2 ,...., alors 6 t est indépendant

^{du passé constitué par les variables X}t 1^{, X}t 2 ^....Xt h ^{pour h 2 0 )}

Equations de Yule-Walker

Multiplions líéquation (1) par Xt h et prenons líespérance des deux cotés, on obtient :

E(XtXt h) 6 2 1E(Xt 1Xt h) ) 2 2 E(Xt 2 Xt h) ) ... ) 2 p E(Xt p Xt h) ) E(6 tXt h)

Pour h 6 0 on obtient :

(

7 $ 6 2 17 1 ) 2 2 7 2 ) ...... ) 2 p 7 p ) ) ²

Pour h 2 0 on obtient :

7 h 6 2 1 7 h 1 ) 2 2 7 h 2 ) .......... ) 2 p ! 7 h p , .........(2)

En divisant (2) par 7 $ on obtient :

p h 6 2 1p h 1 ) 2 2 p h 2 ) ........... ) 2 p p h p , ...........(3 )

Si nous réitéronslíéquation (3 ) pour h 6 1, ] nous obtenons le systeme de Yule-Walker sui- vant :

^p 1 ^{6 2} 1 ^{) 2} 2 ^p 1 ^{) ....... ) 2} p ^p p 1

^p 2 ^{6 2} 1^p 1 ^{) 2} 2 ^{) ........ ) .2} p ^p p 2

4

p p 6 2 1p 1 ) 2 2 p 2 ) ..... ) .2 6

Díou líécriture matricielle suivante :

⁰ p 1 ¹

⁰ 1 p 1 p 2 . . p p 1 ^{1 0}

2 1 ¹

^{I p} 2 ^{I I}

.

^{I I I}

6

^{I I I}

.

^{I I I}

^{I I I}

.

^{I I I}

^{6 7 6}

p p

^p 1 ^{1 p} 1 ^{. . p} p 2 ^{I I}

^{I I}

.

. . 1 . . . ^{I I}

^{I I}

.

. . . 1 . . ^{I I}

^{7 6}

. . . . 1 . ^{I I}

.

.

.

.

1

^p p 1

2 2 I I I I I

^I

⁷

.

2 p

Donc estimer les parametres du modele 4R(]) revient ‡ résoudre le systeme linéaire (ou ma-

tricielle) des ] équations de Yulle-Walker ‡ ] inconnus 2 1, 2 2 , ..........2 p et les valeurs estimées

^>

de p h, sont p h

Remarque

ó 1. Le corrélogramme díun modele 4R est un corrélogramme dont les valeurs abso- lues diminuent, jusquí‡ quíelles deviennent nulles.

ó 2. Il níest toujours facile díidentiÖer un modele autoregréssif par sa fonction díauto- corrélation, sauf dans le cas 4R(1), cíest la raison pour laquelle nous avions eu

recours aux autocorrélations partielles.

Fonction díautocorrelation díun MA(q)

Considérons le modele @ 4(1) vériÖant líéquation suivante :

^Xt ^{6 6} t ^# 1⁶ t 1

² O ov (X , X

) 6 O ov (6

# 6 , 6

# 6 )

^{) t t 1}

t 1 t 1 t 1

1 t 2

^{O ov (X}t^{, X}t 1^{) 6 O ov (6} t ^# 1⁶ t 1^{, 6} t 1 ^# 1⁶ t 2 ⁾

^{3 O ov (X}t^{, X}t 1^{) 6 7} 1

²

⁾

⁷ h ⁶

³

(1 ) # ² )) ² , h 6 0

# 1) ² , h 6 1

0 , h 2 1

Ainsi, par récurrence on trouve que la fonction díautocovariance díun @ 4(q ) síécrit comme

suit :

1

² (1 ) # ²

⁾⁵

2

) # ²

H

) ....... ) # ² )) ² , h 6 0 ,

7 h 6

( # h ) # 1# h# 1 ) ....... ) # H h# q ))

0 , h 2 q ,

² , 0 0 h 0 q ,

Díoü la fonction díautocorrélation :

2

7 h ⁵⁾

1, h 6 0 ,

( # h ) # 1# h# 1 ) ....... ) # H h# q )

7

^p h ^{6 6}

^{$ 5}

1

(1 ) # ²

2

H

) # ²

) ....... ) # ² ) ^{, 0 0 h 0 q ,}

0 , h 2 q

On remarque que la fonction díautocorrélation síannule ‡ partir díun décalage supérieur ‡

q , on dit quelle est tronquée au-del‡ du retard q . Donc on peut identiÖer un @ 4(q ) ‡ partir

du corrélogramme qui síannule ‡ partir díun retard supérieur ‡ q .

Fonction díautocorrelation díun & / , & (: , ; )

Pour calculer les autocorrélations díun modele 4R@ 4, on procede comme dans le cas des modeles 4R. A partir de líéquation

Xt 2 1Xt 1 2 2 Xt 2 ......... 2 p Xt p 6 t t # 1t t 1 # 2 t t 2 ......... # q t t q

1

On peut, en multipliant les deux membres par Xt h et en introduisant líespérance, on obtient líéquation suivante :

^! Xt

⁷ $

1

2 1E(Xt 1

^Xt h

) ........ 2

p E(Xt p

^Xt h

)^" 6

^{8 E(t} t^t t h^{) #} 1^E(t t 1^t t h^{) ........ #} q ^E(t t q ^t t h^)]

7

$

Comme t t est un bruit blanc, et par conséquent non corrélé avec le passé du processus Xt,

donc E(t tXt h) 6 0 , on obtient

^V

^p h ² 1^p h 1 ^{........ 2} p ^p h p ^{6 0 , h 2 q ,}

p

p h 6

^z

i l 1

2 i p h i , V h 2 q

3.9.5 Fonction díautocorrelation partielle

Fonction díautocorrelation partielle díun 4R(])

On considere le modele 4R(X), les équations de Yule-Walker :

p j 6 2 k 1p (j 1) ) 2 k 2 p (j 2) ) ...... ) p (j X), j 6 1, >

oü 2 k j est le j^{? E ?} coecents cient du modele autoregréssif díordre X.

2

2 k k est la fonction díautocorrélation partielle díordre X.

Líautocorrélation partielle entre X1et Xk mesure la corrélation entre X1et Xk lorsque nous avions supprimé líe§et de X2 , X3 , X4 , ....., Xk 1.

Soit le systeme suivant :

^{0 p} 1 ¹

^{0 1 p} 1 ^p 2 ^{. . p} k 1 ^{1 0} k 1 ¹

.

I I I I I I

⁶

Donc :

^p 2 ^{I I}

^{I I}

6

^{I I}

.

^{I I}

^{I I}

^{I I}

^{7 6}

.

p k

^p 1 ^{1 p} 1 ^{. . p} k 2 ^I

^I

. . 1 . . . ^I

^I

. . . 1 . . ^I

⁷

. . . . 1 . ^I

.

.

.

.

1

^p k 1

^{I 2} k 2 ^I

.

^{I I}

^{I I}

.

^{I I}

^{I I}

.

^{I I}

^{6 7}

² k k

2 k k 6

^% 1 p 1 p 2 ......... p k 1 ^%

^%

^%

^%

^%

^{% p} 1 ^{1 p} 1^{......... p} k 2 ^%

^%

^%

^% ..................... ^%

^%

^%

^{% p} k 1 ^p k 2 ^{............p} k ^%

^%

^%

^% 1 p 1 p 2 ......... p k 1 ^%

^%

^%

^{% p} 1 ^{1 p} 1^{......... p} k 2 ^%

^%

^%

^%

^%

^% ..................... ^%

Avec

^{% p} k 1 ^p

k 2 ^{.............1 %}

^%

^% 1 p 1 p 2 ......... p k 1

^%

^{% p} 1 ^{1 p} 1^{......... p} k 2

^%

^% .....................

^%

^%

^%

^%

^% 6 0

^%

^%

^%

^{% p} k 1 ^p

k 2 ^{.............1 %}

On peut donc lire líordre ] díun modele autoregréssif sur le corrélogramme 2 des autocorré- lations partielles, ce dernier síannule ‡ líordre ] ) 1

Ainsi, si la fonction díautocorrélation partielle díune série est calculée et si elle parait tronquée, on peut modéliser la série par un modele autoregréssif.

Fonction díautocorrelation partielle , & (; )

AÖn de calculer les autocorrélations partielles díun modele @ 4, nous utilisons líalgorithme

de Durbin. Contrairement au modele 4R(]), la fonction díautocorrélation díun modele @ 4

nía pas díexpression explicite.

Xt 6 t t & t t 1

avec t t est un bruit blanc et 5 & 5 0 1. La fonction díautocovariance de ce processus est :

7 $ 6 E(XtXt) 6 E 8 (t t & t t 1) (t t & t t 1)] 6 ⁽1 ) & ²

2

2

) ( , h 6 0 ,

⁷ 1 ^{6 E(X}t^Xt 1^{) 6 E 8 (t} t ^{& t} t 1^{) (t} t 1 ^{& t} t 2 ^{)] 6 & )} ( ^{, h 6 1,}

⁷ h ^{6 E(X}t^Xt h^{) 6 E 8 (t} t ^{& t} t 1^{) (t} t 1 ^{& t} t h 1^{)] 6 0 , h % 2,}

On en déduit la fonction díautocorrélation

²

⁵)

p h 6

⁵³

1, h 6 0

&

1 ) & ^{2 h 6 1,}

^{0 , h > 2}

Les autocorrélations partielles sont donc données récursivement par líalgorithme de Durbin.

Nous avons :

²

^{I 2} 11 ^{6 p} 1 ⁶

^I

9

2

1 ) 9 ^{2 ,}

2 22

p 2 2 11p 1 p 1

6 6 2

^{1 2} 11^p 1

I

1 p 1

I p 3 2 2 1p 2 2 22 p 1

2 22 p 1

² 33 ⁶

1 2 2 1p 1

6

² 22 ^p 2

1 2 22 p 1

Comme nous avons :

2 2 1 6 2 11 2 22 2 11(1 2 22 ) 6

^{p 1} ,

1

^{1 p 2}

Nous déduisons la valeur de líautocorrélation partielle 2 33

p 3

² 33 ⁶

1

1

1 p ²

Nous pourrons par la suite poursuivre les calculs pour déterminer les autocorrélations par- tielles díordre supérieur, en exprimant les autocorrélations en fonction de 9 pour obtenir une

suite récurrente on a :

2 22 6

^{p 2}

1

1

1 p ²

9 ²

et p 1 6

9

1 ) 9 ²

² 33 ⁶

1 ) 9 ² ) 9 ⁴

On remarque que

*

(1 ) 9 2 ) 9 4 ) 6 ^{1 9}

donc 2 22 6

1 9 ²

9 ² (1 9 ² )

1 9 ^*

En raisonnant de la même maniere pour 2 33 on trouve

9 ³ (1 9 ² )

² 33 ⁶

1 9 ^,

La formule de récurrence pour les autocorrélations partielles díun modele @ 4(q ) est alors

donnée par :

2 k k 6

9 ^k (1 9 ² )

1 9 2 ! k # 1)

3.9.6 Series non stationnaires

Les chroniques économiques sont rarement des réalisations de processus aléatoires sta- tionnaires. La non stationnarité des processus peut concerner aussi bien le moment du pre- mier ordre (espérance mathématique) que celui du second ordre (variance et covariance du processus). Celle-ci peut être repérée graphiquement (tendance, cycle long, saisonnalité ex- plosive, modiÖcation de structure...) ou encore au moyen de la fonction díautocorrélation (fonction díautocorrélation lentement décroissante). Mais la plupart des résultats et des mé- thodes utilisées dans líanalyse des séries temporelles repose sur la notion de stationnarité

du second ordre, ce qui nous mene ‡ appliquer ‡ la chronique non stationnaire certaines

transformations(di§érence ordinaire, di§érence saisonniere, la formule de Box-Cox...). Parmi

les processus aléatoires non stationnaires, on peut distinguer deux grandes classes, ‡ savoir

les processus T F et les processus 7F.

DeÖnition et description des processus 1 0 et ( 0

DeÖnition

Un processus 1 0 (trend stationnary) represente une non stationnarite de type deterministe, il síecrit sous la forme Xt 6 S t ) t t ocents S t est une fonction polyno- miale qui depend du temps, lineaire ou non lineaire, et t t est un processus de

type & / , & .

Le processus T F le plus simple est représenté par une fonction polynomiale de degré 1. Le processus síécrit :

Xt 6 a$ ) a1t ) t t

Si t t est un bruit blanc, les caractéristique de ce processus sont alors :

2

^{) E8 X}t^{] 6 a}$ ^{) a}1^{t ) E8 t} t^{] 6 a}1^{t ) a}$

#

^{I a_8 X}t^{] 6 0 ) I a_8 t} t^{] 6 ) 2}

^{3 O ov (X}t^{, X}t ^{) 6 0 pour t 6 t#}

Nous constatons que le processus T F est caractérisé par une espérance mathématique ‡ ten-

dance déterministe, une variance constante au cours du temps et par des covariances nulles, dans un tel modele la réalisation des prévisions níest pas une tche facile.

DeÖnition

Les processus ( 0 (di§erncy stationnary) sont des processus non stationnaires

aleatoires quíon peut rendre stationnaire par líutilisation díun Öltre aux di§e- rences : (1 B)^> Xt 6 B ) t t5 oü t t est un processus bruit blanc, B est une constante reelle, et Q est líordre du Öltre aux di§erences.

Ces processus sont souvent représentés en utilisant le Öltre aux di§érences premieres (Q 6 1)

le processus est dit alors du 1^?I ordre il síécrit :

(1 B)Xt 6 B ) t t

Un processus 7F síécrit sous la forme suivante :

Xt 6 p Xt 1 ) ) t t oü t t est un processus stationnaire. Nous pouvons écrire ce processus sous une autre forme :

^Xt ^{6 p 2 X}t 2 ^{) p ) p t} t 1

^{) ) t} t^,

Xt 6 p ³ Xt 3 ) p ² ) p ² t t 2

Par récurrence on obtient :

) p ) p t t 1

) ) t t.

Xt 6 p r Xt r ) ^{z r 1} p 3 ) ^{z r 1} p 3 t t 3

3 l 0

3 l 0

Nous supposons que 5 p 5 6 1 et que * 6 t nous aurons donc

3 l 1

^Xt ^{6 X}0 ^{) t ) z t t} 3

^{oü X}0 ^{désigne le premier terme de la série X}t^.

Passons maintenant ‡ líétude des caractéristiques de ce processus

3 l 1

a) E (Xt) 6 E ^& X0 ) t ) ^{z t}

t 3 ^' 6 E(X0 ) ) t ,

b ) I (Xt) 6 E (Xt E (Xt))²

0

6 E ^{& z}

1

2

t

3 l 1

t 3 '

^, t

^{6 E z t} i

i l 1

t ^-

^{z t} 3 ^,

3 l 1

t

6 E ^{I z}

t

t 2 ) ^z

t

^z t i t 3 ^I

t

6 ^z E (t 2 ) ) 0 6 t) 2 ,

⁶ i l 1 ⁱ

i l 1 3 l 1

i l 3

⁷ i l 1 ^{i (}

^{P ) O ov (X}t^{, X}s^{) 6 E 8 (X}t ^{E (X}t^{)) E (X}s ^{E (X}s^{))] ,}

^{. (} t

^{6 E z t} 3

i l 1

^{) ,} t ^{- /}

^{z t} 3 ^,

3 l 1

(

6 @ i[ (t, ` ) ) ²

V t 6 `

Nous constatons que le processus 7F est caractérisé non seulement par une non station-

narité de type déterministe, provenant du fait que son espérance est une fonction évolutive

dans le temps, mais aussi par une non stationnarité de nature stochastique par le biais des perturbations dont la variance est une fonction acents ne du temps dont le coecents cient est la variance du processus bruit blanc ; de ce fait nous pouvons conclure que dans ce type de pro- cessus, chaque perturbation aléatoire est persistante et possede un e§et durable et cumulatif

sur le comportement de la série.

Connaissant les di§érences qui existent entre les processus T F et 7F, nous concluons que la distinction entre ces deux types de processus est díune grande importance, puisque si líon est en présence díun processus T F et que líon traite comme un processus 7F, et vice versa, on aboutie ‡ une mauvaise stationnarisation.

3.9.7 Test de Dickey-Fuller

Test de Dickey-Fuller simple (DF)

Les modeles suivant de base ‡ la construction de ces tests sont au nombre de trois, et dans ce qui suit t t est un processus bruit blanc

8 1] : Modele sans constante ni tendance déterministe

Xt 6 p Xt 1 ) t t

8 2] : Modele avec constante et sans tendance déterministe

Xt 6 c ) p Xt 1 ) t t

8 3 ] : Modele avec constante et avec tendance déterministe

Xt 6 c ) b t ) p Xt 1 ) t t

On teste líhypothese nulle ;0 de présence de racine unitaire (Xt est intégré díordre 1,< (1), donc non stationnaire) contre líhypothese alternative ;1 en líabsence de racine unitaire (Xt

est intégré díordre 0 , cíest ‡ dire que Xt est stationnaire). Líhypothese du test comme suit 4

^* ;0 4 p 6 1

^;1 ^{4 5 p 5 0 1}

En síinspirant du modele 1.

Xt 6 p Xt 1 ) t t ...(1)

retranchons Xt 1de chaque coté de líéquation (1)

Xt Xt 1 6 p Xt 1 Xt 1 ) t t

Xt 6 (p 1)Xt 1 ) t t

En pratique et en posant b 6 (p 1) on estime les modéles suivants :

modéle8 .] :

Xt 6 b Xt 1 ) t t

modéle8 / ] :

Xt 6 c ) b Xt 1 ) t t

modéle8 6] :

Xt 6 c ) b t ) b Xt 1 ) t t

Ce qui revient ‡ dire que le test de racine unitaire repose sur le test de líhypothése nulle

b 6 0 (non stationnaire) contre líhypothése alternative 5 b 5 6 0 (stationnaire), et donc le systéme díhypothése devient :

^* ;0 4 b 6 0

^;1 ^{4 5 b 5 6 0}

Principe des Tests de Dickey-Fuller

Sous líhypothése ;0 , le processus Xt níest pas stationnaire quelque soit le modéle retenu. Les régles habituelles de líinférence statistique ne peuvent donc pas être appliquées pour tester cette hypothése, en particulier la distribution de Student du paramétre p . Dickey et Fuller

ont étudiés la distribution asymptotique de líestimateur du paramétre p sous líhypothése ;0

‡ líaide des simulations de Monte-Carlo, ils ont tabulé les valeurs critiques pour des échan- tillons de tailles di§érentes.

Soit la t-statistique notée (t'b

^{critique t}t; < L D ? ^:

) tel que t'b 6

bç

)

^{ç 'b}

1

^{, on compare alors la t}'^b

avec la valeur

ó Si t'b

^{% t}t; < L D ?

alors on accepte líhypothése ;0 , il existe une racine unitaire.

ó Sinon on rejette líhypothése ;0

Remarque

ó 1 Ces tests révélent líexistence díune racine unitaire mais restent insucents sants pour

discriminer entre les processus T F et 7F, cíest ainsi quíon adopte un algorithme

en trois étapes.

ó 2 On dit que la tendance est signiÖcativement di§érente de 0 ssi t'b

^{% t}t; < L D ?

alors

la tendance existe sinon elle est dite non signiÖcativement di§érente de 0 .

ó 3 On dit que la constante est non signiÖcativement di§érente de 0 :

ssi sa t-statistique 0 valeur critique sinon elle est dite signiÖcativement di§érente

de 0.

Enonce de líalgorithme

Etape (1) : dans cette étape on estime le modéle 8 3 ] , et on teste la signiÖcativité de la tendance.

ó Si la tendance níest pas signiÖcativement di§érente de 0 , aller ‡ líétape (2).

ó Sinon (la tendance est signiÖcativement di§érente de 0 ) on teste líhypothése nulle

^{;0 (on compare t}'^b

avec les valeurs critiques de 7F )

ó Si ;0 est acceptée, Xt est non stationnaire donc de type 7F, on di§érencie Xt et on recommence les tests précités sur la série aux di§érences premiéres.

ó Sinon (;0 rejetée), Xt est stationnaire donc de type T F ; on peut directement analyser cette série.

Etape(2) : cette étape níest e§ectuée que si la tendance níest pas signiÖcativement

di§érente de 0 , on estime le modéle8 2] (avec constante et sans tendance).

ó Si la constante níest pas signiÖcative, aller ‡ líétape 3

ó Sinon (la constante est signiÖcative) on teste líhypothése ;0 .

ó Si ;0 est acceptée, Xt est non stationnaire on di§érencie Xt et on recommence.

ó Sinon (;0 rejetée), Xt est stationnaire.

Etape(3) : cette étape níest e§ectuée que si la constante níexiste pas, on estime dans ce cas le modéle[1] et on teste ;0

^{ó Si ;}0 ^{est acceptée, X}t ^{est non stationnaire on doit la di§érencie.}

ó Sinon, Xt est stationnaire, dans ce cas on analyse la série.

3.9.8 Test de Dickey-Fuller augmente

Transformation des modËles de base

Dans les modéles précédents, utilisés par les Tests de Dickey-Fuller simple, le processus t t est par hypothése un bruit blanc. Or il níy a aucune raison pour que ‡ priori, líerreur soit non corrélée ; on appelle tests de Dickey-Fuller augmentés (47F , 192 1) la prise en compte de

cette hypothése. Les tests 47F síe§ectuent exactement comme les tests 7F sur les modéles suivants :

modéle 8 .] :

Xt 6 b Xt 1 )

modéle 8 / ] :

p

^z

j l 1

b j - Xt j ) t t

Xt 6 b Xt 1 )

modéle 8 6] :

p

^z

j l 1

b j - Xt j ) t t ) C

Xt 6 b Xt 1 )

p

^z

j l 1

b j - Xt j ) t t ) C ) b t

On pratique nous allons utiliser les tests de 47F

Remarques

ó 1 Avant díappliquer le test 47F il faut préciser líordre de décalage ] en utilisant le critére díAkaÔke.

ó 2 Les principaux logiciels díanalyse de séries temporelles calculent automatiquement

les valeurs critiques ‡ líinstar de EVIEWS 4.0.

3.9.9 Analyse de la saisonnalite

Une série chronologique saisonniére est une série dont les données relatives ‡ une même période (la période est plus courte quíune année) de di§érentes années ont tendance ‡ se situer

de faÁon analogue par rapport ‡ la moyenne annuelle. Elle peut se relier ‡ des observations trimestrielles et mensuelles aussi bien que díheure en heure ou aux observations quotidiennes.

Il est possible de détecter cette saisonnalité par un examen graphique de la série, qui se

manifeste par la répétition díun certain phénoméne dans chaque période. Ou par un examen fait sur le corrélogramme de la série étudiée, qui laisse apparaÓtre des pics trés marqués aux retards 1, S, 2S, ....

On en déduit une saisonnalité de périodicité S (S 6 3 , 6, 12, ..).

3.9.10 Test de Fisher sur la saisonnalite

On a recours ‡ ce test pour détecter líexistence díune éventuelle saisonnalité dans une série ‡ partir de líanalyse de la variance, soit :

N 4 Le nombre díannées.

P 4 Le nombre díobservations dans líannée (périodicité), pour des données mensuelles P 6 12,

trimestrielles P 6 ..

La procédure du test est comme suit :

^{Calcul de la somme des carrees : S}T

4 6

ST 6 ^{< <}

^(c i a ^{c )2}

Avec :

i l 1 a l 1

c i a 4 est la valeur de la série pour la i^{? E ?} année et la j ^{? E ?} période.

c 4 est la moyenne générale de la série sur les N ! P observations.

4

c 6 ^{1 z}

6

^z c i a

N ! P

6

^{Calcul de la somme des carres annuels : S}A

i l 1 a l 1

4

SA 6 P ^z

(c i c )² avec c i 6

1

^<

c i a est la moyenne de líannée i

i l 1

P

^{a l 1}

^{Calcul de la somme des carres periodiques : 0} 6

S6 6 N

6

^<

a l 1

(c a c )² avec c a 6

4

^{1 <} c

N ^{i a}

^{i l 1}

est la moyenne de la période j .

^{Calcul de la somme des carres residuels : S}R

SR 6

4

^<

i l 1

6

^< (c i a c i c a ) c )²

a l 1

Calcul des variances :

SA

^{Variance de líannée : I 4RA 6} N 1

S6

^{Variance de la période : I 4R6 6} P 1

SR

^{Variance des résidus : I 4R}R ⁶

(P 1)(N 1)

ST

^{Variance totale : I 4R}T ⁶

N (P 1)

Le test de saisonnalité est construit ‡ partir des hypothéses suivantes :

^* H0 : Pas de saisonnalité

^Hi ^{: Il existe une saisonnalité}

On a : F . 6

^{I 4R}6

I 4R

R

Si F . > F ^a (P 1, (N 1) x (P 1)), alors on accepte líhypothése Hi selon laquelle la série

est a§ectée díune saisonnalité

Le test de tendance est construit ‡ partir des hypothéses suivantes :

^* H0 : Pas de tendance

^Hi ^{: Il existe une tendance}

^{On a : F} . ⁶

^{I 4R}A

I 4R

R

Si F . > F ^a (P 1, (N 1) x (P 1)), alors on accepte líhypothése Hi selon laquelle la série

est a§ectée díune tendance.

Desaisonnalisation

Pour exprimer ce quíaurait été líináuence de la série sans líináuence saisonniére, on utilise

la série corrigée des variations saisonniéres X

Dans le modéle additif : Xt 6 Xt St

Si : Coecents cient saisonnier brut pour chaque saison j (Si 6 moyenne des di§érences de la saison j ). Si 6 Si Si : coecents cient saisonnier

Dans le modéle multiplicatif : Xt 6 Xt/ St

Si : Coecents cient saisonnier brut pour chaque saison j (Si 6 moyenne des rapport de la saison j )..........Si 6 Si / Si : coecents cient saisonnier.

3.9.11 Extension des modËles 4R@ 4

Líhypothése de stationnarité, présente-sous certaines conditions dans les modéles 4R@ 4, níest que rarement vériÖée pour les séries économiques ; Elles comportent également une ten- dance, une saisonnalité ou même une structure plus complexe. Par conséquent, líintérêt des modéles 4R@ 4 semble assez limité.

ModËles autoregressif moyenne mobile integre díordre (: , 6 , ; ) : & / * , & (: , 6 , ; )

Un processus Xt est un modéle 4R< @ 4(], Q , q ) síil vériÖe une équation de type :

# (B)(1 B)^> Xt 6 ! (B)t t pour tout t % 0

^* # (B) 6 1 b iB b 2 B2 .... b 6 B6 oü b 6 6 0

oü

^{! (B) 6 1 9} i^{B 9} 2 ^{B2 .... 9} q ^{Bq oü 9 q 6 0}

Sont des polynOmes dont les racines sont de module supérieurs ‡ 1 et aucune des racines de

# (B) níest égale ‡ une racine de ! (B).

Les coecents cients réels b i , i 6 1, ..., ] et 9 i j 6 1, ..., q , sont Öxés et 3 t t4 est un bruit blanc.

La famille 4R< @ 4 désigne parfois la classe de tous les modéles, stationnaires et non sta- tionnaires, en convenant que les 4R< @ 4 (], 0 , q ) sont les 4R@ 4(], q ).

Propriete : Soit Xt un modéle 4R< @ 4(], Q , q ) alors le processus(8 ^> Xt) converge vers un modéle 4R@ 4(], q ) stationnaire.

ModËles & / * , & saisonnier, 0 & / * , &

Une classe plus générale de modéles est constitué par les S4R< @ 4 qui permettent de rendre compte des phénoménes périodiques et de non stationnarité.

On dit quíun processus Xt suit un modéle S4R< @ 4(], Q , q ) x (P, 7, D )9 si :

9

V t, # p (B)# 6 *9 (B⁹ )8 ^> 8 ^/ Xt 6 ! q (B)! 7 *9 (B⁹ )t t,

Oü S est la période de la saisonnalité, 8 ^> est líopérateur de di§érence ordinaire

9

de degrés Q , 8 ^/

est líopérateur de di§érence saisonniére de degrés 7 ;

^# p ^{(B) est un polynOme de degré ] en B, appelé polynOme autoregressif ordinaire ;}

! q (B) est un polynôme de degré q en B, appelé polynôme moyenne mobile ordinaire ;

# P ,S (B^S ) 6 1 b 1,S B^S b 2 ,S B^{2 S} .... b P ,S B^{P S} est appelé polynôme autoregressif saisonnier ;

! Q ,S (B^S ) 6 1 ) & 1,S B^S & 2 ,S B^{2 S} .... & Q ,S B^{Q S} est appelé polynôme moyenne mobile saisonnier ;

S

Xt est déÖni aussi comme un modéle S4R< @ 4(], Q , q ) x (P, 7, D )S díordre S si 8 ^> 8 ^/ Xt

est un modéle S4R@ 4(], q ) x (P, D )S . En pratique Q 6 0 , 1, 2 et 7 6 0 , 1.

ModËles & / , & saisonnier, 0 & / , &

Un processus Xt satisfait une représentation 4R@ 4 saisonniére (ou S4R@ 4), notée 4R@ 4S ,S (], q ), si :

p

^<

i l 0

b i S Xt i S 6

q

^<

i l 0

b i S t t i S ( ) #

p ,S

(B^S )8

/

S Xt 6 !

q ,S

(B^S

)t t

(

^{Avec V j 0 ], b} i ^{E R, V j 0 q , &} i ^{E R, b} 0 ^{6 &} 0 ^{6 1 et (b} P ^{, &} q ^{) E R, , t} t ^{est iid (0 ,) 2 ) et oü}

` désigne la période de la saisonnalité de la composante 4R et ` désigne la période de la saisonnalité de la composante @ 4 ; ] et q indiquent líordre respectif des deux modéles 4R

et @ 4 combinés.

3.9.12 Transformation des donnees

Diverses transformations peuvent être apportées aux données avant toute modélisation, aÖn de prendre en compte des tendances exponentielles, des ruptures, des points aberrants,

des phénoménes saisonniers. Ainsi pour certaines séries, on ne pourra pas atteindre la sta- tionnarité en appliquant juste líopérateur de di§érence.

Parmi ces transformations nous avons les données transformées par fonction puissance :

8 (Xt)^% ) a] / b , a E R, b E R, A E R .

La classe de transformation la plus répandue en économétrie, est celle de Box-Cox dans un trés célébre article, correspond a cette famille, avec a 6 1 et b 6 A

X %

B(Xt, A ) 6

^* t ¹

A

quand A 6 0

oü Xt doit être positif 0 < A < 1

^{? B= (X}t^{) quand A 6 0}

Une des raisons de la popularité de la transformée de Box-Cox est quíelle incorpore a la

fois la possibilité díaucune transformation (quand A 6 1) et la possibilité díune transforma-

X %

tion logarithmique quand (A 6 0 ; Lim

^{t 1} 6 Log (X )).

t

^{% " 0} A

En générale, on choisit le logarithme des valeurs pour atténuer une croissance exponen- tielle ou amoindrir le phénoméne de saisonnalité.

Chapitre 4

MÈthodologie de Box et Jenkins

La méthodologie de Box et Jenkins (1910 ) permet de trouver en plusieurs étapes, un modéle 4R@ 4 susceptible de représenter une série chronologique. Elle níest en fait que líapplication de la méthode scientiÖque aÖn díobtenir le modéle 4R@ 4 réel générant la série. Rappelons que la méthode scientiÖque consiste a formuler des suppositions sous forme díun modéle a les mettre a líépreuve et a réviser le modéle en conséquence. Ces étapes étant répétées autant de fois que nécessaire. Une fois le modéle 4R@ 4 connu, on peut déterminer mécaniquement les prévisions. Comme il faut encore pouvoir représenter la tendance et la saisonnalité, on étend la classe des modéle 4R< @ 4 et S4R< @ 4. Cette méthode síe§ectue

en trois grandes étapes a savoir : líidentiÖcation du modéle, líestimation des paramétres et

la validation.

38

4.1 IdentiÖcation du modËle

Cette étape consiste a identiÖer le modéle 4R@ 4 susceptible de représenter la série, cíest pour cela quíil est important de se familiariser avec les données en examinant le graphe

de la série chronologique (présence de saisonnalité, stationnarité,...) qui permet de faire une analyse préliminaire qui consiste par exemple a corriger les données aberrantes, transfor- mer les données (transformation logarithmique, inverse, racine carrée,...) puisquíil faut se ramener a un modéle 4R@ 4 stationnaire, le recours aux di§érence premiére ordinaire, dif- férence premiére saisonniére, di§érence ordinaire et saisonniére voir en di§érence seconde est primordiale. Le choix est dicté par líallure graphique de la série. Díailleurs le choix de la transformation des données est plus facile aprés avoir appliquer les opérateurs de di§érence adéquats.

Il est conseillé de comparer les variances des di§érentes séries. La série avec la plus petite

variance conduit souvent a la modélisation la plus simple. Comme líinspection des autocor- rélations partielles (P 4O ) donne une idée sur líordre du modéle autoregréssif et celle des autocorrélations simples (4O ) donne une idée sur líordre du modéle moyenne mobile, líétude

des corrélogrammes sera díun apport important dans cette étape.

4.2 Estimation

Líobjectif est de trouver les estimateurs des paramétres de la partie 4R et @ 4 du modéle de la chronique. Líestimation du modéle 4R@ 4 repose sur la méthode de maximum

de vraisemblance. Plus spéciÖquement la technique consiste a construire une fonction appelée fonction de vraisemblance et a maximiser son logarithme par rapport aux paramétresb i et & i (avec i : 6 1, ] et j : 6 1, q ) permettant de trouver la valeur numérique la plus vraisemblable pour ces paramétres

Líétape díestimation achevée, líétape suivante va nous permettre de valider le(s) modéle(s)

estimé(s).

4.3 Validation

A líétape de líidentiÖcation, les incertitudes liées aux méthodes employées font que plu- sieurs modéles en générale sont estimés et cíest líensemble de ces modéles qui subissent alors líépreuve des tests, Il existe de trés nombreux permettant díune part de comparer les per- formances entre modéles, on peut citer les tests sur le modéle, les tests sur les paramétres et

les tests sur les résidus.

4.3.1 Tests sur le modËle :

Il faut vériÖer si :

ñLes coecents cients estimés satisfont aux conditions de stationnarité et díinvesrsibilité.

ñLes composantes AR et M A de líARM A níont pas de racine communes.

Ces questions ont une réponse immédiate puisque le logiciel utilisé fournit les inverses des racines des deux polynômes AR et M A, il sucents t de voir si les racines sont :

Strictement supérieure a 1 (a líextérieur du disque unité, les inverses a líintérieur).

Sont distincts, au cas contraire, on peut alors se ramener a une représentation minimale excluant ces racines, dont les degrés de la représentation ARM A seront strictement inférieurs

a ceux de la représentation initiale. Cette représentation sera préférable selon le principe de parcimonie.

4.3.2 Test de Student sur les paramËtres

Le premier test que líon peut mener consiste a tester líhypothése nulle p¹ 6 p 1 et q ¹ 6 q

On regarde si líon peut diminuer díune unité le nombre de retards intervenants dans la partie

AR Ce test est trés simple a mettre en oeuvre puisquíil síagit díun test de signiÖcativité usuel

bç p

^{sur le coecents cient b p ) On calcule donc la statistique de Student du coecents cient (t}'^b# ⁶

)

^{ç 'b}#

) que

líon compare a la valeur critique lue dans la table de la loi de Student. La régle de décision est alors :

^%

^%

Si ^% t

^% 0 ti

, on accepte líhypothése nulle de modéle ARM A(p 1, q ),

^{% 'b}# ^% 2

^%

Si ^% t

%

^% > ti ,líhypothése nulle est rejetée et on retient un modéle ARM A(p, q ),

^{% 'b}# ^% 2

i

a

Oü t

²

est le quantile díordre (1

2 ^{) de la loi de Student (T h) degrés de liberté, h étant}

le nombre de paramétres estimés.

Bien entendu, on peut appliquer un raisonnement similaire au test de líhypothése nulle p¹ 6 p

et q ¹ 6 q 1.

Remarque

De faÁon symétrique, il est possible de mener un deuxiéme test de líhypothése nulle de processus p* 6 p ) 1 et q * 6 q .

4.3.3 Tests sur les residus

Le processus estimé est évidemment de bonne qualité si la chronique calculée suit les évolutions de la chronique empirique. Les résidus entre les valeurs observées et les valeurs calculées par le modéle, doivent se comporter comme un bruit blanc normal.

Pour montrer que les t t sont un bruit blanc, on doit vériÖer si :

ñLa moyenne des résidus est nulle, sinon il convient díajouter une constante au modéle.

ñ Le graphe des résidus en fonction du temps semble approximativement compatible avec une suite de variables aléatoires non corrélées.

Cíest ainsi que nous proposerons une multitude de tests concernant les caractéristiques du

résidu souhaité.

Test de normalite

Le test de Jarque & Bera (192 .) peut síappliquer pour tester la normalité des résidus. Ce dernier est fondé sur la notion skewness (moment díordre 3 , líasymétrie de la distribution) et Kurtosis (moment díordre . et líaplatissement - épaisseur des queues de distribution). Soit

^% k ^{le moment empirique díordre X du processus}

ç

Skewness

^ç

4

t t E 8 t t]] ^K 6

1 ^<

N

^{tl i}

^ç

(t t t t)

Le skewness est une mesure de líasymétrie de la distribution de la série autour de sa moyenne.

% 3

Le coecents cient du skewness (Sk )est déÖni par : (Sk )^{i+ 2} 6

4

3 + 2

%

2

& N (0 , ^{C *} ).

4

^{" $}

Le skewness díune distribution symétrique, telle que la distribution normale est nulle. Le

skewness positive signiÖe que la distribution a une queue allongée vers la droite et le skew- ness négative signiÖe que la distribution a une queue allongée vers la gauche.

Kurtosis

Le Kurtosis mesure le caractére pointu ou plat de la distribution de la série. Le coecents cient

du Kurtosis (ku ) est déÖni par : ku 6

^&

% 4

4

% 3 ^{" $}

N (3 ,

^C 24

4 ^{). Le Kurtosis de la distribution}

normale est 3 . Si le Kurtosis est supérieure a 3 , la distribution est plutôt pointu relativement

a la normale ; si le Kurtosis est inférieure a 3, la distribution est plutôt plate relativement a

la normale.

On construit alors les statistiques centrées réduites correspondantes a (Bk )^{i+ 2} et ku que líon compare aux seuils díune loi normale centrée réduite

(Bk )^{i+ 2}

4

^{. C} *

4

& N (0 , 1)

^{" $}

^ku ³

4

^C 24

4

& N (0 , 1)

^{" $}

^{Si la statistique centrée réduite de (B}k ^{)i+ 2 est inférieure au seuil 1, 96 a 5 % , on accepte líhy-}

pothése de symétrie et líhypothése de normalité. Si la statistique centrée réduite de ku est inférieure au seuil 1, 96 a 5 % , on accepte líhypothése de queue de distributions plates et líhypothése de normalité.

Jarque-Bera

Le Jarque-Bera est une statistique de test pour examiner si la série est normalement distri- buée. La statistique mesure la di§érence du skewness et du Kurtosis de la série avec ceux de

la distribution normale. La statistique est calculée comme suit :

J B 6

N

6 ^{Bk )}

N

^&

(ku 3 )²

^{2. 4 " $}

x ² (2)

^{Oü B}k ^{est le skewness, k}u ^{est le Kurtosis. Sous líhypothése nulle díune distribution normale,}

i a

la statistique de Jarque-Bera suit asymptotiquement une loi de x ²

avec deux degrés de

i a

liberté ( 6 5 % ), aussi, si J B > x ²

^{(2) on rejette líhypothése H}O ^{de normalité des résidus}

au seuil . La probabilité rapportée associée a cette statistique est la probabilité que la statistique de Jarque-Bera dépasse (en valeur absolue) la valeur observée. Une probabilité faible conduit a rejeter líhypothése nulle díune distribution normale.

Test de Durbin Watson

Le test de Durbin Watson permet de détecter une autocorrélation des résidus díordre 1, sous

la forme t t 6 p t t 1 ) " t oü " t s N (0 , )

Le test díhypothése síécrit :

² )e

^{* H}O ^{: p 6 0 (absence de corrélation)}

^H1 ^{: p 6 0 (présence de corrélation)}

Pour tester líhypothése HO , la statistique de Durbin Watson utilisée est

F

2

^< (t t ç )

7J 6

ç

tl 2

F

^t t 1

^< t ²

^{ç t}

tl 1

t

Oü t sont les résidus de líestimation du modéle.

^ç

De part sa construction, cette statistique est comprise entre 0 et .. On peut aussi montrer

p =0 (p étantp observée). AÖn de tester HO , Durbin Watson ont tabulé

que 7J 6 2 lorsque ç ç

des valeurs critiques7J au seuil de 5 % oü on présentera la table dans líannexe appropriée,

ainsi que le mécanisme du test.

Test de Box - Peirce (1970) (portementeau)

Ce test, encore appelé "test portmenteau", a pour objet de tester le caractére

non autocorrélé des résidus. Le test de Box- Peirce établi a partir de la statistique de que-

p ²

1

nouille Q 6 T ^z

ç h(t )e

hl 1 ^ç

p 2

^ç

^{oü : ç} h^{(t ) est le coecents cient díautocorrélation díordre h des résidus estimés, et H est le nombre}

maximal de retards sous les hypothéses suivantes :

^* HO : p (1) 6 p (2) 6 eeeee 6 p (h) 6 0

^H1 ^{:0 j tel que b} i ^{6 0}

! 1 a )

Cette statistique Q en líabsence díautocorrélation obéit a un x ²

(H p q ) degrés de

liberté oü : p est líordre de la partie AR (saisonnier ou non), q est líordre de la partie M A

et H est le nombre de retards choisis pour calculer les autocorrélations.

4

Pour e§ectuer ce test il est conseillé de choisir H 6 ^T (díaprés Box et Jenkins). Líhypothése

HO est rejetée au seuil de 0 e05 si Q est supérieur au quantile 0.95 de la loi x ² , autrement dit

les régles du test portemanteau sont :

! 1 a )

ñSi Q < x ²

! 1 a )

ñSi Q > x ²

^{(H p q ) on accepte H}O ^{6 ) les p} h

(H p q ) on rejette HO 6 ) les p h

forment un bruit blanc.

ne forment pas un bruit blanc.

Test de Ljung-Box

Ce test est a appliquer, de préférence au test de Box - Peirce, lorsque líéchantillon est de petite taille. La distribution de la statistique du test de Ljung-Box est en e§et plus proche de celle de Khi-deux en petit échantillon que ne líest celle du test de Box - Peirce. La statistique

^ç h^{(6 )}

p

¹ 2

de test síécrit : LB(h) 6 T (T ) 2)^{< ç}

T h

^{hl 1}

Sous líhypothése nulle díabsence díautocorrélation :

p 2 6 t).

⁶ 2 ^{) 6 ....... 6 ç} h^{( ç}

La statistique LB(h) suit une loi de Khi-deux a (H p q ) degrés de liberté.

Test de nullite de la moyenne des residus

Un bruit blanc est díespérance mathématique nulle. On e§ectue donc sur les résidus 6 t prévi- sionnels du modéle un test de nullité de leur moyenne. Pour [ sucents samment grand ([ > 30 )

6 N (m 5 ^{a 8} ) et ^{6 m}

^{' 7 [ a} 8

⁷ [ ' N (0 5 1). Sous líhypothése HO de nullité de la moyenne et un

a 8 a 8

^{seuil díacceptation a 95 % , líintervalle de conÖance de 6 est : 1, 96 7} [ ^{< 6 < 1, 96 7} [

Remarque

[ est le nombre díobservations de la chronique des résidus.

Dans la construction des séries temporelles, on estime souvent plusieurs spéciÖcations. Il peut arriver que deux ou plusieurs modéles soient adéquats, dans ce cas, des tests supplé- mentaires devraient être utilisés pour déterminer la meilleure spéciÖcation, cíest ainsi que nous introduisons les critéres de pouvoir prédictifs portant sur la qualité de líinformation et

du modéle.

CritËre de pouvoir predictif

Dans un modéle ARM A, líerreur de prévision a horizon 1 dépend de la variance du résidu.

On peut alors choisir le modéle conduisant a la plus petite erreur de prévision. Plusieurs indicateurs sont alors possibles :

1 La variance du résidu a ² ,ou la somme des carrés des résidus 8C R.

2 Le coecents cient de determination R² , correspond a une normalisation de la variance.

3 Le coecents cient de determination modife R² .

. La statistique de Fisher.

Le but est de minimiser 1 ou de maximiser 2,3 ou ..

CritËre díinformation

Cette approche a ete introduite par Akaike en 1969, cette mesure de líecart entre le modèle propose et la vraie loi peut être obtenue a líaide de la quantite díinformation de Kullback , cette mesure etant inconnue on essayera de minimiser son estimateur.

Plusieurs estimateurs de la quantite díinformation ont ete propose :

A< C (p, q ) 6 Yo g a ² ) ^{2p ) q} ,

ⁿ

8C (p, q ) 6 Yo g a ² ) (p ) q ) ^{? B= n} , cet estimateur a ete introduit par Schwarz.

ⁿ

Remarques

En pratique, il faut toujours síassurer que le modèle le plus simple est applique Cíest

le principe de parcimonie de la methode de Box & Jenkins. Cíest a dire quíil est parfois preferable de choisir un modèle juge moins bon mais qui contient moins de paramètres. Le modèle obtenu níest pas necessairement le vrai modèle mais cíest celui qui síen approche le plus.

Les tests qui suivent ne fgurent pas dans la demarche de Box & Jenkins, mais nous les utilisons comme complementaires aux tests de validation de cette demarche.

Test de stabilite

Pour examiner si les paramètres du modèle estime sont stables a travers divers sous echan- tillons de líensemble des donnees. La technique empirique recommande le partage de líen- semble des observations n , en 2 sous ensembles :

n 1 líensemble díobservations a employer pour la reestimation du modèle trouve pour líen- semble n et líevaluation.

n 2 (n 2 6 n n 1) líensemble des informations a employer pour les comparer aux valeurs prevues.

Employer toutes les observations disponibles de líechantillon pour líevaluation favorise la recherche des specifcations avec les meilleurs ajustements de líensemble des donnees speci-

fques, mais ne permet pas de tester les previsions du modèle avec les donnees qui níont pas

ete employees en líestimant, ni de determiner la constance, la stabilite et la puissance des paramètres du rapport estime.

Dans le travail de serie chronologique on prend habituellement les premières observations pour líevaluation et les dernières pour le test. Une règle generalement utilisee, est díem- ployer 25 % a 90 % des observations pour líevaluation et le reste pour tester.

4.4 Prevision

Líobjectif de la methode de Box & Jenkins est de realiser des previsions. une fois que

le modèle AR< M A(p, Q , q ) a ete choisi, estime et valide pour les observations X1, ...., Xt, on calcule les previsions.

On suppose quíon se trouve a líinstant t, et quíon desir prevoir la valeur de x t+ h, tel que alors on utilise líestimateur X^X t(h) líesperance conditionnelle de Xt+ h, tel que :

^X

^x t^{(h) 6 E[ X}t+ h^{/ X}t^{, X}t 1^{, ..., X}1^{]; oü XX} t^{(h) est la prevision, t est líorigine de la previson, et}

h líhorizon de prevision.

Sous les hypothèses suivantes :

E[ Xt j / Xt, Xt 1, ..., X1] 6 Xt j , V ) > 0 ;

^{E[ X}t+ j ^{/ X}t^{, X}t 1^{, ..., X}1^{] 6}

^XX t^{() ), V ) > 1;}

E[ 6 t j / Xt, Xt 1, ..., X1] 6 6 t j , V ) > 0 ;

E[ 6 t+ j / Xt, Xt 1, ..., X1] 6 0 , V ) > 1.

4.4.1 Prevision a líaide díun modËle autorogressif moyenne mobile integre ARIMA

On considère un modèle AR< M A(p, Q , q ) ecrit sous forme canonique tel que :

# p (B)8 ^> Xt 6 ! q (B)6 t. Oü # p (B) 6

p

^z

i l 1

b i Bⁱ , ! q (B) 6

q

^z

i l 1

& i B^q et 8 ^> 6 (1 B)^>

On peut ecrire : Xt 6

p + >

^z

i l 1

$ i Xt j ) 6 t

q

^z

j l 1

^& t j ⁶ t j

Oü W (B) 6 # p (B)8 ^> et donc Xt+ h 6

p + >

^z

i l 1

^W i ^Xt h+ j ^{) 6}

t+ h

q

^z &

j l 1

t j ⁶

t+ h j

Il síensuit que la prevision optimale a la date t ) h, faite compte tenu de toute líinformation

t

disponible jusquía la date t, notee x (h); est donne par :

^X

^X

x t(h) 6 E[ Xt+ h/ Xt, Xt 1, ..., X1, M 1] alors : X^X t(h) 6

p + >

^z

i l 1

W i X^X t(h i) ) 0

q

^z

j l 1

⁶ t

& t j X

(h ) )

^{Oü XX} t^{(h i) 6 X}t+ h i ^{pour h > q , on obtient une relation de recurrence de la forme :}

p + >

^XX t^{(h) 6}

^z

i l 1

^W i ^XX t^{(h i)}

Conclusion

Avantages

ñFournit des previsions inconditionnelles.

Peut être entièrement faite automatiquement. en employant des systèmes experts pour líidentifcation des modèles.

ñLes modèles sont parcimonieux en ce qui concerne les coecents cients.

Incovenients

Exige un grand nombre díobservations pour líidentifcation du modèle. Compliquee a expliquer et interpreter aux utilisateurs inities.

Ne prend pas en consideration les dependances croises entre les di§erentes series.

Chapitre 5

Application de la mÈthodologie de

Box-Jenkins

Presentation generale des donnees :

La consommation du gaz naturel en Algerie se presente sous trois aspects di§erents

a savoir :

Consommation des distributeurs publics : elle represente la consommation des menages y compris celles des petites entites commerciales tel que les boulangeries, les res- taurants, etc.

Consommation industrielle : elle englobe la consommation des usines de production

et de transformation tel que les briqueteries...

Consommation des producteurs díelectricite : la production díelectricite en Algerie provient essentiellement du gaz naturel, on peut citer comme centrale electrique celle díEL HAMMA.

Chacune de ces consommations est etudiee separement, cíest ainsi que nous obtenons trois

series de consommation :

La consommation des distributeurs publics a la date t : DPt

La consommation industrielle a la date t : C It

La consommation des producteurs díelectricite a la date t : C Et

Remarques :

- La modelisation et par suite la prevision sont faites sur la base de donnees mensuelles pour une duree de 2 ans.

- Ces donnees ont pour unite de mesure le mètre cube.

48

5.1 Etude de la serie de consommation des distribu- teurs publics (DP)

5.1.1 IdentiÖcation

La série DPt représente líévolution mensuelle de la consommation nationale du gaz na- turel des distributeurs publics sur une période allant de janvier 1991 a décembre 20 0 ..

Avant toute analyse de série temporelle, il est indispensable díétudier avec soin le graphe représentant son évolution, car ce dernier fournit a priori une idée globale sur la nature et

les caractéristiques du processus générant cette série a savoir : tendance, saisonnalité,....etc.

^{Representation de la serie brute ( .} t ^:

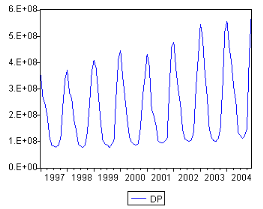
^{FIG.I.1ó Graphe de la sÈrie brute DP} t

Globalement, la représentation graphique (Fig.I 1) de la série présente les caractéristiques suivantes :

^{Une non stationnarité en variance, caractérisée par un accroissement de la variabilité par}

rapport au temps.

Une légére tendance a la hausse due a líaugmentation du nombres de foyers alimentés en

gaz de ville obéissant au programme national du gaz (PNG).

Un phénoméne périodique caractérisé par des mouvements ascendants suivis par díautres descendants autour des valeurs 10 ^, et 6.10 ^, , ces mouvements sont dus au rythme des saisons

car la consommation gaziére accroÓt durant líhiver oü le citoyen se penche vers líutilisation

des chau§ages fonctionnant au gaz qui sont beaucoup plus attractifs que les chau§ages électriques en terme de factures de consommation, puis la consommation décroÓt durant líété.

b-Introduction du logarithmique

Pour analyser la série DPt par líapproche proposée par Box-Jenkins, une modifcation doit être apportée sur les données afn díatténuer la variabilité qui a§ecte la série chronologique,

la série LDPt est générée par líintroduction du logarithme népérien a la série brute DPt. Cíest a dire

LDPt 6 Log (DPt) pour tE 3 1, 2, .....964

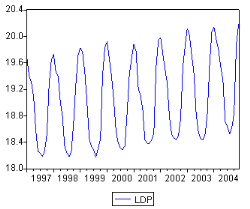
FIG.I.2ó Graphe de la sÈrie LDPt

On remarque que la représentation graphique de la série (FIG.I .2) LDPt garde la même allure que celle de la série DPt mais avec des pics moins importants, amortis suite a la transformation logarithmique appliquée. En e§et, líéchelle de mesure est réduite, elle áuctue

de 12 , 1 a 20 , 2. Ce qui est de la saisonnalité, celle-ci est toujours apparente, líexamen du corrélogramme de la série LDPt nous permettra de conforter nos observations.

a-Analyse preliminaire de la serie + ( . t

Examen du correlogramme de la serie LDPt

Líanalyse du corrélogramme simple et du corrélogramme partiel de la série LDPt (Fig.I .3 )

donné par le logiciel EVIEWS 4.0, nous indique une non stationnarité de la série en terme

de la saisonnalité, tel que le montre bien le corrélogramme simple.

En e§et, la fonction díautocorrélation simple estimée (colonne AC ) ne décroÓt pas de ma- niére rapide vers zéro, et de plus elle est caractérisée par un mouvement sinusoÔdal apparent quíon soupÁonne de périodicité 8 6 12 , ce qui nous pousse a e§ectuer une etude sur la saisonnalité de la série.

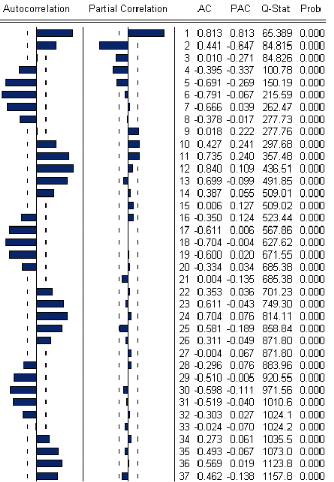
^{FIG.I .3 Corrélogramme de la série LDP}t

Etude de la saisonnalite de la serie LDPt

Les résultats du test de saisonnalité sont regroupés dans le tableau ci-dessous, oü :

8C : représente la somme des carrés.

M C : moyenne des carrés.

Source des variations	8C	d.liberté	M C	F	P _o b	F critique
Lignes	23 50 1.5	11	20 71.7	6.64	1.93 E 05	1.8 7

11

^{On a F} = ^{6 6.64 > F O ) O)}

^{6 1.8 7, donc on peut dire que la série LDP}t ^{est a§ectée díune}

saisonnalité.

Desaisonnalisation de la serie LDPt

Etant donné que la stationnarité de la série ne dépend pas uniquement de la présence

ou non de la tendance, mais aussi du phénoméne saisonnier, une désaisonnalisation de la série LDPt síimpose pour la suite de notre étude, cíest ainsi quíon obtient une série corrigée

^{de líe§et saisonnier LDP 8A}t ^{par líintroduction díune di§érentiation díordre 12 sur la série}

^LDPt^.

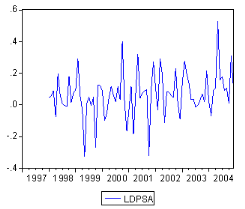
^{FIG.I .4 ó Graphe de la sÈrie LDP 8A}t

En observant le graphe de la série LDP 8At (Fig.I .5 ), nous remarquons que la saisonna- lité été absorbée.

Examen du correlogramme de la serie LDP 8At

Líexamen du corrélogramme de la série LDP 8At (Fig.I .4) nous confrme le succés de la désaisonnalisation de la série LDPt puisque celle-ci a été absorbée. Concernant la station- narité de la série, nous ne pouvons dire quíelle est stationnaire. Un recours au test de racine unitaire permet díacents rmer ou díinfrmer la stationnarité de la série en question.

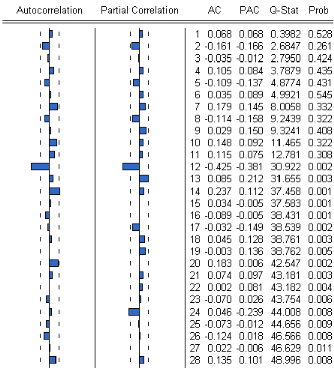
^{FIG.I .5 ó Corrélogramme de la série LDP 8A}t

Test de racine unitaire (Dickey-Fuller) sur la serie LDP 8At

A partir du logiciel EI I EJ 8 4.0 , on procéde a líestimation par la méthode des moindres carrées avec p 6 1 des trois modéles [ 4] , [ 5 ] , [ 6] de DickeyñFuller sur la série LDP 8At (car

les résidus forment un bruit blanc), dont les résultats díanalyse sont représentés ci-dessous

Modèle[6] A LDP SAt 6 LDP SAt 1 ) b j A LDP SAt j ) b t ) 6 t

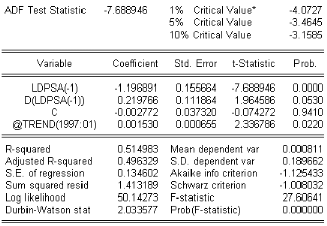
Le test montre que la statistique t' 6 7.68 8 9 est inférieure aux di§érentes valeurs critiques relatives aux seuils 1% , 5 % et 10 % . Líhypothése HO est rejetée, donc la série LDP SAt ne posséde pas de racine unitaire.

La probabilité de nullité du coecents cient de la tendance qui est égale a 0 .0 2 est infé- rieure au seuil de 5 % , aussi la valeur empirique de la statistique de Student relative a la tendance(7 T REN D) qui est égale a 2.33 67 est supérieure aux valeurs tabulées (1.95 ) au seuil 5 % et (1.64) au seuil 10 % . On rejéte donc líhypothése du nullité du coecents cient de la ten- dance (il est signifcativement di§érent de zéro). Ce qui concerne la constante on remarque

la t-statistic associée qui est égale 0 .00 742 est inférieure aux valeurs tabulées relatives aux

seuils 5 % et 10 % , donc la constante est non signifcativement di§érente de zéro.

Sachant que la série ne posséde pas de racine unitaire et que la tendance est signifcativement di§érente de zéro, on peut acents rmer que le processus est de type T S (trend stationnary), une regression de la série LDP SAt sera entreprise pour la stationnariser.

Test de racine unitaire (Dickey-Fuller) sur la serie di§erenciee ( (+ ( . 0 & t)

Modèle[6] A D(LDP SAt) 6 DLDP SAt 1 )

2

^z

j l 1

b j A D(LDP SAt j ) ) b t ) 0 ) 6 t

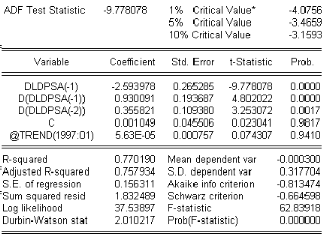
Modèle[5] A D(LDP SAt) 6 D(LDP SAt 1) )

2

^z

j l 1

b j A D(LDP SAt j ) ) 0 ) 6 t

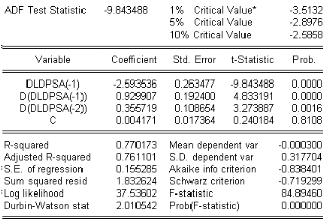
Modèle[4] A D(LDP SAt) 6 D(LDP SAt 1) )

2

^z

j l 1

b j A D(LDP SAt j ) ) 6 t

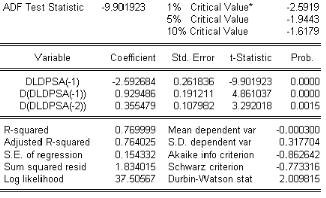
^{Les statistiques empiriques t}' ^{associées aux trois modéles sont inférieures aux valeurs cri-}

tiques aux seuils 1% , 5 % et 10 % , donc il níexiste pas de tendance stochastique (DS). Dans

le modéle [6], nous avons la t-statistic associée a la tendance, qui est égale a 0 .0 74, est inférieure a toutes les valeurs tabulées aux seuils 1% , 5 % et 10 % avec une probabilité (prob6 0 .94 > 0 .05 ), donc le coecents cient de la tendance du modéle [6] níest pas signifca- tivement di§érent de zéro, le processus níest pas de type T S. La série D(LDP SAt) níadmet

ni tendance déterministe, ni tendance stochastique, elle est donc stationnaire.

Correlogramme de la serie ( (+ ( . 0 & t)

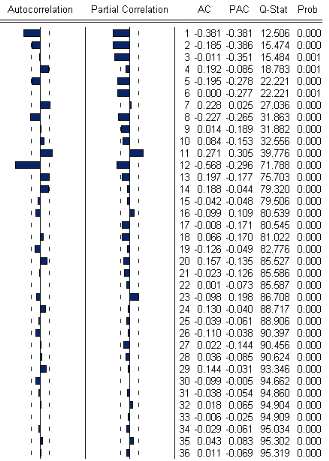
FIG.I .6 ó Corrélogramme de la série D(LDP SAt)

SpeciÖcation des modèles

Líanalyse du corrélogramme partiel de la série stationnaire D(LDP SAt) (Fig.I .6) montre quíaux retards (k 6 1, 2, 3 , 5 ,6, 8 , 11, 12) les termes sont signifcativement di§érents de zéro et

ce qui concerne le corrélogramme simple, on remarque quíaux retards (k 6 1, 2, 7, 8 , 11, 12)

les termes sont aussi a líextérieur de líintervalle de confance, par conséquent nous avons plusieurs modéles candidats (SARI M A(0 , 1, 1), SARI M A(0 , 1, 2),

SARl M A(12, 1, 0 ), SARl M A(10 , 1, 11),......) parmi lesquels nous avons estimé les modéles

SARl M A(0 , 1, 12) x (0 , 1, 1), SARl M A(12, 1, 12) x (1, 1, 1).

Choix du modèle

Entités statistiques	0 & / * , & (! " , ! , ! " ) x (! , ! , ! )	0 & / * , & (! " , ! , ! ) x (! , ! , )
R^2	0 .70 20	0 .4971
2 ^R	0 .68 40	0 .48 98
Al O	1.4919	1.3 78 7
F	1.33 26	1.00 26
SO R	0 .8 122	1.465 9

Suivant les critéres de pouvoir prédictif et les critéres díinformation mentionnés dans le

tableau ci-dessus, le modéle SARl M A(12, 1, 12) x (1, 1, 1) sera choisi pour représenter le processus 3 D(LDP SAt)4 t.

5.1.2 Estimation du modèle SARl M A(12, 1, 12) x (1, 1, 1)

Líestimation des coecents cients du modéle SARl M A(12, 1, 12) x (1, 1, 1) est donnée par la table ci-dessous

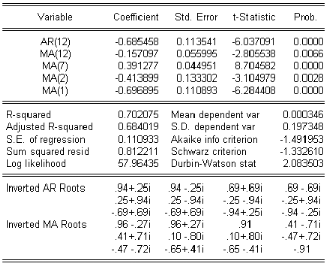
0 & / * , & (! " , ! , ! " ) x (! , ! , ! )

Remarque

1-Le modéle SARl M A(12, 1, 12) x (1, 1, 1) est le modéle qui presente les meilleurs critéres

de pouvoir predictif (a savoir R² , R² , statistique de Fisher : maximum ; et SSR, Al O , SO :

minimum.

2- La statistique de Durbin-Watson=2.08 presage un bon ajustement.

5.1.3 Validation du modèle

Tests sur le modèle

Les racines des deux polynômes autoregressif et moyenne mobile sont superieures en module

a 1, car leurs inverses calculees par EVIEWS sont tous inferieurs a 1, ainsi les conditions

de stationnarite et díinversibilite sont verifees. Les composantes AR et M A de líARM A níont pas de racines communes (leurs inverses sont distinctes), il en resulte donc que notre representation SARl M A(12, 1, 12) x (1, 1, 1) est minimale par le principe de parcimonie. Tests sur les estimations

Les coecents cients des paramétres du modéle SARl M A(12, 1, 12) x (1, 1, 1) sont signifcative-

ment di§erents de zero ( 0 .69, 0 .16, ) 0 .3 9, 0 .41, 0 .70 ), díailleurs le test de Student le confrme puisque les t-statistic associes aux paramétres du modéle ( 6.03 , 2.80 , 8 .70 , 3 .10 ,

6.28 ) en valeurs absolues, sont superieurs aux valeurs theoriques (1.64) au seuil 5 % et (1.95 )

au seuil 10 % .

Representation graphique des series : residuelle (6 t), actuelle et estimee

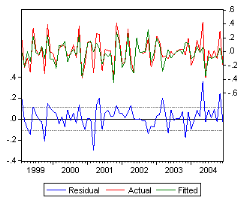
FIG.l .7. G. des SÈries estimÈ, rÈelle et rÈsiduelle

En analysant la représentation graphique (FIG.l .7) , nous constatons que le graphe de la série estimée est presque semblable a celui de la série réelle, a quelque pics prés. Mais globalement

le modéle SARl M A(12, 1, 12) x (1, 1, 1) explique bien le processus 3 D(LDP SAt)4 t

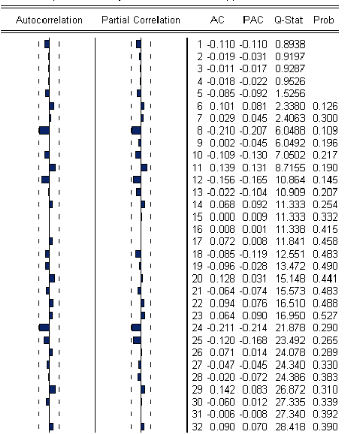
FIG.I .8 OorrÈlogramme des rÈsidus

Test de Ljung-Box

Líanalyse du corrélogramme des résidus, associé a la fgure l .8 montre que tous les termes sont a líintérieur de líintervalle de confance (illustré par des pointillés sur le logiciel Eviews),

ce qui est confrmé par la Q s tat pour tous les retards en particulier Q s tat 6 24.3 4 (au

O ,O5

retard > 6 27) 0 x ²

(22) 6 33 .92, donc les residus se comportent comme un bruit blanc.

Donc le modèle est valide et il síecrit comme suit :

D(LDP SAt) 6 D(LDP SAt 1) ) 0 .3 1D(LDP SAt 12 ) 0 .3 1D(LDP SAt 13 )

) 0 .69D(LDP SAt 24 ) 0 .69D(LDP SAt 25 ) ) 6 t ) 0 .76 t 1

^{) 0 .416} t 2 ^{0 , 3 96} t 7 ^{) 0 .166} t 12

Test de stabilite

Pour faire ce test nous sommes amenes a reestimer le modèle choisi sur les 79 premières observations de la serie D(LDP SAt), donc de Decembre 1997 a Juin 20 0 4.

EVIEWS nous donne líestimation suivante :

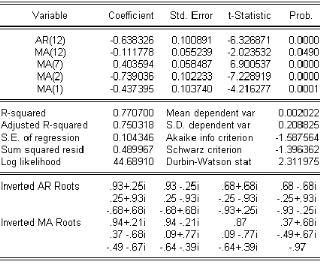
On constate que :

Tous les coecents cients du modèle estime sont signifcativement di§erents de zero au seuil

5 % .

Les conditions díinversibilite et de stationnarite sont verifees.

On calcule maintenant les previsions de la consommation publique sur la periode de Avril

20 03 a Decembre 20 0 4 que nous comparons avec les observations reelles sur la même periode.

Representation graphique

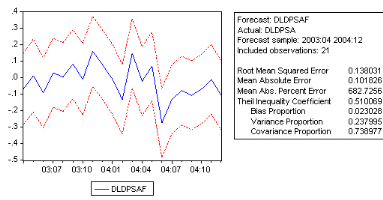
Fig.I .8 .Graphe des previsions D(LDP SAF t) (0 4/ 20 03 12/ 20 0 4)

On remarque que les previsions de la consommation publique sur la periode 0 4/ 20 03 au

12/ 20 0 4 (en couleur bleu) donnees par le modèle SARl M A(12, 1, 12)x (1, 1, 1) appartiennent

a líintervalle de confance (en pointilles rouges, voir Fig.l .8 ), ce qui acents rme la stabilite du modèle precite et donc il peut être generateur de la serie D(LDP SAt).

Test de normalite

Les tests sont e§ectues a partir des valeurs empiriques des coecents cients de Skewness, Kurtossis

et la statistique de Jarque-Berra donnees par le logiciel EVIEWS. En utilisant le logiciel on a líhistogramme suivant :

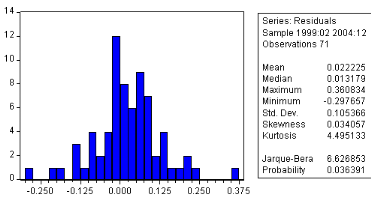
^% (Sk )1+ 2 ^%

Test de Skewness : (SK )^{1+ 2} 6 0 .03 4 ' 7 1 6

^{% %}

^A 6

,4

6 0 .1272 0 1.96

Test de Kurtossis : ku 6 4.495 1 ' 7 2 6

^ku ³

^A 24

,4

6 2.7970 > 1.96

Donc, díaprès le resultat du test, nous rejetons líhypothèse de normalite en ce qui concerne

líaplatissement de la distribution, ce qui est confrme par la statistique de Jarque-Berra :

J B 6

8 4

6 ^{SK )}

8 4

0 ,05

(ku 3 )² 6 6.62 > x ²

²⁴

(2) 6 5 .911

Conclusion : Les residus ne forment pas un bruit blanc gaussien.

5.1.4 Prevision

Après avoir choisi le meilleur modèle, on passe aux previsions pour un horizon h.

Le modèle est represente par líequation suivante :

D(LDP SAt) 6 D(LDP SAt 1) ) 0 .3 1D(LDP SAt 12 ) 0 .3 1D(LDP SAt 13 )

) 0 .69D(LDP SAt 24 ) 0 .69D(LDP SAt 25 ) ) 6 t ) 0 .76 t 1

) 0 .416 t 2 0 , 3 96 t 7 ) 0 .166 t 12

Pour faire les previsions, nous avons quía remplacer dans líequation du modèle

SARl M A(12, 1, 12) x (1, 1, 1), t par t ) h

Nous aurons donc : Pour h 6 1

D(L^\DP SAt)(1) 6 D(LDP SAt) ) 0 .3 1D(LDP SAt 11) 0 .3 1D(LDP SAt 12 )

) 0 .69D(LDP SAt 23 ) 0 .69D(LDP SAt 24 ) ) 0 .76 t ) 0 .416 t 1

^{X X}

0 , 3 96 t 6 ) 0 .166 t 11

^{X X}

Pour h 6 2

D(L^\DP SAt)(2) 6

D(LD^\P SAt)(1) ) 0 .3 1D(LDP SAt 10 ) 0 .3 1D(LDP SAt 11)

) 0 .69D(LDP SAt 22 ) 0 .69D(LDP SAt 23 ) ) 0 .416 t 0 , 3 96 t 5

Pour h 6 12

^{X X}

^X

) 0 .166 t 10

D(D^\P SAt)(12) 6

D(LD^\P SAt)(11) ) 0 .3 1D(LDP SAt) 0 .3 1D(LDP SAt 1)

^X

) 0 .69D(LDP SAt 12 ) 0 .69D(LDP SAt 13 ) ) 0 .166 t

Pour h > 12

D(D^\P SAt)(h) 6

D(LDP^\SAt)(h 1) ) 0 .3 1D(LDP SAt+ h 12 ) 0 .3 1D(LDP SAt+ h 13 )

^{) 0 .69D(LDP SA}t+ h 24 ^{) 0 .69D(LDP SA}t+ h 25 ⁾

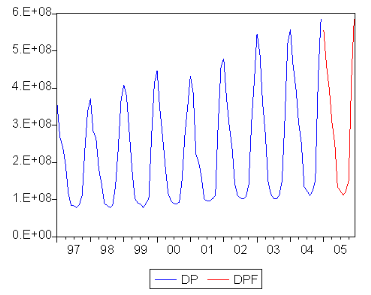
FIG.I .9 -Graphe des previsions de la consommation publique

Les previsions de la consommation publique pour líexercice 20 0 4/ 20 05 sont donnees dans le tableau ci-dessous

Mois	Previsions (m ^3)
Jan	55 622773 25 .05 6
Fev	460 2773 25 .113
Mar	3 983 77783 .88 6
Avr	30 5 95 2699.0 2
Mai	25 0 946120 .7
Jui	13 3 77920 9.425
Juil	123 297767.964
Aou	1114200 3 6.05 8
Sep	12298 95 95 .977
Oct	15 143 48 0 4.0 74
Nov	42765 28 5 1.78 3
Dec	58 670 4969.141

Nous pouvons dire que les previsions obtenues sont en harmonie avec líallure generale de la serie, puisque le phenomène de periodicite est reproduit mais avec une certaine augmentation, ceci est explique du faite que le nombre díabonnes dans la classe des consommateurs publics accroÓt avec un taux annuel de 27% .

5.2 Etude de la Serie de consommation des centrales electriques (CE)

5.2.1 IdentiÖcation

La série O Et représente líévolution mensuelle de la consommation nationale du gaz na- turel des centrales électriques sur une période allant de janvier 1997 a décembre 20 0 4.

^{a-Representation graphique de la serie brute O E}t

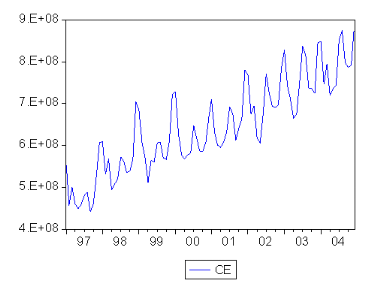
^{FIG.II.1ó Graphe de la serie brute O E}t

La représentation graphique de la série présente les caractéristiques suivantes :

Une tendance a la hausse avec des valeurs áuctuant autour de 4, 4.E ) 0 8 et 9.E ) 0 8 . Une non stationnarité en moyenne, témoignée par la tendance .

Un mouvement périodique caractérisé par des áuctuations ascendantes et descendantes tout au long de la période allant de Janvier 1997 a Décembre 20 0 4.

b-Examen du correlogramme de la serie O Et

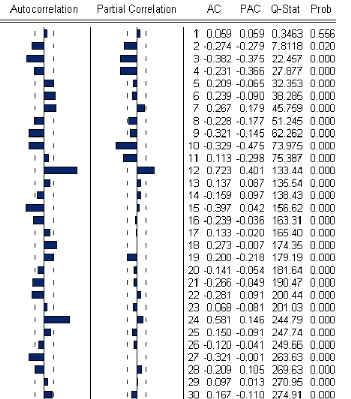
FIG.II.2ó Corrélogramme de la série O Et

Les corrélogrammes simple et partiel font apparaÓtre un "pic" important au retard k 6 12

ce qui laisse supposer que la série est a§ectée díune saisonnalité et par suite nous poussera a dire quíelle est non stationnaire, cíest ainsi quíun recours au test de Fisher nous permettera

de verifer nos hypothèses.

^{Etude de la saisonnalite de serie O E}t

Source des variations	SO	d.liberté	M O	F	P _o b	F critique
Lignes	1950 1.5	11	10 5 4.7	4.3 4	1.03 E 03	1.8 7

Le test confrme nos doutes concernant la présence díune saisonnalité puisque F 6 6.64 >

F ^{0 ) 05}

11 6 1.8 7.On procède a la désaisonnalisation de série par líapplication de líopérateur de

di§érence saisonnière V S 6 (1 B¹² ), líopération e§ectuée, la nouvelle série générée est

O ESAt

Analyse preliminaire de la serie O ESAt

Examen du correlogramme de la serie

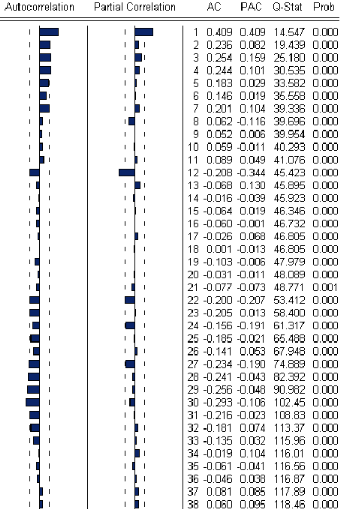
^{FIG.II.3ó Corrélogramme de la série O ESA}t

Líanalyse du correlogramme simple et correlogramme partiel de la serie O ESAt (Fig.l l .3 ) nous indique prealablement que la serie est non stationnaire, puisque la fonction díautocor- relation (visible sur la colonne AO ) ne decroÓt pas de manière rapide. Afn de verifer cette hypothèse, il convient díappliquer le test de racine unitaire.

Test de racine unitaire (Dickey-Fuller) sur la serie O ESAt

A partir du logiciel EVIEWS 4.0, on procède a líestimation par la methode des moindres carrees avec p 6 0 des trois modèles [ 4] , [ 5 ] , [ 6] de DickeyñFuller sur la serie O ESAt (car les residus forment un bruit blanc), dont les resultats díanalyse sont representes ci-dessous

, 9 6 7 8 7 [ % ] A O ESAt 6 b O ESAt 1 ) O ) b t ) 6 t

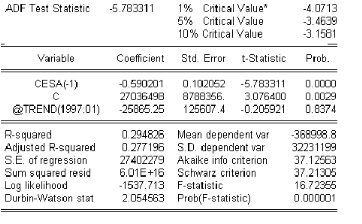
A la lecture de tableau ci dessus, on remarque que la statistique t' 6 5 .78 est inferieure

aux di§erentes valeurs critiques relatives aux seuils 1% , 5 % et 10 % : Líhypothèse H0 est rejetee, donc la serie O ESAt ne possède pas de racine unitaire, elle est donc stationnaire.

La probabilite de nullite du coecents cient de la tendance 0 .83 74 est superieure au seuil de 5 % , aussi la valeur empirique de la statistique de Student relative a la tendance(7 T REN D)

qui est egale a 0 .20 5 9 est inferieure aux valeurs tabulees (1.95 ) au seuil 5 % et (1.64) au seuil 10 % . On accepte donc, líhypothèse du nullite du coecents cient de la tendance (il níest pas signifcativement di§erent de zero), le processus níest pas de type T S (trend stationnary).De

la on estime le modèle [ 5 ]

, 9 6 7 8 7 [ $ ] A O ESAt 6 b O ESAt 1 ) O ) 6 t

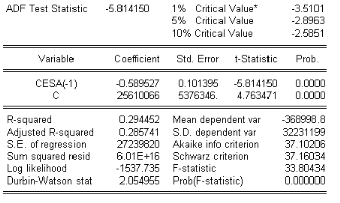
Contrairement a la tendance, la probabilite de nullite de la constante est nulle et elle est inferieure au seuil 5 % , aussi la valeur empirique de la statistique de Student (t-statistic) relative a la constante O qui est egale a (4.763 4) est superieure aux valeurs tabulees (1.95 )

au seuil 5 % et (1.64) au seuil 10 % . On rejette donc, líhypothèse de nullite de la constante

(elle est signifcativement di§erente de zero).

Le fait que la statistique t' 6 5 .8 141 est inferieure aux di§erentes valeurs critiques relatives aux seuils 1% , 5 % et 10 % : líhypothèse H0 est rejetee, donc la serie O ESAt ne possède pas de racine unitaire, elle est donc bien stationnaire. Líestimation des paramètres sera entamee a la base du modèle[ 5 ] .

SpeciÖcation du modèle

Líanalyse du correlogramme partiel de la serie O ESAt (Fig.l l .3 ) montre quíaux retards

(k 6 1, 12, 22) les termes sont a líexterieur de líintervalle de confance et ce qui concerne le correlogramme simple, globalement, on remarque que les valeurs des fonctions díautocorrela- tion simples sont elevees au di§erents retards (k 6 1, 2, 3 , 4, 7, 12, 27, 28 , 29, 30 ....), ce qui nous amène a avoir plusieurs modèles candidats : SARM A(1, 1), SARM A(2, 0 ), SARM A(3 , 12), .. ect. Après une selection nous allons representer le modèle le plus adequat estime a líaide du logiciel EVIEWS 4.0 a savoir : SARl M A(p, Q , q ) x (P, D, Q ).

5.2.2 Estimation des paramètres

0 & / * , & (! , , ! " ) x ( , ! , ! )

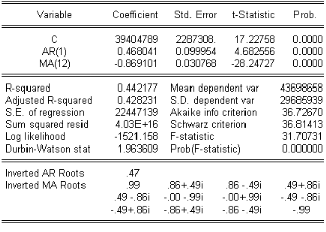
Remarque

1 Le modèle SARI M A(1, 0 , 12) x (0 , 1, 1) a été choisi, car il présente des critères de pouvoir prédictif meilleur que ceux des autres modèles estimés (a savoir : R² , R, statistique de Fisher : maximum ; et SSR, AI O , SO : minimum.

2 La statistique de Durbin-Watson 6 1.96, présage un bon ajustement.

5.2.3 Validation du modèle

Tests sur le modèle

Les racines des deux polynômes autoregressif et moyenne mobile sont supérieures en module

a 1, car leurs inverses calculés par EVIEWS sont tous inférieurs a 1, ainsi les conditions de stationnarité et díinversibilité sont vérifées.

Les composantes AR et M A de líARM A níont pas de racines communes (leurs inverses sont distinctes), il en résulte donc que notre représentation SARI M A(1, 0 , 12) x (0 , 1, 1) est minimale par le principe de parcimonie.

Tests sur les estimations

Les coecents cients des paramètres du modèle SARI M A(1, 0 , 12) x (0 , 1, 1) sont signifcative- ment di§érents de zéro, díailleurs le test de Student le confrme.

Test sur les residus

^{Representation graphique des series : residuelle (6} t^{), actuelle (O ESA}t^{) et estimee}

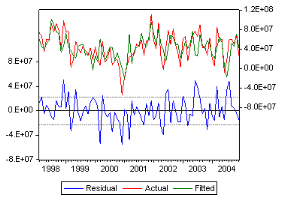
FIG.I I .4 Graphique des series estimee, reelle et celle des residus

Test de Ljung-Box

Le corrélogramme des résidus ne fait apparaÓtre aucun terme en dehors de líintervalle de confance au seuil 5 % , ce qui est confrmé par la Q s tat pour tout les retards en particulier

0 ) 05

Q s tat 6 25 .28 2 (au retard K 6 29) 0 x ²

(26) 6 3 8 .92, on peut donc assimilé les résidus

a un bruit blanc.

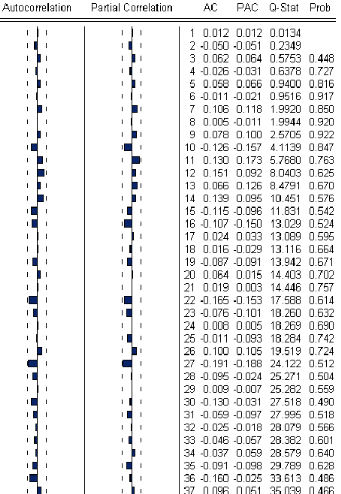
FIG.II.5 Oorrelogramme des residus

Líestimation du modèle SARI M A(1, 0 , 12) x (0 , 1, 1) est donc validée, la série G ESAt peut être valablement représentée par un processus de type SARI M A(1, 0 , 12) x (0 , 1, 1) et il síécrit :

^{G ESA}t ^{6 3 940 478 9 ) 0 .47G ESA}t 1 ^{) G ESA}t 12 ^{0 .47G ESA}t 13 ^{) t} t ^{) 0 .8 7t} t 12

Test de stabilite

Réestimons le modèle obtenu précédemment sur les 66 premières observations, cíest a dire sur la période (1997 : 0 1 20 03 : 0 6).

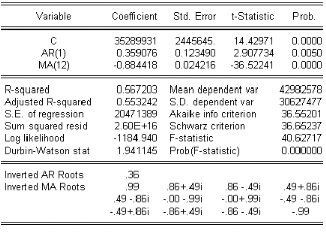
Les coecents cients du modèle sont signifcativement di§érent de zéro pour un seuil de 5 % (les valeurs empiriques t-statistic sont toutes supérieures aux valeurs tabulées au seuil 5 % ), et

les conditions de stationnarité et díinversibilité sont vérifées.

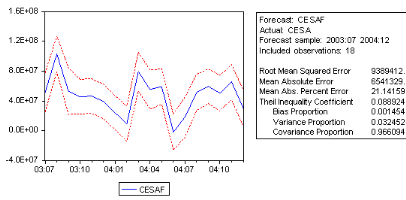
Fig.II.6.Graphe des previsions (C ESAF t) (0 7/ 20 03 12/ 20 0 4)

On remarque que les valeurs obtenues sont a líintérieur de líintervalle de confance, par

conséquent le modèle est stable.

Test de normalite

Les tests sont e§ectués a partir des valeurs empiriques des coecents cients de Skewness, Kurtossis

et la statistique de Jarque-Berra données par le logiciel EVIEWS. En utilisant le logiciel on

a líhistogramme suivant :

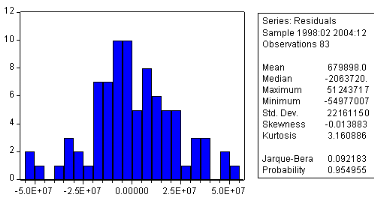
^% (Bk )1/ 2 ^%

^{Test de Skewness : (B}K ^{)1/ 2 6 0 .0 1 ' 7} 1 ^{6 %}

ku 3

^%

^A

6

,3

6 0 .33 88 < 1.96.

^{Test de Kurtossis : k}u ^{6 3 .16 ' 7} 2 ⁶

^A 24

,3

6 0 .2975 < 1.96.

Donc, díaprès le résultat du test, nous acceptons líhypothèse de normalité en ce qui concerne

la symétrie et líaplatissement de la distribution, ce qui est confrmé par la statistique de

Jarque-Berra :

J B 6

83

6 ^{BK )}

83

0 ,05

(ku 3 )² 6 0 .0 9 < x ²

²⁴

(2) 6 5 .911.

Conclusion : Les résidus forment un bruit blanc gaussien.

5.2.4 Prevision

Líéquation du modèle BARI M A(1, 0 , 12) x (0 , 1, 1) représentant la série C EBAt est don-

née par :

O ESAt 6 3 940 478 9 ) 0 .47O ESAt 1 ) O ESAt 12 0 .47O ESAt 13 ) t t ) 0 .8 7t t 12

Les prévisions seront calculées a líaide de líEVIEWS pour un horizon h 6 12 mois depuis líorigine 12/ 20 0 4

Soit O^\ESAt(h) la prévision a líorigine t, a un horizon h :

Pour h 6 1 :

^X

O^\ESAt(1) 6 3 940 478 9 ) 0 .47O ESAt ) O ESAt 11 0 .47O ESAt 12 ) 0 .8 7t t 11

.

^X

O^\ESAt(12) 6 3 940 478 9 ) 0 .47O^\ESAt(11) ) O ESAt 0 .47O ESAt 1 ) 0 .8 7t t

Pour h > 12 :

O^\ESAt(h) 6 3 940 478 9 ) 0 .47O^\ESAt(h 1) ) O ESAt+ h 12 0 .47O ESAt+ h 13

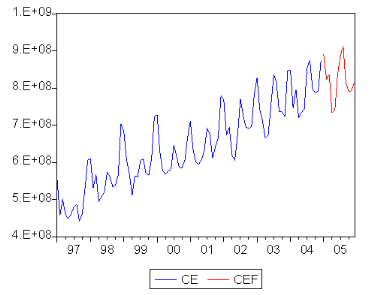
Fig.II.6-Graphe des previsions de la consommation des centrales electriques

Les prévisions sont données dans le tableau suivant :

Mois	Previsions (m ^3)
Jan	8 905 6640 1
Fev	8 24114942
Mar	83 60 73 93 4
Avr	73 38 03 203
Mai	740 4700 3 1
Jui	83 53 45 929
Juil	88 5 95 9278
Aou	913 7777162
Sep	8 140 77793
Oct	7915 9475 2
Nov	7925 5 73 97
Dec	8 15 78 78 2649

5.3 Etude de la serie de consommation industrielle (CI)

5.3.1 IdentiÖcation

La série O It représente líévolution mensuelle de la consommation nationale du gaz naturel

de líindustrie algérienne sur une période allant de janvier 1997 a décembre 20 0 4.

^{a-Representation graphique de la serie brute ' *} t

^{FIG.III.1ó Graphe de la serie brute O I}t

Globalement, la représentation graphique de la série présente des variations montrant un mouvement ascendant suivis par díautres descendants áuctuant entre des valeurs 10 ^, et

1, 9E ) 08 ainsi que de nombreux pics compensés souvent par des creux. Pour absorber le

phénomène de variabilité líintroduction díune transformation logarithmique est nécessaire pour la suite de notre étude.

b-Introduction du logarithmique

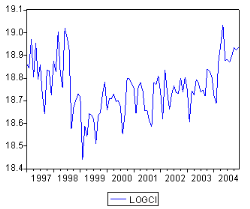
^{FIG.III.2ó Graphe de la serie brute LB : O I}t

Cette représentation, a une allure similaire a celle de la série brute O It, mais la transformation logarithmique a amorti les pics et les creux, líéchelle de mesure est réduite (les valeurs áuctuent entre 18 .4 et 19.1), on peut remarquer que la série est a§ectée díune tendance qui peut être stochastique ou déterministe.

c-Analyse preliminaire de la serie + - ) ' * t

Examen du correlogramme de la serie

Líanalyse du corrélogramme simple et partiel nous indique une non stationnarité de la série. Pour la saisonnalité, le corrélogramme ne montre aucun signe de sa présence, néanmoins un test de saisonnalité sera entrepris pour e§acer équivoque.

En e§et, la fonction díautocorrélation simple ne décroÓt pas de manière rapide vers zéro

et le premier terme du corrélogramme partiel est très important (0 .5 90 ) ceci nous mène a tester líexistence díune tendance déterministe ou stochastique par líemploi du test de racine unitaire.

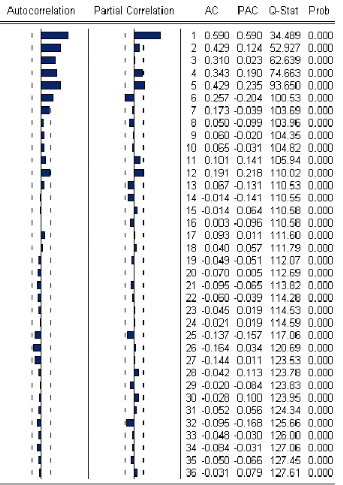
^{FIG.III.3ó Corrélogramme de la série + - ) ' *} t

^{Etude de la saisonnalite de la serie LB : O I}t

Source des variations	SO	d.liberté	M O	F	P _o b	F critique
Lignes	1250 .5	11	15 2.1	1.3 2	1.23 E 4	1.8 7

11

Etant donné que F 6 1.3 2 < F ^{0 ) 05}

6 1.8 7, nous pouvons dire que la série en question

est dépourvue díun caractère saisonnier. La consommation industrielle, contrairement a la

consommation publique et celle des centrales électriques níobéÓt pas au phénomène saison- nier, elle est plutôt tributaire de líétat socio-économique du pays.

Test de racine unitaire (Dickey-Fuller) sur la serie + - ) ' * t

Donc a líaide du logiciel EVIEWS, les paramètres des modèles [ 4] , [ 5 ] et [ 6] sont estimés par la méthode des moindres carrés ordinaires avec p 6 0 , les résultats díanalyse sont repré- sentés ci-dessous.

, 9 6 7 8 7 [ % ] A LB : O It 6 b LB : O It 1 ) O ) b t ) t t

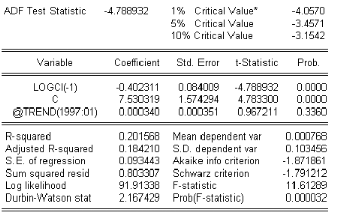
, 9 6 7 8 7 [ $ ] A LB : O It 6 b LB : O It 1 ) O ) t t

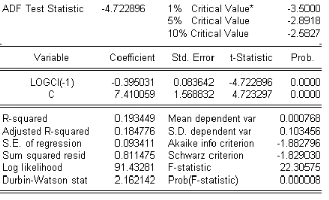
Les statistique t^X' associées aux modéles [ 5 ] et [ 6] respectivement sont supérieurs a toutes

les valeurs critiques relatives aux seuils 1% , 5 % et 10 % : líhypothése H0 est rejetée la série + - ) ' * t ne posséde pas de racine unitaire, elle est donc stationnaire.

La probabilité de nullité du coecents cient de la tendance est supérieure au seuil 5 % , la va- leur empirique t-statistic est inférieur aux valeurs critiques tabulées par Dickey-Fuller. On accepte donc líhypothése de nullité du coecents cient de la tendance et le processus níest pas de type T S. La probabilité de nullité de la constante est inférieure au seuil 5 % , et sa valeur em- pirique t-statistic est supérieure aux valeurs critique tabulées par Dickey-Fuller. On rejette donc líhypothése de nullité de la constante.

La série + - ) ' * t níadmet ni tendance déterministe ni stochastique donc le processus est stationnaire.

SpeciÖcation du modèle

Díaprés le corrélogramme nous sommes amenés a avoir plusieurs modéles candidats ARM A(1, 1), ARM A(4, 4), ARM A(6, 6), ...., suivant les Critéres de pouvoir prédictif et les critéres díin- formations nous avons choisi le modéle ARM A(1, 12)

5.3.2 Estimation des paramètres du modèle ARM A(1, 12)

ARM A(1, 12)

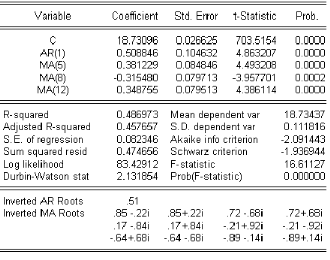
Remarques

1-Le modéle ARM A(1, 12) est le modéle qui présente les meilleurs critéres de pouvoir prédictif (a savoir R² , R² : maximum ; et SSR, AI O, SO : minimum)

2- La statistique de Durbin-Watson 6 2.14, présage un bon ajustement.

5.3.3 Validation du modèle

Tests sur le modèle

Les racines des deux polynômes autoregressif et moyenne mobile sont supérieures en mo- dule a 1, car leurs inverses calculés par EVIEWS sont tous inférieurs a 1, ainsi les conditions

de stationnarité et díinversibilité sont vérifées.

Les composantes AR et M A de líARM A níont pas de racines communes (leurs inverses sont distinctes), il en résulte donc que notre représentation ARM A(1, 12) est minimale par

le principe de parcimonie.

Tests sur les estimations

Les coecents cients des paramétres du modéle ARM A(1, 12) sont signifcativement di§érents

de zéro, díailleurs le test de Student le confrme.

Test sur les residus

^{Representation graphique des series : residuelle (t} t^{), actuelle et estimee}

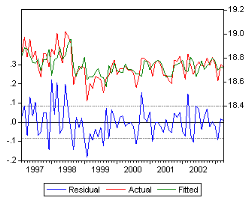
FIG.III.4 Graphique des series estimee, , reelle et celle des residus

Test de Ljung-Box

Líanalyse du corrélogramme des résidus (Fig.I I I .5 ) montre que tous les termes sont a líintérieur de líintervalle de confance (illustré par des pointillés sur le logiciel Eviews), ce qui

est confrmé par la Q s tat pour tous les retards en particulier Q s tat 6 17.0 7(au retard

0 ,05

K 6 27) < x ²

(22) 6 3 3 .92, donc les résidus se comportent comme un bruit blanc

Díoü le modéle est validé, et il síécrit comme suit :

LB : O It 6 18 .76 ) 0 .5 9LB : O It 1 ) t t 0 .41t t 5 ) 0 .29t t 8 0 .33 t t 12

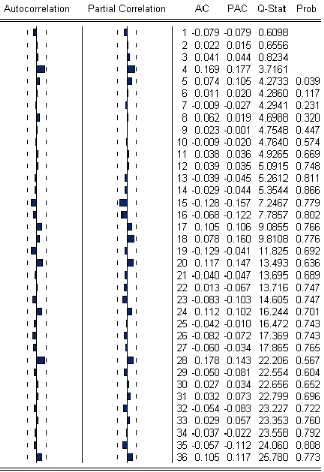
FIG.III.5ó Corrélogramme des résidus

Test de stabilite

On résetime le modéle ARM A(1, 12) sur les 65 premiéres observations de la série LB : O It ,

de Janvier 1997 a Avril 20 03 .

Le logiciel EVIEWS donne líestimation suivante

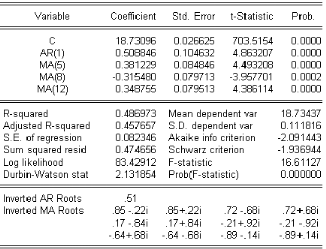
Les coecents cients du modéle estimé sont signifcatifs au seuil 5 % .

Les conditions de stationnarité et díinversibilité sont vérifées.

On remarque que les valeurs obtenues sont a líintérieur de líintervalle de confance, par conséquent le modéle est causal et inversible.

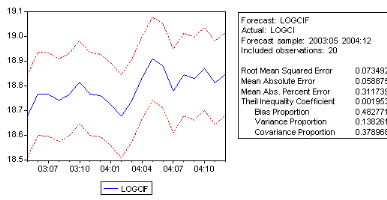
Fig.III.6.Graphe des previsions (LO G O I F t) (05 / 20 03 12/ 20 0 4)

Test de normalite

Les tests sont e§ectués a partir des valeurs empiriques des coecents cients de Skewness, Kurtossis

et la statistique de Jarque-Berra données par le logiciel EVIEWS. En utilisant le logiciel on

a líhistogramme suivant :

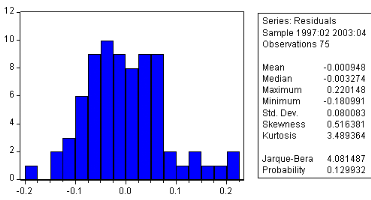
^% (Sk )1/ 2 ^%

Test de Skewness :(SK )^{1/ 2} 6 0 .5 163 ' 7 1 6

^{% %}

^A 6

-5

6 0 .95 677 < 1.96.

Test de Kurtossis : ku 6 3 .48 93 ' 7 2 6

^ku ³

^A 24

-5

6 0 .223 6 < 1.96.

Donc, díaprés le résultat du test, nous acceptons líhypothése de normalité en ce qui concerne

la symétrie et líaplatissement de la distribution, ce qui est confrmé par la statistique de

Jarque-Berra :

J B 6

95

6 ^{SK )}

95

0 ,05

(ku 3 )² 6 4.08 14 < x ²

²⁴

(2) 6 5 .911 .

Conclusion : Les résidus forment un bruit blanc gaussien.

5.3.4 Prevision

Líéquation du modéle síécrit comme suit :

LO G O It 6 18 .73 ) 0 .5 1LO G O It 1 ) t t 0 .38 t t 5 ) 0 .3 2t t 8

0 .35 t t 12 .

Les prévisions seront calculées a líaide de líEVIEWS pour un horizon h 6 12 mois, Soit

L^\O G 0 1 (h) la prévision a líorigine t, a un horizon h

L\O G 0 1 (1) 6 18 .73 ) 0 .5 1LO G 0 1t 0 .38 t t 4 ) 0 .3 2t t 7

^{X X}

^X

0 .35 t t 11.

.

^X

L^\O G 0 1 (12) 6 18 .73 ) 0 .5 1LO^\G 0 1t(11) 0 .35 t t.

Pour h > 12 :

L^\O G 0 1 (h) 6 18 .73 ) 0 .5 1LO^\G 0 1t(h 1).

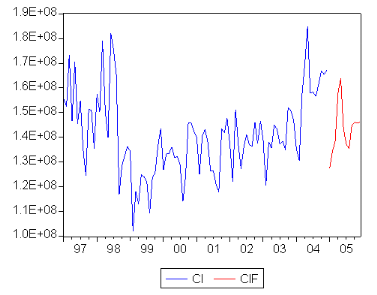
Fig.III.7-Graphe des previsions de la consommation industrielle

Le tableau des prévisions sera donné comme suit :

CHAPITRE 5. APPLIOATION DE LA M...THODOLOGIE DE BOX-JENKINS 90

Mois	Previsions (m ^3)
Jan	15 55 0 68 28
Fev	13 43 3 10 40
Mar	13 85 24238
Avr	15 80 77120
Mai	1638 038 58
Jui	1433 98 25 2
Juil	13 71210 27
Aou	13 5 4660 35
Sep	14478 40 5 7
Oct	14610 25 0 9
Nov	145 7458 67
Dec	14618 23 95

5.3.5 Conclusion

Líanalyse des trois séries représentant les di§érents types de consommation, suivant la démarche de Box & Jenkins, nous a permis de mettre en évidence les remarques suivantes : Les séries de consommation publique et industrielle exhibant une certaine variabilité ont nécessité une transformation logarithmique qui nía fait quíamortir les pics et les creux qui caractérisent ces séries.

Les chroniques associées aux consommation publique et celles des centrales électriques carac-

térisées par un mouvement saisonnier de périodicité annuelle, ont nécessité une di§érentiation díordre 12.

Mis a part la série de consommation publique qui a nécessité une di§érence ordinaire pour être

stationnaire, les autres séries Aprés transformations ont aboutis a des séries stationnaires. Pour chaque série nous avons spécifé des modéles bien précis tel quíon a :

Modéle SAR1 M A(12, 1, 12) x (1, 1, 1) pour la consommation publique.

Modéle SAR1 M A(1, 0 , 12) x (0 , 1, 1) pour la consommation des centrales électriques. Modéle ARM A(1, 12) pour la consommation industrielle.

Ces modéles sont les plus adéquats et ils sont caractérisés par des résidus de type bruit blanc

gaussien a líexeption de la premiére série associée a la consommation publique.

Nous souciant de la qualité des prévisions obtenues, et sachant que la méthodologie de Box

& Jenkins ne prend pas en considération la corrélation entre les séries, nous allons essayer díintroduire les modéles I AR a la base de nos séries pour une amélioration éventuelle.

Chapitre 6

MODELES VAR

6.1 Introduction

Dans le chapitre précédent ont été intéressé par líétude de líévolution des séries chronolo- giques des trois types de consommation du gaz naturel a savoir la consommation publique, la consommation des centrales électriques et la consommation industrielle. Les modéles de sé- ries chronologiques univariés leurs associés ont été identifés, estimés et validés. Ces modéles ont été exploité par la suite pour líobtention des prévisions a court terme.

Les mécanismes engendrant les séries observées individuellement ne peuvent pas fournir

des informations et de renseignement sur plusieurs questions intéressantes pour une variété díobjectifs comme a titre díexemple la relation de líévolution de la consommation industrielle avec celle des centrales électriques. La théorie économique nous informe que ces facteurs sont

liés dans le cadre du développement díun pays.

Dans le chapitre présent nous développons les modéles de séries chronologiques multiva- riés I ARM A, en particulier les modéles I AR,qui peuvent répondre a plusieurs préoccupa- tions liées aux comportement simultanés des trois séries sous-jacentes.

91

6.2 Processus multivaries

DeÖnition

un processus3 Xt, t E Z4 multivarié est une famille de variables aléatoires vectorielles défnies sur R^F.

Comme dans le cas univarié, la stationnarité joue un rôle important dans la théorie des processus, cíest ainsi quíon síétalera a étudier les processus multivariés sationnnaires dans

ses di§érents champs.

6.2.1 Fonction díautocovariance díun processus multivarie

Considérons un processus multivarié 3 Xt, t E Z4 de moyenne % , la covariance entre Xt

et Xs est donnée par

7 (t, s ) 6 0 ov (Xt, Xs) 6 E ^! (Xt % ) (Xs % ) ^" , V t, s E Z.

6.2.2 Processus multivarie fortement stationnaire

Soit un processus multivarié3 Xt, t E Z4 , le processus est dit fortement (ou stricte- ment) stationnaire si : V n E N , V (t1, t2 ,..., tF) et V h E Z, le vecteur (Xt1 + h, ..., Xt" + h) a

^{la même loi de probabilité que la suite (X}t1 ^{, ..., X}t" ^{), autrement dit :}

P (Xt1 < x 1, ..., Xt" < x F) 6 P (Xt1 + h < x 1, ..., Xt" + h < x F) ,

V (t1, t2 ,..., tF) E Z^F, V (X1, X2 ,..., XF) E R^F, V h E Z.

Ainsi tous les moments díordre, díun processus multivarié strictement stationnaire sont in- variants pour toute translation dans le temps, or cette défnition est rarement vérifée en pratique, cíest ainsi que nous nous intéressons a un second type de stationnarité des proces-

sus multivariés, dit du second ordre.

6.2.3 Processus multivarie faiblement stationnaire

Le processus multivarié 3 Xt, t E Z4 est dit faiblement stationnaire (du second ordre) si

sa moyenne est fnie indépendante du temps et de plus le processus est stationnaire en sa

covariance, ie :

ó 1. E (Xt) 6 E (Xt+ h) 6 % (constante) , V t E Z,

ó 2. 0 o v (Xt, Xt+ h) 6 E ^! (Xt % t)(Xt+ h % t+ h)^{1 "} 6 F (h) , V t, h E Z,

oü F (h) est la fonction díautocovariance matricielle du processus{ Xt, t E Z} .

Proposition

Si { Xt, t E Z} stationnaire alors V i E { 1, .., n } (Xi t,) stationnaire. La reciproque est fausse.

Remarque

Dans ce qui suit le terme stationnaire, sauf mention contraire signifera la stationnarite du second ordre.

6.2.4 Processus bruit blanc multvarie

Un vecteur bruit blanc multivarie { t t, t E Z} est une suite de variables aleatoires non correlees de moyenne nulle et de matrice de covariance " , ie :

^* E (t t) 6 0 ,

^E(t t^t t^{) 6 " . V}

t E Z

Et en consequence sa fonction díautocovariance est donnee par :

^* " , h 6 0 ,

^{F (h) 6 E (t} t ^t t+ h^{) 6}

0 , h 6 0 .

Remarque

On suppose que " est non singuliére.

Proprietes

F ( h) 6 F (h) , V h E Z, (la fonction díautocovariance níest pas symetrique)

Estimateur

En pratique la fonction díautocovariance est estimee a líaide de líestimateur suivant :

1

T h

z ( (

F^X (h) 6

^{T h} tl 1

^Xt ^X t

1

^Xt+ h ^X t+ h ^,

T h

z

^{avec X} t h ⁶

Xt

T

^{T h} tl 1

et X t 6

^{1 z} X

t

^T tl 1

6.2.5 Fonction díautocorrelation

La fonction díautocorrélation díun processus stationnaire multivarié faiblement station- naire de moyenne % et de matrice de covariance F (h) , notée Ah 6 (p i j (h)) est défnie par

7 i j (h)

^Ah ⁶

^A ,

⁷ ii ^{(0 )7} j j ^{(0 )}

6.2.6 Decomposition de Wold -Cramer

Le théoréme de Wold, est également valable dans le cas multivarié.

Theorème de Wold :

Tout processus stationnaire { Xt, t E Z} peut se decomposer en la somme díune composante regulière previsible (deterministe) et díune expression lineaire sto- chastique tel que :

z$

^Xt ^{6 H} t ⁾

j l 0

^Oj ⁶ t j

oü Oj est une suite de matrices carrees de taille n x n avec O0 6 1F et { 6 t} E R^F

avec 6 t bruit blanc de matrice de covariance ^z .

z$

Etant donné que la série

j l 0

^Oj ⁶ t j ^{doit être convergente, cíest a dire que les termes O}j ⁶ t j ^{6 0}

lorsque j -- + , donc la décomposition de Wold peut être approximée par une représentation

vectorielle moyenne mobile I M A(+ ), et comme le passage díune représentation moyenne mobile vers une représentation autoregressive est possible, on peut approximer la décompo- sition de Wold par une représentation vectorielle autoregressive I AR(+ ).

6.2.7 Modèle autoregressif moyenne mobile Multivarie I ARM A(p, q )

Le processus stationnaire satisfait une representation & / , & multivarie, note

2 & / , & díordre (: , ; ), síil est solution de líequation aux di§erences stochastique suivante :

p

^Xt ^z

j l 1

b j Xt j 6 6 t

q

^z

j l 1

^& j ⁶ t j

Le modéle I ARM A(p, q ), síécrit sous la forme suivante

Xt 6 b 0 ) b 1Xt 1 ) .... ) b p Xt p ) 6 t ) & 16 t 1 ) .... ) & q 6 t q

Soit encore :

^{# (L)X}t ^{6 ! (L)6} t ^{) b} 0

oü # (L) 6 I

p

^z

i l 1

# i Lⁱ et ! (L) 6 I

q

^z

i l 1

# j L^j

Ou encore # est un polynôme matriciel díordre p et ! un polynôme matriciel díordre q .

Dans la suite, on síintéresse a un type particulier de modéles I ARM A(p, q ), a savoir les modéles I AR(p)

6.2.8 Modèle Autoregressif Multivarie I AR(p)

Les modéle I AR(p) (vector autoregressif) constituent une généralisation des modéle AR

au cas multivarié

DeÖnition

Le processus du second ordre n -varie admet une representation I AR (au- toregressif vector) díordre p note (I AR(p)) síil est solution de líequation aux di§erences stochastique suivante :

Xt 6 b 0 ) b 1Xt 1 ) .... ) b p Xt p ) 6 t.

oü {6 t}est un bruit blanc vectoriel.

En introduisant líopérateur de retard L, on peut réécrire líéquation précédente sous la forme symbolique suivante :

# (L)Xt 6 b 0 ) 6 t

oü # (L) 6 I

p

^z

i l 1

# i Lⁱ

avec L^j Xt 6 Xt j

Remarque 1

Tout modéle I AR (p) peut síécrire sous la forme díun I AR (1), mais de dimension supérieur

(n p au lieu de n ).

Soit le modéle I AR(p) :

# (L)Xt 6 q 0 ) 6 t

Posons :

On peut écrire alors :

0

^I

5 t 6 ^I

^I

⁶

Xt 1

.

^Xtt1 ^I I I

⁷

^Xttp p t1)

avec :

⁵ t ^{6 q 5} tt1 ⁾

^qA 0 ^{) 6} t

^A

0

q 1 q 2 .. q p ¹

⁰

I

^I

q^A 0 6 ^I

^q 0 ¹

^I

0 ^I

. I

^{0 6} t ¹

^I

^I 0 ^I

t

^I

.

6 6 ^I

^A I

^I In 0 .. ^I

^I

^I

^I 0 In 0 ^I

q

I I

^{6 . 7}

0

^{6 . 7}

0

^{I .} . . ^I

.

^{6 7}

0

^{oü I}n ^{désigne la matrice identité de dimension n x n . En e§et :}

0 Xt 1

⁰ q 1 q 2 .. q p ^{1 0}

^I In 0 .. ^I

^Xtt1 ¹

6

0 q 0 1 0 t 1

^I

5 t 6 ^I

I

^Xtt1

.

^{I I} 0 In 0

6

^{I I}

I I

^{I I} Xttt2 ^{I I}

^{I I I I}

.

)

I I I I

0 ^{I I} 0 ^I

^I

^I

^I

. I ) ^I . I

^I

.

^{6 . 7 .}

^{Xttp p t1) 6} 0

^{. .} .

^{I 6 . 7}

^{7 X}ttp

^{6 . 7}

0

^{6 . 7}

0

est alors un I AR (1) de dimension n p.

6.2.9 Caracteristiques des modèles I AR

Etudions les principales caractéristiques des modéles I AR. Concidérons un modéle I AR (1)

^Xt ^{6 q} 0 ^{) q} 1^Xtt1 ^{) 6} t

Oü 6 t & BB(0 , " )

Esperance

On a

^{E[ X}t^{] 6 E[ q} 0 ^{) q} 1^Xtt1 ^{) 6} t^]

Le processus étant stationnaire, on a : E[ Xt] 6 E[ Xtt1] . On peut donc écrire (sachant que

^{E[ 6} t^{] 6 0 ) :}

Díou

^{E[ X}t^{] 6 q} 0 ^{) q} 1^{E[ X}t^]

E[ Xt] 6 (I q 1)^t1q 0

Fonction díautocovariance

Considérons le processus centré : 5 t 6 Xt E[ Xt] , soit :

5 t 6 q 15 tt1 ) 6 t

La fonction díautocovariance F est donnée par :

F (0 ) 6 E[ 5 t5 t ] 6 E[ q 15 tt15 t ) 6 t5 t ] (" )

Or

E[ 6 t5 t ] 6 E[ 6 t(5 tt1q 1 ) 6 t)] 6 q 1E[ 6 t5 tt1] ) E[ 6 t6 t]

Comme 6 t est BB alors

E[ 6 t5 tt1] 6 0

On a donc

E[ 6 t5 t ] 6 E[ 6 t6 t] 6 "

On remplaÁant dans (" ) on aura

F (0 ) 6 q 1E[ 5 tt15 t ] ) "

On remarque que E[ 5 t5 tt1] 6 F (1), on en déduit :

F (0 ) 6 q 1F (1) ) "

On calcule la matrice díautocovariance díordre 1 :

F (1) 6 E[ 5 t5 tt1] 6 E[ (q 15 tt1 ) 6 t)5 tt1] 6 q 1E[ 5 tt15 tt1] 6 q 1F (0 )

On en déduit la formule de récurrence suivante pour la matrice díautocovarinace díordre h

díun modéle I AR (1) :

F (h) 6 q 1F (h 1) V h > 1

Representation canonique

Considérons un modéle I AR centré, cíest a dire avec q 0 6 0

on peut écrire :

^{# (L)X}t ^{6 6} t

DeÖnition

# (L)

1 ^A

Xt 6 # ^t (L)6 t 6

^{; < D # (L)}

6 t.

Si toutes les racines du déterminant de # (L) sont du module supérieur a 1, alors líéquation

# (L)Xt 6 6 t défnit un unique modéle I AR(p) stationnaire. On dit que Xt est en représen- tation canonique et 6 t est appelé résidu du processus.

Remarque 1

Si les racines de Q R t # (L) sont de module inférieur a 1, on peut changer les racines en leurs inverses et modifer le bruit blanc associé afn de se ramener a la représentation canonique. Remarque 2

Si au moins une des racines de Q R t # (L) est égale a 1, le processus níest plus stationnaire et

on ne peut pas se ramener a une représentation canonique.

Remarque 3

En représentation canonique, la prévision síécrit :

E[ Xt+ 1 5

t ] 6

p

^z

i l 1

^# i ^Xt+ 1ti

oü Xt désigne le passé de X jusquía la date t incluse.

6.2.10 Estimation des paramètres díun I AR (p)

Les paramétres díun modéle I AR ne peuvent être estimés que sur les séries temporelles

stationnaires (sans saisonnalité et sans tendance) par la méthode M O O . Pour les modéle

I AR non contraints-ou plus généralement par la technique du maximum de vraisemblance.

Estimation par la methode des moindres carres ordinaires des modèle 2 & /

non contraints

Considérons le modéle I AR (p) :

^{# (L)X}t ^{6 6} t

^{Oü 6} t ^{& BB(0 , " ).}

Déterminons tout díabord le nombre de paramétres a estimer.

n (n ) 1)

paramétres a estimer dans "

²

n ² p paramétres a estimer dans # .

Au totale, on a donc n ² p ) ^{n (n ) 1)} paramétres a estimer pour un I AR (p)

²

Décomposons líécriture du I AR (p). La j ^{i e E e} équation síécrit :

^I

⁰ X0 X1 p ¹

⁰

I I

j

6 ^I I

Xj 1 ¹

^I

^I

X

.

Xj 2 ^{I 1}

.

^I

6

^I

I I

^t

^X2 tp

I I I

^I

^I W j ) 6 j ; avec j 6 1, 2, .., p

.

^I

^I

. ^I

^I

^I

^{6 . 7}

^{I X}tt1 ^Xttp ^I

.

^I

^I

Soit encore

^Xj T

⁶

^XT t1

⁷

^XT tp

^X j ⁶

Oü

^W j ^{) 6} j

⁰

I

^I

.

6 j 6 ^I

^I

^I

⁶

⁶ j 1 ¹

.

.

⁶ j 2 ^I I I I I

⁷

⁶ j T

^{La variable X} j ^{contient T observations. La matrice X est de format (T , n p).}

Soit une ligne Xt de cette matrice :

^Xt ^{6 (X}1tt1^X2 tt1 ^Xntt1^X1tt2 ^Xntt2 ^X1ttp ^Xnttp ⁾

Le modéle est un modéle I AR (p) a n composantes indicées par le temps t. W j est de di- mension (n p, 1). On a

⁰

I I I

q

^I

W j 6 ^I

^I

^I

^I

^I

⁶

1

q

¹

1j

q

2

1j ^I

.

. ^I

^I

^I

n ^I

^I

1j

^I

ⁿ

q

^I

2 j

. ^I

^{. 7}

q

n p j

0

I

^I

6 j 6 ^I

^I

^I

⁶

⁶ j 1 ¹

.

.

⁶ j 2 ^I I I I I

⁷

.

⁶ j T

La matrice X ne dépend pas de j :

^X j ⁶

^W j ^{) 6} j

.

On empile les n équations pour retrouver le I AR :

⁰ X 1 ¹

I X 2 I

^{0 X}11 ¹

^{I X}12 ^I

^I . ^I

0

⁰ 0 0 ¹

I

W 1 1

W 2 I

^{0 6} 11 ¹

^{I 6} 22 ^I

^I . ^I

^I

^{I I I}

.

6

^{I I I}

.

^I

^{I I I}

.

^{I I I}

^{6 7 I}

⁶

X n ^I

. ^I

6

^I

X1T ^I

⁶

^I

X2 T ^I

^I

.

^I

⁷

^XnT

0 X 0 ^{I I}

^I

^I

^I

.

^. . ^{I I}

^I

^{7 I}

X ⁶

I

^{I I}

.

)

^{I I}

^I

^I

. ^{I I}

^I

^{. 7 I}

W n ⁶

. ^I

^I

6 1T ^I

.

^I

6 2 T ^I

^I

^I

⁷

.

⁶ nT

^{On cherche a estimer (W} 1^W 2 ^{. . . W n ) .}

La matrice de variance-covariance des erreurs devient un peu plus compliquée et síécrit :

^{0 0} a 11 0 . . . 0

I I 0 . .

^{1 0} a 12 0 . . . 0 ^{1 1}

I I . . I I

^{I 6} .

^{7 6} 0 ^{. 7 I}

^I

^I 0 a 11

⁰

^I

^I a 2 1 0 . . . 0 ^{1 0}

^{I I}

^I 0 . . I I

0 a 12 ^I

^I

^I

a 12 0 . . . 0 ^{1 I}

^I

. . I ^I

^{I 6} .

^{7 6} 0 ^{. 7 I}

^I

^I 0 a 2 1

^I

^I

^I

^I

^I

^I

^I

⁶

0 a 12

. . .

^I

^I

^I

^I

^I

^I

⁰ a nn 0 . . . 0 ^{1 I}

0

^I

^{I .} . . ^{I I}

^{6 7 7}

^{0 a} nn

Líobservation de cette matrice indique la présence díhétéroscédasticité (il y a en e§et, aucune

raison pour que a 11 6 a 22 6 6 a nn) et díautocorrélation.

Il se pose en conséquence un probléme pour líapplication de la méthode M O O . Rappelons en e§et que les estimateurs sont sans biais, mais ne sont plus de variance minimale. Il convient

dés lors díutiliser la technique des moindres carrés généralisés (M O G ) qui fournit un esti- mateur BLH E (Best Linear Unbiaised Estimator).

On peut réécrire la matrice de variance-covarince comme suit :

I [ 6 ] 6 " # I 6 2

oü " 6 (a i j ) et # désigne le produit de Kronecker. Rappelons que :

⁰

A # B 6 I

. ¹

a B ^I

^{6 i j 7}

.

Nous venons de voir que la matrice de variance-covariance des résidus est telle que

líon devait théoriquement appliquer la méthode M O G . Cependant, puisque la matrice des variables explicatives est bloc diagonale, on peut appliquer les M O O bloc par bloc. Le théo- réme de Zellner nous montre ainsi quíestimer chacune des n équations par les M O O est équivalent a estimer le modéle par la méthode M O G . Afn de le prouver, considérons le modéle suivant :

Oü 6 est un bruit blanc.

5 6 X a ) 6

Rappelons que líestimateur de la méthode M O O est donné par :

^X

^a3 . 5

6 (X X )^t1X 5

et que líestimateur de la méthode M O G síécrit :

^X

^a3 . 0

6 (X 2 ^t1X )^t1X 2

^t15

oü 2 désigne la matrice de variance-covariance de 6 .

Dans notre cas, on a :

⁰

I

^I

^{X 6} I

⁶

X 0 0 ¹

0 X 0 ^I

^I

^. . . ^I

⁷

X

6 I # X

oü I est la matrice identité.

Remarque

Avant díappliquer la méthode des M O G , rappelons que líon a les égalités suivantes concer- nant le produit de Kronecker :

(A # B)(O # D) 6 AO # BD

(A # B) 6 A # B

1

(A # B)

6 A^t1 # B^t1

Afn de calculer l¹ estimateur des M O G , commenÁons par étudier la matrice X 2 ^t1X :

X 2 ^t1X 6 (I # X )(" ^t1 # I )(I # X )

6 " ^t1 # X X

avec 2 ^t1 6 " ^t1 # I .

On en déduit :

(X 2 ^t1X )^t1 6 " ^t1 # ( X X )^t1

pour le vecteur X 2 ^t15 , il vient :

X 2 ^t15 6 (I # X )(" ^t1 # I )5

6 (" ^t1 # X )5

on a donc :

^X

^a3 . 0

6 " # (X X )^t1("

^t1 # X )5

díou

6 (I # (

X )^t1 X )5

0 1

⁰

^X

⁷

a3 . 0 6 ^I

⁶

( X X )^t1X 0 . . .

0 ^{. .} .

¹

^I

I I I

( X X )^t1 X ⁶

⁵ 1

^I

5 2 ^I

^I

.

^{. 7}

⁵ n

⁰ ( X X )^t1

.

t1

⁵ 1 ¹

I

6

^I (X X )

^I

^I

⁶

X 5 2

^I

^I

⁷

( X

^{)t1X 5} n

On retrouve líestimateur des M O O équation par équation.

Cependant, cette technique díestimation des I AR níest plus valable des lors quíil existe

des contraintes sur les paramétres. Il convient alors díutiliser la technique du maximum de vraisemblance.

Estimation par la methode du maximum de vraisemblance

Considérons un modéle I AR (p)

Xt 6 q 1Xtt1 ) .... ) q p Xttp ) 6 t

Oü 6 t est un bruit blanc de matrice de variance covariance " .

On écrit la vraisemblance conditionnellement a toute valeurs passées du processus :

L(q 1, q 2 , . . . , q p , _ 5 Xtt1) 6

T

^;

tl 1

L(XtXtt1)

oü Xtt1 désigne tout le passé de Xt jusquía la date (t 1) incluse la vraisemblance síécrit alors :

L(q 1, q 2 , . . . , q p , _ 5 Xtt1) 6

T

^;

tl 1

(7 2'

1

n ⁷

^{; < D _}

T

2

x < E C [ ^{1 z}

tl 1

(Xt q 1Xtt

^<

1 .... q p Xttp )

(Xt

^q 1^Xtt1

.... q p Xttp )]

On en déduit líexpression de la log-vraisemblance :

? B= L(X1 . . . Xt) 6

T

^T ? B= 2' ^T ? B= ; < D _ ^{1 z}

L t_ ^t1L t.

2 2 2

tl 1

On maximise ensuite cette expression afn díobtenir les estimations q 1, . . . q p et de _ .

6.2.11 Validation : tests de speciÖcation

Test du rapport de maximum de vraisemblance

On peut e§ectuer des tests sur líordre p du I AR .Considérons le test suivant :

H0 : # p + 1 6 0 : Modéle I AR (p)

H1 : # p + 1 6 0 : Modéle I AR(p ) 1)

La matrice díinformation de Fisher est dicents cile a calculer, ce qui explique que líon uti-

lise un test du rapport du maximum de vraisemblance. La technique consiste a estimer un modéle contraint I AR (p) et un modéle non contraint I AR (p ) 1) et a e§ectuer le rapport

des log-vraisemblances. Rappelons que la log-vraisemblance díun modéle I AR síécrit :

T

? B= L(X1 . . . Xt) 6 ^{n T} ? B= 2' ^T ? B= ; < D _ ^{1 z}

L t_ ^t1L t.

2 2 2

tl 1

T

^z

tl 1

L t_ ^t1L t.est un scalaire, on a donc, on notant T _ la trace :

T

^z

tl 1

T

^L t^{_ t1L} t ^{6 T _(z}

tl 1

T

^L t^{_ t1L} t^{) 6 T _(_ t1 z}

tl 1

L tL t)

T

T

6 T _(T _ ^{t1 1 z}

L tL t)

tl 1

6 T _(T _ ^t1_ ) 6 T _(T In) 6 n T

Soient l og L^c la log vraisemblance estimée du modéle contraint :

l og Lc 6 ^nT l og 2' ^T l og ; < D _X c ¹ n T

2 2 2

Soient l og L^nc la log vraisemblance estimée du modéle non contraint :

l og Lnc 6 ^nT l og 2' ^T l og ; < D _X nc ¹ n T

2 2 2

oü _^{X c} (respectivement _^{X nc} ) désigne líestimateur de la matrice de variance-covariance

des résidus du modéle contraint (respectivement non contraint).

On calcule la statistique de test & 6 T x RM I . Oü RM I désigne le rapport du maxi- mum de vraisemblance :

& 6 T l og

^, ; < D _^{X c -}

; < D _^{X nc}

Sous líhypothése nulle, cette statistique suit une loi de khi-deux a _ degrés de liberté

oü _ désigne le nombre de contraintes.

Si líon accepte líhypothése nulle, on peut e§ectuer un deuxiéme test :

HO : # p 6 0 : Modéles I AR(p 1)

H1 : # p 6 0 : Modéles I AR (p)

Ce test síe§ectue de la même faÁon que précédemment. On a ainsi une séquence de tests emboÓtés dont le but est de déterminer líordre p du modéle I AR

Remarque

Dans le cas díun modéle AR, en plus des tests sur les paramétres, on e§ectue des tests

sur les résidus afn de valider le modéle. Dans le cas des modéles I AR, ces tests ne sont pas trés puissants et líon préfére réaliser un graphe des résidus. Notons cependant quíil convient díexaminer attentivement les résidus surtout lors díutilisation des modéles I AR

pour líanalyse de réponse impulsionnelle oü líabsence de corrélation des résidus est cruciale

pour líinterprétation.

Critères díinformation

Afn de déterminer líordre p du I AR, on peut également utiliser des Critéres díinformation. Ainsi, on estime un certain nombre de modéles I AR pour un ordre p allant de 0 a h, oü

h est le retard maximum. On retient le retard p qui minimise les Critéres AI O , SI O et

Hannan-Quinn (H Q ).défnis comme :

AI O 6 l og Q R t _^X )

2n ² p

T

SI O 6 l og Q R t _^X

) n ² p

l og T

T

H Q 6 l og Q R t _^X

) n ² p

2 l og (l o g T )

T

oü n est le nombre de variables du systéme, T est le nombre díobservations et _^X

estimateur de la matrice de variance covariance des résidus.

Remarque

est un

Les Critéres SI O et H Q conduisent a des estimateurs convergents de p, le critére AI O

donnant des estimateurs ecents caces de p.

6.2.12 Prevision des modèles VAR

Considérons un modéle I AR (p)

^Xt ⁶

^qX 1^Xtt1 ^{) .... )}

^qX p ^Xttp ^{) L} t

^{On suppose que p a été choisi, que les qX} i ^{ont été estimés et que la matrice de variance-}

covariance associée a L t a été estimée.

Afn de réaliser des prévisions, il est nécessaire de vérifer que le modéle est bien

en représentation canonique. Pour cela, on calcule le déterminant du polynôme # (L) et on regarde si les racines sont bien a líextérieur du disque unité. Si tel est le cas, alors la prévision

en (T ) 1) du processus est :

^{E[ X}T + 1 ^{5 X}T ^{] 6}

^qX 1^XT ^{) .... )}

^qX p ^XT tp + 1

oü T désigne le passé de X jusquía la date T incluse.

Chapitre 7

APPLICATION DE LA MODELISATION MULTIVARIEE

Suite a líapplication de la méthodologie de Box & Jenkins sur les di§érentes séries de consommation celles-ci sont rendues stationnaires, nous pouvons donc appliquer la modéli- sation multivarié I AR.

7.1 Etude multivariee des series de consommation

(O Et, DPt, O It)

Dans la suite de notre étude nous considérons le vecteur M t 6 (O ESAt, DLDP SAt,

LO G O It)

et L t 6 (R 1t, R 2 t, R 3 t) vecteur résiduel associée a M t de matrice de variance-covariance ^z

7.1.1 IdentiÖcation du modèle VAR(P)

A líinstar de la méthodologie de Box & Jenkins líidentifcation est une étape cruciale, pour mener a bien cette démarche on a recours aux critéres díinformations AI O, SO et le maximum de vraisemblance (LI ) pour déterminer le nombre de décalages p.

A cette fn, nous avons estimé divers modéles I AR pour des ordres de retards p allant de 1 a

14. Pour chaque modéle, nous avons calculé les critéres díinformations précédemment cités.

Le tableau TAB.I I.1 reporte les résultats obtenus. On constate que deux des trois critéres nous conduisent a retenir un modéle I AR(14).

106

TAB * 2 .!

p	LI	AI O	SO
1	140 9.75	3 7.67	35 .0 2
2	13 83 .28	3 7.67	35 .29
3	13 63 .68	3 6.8 4	35 .13
4	13 43 .96	3 6.0 1	3 6.18
5	13 19.45	35 .98	3 6.50
6	13 0 1.3 4	35 .58	3 7.0 1
7	1291	35 .3 4	3 7.74
8	1267.41	35 .23	3 7.74
9	125 4.65	35 .20	38 .65
10	1227.33	35 .17	38 .98
11	1205	35 .12	3 9.0 7
12	118 2.47	35 .0 7	3 9.5 4
13	1160	3 4.8 4	40 .42
14	113 1.0 2	3 4.43	40 .5 1

Líastérisque indique líordre p a retenir.

Les comparaison des modéles suivant les critéres AI O et LI nous pousse a choisir le modéle

I AR(14)

7.1.2 Estimation du modèle VAR(14)

a-Estimation du modèle 2 & / (! # ) avec constante

Le modéle I AR(14) avec constante síécrit sous la forme suivante

M t 6 # O ) # 1M tt1 ) ....... ) # p M tt14 ) L t

oü # O 6 (aO , aO , aO ) représente líestimation de la consatante et # p (p 6 1, ..., 14) sont des

1 2 3

0 a1 2 3 1

1p ^a1p ^a1p

a

2 p

^{matrices carrées díordre 3 tel que #} p ^{6 6 1}

a

1

3 p

les coecents cients estimés.

2 3

a

a

2 p 2 p

a

a

2 3

3 p 3 p

^j (i, j 6 1, 2, 3 ) représentent

^{7 les a}i p

^X

Donc on doit estimer 9 paramétres pour ^z?

et 13 2 paramétres a estimer pour # p . On e§ectue

líestimation en utilisant le logiciel EVIEWS, nous obtenons le tableau qui sera présenté comme suit :

Le tableau contient 3 colonnes au nombre des variables du modèle I AR.

Ce tableau peut être décomposé en 3 blocs, chaque bloc est associé a une série

Chaque bloc contient p 6 14 lignes

La ligne i (i 6 1...14) díun bloc précis correspond a la série associée a líinstant t i. Chaque ligne contient les coecents cients au retard i (donnés en haut), ainsi que les t-

statistic associées (données en bas entre crochets).

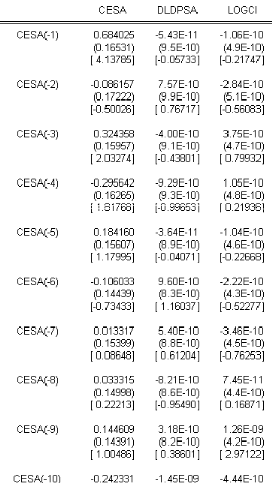
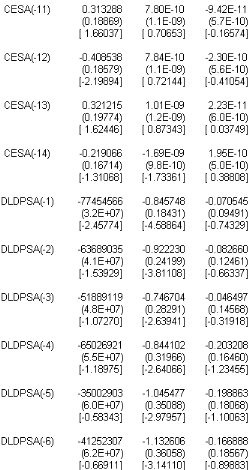
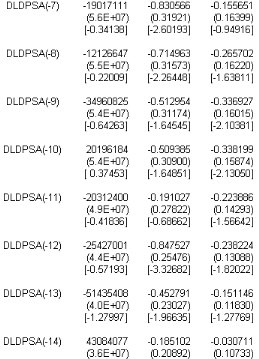
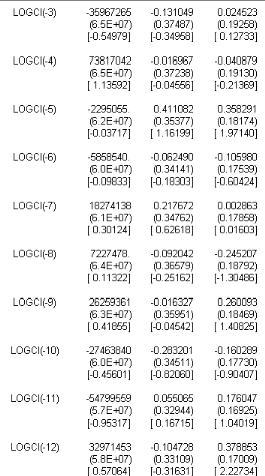
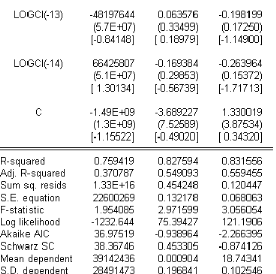
TAB.I I.2 Estimation I AR(14) avec O

A la lecture du tableau TAB.I I.2 on constate que la constante est non signifcative aux seuils

1% , 5 % et 10 % puisque les t-statistic (données par les valeurs entre crochets) sont inférieures aux di§érentes valeurs critiques. De la on réestime le modèle I AR(14) sans constante.

b-Estimation du modèle VAR(14) sans constante

Líéquation du modèle I AR(14) sans constante síécrit :

M t 6 # 1M tt1 ) ....... ) # p M tt14 ) L t

^{Donc on doit estimer 14 matrices #} p ^{, ainsi que la matrice variance-covariance z?}

associée au

résidu L t, nous obtenons le tableau suivant :

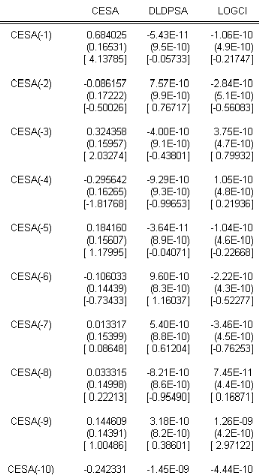
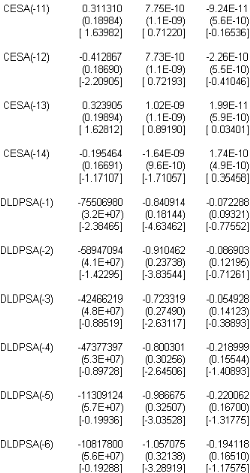
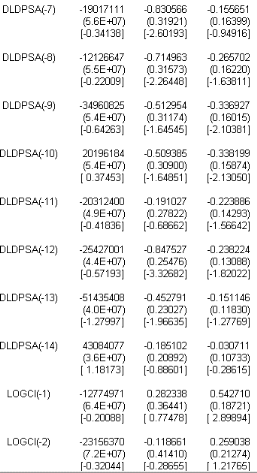
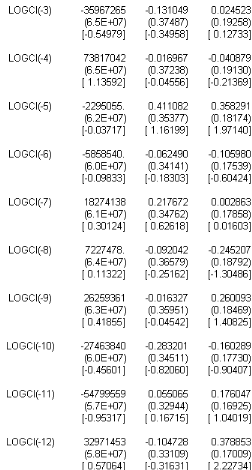
TAB.I I.3 Estimation I AR(14) sans O

A partir TAB I I.3 du tableau nous obtenons líéquation suivante :

0

M t 6 ⁶

0 .68 75 50 6980 12779471

5 .43 E 11 0 .8 4 0 .28

1.0 6E 10 0 .0 7 0 .5 4

1

^{7 M} tt1

⁰ 0 .08 58 8 9470 94 23 15 63 70

) ⁶ 7.5 7E 10 0 .91 0 .12

2.8 4E 10 0 .0 9 0 .26

⁰ 0 .3 2 424661219 35 967265

) ⁶ 4E 10 0 .72 0 .13

3 .75 E 10 0 .05 0 .0 2

⁰ 0 .3 1 65 0 26921 73 8 170 42

1

^{7 M} tt2

1

^{7 M} tt3

1

) ⁶ 9.58 E 10 0 .8 4 0 .0 2

3 .75 E 10 0 .20 0 .0 4

⁰ 0 .18 1130 9124 2295 05 5

) ⁶ 4E 10 0 .99 0 .41

3 .75 E 10 0 .22 0 .3 6

^{7 M} tt4

1

^{7 M} tt5

⁰ 0 .11 10 8 1780 0 58 58 5 40

) ⁶ 9.6E 10 1.05 70 75 0 .0 6

2.22E 10 0 .19 0 .11

⁰ 0 .0 1 190 17111 18 27413 8

) ⁶ 5 .4E 10 0 .83 0 .83

3 .46E 10 0 .15 0 .00 3

¹

^{7 M} tt6

1

^{7 M} tt7

⁰ 0 .03 12126647 7277478

) ⁶ 8 .21 10 0 .71 0 .0 9

7.45 E 11 0 .26 0 .25

1

^{7 M} tt8

⁰ 0 .14 3 49608 25 2625 93 61

) ⁶ 3 .18 E 10 0 .5 2 0 .0 2

1.26E 9 0 .3 4 0 .26

1

^{7 M} tt9

⁰ 0 .24 20 19618 4 274638 40

) ⁶ 1.45 E 9 0 .5 1 0 .28

4.4E 10 0 .3 4 0 .16

1

^{7 M} tt10

⁰ 0 .3 1 20 3 1240 0 5 479955 9

) ⁶ 7.75 E 10 0 .19 0 .05

9.24E 11 0 .22 0 .18

⁰ 0 .41 25 42700 1 5 479955 9

) ⁶ 7.73 E 10 0 .85 0 .11

2.26E 10 0 .24 0 .38

1

^{7 M} tt11

1

^{7 M} tt12

⁰ 0 .3 2 5 143 5 408 5 485 5 771

) ⁶ 1.0 2E 9 0 .45 0 .05

1.99E 11 0 .15 0 .18

1

^{7 M} tt13

⁰ 0 .2 430 8 40 77 5 93 3 65 70 6

) ⁶ 1.64E 9 0 .19 0 .19

1.74E 10 0 .03 0 .26

1

^{7 M} tt14 ^{) L} t

Bien entendu cette écriture du modèle subira un remaniement après líépreuve des tests suite

a líétape de validation.

Nous obtenons également la matrice de variance-covariances suivante :

0

z? 6 6

1

7

5 .17E ) 14	0 .0 45	0 .13 5
0 .0 45	625 78 9	0 .0 11

0 .13 5 0 .0 11 5 .11E ) 11

7.1.3 Validation

Test sur le nombre de decalages p :

Afn de valider líordre p 6 14 du modèle I AR(14), on utilise en plus des critères díinforma- tions précédents, le critère de Hannan-Quinn qui est a minimiser. Ainsi on estime un certain

nombre de modèles I AR pour p allant de 1 a 14, on obtient le tableau suivant

P	H Q
1	124.41
2	10 5 .5 9
:
:
:
:
14	28 .8 1

Le résultat du test confrme líordre du décallage (p 6 14) jugé nécessaire.

Test sur les residus :

De la même faÁon que la méthodologie de Box & Jenkins, il convient de vérifer si les rési- dus forment un bruit blanc, une observation des corrélogrammes des résidus des trois séries síimpose.

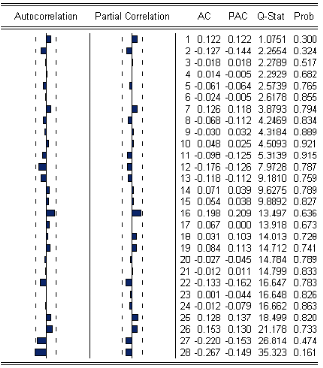
^{FIG.I I.4 Corrélogramme des résidus de la série O ESA}t

Líanalyse du corrélogramme des résidus de la série O ESAt (Fig.I I.4) montre que tous termes sont a líintérieur de líintervalle de confance, ce qui est confrmé par la Q s tat pour

0 ,05

tous les retards en particulier Q s tat 6 26.8 1 (au retard K 6 27) < x ²

(22) 6 33 .92,

donc les résidus se comportent comme un bruit blanc.

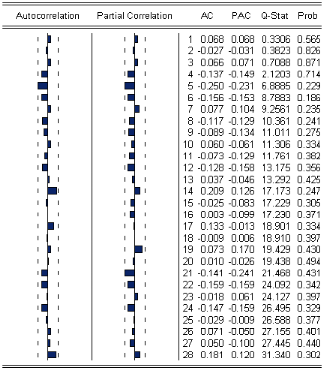
^{FIG.I I.5 Corrélogramme des résidus de la série DLDP SA}t

Líobservation du corrélogramme des résidus de la série DLDP SAt nous montre que les

résidus en question forment un bruit blanc.

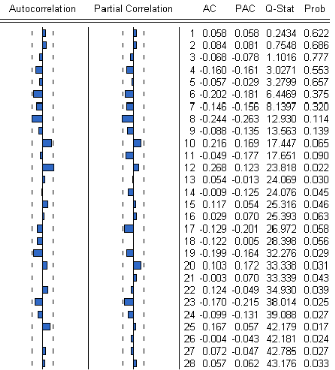
^{FIG.I I.6 Corrélogramme des résidus de la série LO G O I}t

Globalement, líanalyse des trois corrélogrammes nous montre que tous les termes sont a líintérieur de líintervalle de confance de la on déduit une absence de corrélation, donc les résidus des séries une a une forment un processus bruit blanc.

Etant donné que nous sommes dans líobligation díavoir un vecteur résiduel de type bruit blanc, líobservation des corrélogrammes simples ne sucents t pas, cíest ainsi quíon examinera les corrélogrammes croisés des résidus.

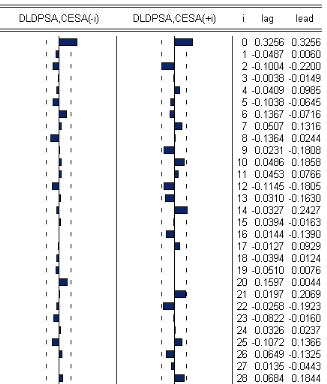
^{FIG.I I.7 Corrélogramme des résidus croisés entre DLDP SA}t ^{et O ESA}t

En observant la fgure I I.7 on remarque que tous les termes sont a líintérieur de líin- tervalle de confance ce qui traduit une absence de corrélation entre les résidus des séries

^{DLDP SA}t ^{et O ESA}t^.

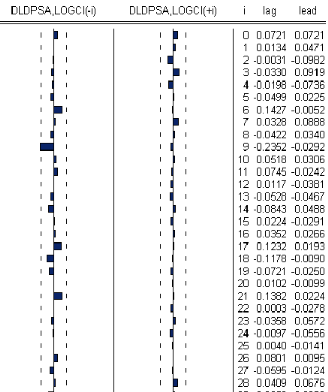
^{FIG.I I.8 Corrélogramme des résidus croisés entre DLDP SA}t ^{et LO G O I}t

De la même faÁon et pour les mêmes arguments, les résidus des séries DLDP SAt et

^{LO G O I}t ^{sont non corrélées.}

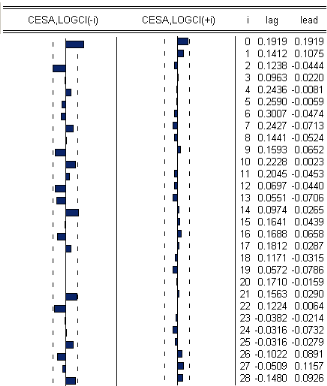
^{FIG.I .5 Corrélogramme des résidus croisés entre O ESA}t ^{et LO G O I}t

A la base de líétude des corrélogrammes simples et croisés des résidus, on déduit que les résidus associés au modèle I AR(14) forment un vecteur bruit blanc.

Tests sur les estimations :

En tenant compte du tableau des estimations (Tab I I.3 ) et le faite quíun coecents cient est signifcativement di§érent de zéro au seuil 5 % , si la t-statistic associée est supérieure a 1.96,

et en vertu des résultats des tests précédents, le modèle I AR(14) est validé et il síécrit de

la faÁon suivante :

11

² O ESAt 6 7750 6980 DLDP SAtt1 5 .43 e ^t

I

O ESAtt1

^I 4e ^t10

I

^{O ESA}tt3

) 7.73 e

t10

^{O ESA}tt12

^{) e} 1t

^{I DLDP SA}t ^{6 0 .8 4DLDP SA}tt1 ^{0 .91DLDP SA}tt2 ^{0 .73 DLDP SA}tt3

^{)I 0 .8 DLDP SA}tt4 ^{0 .98 DLDP SA}tt5 ^{1.05 DLDP SA}tt6

0 .83 DLDP SAtt7 0 .71DLDP SAtt8

^I

^I 0 .85 DLDP SAtt12 0 .45 DLDP SAtt13 ) e 2 t

I

^I LO G O It

^I

6 0 .3 4DLDP SA

tt9

0 .3 4DLDP SA

tt10

) 1.26e ^t9 O ESA

tt9

^{3 ) 0 .5 4LO G O I}tt1 ^{) 0 .3 6LO G O I}tt5 ^{) 0 .38 LO G O I}tt12 ^{) e} 3 t

Remarque

On constate que la série DLDP SAt síécrit uniquement en fonction de ses valeurs passées, ceci nous pousse a penser que líapproche multivarié níapportra en rien en terme de prévisions par rapport a líapproche univarié concernant la consommation publique.

7.1.4 Prevision

Le modèle étant validé, líexpression de la prévision pour un horizon h 6 1 a partir de líinstant présent t est donnée par :

² O^DESA(1) 6 7750 698 0 DLDP SAt 5 .43 e ^t11O ESAt

^I

^I 4e ^t10

^I

^D

I

^{O ESA}tt2 ^{) 7.73 e}

t10

^{O ESA}tt11

^{I DLDP SA(1) 6 0 .8 4DLDP SA}t ^{0 .91DLDP SA}tt1 ^{0 .73 DLDP SA}tt2

^{0 .8 DLDP SA}tt

3 ^{0 .98 DLDP SA}

tt4

1.05 DLDP SA

tt5

I ^{0 .83 DLDP SAtt6 0 .71DLDP SAtt7}

^I

^{I 0 .85 DLDP SA}tt11 ^{0 .45 DLDP SA}tt12

I 9

^{I LDO G O I (1) 6 0 .3 4DLDP SA}tt8 ^{0 .3 4DLDP SA}tt9 ^{) 1.26e t O ESA}tt8

^{) 0 .5 4LO G O I}t ^{) 0 .3 6LO G O I}tt

4 ^{) 0 .38 LO G O I}

tt11

Pour un horizon h 6 12, on obtient :

² D D

t11 D

O ESA(12) 6 7750 6980 DLDP SA(11) 5 .43 e

^I

O ESA(11)

^I 4e ^t

^I

¹⁰ O^DESA(9) ) 7.73 e

t10

^{O ESA}tt1

^I

^I DL^DDP SA(12) 6 0 .8 4DL^DDP SA(11) 0 .91DL^DDP SA(10 ) 0 .73 DL^DDP SA(9)

^)I 0 .8 DL^DDP SA(8 ) 0 .98 DL^DDP SA(7) 1.05 DL^DDP SA(6)

I ^{0 .83 DLDDP SA(5 ) 0 .71DLDDP SA(4)}

^I

^{I 0 .85 DLDP SA}t ^{0 .45 DLDP SA}tt1

^I

^I L^DO G O I (12) 6 0 .3 4DL^DDP SA(3 ) 0 .3 4DL^DDP SA(2) ) 1.26e ^t9 O^DESA(3 )

^3I ) 0 .5 4L^DO G O I (11) ) 0 .3 6L^DO G O I (7) ) 0 .38 LO G O It

Pour h > 12 on obtient le système díéquations suivant :

² D D

t11 D

O ESA(h) 6 7750 6980 DLDP SA(h 1) 5 .43 e

^I

O ESA(h 1)

^I 4e ^t

^I

¹⁰ O^DESA(h 3 ) ) 7.73 e

t10

^{O ESA}t+ ht11

^I

^I DL^DDP SA(h) 6 0 .8 4DL^DDP SA(h 1) 0 .91DL^DDP SA(h 2)

^I)^I 0 .73 DL^DDP SA(h 3 ) 0 .8 DL^DDP SA(h 4) 0 .98 DL^DDP SA(h 5 )

1.05 DL^DDP SA(h 6) 0 .83 DL^DDP SA(h 7) 0 .71DL^DDP SA(h 8 )

^I

^{I 0 .85 DLDP SA}t+ ht12 ^{0 .45 DLDP SA}t+ ht13

^I

^I L^DO G O I (12) 6 0 .3 4DL^DDP SA(h 9) 0 .3 4DL^DDP SA(h 8 )

^I

I t9 D D D

) 1.26e

^I

O ESA(h 9) ) 0 .5 4LO G O I (h 1) ) 0 .3 6LO G O I (h 5 )

^{3 ) 0 .38 LO G O I}t+ ht12

Les graphes des prévisions des trois séries de consommation ainsi que les tableaux asso-

ciés sont données ci-dessous :

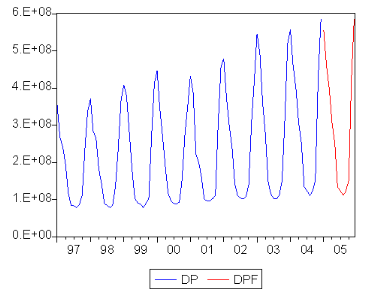
^{FIG.I I.9 Graphe des prévisions de la série DP}t

Les prévisions de la consommation publique pour un horizon díune année sont comme

suit :

Mois	Previsions (m ^3)
Jan	55 622773 25 .05 6
Fev	460 2773 25 .113
Mar	3 983 77783 .88 6
Avr	30 5 95 2699.0 2
Mai	25 0 946120 .7
Jui	13 3 77920 9.425
Juil	123 297767.964
Aou	1114200 3 6.05 8
Sep	12298 95 95 .977
Oct	15 143 48 0 4.0 74
Nov	42765 28 5 1.78 3
Dec	58 670 4969.141

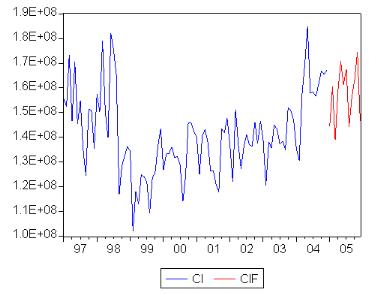
^{FIG.I I.10 Graphe des prévisions de la série O I}t

Les prévisions de la consommation industrielle sont contenues dans le tableau suivant :

Mois	Previsions (m ^3)
Jan	1445 18 77.75 3
Fev	1605 538 5 6.698
Mar	13 8 93 40 61.38 3
Avr	15 93 0 1628 .8 7
Mai	170 608 15 6.0 65
Jui	16128 60 41.20 3
Juil	16773 40 08 .5 15
Aou	14423 1470 .35 2
Sep	15 63 0 190 7.5 92
Oct	163 298 43 9.196
Nov	1745 793 63 .261
Dec	1463 95 145 .53 1

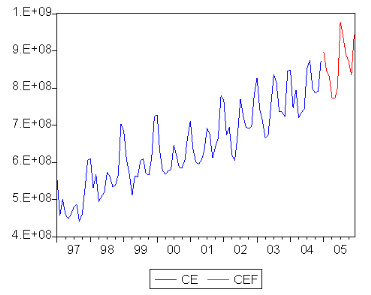
^{FIG.I I.11 Graphe des prévisions de la série O E}t

Les prévisions de la consommation des centrales électriques a partir de janvier 20 05

jusquíau mois de Décembre de la même année sont résumées dans le tableau suivant :

Mois	Previsions (m ^3)
Jan	8 98 12260 4
Fev	8 474198 20
Mar	83 2480 100
Avr	7743 90 419
Mai	77228 7470
Jui	80 0 95 473 4
Juil	97772190
Aou	93 8 7355 88
Sep	8 90 74173 1
Oct	8 7163 15 79
Nov	83 43 440 8 2
Dec	945 147935

7.2 Conclusion

Líétude multivariée achevée, nous pouvons tirer les enseignements suivants :

1 Le modèle I AR(14) a été retenu pour modéliser le vecteur composé des trois séries de consommation.

2 On constate que líordre du décallage retenu (p 6 14) pour la modélisation I AR(14) est

assez élevé ceci nous amène a estimer 13 2 paramètres.

3 Le modèle I AR(14) validé, il a été exploité pour e§ectuer des prévisions, en examinant

les équations liées aux prévisions et plus précisément celle de la série relative a la consom- mation publique, nous constatons que celle ci síécrit uniquement en fonction de ses valeurs passées.

4 Toujours concernant les prévisions, et ce qui concerne la consommation des centrales élec- triques, nous remarquons que durant le premier semestre de líannée 20 05 une consommation assez élevée est prévue, ce qui est visible sur le graphe des prévisions associé (Fig I I.11).

A cette étape bien précise nous sommes en possession de deux groupes de résultats associés

a deux approches di§érentes pour un objectif commun a savoir e§ectuer des prévisions. Pour choisir les meilleurs résultats une comparaison sera entreprise par la suite pour ne pas perdre

de vue le but de notre étude.

Comparaison

La comparaison des résultats prévisionnels obtenues par les deux méthodes a savoir la métho- dologie de Box & Jenkins et la modélisation I AR est basée sur la somme des carrées résidus

(RM SE) entre les observations prévues et les réalisations des séries de consommation.

Les prévisions díune méthode sont jugées plus fables son RM SE est la plus faible par rap- port a celle de líautre méthode.

h

Le calcul du RM SE est donné par la formule suivante :

RM SE(e ) 6

^D 1

^z (Xt

XX t)

Remarque

ⁿ tl 1

Faute de données réelles pour le premier semestre de líannée 20 05 , le RM SE a été calculé

a partir des valeurs prévues pour líannée 20 0 4 obtenues a partir du modèle réestimé pour la circonstance.

Le tableau suivant donne le RM SE calculée a partir de la modélisation I AR pour la consom-

mation industrielle :

Annee 2004	Valeurs reelles O Et	^Valeurs prevues ^O@Et	Erreurs de prevision L t
Jan	848460874	846634885	1825989
Fev	746719220	799828686	-53109466
Mar	795301680	722915250	72386430
Avr	719928389	689394162	30534227
Mai	735060340	729374760	5685580
Jui	743660994	823665332	-80004338
Juil	853005290	892070433	-39065143
Aou	874196128	877568835	-3372707
Sep	797446831	800584608	-3137777
Oct	786482709	766451183	20031526
Nov	791780442	727083265	64697177
Dec	873030005	727083265	145946740
RMSE	/	/	51028390

Pour ce qui est de la méthodologie de Box & Jenkins, nous obtenons les résultats suivants :

Annee 2004	Valeurs reelles Xt	^Valeurs prevues XXt	Erreurs de prevision L t
Jan	848460874	803232848	45228026
Fev	746719220	730444495	16274725
Mar	795301680	735636675	59665005
Avr	719928389	670431474	49496915
Mai	735060340	682643337	52417003
Jui	743660994	702716222	40944772
Juil	853005290	796989085	56016205
Aou	874196128	794207214	79988914
Sep	797446831	742553190	54893641
Oct	786482709	732049804	52632905
Nov	791780442	754378439	37402003
Dec	873030005	833417694	39612311
RMSE	/	/	144359199.3

Ainsi, la comparaison entre les deux méthodes utilisées síe§ectuera a partir du tableau sui-

vant :

Series/approches	RMSE1	RMSE2
RMSE (DP)	36677021	38664551
RMSE (CE)	144359199.3	51028390
RMSE (CI)	19705471	11444266

Remarque : RM 8E1 et RM 8E2 sont associées a la méthodologie de Box & Jenkins et la

modèlisation I AR respectivement.

Pour la consommation publique RM 8E1 > RM 8E2.

Pour la consommation industrielle RM 8E1 < RM 8E2.

Pour la consommation des centrales électriques RM 8E1 < RM 8E2.

Nous concluons que les prévisions obtenues par la modélisation I AR sont plus fables que celles obtenues par la méthodologie de Box & Jenkins pour la consommation industrielle et celle des centrales électriques, par contre pour la consommation publique la méthodologie de Box & Jenkins donne de meilleurs résultats.

Chapitre 8

Conclusion generale

Ces dernières décennies, une place importante a été consacrée au gaz en raison de ses caractéristiques économiques et écologiques.

En e§et, le gaz naturel représente une des sources díénergie la plus utilisée dans le monde, voir la plus prometteuse puisquíelle bénéfcie avec la montée des préoccupations environne- mentales díune considération importante. LíAlgérie est un pays producteur et exportateur de cette énergie, il a été donc primordial pour la SONELGAZ díanalyser líévolution temporelle

de la consommation nationale du gaz naturel dans ces di§érents aspects afn de comprendre

le mécanisme qui gère cette consommation et de tirer par la suite des informations et des conclusions utiles a la phase de prise des décisions liées aux di§érents projets et plus préci- sément le projet nommé programme national du gaz (PNG).

Notre étude a porter donc sur líanalyse des séries chronologiques représentant líévolution

de la consommation mensuelle du gaz naturel pour les distributeurs publics, les centrales électriques et de líindustrie. Líanalyse permet de construire un modèle mathématique qui explique le phénomène de líévolution de la consommation.

A travers cette étude, nous avons proposé dans un premier temps díétudier individuellement

les séries représentant la consommation publique, la consommation industrielle et celle des producteurs díélectricité.

Chaque série a été étudiée séparément, négligeant líe§et des autres séries suivant la métho- dologie de Box & Jenkins qui permet en plusieurs étapes de trouver un modèle susceptible

de représenter la série chronologique.

Líétude de la série représentant la consommation publique a révélé la présence díune sai-

133

sonnalité due aux rythmes des saisons, après désaisonnalisation et di§érentiation, la série obtenue était stationnaire, líanalyse du corrélogramme de la série a permis díidentifer plu- sieurs modèles candidats quíon a estimé et parmi lesquels nous avons choisi le meilleur, le modèle spécifé est de type 8ARM A(p, Q , q ) x (P, D, Q ).

Après estimation des paramètres, les tests relatifs a líétape de validation nous ont permis

de vérifer líadéquation de ce modèle aux données dont nous disposons. Une fois le modèle choisi, estimé et validé, nous avons calculé les prévisions pour un horizon de 12 mois.

De la même manière nous avons étudié la série représentant la consommation des centrales électriques oü líobservation du graphe représentant cette série et le corrélogramme associé nous a incité a e§ectuer le test de Fisher relative a líétude de la saisonnalité puisque que celle ci était caractérisée par un mouvement saisonnier apparent, tout comme la série de consommation publique une désaisonnalisation a été entreprise pour donné lieu a une série stationnaire, le modèle qui a généré cette série est de type 8ARI M A(p, 0 , q ) x (P, D, Q ) grce auquel on a pu faire des prévisions pour un un horizon díune année.

Le même cheminement a été suivi pour líétude de la série associée a la consommation in-

dustrielle oü celle ci a subit une transformation logarithmique pour atténuer les pics et les creux qui caractérisent cette série, la série est ainsi devenu stationnaire, le modèle retenu est

de type ARM A(p, q ) qui a été exploité pour e§ectuer des prévisions pour líannée 20 05 . Cependant la méthodologie de Box & Jenkins ne prend pas en compte líinterdépendance

des séries, pour cette raison nous avons proposé par la suite une approche multivariée pour

paraÓtre aux insucents sances de líapproche univarié.

Etant donné quía líissue de la méthodologie de Box & Jennkins les séries sont rendues sta- tionnaires, líapplication de la modélisation I AR(p) a la base de ces séries est possible, en utilisant les critères díinformations díAkaike et le maximum de vraisemblance nous obtenons

un ordre de décallage p 6 14, a líinstar de la méthode précédente, le modèle I AR(14) subira

líépreuve des tests pour quíil soit par la suite validé afn díêtre exploité pour les prévisions. Néanmoins líordre du décallage p 6 14 retenu est important, ce qui níest pas pour diminuer

le nombre de paramètres a estimer qui avoisine 13 2 paramètres, nous aurons pu diminuer líordre du décallage en introduisant une composante moyenne mobile mais le logiciel EVIWS

ne traite pas les modèles I ARM A.

Nous achevons notre étude par une comparaison entre les deux méthodes a la base du cri-

tère RM 8E qui permet de conclure que líapproche multivarié nous a permis díaméliorer les prévisions pour les séries de consommation industrielle et celles des centrales électriques par rapport a la méthodologie de Box & Jenkins et díacents rmer que cette dernière donne de bons résultats pour la consommation publique.

Toutefois une étude explicative sur la consommation du gaz naturel est très importante et par conséquent, trouvera un intérêt particulier dans cette étude, on peut citer a titre díexemple

les facteurs météorologiques qui ináuent sur les consommations industrielle, publique et les producteurs díélectricité.

^{Première partie}

ANNEXE[A]

137

8.1 Methodes díestimation

8.1.1 Methodes des moindres carrees ordinaires (M O O )

E§ectuer une estimation au sens des moindres carrées, cíest choisir dans une famille de

modèles théoriques celui pour lequel la moyenne des carrés des écarts entre les données et le modèle est minimale.

La méthode des moindres carrés ordinaires (M O O ) est sans doute la plus commune parmi

les di§érentes techniques qui permettent díestimer les paramètres b i de líéquation suivante :

Y t 6 b 0 ) b 1Xt1 ) ....... ) b 1Xtp ) L t; t 6 1, ..., n (1)

Oü Y t variable quantitative a expliquer (variable exogène ou indépendante) ; Xt1,....., Xtp

sont p variables quantitatives explicatives

(variables endogènes ou indépendantes) ; b i paramètre du modèle (1), i 6 1, ..., p; L t : erreurs. Sous forme matricielle, le modèle (1) síécrit :Y 6 X b ) L ;

Avec X une matrice (n x (p ) 1)) de terme général Y t et les vecteurs L 6 (L 1, L 2 , ...., L p ) et

b 6 (b 1, b 2 , .., b p ) .

On suppose que les L t sont des termes díerreurs díune variable L indépendantes et identique- ment distribuées ;

8

E(L t) 6 0 ; I AR(LL ¹ ) 6 a ² I oü I est la matrice identité de dimension n x n

Estimation des coecents cients :

La méthode des moindres carrés consiste a choisir b de telle faÁon a minimiser la somme des

carrés des résidus :

m in

^*

88R(b ) 6

n

^z

tl 1

⁺

2

(Y t b 0 tb 1Xt1 ..... Xtp )

6 m > A

<

2

6 Y X b 6

6 m > A (LL ¹ ) 6 ^# (Y X b ) (Y X b )^$

<

Par dérivation matricielle (par rapport a b ) de la dérnière équation on obtient les Héquations normalesH : X Y X X b 6 0 , dont la solution correspond bien a un minimum car la matrice hessienne 2X X est défnie positive. Alors líestimation des paramètres b i est donnée par :

^Xb 6 (X X )^t1X Y .

Theorème :

Si le modèle est identiÖe, líestimateur des , ' - existe et il est unique : ^Xb 6 (3 3 )^t13 Y.

Proprietes :

Les estimateurs des M O O b 0 , b 1, .., b p sont des estimateurs sans biais : E(^Xb ) 6 b

La somme des carrés des résidus permet díestimer la variance et líécart-type de líaléa et des estimateurs des coecents cients.

Les estimateurs des M O O des coecents cients suivent une loi normale et permettent les tests

de signifcativité de Student, ainsi que le test de Fisher díhypothèses linéaires

8.1.2 Methode de maximum de vraisemblance (EM I )

Líestimation du maximum de vraisemblance sur la notion de vraisemblance díun en- semble donné díobservations relatives au modèle.

Plus spécifquement, la technique consiste a construire une fonction appelée fonction

de vraisemblance (construite a partir de la fonction de densité) et la maximiser par rap- port aux paramètres inconus, permetant de la valeur numérique la plus samblable pour ces paramètres.

Désignons parX1.....Xn les observations succesives e§ectuées sur un processus. Ces ob- servations sont indépendantes et chaqueXt a une densité de probabilité Lt(Xt, & ) connue analytiquement mais dont líun des paramètres & est inconu.

La fonction de vraisemblance, qui est défnie comme la fonction de densité conjointe des

n observations est calculée comme le produit des fonctions de densité des observations indé- viduelles (car les observations sont indépendantes) : L(X, & ) 6 Lt(Xt, & )

Dans la pratique on utilise la fonction de logvraisemblance Y(X, & ) 6 l o g (L(X, & )) plutôt que la fonction de vraisemblance (il est plus faÁile de maximiser une somme quíun produit).

^X

On appel estimateur du maximum de vraisemblance toute solution & au problème m : E Y(X, & ).

$

Ainsi un EM I peut se défnire comme une solution aux équations de vraisemblance qui correspond précisément aux conditions du premier ordre suivantes

8(& ) 6

gradient.

3 Y(X, & )

6

^{3 &}

n

^<

tl 1

3 Y(Xt, & )

3 &

6 0 avec

3 ² Y(X, & )

3 & ²

< 0 ,oü 8 E R^K est le vecteur

Proprietes

La méthode de maximum de vraisemblance présente díintéressantes propriétés díoptima- lité. Sous des hypothèses relativement larges, habituellement appelées condition de régularité

les EM V sont :

Consistants : cíest a dire quand la taille de líéchantillon augmente, LíEM V tend en pro- babilité vers la vrai valeur du paramètre. Díailleurs pour une grande dimension de líéchan- tillon, líestimateur du maximum de vraisemblance aura une distribution normale approxi- mativement centrée et tend vers la vraie valeur du paramètre.

Ecents cace : signife que les EM V auront une variance (asymptotique) plus petite que díautres estimateurs consistants.

Quand le modèle est spécifé, les estimateurs du maximum de vraisemblance peuvent perdre certaine de leur propriétés souhaitables. Cependant il a été montré que sous les hypo- thèses de régularité, les estimateurs du maximum de vraisemblance auront une probabilité limite bien défnie et seront approximativement normalement distribués.

8.1.3 Methode des moindres carres generalises (M O G )

Dans de nombreux cas, une hypothèse est violée : Líhypothèse díhomoscédasticité ou díindépendance des perturbations. Cette violation se produit, généralement, lorsquíil yía agrégation temporelle des données, ou auto corrélation des résidus. La matrice de covariance

des résidus, níest plus égale a a ² I , mais plus généralement a E(LL ) 6 a ² 2 , oü 2 étant une matrice semi défnie positive.

Líestimateur des M O G de est solution du problème :

0

m > A { 8O RG ( ) 6 (Y X )¹ 2 ^t1(Y X )}

La matrice hessienne de 8O RG ( ) est défnie-positive, donc les conditions du premier ordre sont nécessaire est sucents santes :

" S . R 0 p )

t1 1

1 t1 1 t1

" ^{6 0 ( ) X 1 2} 0 ^{(Y X )}

^{6 0 ( ) X 2} 0 ^X

^{6 X 1 2} 0 ^Y

et nous obtenons ainsi, líestimateur de :

1 6 (X 1 2 t1X )t1X 1 2 t1

0 0 ^Y

Theorème

Si le modèle est identifé líestimateur des M O G existe et est unique :

1 6 (X 1 2 t1X )t1X 1 2 t1

0 0 ^Y

Líestimateur des M O G est sans biais, on a :

E( 1 5 X ) 6 E((X 1 2 t1X )t1X 1 2 t1Y 5 X ) 6 (X 1 2 t1X )t1X 1 2 t1E(Y 5 X )

0 0 0 0

6 (X 1 2 t1X )t1X 1 2 t1

de plus :

0 0 ^X 0 ⁶ 0 ^,

^{E(L 1 5 X ) 6 E(Y Y 1 5 X ) 6 E(Y 5 X ) E(Y 1 5 X ) 6 X} 0 ^X 0 ^{6 0 .}

Cíest donc un estimateur sans biais, a variance minimale.

^{Deuxième partie}

ANNEXE[B] Tableaux statistiques

142