Dosimétrie des photons de haute énergie

République Algérienne Démocratique et Populaire
Ministère de l'Enseignement Supérieur et de la Recherche Scientifique

Université Abou Bekr Belkaid Tlemcen
Faculté des Sciences
Département de Physique

MÉMOIRE

Pour l'obtention du diplôme de
MASTER en Physique Médicale
Option : Radioprotection et Imagerie Médicales

THÉME

Dosimétrie des photons de haute énergie

Réalisé par

AISSANI Marwa YAHOUNI Imène

Établissement d'accueil
Centre Anticancéreux "Emir Abdelkader" d'ORAN (CAC)

Soutenu en Novembre 2011 devant le Jury:

Mr Kaouel MEGUENI Professeur (hospitalo-universitaire Tlemcen) Président

Mr Belkacem HATTALI Physicien médicale (CAC d'Oran) Encadreur

Mme M. BENSENANE Maître-assistant (hospitalo-universitaire Tlemcen) Examinateur

Mme I.MEGNOUNIF Maître-assistant (université Tlemcen) Examinateur

Mr B .TABETTI Doyen de la faculté des sciences Tlemcen Invité

Mr M.BENMOUNA Professeur (université Tlemcen) Invité

Remerciement

On tient tout d'abord à remercier vivement le bon dieu, de nous avoir donné la force pour suivre ainsi que l'audace pour dépasser toutes les difficultés, grace à son aide que nous avons réalisées ce modeste travail.

On présente nos premiers remerciements à notre promoteur Monsieur HATTALI

Belkacem, physicien médical au sein du CAC pour nous avoir permis de réaliser ce travail de recherche, pour tout le temps qu'il nous a consacré et pour avoir assuré avec intérêt la direction et le suivi de ce travail.

Nos remerciements les plus sincères sont adressés à Monsieur B. TABTI le doyen de la faculté des sciences, ainsi à Monsieur M. BENMOUNA pour ses soutiens moral inconditionnel durant ces quelque mois, ses conseils précieux et ses encouragements.

Nous tenons également à remercier très chaleureusement :

Monsieur K. MEGUENI, Professeur à la faculté de médecine de Tlemcen et médecin chef au service de l'épidémiologie à CHUT.

Madame m. Bensnane Maître-assistant hospitalo-universitaire Tlemcen . Madame I. MEGNOUNIF Maître-assistant à l'université de Tlemcen.

À avoir participé a notre nombre de jury.

On remercie encore nos enseignent de master de la faculté de médecine et la faculté des sciences.

On n'oublierait pas de remercier les employeurs du CAC d'Oran surtout Monsieur M. BOUROUINA et les dosimétriste pour leur aide et leur gentillesse.

Merci également à toutes personnes partageant ses connaissances du loin ou du proche, tous ceux qui ont publié leurs résultats de recherche pour que tout le monde puisse les exploiter et les achever et que l'on puisse rendre leurs travaux plus utiles pour le développement de l'humanité.

Je dédie ce travail

A mes très chers parents
YAHOUNI FETHI
LARBAOUI DALILA

Pour leur sacrifices et leur encouragements, etqui gráce à eux j'ais pu continuer mes études. Merci pour votre compréhension, et votre soutien permanent. Merci d'avoir toujours été là.

A mes très chers frères et soeurs

Nesrine et son mari Réda

Ma petit soeur Fedwa

Mon cher frère Walid

Merci de m'avoir encouragé et soutenu pour réalisée ce mémoire A mes amis, de tout le long cycle d'étude, pour leurs présences et leurs encouragements.

A tous ceux qui deprès ou de loin, ont contribués à la réalisation de ce travail et à ce qui me son chers.

Je dédie ce travail

À mes très chers parents
AISSANI MOSTEFA
KALACHE FAWZIA

J'y puise une ouverture d'esprit, un soutien, une confiance et un amour indéfectibles que j'espere rendre pareillement et transmettre a mon tour.

À mes très chers frères et soeurs

Mansouriya et Nacera

Ma petit soeur Zineb

Mon cher frère Mohamed

Merci de m'avoir encouragé et soutenu pour réalisée ce mémoire À ma famille, mes amis et à ceux qui m'aiment et qui attendent avec impatience ma réussite.

En espérant être toujours à la hauteur de leurs attentes et de leurs espérances.

Remerciement .i

D édicace . ii

Table des matieres ... ..iv

L iste des tableaux .. x

L iste des figures ...... xi

Glossaire ... .....xv

Introduction générale 1

Chapitre I. Interaction rayonnements matière, grandeurs et unités dosimétriques des rayonnements

I.1. Rappel sur les rayonnements ionisants 4

I.1.1. Introduction . 4

I.1.2. Définition et classification 4

I .2. Interactions des particules avec la matière ...7

I.3. Interaction des particules chargée avec la matière .......8

I.3.1. Interaction des électrons avec la matière 9

I.3.1.1. Phénomène d'excitation et d'ionisation 9

I.3.1.2. Rayonnement de freinage . 11

I.4. Interaction des particules chargées lourds avec la matière .. 11

I.5. Interaction des neutrons avec la matière . 12

I.6. Grandeurs Caractéristiques de ces interactions ..14

I.6.1. Ralentissement des particules et pouvoir d'arret .14

I.6.2. Transfert linéique d'énergie (TEL) .14

I.6.3.Parcours .16 I.7. Interactions du rayonnement électromagnétique (photons) avec la
matière................................................	....................................16
I.7.1. Effet photoélectrique	17
I.7.2. Effet Compton	19
I.7.3. Production de paires	. .20
I.7.4. Section efficace	22

I.7.4.1. Définitions et notations 22

I.7.4.2. Domaine de prépondérance de chacun des effets 22

I.7.5.Atténuation des rayonnements électromagnétiques 24

I.7.5.1. Loi d'atténuation .24

I.7.5.2.Couche de demi-atténuation(CDA) 25

I.8. La dosimétrie des rayonnements ionisants 25

I.8.1. Définition ..26

I.9. Grandeurs et unités dosimétriques.............................................26

I.9.1. Exposition	..26
I.9.2. Kerma	27
I.9.3. La dose absorbée	30
I.9.4. Débit de dose absorbée	.30
I.9.5. L'équilibre électronique	. 31

Chapitre II. Paramètres physiques et dosimétriques des unités d'irradiation

II.1. Introduction........................................................................34

II.2. Rayonnement électromagnétique X...........................................34

II.3. Origine des rayons X.............................................................34

II.4. Production de rayons X..........................................................35

II.5. Principe du tube à rayons X.....................................................35

II.6. Spectre de rayons X...............................................................37

II.7. Dosimétrie des faisceaux de photons..........................................39

II.7.1. Caractéristiques physiques d'un faisceau de photons dans le vide		39	II.7.1.1. La distribution spectrale ..
39		II.7.1.2. Les paramètres énergétiques ..
.40		II.7.1.3. La distribution spatiale ..
.41		II.7.1.4. Lois fondamentales de l'atténuation des faisceaux de photons
41		II.7.2. Caractéristiques physiques d'un faisceau traversant un matériau
41

II.8. Pénétration du faisceau de photons dans l'eau..............................42 II.9. Paramètres de traitement........................................................44			II.9.1. La taille du champ du faisceau de rayonnement
.44		II.9.2. Facteur de collimateur
.44		II.9.3. Le facteur de diffusions au pic (PSF)
...45		II.9.4. Le débit de la machine relative (output) .
46

II.10. Courbes de distribution de doses.............................................48 II.10.1. Le rendement en profondeur . 48

II.10.2. Le profile de dose . 49

II.10.3. La pénombre géométrique 49

Chapitre III. Matériels et équipements utilisés

III.2.1 La Voie de photons .54 III.2. 2 La Voie d'électrons 55 La dosimétrie 57
III.3.1. Introduction	..57
III.3.2.Chambres d'ionisation	57
III.3.2.1.Chaine de mesure chambre-électromètre	.58
III.3.2.2.Principe de fonctionnement	.59
III.3.2.3.Propriétés des chambres d'ionisation	60
III.3.2.4.Les différents types de chambres	.60

III.1. Introduction.......................................................................52 III.2. Description générale sur Les Accélérateurs Linéaires «««««..................52

III.3.

III.3.2.4.1.Chambres cylindriques ..61

III.4. Le milieu de référence (Le fantôme) 63

III.5. L'électrom~tre....................................................................65
III.6. Thermomètre et baromètre....................................................66

Chapitre IV. Résultats et discussion

IV1. Introduction........................................................................68 IV.2. Les données de photon à scanné..............................................68

IV. 2.1.Méthode et dispositifs utilisés . .68

IV. 2.1.1. Medical Physics Control Center MEPHYSTO mc² .. 69

IV. 2.1.2. Le positionnement des chambres d'ionisation 70

IV. 2.2. Résultats .70

IV. 2.2.1 Les courbes rendements en profondeur (PDD) pour les champs ouverts ^àl'axe central . 71

IV. 2.2.1.1. Discutions et Interprétation 74

IV. 2.2.2. Mesure des profils latéraux de doses 74

IV. 2.2.2.1. Profil de dose pour un champ ouvert 75

IV. 2.2.2.1.1 Discutions et interprétation 81

IV. 2.2.2.2. Profil de dose diagonale 82

IV. 2.2.2.3. Profil de dose pour un champ MLC 83

IV. 2.2.2.3.1. Discutions et interprétation 84

IV. 2.2.2.4. Profil de dose pour un champ avec filtre en coin 84

IV. 2.2.2.4.1. Discutions et interprétation 95

IV.3. Les données photon non -scan 96

IV.3.1. Mesure des facteurs de diffusion totale et d'output du collimateur 96

IV.3.2 : facteurs de transmission de block et porte cache 99

IV.4. comparaison entre les données mesurer et calculer 101

IV.4.1. Pour les rendements en profondeur 101

IV.4.1.1. Discutions et interprétation .103

IV.4.2. Pour les profils de dose avec filtre en coins 103

IV.4.3. Pour les profils de dose avec champ ouvert 114

IV.4.4. Pour les profils de dose diagonale 120

IV.4.5. Interprétation des résultats 122

Conclusiongénérale ............................................................... 124

Bibliographies & Références......................................................126

Liste des Tableaux

Tableau 1.1 classification des neutrons............................................13

Tableau 4.1Valeur de COF, TSCF et PSCF pour les faisceaux de photons de 6

et18 MeV.................................................................................97

Tableau 4.2Valeur obtenue pour les deux faisceaux RX avec et sans port

cache......................................................................................99

Tableau 4.3Valeur obtenue pour les deux faisceaux RX avec et sans

BLOC....................................................................................100

Tableau 4.4 Valeur obtenue pour la transmission par bloc....................100

Figure 1.1 Classification des rayonnements 5

Figure1.2 Phénomène d'ionisation 10

Figure1.3 Phénomène d'excitation 10

Figure1.4 Phénomène de freinage 11

Figure1.5 Variation du TLE des électrons dans les tissus en fonction de l'énergie 15

Figure1.6 Effet photoélectrique 19

Figure1.7 Effet Compton .........20

Figure1.8 Effet de production des paires .........21

Figure1.9 Phénomène d'annihilation de la matière 21

Figure 1.10 Probabilités de réalisation des effets photoélectrique, Compton et de production
de paires dans les tissus biologiques en fonction de l'énergie .23
Figure1.12 Représentation schématique du transfert d'énergie d'un photon au milieu

travers 28

Figure1.13 L'équilibre électronique 32

Figure 2.1 Principe du tube à rayons X 36

Figure 2.2 Exemple d'un spectre de rayons X, représenté en fonction de la longueur
d'onde 38

Figure 2.3 Exemple d'un spectre de rayons X, pour une haute tension de 100 KV,

représenté en fonction de l'énergie .38

Figure 2.4 Caractéristiques physiques d'un faisceau de photons dans le vide ..39

Figure 2.5 Caractéristiques physiques d'un faisceau traversant un matériau 42

Figure 2.6 Schématisation d'une courbe de rendement en profondeur 43

Figure 2.7 Mesure du PSF. La mesure dans l'air s'effectue avec un capuchon de build-up .46

Figure 2.8 Mesure du (HSF) et du (RDF) 48

Figure 2.9 Profile de dose 49
Figure 2.10. Profil latéral de dose et leur régions (la partie centrale >80%, la partie de

pénombre entre 20% et 80%, la partie de transmission >20%)		.50
Figure 3.1 Schéma d'un accélérateur SIEMENS		..52
Figure 3.2 Le schéma des différents composants d'un accélérateur linéaire		54
Figure 3.3 Chaine de mesure chambre-électrometre		58
Figure 3.4 Principe de fonctionnement d'une chambre d'ionisation		59
Figure 3.5 Schéma d'une chambre de type Farmer		61
Figure 3.6 Chambre d'ionisation de type Farmer		62
Figure 3.7 Chambres d'ionisations de type Semiflex		.63
Figure 3.8 Fantôme d'eau MP3-P		64
Figure 3.9 Mini-fantômes ESTRO		65
Figure 3.11 Electromètre PTW UNIDOS		.66
Figure 3.12 Thermomètre baromètre		66
Figure 4.1. Système d'acquisition des données le software MEPHYSTO mc^2	..	69
Figure 4.2. Moyenne de positionnement de la chambre d'ionisation		....70
Figure 4.3. Rendement en profondeur pour les faisceaux RX de 6MV		71
Figure 4.4 Rendement en profondeur pour les faisceaux RX de 18MV		72
Figure 4.5 Rendement en profondeur pour différent fitre en coin (W15, W30, pour les faiseaux RX de 6MV	W45,	W60) ..73
Figure 4.6 Rendement en profondeur pour différent filtre en coin (W15, W30, pour les faiseaux RX de 18MV	W45,	W60) 73
Figure 4.7. Profils de dose pour champ ouvert de 5×5 avec une énergie de 6MeV		...75

Figure 4.8. Profils de dose pour champ ouvert de 10×10 avec une énergie de 6MeV 75

Figure 4.9. Profils de dose pour champ ouvert de 15×15 avec une énergie de 6MeV ..76

Figure 4.10. Profils de dose pour champ ouvert de 20×20avec une énergie de 6MeV ..76

Figure 4.11. Profils de dose pour champ ouvert de 25×25 avec une énergie de 6MeV 77

Figure 4.12. Profils de dose pour champ ouvert de 30×30 avec une énergie de 6MeV........77

Figure 4.13. Profils de dose pour champ ouvert de 5×5 avec une énergie de 18MeV 78

Figure 4.14. Profils de dose pour champ ouvert de 10×10 avec une énergie de 18MeV 78

Figure 4.15. Profils de dose pour champ ouvert de 15×15 avec une énergie de 18MeV. 79

Figure 4.16. Profils de dose pour champ ouvert de 20×20 avec une énergie de 18MeV 79

Figure 4.17. Profils de dose pour champ ouvert de 25×25 avec une énergie de 18MeV 80

Figure 4.18. Profils de dose pour champ ouvert de 30×30 avec une énergie de 18MeV 80

Figure 4.19. Profils de dose diagonale pour une énergie de 6MeV 82

Figure 4.20. Profils de dose diagonale pour une énergie de 18MeV ..82

Figure 4.21. Profils de dose pour un champ MLC avec une énergie de 6MeV ..83

Figure 4.22. Profils de dose pour un champ MLC avec une énergie de 18MeV 83

Figure 4.23. Profils avec filtre en coin de 15° pour un champ de 10×10 et une énergie de 6MeV 84

Figure 4.24. Profils avec filtre en coin de 15° pour un champ de 20×20 et une énergie de 6Mev...85 Figure 4.25. Profils avec filtre en coin de 15° pour un champ de 25×25 et une énergie de 6MeV 85 Figure 4.26. Profils avec filtre en coin de 15° pour un champ de 10×10 et une énergie de 18MeV 86 Figure 4.27. Profils avec filtre en coin de 15° pour un champ de 20×20 et une énergie de 18MeV 86 Figure 4.28. Profils avec filtre en coin de 15° pour un champ de 25×25 et une énergie de 18MeV 87 Figure 4.29 Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de 6MeV 87 Figure 4.30. Profils avec filtre en coin de 30° pour un champ de 20×20 et une énergie de 6MeV 88 Figure 4.31. Profils avec filtre en coin de 30° pour un champ de 25×25 et une énergie de 6MeV 88 Figure 4.32. Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de 18MeV 89 Figure 4.33. Profils avec filtre en coin de 30° pour un champ de 20×20 et une énergie de 18MeV .89 Figure 4.34. Profils avec filtre en coin de 30° pour un champ de 25×25 et une énergie de 18MeV .90 Figure 4.35. Profils avec filtre en coin de 45° pour un champ de 10×10 et une énergie de 6MeV 90 Figure 4.36. Profils avec filtre en coin de 45° pour un champ de 20×20 et une énergie de 6MeV 91 Figure 4.37. Profils avec filtre en coin de 45° pour un champ de 25×25 et une énergie de 6MeV 91 Figure 4.38. Profils avec filtre en coin de 45° pour un champ de 10×10 et une énergie de 18MeV .92 Figure 4.39. Profils avec filtre en coin de 45° pour un champ de 20×20 et une énergie de 18MeV .92

Figure 4.40. Profils avec filtre en coin de 45° pour un champ de 25×25 et une énergie de 18MeV 93 Figure 4.41. Profils avec filtre en coin de 60° pour un champ de 10×10 et une énergie de 6MeV 93 Figure 4.42. Profils avec filtre en coin de 60° pour un champ de 20×20 et une énergie de 6MeV 94 Figure 4.43. Profils avec filtre en coin de 60° pour un champ de 10×10 et une énergie de 18MeV ....94 Figure 4.44. Profils avec filtre en coin de 60° pour un champ de 20×20 et une énergie de 18MeV ....95 Figure 4.45.Variation du CF, du TSCF et du PSCF en fonction de la taille du champ pour le faisceau X6 98 Figure 4.46. Variation du CF, du TSCF et du PSCF en fonction de la taille du champ pour le faisceau X18 .98 Figure 4.47. Dispositif expérimental pour la mesure du facteur de transmission du porte cache .99 Figure 4.48. Comparaison entre les rendements en profondeur pour les faisceaux RX de 6MV mesurer et calculer .101 Figure 4.49. Comparaison entre les rendements en profondeur pour différent filtre en coin (W15, W30, W45, W60) pour les faiseaux RX de 6MV Mesurer et calculer 101 Figure 4.50. Comparaison entre les rendements en profondeur pour différent filtre en coin (W15, W30, W45, W60) pour les faiseaux RX de 18MV Mesurer et calculer .102 Figure 4.51. Comparaison entre les rendements en profondeur pour les faisceaux RX de 18MV mesurer et calculer ..102 Figure 4.52. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de 10×10 et une énergie de 6MeV 103 Figure 4.53. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de 20×20 et une énergie de 6MeV 104 Figure 4.54. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de 25×25 et une énergie de 6MeV 104 Figure 4.55. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de 6MeV 105 Figure 4.56. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de 20×20 et une énergie de 6MeV .105 Figure 4.57. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de 25×25 et une énergie de 6MeV 106 Figure 4.58. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de 10×10 et une énergie de 6MeV 106 Figure 4.59. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de 20×20 et une énergie de 6MeV .107 Figure 4.60. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de 25×25 et une énergie de 6MeV 107 Figure 4.61. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de 10×10 et une énergie de 6MeV 108 Figure 4.62. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de 20×20 et une énergie de 6MeV ....108 Figure 4.63. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de 10×10 et une énergie de 18MeV .109

Figure 4.64. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de 20×20 et une énergie de 18MeV ..109 Figure 4.65. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de 25×25 et une énergie de 18MeV 110 Figure 4.66. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de 18MeV ...110 Figure 4.67. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de 20×20 et une énergie de 18MeV 111 Figure 4.68. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de 25×25 et une énergie de 18MeV 111 Figure 4.69. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de 10×10 et une énergie de 18MeV 112 Figure 4.70. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de 20×20 et une énergie de 18MeV .112 Figure 4.71. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de 25×25et une énergie de 18MeV 113 Figure 4.72. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de 10×10et une énergie de 18MeV 113 Figure 4.73. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de 20×20et une énergie de 18MeV 114 Figure 4.74. Comparaison entre les Profils pour un champ ouvert de 5×5et une énergie de 6MeV 114 Figure 4.75. Comparaison entre les Profils pour un champ ouvert de 10×10 et une énergie de 6MeV .115 Figure 4.76. Comparaison entre les Profils pour un champ ouvert de 15×15et une énergie de 6MeV 115 Figure 4.77. Comparaison entre les Profils pour un champ ouvert de 20×20et une énergie de 6MeV 116 Figure 4.78. Comparaison entre les Profils pour un champ ouvert de 25×25et une énergie de 6MeV .116 Figure 4.79. Comparaison entre les Profils pour un champ ouvert de 30×30et une énergie de 6MeV ....117 Figure 4.80. Comparaison entre les Profils pour un champ ouvert de 5×5et une énergie de 18MeV 117 Figure 4.81. Comparaison entre les Profils pour un champ ouvert de 10×10et une énergie de 18MeV 118 Figure 4.82. Comparaison entre les Profils pour un champ ouvert de 15×15et une énergie de 18MeV 118 Figure 4.83. Comparaison entre les Profils pour un champ ouvert de 20×20et une énergie de 18MeV .119

Figure 4.84. Comparaison entre les Profils pour un champ ouvert de 30×30et une énergie de 18MeV 119 Figure 4.85. Comparaison entre les Profils diagonale avec une énergie de 6MeV .120

Figure 4.86. Comparaison entre les Profils diagonale avec une énergie de 6MeV .120

Figure 4.87. Comparaison entre les Profils diagonale avec une énergie de 18MeV 121

Figure 4.88. Comparaison entre les Profils diagonale avec une énergie de 18MeV 121

3D: Trois dimensions

CAX : Central axis

CDA : Couche de demi-atténuation

CF: Collimator factor

D : La dose absorbée

Débit de dose absorbée

ERI : Energie de Rayonnement Ionisant

ESTRO: European Society for Therapeutic Radiation Oncology FOC : Facteur d'Ouverture de Collimation

Gy: Gray

HVL: Half Value Layer

ICRU: International Commission on Radiation Units and measurements J : Joule

Kerma: Kinetic Energy Released per unit Mass in the medium KeV: Kilo Electro Volt

L'IAEA: International Atomic Energy Agency (AIEA : Agence Internationale de l'Energie Atomique)

MEPHYSTO: Medical Physics Control Center

MeV: Mega Electro Volt

MLC : Multi Leaf Collimator (CML : Collimateur Multi Lames) PDD : Percentage Depth Dose

PMMA: Poly Methyl Meth Acrylat

PSF: Peak Scatter factor

PTW: Physikalisch-Technische Werkstätten

RDF : Relative dose factor (facteur de dose relative)

SAD : Source-Axis Distance

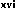
SI : Système International des unités SSD : Source-Surface Distance TBA: Therapy Beam Analyzers TEL : Transfert linéique d'énergi

TPS : Treatment Planning System (Système de planification des traitements)

TRS: Technical Reports Series TSF: Total Scatter Factor

UNIDOS : Universelle Dosimètre WF: Wedge Factor

Z : Numéro atomique d'un atome

Les photons sont des rayonnements ionisants qui créent des particules chargées (électrons et positrons) dans le milieu ; ces particules chargées à leur tour vont ioniser le milieu. Les interactions prépondérantes des photons de hautes énergies utilisés en radiothérapie avec le tissu sont : effet Compton et création de paires. Toutes ces interactions conduisent à la production d'électrons de hautes énergies.

Autrement dit, les électrons sont vite absorbés et déposent toute leur énergie dans le tissu sous forme d'ionisations ; ceci permet d'atteindre des doses importantes nécessaires pour la stérilisation des tumeurs. Les photons sont atténués exponentiellement avec la distance. L'effet biologique sur le tissu est proportionnel aux ionisations crées. Donc, même si les photons sont utilisés en radiothérapie, ce sont les électrons créés dans le tissu qui sont responsables des dommages au niveau de la cellule vivante.

Les rayonnements ionisants sont les plus utilisées en radiothérapie, pour le traitement des cancers qui consiste à tenir de manière optimale l'ensemble des irradiations qu'il va falloir appliquer au patient dans le but de détruire complètement sa tumeur.

D'autre part l'utilisation des rayonnements ionisants présente de danger pour la santé humaine, qu'on-t-il dépasse un seuil de sûreté. D'où la nécessité de la précision sur la dose délivrée à la tumeur au cours du processus d'irradiation. Ceci fait l'objet de la dosimétrie qui permet le contrôle de la qualité des traitements par ionisations. Elle mesure au mieux les rayonnements en un lieu ou sur une personne, pour fournir une estimation de l'équivalent de dose et de dose efficace. Il est, donc, important de tout mettre en oeuvre pour améliorer l'exactitude et la précision de la dose en radiothérapie afin d'assurer le succès du traitement.

Il est évident que l'exactitude sur la dose absorbée de référence doit être meilleure que l'exactitude sur la dose absorbée délivrée au volume cible. En conséquence le débit de référence du faisceau clinique est le premier paramètre à contrôler.

Une combinaison appropriée de ces fonctions va nous permettre de calculer le débit de dose en n'importe quel point dans le fantôme à partir du débit de dose de référence de l'appareil de traitement.

Le travail a été réalisé dans le cadre du présent mémoire de fin d'étude, consiste à déterminer les paramètres dosimétriques nécessaire pour le système de calcule de dose (TPS), ces mesures de qualité applicable au programme de contrôle de dose pour des faisceaux de photons de haute énergie à l'aide de chambres d'ionisation. Les mesures des ces paramètre pour le TPS on été fait depuis l'installation des accélérateurs dans le service de radiothérapie en 2008. Les procédures de contrôle qualité exigent que ces données serrant contrôler chaque année. S'il y a des changements important entre les nouvelles valeurs et les anciennes valeurs le physicien doit intervenir et rectifier les données dans le TPS.

Dans ce projet, nous avons procédé l'organisation suivante :

Le premier chapitre sera consacré aux notions fondamentales de la dosimétrie des rayonnements ionisants. Il s'attache essentiellement à la description de l'interaction des rayonnements avec la matière ainsi une description générale sur les grandeurs et les unités dosimétriques utilisés en radiothérapie.

Le second chapitre est consacré aux aspects physiques et dosimétriques des unités de traitement.

Le troisième chapitre est consacré aux matériels et méthodes expérimentales utilisés pour effectuer ce travail.

Le quatrième chapitre est réservé à la partie expérimentale et à l'interprétation des résultats obtenus.

Enfin, nous clôturons par une conclusion qui décrit panoramiquement le travail réalisé et résultats obtenu.

Chapitre I

Interaction rayonnements matière, grandeurs

et unités dosimétriques des rayonnements

I.1. Rappel sur les rayonnements ionisants : I.1.1. Introduction :

L'homme est exposé aux rayonnements depuis son apparition sur terre. Il est exposé à la lumière visible provenant du Soleil, laquelle s'accompagne de rayonnements invisibles connus sous le nom de rayonnements ultraviolets et infrarouges. Ces rayonnements sont des ondes électromagnétiques comm

les rayons X et les rayons gamma [1].

En médecine et en biologie, les rayonnements ionisants rencontrés sont principalement

Constitués soit par des particules matérielles chargées (électrons, protons, deut ions...) ou neutres (neutrons), soit par des photons (essentiellement les rayons x et ã) [2].

I.1.2. Définition et classification :

On appelle rayonnement ou radiation le processus d'émission ou de transmission d'énergie sous la forme d'ondes électromagnétiques ou de particules [3].

0 ,Rayonnement ionisant : Un rayonnement est dit ionisant quand il est susc

d'arracher des électrons à la matière.

0 ,Rayonnement non-ionisant : l'énergie est insuffisante pour ioniser l'atome [4].

Tout particules ou photons dont l'énergie est supérieure à l'énergie de liaison des électrons les moins liés des atomes constituant la matière vivante ERI=12.4 eV [1].

Un rayonnement ionisant est un transport d'énergie sous la forme de particules ou d'ondes électromagnétiques d'une longueur d'ondes inférieure ou égale à 100 nanomètres, soit d'une fréquence supérieure ou égale à 3 ×1015 hertz, pouvant produire des ions directement ou indirectement.

Ces définitions réglementaires, assez ardue de prime abord, laisse transparaitre deux termes

importants :

'une façon bien

caractéristique [3]. :

On peut classer les rayonnements selon leur façon de produire des ionisations dans la matière en utilisant leur propre pouvoir d'ionisation :

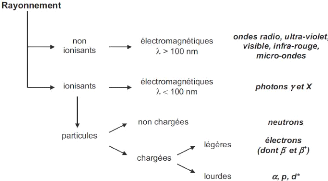
Figure 1.1. Classification des rayonnements

> Radiations directement ionisantes : comme les électrons, particules á, positrons, protons, deutons...

> Radiations indirectement ionisantes : comme les neutrons, rayons X, rayons ã.

· Les particules ou rayonnements particulaires : qui ont une masse au repos. L'énergie totale de ces particules est donnée par la relation d'Einstein :

E (1.1)

Ou est la masse et c la vitesse de la lumière (3.108 ms.-1) [1].

* 1 p p 1 eu 1 (noyaux de deutérium)

Cette énergie totale peut elle-même être décomposée de la façon suivante :

E = mc²= T + +moc² (1.2)

Ou T est l'énergie cinétique de la particule et noc² l'énergie équivalent a la masse au repos de cette même particule [3].

· les rayonnements électromagnétiques : qui sont constitues par un flux de photons et donc n'ont pas de masse.

On emploie parfois à leur égard le terme << énergie qui se déplace >>. Cette énergie est donnée par la relation :

E = hv = h (1.3)

Ou h est la constante de Planck (6,6.10-34 J.s) et ~ la fréquence du rayonnement (en s-1) égale au rapport entre c et la longueur d'onde a du rayonnement (en m) [1].

Selon la définition précédente, un rayonnement non ionisant aura une énergie insuffisante pour ioniser la matière.

D'après la figure 1.1, on s'aperçoit que ce type de rayonnement est constitue essentiellement de rayonnements électromagnétiques de longueur d'onde supérieure a 100 nm.

Par opposition, un rayonnement ionisant aura une énergie insuffisante pour ioniser la matière et une longueur d'onde inférieure à 100 nm.

Les rayons ã et X entrent dans cette catégorie. L'équivalent en énergie de la valeur de longueur d'onde 100 nm est égal a 12,4 eV.

Pour en savoir plus on peut connaitre l'énergie minimale en électron-volt susceptible de provoquer l'ionisation de la matière, il suffit d'appliquer la formule :

Longueur d'onde correspondante (100nm). Application numérique :

E = h^c = 6 6 10- ^34 x 3. , . 1 100.

-9 = 1, 9 8.10- ^18J (1.4)

Soit en électronvolt :

1_' 9 8.10- 18J

E = = 12,4 e V (1.5)

1,6. 10- 19

I .2. Interactions des particules avec la matière :

Les rayonnements rencontrés en médecine et en biologie sont constitués, soit par des particules matérielles, chargées (électrons, positons, deutons et alphas), ou neutres (neutrons), soit par des photons (rayonnement y et X). Les électrons, positons et particules alpha sont des produits de désintégration des sources radioactives.

Les accélérateurs de particules produisent également des protons, des deutons et des alphas de grande vitesse, ainsi que des électrons accélérés. Ces particules traversent la matière cèdent leur énergie cinétique par suite de collisions (excitation et ionisation) avec les atomes de la matière.

Les particules sous-atomiques impliquées dans la physique des noyaux et des particules sont trop petites pour être observées visuellement. La détection de ces particules est basée plutôt sur leurs interactions avec la matière, où, en général une partie de l'énergie d'une particule est déposée, signalant sa présence [5].

L'énergie en excès contenue dans le noyau des isotopes radioactifs, était libérée sous la forme de rayonnements ionisants, d'énergies et de natures différentes.

La nature de ces Rayonnements dépend à la fois de la quantité d'énergie en excès contenue dans le noyau Instable et de la structure de ce dernier (noyaux, lourds de fort numéro atomique Z, noyau avec un excès de protons ou un excès de neutrons).

Ces rayonnements pourvus d'énergie vont interagir avec les structures constitutives de la matière c'est-a-dire essentiellement les électrons et les noyaux des atomes. En interagissant, le rayonnement va céder tout ou une partie de cette énergie à la matière.

En contrepartie, cette dernière subit des modifications du fait de cette interaction [3].

Notre objectif est de décrire le comportement des rayonnements ionisants après leur formation suite à une désintégration ou une désexcitation d'un noyau radioactif [3] :

On peut citer trois tirées de l'importance de cette étude :

> L'interaction entre un rayonnement et la matière se traduit par un transfert d'énergie.

> Une interaction est nécessaire pour détecter un rayonnement, d'où l'importance de cette notion en imagerie diagnostique.

> De mrme, un transfert d'énergie est la première étape de l'action biologique des rayonnements.

Nous étudierons successivement le cas des particules chargées, des photons, puis des neutrons [1].

I.3. Interaction des particules chargée avec la matière :

En général, les particules chargées perdent de leur énergie principalement par les Interactions électrostatiques avec les électrons de l'atome. Lorsque l'énergie transférée aux électrons dans un atome est suffisante pour faire monter le niveau d'énergie des électrons à un niveau supérieur, ce processus est appelé excitation.

Si l'énergie transférée est encore plus grande, alors l'électron est éjecté en dehors du système ce processus est nommé ionisation.

L'électron éjecté perdra son énergie cinétique et s'attachera à un autre atome, faisant ainsi de cet atome un ion négatif.

L'atome est chargé positivement et l'ion négatif forme une paire d'ions.

Quelques uns des électrons éjectés peuvent avoir une énergie suffisante pour produire une ionisation [7].

I.3.1. Interaction des électrons avec la matière :

Les électrons sont des particules légères porteuses d'une charge électrique élémentaire, négative pour les « négatons » et positive pour les « positons » [1].

Un électron traversant un milieu matériel perd de l'énergie par :

· "Collisions", c'est-à-dire interactions coulombiennes avec les électrons des atomes du

Milieu traversé, ce qui conduit à l'ionisation ou à l'excitation de ces atomes,

Deux cas de figure peuvent se présenter : les électrons agissent soit avec les électrons des

atomes constituant le milieu, soit avec leur noyau [8].

Dans le cas d'une interaction « électron-électron », on parlera de collision. Il en existe deux types : l'ionisation et l'excitation ; dans le cas d'une interaction « électron-noyau », on parlera de sur les rayonnements de freinage.

I.3.1.1. Phénomène d'excitation et d'ionisation :

Ces interactions sont les plus probables. L'électron incident transfère une partie de son Énergie cinétique a l'électron atomique ; selon la valeur de la quantité d'énergie transférée, L'une ou l'autre de ces réactions aura lieu [3] :

Notons ÄE l'énergie cinétique de l'électron incident et WL l'énergie de liaison de l'électron de l'atome cible.

Selon que ÄE est suffisante ou non pour éjecter l'électron de son orbite, deux phénomènes peuvent se produire : [1]

Si ÄE = WL : l'e^-de la cible est éjecté de son orbite avec une énergie cinétique (ÄE-WL), et il se produit une ionisation de l'atome cible. L'électron éjecté, dit électron secondaire, peut à son tour créer d'autres ionisations si son énergie cinétique est suffisante.

Figure1.2. Phénomène d'ionisation

Si ÄE < WL : le transfert d'énergie ÄE ne peut produire aucune ionisation mais, peut porter l'électron cible à un niveau énergétique supérieur, avec excitation de l'atome cible.

Figure1.3. Phénomène d'excitation.

Si E << WL : cette excitation aboutit à une dissipation thermique (par augmentation de l'énergie de translation, de rotation ou de vibration des molécules cibles.

I.3.1.2. Rayonnement de freinage :

Plus rarement, les électrons incidents peuvent interagir avec les noyaux des atomes de la substance traversée. Ils subissent l'influence du champ coulombien du noyau : ils sont alors dévies et cèdent une partie de leur énergie au noyau.

Cela se manifeste par un ralentissement ou freinage. L'énergie perdue est émise sous la form de rayonnements X, dits de << freinage >>.

Dans la littérature, on emploie aussi le terme de << bremsstrahlung >> (<< rayonnement de freinage >>, en allemand).

Ce phénomène n'est important que dans le cas d'électrons de forte énergie (supérieure a 1 MeV) traversant une matière constituée d'atomes lourds (numéro atomique Z élevé) [3].

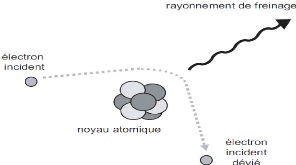
Figure1.4 : Phénomène de freinage.

I.4. Interaction des particules chargées lourds avec la matière :

Les particules lourdes chargées (protons, deutons, particulesa), ayant l'énergie de l'ordre de
quelques MeV, sont émises par des réactions nucléaires, désintégrations radioactives

spontanées ou réactions provoquées par bombardement de noyau avec des particules accélérées, ou accélérées artificiellement avec des cyclotrons (énergies de plusieurs dizaines de MeV).

Une particule lourde chargée qui traverse la matière perdre de l'énergie principalement par l'ionisation et l'excitation des atomes.

Une particule lourde chargée peut transférer seulement une petite fraction de son énergie lors d'une collision électronique simple. Sa déflection lors de la collision est négligeable.

Toutes les particules lourdes voyagent essentiellement selon une trajectoire directe dans la matière [7].

Les particules chargées lourdes (m>>me), telles que les particules á les protons ou les noyaux
d'atomes ionisés, interagissent principalement par les forces coulombiennes entre leur propre
charge positive et la charge négative des électrons orbitaux des atomes du matériau absorbeur.

L'interaction directe de ces particules avec les noyaux (diffusion de Rutherford) est possible, mais beaucoup plus rare et donc en pratique négligeable pour modéliser leur ralentissement.

La valeur très élevée du pouvoir d'arr~t à des conséquences importantes : le parcours des particules lourdes est, a l'énergie égale, beaucoup plus petit que celui des électrons et le TEL au long de la trajectoire est très élevée ce qui confère a ces particules une efficacité biologique élevée [9] [10].

I.5. Interaction des neutrons avec la matière :

Le neutron est une particule non chargée de masse voisine de celle du proton. Il est instable lorsqu'il n'est pas lié, avec une demi-vie de 12 minutes. Les neutrons sont généralement classés en fonction de leur énergie.

Cette classification est résumée dans le tableau suivant :

Neutron	Energie cinétique
thermique	inferieure a 0,4 eV
intermédiaire	comprise entre 0,4 eV et 200 keV
rapide	comprise entre 200 keV et 10 MeV
relativiste	supérieure à 10 MeV

Tableau 1.1 : classification des neutrons

Les neutrons n'interagissent qu'avec les noyaux des atomes du matériau traverse En raison de leur charge nulle, Ces interactions se divisent en deux catégories : celles qui entraînent la disparition du neutron, que l'on nomme absorptions et celles qui ne contribuent qu'à diminuer l'énergie du neutron que l'on nomme diffusions.

Les neutrons rapides perdent leur énergie cinétique au cours de chocs avec les noyaux atomiques, transférant une partie de son énergie au noyau heurte. Le transfère d'énergie est faible lorsque le noyau cible à une masse élevée et cette interaction entraine seulement la diffusion du neutron.

Lorsque la masse du noyau est égale à celle du neutron on a un choc frontal et pour arrester les neutrons on utilise des milieux riches en hydrogène (paraffine). Les neutrons thermiques, ayant leur énergie cinétique réduit à une valeur très faible, correspondant à l'énergie cinétique de l'agitation thermique, sont absorbés dans le milieu par capture nucléaire et il en résulte la production d'un isotope souvent radioactif.

Les applications principales des neutrons sont la production des radioéléments et l'analyse par activation, mais la présence de neutrons au voisinage des piles atomiques des accélérateurs soulève des problèmes de protection.

I.6. Grandeurs Caractéristiques de ces interactions :

I.6.1. Ralentissement des particules et pouvoir d'arrêt :

On appelle pouvoir d'arret ou coefficient de ralentissement d'un matériau par une particule d'énergie E la perte d'énergie S subie par la particule dans le matériau par unité de longueur

E

(1.6)

Le ralentissement des électrons est surtout dû aux interactions, mais aussi au freinage.

U

S s'exprime en MeV.cm-1.

U

On peut séparer S = Sc + Sr avec Sc pouvoir d'arret par collision et Sr pouvoir d'arret par

freinage.

On peut également utiliser le pouvoir massique d'arret [11,10].

I.6.2. Transfert linéique d'énergie (TEL) :

Les trois mécanismes décrits précédemment perm

énergie à la matière traversée.

L'expérience montre que les faibles transferts d'énergie sont très favorisés ; les électrons doivent donc subir un très grand nombre d'interactions avant d'être stoppés.

Il en résulte que le ralentissement peut être considéré comme un phénomène progressif et

continu qui peut etre caractérisé par le transfert linéique d'énergie (TEL ou TLE).

On appelle transfert linéique d'énergie (TEL) la quantité d'énergie transférée au milieu cible

Le TEL s'exprime classiquement en keV/um ou keV.cm-1.

Pour des particules de vitesse faible devant celle de la lumière, le TEL est donnée par la formule approchée :

T. L. E v ² nZ (1.7)

Avec K une constante ; z la charge de la particule incidente ; v sa vitesse ; n : le nombre d'atomes de la cible/unité de volume et Z le numéro atomique de la cible.

Dans le cas particulier des tissus vivants,

Les<< dégâts biologiques >> créés par les électrons sont d'autant plus importants que l'énergie cédée localement aux cellules est grandes :

Le TEL est donc une grandeur importante dans la détermination de << efllft BRlRIIDf >>.

La figure 1.5 décrit les variations du TEL dans les tissus en fonction de l'énergie des électrons.

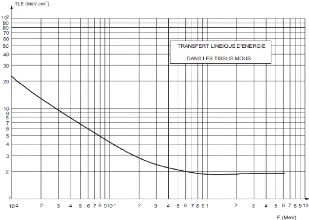
Figure1.5. Variation du TLE des électrons dans les tissus en fonction de l'énergie.

On peut déduire de la figure :

Dans le cas de basse énergie : le TLE est une fonction décroissante de l'énergie. On peut en
déduire que plus les électrons sont ralentis, plus la quantité d'énergie cédée à la matière par

interaction est grande, plus leur aptitude à léser les cellules constitutives des tissus devient grande. Les électrons sont donc plus dangereux à la fin de leur parcours ;

Dans le cas de 500 keV < E < 5 MeV, le TLE peut être considère comme sensiblement Constant est égal à environ 2 MeV.cm-1.

I.6.3.Parcours :

Le parcours est par définition le trajet effectué par une particule cédant toute son énergie cinétique. Le parcours total effectué par une particule d'énergie E est donnée par la relation :

~ ^E E E ^(1.8)

Sous la forme différentielle l'équation (1.8) s'écrit sous la forme :

E (1.9)

Ce qui conduit à :

E E (1.10)

I.7. Interactions du rayonnement électromagnétique avec la matière :

Le comportement des rayonnements électromagnétiques dans la matière est fondamentalement différent de celui des particules chargées. En une seule interaction, le Photon peut ~tre complètement absorbé et disparaître. Mais, à l'inverse, il est susceptible de traverser des quantités importantes de matière (par exemple un centimètre d'épaisseur de plomb) sans interagir du tout, ce qui est exclu pour les particules chargées qui, en pénétrant.

Un photon peut interagir avec les électrons atomiques, le noyau ou les champs électromagnétiques présents autour des électrons ou du noyau.

Le transfert de l'énergie de radiation aux électrons de la matière se fait soit par excitation en faisant passer l'électron de l'atome cible à un niveau énergétique supérieur, soit en l'éjectant hors de l'atome par ionisation.

Lors d'une interaction, le photon peut "rebondir" sans perd d'énergie (diffusion élastique), perdre une partie de son énergie (diffusion inélastique), ou perdre toute son énergie (absorption).

L'interaction entre les photons et la matière par laquelle les photons individuels sont enlevé ou défléchis du faisceau primaire de rayons X ou de rayons y peut être classifiée selon :

> Le type de cible : par exemple, les électrons, les atomes ou les noyaux avec lesquels le photon interagit.

> Le type d'événement : par exemple : diffusion, absorption, production de paires, etc. qui se produit [7].

Les interactions qui se produisent avec les électrons atomiques sont :

> L'effet photoélectrique (absorption)

> La diffusion de Rayleigh (diffusion)

> La diffusion de Compton (diffusion)

> La diffusion de Compton à deux photons (Effet multi photonique)

Les principales interactions possibles sont : l'effet photoélectrique, l'effet Compton et création de paires, d'autres effets de moindre importance : l'effet Thomson-Rayleigh et photo nucléaire [12].

I.7.1. Effet photoélectrique :

L'effet photoélectrique est le mode dominant d'interaction pour les photons de basse énergie (0.01 et 0.1 MeV) [2]

C'est un processus par lequel le photon incident, cède toute son énergie à un électron des

couches profondes (couche K ou L), qui est alors éjecté de l'atome : il y a absorption totale du photon et ionisation de l'atome [12].

L'énergie de l'électron E_ci_nest égale à l'énergie du photon incident, moins l'énergie de liaison de l'électron qui a été éjecté :

ki_n= h v --We (1.11)

Où We est l'énergie de liaison d'un électron atomique et hí l'énergie initiale du photon Incident.

Comme les énergies de liaison sont relativement faibles, l'énergie de l'électron secondaire est
Le mode de désexcitation radiatif correspondant à l'émission d'un rayonnement de

Le mode de désexcitation

nom "d'effet Auger"[2].

La probabilité d'interaction par effet photoélectrique est caractérisée par le coefficient d'atténuation massique.

Cette probabilité est grande quand l'énergie du photon incident est supérieure, mais voisine à l'énergie de liaison d'un électron sur sa couche ; la probabilité décroit très vite avec l'énergie.

On peut conclure que l'effet photoélectrique = Absorption complète du photon incident par

l'atome et éjection conséquente d'un électron de l'atome.

C'est-à-dire Quand l'énergie du photon augmente, des électrons des couches plus profondes peuvent être éjectés [4].

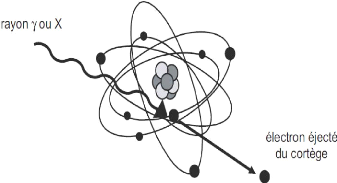
Figure1.6. effet photoélectrique

La figure 1.6 représente l'interaction d'un photon par effet photoélectrique et la désexcitation
radiative de l'atome cible avec émission d'un photon de fluorescence ou d'un électron Auger.

La désexcitation non radiative est prépondérante dans le cas d'atomes cibles légers qui subissent principalement des photo-ionisations en couche K et deviennent donc émetteur d'électrons Auger.

I.7.2. Effet Compton :

Cet effet est produit si le photon incident possède une énergie de 0.1 à 0.5 MeV.

Le photon interagit avec un électron libre ou peu lié et l'interaction conduit l'éjection de l'électron, et le photon incident subit une diffusion avec une énergie inférieure à son énergie initiale.

L'énergie du photon diffusé et électron de Compton est donnée simplement, en appliquant les lois de la conservation de l'énergie et du moment cinétique au choc du photon avec un électron libre, ce qui donne la relation suivante [2] :

in (1.12)

by est l'énergie du rayonnement électromagnétique incident (ici un rayon ã), et E_ci est l'énergie cinétique de l'électron éjecté.

Au cours de l'interaction, une partie de l'énergie du photon est transmise à l'électron, qui recule et le reste de l'énergie, hí apparaît sous la forme d'un photon diffusé.

Figure1.7. Effet Compton. I.7.3. Production de paires :

Dans le champ électrique intense qui règne au voisinage du noyau, le photon peut se matérialiser sous forme d'un électron et d'un positon.

Une énergie de 2 x 0.51 MeV, correspondant à leurs masses, est dépensée pour créer l'électron et le positon (figure 1.8). L'excédent d'énergie se répartit, sous forme d'énergie cinétique, entre les deux particules. La production d'une paire e +, e^- n'est donc possible que si l'énergie du photon est supérieure à 2m, c² [10].

La conservation de l'énergie s'écrit :

E= 2E0 + E_e-- +Ey_e+ (1.13)

Oil E0 est l'équivalent énergétique de la masse de l'électron ( E0 =m, c² =0,511 MeV), E_e+ et E_e^- sont respectivement les énergies cinétiques de l'électron et du positron.

L'électron et le positron sont ralentis dans la matière.

A la fin de son parcours, le positron interagit avec un électron et s'annihile ce qui engendre l'émission de deux photons gamma d'énergie 511 keV à 180° l'un de l'autre (voire figure 1.8 et figure 1.9) [2].

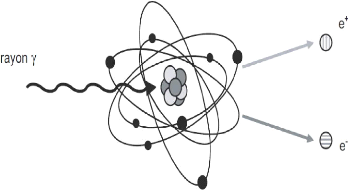
Figure1.8. effet de production des paires.

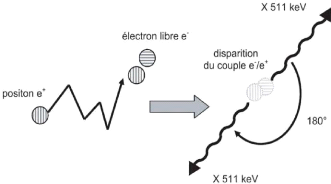
Figure1.9. Phénomène d'annihilation de la matière.

I.7.4. Section efficace :

I.7.4.1. Définitions et notations :

En physique nucléaire ou en physique des particules, la section efficace est une grandeur physique reliée à la probabilité d'interaction d'une particule pour une réaction donnée. L'unité de section efficace est une unité de surface ; on utilise traditionnellement le barn (b) :

1 b = 10^-24 cm² = 100×10^-30 m², soit la surface d'un carré de dix femto mètres de côté (c'est-àdire l'ordre de grandeur du diamètre d'un noyau atomique).

La section efficace représente « la probabilité intrinsèque » d'une interaction et elle est indépendante des variables du faisceau et de la cible : la géométrie, la densité et l'intensité

A chacun de ces modes d'interaction est associée une section efficace, qui dépend de l'énergie
des photons incidents et du numéro atomique Z du matériau traversé. L'importance relative de

ces trois modes en fonction de E et Z est représentée sur la figure 1.10, avec 0_p h, 0 _c et

⁰pair

les sections efficaces des effets photoélectriques, Compton et création de paires respectivement [5,13].

L'interaction des photons avec la matière a comme section efficace la somme de toutes les sections efficaces des différents processus. Elle est donnée par :

⁰t ot = 0p _h + 0 _c + ⁰pai r (1.14)

I.7.4.2. Domaine de prépondérance de chacun des effets :

L'importance relative des différents types d'interaction est en fonction de l'énergie de la radiation et du numéro atomique du milieu, on peut reporter dans le plan (hí, Z) les lieux de probabilité des effets :

Ceci permet de définir trois zones :

> ) IIFlDIfcHJIL IGeAISERtRnAIEIIhaXtIZ I: ISIIGRP KIKFTIGeIl'eIII1Iphotoélectrique.

> e WJiI IP R\ IInIIRIZ IP R\ enI: ISIéGRP KIKFT IGeIllflItlIErRP SIRn.

> Énergie élevée et Z élevé : prédominance de la production de paires.

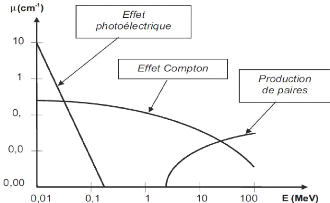
Figure 1.10. Probabilités de réalisation des effets photoélectrique, Compton et de
production de SIIIIAITIIfRnFIRnIGeIlVQ-rJll.

IESLIA IliIfIJXrH, IRIESSEEMIIXeI:

> (T-IIIIISERtRVDFUIXeISIéGRP ineIIXx IIIAAIAIé(IIJieA. ILIISIREIHlitéIG'RFFXrHIFeIIAtI Xne I1RnFtIRnIGéFrRiAAMeIGeIl'KHJILIGXIIa\ RnneP WIinFiG1ntI;

> (VIIIIErRP SIRnIIANIl'eIIIIISIfGominant aux énergies intermédiaires et la valeur du IIFteXrIEINEUe IrMMIP 11tISIXIenIfRnFIRnIGEIlKHJieI;

> OEISIREIEIlitéIG'RFFXrrenFeIGeIl'efIIIIGE ISIRGXFtIRnIGeISIIIIA, IaX-dessus de son seuil GwSSmaiRnIGeI1,rE2 ID tp ,IeAtIXP IfRnFtIRnIFIRiAAMeIGe WIJII.

Pour les énergies des rayonnements ã émis par les radionucléides (0,1 a quelques MeV), on peut constater que l'effet Compton est le mode d'interaction privilégie ou prépondérant dans les tissus biologiques [3].

I.7.5.Atténuation des rayonnements électromagnétiques :

I.7.5.1. Loi d'atténuation :

L'étude de probabilités d'interaction des photons avec la matière conduit à la définition des lois d'atténuation d'un faisceau de photons.

Au contraire des particules chargées qui cèdent progressivement leur énergie à la matière au cours d'interactions successives, les rayonnements électromagnétiques disparaissent brutalement à la suite d'une interaction.

On ne peut plus parler de ralentissement, il faut y substituer la notion d'atténuation en nombre.

Dans le cas d'un faisceau parallèle mono énergétique (dont les rayonnements ont la même énergie), le nombre de rayons émergeants N n'ayant subi aucune interaction dans la traversée d'un écran d'épaisseur x est lie au nombre de rayons incidents No par une relation exponentielle du type :

N = N0 e^- i^ix (1.15)

Ou ì est le coefficient d'atténuation linéique dont la valeur dépend de l'énergie du rayonnement et de la nature de l'écran : si x, épaisseur de l'écran, est exprimé en cm par exemple, ì devra etre exprimé en cm-1.

Sur papier semi-logarithmique, la représentation graphique de cette loi d'atténuation est une droite de pente -ì.

Il est important de noter que cette loi ne permet pas de calculer que le nombre de
rayonnements électromagnétiques sortant de l'écran avec l'énergie initiale (donc vierges de

toute interaction). Ceux-ci ne représeQtAQtVDIPQe Satie nGWIED RQQeP eQts électromagnétiques émergeants, ils ne prennent pas en compte, en particulier, les rayonnements diffuses Compton.

I.7.5.2.Couche de demi-atténuation(CDA) :

On appelle couche de demi-atténuation (CDA) l'épaisseur de matière nécessaire pour GiP iQueI GH P Ri3ip11¹iQteQsitp GuMisHeDO

L112 Tel que :

L112) = 2° (1.16)

Appliquant (1.12) pour x = L ₁₂₁ , on obtient :

L n2

L112 = (1.17)

ii

Comme L 121, ii GpSeQG Ge l'pQHJiL IGeNSERtRQs EI GIIMP 11i41FDIEYIIspe [10] [14].

I.8. La dosimétrie des rayonnements ionisants :

L'hétérogénéité de l'émission de la source de rayonnements, les caractéristiques du rayonnement utilisent, les distances de la source par rapport aux différentes parties du volume des produits traites et la structure du produit ne permettent pas d'obtenir une dose identique GEQsVIRut OIYROP HGXESIRGuit. D¹Rù la nécessite de procéder à la dosimétrie [15].

/ IHRESEiRlRTiINE TREteQuClRLI Ge1l¹i1BGiDiRQ GE DITP 13i4111YiY1Q26FSarDQ rD RQQ1P eQt dépend, essentiellement de la nature du ID RQQeP IQt eINGeTI'pQHgie ITENRIEpH SEURNP 13i41e irradiée.

La dosimétrie a pour but de déterminer cette énergie absorbée. Cette détermination est essentielle :

ü Pour estimer le danger potentiel des techniques de diagnostique utilisant, in vivo, les radiations ionisantes.

ü Pour prévoir en radiothérapie, les effets du traitement sur les tissus tumoraux et sur les tissus sains adjacents.

ü Pour définir les normes de radioprotection individuelle et collective [2].

I.8.1. Definition :

La dosimétrie est un moyen de mesure de la dose des rayonnements, absorbée par la matière et de contrôle du bon fonctionnement de l'installation. Comme elle représente une assurance de résultats et de qualité pour les produits traites [16] et une maintenance des performances des mesures acceptables [17].

I.9. Grandeurs et unités dosimétriques :

Les définitions évoquées dans cette partie sont celles des grandeurs qui représentent l'outil nécessaire pour corréler des mesures physiques aux effets des irradiations. Ce sont des grandeurs macroscopiques se rapportant aux effets dans un milieu, pouvant être utilisées pour prévoir les conséquences d'une irradiation [18].

L'action d'un rayonnement ionisant est définie par plusieurs grandeurs, auxquelles correspondent des unités particulières. Les grandeurs usuellement utilisées en dosimétrie, sont : [17]

I.9.1. Exposition :

L'exposition ne s'applique qu'à des rayonnements indirectement ionisants et parmi ceux-ci uniquement aux rayons X et ã.

Cette quantité d'exposition est définie par l'ICRU (International Commission on Radiation Units and measurements) comme le quotient de la charge par le volume d'air de masse
[19, 2,13]

(1.18)

L'unité : C. -

L'ancienne unité utilisée était le Roentgen (R 1R = 2.58. - C. - [20]

Oil est la charge électrique totale de tous les ions d'un signe donné produits dans l'air

quand tous les électrons secondaires libérés par les photons dans un volume d'air de masse Sont complètement arr~tés par l`air.

Les ions produits par l'absorption des rayonnements de freinage émis par les électrons secondaires très énergétiques n'entrent pas dans la charge .

I.9.2. Kerma :

Le Kerma représente l'énergie cinétique libérée dans le milieu par le rayonnement indirectement ionisant (photon, neutron).

Le transfert d'énergie par un flux de photons à un milieu se fait en deux étapes [21] [13] :

> La première est l'interaction des photons avec les atomes du milieu mettant ainsi les électrons en mouvement par les interactions de photons (effet photoélectrique, Compton, création de paire, etc...) (figure 1.11(a))

> La deuxième étape concerne le transfert d'énergie qui se fait entre ces électrons de haute énergie et le milieu par excitations et ionisations (figure 1.11. (b)).

Figure1.11 : Représentation schématique du transfert d'énergie d'un photon au milieu
traversé

La quantité dénommée Kerma (Kinetic Energy Released per unit Mass in the medium).

Elle traduit le premier acte du transfert d'énergie par collision aux particules secondaires. Elle présente la somme des énergies cinétiques initiales de toutes les particules chargées mises en mouvement par les rayonnements dans le volume de masse dm du milieu :

Ecin (1.19)

Dans le système international des unités (SI), le kerma est exprimé en gray (symbole : Gy) : 1Gy = 1 J/kg. Bien que son usage ne soit plus autorisé depuis 1er janvier 1986, une ancienne unité est encore souvent employée le rad (1 rad = 10^-2Gy).

Le Kerma s'applique quelle que soit la nature du rayonnement indirectement ionisant. Lorsque le milieu absorbant est l'air, on parle de Kerma et de débit de Kerma dans l'air [22].

Le Kerma se divise en Kerma de collision K_coiet Kerma radiatif K_rad [13].

Kerma de collision o est l'énergie transférée aux électrons secondaires qui est perdue lors des collisions.

Kerma radiatif est l'énergie transférée aux électrons qui est perdue par des processus

radiatifs.

onc, le kerma s'écrit :

a (1.20)

La fraction moyenne de l'énergie transférée aux électrons qui est perdue par des processus radiatifs est représentée par un facteur désigné sous le nom de la fraction radiative ~. Par

conséquent, la fraction d'énergie perdue lors des collisions est (1 i- ~).

Une relation fréquemment utilisée entre le kerma 0 de collision et le kerma total K peut

être écrite comme suit :

- ~) (1.21)

Le débit de Kerma est le quotient de la variation du Kerma pendant un intervalle de temps

.

t

(1.22)

Son unité est le gray par minute.

I.9.3. La dose absorbée :

C'est une grandeur plus intéressante en radiothérapie et en radiobiologie.

La différence entre le Kerma et la dose absorbée peut être mise en évidence en remarquant

que dans l'énergie transférée à l'électron une partie est déposée dans le milieu, l'autre est perdu sous forme de rayonnement de freinage [2]

La dose absorbée, D est le quotient E par dm, où E est l'énergie moyenne cédée par le

rayonnement ionisant à la matière de masse dm

(1.23)

U nité S.I. : J. Kg- ¹ Le nom spécial de l'unité de dose absorbée est le gray (symbole : Gy) : 1Gy = 1 J. K -

L 'ancienne unité de dose absorbée, rad, a pour valeur correspondante : 1 rad = 10^-2J. Kg^-

Pour une source de photon et sous les conditions de l'équilibre électronique, la dose absorbée,

D peut être exprimée comme suit :

. _E. gen (1.24)

m ù :

2

E = énergie du rayonnement ionisant (J), et ( fte _n /yl)) = Le coefficient massique d'absorption d'énergie ( 2 / kg) [23] [18]

I.9.4. Débit de dose absorbée :

Le débit de dose absorbée, 13 est le quotient de dD par dt, où dD est l'incrément de dose

ps dt correspondant :

(1.25)

t

Unité S.I: J. Kg- 1_{. s}- 1

Le nom spécial, gray (Gy), peut être substitué au joule par kilogramme : 1Gy. s^{- 1} = 1 J. Kg^- 1. s-1

L'ancienne unité de débit de dose absorbée, rad. s^{- 1} , a pour valeur correspondante : 1 rad. _s- 1= 10-2 J. Kg^{- 1}s^{- 1}[23, 17,18].

I.9.U ZI VEXiliFILWITURniEXe :

Le Kerma et la dose absorbée s'expriment avec la mrme unité. Cependant, ce n'est que lorsque l'équilibre électronique est atteint dans le milieu que les quantités

Kerma et dose

absorbée sont égales.

Un rayonnement gamma interagit avec la matière pour donner des électrons secondaires qui cèdent leur énergie à la matière selon différents processus (excitation, ionisation). Considérons un faisceau de photons pénétrant dans un milieu matériel ; les électrons mis en mouvement ont un certain parcours en fonction de leur énergie (figure 1.12) [13,2].

Au fur et à mesure que le faisceau de photons pénètre dans le milieu, il met en mouvement des électrons et la fluence de ces électrons sur des couches successives du milieu augmente progressivement ceci jusqu'à une profondeur égale au parcours des électrons d'énergie maximale mis en mouvement dans le milieu, c'est la profondeur de l'équilibre électronique.

- g) (1.26)

Lorsque celui-ci est éteint, le flux d'électrons est proportionnel au flux de photons ; mais celui-ci étant atténué le flux d'électrons diminue alors parallèlement tout en restant proportionnel au flux de photons.

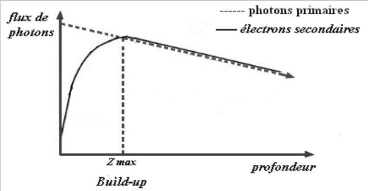
Figure1.12 : L'équilibre électronique

Chapitre II

Paramètres physiques et dosimétriques

des unités d'irradiation

II .1. Introduction :

Dans le domaine médical, les rayons X de basse énergie sont utilisés en radiodiagnostic et en radiothérapie conventionnelle, encore appelée radiothérapie « basse énergie », alors que la radiothérapie dite « haute énergie » met en oeuvre des rayonnements X produits par des accélérateurs [3].

Les faisceaux de photons externes sont tous caractérisés par des paramètres physiques, mais tombent dans différentes catégories selon leur origine, des moyens de production et l'énergie. En ce qui concerne les rayons X qui sont originaires d'un objectif de bombardement d'électrons énergétiques. En ce qui concerne les moyens de production des rayons X sont produits soit dans un tube à rayons X (rayons x superficielle ou orthovoltage) ou dans un accélérateur linéaire (mégavoltage rayons X) [16].

II.2. Rayonnement électromagnétique X :

Les rayons X ont été découverts en 1895 par le physicien allemand Röntgen, ils appartiennent au rayonnement électromagnétique à haute fréquence, avec une longueur d'onde comprise entre cinq picomètre et dix nanomètres.[27]

Ils s'inscrivent dans le large domaine des ondes électromagnétiques, Sur le spectre en énergie des rayonnements électromagnétiques, les rayons X se situent après l'ultraviolet Selon le mode de production, ils peuvent avoir une énergie plus ou moins élevée, de quelques KeV à des centaines de MeV [27,3].

II.3. Origine des rayons X :

Si les rayons X sont des rayonnements électromagnétiques de même nature que les photons gamma, ils en différent par leur origine.

Les photons gamma sont issus du noyau de l'atome, alors que les rayons X prennent
naissance au niveau du cortège électronique ou dans le champ électrostatique qui entoure le

noyau. Ils résultent des interactions des électrons avec la matière, qui peuvent prendre deux formes selon l'énergie des électrons et la nature du milieu traverse :

· Interaction des électrons avec le noyau, qui crée un rayonnement X de freinage.

· Interaction des électrons incidents avec les électrons du cortège électronique donnant lieu à une ionisation ou à une excitation, dont la conséquence directe sera un réarrangement du cortège [3].

II.4. Production de rayons X :

La théorie du rayonnement électromagnétique prévoit que lorsqu'une particule chargée subit une modification de sa trajectoire, elle rayonne de l'énergie. Ainsi, une particule accélérée ou décélérée subit une perte de son énergie sous forme de rayonnement électromagnétique.

Ce processus porte le nom de rayonnement de freinage ou Bremsstrahlung. Cette perte d'énergie par rayonnement de freinage dépend en partie de la masse de la particule incidente. Ce processus est important pour les particules légères comme les électrons et il est pratiquement négligeable pour les particules lourdes.

La production des rayons X s'effectue sur la base de ce processus en créant un faisceau de particules chargées que l'on freine ensuite dans un matériau cible, c'est le principe du tube à rayon X [27].

II.5. Principe du tube à rayons X :

Pour disposer de faisceaux de rayons X utilisables, le procédé technologique consiste à créer des électrons et a les envoyer sur une cible pour obtenir des rayonnements de freinage en grand nombre.

Un courant électrique circule dans un filament et crée des électrons par chauffage (effet
thermo-ionique). Ce filament constitue la cathode du tube a rayons X ; il est porté à un
potentiel négatif. Les électrons formés sont accélérés par une haute tension appliquée entre la

cathode et une cible, ou anode (parfois aussi appelée anticathode), qui est portée à un potentiel fortement positif pour attirer les électrons.

L'ensemble est placé dans une ampoule en verre dans laquelle est réalisé un vide Poussé pour éviter la dispersion des électrons (Figure 2.1).

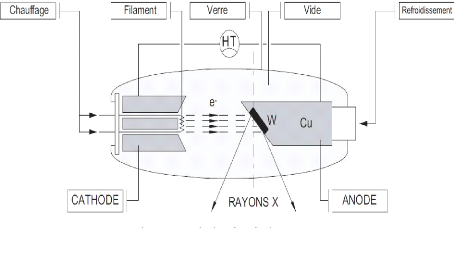
Figure 2.1. Principe du tube à rayons X

Pour favoriser la production de rayonnement de freinage, l'anode est constituée d'un matériau de numéro atomique élevé résistant à la chaleur. Le tungstène, de numéro atomique 74 (et de symbole chimique W) répond bien a ces deux exigences et constitue très souvent la cible des tubes a rayons X. Selon les applications envisagées, celle-ci peut être également en molybdène, or, cuivre, fer, cobalt. . .

Le rendement de la cible en rayonnement de freinage reste toujours limite (2 %). Les nombreuses ionisations et excitations créées par les électrons dans la cible produisent une importante élévation de température. Celle-ci est donc souvent enchâssée dans du cuivre pour assurer la diffusion de la chaleur et nécessite un refroidissement par air, huile ou eau.

L'anode est le plus souvent inclinée par rapport à la direction des électrons et les rayons X sont émis préférentiellement dans un cône dont l'axe dépend de la pente de l'anode. Les rayons X traversent la paroi du tube et sortent par une fenêtre en matériau léger (béryllium ou aluminium) aménagée dans la gaine plombée qui entoure le tube.

Cette fenêtre va arrêter une partie des rayons X, en particulier ceux qui auront une énergie faible. De plus, pour limiter le faisceau à sa partie utile, un collimateur est placé après la fenêtre de sortie.

II.6. Spectre de rayons X :

Le spectre en énergie des rayons X émis par l'anode est le résultat de la superposition de deux spectres indépendants :

- le spectre continu des rayonnements de freinage, de 0 à ;

- le spectre de raies caractéristiques liées au réarrangement du cortège électronique.

Ce spectre global peut être représenté de deux manières :

- en fonction des longueurs d'onde, comme sur la (figure 2.2.) : le spectre présentera alors une longueur d'onde minimale

~ (2.1)

- en fonction de l'énergie, comme sur la (figure 2.3.) Dans ce cas, l'énergie des rayons

X ne pourra pas dépasser une valeur maximale correspondant à la haute tension
appliquée. En aucun cas l'énergie du photon X de freinage ne peut être supérieure à celle de l'électron qui lui a donné naissance :

(2.2)

Ou, plus simplement : (en KeV) = haute tension (KV) (2.3)

La forme exacte du spectre émis par un tube à rayons X dépend de nombreux paramètres tels que la nature de l'anode, la valeur de la haute tension et la filtration totale. L'intensité électrique du courant parcourant le filament permet de modifier le nombre d'électrons émis, donc celui de rayons X produits par le tube.

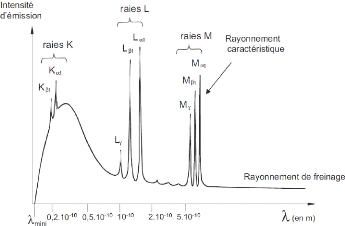
Figure 2.2. Exemple d'un spectre de rayons X, représenté en fonction de la longueur
d'onde

Figure 2.3. Exemple d'un spectre de rayons X, pour une haute tension de 100 KV,
représenté en fonction de l'énergie

II.7. Dosimétrie des faisceaux de photons :

II.7.1. Caractéristiques physiques d'un faisceau de photons dans le vide :

Considérons un faisceau de photons issu d'une source S supposée ponctuelle et qui se propage dans le vide [2].

Un faisceau de photons issu d'une source sera caractérisé par trois types de grandeur : sa distribution spectrale, par ses paramètres énergétiques et par sa distribution spatiale.

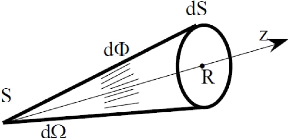
Figure 2.4. Caractéristiques physiques d'un faisceau de photons dans le vide

II.7.1.1. La distribution spectrale :

C'est-à-dire les proportions relatives des énergies qui sont représentées dans le faisceau

Par exemple : Source radioactive --* spectre de raies Tube de Coolidge --* spectre continu

Pour tous les autres paramètres, on raisonnera sur un faisceau monoénergétique.

Pour les faisceaux polyénergétiques, on procède par addition (spectre de raies) ou par intégration (spectre continu).

II.7.1.2. Lesparamètres énergétiques :

1. Flux énergétique ( ) :

C'est énergie totale transportée par le faisceau par unit

est finie, donc le flux transporté dans l'angle solide qui voit la matière à partir de la source.

2. Intensité énergétique (I) : dans une direction donnée

I = (2.4)

17 nité : Watt/stéradian d est pris suffisamme

3. L'énergie totale (W) : L'énergie totale

~

W = ) (2.5)

17 nité : Joules

4. Fluence énergétique (?) : Cette quantité de densité de puissance peut être cumulée dans
le temps pour aboutir à l'énergie totale qui a traversé dS pendant le temps d'irradiation, on parle de fluence énergétique.

W

y7 (2.7)

17 nité : Joules/

II.7.1.3. La distribution spatiale :

On caractérise la distribution spatiale d'un rayonnement par l'indicatrice d'intensité énergétique ; si l'intensité énergétique I ne dépend pas de la direction d'observation, l'indicatrice d'intensité énergétique est une sphère et le faisceau est dit isotrope.

I = ?/4j (2.8)

C'est le cas d'une source radioactive de faibles dimensions [2].

II.7.1.4. Lois fondamentales de l'atténuation des faisceaux de photons :

Considérons un faisceau mince issu d'une source ponctuelle S et se propageant dans le vide. Quand on s'éloigne de la source, la surface traversée par ce flux augmente. La fluence énergétique ? est proportionnels à 1/ .

Par contre, l'intensité énergétique I ne varie pas quand on s'éloigne de la source [2].

II.7.2. Caractéristiques physiques d'un faisceau traversant un matériau :

Au voisinage d'un point P du matériau, on observe non seulement des photons provenant du faisceau initial, mais également des photons diffusés dont la direction de propagation et la distribution spectrale ne sont pas uniformes (figure 2.5) [2].

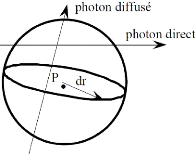
Figure 2.5. Caractéristiques physiques d'un faisceau traversant un matériau

Dans l'élément de sphère de rayon dr, la surface de section qui est perpendiculaire au rayonnement diffusé est toujours it. (dr) ² quelle que soit la direction du rayonnement diffusé. Il convient donc d'adapter les définitions qui font intervenir une surface fixée dS, donc on aura : [28]

- la fluence énergétique ~ =dW

ir.(dr) 2 (2.11)

II.8. Pénétration du faisceau de photons dans l'eau :

Dans l'étude de la distribution de la dose sur l'axe du faisceau de photons pénétrant dans un milieu équivalent tissu, on obtient une courbe dont la forme dépend de l'énergie et des paramètres géométriques de l'irradiation (section de faisceau, distance source surface SSD). Ces paramètres dépendent beaucoup d'appareillages utilisés.

Le plus souvent, la dose absorbée en un point de l'axe est exprimée en pourcentage de la dose maximale sur l'axe, la courbe obtenue, appelée courbe de rendement en profondeur, présente toujours trois parties distinctes figure (2.6).

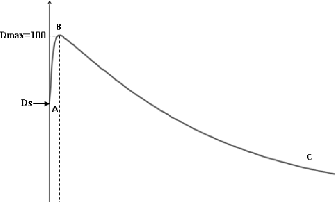
Figure 2.6. Schématisation d'une courbe de rendement en profondeur

La région d'accroissement de dose, AB, correspondant d'une part, à la mise en mouvement des électrons secondaires dans le milieu par les photons primaires et, d'autre part, a l'effet des rayonnements diffusés provenant de la tête d'irradiation et des éventuels accessoires placés sur le trajet du faisceau. Elle est caractérisée par la dose à la surface D.

La région du maximum, B, correspondant à un équilibre électronique, est d'autant plus plate que l'énergie est plus élevée et est caractérisée par la profondeur du maximum .

La région de la décroissance de dose en profondeur, BC, est pratiquement exponentielle.

Le rendement en profondeur dépend de la distance séparant la source de photons à la surface du milieu équivalent-tissu.

II.9. Paramètres de traitement :

II.9.1. La taile du champ du faisceau de rayonnement :

Les Faisceaux utilisés pour la radiothérapie ont des formes différentes que représentent habituellement un compromis entre la forme de la cible réelle et le besoin de simplicité et d'efficacité dans le faisceau de façonnage. Généralement les formes utilisées : carrée, rectangulaire, circulaire et irrégulières.

Les champs circulaires avec collimateurs spéciaux attachés à la machine de traitement, et les champs irréguliers qui ceux faits avec des blocs de blindage ou avec des collimateurs mutilâmes attaché à une machine de traitement.

Un champ arbitraire rectangulaire avec des côtés a et b sera à peu près équivalente à un champ carré avec des côtés a lorsque les deux champs ont la même aire / périmètre (règle de la journée), c'est-à-dire,

(2.12)

Un champ arbitraire carré avec des côtés a sera équivalent à un champ circulaire avec un rayon lorsque les deux champs ont la même zone, à savoir

r (2.13)

II.9.2. Facteur de coiimateur :

Lorsque l'ouverture du collimateur augmente, le Build-up (profondeur où la dose est maximale) se rapproche de la surface. Ceci est dû à l'augmentation du flux des électrons secondaires et des photons diffusés par le collimateur lorsque sa surface interne croît.

L'augmentation de la section du faisceau entraîne celle du volume diffusant ; il en résulte un
accroissement du flux des électrons secondaires et donc de la dose sur l'axe. Ainsi, on

détermine un facteur correctif (Facteur d'Ouverture de Collimation "F.O.C") pour tenir compte de l'influence de l'ouverture du champ.

Le facteur de collimation (F.O.C) est défini dans l'ICRU24 comme le rapport du débit d'exposition ou débit de dose d'un champ donné à celui d'un champ de référence. Il s'obtient en mesurant les doses reçues (D) par une chambre d'ionisation placée à une distance de référence , à la profondeur de référence , pour un champ de dimension C, à la dose (D ) mesurée à la même distance et à la même profondeur pour le champ de référence, : [2,29]

F (2.14)

Les détecteurs habituellement recommandés pour ce type de mesures en radiothérapie conventionnelle sont une chambre d'ionisation de type Farmer (cylindrique de 0,6 cm3).

II.9.3. Le facteur de diffusions au pic (PSF) :

C'est le facteur PSF défini à la profondeur de maximum de dose (figure 2.7). Il représente le rapport entre la dose absorbée totale et la dose des photons primaires à la profondeur de maximum de dose.

D'après cette définition, le PSF tend vers 1 si la taille du champ tend vers 0. [30,13]

) P F ) u		) (2.15)

Figure 2.7. Mesure du PSF. La mesure dans l'air s'effectue avec un capuchon de build-up

II.9.4. Le débit de la machine relative (output) :

Le facteur d'output d'un appareil de traitement est défini dans l'ICRU24 (ICRU, 1976) comme le rapport du débit d'exposition ou du débit de dose d'un champ donné à celui d'un champ de référence ( f, f). Il est noté RDF (facteur de dose relative) . (figure 2.8).

r .f)

) r j r j) (2.16)

La séparation d'output total (`output dans l'eau ') en facteur de diffusion dans la tête d'irradiation , et le facteur de diffusion dans le fantôme , a été proposée par Holt (1970). Dans ce cas, le facteur d'output , est égale à :

(2.17)

: est appelé aussi output dans l'air. Il est mesuré dans un mini-fantôme selon les mêmes conditions géométriques que le .

i i .f r j ~ i i j r j

(2.18)

: Facteur de diffusion dans le fantôme. Il est souvent estimé par le rapport du facteur d'output (facteur de diffusion total, ) et le facteur de diffusion dans la tête de traitement

car la mesure de fait appel à des techniques souvent difficiles à réaliser expérimentalement.

(2.19)

La variation de l'output avec la taille du champ au point de référence est fortement liée au rayonnement diffusé dans la tête d'irradiation. Il dépend donc de la structure de la tête qui varie d'une machine à l'autre. Cette variation dépend moins des diffusions dans le patient qui sont directement proportionnelles à la surface irradiée au point de mesure, car pour les photons de hautes énergies les diffusions se font plutôt en amont que latéralement. Ainsi, le facteur de diffusion dans la tête ( ou HSF) et le facteur de diffusion dans le fantôme peuvent être déterminés séparément et puis leur combinaison donne le facteur de diffusion totale (facteur d'output).

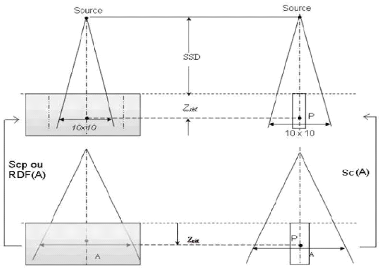
Figure 2.8. Mesure du (HSF) et du (RDF)

II.10. Courbes de distribution de doses :

II.10.1. Le rendement en profondeur :

La courbe donnant la variation de la dose absorbée en fonction de la profondeur dans l'eau sur l'axe du faisceau d'irradiation à une distance source-surface du fantôme fixe, est appelée courbe de rendement en profondeur : PDD(z) (figure 2.6).

Le rendement en profondeur (PDD) correspond à la variation de la dose absorbée le long de l'axe du faisceau en fonction de la profondeur du point de mesure, pour différentes tailles de champ.

La distance source-surface du fantôme est constante et la distance source détecteur varie avec la profondeur du point de mesure ; ces courbes sont normalisées au point du maximum de dose.

Certaines grandeurs dosimétriques peuvent être définies à partir de la courbe de rendement en profondeur : la dose à la surface, la dose de sortie et la profondeur de maximum de dose (profondeur de l'équilibre électronique): .

II.10.2. Le profile de dose :

Les courbes décrivant La variation de la dose absorbée en fonction de la distance dans un plan perpendiculaire à l'axe du faisceau et à différentes profondeurs et pour différentes tailles de champ est appelée profil latéral de dose.

Figure 2.9. Profile de dose

On peut définir à partir de la courbe de profile de dose : la pénombre, la taille du champ, les corrections hors axe central et la profondeur de mesure. [28,29]

II.10.3. La pénombre géométrique :

Physiquement, la pénombre est la région en bordure de champ où la dose change rapidement en fonction de la distance de l'axe centrale. Géométriquement, la pénombre est la différence entre le faisceau tracé à partir du centre de la source et le faisceau tracé à partir des extrémités de la source. La pénombre géométrique est mesurable sur la courbe de profile de dose. La pénombre physique inclut de plus les diffusions dans les collimateurs et leur contribution aux extrémités du champ d'irradiation Figure (2.10). [28]

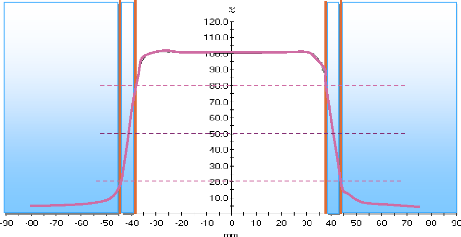
Figure 2.10. Profil latéral de dose et leur régions (la partie centrale >80%, la partie de
pénombre entre 20% et 80%, la partie de transmission >20%).

Chapitre III

Matériels et équipements utilisés

III.1. Introduction :

La radiothérapie est l'une des armes les plus puissantes pour la lutte efficace contre la maladie douloureuse du cancer humain. Les techniques de traitement et de l'équipement d'irradiation ont été développés en permanence dans le passé pour répondre aux objectifs d'offrir des charges de rayonnement aux tissus du cancer pour but de détruire les cellules cancéreuses dans une manière optimale et de protéger les patients contre les dégâts d'irradiation[31].

En radiothérapie du cancer, le mode de traitement le plus répandu est celui utilisant des photons de haute énergie. Le mode de traitement utilisant les électrons est quant à lui classé en deuxième position. Dans le Centre de radiothérapie du cancer, la production de photons et d'électrons de haute énergie s'obtient à l'aide d'un accélérateur linéaire de particules [32].

III.2. Description générale sur Les Accélérateurs Linéaires :

L'accélérateur linéaire d'électron étudié au cours de ces travaux est de type Primus élaboré par le constructeur SIEMENS (figure 3.1). Conçu pour le traitement en radiothérapie [32], est composé essentiellement de deux parties indépendantes : l'accélérateur et sa tête.

Pour situer ces composantes, le schéma d'un accélérateur linéaire est présenté à la (figure 3.1)

Figure 3.1. Schéma d'un accélérateur SIEMENS

La numérotation des composantes sur la figure 3.1 correspond à :

(1) Klystron ou Magnétron.

(2) accélérateur par ondes stationnaires ou par ondes progressives.

(3) aimant de recourbement.

(4) carrousel des collimateurs primaires.

(5) miroir.

(6) mâchoires primaires.

(7) mâchoires mutilâmes.

Les composantes (4), (5), (6) et (7) font partie de la tête de l'appareil.

Les trois autres composantes constituent le circuit des électrons pour un accélérateur linéaire de basse et/ou de haute énergie.

Des électrons de basse énergie sont d'abord générés par un klystron. Celui-ci est connecté au tube de l'accélérateur. À l'intérieur de l'accélérateur, les électrons sont accélérés aux énergies d'intérêt, soit supérieures à un méga électron-volt (MeV). À la sortie, la configuration horizontale de la machine fait en sorte que le faisceau doit être courbé et redirigé verticalement en direction du patient. Un champ magnétique est utilisé pour contraindre les électrons à effectuer une rotation pour ensuite sortir par une fenêtre.

Dans notre cas, le faisceau passe dans un aimant de recourbement qui effectue une boucle de 270 degrés. L'avantage de ce type de boucle est de réaliser un filtrage de l'énergie des particules à l'aide du champ magnétique. L'orbite des électrons sera proportionnelle à la racine carrée de l'énergie, créant ainsi une dispersion spatiale des particules selon l'énergie au niveau de la fenêtre de sortie.

En ajustant l'intensité du champ magnétique et l'énergie des particules à la sortie du tube, on filtre les électrons déviés de leur trajectoire par rapport à l'ouverture de la fenêtre. Les électrons, une fois passés celle-ci, sont à l'intérieur de la tête de l'appareil. Le rôle de la tête est de générer le faisceau de photons ou d'électrons utilisés pour le traitement. Avec ces types de faisceaux, les électrons frappent tout d'abord une cible de numéro atomique élevé. Des photons de bremmstrahlung sont ainsi créés. Un premier filtre est disposé afin d'éliminer la contamination en électrons du faisceau. Les photons sont ensuite injectés dans le collimateur

primaire oil un second filtre est utilisé pour équilibrer la distribution en énergie et en fluence des particules.

La forme du champ est ensuite modelée à l'aide des collimateurs secondaires qui est un dispositif spécifique fixé à la tte de l'accélérateur linéaire. Il est constitué de lamelles de tungstène parallèles, qui se déplacent les unes par rapport aux autres de façon à conformer le faisceau à la planification [33]. Le faisceau est ainsi mieux adapté à la forme de la tumeur [34].

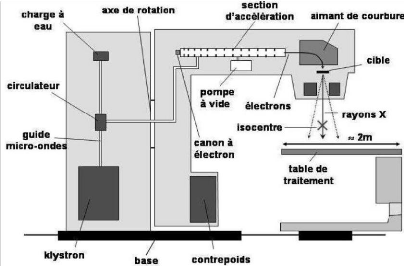
Figure 3.2. Le schéma des différents composants d'un accélérateur linéaire.

L'accélérateur linéaire possède deux voies de faisceau d'irradiation. La première est une voie de photons et la deuxième sert dans le traitement par électrons [32].

III.2.1 La Voie de photons :

Pour cette voie, le Primus possède une seule cible identique pour deux énergies : une basse
aux environs de 6 MeV, c'est le mode 6MeV et une haute à 18 MeV, c'est le mode 18 MeV.
La cible est constituée de trois couches successives d'épaisseurs différentes. Le siège de la

création des photons par bremsstrahlung est la première couche d'or de quelques dixièmes de millimètres d'épaisseur. Elle est de section efficace élevée. La dernière couche est constituée de graphite et sert à atténuer au maximum les électrons primaires et ainsi éviter une contamination du faisceau.

Le faisceau de photons est produit par les électrons de haute énergie qui viennent interagir avec une cible en tungstène, Lorsque le faisceau sort de la cible il pénètre directement dans le collimateur primaire. Ce dernier va confiner le faisceau, c'est lui qui définit le champ maximum d'irradiation par son ouverture supérieure et sa forme en cône.

Suite à cela, le faisceau passe dans une chambre moniteur qui mesure la fluence au cours du traitement. Elle est multi-segmentée de manière à s'assurer de la symétrie du faisceau d'irradiation. Elle est suivie d'un miroir semi-réfléchissant permettant de projeter un champ lumineux dans l'axe d'irradiation. Celui-ci présente deux intérêts :

n il constitue une preuve visuelle pour le praticien concernant ce qu'il fait

n il projette sur la table de traitement une échelle métrique donnant la distance à la source.

Après il traverse un filtre égalisateur placé à la sortie de la cible qui atténue le faisceau sur l'axe central davantage que sur les bords, réalisant ainsi son uniformité.

En place finale dans la voie de faisceau, on distingue la partie de collimation secondaire constituée par une paire de mâchoires et par le collimateur multimâle, permet d'obtenir des dimensions de faisceau variables.

III.2. 2 La Voie d'électrons :

La voie d'électrons génère des faisceaux aux environs de 6, 9, 12, 15 ,18 et 21 MeV. Pour le but d'obtenir un faisceau d'électrons de haute qualité pour la thérapie du cancer, le faisceau accéléré dévié et conduit dans la tte d'irradiation, doit ~tre large et uniforme.

Ainsi on ne trouve plus sur le trajet de faisceau ni cible ni absorbeur. Les composants majeurs dans la modification du faisceau sont des couches minces qualifiées de "feuilles de diffusion". Le rôle principal de cette partie est de diffuser le faisceau quasi mono-incident en sortie de la déviation magnétique. L'utilisation de métal dense se justifie par le besoin de diffuser les électrons sans pour autant entraîner une perte d'énergie conséquente.

Toutefois, la dégradation inévitable du spectre énergétique par le phénomène de bremsstrahlung oblige à limiter l'épaisseur, ce qui ne permet pas d'atteindre une homogénéité convenable pour le faisceau. C'est ce qui explique la dualité des feuilles de diffusion.

pour disperser le faisceau d'électrons et pour lui donner une largeur utile , le métal et l'épaisseur dépendent de l'énergie utilisée et sont propres à chacune des énergies disponibles afin de limiter au maximum la contamination inévitable du faisceau par des électrons d'énergie plus faible et par des rayonnements X de freinage, tout en obtenant un champ égalisé de la plus grande dimension possible.

Le faisceau traverse un ensemble de deux chambres d'ionisation à transmission indépendante qui autorisent une double mesure de la dose délivrée ainsi qu'une vérification de la symétrie du faisceau.

Juste à la suite on trouve un collimateur primaire plus destiné à stopper les quelques électrons diffusés à des angles importants qu'à véritablement collimater le faisceau.

Concernant le système de collimation, les mâchoires et le multi lame jouent le rôle de collimateur intermédiaire. Pour chaque champ, leur ouverture est supérieure à la taille de ce dernier de plusieurs centimètres : ce n'est donc pas ce système qui délimite l'irradiation. C'est l'applicateur qui agit vraiment dans ce sens sur le faisceau. [35,32]

III.3. La dosimétrie : III.3.1. Introduction :

La dosimétrie des faisceaux de rayonnements consiste à mesurer une quantité dosimétrique expérimentalement en utilisant un système de dosimétrie qui doit posséder au moins un effet physique qui est une fonction de la quantité dosimétrique mesurée.

Les caractéristiques qui déterminent l'utilisation d'un détecteur donné de radiation dans une situation sont :

1) la linéarité de la réponse en fonction de la dose,

2) la dépendance de la réponse en fonction du débit de dose,

3) la dépendance de la réponse en fonction de l'énergie du faisceau,

4) la dépendance en fonction de sa direction par rapport au faisceau,

5) la résolution spatiale élevée et ses dimensions.

Bien qu'il existe plusieurs types de systèmes dosimétrique tel que les films et les dosimètres thermoluminescences, la chambre d'ionisation est généralement la mieux adaptée pour les mesures en radiothérapie. Contrairement au film, la réponse dépend peu de l'énergie du rayonnement incident, et par rapport aux dosimètres thermoluminescents, elle est beaucoup plus facile et rapide à utiliser surtout pour les mesures relatives.

III.3.2.Chambres d'ionisation :

L'émission des rayonnements est toujours associée à la radioactivité. Aucun des sens dont dispose l'tre humain n'est sensible aux rayonnements émis par les substances radioactives. On ne peut détecter ces rayonnements donc déceler la radioactivité qu'en utilisant deux types d'interaction entre les rayonnements ionisants et la matière : l'ionisation et l'excitation. [36]

La chambre d'ionisation constitue un des systèmes les plus simples de détection des rayonnements [37]. Dans le domaine de la physique médicale, l'application principale de la chambre d'ionisation est la dosimétrie des faisceaux de radiothérapie. Une propriété importante d'une chambre d'ionisation réside dans le matériau constituant sa paroi.

Ceci est lié au fait que, dans le cas de la dé21-F2iRQ d'PQ rI RQQ1-P 1-Q2 iQdiI1-F21-P 1-Q2 iRQiAIQ2 (comme les photons), ce sont les particules chargées secondaires produites dans la paroi (principalement les électrons) qui sont mesurées dans le volume de la chambre.

Selon les fabricants et les conditions de mesure, le volume sensible des chambres d'ionisation est généralement compris entre quelques et quelques dizaines de . / lpSIiAA1-Pr 1-2 la nature de ce matériau sont à choisir selon les conditions spécifiques de la mesure. Les qualités habituelles de ces détecteurs (stabilité, linéarité, polarité, influence du débit, de l'angle

GIiQTIG1-QF1- U ra RQQ1-P 1-Q2, I ARQ2 pYIG1-P P 1-Q2 iQdiAS1-QAaFl1-A. / pO1-F2IRP q2I1- aAARFIp dRi2

être adapté et capable de mesurer des charges très faibles [38,2].

III.3.2.1.Chaine de mesure chambre-électromètre :

/ a FKEP EU1- 3VRQiAa2ARQ 1-A2 2RujROrA u2iliAp1- 1Y1-F uQ pl1-F2rRP q2I1-, uQ diASRAi2II SRX P 1-Aur1-1 (1- FROraQ2 iQdui2 SU l1- SIAAEI1- (X U RQQ1-P 1-Q2 GEQA GE FhaP Er1-, d1- l'RUI1- de 1 ,1 4 1 utilisé en même temps INPQ1- FX[P br1- d'iRQiAI2IRQ.

Un amplificateur opérationnel avec une résistance standard ou un condensateur standard

S1-rP 1-2 d1- I1-QP1- F1-A FROIaQ2A IIIR1-A P 1-AuarEl1-A SEr l'pl1-F2IRP q2I1-.

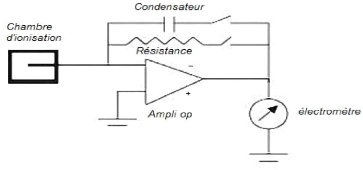
Figure 3.3. Chaine de mesure chambre-électromètre

¹ Ampère

III.3.2.2.Principe de fonctionnement :

Une chambre d'ionisation est constituée par une enceinte délimitant un certain volume gazeux, compris entre des électrodes portées à une tension de l'ordre d'une centaine de volts. En générale, le principe de la chambre d'ionisation est de ce placer dans les conditions où le nombre d'ions collectés est égale au nombre d'ions formés lors de l'irradiation, ce qui permet de mesurer la quantité d'électricité transportée par ces ions [37].

La mesure d'une dose absorbée dans un matériau m peut se traduire en fait par la mesure

d'une quantité d'ions, ou d'un courant d'ionisation créé dans un volume gaz entouré d'une
paroi en matériau m (ou équivalent à m) .Ceci étant, une chambre d'ionisation est simplement
constituée d'un volume utile de gaz qui est délimité par deux électrodes soumis à une

L'électrode centrale est portée à une haute tension positive ou négative, alors, que l'enceinte

est en général mise à la masse. Ce qui va créer un champ électrique, entre la paroi de

l'enceinte et l'électrode centrale. Le rayonnement incident ionise le gaz et les ions créés dans

le gaz remplissant l'enceinte sont donc, attirés par l'une des électrodes suivant leur signe et

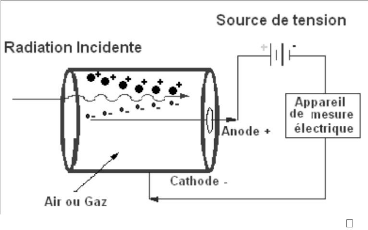
Figure 3.4. Principe de fonctionnement d'une chambre d'ionisation

collectés par cette électrode, d'où l'apparition d'un courant proportionnel à la dose de rayonnement reçue [23].

III.3.2.3.PropripFpsrdesrEhDP EtHrI'iRnisDFiRn :

Des chambres d'ionisation sont employées en radiothérapie et en radiologie diagnostic pour la

détermination de la dose de rayonnement.

Elles viennent dans diverses formes et tailles, selon les conditions spécifiques, mais généralem

1. Une chambre d'ionisation est fondamentalement une cavité remplie par gaz entourée d'un mur externe conducteur et en ayant une électrode de rassemblement centrale. Le mur et l'électrode de rassemblement sont séparés avec un isolateur de qualité pour réduire le courant
de fuite quand une tension de polarisation est appliquée à la chambre.

2. L'électrode de garde est habituellement fournie dans la chambre pour réduire plus loin la fuite de chambre. Elle arrête la fuite courante et lui permet de couler dans la terre, déviant
l'électrode de rassemblement. Elle assure également l'uniformité améliorée de champ en volume actif ou sensible de la chambre, avec une meilleure collection de charge.

3. Les mesures avec des chambres d'ionisation exigent une correction de la température et

de pression.

III.3.2.4.Les différents types de chambres :

Il existe différents types de chambre d'ionisation comme la volumineuse chambre à paroi d'air (utilisée uniquement dans les laboratoires standards), les chambres plates utilisées pour la dosimétrie des électrons (énergie inférieure à 10 MeV) ainsi que des photons de basse énergie,[39] sont principalement utilisées pour l'étalonnage des faisceaux d'électrons et les

mesures dans la

Et la chambre c

radiothérapie).

III.3.2.4.1.Chambres cylindriques :

La chambre d'ionisation cylindrique la plus utilisée en radiothérapie, est la chambre de type

Farmer (figure 3.5) qui est à l'origine construite par Baldwin, mais maintenant fourni par plusieurs fournisseurs, qui sert habituellement pour la calibration² absolue de faisceau de photon en radiothérapie.

E lle mesure l'ionisation produite dans son petit volume d'air (0.6 cm³) en collectant les
charges par deux électrodes (environ 300 V). La paroi de la chambre est faite d'un matériau qui est considéré comme équivalent à l'air (graphite) ou au tissu (PMMA).

La chambre est également connue comme chambre de dé³.

Figure 3.5. Schéma d'une chambre de type Farmer

D'autre chambre d'ionisation utilisée est de type Sem mesures de photon et d'électron de haute énergie.

E lle a les caractéristiques suivantes :

· Volumes utiles non étanches à l'air de 0,125 cm³ et 0,3 cm³.

· Appropriées pour une utilisation dans des fantômes d'eau.

· Réponse en énergie plate au sein d'une large plage d'énergie.

² La détermination de dose en états d'irradiation de référence IA

³ Vu que son volume sensible ressemble à celui du dé

Les chambres Semiflex sont conçues pour la dosimétrie thérapeutique, essentiellement pour les mesures de distributions de dose dans des fantômes d'eau motorisés. Elles sont pourvues d'une tige courte pour le montage et d'un câble de raccordement flexible. Pour l'énergie, la plage d'utilisation nominale s'étend de 30 KeV à 50 MeV (pour les photons) et de 6 MeV à 50 MeV (pour les électrons).

La paroi se compose de graphite recouvert d'une couche de protection en acrylique. Les anneaux de garde sont conçus pour atteindre le volume de mesure. Un capuchon d'accumulation en acrylique pour une mesure dans l'air.

Une correction de la densité de l'air est requise pour chaque mesure, et un appareil de contrôle de radioactivité est disponible en option. Les chambres possèdent un diamètre intérieur de 5,5 mm, elles se distinguent uniquement par la longueur du volume de mesure.

La chambre 0,125 cm³ est idéale pour la dosimétrie 3D dans des fantômes d'eau, car le volume de mesure est à peu près sphérique. Il en résulte donc une réponse angulaire plate sur un angle de #177; 160° et une résolution spatiale uniforme sur les trois axes du fantôme d'eau.[42]

Les chambres d'ionisation cylindriques utilisées dans le cadre de notre travail sont :

ü TM30013 chambre étanche Fermer PTW (figure 3.6).

ü TM31010 chambre Semiflex de 0,125 cm³(figure 3.7).[46]

Figure 3.6. Chambre d'ionisation de type Fermer

Figure 3.7. Chambres d'ionisations de type Semiflex

III.4. Le milieu de référence (Le fantôme) :

L'eau est recommandée dans l'AIEA (Code of Practice TRS -277 et TRS -381) comme milieu de référence pour mesure de la dose absorbée pour les deux faisceaux photons et électrons [43].

Le milieu de référence pour la dosimétrie en radiothérapie, est un fantôme de matériau pouvant absorber et diffuser les rayonnements ionisants de la même façon que le tissu biologique.

A cet effet, le fantôme doit avoir des densités électroniques et volumiques qui se rapprochent de celles des tissus. Cependant, ce sont les fantômes d'eau qui ont ces particularités (les tissus biologiques sont constitués de plus de 80 % d'eau) et sont les plus fréquemment utilisés. Ces fantômes sont recommandés par les protocoles dosimétriques les plus récents.

Le fantôme utilisé dans le présent travail est un fantôme MP3-P réservoir d'eau 3D motorisé pour les faisceaux de radiothérapie (figure 3.9), le MP3-P à la caractéristique suivante [41]:

· Réservoir d'eau 3D de haute précision.

· Taille et plage de déplacement optimisées pour le faisceau horizontal.

· Ouverture d'entrée étroite pour une précision optimale.

· Système intégré pour les tâches les plus exigeantes de dosimétrie relative et absolue dans une grande variété d'applications.

· Robuste, entièrement automatique de l'eau pour les scans 3D, équipé de parois du réservoir renforcé pour éviter toute déformation ou fuite.

· Tout-en-un avec table élévatrice facile manoeuvrable et intégré dans le réservoir d'eau pour pratique, «une installation rapide ».

· Dispositif de positionnement pour l'alignement du réservoir routable, précis, horizontal et vertical [44].

Figure 3.8. Fantôme d'eau MP3-P

Il existe d'autre type comme les Mini-fantômes cylindriques en acrylique sont conçus pour des mesures dans l'air ou pour mesurer des rapports de diffusion en volume conformément aux recommandations ESTRO (figure 3.10)

Le fantôme a une dimension extérieure de 40 mm de diamètre par 240 mm de hauteur, accueille un type de chambre d'ionisation Fermer parallèle à l'axe de fantôme, à une profondeur de 100 mm. [31,45]

Figure 3.9. Mini-fantômes ESTRO

Alternativement, on peut aussi utiliser comme fantômes des plaques constituées de plastique tels que le polystyrène, PMMA « PolyMethyl MethAcrylate » connu aussi sous des noms Commerciaux comme Lucite, Plexiglas ou Perspex, et certains plastiques équivalents eau, mais la détermination de la dose absorbée doit toujours se référer à l'eau. [41]

III.5. / VOITIRP~Tre :

La charge collecté (ou intensité) produite dans une chambre d'ionisation est extr~mement faible, sa mesure exige un dispositif très sensible appelé électromètre, dont l'impédance d'entrée est très élevée (> 10¹⁴ Ù).

Un électromètre idéal devrait posséder un affichage numérique et avoir un pouvoir de résolution de quatre chiffres ou 0.01%.

L'électromètre et la chambre d'ionisation peuvent ~tre étalonnés séparément. Cependant, il arrive que l'électromètre fasse partie intégrante du système de dosimétrie, et il faut alors étalonner la chambre d'ionisation et l'électromètre comme étant un seul système de mesure

[2, 40,41].

Figure 3.10. Electromètre PTW UNIDOS

III.6. Thermomètre et baromètre

Les mesures effectuées avec une chambre d'ionisation doivent être corrigées pour la température et la pression. Cette correction, dont le formalisme est donné par tous les protocoles dosimétriques existants, est indispensable pour ramener la valeur de la lecture donnée par la chambre aux conditions standards pour lesquelles cette chambre a été étalonnée.

La précision des baromètres et le thermomètre sont utilisés pour déterminer les facteurs de correction de la densité d'air pour la dosimétrie absolue.

L'instrument utilisé pour la mesure de la température et de la pression est illustré par la figure 3.12 [31,2].

Figure 3.11. Thermomètre baromètre

Chapitre IV

Résultats et discussion

IV .1. Introduction :

L'accélérateur SIEMENS PRIMUS du service de radiothérapie d'Oran fournit deux énergies en régime photon (choisir parmi une combinaison de six énergies disponibles, avec une un minimum de 6 MeV et un maximum de 18 MeV). Les données dosimétriques de base nécessaires pour l'exploitation, en routine clinique de l'accélérateur sont : pour les faisceaux de photons : les courbes de rendement en profondeur (PDD) pour champs ouverts et champs avec filtre en coin, les profils de doses latéraux pour champs ouverts, champs avec filtre en coin et pour un champ MLC, les facteurs d'output du collimateur (COF), les rapports de diffusion totale (TSF). De plus, nous avons mesuré la transmission de Block et porte cache pour un champ de 10x10.

Dans ce domaine, la précision requise est importante car elle est directement liée à la dose délivrée aux patients. De ce fait, avant l'utilisation de l'appareil, ces paramètres dosimétriques doivent être soigneusement vérifiés. Les procédures de vérification rentrent dans le cadre du contrôle de qualité de l'appareil. Dans le présent travail, nous avons procédé au contrôle des plus importants des paramètres dosimétriques. [2,47]

IV.2. Les données de photon à scanné :

IV. 2.1. Méthode et dispositifs utilisés :

Les mesures des courbes de rendement en profondeur et des profiles de dose ont été effectués a l'aide d'un fantôme de type PTW MP3, connecté a un micro-ordinateur pc, le système est piloté pour l'acquisition des données dosimétrique par un software MEPHYSTO mc². [47]

Les mesures dosimétrique sont effectuées à l'aide d'une chambre d'ionisation semiflex, de 0.125 3 de volume sensible de type PTW 31010. La chambre utilisée pour l'acquisition peut se déplacer dans les trois directions. Les dose absolues ont été mesurés avec une chambre d'ionisation cylindrique de type FARMER de volume sensible 0.6 ³, associé à un électromètre de type UNIDOS.

Page 68

IV. 2.1.1. Medical Physics Control Center MEPHYSTO mc2:

MEPHYSTO est un Logiciel pour l'acquisition des données de faisceaux thérapeutiques et l'analyse des données en radiothérapie, les caractéristiques de ce système sont :

> Centre de commande personnalisable pour toutes les tâches de dosimétrie en radiothérapie.

> Acquisition rapide des données de faisceaux avec graphique intégré.

> Liste des tâches.

> Mise en service rapide et précise avec une conversion par lots structurée pour tous les TPS reconnus.

> Supporte tous les protocoles d'analyse internationaux reconnus ainsi que les spécifications des distributeurs d'accélérateurs linéaires.

> Supporte l'analyse des données en ligne avec la Linear Array.

Figure 4.1. Système d'acquisition des données le software MEPHYSTO ^mc2

MEPHYSTO est l'interface utilisateur la plus avancée, vaste et auto-explicative pour la commande TBA et l'évaluation des données. Des solutions à toutes les tâches de dosimétrie importantes en radiothérapie sont implémentées dans des modules avec des flux de travail optimisés. MEPHYSTO est personnalisable et permet l'adaptation aux équipements disponibles. Un logiciel ou des documents supplémentaires sont intégrés. [48]

Page 69

IV. 2.1.2. Le positionnement des chambres affRQBDtiRn

:

Le positionnement de la chambre d'ionisation ce fait en suivant les étapes suivants :

> La chambre doit être verticale dans le fantôme.

> Fixer le système d'acquisition utilisé, si on prend des données à une SSD = 100 cm, la chambre sera fixé a une profondeur de 10 cm, donc les lasers ce coïncide avec la surface de l'eau (technique SSD). Si on prend les données à une SSD=90 cm, la position de la chambre et de 10 cm dans l'eau, la projection des lasers sera dans la chambre de meure (technique SAD).

La chambre est centrée approximativement sur l`axe centrale faisceau. le balayage de la chambre doit être horizontale et verticale dans le fantôme. [47,49]

Figure 4.2. Moyenne de positionnement de la chambre d'ionisation

IV. 2.2. Résultats :

Les données nécessaires pour chaque énergie de photon pour une SSD nominale de 90 cm on peut les prendre dans une autre SSD (100 cm).

Page 70

IV. 2.2.1 Les courbes de rendements en profondeur (PDD) pour les HUY MIMI-1tM7 11 ^RUxI- central :

Les courbes de rendement en profondeur ( PDD) pour les champs ouverts ont été mesurées pour les tailles de champs de : 3x3, 4x4, 5x5, 7x7 ,10x10 ,12x12 ,15x15 ,20x20 ,25x25 ,30x30, 35x35, 40x40 cm².

Les courbes de rendement en profondeur ont été mesurées à partir d1- 111 IVXIIc1-INIVIM une profondeur de 40 cm pour les deux faisceaux de photon.

Les figures 4.3 et 4.4 montrent les courbes de rendement en profondeur pour les faisceaux RX de 6 et 18MeV.

	120%
				3x3 4x4 5x5 7x7 10x10 12x12 15x15 20x20 25x25 30x30
	100% 80% 60% 40% 20%
D/Dmax (%)

0%

0 50 100 150 200 250 300 350

profondeur (mm)

Figure 4.3. Rendement en profondeur pour les faisceaux RX de 6MV

Page 71

CHAPITRE IV	RÉSULTATS ET DISCUSSION
			3x3 4x4 5x5 7x7 10x10 12x12 15x15 20x20 25x25 30x30 35x35 40x40

120%

100%

80%

D/Dmax (%)

60%

40%

20%

0%

0 50 100 150 200 250 300 350

profondeur(mm)

Figure 4.4 Rendement en profondeur pour les faisceaux RX de 18MV

Pour les champs avec filtre en coin, l'accélérateur dispose de quatre filtres avec des angles de 15°, 30°, 45° et 60°. Les courbes de rendement en profondeur ont été mesurés, pour les filtre de 15°, 30° et 45° pour les tailles de champs de 10×10, 20×20 et 25×25 alors que pour le

filtre de 60° les mesures ont été faites pour les tailles de champs de 10×10 et 20×20 .

Les figures 4.5 et 4.6 montrent les courbes de rendement en profondeur Pour les champs avec filtre en coin des faisceaux de RX pour l'énergie 6 et 18MeV.

Page 72

CHAPITRE IV

RÉSULTATS ET DISCUSSION

(W15) 5x5 (W15) 10x10 (W15) 20x20 (W15) 25x25 (W30) 5x5 (W30) 10x10 (W30) 20x20 (W30) 25x25 (W45) 5x5 (W45) 10x10 (W45) 20x20

D/Dmax (%)

120% 100% 80% 60%

40%

20%

0%

0 50 100 150 200 250 300 350

profondeur (mm)

Figure 4.5 Rendement en profondeur pour différent fitre en coin (W15, W30, W45, W60)
pour les faiseaux RX de 6MV

(W15) 5x5 (W15) 10x10 (W15) 25x25 (W30) 5x5 (W30) 10x10 (W30) 20x20 (W30) 25x25 (W45) 5x5 (W45) 10x10 (W45) 20x20 (W45) 25x25 (W60) 20x20

0 50 100 150 200 250 300 350

profondeur (mm)

120%

100%

D/Dmax (%)

80% 60% 40%

20%

0%

Figure 4.6 Rendement en profondeur pour différent filtre en coin (W15, W30, W45, W60)
pour les faiseaux RX de 18MV

Page 73

IV. 2.2.1.1. Discutions et Interprétation :

Nous remarquons d'après les résultats obtenus que les rendements en profondeur, mesurés à l'aide d'une chambre d'ionisation pour différents taille du champ et filtre en coin sont confondus. Ceci constitue un très bon résultat.

IV. 2.2.2. Mesure des profils latéraux de doses :

Les profils de dose pour les champs ouverts ont été mesurés pour les mêmes tailles de champs
que les courbes de rendements en profondeur (5×5, 10×10, 15×15, 20×20, 25×25,
30×30 ) avec l'explorateur de faisceau MEPHYSTO. Les profondeurs auxquelles ont été

mesurés les profils sont : d , 5, 10, 20, 30 .avec un incrément de 2 .

Pour les profils de dose diagonale ont été mesurés pour la plus large taille de champ de
l'accélérateur, les profondeurs auxquelles ont été mesurés les profils sont : - d , d -0.5,

d +0.5, 0.5, 1.0, 2.0, 3.0, 5.0, 10.0, 20.0, 30.0 .

Les profils de dose pour un champ MLC, ont été mesurés pour une taille de champ de 20x20 avec un port large de 10 cm asymétriques MLC avec une banque de feuilles à 7,5 cm du CAX et d'autres banque de feuilles au 2,5 cm de CAX (à l'isocentre). Pour les profondeurs - d , 5,0, 10,0 et 20,0 cm.

Pour les champs avec filtre en coin, les profils ont été mesurés, pour les filtre de 15°, 30° et

45° pour les tailles de champs de 10×10, 20×20 et 25×25 alors que pour le filtre de 60°

les mesures ont été faites pour les tailles de champs de 10×10 et 20×20 . Les profondeurs

de mesures sont : 5, 10 et 20 . Avec un incrément de 2 .

Les données des mesures des profils, pour les champs ouverts, les profils de dose diagonale et les profils pour les champs avec filtre en coin, sont présentées dans les figures suivant.

Page 74

IV. 2.2.2.1. Profil de dose pour un champ ouvert :

OCR (%)

-80 -60 -40 -20 0 20 40 60 80

Y (mm)

dmax 5cm 10cm

20cm 30cm

OCR(%)

-100 -50 0 50 100

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.7. Profils de dose pour champ ouvert de 5×5 avec une énergie de 6MeV

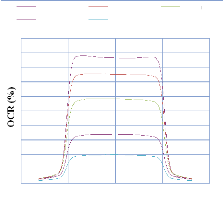
-100 -50 0 50 100

Y (mm)

dmax 5cm 10cm

20cm 30cm

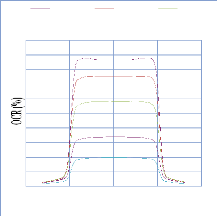
dmax 5cm 10cm

20cm 30cm

-100 -50 0 50 100

X (mm)

Figure 4.8. Profils de dose pour champ ouvert de 10×10 avec une énergie de 6MeV

-150 -100 -50 0 50 100 150

Y (mm)

dmax 5cm 10cm

20cm 30cm

-200 -100 0 100 200

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.9. Profils de dose pour champ ouvert de 15×15 avec une énergie de 6MeV

dmax 5cm 10cm

20cm 30cm

-200 -100 0 100 200

Y (mm)

dmax 5cm 10cm

20cm 30cm

-200 -100 0 100 200

X (mm)

Figure 4.10. Profils de dose pour champ ouvert de 20×20avec une énergie de 6MeV

Page 76

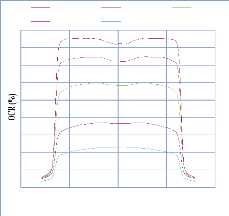
-200 -100 0 100 200

Y (mm)

dmax 5cm 10cm

20cm 30cm

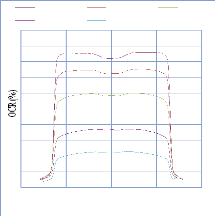
-200 -100 0 100 200

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.11. Profils de dose pour champ ouvert de 25×25 avec une énergie de 6MeV

-400 -200 0 200 400

Y (mm)

dmax 5cm 10cm

20cm 30cm

-400 -200 0 200 400

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.12. Profils de dose pour champ ouvert de 30×30 avec une énergie de 6MeV

Page 77

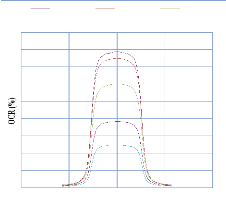
-100 -50 0 50 100

Y (mm)

dmax 5cm 10cm

20cm 30cm

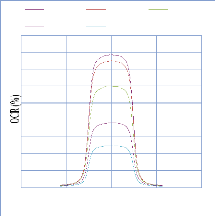
dmax 5cm 10cm

20cm 30cm

-100 -50 0 50 100

X (mm)

Figure 4.13. Profils de dose pour champ ouvert de 5×5 avec une énergie de 18MeV

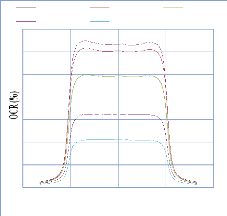
-100 -50 0 50 100

Y (mm)

dmax 5cm 10cm

20cm 30cm

-100 -50 0 50 100

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.14. Profils de dose pour champ ouvert de 10×10 avec une énergie de 18MeV

Page 78

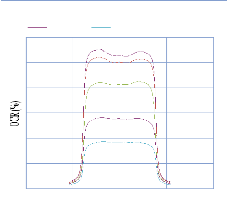
-200 -100 0 100 200

Y (mm)

dmax 5cm 10cm

20cm 30cm

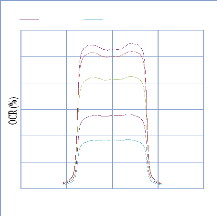
-200 -100 0 100 200

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.15. Profils de dose pour champ ouvert de 15×15 avec une énergie de 18MeV

-200 -100 0 100 200

Y (mm)

dmax 5cm 10cm

20cm 30cm

-200 -100 0 100 200

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.16. Profils de dose pour champ ouvert de 20×20 avec une énergie de 18MeV

Page 79

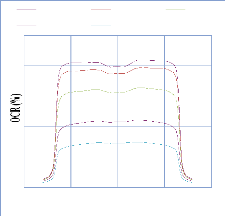
-200 -100 0 100 200

Y (mm)

dmax 5cm 10cm

20cm 30cm

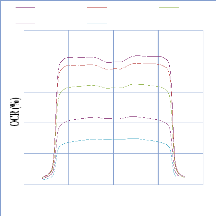
-200 -100 0 100 200

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.17. Profils de dose pour champ ouvert de 25×25 avec une énergie de 18MeV

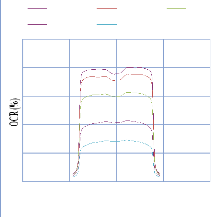
-400 -200 0 200 400

Y (mm)

dmax 5cm 10cm

20cm 30cm

-400 -200 0 200 400

X (mm)

dmax 5cm 10cm

20cm 30cm

Figure 4.18. Profils de dose pour champ ouvert de 30×30 avec une énergie de 18MeV

IV. 2.2.2.1.1 Discutions et interprétation :

On observe dans les figures des résultats un large plateau pour les différent taille du champ représente le maximum de dose ce qui permet de situer la zone d'homogénéité dans laquelle la dose décroît plus ou moins vite, elle correspond à la pénombre et elle est définie par la distance séparant l'isodose 80% et l'isodose 20% de la dose maximale sur l'axe du faisceau.

Les profils obtenus étant symétriques par rapport au centre, on peut déduire que la source est bien centrée sur l'axe du collimateur.

Page 81

IV. 2.2.2.2. Profil de dose diagonale :

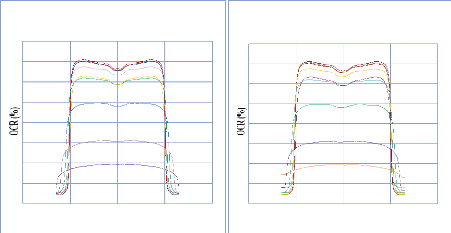
-400 -200 0 200 400

X(mm)

dmax dmax-0.5 dmax+0.5

5cm 30cm 50cm

100cm 200cm 300cm

-400 -200 Y 0 (mm) 200 400

dmax dmax-0.5 dmax+0.5

5cm 30cm 50cm

100cm 200cm 300cm

Figure 4.19. Profils de dose diagonale pour une énergie de 6MeV

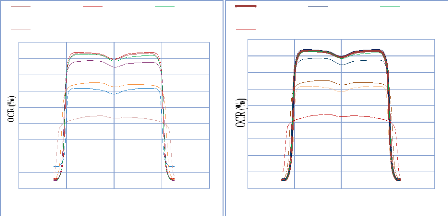
-400 -200 0 200 400

X(mm)

dmax dmax-0.5 dmax+0.5

50cm 100cm 200cm

300cm

-400 -200 0 200 400

Y(mm)

dmax dmax-0.5 dmax+0.5

50cm 100cm 200cm

300cm

Figure 4.20. Profils de dose diagonale pour une énergie de 18MeV

Page 82

IV. 2.2.2.3. Profil de dose pour un champ MLC :

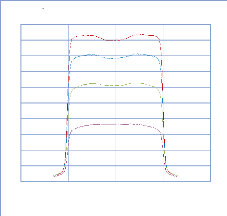
Dose en %

-200 -100 0 100 200

Y ( mm)

dmax 5cm 10cm 20cm

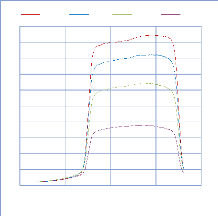
Dose en %

-100 -50 0 50 100

X (mm)

dmax 5cm 10cm 20cm

Figure 4.21. Profils de dose pour un champ MLC avec une énergie de 6MeV

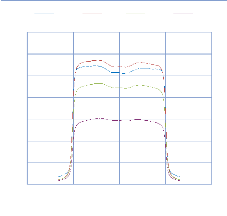
Dose en %

-200 -100 0 100 200

Y (mm)

dmax 5cm 10cm 20cm

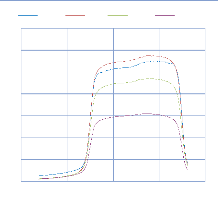
Dose en %

-100 -50 0 50 100

X (mm)

dmax 5cm 10cm 20cm

Figure 4.22. Profils de dose pour un champ MLC avec une énergie de 18MeV

Page 83

IV. 2.2.2.3.1. Discutions et interprétation :

On observe dans les figures des résultats pour un champ MLC que la zone d'homogénéité du faisceau est entre -10cm et +10cm pour l'axe Y et entre -5cm et +5cm pour l'axe X.

Les profils obtenus étant symétriques par rapport au centre pour l'axe Y mais décaler pour l'axe X, on pue dire que lorsque on utilise un champ MLC on a une optimisation de la distribution de la dose et les faisceaux de photons son atténuer.

IV. 2.2.2.4. Profil de dose pour un champ avec filtre en coin :

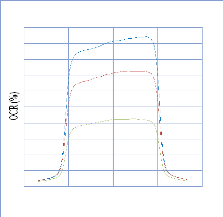
-100 -50 0 50 100

Y(mm)

5cm 10cm 20cm

-100 -50 0 50 100

X(mm)

5cm 10cm 20cm

Figure 4.23. Profils avec filtre en coin de 15° pour un champ de 10×10 et une énergie de
6MeV

Page 84

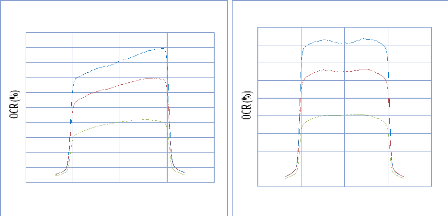
5cm 10cm 20cm

-200 -100 0 100 200

Y(mm)

5cm 10cm 20cm

-200 -100 0 100 200

X(mm)

Figure 4.24. Profils avec filtre en coin de 15° pour un champ de 20×20 et une énergie de
6MeV

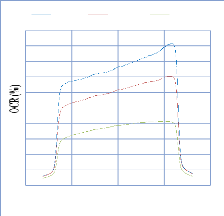
-200 -100 0 100 200

Y(mm)

5cm 10cm 20cm

-200 -100 0 100 200

X(mm)

5cm 10cm 20cm

Figure 4.25. Profils avec filtre en coin de 15° pour un champ de 25×25 et une énergie de
6MeV

Page 85

5cm 10cm 20cm

-100 -50 0 50 100

Y(mm)

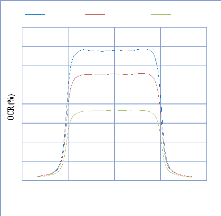
-100 -50 0 50 100

X(mm)

5cm 10cm 20cm

Figure 4.26. Profils avec filtre en coin de 15° pour un champ de 10×10 et une énergie de
18MeV

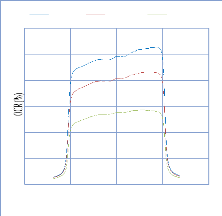
-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

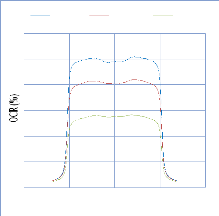
-200 -100 0 100 200

X(mm)

5cm 10cm 20cm

Figure 4.27. Profils avec filtre en coin de 15° pour un champ de 20×20 et une énergie de
18MeV

Page 86

-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

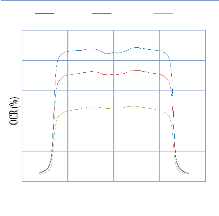
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.28. Profils avec filtre en coin de 15° pour un champ de 25×25 et une énergie de
18MeV

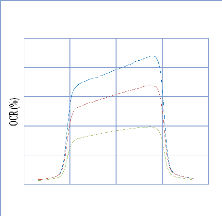
-100 -50 0 50 100

Y (mm)

5cm 10cm 20cm

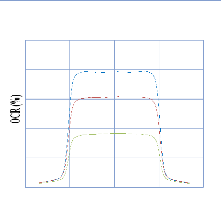
-100 -50 0 50 100

X (mm)

5cm 10cm 20cm

Figure 4.29 Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de
6MeV

-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

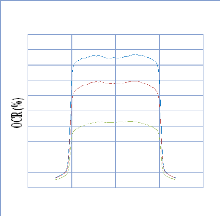
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.30. Profils avec filtre en coin de 30° pour un champ de 20×20 et une énergie de
6MeV

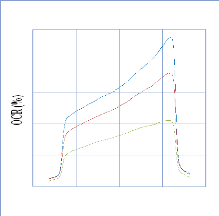
-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

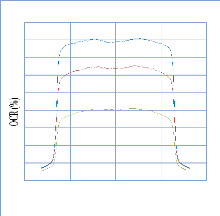
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.31. Profils avec filtre en coin de 30° pour un champ de 25×25 et une énergie de
6MeV

-100 -50 0 50 100

Y (mm)

5cm 10cm 20cm

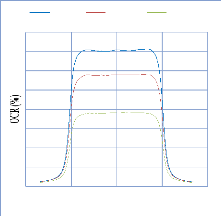
-100 -50 0 50 100

X(mm)

5cm 10cm 20cm

Figure 4.32. Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de
18MeV

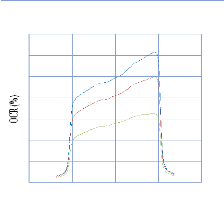
5cm 10cm 20cm

-200 -100 0 100 200

Y (mm)

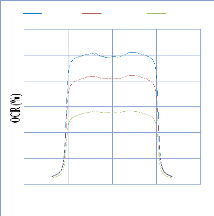
-200 -100 0 100 200

X(mm)

5cm 10cm 20cm

Figure 4.33. Profils avec filtre en coin de 30° pour un champ de 20×20 et une énergie de
18MeV

-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

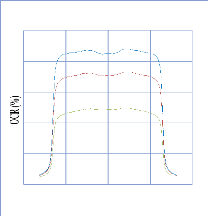
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.34. Profils avec filtre en coin de 30° pour un champ de 25×25 et une énergie de
18MeV

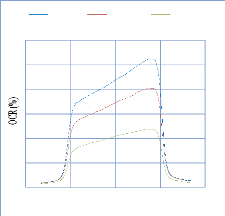
-100 -50 0 50 100

Y (mm)

5cm 10cm 20cm

-100 -50 0 50 100

X (mm)

5cm 10cm 20cm

Figure 4.35. Profils avec filtre en coin de 45° pour un champ de 10×10 et une énergie de
6MeV

-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

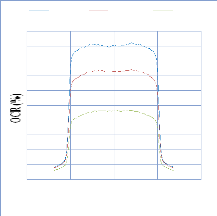
5cm 10cm 20cm

-200 -100 0 100 200

X(mm)

Figure 4.36. Profils avec filtre en coin de 45° pour un champ de 20×20 et une énergie de
6MeV

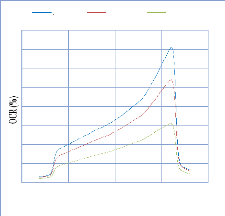
-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

-200 -100 0 100 200

X(mm)

5cm 10cm 20cm

Figure 4.37. Profils avec filtre en coin de 45° pour un champ de 25×25 et une énergie de
6MeV

5cm 10cm 20cm

-100 -50 0 50 100

Y (mm)

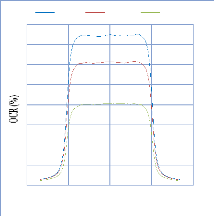
-100 -50 0 50 100

X (mm)

5cm 10cm 20cm

Figure 4.38. Profils avec filtre en coin de 45° pour un champ de 10×10 et une énergie de
18MeV

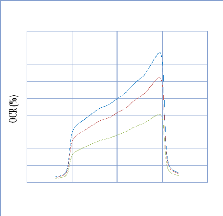
5cm 10cm 20cm

-200 -100 0 100 200

Y (mm)

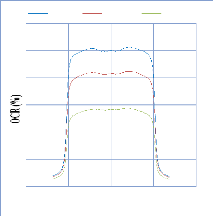
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.39. Profils avec filtre en coin de 45° pour un champ de 20×20 et une énergie de
18MeV

-200 -100 0 100 200

Y (mm)

5cm 10cm 20cm

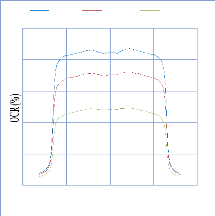
-200 -100 0 100 200

X(mm)

5cm 10cm 20cm

Figure 4.40. Profils avec filtre en coin de 45° pour un champ de 25×25 et une énergie de
18MeV

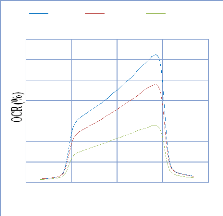
-100 -50 0 50 100

Y (mm)

5cm 10cm 20cm

-100 -50 0 50 100

X (mm)

5cm 10cm 20cm

Figure 4.41. Profils avec filtre en coin de 60° pour un champ de 10×10 et une énergie de
6MeV

5cm 10cm 20cm

-200 -100 0 100 200

Y (mm)

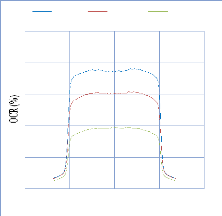
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.42. Profils avec filtre en coin de 60° pour un champ de 20×20 et une énergie de
6MeV

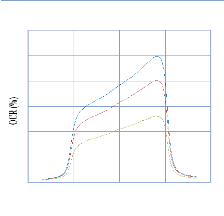
-100 -50 0 50 100

Y (mm)

5cm 10cm 20cm

-100 -50 0 50 100

X (mm)

5cm 10cm 20cm

Figure 4.43. Profils avec filtre en coin de 60° pour un champ de 10×10 et une énergie de
18MeV

Page 94

5cm 10cm 20cm

-200 -100 0 100 200

Y (mm)

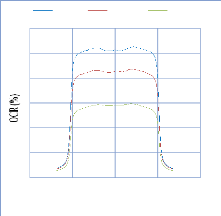
-200 -100 0 100 200

X (mm)

5cm 10cm 20cm

Figure 4.44. Profils avec filtre en coin de 60° pour un champ de 20×20 et une énergie de
18MeV

IV. 2.2.2.4.1. Discutions et interprétation :

On observe dans les figures des résultats pour un champ avec filtre en coin que les courbes de profil pour l'axe Y sont déformées donnant une direction oblique par rapport à l'axe du faisceau.

L'atténuation du faisceau est plus importante du coté où l'épaisseur du filtre est plus grande.

Page 95

IV.3. Les données photon non -scan :

IV.3.1. Mesure des coiimateur :

Le facteur de diffusion total (Total scatter factor TSCF'S ou Scp) est mesurée dans un fantôme d'eau MP3-P à la profondeur du maximum de dose pour les mêmes tailles de champ de rendement en profondeur.

La valeur du facteur du collimateur (COF collimator factor ou Sc) est effectuée dans un mini-fantôme en acrylique à la profondeur du maximum de dose pour les mêmes tailles de champ.

Les mesures du COF et TSCF ont été effectuées avec une chambre cylindrique de type Fermer de 0.6 cm³ de volume sensible (TM30013) connectée à un électromètre du type PTW UNIDOS.

La valeur de COF et de TSCF vont être utilisée pour la détermination du PSCF (Peak Scatter Factor).

PSCF = T

(4.1)

Pour chaque énergie de photon, les données sont mesurées à la profondeur de référence (10 cm)

Les figures 4.43 et 4.44 montrent la variation du COF du TSCF et du PSCF en fonction de la taille de champ pour les faisceaux de photons de 6 et 18 MeV.

Les valeurs de ces coefficients sont données dans le tableau 4.1.

Page 96

	6 MeV			18 MeV
Taille de champ (cm Xcm)	TSCF	CF (Sc)	PSCF	TSCF	CF (Sc)	PSCF
3 X3	0.807	0.920	0.877	0.819	0.906	0.904
4 X4	0.856	1.028	0.832	0.882	0.945	0.933
5 X5	0.887	0.962	0.921	0.916	0.922	0.993
7 X7	0.939	0.981	0.957	0.958	0.977	0.980
10 X10	1	1	1	1	1	1
12 X12	1.03	1.009	1.020	1.020	1.006	1.013
15 X15	1.064	1.008	1.055	1.042	1.012	1.029
20 X20	1.104	1.027	1.074	1.067	1.022	1.044
25 X25	1.132	13.00	1.099	1.083	1.025	1.056
30 X30	1.184	1.032	1.147	1.094	1.029	1.063
35 X35	1.165	1.034	1.127	1.104	1.029	1.073
40 X40	1.179	1.034	1.14	1.110	1.025	1.082

Tableau 4.1. Valeur de COF, TSCF et PSCF pour les faisceaux de photons de 6 et 18 MeV.

Page 97

CHAPITRE IV		RÉSULTATS ET DISCUSSION
1,3 1,2 1,1 1 0,9 0,8 0,7				TSCF CF PSCF

0 5 10 15 20 25 30 35 40 45

Figure 4.45.Variation du CF, du TSCF et du PSCF en fonction de la taille du champ
pour le faisceau X6

1,15 1,1 1,05 1 0,95 0,9 0,85 0,8

TSCF CF PSCF

0 5 10 15 20 25 30 35 40 45

Figure 4.46. Variation du CF, du TSCF et du PSCF en fonction de la taille du
champ pour le faisceau X18

Page 98

IV.3.2. Facteurs de transmission de block et porte cache :

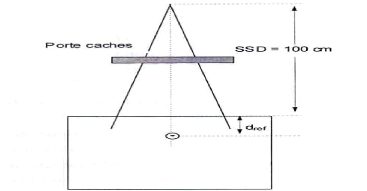
Figure 4.47. Dispositif expérimental pour la mesure du facteur de transmission du

porte cache.

Pour la détermination des facteurs de transmission des porte s caches nous avons mesuré la valeur de la dose absorbée pour un champ de 10 x 10 cm à une distance source-surface de 100 cm, à une profondeur de référence de 10 cm avec et sans porte cache. La valeur du facteur de transmission est obtenue par le rapport des deux mesures.

Les valeurs obtenues pour les deux faisceaux RX sont données dans le tableau 4.2

Avec Port cache

Sans Port cache

6MeV

18MeV

6MeV

18MeV

12.18nC

14.23nC

12.33nC

14.44nC

Tableau 4.2. Valeur obtenue pour les deux faisceaux RX avec et sans port cache

La transmission par blocs peut ~tre mesuré on utilise un fantôme d'eau, les mesure sont effectué avec une chambre d'ionisation positionner à l'isocentre. L'épaisseur de blocs et de 7.5 à 8cm.

Mesurent le débit de dose pour un champ 10 )(10 cm² jà l'isocentre avec le bloc de cerrobend, ensuite on enlève le bloc de cerrobend et on mesure le débit de dose.

Le rapport des lectures est la transmission par bloc. Le nombre de HVL peut être calculé par la formule suivante

) (4.2)

Avec BLOC

Sans BLOC

6MeV

18MeV

6MeV

18MeV

0.4625nC

0.5825nC

12.33nC

14.44nC

Tableau 4.3. Valeur obtenue pour les deux faisceaux RX avec et sans BLOC

	T= (Rb/RWb	HVL
6MeV	0.0375	4.73
18MeV	0.0403	4.63

Tableau 4.4. Valeur obtenue pour la transmission par bloc

IV.4. comparaison entre les données mesurer et calculer :
IV.4.1. Pour les rendements en profondeur :

3x3 calculer 4x4 calculer 5x5 calculer 7x7 calculer 10x10 calculer 12x12 calculer 15x15 calculer 20x20 calculer 25x25 calculer 30x30 calculer 35x35 calculer 40x40calculer 3x3 mesurer 4x4 mesurer 5x5 mesurer 7x7 mesurer 10x10 mesurer 12x12 mesurer

0%

0 50 100 150 200 250 300 350 400 450

profondeur (mm)

D/Dmax (%)

100%

40%

80%

60%

20%

120%

Figure 4.48. Comparaison entre les rendements en profondeur pour les faisceaux RX de
6MV mesurer et calculer

(W15) 5x5 calculer (W15) 10x10 calculer (W15) 20x20 calculer (W15) 25x25 calculer (W30) 5x5 calculer (W30) 10x10 calculer (W30) 20x20 calculer (W30) 25x25calculer (W45) 5x5 calculer (W45) 10x10 calculer (W45)20x20 calculer (W45) 25x25 calculer (W60) 5x5 calculer (W60) 10x10 calculer (W60) 20x20 calculer (W15) 5x5 mesurer (W15) 10x10 mesurer (W15) 20x20 mesurer (W15) 25x25 mesurer (W30) 5x5 mesurer (W30) 10x10 mesurer (W30) 20x20 mesurer

D/Dmax (%)

120%

100%

40%

80%

60%

20%

0%

0 100 200 300 400 500

profondeur (mm)

Figure 4.49. Comparaison entre les rendements en profondeur pour différent filtre en coin
(W15, W30, W45, W60) pour les faiseaux RX de 6MV Mesurer et calculer

D/Dmax (%)

120%

100%

40%

80%

60%

20%

0%

(W15) 5x5 calculer (W15) 10x10 calculer (W15) 20x20 calculer (W15) 25x25 calculer (W30) 5x5 calculer (W30)10x10 calculer (W30) 20x20 calculer (W30) 25x25 calculer (W45) 5x5 calculer (W45) 10x10 calculer (W45) 20x20 calculer (W45) 25x25 calculer (W60) 5x5 calculer (W60) 10x10 calculer (W60) 20x20 calculer (W15) 5x5 mesurer (W15) 10x10 mesurer (W15) 25x25 mesurer (W30) 5x5 mesurer

0 100 200 300 400 500

profondeur (mm)

Figure 4.50. Comparaison entre les rendements en profondeur pour différent filtre en coin
(W15, W30, W45, W60) pour les faiseaux RX de 18MV Mesurer et calculer

0 50 100 150 200 250 300 350 400 450

profondeur (mm)

D/Dmax (%)

120%

100%

40%

80%

60%

20%

0%

3x3 calculer 4x4 calculer 5x5 calculer 7x7 calculer 10x10 calculer 12x12 calculer 15x15 calculer 20x20 calculer 25x25 calculer 30x30 calculer 35x35 calculer 40x40 calculer 3x3 mesurer 4x4 mesurer 5x5 mesurer 7x7 mesurer 10x10 mesurer 12x12 mesurer 15x15 mesurer 20x20 mesurer 25x25 mesurer 30x30 mesurer 35x35 mesurer 40x40 mesurer

Figure 4.51. Comparaison entre les rendements en profondeur pour les faisceaux RX de
18MV mesurer et calculer

IV.4.1.1. Discutions et interprétation :

La courbe de rendement en profondeur déterminée expérimentalement a été comparée à celle calculer par le TPS.

DIESrèAR:Ds courbes 4.46, 4.47, 4.48 et 4.49 OURVIFIRît aWIFITILSIRIRQWENIIX 3741Qdr11 un maximum à Z max .-,' 15 mm oil il y a un dépôt maximum de dose (région de build-up), puis une décroissance de dose en profondeur, pratiquement exponentielle, correspondant à (¹134éQuEARQ du IaBFID.

La variation de dose en profondeur concorde parfaitement avec ce qui est calculé par le TPS La différence de la profondeur de dose maximale qui devrait être de 5 mm, est due au fait que ClfFKEP EURVRQiADARQ MIEVI Q'Fst SIN ITORut EEESYCSRMIRTRQIIGIEDNd-up.

IV.4.2. Pour les profils de dose avec filtre en coins:

-150 -100 -50 0 50 100 150

5cm calculé 10cm calculé 20cm calculé

5cm mesuré 10cm mesuré 20cm mesuré

Figure 4.52. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de
10×10 et une énergie de 6MeV

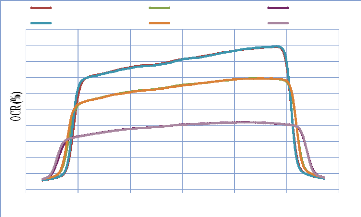
-150 -100 -50 0 50 100 150

5cm calculer 10cm calculer 20cm calculer

5cm mesurer 10cm mesurer 20cm mesurer

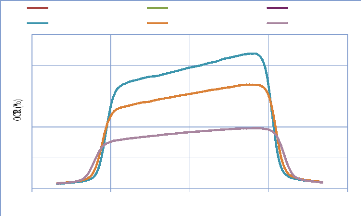
-100 -50 0 50 100

5 cm calculé 1O cm calculé 20 cm calculé

5 cm mesuré 10 cm mesuré 20 cm mesuré

-300 -200 -100 0 100 200 300

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

-200 -150 -100 -50 0 50 100 150 200

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

Figure 4.53. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de
20×20 et une énergie de 6MeV

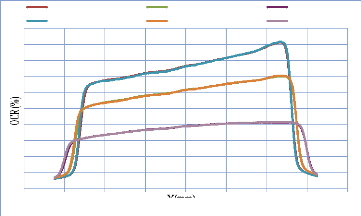
-200 -150 -100 -50 0 50 100 150 200

5cm calculer 10 cm calculer 20cm calculer

5cm mesurer 10cm mesurer 20cm mesurer

Figure 4.54. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de
25×25 et une énergie de 6MeV

Figure 4.55. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de
10×10 et une énergie de 6MeV

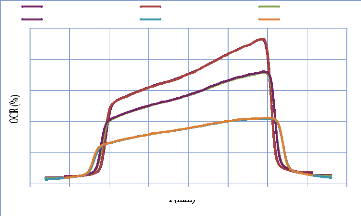
-200 -150 -100 -50 0 50 100 150 200

5cm calculé 5m mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

Figure 4.56. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de
20×20 et une énergie de 6MeV

Figure 4.57. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de
25×25 et une énergie de 6MeV

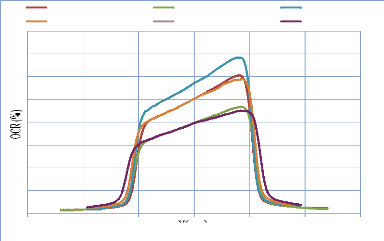
-150 -100 -50 0 50 100 150

5 cm 10 cm 5cm mesuré

10cm mesuré 20cm mesuré 20cm calculé

Y(m

Figure 4.58. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de
10×10 et une énergie de 6MeV

Figure 4.59. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de
20×20 et une énergie de 6MeV

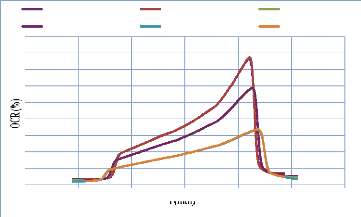
-300 -200 -100 0 100 200 300

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

Figure 4.60. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de
25×25 et une énergie de 6MeV

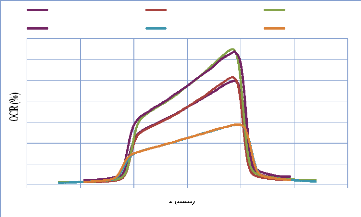
-150 -100 -50 0 50 100 150

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

-150 -100 -50 0 50 100 150

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

-200 -150 -100 -50 0 50 100 150 200

5 cm calculé 10 cm calculé 20 cm calculé

5 cm mesuré 10 cm mesuré 20 cm mesuré

-200 -150 -100 -50 0 50 100 150 200

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

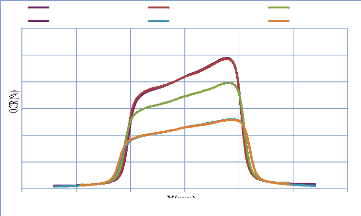
-150 -100 -50 0 50 100 150

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20cm mesuré

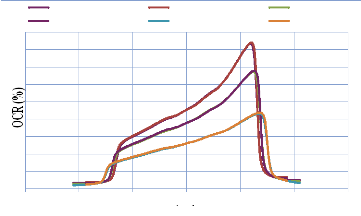
-300 -200 -100 0 100 200 300

5cm calculé 5cm mesuré 10cm calculé

10cm mesuré 20cm calculé 20 mesuré

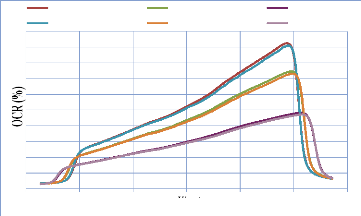
-150 -100 -50 0 50 100 150

5 cm calculé 10 cm calculé 20 cm calculé

5 cm mesuré 10 cm mesuré 20 cm mesuré

Figure 4.61. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de
10×10 et une énergie de 6MeV

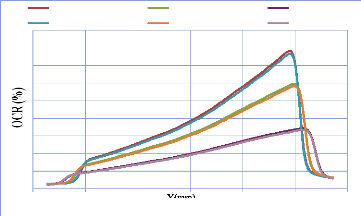
-150 -100 -50 0 50 100 150

5cm calculé 10cm calculé 20cm calculé

Y⁽mm

5cm mesuré 10cm mesuré 20cm mesuré

Figure 4.62. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de
20×20 et une énergie de 6MeV

Figure 4.63. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de
10×10 et une énergie de 18MeV

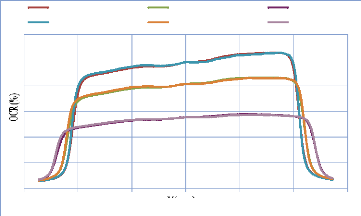
-150 -100 -50 0 50 100 150

5cm calculé 10cm calculé 20cm calculé

Y⁽

5cm mesuré 10cm mesuré 20cm mésuré

Figure 4.64. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de
20×20 et une énergie de 18MeV

Figure 4.65. Comparaison entre les Profils avec filtre en coin de 15° pour un champ de
25×25 et une énergie de 18MeV

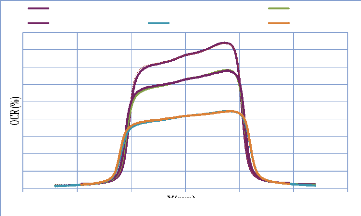
-150 -100 -50 0 50 100 150

5cm calculé 5cm mesuré 10cm calculé

Y⁽mm

10cm mesuré 20cm calculé 20cm mesuré

Figure 4.66. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de
10×10 et une énergie de 18MeV

Figure 4.67. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de
20×20 et une énergie de 18MeV

-300 -200 -100 0 100 200 300

5cm calculé 5cm mesuré 10cm calculé

Y(mm

10cm mesuré 20cm calculé 20cm mesuré

Figure 4.68. Comparaison entre les Profils avec filtre en coin de 30° pour un champ de
25×25 et une énergie de 18MeV

Figure 4.69. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de
10×10 et une énergie de 18MeV

-200 -150 -100 -50 0 50 100 150 200

5cm calculé 5cm mesuré 10cm calculé

Y(mm

10cm mesuré 20cm calculé 20cm mesuré

Figure 4.70. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de
20×20 et une énergie de 18MeV

Figure 4.71. Comparaison entre les Profils avec filtre en coin de 45° pour un champ de
25×25et une énergie de 18MeV

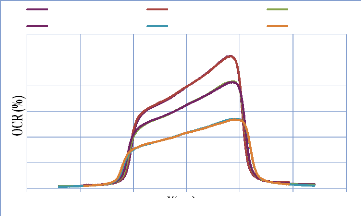
-150 -100 -50 0 50 100 150

5cm calculé 5cm mesuré 10cm calculé

Y⁽mm

10cm mesuré 20cm camculé 20cm mesuré

Figure 4.72. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de
10×10et une énergie de 18MeV

Figure 4.73. Comparaison entre les Profils avec filtre en coin de 60° pour un champ de
20×20et une énergie de 18MeV

IV.4.3. Pour les profils de dose avec champ ouvert :

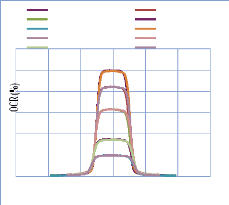
dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

-150 -100 -50 0 50 100 150

y(mm)

	dmax calculé 5cm calculé 10cm calculé 20cm calculé 30cm calculé dmax mesuré 5cm mesuré 10cm mesuré 20cm mesuré 30cm mesuré
-200 -100 0 100 200 X(mm)

Figure 4.74. Comparaison entre les Profils pour un champ ouvert de 5×5et une énergie de
6MeV

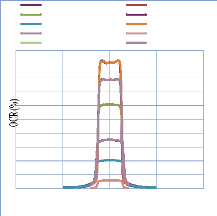
-400 -200 0 200 400

X(mm)

dmax calculé 5cm calculé

10cm calculé 20cm calculé

30cm calculé dmax mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

	dmax calculé 5 cm calculé 10 cm calculé 20 cm calculé 30 cm calculé dmax mesuré 5 cm mesuré 10 cm mesuré 20 cm mesuré 30 cm mesuré
-400 -200 0 200 400 Y(mm)

Figure 4.75. Comparaison entre les Profils pour un champ ouvert de 10×10 et une énergie
de 6MeV

-300 -200 -100 0 100 200 300

X(mm)

dmax calculé 5cm calculé

10cm calculé 20cm calculé

30cm calculé dmax mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

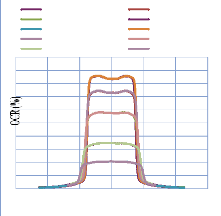
-300 -200 -100 0 100 200 300

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.76. Comparaison entre les Profils pour un champ ouvert de 15×15et une énergie
de 6MeV

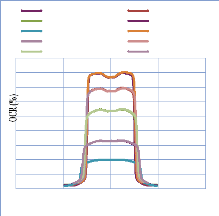
dmax calculé 5cm calculé

10cm calculé 20cm calculé

30cm calculé dmax mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

-400 -200 X(mm) 0 200 400

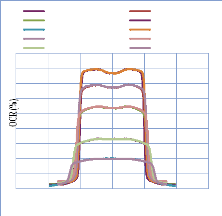
-300 -200 -100 0 100 200 300

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.77. Comparaison entre les Profils pour un champ ouvert de 20×20et une énergie
de 6MeV

-400 -200 0 200 400

X(mm)

dmax calculé 5cm calculé

10cm calculé 20cm calculé

30cm calculé dmax mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

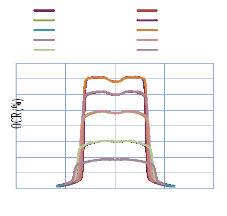
-400 -200 0 200 400

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.78. Comparaison entre les Profils pour un champ ouvert de 25×25et une énergie
de 6MeV

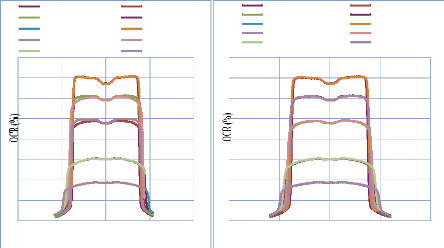
-400 -200 0 200 400

X(mm)

dmax calculé 5cm calculé

10cm calculé 20cm calculé

30cm calculé dmax mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

-400 -200 0 200 400

y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

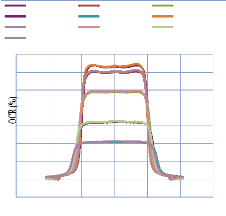
-150 -100 -50 0 50 100 150

3cm calculé 5cm calculé 10cm calculé

20cm calculé 30cm calculé 3cm mesuré

5cm mesuré 10cm mesuré 20cm mesuré

30cm mesuré

X(mm)

-100 -50 0 50 100

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.79. Comparaison entre les Profils pour un champ ouvert de 30×30et une énergie
de 6MeV

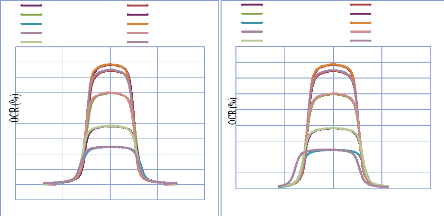
-100 -50 0 50 100

X(mm)

3 cm calculé 5cm calculé

10 cm calculé 20cm calculé

30cm calculé 3cm mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

-100 -50 0 50 100

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.80. Comparaison entre les Profils pour un champ ouvert de 5×5et une énergie de
18MeV

Figure 4.81. Comparaison entre les Profils pour un champ ouvert de 10×10et une énergie
de 18MeV

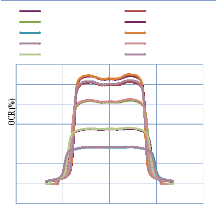
-200 -100 0 100 200

3 cm calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé 3 cm mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

X(mm)

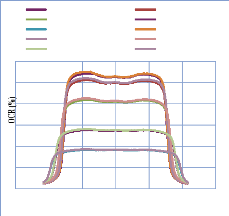
-150 -100 -50 0 50 100 150

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.82. Comparaison entre les Profils pour un champ ouvert de 15×15et une énergie
de 18MeV

-200 -100 0 100 200

3cm calculé 5cm calculé

10cm calculé 20cm calculé

30cm calculé 3cm mesuré

5cm mesuré 10cm mesuré

20cm mesuré 30cm mesuré

X(mm)

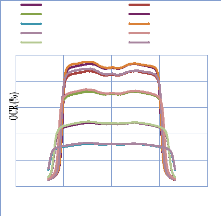
-200 -100 0 100 200

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.83. Comparaison entre les Profils pour un champ ouvert de 20×20et une énergie
de 18MeV

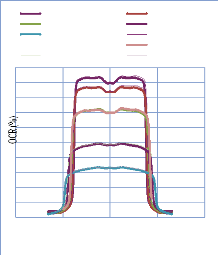
-400 -200 0 200 400

X(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax calculé

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

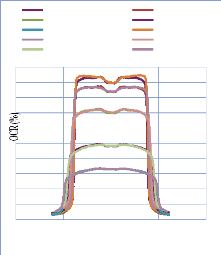
-400 -200 0 200 400

Y(mm)

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Figure 4.84. Comparaison entre les Profils pour un champ ouvert de 30×30et une énergie
de 18MeV

-300 -200 -100 0 100 200 300

X(mm)

dmax mesuré dmax-0.5 mesuré dmax+0.5 mesuré 50cm mesuré 100cm mesuré 200cm mesuré 300cm mesuré dmax calculé dmax-0.5 calculé dmax+0.5 calculé 50cm calculé 100cm calculé 200cm calculé 300cm calculé

IV.4.4. Pour les profils de dose diagonale :

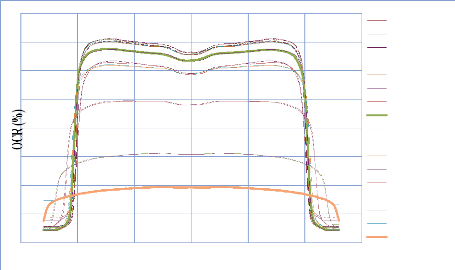
-300 -200 -100 0 100 200 300

X(mm)

dmax mesuré dmax calculé dmax-0.5 mesuré dmax-0.5 calculé dmax+0.5 mesuré dmax+0.5 calculé 5cm mesuré

5cm calculé

30cm mesuré 30cm calculé 50cm mesuré 50cm calculé 100cm mesuré 100cm calculé 200cm mesuré 200cm calculé 300cm mesuré 300cm calculé

Figure 4.85. Comparaison entre les Profils diagonale avec une énergie de 6MeV

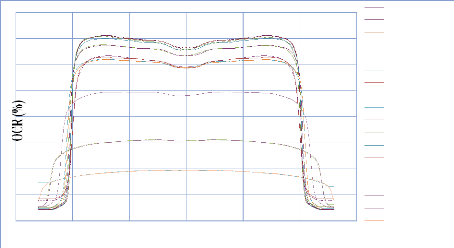
-300 -200 -100 0 100 200 300

Y(mm)

dmax mesuré dmax-0.5 mesuré dmax+0.5 mesuré 5cm mesuré 30cm mesuré 50cm mesuré 100cm mesuré 200cm mesuré 300cm mesuré dmax calculé dmax-0.5 calculé dmax +0.5 calculé 5cm calculé

30cm calculé 5cm calculé 100cm calculé 200cm calculé 300cm calculé

Figure 4.86. Comparaison entre les Profils diagonale avec une énergie de 6MeV

Figure 4.87. Comparaison entre les Profils diagonale avec une énergie de 18MeV

-300 -200 -100 0 100 200 300

Y(mm)

dmax mesuré dmax calculé dmax-0.5 mesuré dmax-0.5 calculé dmax+0.5 mesuré dmax+0.5 calculé 5cm mesuré

5cm calculé

50cm mesuré 50cm calculé 100cm mesuré 100cm calculé 200cm mesuré 200cm calculé 300cm mesuré 300cm calculé

Figure 4.88. Comparaison entre les Profils diagonale avec une énergie de 18MeV

IV.4.5. Interprétation des résultats:

dmax calculé 5 cm calculé 10 cm calculé 20 cm calculé 30 cm calculé dmax mesuré 5cm mesuré 10 cm mesuré

6 MeV

Max(%)

Min%

Moyenne%

Partie central

-0.02

-0.22

- 0.10

-150 -100 -50 0 50 100 150 Y(mm)

Profils pour un champ ouvert de 5×5et une énergie de 6MeV

5cm calculé 10cm calculé 20cm calculé

5cm mesuré

10cm mesuré 20cm mesuré

18 MeV

Max(%)

Min%

Moyenne%

Partie central

0,92

-0.45

0,23

-200 -100 0 100 200

Y(mm) Profils avec filtre en coin de 30° pour un champ de 10×10 et une énergie de 18MeV

Profils d'un champ ouvert de 25×25, énergie
de 6MeV

Profils diagonale avec une taille du champ
de40x40 une énergie de 18MeV

-400 -200 0 200 400

Y(mm)

-400 -200 0 200 400

Y(mm)

dmax mesuré dmax calculé

dmax-0.5 mesuré dmax-0.5 calculé

dmax+0.5 mesuré dmax+0.5 calculé

dmax calculé 5 cm calculé

10 cm calculé 20 cm calculé

30 cm calculé dmax mesuré

5 cm mesuré 10 cm mesuré

20 cm mesuré 30 cm mesuré

Partie central

Partie central

18 MeV

18 MeV

Max(%)

Max(%)

0,83

0,53

Min%

Min%

-11.96

-0.21

Moyenne%

Moyenne%

-5,72

0,31

L'objectif du travail effectué, dans le cadre du présent mémoire de fin d'étude, était :

D'une part de développer un système de qualité applicable au programme de contrôle de dose délivré par l'accélérateur, pour des faisceaux de photons de haute énergie à l'aide de chambres d'ionisation.

D'autre part on a réalisé des mesures pratiques issues de l'accélérateur PRIMUS de Centre Anti Cancéreux Oran, Consiste à comparer les paramètres dosimétriques mesurées en utilisant le milieu de référence (fantômes) directement sous les appareils de traitement avec celles calculées par le TPS (Système de Planification des Traitements). Les données mesurées sur le TPS sont basé sur des mesures réales effectuées sur l'accélérateur. Des recommandations internationales exigent des contrôles annuels des données délivrées par les accélérateurs.

Dans ce travail nous avant effectuer des mesures sur l'accélérateur et nous avons comparés ces mesures aux ancien valeurs.

De la on peut conclure :

Dans une première partie nous avons trouvé que les données scanné sont :

> Les allures de rendements en profondeur, pour les deux faisceaux de photons (6 et 18 MeV) déterminés par le logiciel MEPHYSTO, en fonction de la taille du Champ coïncident parfaitement avec celles mesurés auparavant. Pour les valeurs de Dmax des deux énergies sont 1.5cm pour 6Mv et 3cm pour 18Mv.les déviation entre les courbes de PDD et de 2% au maximum.

> La courbe de profil traduit la variation de la dose absorbée en fonction de la position sur une ligne perpendiculaire à l'axe du faisceau. Les profils de dose pour l'accélérateur PRIMUS ce coïncide avec les ancien mesures. Pour les tailles de champs la valeur ne dépasse pas 2mm.

Page 124

> La mesure du profil du faisceau nous indique si le faisceau est uniforme sur toute la grandeur du champ. Cette caractéristique est nécessaire pour donner une dose uniforme au patient.les mesures de la planéité et de la symétrie sont inférieur a 3%.

Dans une second partie : donnée non scan

Nous avons déterminé les facteurs (TSCF, CF, PSCF) en fonction de la taille du champ, nous avons utilisé un autre type de fantômes (mini fantôme) avec une profondeur de référence (10 cm) pour les deux énergies (6 et 18 MeV). Les mesures sont parfait seulement pour la taille de champs de 30x30 les valeurs ne ce coïncide pas avec les ancien, cette variation peut être à cause des erreurs de positionnement de la chambre.

La taille du champ, est le paramètre le plus influent par rapport au SSD, son influence est négligeable. Par ailleurs, le fantôme d'eau reste le fantôme le plus recommandé pour la détermination des paramètres qui caractérise un faisceau de photon.

Page 125

[1]. Dr. MEGHELLI. "Interactions entre les rayonnements ionisants et la matière ", Biophysique-Médicale. Service Médecine Nucléaire, CHU Tlemcen.

[2]. MELLE. BERKOK HOURIA, MR. FARSI ABDELSAMAD. " Détermination de la qualité des faisceaux de photons de haute énergie utilisés en radiothérapie à l'aide des différents fantômes". Physique médicale. Université de Science et de la TechnologieMohamed Boudiaf. Oran : s. n, 2009. Projet de Fin d'Etudes.

[3]. CHRISTINE JIMONET ET HENRI METIVIER. "Personne compétente en radioprotection". Principes de radioprotection-réglementation. EDP Sciences 2007. France. ISBN : 978-2-86883-948-0

[4]. TIINA SUOMIJÄRVI. Physique Nucléaire et Applications ; IPN-Orsay.

[5]. CHAPITRE 6. INTERACTIONS DES PARTICULES AVEC LA MATIERE. http://dpnc.unige.ch/atlas/xin/noyaux/pdf/chapitre-6.pdf

[6]. MICHAËL BEUVE. " Modélisation de l'interaction des ions de haute énergie avec la matière inerte, la matière vivante et la matière en mouvement". Université CLAUDE
BERNARD - LYON 1: s. n, 2007.Projet HDR.

[7]. TILAHUN TESFAYE. "Physique nucléaire". Université Virtuelle Africaine Addis Ababa, License (Creative Commons), Version 2.5.

[8]. AIP. "Interaction des particules ou rayonnements ionisants Avec la matiere". http://archiveweb.epfl.ch/ipn.epfl.ch/webdav/site/ipn/shared/.../AIp.pdf

[9]. PHENOMENES DE FREINAGE. [Online], [cité : Août, 2011]. ].. http://malek kadri.blogspot.com/2011/08/phenomenes-de-freinage.html

[10]. SPECTRO-ALPHA3. "Spectrométr ie " http://www.cesr.fr/~jean/SpectroAlpha3.pdf

[11]. INTERACTION DES PARTICULES AVEC LA MATIERE. [Online], [cité : mai, 2011] http://www.medecineweb.com/2011/05/interaction-des-particules-avec-la.html

[12]. INTERACTION DES PARTICULES CHARGEES AVEC LA MATIERE. [Online]. http://coursp1bichat-lariboisiere.weebly.com

[13]. CHRISTOPHE CHAMPION. " Interaction des ondes et des particules avec la matière biologique". Laboratoire de physique moléculaire et des collisions ; Institut de physique de Metz ; Université de Metz, Technopôle 2000, Doc.

[14]. ZIAD FRANCIS. "Simulations Monte-Carlo et étude micro dosimétrique pour des irradiations cellulaires à faibles doses en neutrons de 14 MeV". Physique corpusculaire ;

Page 126

école doctorale des sciences Fondamentales ; université blaise pascal (U.F.R. de Recherche Scientifique et Technique) : s. n, 2007. Thèse de doctorat.

[15]. Y. ARNOUD. LPSC GRENOBLE. " Interactions et Détecteurs". [Online]. http://lpsc.in2p3.fr/arnoud/Cours, Master 1 ITDD; 2008-2009.

[16]. ERVIN B. PODGORSAK. "Review of Radiation Oncology Physics": A Handbook for Teachers and Students; Department of Medical Physics McGill University Health
Centre Montréal, Québec, Canada. Sponsored by: International Atomic Energy Agency, Vienna, 2005. ISBN 92-0-107304-6.

[17]. PR. MALIKA ÇAOUI. " Interaction des rayonnements ionisants avec la matière". Université Mohamed V-Souissi. : s. n, 2009

[18]. ASMA MARZOUK. " Etude d'une solution d'Alanine par Spectrophotométrie UV-Visible pour une application dosimétrique". Chimie Industrielle. Institut national de Sciences Appliquées et de Technologie. Université de 7 Novembre. Carthage : s .n ,2007. Projet de Fin d'Etudes.

[19]. HIGH-DOSE DOSIMETRY. IAEA, International Atomic Energy Agency, Vienna, 1985

[20]. M.A.MISDAQ. "Introduction à la physique et aux techniques nucléaires", AfriqueOrient, Casablanca, 1990.

[21]. KHALED FARAH. "Etudes spectroscopiques des verres irradies : Application en dosimétrie nucléaire". Physique. Université de Monastir, Faculté des sciences de Monastir: s. n, 2010.Thèse de doctorat.

[22]. ICRU 33 (International Commission of Radiological Units and measurement).

[23]. THE PHYSICS OF RADIOLOGY. 4éme edition. Harold Elford Johns- John Robert Cunningham.

[24]. ABDEL-MJID NOURREDDINE. "Métrologie des rayonnements ionisants et mesures environnementales". Institut Pluridisciplinaire Hubert Curien.

[25]. KHALED FARAH. "Caractérisation de plusieurs types de détecteurs solides pour la dosimétrie du traitement par rayonnements ionisants". Instrumentations et mesures. Université de Monastir, Faculté des sciences de Monastir: s. n, 2004. Projet de Fin d'Etudes.

[26]. ABDE MJID NOURREDDINE. "Radioprotection et dosimétrie". Groupe de radioprotection et mesures environnementales ; Institut de recherches subatomique ; Université Louis Pasteur. Journée scientifique Algéro-Française, Jijel décembre 2004. Doc

Page 127

[27]. RANA KHOURY. "PIXSCAN : Micro-tomodensitomètre à pixels hybrides pour le petit animal". Instrumentation ; faculté des sciences de luminy ; Université de la méditerranée AIX-Marseille ii: s. n, 2008. Thèse de doctorat.

[28]. DOSIMETRIE. http://www.adacuser.free.fr/modules/archives/download.php?id=2

[29]. S. DERREUMAUX, G. BOISSERIE, G. BRUNET, I. BUCHHEIT, T. SARRAZIN, M. CHEA, C. HUET, I. ROBBES ET F. TROMPIER. " Mesure de la dose absorbée dans les faisceaux de Photons de très petites dimensions utilises en Radiothérapie stéréotaxique ". Société Française de Physique Médicale. Rapport final du groupe de travail IRSN/SFPM/SFRO. Rapport DRPH/SER n° 2008-18.

[30]. PARAMETRES DOSIMETRIQUES CARACTERISANT LES FAISCEAUX DE PHOTONS. http:/www.tech-radiotherapie.info/modules/articles/art/para_dosi.pdf

[31]. DR. PYCHLAU GMBH. "Radiation medicine QA". PTW-Freiburg PhysikalischTechnische Werkstätten. D587.211.00/04 2011-04.

[32]. ERIC FRANCHISSEUR. "Modélisation et validation de l'accélérateur PRIMUS de SIEMENS par le code Monte Carlo PENELOPE dans le cadre de la Radiothérapie du Cancer". PHYSIQUE. Ecole Doctorale de Sciences Fondamentales et Appliquées. UNIVERSITE DE NICE-SOPHIA ANTIPOLIS - UFR Sciences. Nice: s. n, 2007. Thèse de doctorat.

[33]. VINCENT HUBERT-TREMBLAY. "Elaboration des éléments d'une simulation Monte Carlo permettant l'évaluation d'une planification de traitement en radiothérapie externe Compression d'images DICOM à l'aide d'un octree et modélisation de la tête d'un accélérateur linéaire." physique. Faculté des sciences et génie ; Université Laval. Québec : s. n, 2006. Projet de Fin d'Etudes.

[34]. BAPTISTE BLANPAIN. " Vers un calcul en temps réel de la dose dans un fantôme segmente en mailles homogènes. " Radiophysique et imagerie médicales, Laboratoire intelligence Multi-Capteurs et Apprentissage, Université Toulouse III-Paul Sabatier : s. n, 2009. Thèse de doctorat.

[35]. MYRIAM COULIBALY ET BORIS GEYNET. "Evolution technologique en radiothérapie externe" ; Université de Technologie Compiègne 2001.

[36]. DETECTION DES RAYONNEMENTS IONISANTS. http://ead.univangers.fr/~jaspard/Page2/COURS/5RayonIONISANT/Cours6/1Cours6.htm

[37]. SYSTEMES DE DOSIMETRIE DE CHAMBRE D'IONISATION http://www.geniephysiqueusto.unblog.fr/files/2009/03/chambresdionisation.pdf

[38]. ABDELMALEK ADEL. "Caractérisation de trois types de détecteurs plastiques à base de PMMA pour la dosimétrie. " Instrumentation et Maintenance Industrielle

Page 128

nucléaire, Centre National des sciences et Technologies Nucléaires (CNSTN), Institut National des Sciences Appliquées et de Technologie, Université du 7 novembre à Carthage: s. n, 2008. Projet de Fin d'Etudes.

[39]. DAVID BENOIT. " Mise au point et évaluation d'un système fibré de dosimétrie en ligne utilisant des matériaux phosphorescents stimulables optiquement Application à la mesure de dose en radiothérapie et au monitoring de faisceaux. " Radiophysique et Imagerie Médicales, Institut d'Electronique du Sud (UMR UM2-CNRS 5214), l'Université Toulouse III - Paul Sabatier: s. n, 2008. Thèse de doctorat.

[40]. THE USE OF PLANE-PARALLEL IONISATION CHAMBERS IN HIGH-ENERGY ELECTRON AND PHOTON BEAMS: An International Code of Practice for dosimetry, International atomic energy agency. Technical Reports Series No.381. Vienna; IEAE; 1997.

[41]. ABSORBED DOSE DETERMINATION IN EXTERNAL BEAM RADIOTHERAPY BASED ON ABSORBED DOSE TO WATER STANDARDS: An International Code of Practice for dosimetry, International atomic energy agency. Technical Reports Series No.398. Vienna; IAEA; 2000.

[42]. CHAMBRES D'IONISATION SEMIFLEX. http://www.ptw.de/1006. html?&L=2&cId=3296

[43]. ABSORBED DOSE DETERMINATION IN EXTERNAL BEAM RADIOTHERAPY AN INTERNATIONAL: Code of Practice for Dosimetry Based on Standards of Absorbed Dose to Water, Technical reports series no. 398;
INTERNATIONAL ATOMIC ENERGY AGENCY VIENNA, 2000 STI/DOC/010/398.

[44]. FANTOME D'EAU MP3-M. http://ptw.de/mp3-m.html?&L=2

[45]. ESTRO MINI PHANTOMS. http://www.harpell.ca/manufacturer/ptw/estro-miniphantoms

[46]. UNTITLED - MEDITEL http://www.meditel.com.tr/UserFiles/File/ptw.pdf

[47]. MESURES DES DONNEES DOSIMETRIQUE ET PHYSIQUES DES FAISCEAUX DE PHOTONS ET D'ELECTRONS DE L'ACCELERATEUR LINEAIRE SIEMENS PRIMUS DU CAC ORAN. Centre de recherche nucléaire d'Alger, division de la sureté. Aout 2008.

[48]. MEDICAL PHYSICS CONTROL CENTER. MEPHYSTO http://www.scanrad.no/straleterapi/dosimetri/qa-software/600/MEPHYSTO_mcc.pdf

[49]. KLAUS BEICH, DIETMAN NITSCHE et AREL HOFFMANN. "Precise, Fast, Reliable - the Standard for Therapy Beam Analyzers". TBA Systems. Computer assisted scanning devices for beam data acquisition and analysis in radiation therapy.

Page 129

Résumé

La radiothérapie externe utilise des rayonnements ionisants pour le traitement des tumeurs. L'utilisation de ces rayonnements nécessite la plus grande vigilance de la part du physicien médical et du personnel qui les utilise. Cependant, les résultats du traitement dépendent beaucoup de la précision sur la dose délivrée à la tumeur.

Les rayonnements ionisants sont délivrés à partir de l'accélérateur de particules par l'intermédiaire d'un logiciel de planification des traitements (TPS) qui permet de définir une balistique de traitement et de calculer la dose à délivrer aux patients. Il faut donc que le calcul des faisceaux d'irradiation issu du TPS soit le plus proche possible des mesures effectuées sous l'accélérateur de particules.

Le présent travail a pour but de spécifie les éléments d'un système de qualité applicable

au programme de contrôle de dose afin de vérifier les caractéristiques (rendement en profondeur et profil de dose) de nos faisceaux dans un fantôme d'eau placée à une distance source - surface de 100 cm, une comparaison des courbes obtenues par le TPS à celles mesurées expérimentalement est faite pour différentes tailles de champs pour les faisceaux de photons de haute énergie de 6 et 18 MV de l'accélérateur linéaire de particule Primus (siemens) du service de radiothérapie du Centre anticancéreux - Oran.

Mots clés : Radiothérapie externe, rayonnements ionisants, TPS, rendement en profondeur, profil de dose, fantôme d'eau, accélérateurs linéaires

Abstract

The external radiotherapy uses ionizing radiations for the treatment of the tumors. The use of these radiations requires the greatest vigilance on behalf of the medical physicist and the personnel which uses them. However, the results of the treatment depend much on the precision on the amount delivered with the tumor.

The ionizing radiations are delivered starting from the particle accelerator via software of planning of the treatments (TPS) which makes it possible to define ballistics of treatment and to calculate the amount to be delivered with the patients. It is necessary thus that the calculation of the beams of irradiation resulting from the TPS is possible nearest the measurements taken under the particle accelerator.

The purpose of this work is of specifies the elements of a system of quality applicable to the checking routine of amount in order to check the characteristics (in-depth output and profile of amount) of our beams in a water phantom placed at a distance source - surface of 100 cm, a comparison of the curves obtained by the TPS with those measured in experiments is made for various sizes of fields for the beams of photons of high energy of 6 and 18 MV of the linear accelerator of particle Primus (mho) of the service of radiotherapy of the anti-cancer Center - Oran.

Key words: External radiotherapy, ionizing radiations, TPS, in-depth output, profile of amount, water phantom, linear accelerators