Application des méthodes de l'analyse de données sur l'évolution du parc automobile algérien

République Algérienne Démocratique Et Populaire Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Université des Sciences et de la Technologie Houari Boumediene Faculté des mathématiques Département de probabilités et statistiques
Mémoire de fin d'étude En vue de l'obtention du diplôme d'Ingénieur d'Etat THEME : Encadré par : Mlle Kheffache Devant le jury : Mme Djemai Mr Kernane Mlle Kheffache Promotion 2010-2011	en Statistique Présenté par: Mr Bouatta Adel Mr Bensaid Lyes Présidente du jury Examinateur Encadreur

Remerciements

Par sa présence, par ses précieux conseils, sa gentillesse et son soutien,
nous disons un grand merci à notre promotrice Mlle D.Kheffache.

Nous remercions également Mme S.Djemai d'avoir accepté de
présider le jury, nous lui disons merci pour ses conseils et ses
remarques pertinentes ...Merci Madame.

Nous remercions également Mr T.Kernane de nous avoir honoré en
examinant notre travail, nous le remercions vivement pour toutes les
remarques ainsi que pour tous les encouragements qu'il nous a apporté
...Merci monsieur.

Nous tenons à remercier également nos familles, qui nous ont aidé, encouragé et soutenu dans les moments difficiles tout au long de la préparation de ce mémoire.

Enfin, nous remercions toute personne ayant contribué de près ou de loin â l'élaboration de ce travail.

A toutes ces personnes, nous leurs disons merci infiniment.

Dédicaces

Je dédie ce projet de fin d'étude

A tous ceux et à toutes celles qui me sont chers

Aux personnes qui m'ont encouragé et motivé, qui n'ont cessé d'oeuvré pour ma réussite et pour mon bonheur.

A mes parents, qui ont tant sacrifié pour mon succès attendant ce jour
avec impatience, mon frère Ryad et ma soeur Alida.

A mes oncles et mes tantes qui m'ont soutenu et qui n'ont cessé de
m'encourager me réservant
les moyens nécessaires au bon déroulement de mes études
Je remercie chaleureusement mon oncle Hakim pour sa contribution
exceptionnelle pour le bon déroulement de mon travail, sans oublier
aussi mes grands-parents.

A tous les camarades de la promotion 2010 - 2011
probabilité&statistique ainsi qu'aux

Promotions à venir.

A tous mes amis de l'USTHB

A toi Lyes, qui a tant donné pour que nous puissions achever notre
mémoire dans les meilleures conditions

A toute ma famille, mes proches et mes amis.

Adel

Dédicaces

Je dédie ce modeste travail
Aux êtres qui me sont très chers
A ceux qui ont attendu ce jour avec impatience et qui n'ont jamais
cessé de m'encourager et qui se sont toujours sacrifiés pour mon
bonheur.

A mes parents, qui ont humblement attendu avec impatience les
fruits de mon travail, ma soeur Ania et mon frère Koceila.

A mes oncles et tantes qui m'ont tous, soutenus et qui m'ont réservés
les moyens nécessaires tout au long de mes études. Je remercie
chaleureusement ma tante Nacera pour sa contribution exceptionnelle
pour le bon déroulement de mon travail, sans oublier aussi mes grands
parents.

A tous les camarades de la promotion 2010 - 2011
probabilité&statistique surtout Mrs : Adel Djazouli, Adel Mezouani,
Rabie, Sami, Abdelkader, Yacine ainsi qu'aux
Prochaines promotions que je ne manquerai pas d'encourager. Et
aussi à mon très cher ami Guidoum Arsalane dont son aide et ces
conseils m'ont été de grand apport. sans oublier mon voisin et ami
Gherbi Lamine

A toi Adel mon cher binôme, qui a tant donné pour que nous
achevions ce travail

A toute ma famille, mes proches et mes amis.

Eyes

Chapitre I Introduction et problématique

I. Introduction générale ..1

1. Présentation de l'organisme 1

2. Historique 1

3. Le système National statistique 2

4. Le conseil national de la statistique 2

5. Fonctions de l'Office National des Statistiques 3

6. Organigramme de l'office national des statistiques 4

II.Problématique 5

III.Présentation des données 6

IV.Solution proposée 7

Chapitre II Double Analyse en composantes principales

I.Présentation théorique de la méthode DACP 10

II.Présentation générale de la méthode et notations 10

III.Etude de l'interstructure : analyse du nuage des centres de gravite 12

IV.Analyse des T nuages d'individus 12

V.Étude de l'intrastructure : recherche d'un espace de représentation commun 13

1.Généralités : définition des indices 13

2.Sélection du meilleur système d'axes 15

3.Un second critère maximisant l'inertie expliquée 15

4.troisième critère 17

5.recherche globale d'un nouveau système d'axes 18

VI.Compromis et interprétation des trajectoires des individus 18

Chapitre III Application de la DACP

I.Phase1: Etude de l'interstructure 22

II.Phase2: Analyse des 10 nuages d'individus 28

III.Phase3 : Étude de l'intrastructure 31

1.Représentation des individus (les wilayas) 34

Chapitre IV analyse factorielle des correspondances

I.Définition 40

II.Eléments de base de l'analyse 40

1.Tableau de contingence 40

2.Construction des nuages 42

Chapitre V Application de l'AFC

I.Répartition : genre véhicule/ tranche d'âge 45

1.Tableau de contingence : hypothèse d'indépendance 45

2.Teste d'indépendance (X2) 45

3.Valeurs-propres et pourcentages d'inertie 46

4.Coordonnées, contributions et cosinus carrés 46

5.Nuage des points lignes 47

6.Nuage des points colonnes 47

7.Nuage des points (représentation quasi-barycentrique) 48

8.Inteprétation 48

II.Répartition : genre véhicule/ tranche de puissance 50

1.Tableau de contingence : hypothèse d'indépendance 50

2.Teste d'indépendance (X2) 50

3.Valeurs-propres et pourcentages d'inertie 51

4.Coordonnées, contributions et cosinus carrés 51

5.Nuage des points lignes 52

6.Nuage des points colonnes 52

7.Nuage des points (représentation quasi-barycentrique) 53

8.Interprétation 53

Chapitre VI Méthodologie de Box & Jenkins

I.Définitions sur les séries chronologiques 57

1.Qu'appelle-t-on série chronologique? 57

2.Représentation graphique 57

3.Schéma de décomposition d'une chronique 58

4.La procédure de la bande 58

5.Prévision 59

II.Processus stochastique 59

1.Définition 59

2.Processus stationnaire 60

3.Caractéristiques d'un processus stationnaire 61

4.Les opérateurs 63

5.Processus bruit blanc 64

6.Classes des modèles ARMA 64

7.Processus non stationnaires 68

III.Méthodologie de Box & Jenkins 70

1.Définition 70

2.Test de la saisonnalité et de la tendance 70

3.Principe de la méthode 74

4.Choix du modèle 79

5.Prévision 79

IV.Analyse spectrale 81

1.Introduction 81

2.Le périodogramme 81

3.Objectif de l'analyse spectrale 82

4.Concepts de l'analyse harmonique de Fourier 82

Chapitre VII Application de la méthode de Box & Jenkins

I.Série annuelle d'importation des véhicules touristiques(VT) 86

1.analyse préliminaire de la série VT (vehicules tourismes) 86

2.Test de la racine unitaire (Dickey-Fuller) sur la série VT 87

3.Etude de la série RVT 89

4.Test de la racine unitaire (Dickey-Fuller) sur la série RVT : 90

5.analyse spectrale 91

6.Désaisonnaliser la série RVT 92

7.Identification et estimation du modèle a priori 93

8.Test de validation 93

9.Test sur les résidus 94

10.Prévision 99

II.série annuelle d'importation des autocar-autobus(AA) 100

1.analyse préliminaire de la série AA 100

2.Test de la racine unitaire (Dickey-Fuller) sur la série AA 101

3.Test de la racine unitaire (Dickey-Fuller) sur la série TAA 104

4.analyse spectrale 106

5.Identification et estimation du modèle a priori 106

6.Test de validation 107

7.Test sur les résidus 108

8.Prévision 113

Conclusion générale 115

hapitre I

::ntr duction et

D)

Fa

pr biém tique

C

Chapitre I Introduction et Problématique

USTHB Page 1

I. Introduction générale

1. Présentation de l'organisme :

L'Office National des Statistiques est l'Institution Centrale des Statistiques de l'Algérie. C'est un établissement public à caractère administratif chargé de la collecte, du traitement et de la diffusion de l'information statistique socio-économique (tel que recensement de la population et de l'habitat, enquête sur la main d'oeuvre, enquête sur les entreprises industrielles, etc...). L'Office National des Statistiques est placé sous la tutelle du ministère de la Prospective et des Statistiques

2. Historique :

L'Office National des Statistiques fut créé au lendemain de l'indépendance, en 1964, sous l'appellation de Commissariat National pour le Recensement de la Population (C.N.R.P) et ceci afin de réaliser le premier recensement de la population de l'Algérie indépendante en 1966. En 1971, il change de dénomination et devient Commissariat National aux Recensements et Enquêtes Statistiques (C.N.R.E.S). De grands travaux ont été réalisés pendant cette période tels que : le deuxième recensement de la population et de l'habitat en 1977 ; l'enquête démographique en 1972-1973 ; l'enquête cartographique en 1972-1975 qui devrait servir de base à la réalisation du recensement, et l'enquête sur la consommation des ménages en 1979-1980. Par ailleurs, une réorganisation de l'appareil statistique a donné naissance à l'actuel Office National des Statistiques par le biais du décret législatif N° 82484 du 18/12/1982 complété et modifié par le décret N° 85-311 du 17/12/1985.

L'O.N.S est alors chargé de l'organisation et la coordination des travaux statistiques.

De grandes enquêtes ont été réalisées, parmi ces dernières on citera le recensement de la population et de l'habitat de 1987, les enquêtes annuelles auprès des ménages de 1982 à 1992, les enquêtes annuelles auprès des entreprises,.... Enfin,le décret N° 95-159 du 03/06/1995 a donné lieu à une nouvelle réorganisation de l'Office National des Statistiques.

Chapitre I Introduction et Problématique

USTHB Page 2

3. Le système National statistique :

Le système national d'information statistique a été réorganisé par le décret législatif N° 9401 du 15 Janvier 1994, qui définit les principes généraux et fixe le cadre organisationnel ainsi que les droits et obligations des personnes physiques et morales dans les domaines de la production, la conservation, l'utilisation et la diffusion de l'information statistique. Ainsi, toute information quantitative ou qualitative permettant la connaissance des faits économiques sociaux et culturels par des procédés numériques est considérée comme une information statistique.

Suivant le principe de la liberté d'information, toute personne physique ou morale a la faculté de produire, traiter et diffuser l'information statistique. Cependant ne relève du domaine public que l'information statistique qui aura été élaborée par les services de l'Etat ou qui aura bénéficié de l'enregistrement statistique. Au terme du décret législatif cité ci-dessus, "L'enregistrement statistique est la reconnaissance par l'Etat du caractère d'intérêt public des enquêtes, études et travaux statistiques. A ce titre, elle est accessible à tout demandeur. Sans préjudice des procédures juridiques et administratives, sa rétention peut faire l'objet pour son obtention, d'un recours. par ailleurs, dans le cadre du secret statistique, le décret législatif précise que les renseignements individuels figurant sur les questionnaires revêtus de l'enregistrement statistique et ayant trait à la vie personnelle et familiale ne peuvent faire l'objet de communication de la part du service dépositaire ou de publication que conformément à la loi sur les archives nationales. Les renseignements individuels ne peuvent en aucun cas être utilisés à des fins de contrôle fiscal, de répression économique, d'enquêtes judiciaires, d'atteinte à la vie privée des personnes, ou de concurrence.

4. Le conseil national de la statistique :

Le conseil national des statistiques est chargé de l'élaboration de la politique nationale de la statistique et de l'information économique ; de la coordination de l'élaboration et du contrôle d'exécution des programmes nationaux, sectoriels et spécifique de travaux statistiques conforme à la politique nationale arrêtée en la matière ; de se prononcer et d'arrêter les méthodes, procédures et modalités de calcul et composition de tous les indices, indicateurs, agrégats et comptes servant de référence officielles ; de veiller à la garantie effective du secret statistique ainsi qu'au strict respect de l'obligation statistique ; de veiller à la promotion de la circulation de l'information statistique et au perfectionnement permanent des circuits assurant la disponibilité d'informations fiables, régulières et adaptées aux besoins des agents socio-économiques. Il peut être crée auprès du conseil un ou plusieurs comités permanents investis de missions définies par leur texte de création. Le conseil est habilité à recourir à toute compétence ou expertise extérieures au conseil.

Chapitre I Introduction et Problématique

USTHB Page 3

5. Fonctions de l'Office National des Statistiques :

Aux termes du décret législatif 94-01 du 15/01/1994, les prérogatives de l'Office National des Statistiques ont été reconduites et élargies.

C'est ainsi que l'Office National des Statistiques veille à l'élaboration, la disponibilité et à la diffusion d'informations fiables, régulières et adaptées aux besoins des agents économiques et sociaux.

Il assure ou fait assurer la disponibilité régulière des données, analyses statistiques et études économiques nécessaires à l'élaboration et au suivi de la politique économique et sociale des pouvoirs publics.

Il élabore et diffuse régulièrement, en application du programme national statistique, indices, indicateurs de l'économie nationale ainsi que les comptes de la nation.

Il gère les enregistrements statistiques des enquêtes et travaux statistiques, tient et met à jour un répertoire des agents économiques et sociaux auxquels est attribué le Numéro d'Identification Statistique (NIS)

Chapitre I Introduction et Problématique

6. Organigramme de l'office national des statistiques

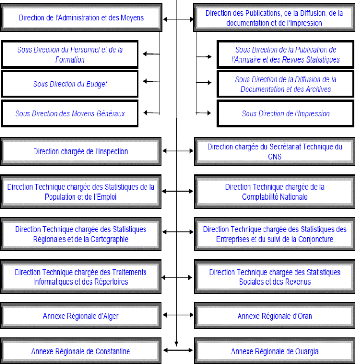
USTHB Page 4

Chapitre I Introduction et Problématique

USTHB Page 5

II. Problématique :

Il n'existe pas aujourd'hui de statistiques réelles précises sur la composition du parc automobile algérien. Les documents qui pourraient servir à l'évaluer ne concernent que certaines catégories de véhicules et ne sont pas systématiquement actualisés, faussant les résultats que l'on pourrait en déduire. Or, la connaissance de la nature et du volume du parc revêt des enjeux économiques, politiques ou environnementaux considérables.

La première étape de notre travail est de collecter toutes les informations disponibles. Afin de mettre en valeur l'évolution technologique du marché des véhicules neufs.

Cette étude détaillée des évolutions passées et présentes des véhicules neufs peut être utilisée à des fins prévisionnelles en vue d'aider aux décisions politiques envisagées à l'égard des véhicules routiers.

L'objectif de notre travail est :

? D'une part, de ressortir l'évolution du parc national pour l'exploration de données récoltées sur une période qui va de 2000 à 2009 en utilisant les méthodes de l'analyse des données.

? D'autre part, de faire une prévision à court terme pour les véhicules les plus répandus sur le parc automobile.

Chapitre I Introduction et Problématique

USTHB Page 6

III. Présentation des données :

Les données que nous avons obtenus proviennent de l'office national des statistiques elles présentent les véhicules circulant en Algérie.

Une partie des données reste inconnue ou n'est pas recensée, ces statistiques ne peuvent donc rendre compte que du parc automobile tel que présenté par l'ONS.

Les véhicules sont classés par genre, nous avons obtenus la répartition de ces genres de véhicules de plusieurs façons qui sont les suivantes :

? 1_ (Genre /Wilaya) : répartition des véhicules dans chacune des 48 wilaya du pays.

Les genres de véhicule concernés sont les suivants : VT: véhicule de tourisme, CM: camion, CMT: camionnette, AA: autocar-autobus, TR: tracteur routier, TA: tracteur agricole. Nous disposons de leurs répartitions dans chacune des 48 wilayas et ce pour chaque année de 2000 à 2009.

? 2_ (Genre /Tranche d'âge) : repartions des véhicules selon leurs âges (anciennetés).

Les genres de véhicule concernés sont les suivants : VT: véhicule de tourisme, CM: camion, CMT: camionnette, AA: autocar-autobus, TR: tracteur routier, TA: tracteur agricole, R: remorque, VS: véhicule spéciale, M: Moto. Nous disposons de la répartition de ces genres de véhicules selon l'ancienneté, les données ont été récoltées en 2009.

? 3_ (Genre/Tranche de puissance) : répartition des véhicules par puissance (chevaux).

Les genres de véhicule concernés sont les suivants : VT: véhicule de tourisme, CM: camion, CMT: camionnette, AA: autocar-autobus, TR: tracteur routier, TA: tracteur agricole, VS: véhicule spéciale, M: Moto. Nous disposons de leurs répartitions par puissance du moteur, les données ont été récoltées en 2009.

L'organisme d'accueil a mis à notre disposition un ensemble de données de type annuel allant de 1963 à 2009, celui-ci concerne l'importation en Algérie des véhicules de type touristiques ainsi que des véhicules de type autocars-autobus.

Chapitre I Introduction et Problématique

USTHB Page 7

IV. Solution proposée :

Lors de la première partie de notre étude, nous exploiterons les données concernant la répartition des différents genres de véhicules dans chacune des 48 wilayas du pays sur la période allant de 2000 à 2009.

La méthode d'analyse des données utilisée à cet effet sera la DACP ou Double Analyse en Composantes Principales.

Apres cela, nous examinerons la répartition des véhicules sur le territoire national selon l'âge (ou ancienneté) et selon la puissance, nous utiliserons à cette occasion la méthode statistique appelé AFC ou analyse factorielle des correspondances.

Enfin, pour finaliser notre analyse du parc national automobile, une partie prévision a été introduite dont l'objectif serai d'emmètre des prévisions à court terme sur le futur nombre d'importation de véhicules de type touristique ainsi que de véhicules de type autocar-autobus.

? Pourquoi utiliser la DACP ?

La DACP s'applique à des données de type cubiques bien précises :

« Les mêmes variables doivent être mesurées (dans la même unité) sur les mêmes individus à différents instants».

L'objectif principal de la DACP est, à l'instar de STATIS et de l'AFM, de comparer globalement l'évolution des liaisons entre les différentes variables et l'évolution des différents individus.

Par rapport aux données que nous avons concernant la répartition genre/ wilaya, la meilleure méthode sera la DACP car les mêmes données se répètent à différents instants, dans notre cas 10 années, et que les variables sont mesurées dans les mêmes unités, aussi l'objectif de notre travail est justement de ressortir l'évolution du parc automobile sur ces dix années, ce qui nous amène à la conclusion que la méthode la plus judicieuse à utiliser sera la DACP.

		lisiyse des données
CCM			hapitre	II

y

ble )0 I se ett

composantes

duel" Ice

Chapitre II Double analyse en composantes principales

USTHB Page 10

La méthode DACP

(Double analyse en composantes principales)

I. Présentation théorique de la méthode DACP :

La double analyse en composantes principales notée DACP a été introduite en 1976 par Jean-Marie Bouroche. La DACP s'applique à des données de type « cubiques » bien précises :

« Les mêmes variables ont été mesurées (dans la même unité) sur les mêmes individus à différents instants ».

Dans le cas où la troisième dimension n'est pas le temps, l'analyse reste possible mais l'interprétation des résultats est beaucoup plus difficile. Le domaine d'application de cette méthode est donc plus restreint que celui de STATIS et de l'AFM, même s'il se rencontre fréquemment en pratique.

L'objectif principal de la DACP est, à l'instar de STATIS et de l'AFM, de comparer globalement l'évolution des liaisons entre les différentes variables et l'évolution des différents individus.

II. Présentation générale de la méthode et notations :

La double analyse en composantes principales peut être décomposée en trois phases distinctes ; ces trois phases sont les suivantes :

-La première étape analyse un phénomène d'analyse globale, qualifié de « déplacement des nuages au cours du temps ». Cette évolution est étudiée par une analyse en composantes principales des centres de gravité des nuages ; elle correspond à ce que nous avons appelé « l'étude de l'interstructure ».

-La seconde étape consiste à étudier la déformation des nuages autour de leur centre de gravité, pour cela, on effectue T analyses en composantes principales des T nuages de points, centrés par rapport à leur centre de gravité pour éliminer le phénomène d'évolution global.

-Enfin, la troisième phase consiste à représenter dans un même espace les évolutions des différents individus au cours du temps ; le problème majeur de cette phase consiste précisément à rechercher un espace de représentation commun. C'est là l'objectif ultime de toutes les méthodes d'analyse des données évolutives ; trouver un espace dans lequel pourront être représentées les trajectoires des individus.

Nous rappelons brièvement les notations utilisées jusqu'à présent : les tableaux étudiés seront

notés , (t=1,..., T), ce sont des tableaux à n lignes (les individus) et p colonnes (les
variables).

Chapitre II Double analyse en composantes principales

USTHB Page 11

Notation des tableaux de données dans la Double ACP :

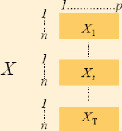
[ =( n

A l'instant t, une variable j est identifiée au vecteur :

Et un individu i sera identifié au vecteur [ ]

Les individus seront munis des poids et on notera :

D_n = [Où les pi vérifient : ?

A l'instant t, le centre de gravité du tableau Xt associé à la matrice est le vecteur défini

par :

=

[ ]

Où : = ?

Enfin, on note ={ , i=1, , , } le nuage des individus définis par le tableau .

Chapitre II Double analyse en composantes principales

III. Etude de l'interstructure : analyse du nuage des centres de gravite :

L'objectif de la première phase de la double analyse en composantes principales est de décrire l'évolution globale de la population d'individu étudiée. Cette phase peut être mise en parallèle avec la première phase de la méthode STATIS, c'est à dire l'étude de l'interstructure. Toutefois, l'approche est légèrement différente puisque STATIS et l'AFM étudient les ressemblances et les différences entre tableaux centrés par rapport à leur centre de gravité, alors que la DACP étudie l'évolution des tableaux par l'intermédiaire de leur centre de gravité

Cette phase ne présente aucune difficulté théorique particulière, elle consiste simplement en une analyse en composantes principales du nuage de points défini par les centres de gravité de chaque tableau.

On obtient alors une image euclidienne des tableaux dans un espace de dimension souhaitée. Souvent, on peut vérifier que le premier axe de cette image s'explique en termes d'évolution globale dans le temps : les centres de gravités 9 ^(t) varient en général de manière continue dans le temps le long de cet axe.

1er étape : on effectue une ACP sur le tableau (de taille T x p) défini par :

	9(1)		(x^1)^(1)	... (xp)^(1)
G=		=	[(x^1)^(t)	... (xp)^(t)
	9(T)		(x ^1)(T)	... (xp)^(T)

IV. Analyse des T nuages d'individus :

Une fois ce phénomène d'évolution dans le temps observé et analysé, il est possible de l'éliminer par centrage des différents tableaux ; nous allons ensuite chercher à faire apparaitre des phénomènes de variation autour de la moyenne.

Pour cela, la méthode proposée ne présente là encore aucune difficulté technique, puisqu'elle consiste en une analyse en composantes principales des T nuages de points-individus, centrés par rapport à leurs centres de gravité.

2eme étape : on effectue T ACP des tableaux (de taille n x p) définis par :

=

pour t=1,...,T

USTHB Page 12

Chapitre II Double analyse en composantes principales

USTHB Page 13

Ces T analyses en composantes Principales vont nous fournir deux types de résultats :

- il sera possible, d'une part, d'interpréter chacune des ACP à l'aide des représentations graphiques et des aides à l'interprétation bien connues de tous ; cette analyse apparait toutefois fastidieuse dès que l'on dispose de nombreux tableaux.

- D'autre part, ces T ACP nous fournissent chacune deux systèmes d'axes orthogonaux. Si l'on note q le nombre d'axes retenus dans les ACP ( q < Min(p,n) ), on a :

- T systèmes de facteurs principaux (vecteur de taille p) pour t=1...T

- T systèmes de composantes principales (vecteurs de taille n) pour

t=1...T

V. Étude de l'intrastructure : recherche d'un espace de représentation commun aux études :

La troisième et dernière phase de la DACP répond à son objectif principal, à savoir : trouver un espace dans lequel il sera possible de représenter les trajectoires des individus au cours du temps.

Quatre critères de sélection d'axes ont été proposés par J-M Bouroche dans sa thèse, nous allons les présenter dans la suite de ce paragraphe.

A. Généralités : définition des indices

Nous disposons, à l'issue de la deuxième phase de la DACP, de 2T systèmes d'axes orthonormés :

- T systèmes de facteurs principaux (vecteurs de taille p) pour t=1...T ; ce

sont les vecteurs propres des matrices M associés aux deux plus grandes valeurs

propres , I=1...q ;

- T systèmes de composantes principales (vecteurs de taille n) pour

t=1...T ; ce sont les vecteurs propres des matrices D, associés aux mêmes q plus

grandes valeurs propres , I=1...q ;

Avant de présenter les quatre critères, nous allons commencer par définir deux indices mesurant la proximité entre les systèmes d'axes.

Chapitre II Double analyse en composantes principales

USTHB Page 14

Les critères de sélection d'axes sont basés sur deux indices :

On a M = et les facteurs principaux sont orthonormés ; la quantité

représente donc l'inertie expliquée par le facteur principal l pour le tableau (t). En se basant sur cette propriété, on peut définir l'inertie expliquée par un facteur quelconque v.

Définition de l'inertie expliquée par un facteur quelconque :

On définit l'inertie expliquée par un facteur v quelconque par la quantité : v.

Pour un système d'axe , on définit alors l'indice Ö (t, v) par :

Ö (t, v) = ? ?

?

Cet indice mesure la perte en pourcentage de l'inertie de nuage des individus définis par

le tableau (t) lorsqu'on le projette sur le sous-espace défini par les au lieu de le

projeter sur ses q premiers facteurs principaux.

En d'autres termes, lorsque l'on projette le nuage sur le sous-espace engendré par les

), son inertie diminue en pourcentage de .

La proximité entre deux facteurs u et v peut également être mesurée par l'angle entre ces deux vecteurs u et v (de dimension p), ou plus précisément par le cosinus carrée de leur angle.

Ainsi, le deuxième indice mesurant la proximité entre un système d'axe et un

système d'axes est : =? .

On écrira également par la suite : =? ?

Cet indice mesure la proximité du système d'axe v= systèmes de facteurs

principaux.

Chapitre II Double analyse en composantes principales

USTHB Page 15

B. Sélection du meilleur système d'axes :

Le premier critère de sélection d'axes consiste à choisir parmi les T systèmes d'axes trouvés celui qui est tel que la somme des pertes d'inertie lorsque l'on projette tous les nuages sur le système d'axe soit minimum. C'est l'indice Ö précédemment défini qui est utilisé. Soit r une

? ?

date comprise entre 1 et T. l'indice : Ö (t, r) =

?

Mesure la perte d'inertie en pourcentage du nuage lorsqu'on le projette sur les q

premiers facteurs principaux du nuage au lieu de le projeter sur ses q premiers facteurs

principaux.

Ainsi, si l'on projette les T nuages , t=1...T sur le sous-espace vectoriel engendré par les

on perd ? (. , r) = ? En moyenne :

Ce premier critère prône de choisir le système d'axe tel que :

Ö(. , r) =

On représentera alors les trajectoires des individus dans l'image euclidienne définie par les q axes suivants :

= pour l=1...q (facteurs principaux).

= pour l=1...q (composantes principales).

En effet, en notant ? la mesure de proximité entre les systèmes

de facteur principaux associés aux nuages et , on peut définir un autre critère de

choix de système d'axes. Ainsi, si l'on représente les T nuages sur le sous-espace vectoriel

engendré par les , la qualité de la représentation (en terme de somme des cosinus

carrés d'angles entre les axes des différents systèmes) se mesure par la quantité :

? = ? ?

On pourrait alors choisir le système tel que : = .

C. Un second critère maximisant l'inertie expliquée :

Notons le système recherché. Alors, l'inertie du nuage expliquée par le

système est égale à la quantité : ? .

Le second critère a pour objectif de maximiser l'inertie de l'ensemble des nuages projetés, ce qui revient à résoudre le problème d'optimisation suivant :

? ?

= ? où V=?

Chapitre II Double analyse en composantes principales

USTHB Page 16

La solution d'un tel problème est classique puisque c'est la base de l'analyse en composantes principales, qui consiste à rechercher des vecteurs orthogonaux maximisant l'inertie du nuage

projeté ; les sont donc les q vecteurs propres de la matrice MV=?

associés à

ses q plus grandes valeurs propres. Quatre remarques importantes :

1. On peut comparer ce second critère avec le précèdent : en effet, le premier critère consiste

en fait à maximiser la fonction ø (. , r) = ? où l'indice ø(t,r)=? Q (t)

représente le pourcentage d'inertie de expliquée par le système

Le premier critère revient donc à rechercher, parmi les T systèmes d'axes connus, le système

tel que la quantité :

? ?

=?

[ ?

] soit maximale.

?

?

Or: ?

Puisque le dénominateur dépend de t ; la solution obtenue par le premier critère ne peut donc pas être considérée comme un sous-optimum de celle obtenue par le second.

2. En fait, nous suggérons de définir là-aussi un critère supplémentaire : il consisterait à considérer les éléments propres non plus de la matrice MV, mais de la matrice M où est

définie par : ?

Ce critère reviendrait alors à « normer » chaque matrice V,

?

par l'approximation d'ordre q de sa trace, cette « norme » est sensiblement différente de celle issue du produit scalaire de Hibert-schmidt. Cette méthode serait intéressante dans des configurations où les objets auraient des « normes » (somme des valeurs propres de M ) très différentes les unes des autres. On s'inspire ainsi de la notion de « pondération des variables » utilisée par l'analyse factorielle multiple.

En effet, dans le cas où des objets de normes élevées influenceraient de façon considérable le système d'axes retenu, diviser chaque objet v par sa « norme » permettrait d'équilibrer l'influence des différents nuages dans la construction de la nouvelle image euclidienne.

La méthode proposée, que l'on retrouve aussi dans STATIS, fournirait des résultats différents de ceux obtenus avec une DACP classique.

Le critère a pour but de résoudre le problème d'optimisation suivant :

? ?

? = ? Où ?

?

La solution de ce problème est obtenue en recherchant les q vecteurs propres de la

matrice M associés à ses q plus grandes valeurs propres.

Chapitre II Double analyse en composantes principales

USTHB Page 17

Il apparait alors, si l'on utilise ce critère, que le recours au premier critère n'est plus indispensable puisque ce dernier conduit à un sous-optimum de ce critère qui est plus difficile à mettre en oeuvre que le premier critère.

3. La matrice V est en fait la matrice d'inertie du nuage = ? Par rapport à son
origine. Le second critère conduit donc à effectuer un ACP sur le nuage des nT individus par rapport à leur centre de gravité et définis par les p variables.

4. Lorsque l'on considère ce second critère on voit apparaitre plus clairement des ressemblances entre l'obtention des trajectoires par les méthodes STATIS duale et DACP :

-d'une part, des objets normés par une norme proche de celle issue du produit scalaire de Hibert-Schmidt se dégager de la DACP.

-d'autre part, la recherche d'un espace commun revient à chercher les éléments propres d'un objet V que l'on pourrait qualifier de « matrice de variance-covariance compromis ». Dans l'image euclidienne ainsi déterminée, on peut représenter les positions compromis des variables, donc les coordonnées correspondent aux corrélations moyennes des variables avec les axes sur la période ainsi que les trajectoires des individus.

D. troisième critère :

Recherche séquentielle d'un nouveau système d'axes :

Ce critère est basé sur le second indice Rappelons

que : ( ) ? ?

La recherche du système d'axe se fait de la manière séquentielle suivante :

On choisit tel que en moyenne, l'angle ( , ) soit minimum, alors est tel que

? soit maximum.

A l'étape 1, on impose à d'être orthogonal au sous-espace engendré par et de

maximiser ? Et ainsi de suite jusqu'à

Un tel système d'axe peut, grâce à cette méthode, être facilement obtenu analytiquement : est le vecteur propre associé à la plus grande valeur propre de matrice :

est le vecteur propre associé à la plus grande valeur propre de la matrice :(? (?

Où I est la matrice identité de taille p et est la matrice de taille p x T définie

par : = [ ]

Chapitre II Double analyse en composantes principales

USTHB Page 18

Cette méthode accorde une importance décroissante aux axes. En effet, elle privilégie les premiers axes par rapport aux derniers puisque la séquence commence à l'axe 1 pour se terminer à l'axe q : on laisse moins de « champs pré » aux derniers axes qu'aux premiers. Cela se justifie dans le sens où les premiers axes sont les plus importants puisqu'ils expliquent le plus d'inertie.

Il est possible de comparer les résultats obtenus avec les trois critères précédents en calculant

les indices : Ö (v) = ? ?4 ?

?

Et : ( ) ? ?

E. recherche globale d'un nouveau système d'axes :

Ce critère consiste à résoudre directement le problème : Max sous la contrainte :

( ) orthonormés.

La résolution d'un tel problème n'est pas possible analytiquement ; par contre il existe des méthodes numériques permettant de trouver une solution.

Enfin, il faut noter que contrairement à la méthode séquentielle, cette méthode attribue une importance identique aux axes (premiers et derniers axes).

VI. Compromis et interprétation des trajectoires des individus :

Les trajectoires des individus sont représentées dans le système d'axes déterminé ; ces axes sont interprétés grâce à leurs corrélations avec les positions-compromis des variables. En fait, les coordonnées des variables correspondent à des corrélations moyennes entre les variables et les axes sur la période.

Utiliser le critère 1 revient à choisir comme compromis l'objet . Les positions -compromis des variables sont obtenues en faisant l'ACP du tableau n°r. Les trajectoires des individus sont obtenues en projetant les individus définis par chaque tableau sur le système d'axes retenu, ce qui revient à mettre en éléments supplémentaires les autres tableaux dans l'ACP du tableau n.

Dans ce cas, on peut définir aussi des positions-compromis des individus, ce sont les positions des individus correspondant à l'année r. on utilisant les critères précédents, on a

respectivement les compromis : V= ? et ?

?

Les positions-compromis des variables sont celles issues de l'ACP de ces compromis. Les trajectoires sont déterminées par les positions des individus dans l'ACP du tableau présenté sur la figure suivante :

Chapitre II Double analyse en composantes principales

USTHB Page 19

Superposition des tableaux de données centrés :

1... ... ....p

1

.

.

Y

. n . 1

.

.

Y??

. n

.

1

.

. Yr

. n

(Références bibliographiques : Ouvrages, [2])

Remarque : La théorie de l'ACP est présente dans l'annexe A.

Chapitre III Application de la DACP

USTHB Page 21

Application de la Double Analyse en Composantes Principales

L'un des objectifs de l'office national des statistiques est de recenser les véhicules présents sur le territoire national. Nous avons choisi d'appliquer la Double Analyse en Composantes Principales sur des données concernant le parc automobile Algérien. Ces recensements de données sont établis chaque année par l'ONS (office national des statistiques), les données sur lesquelles nous avons appliqué la DACP s'échelonnent sur une période qui va de 2000 à 2009, elles concernent la répartition des différents genres de véhicules dans chacune des quarante-huit wilayas du pays.

? Les variables sont les genres de véhicules (p=6), ce sont les suivantes VT: véhicule touristique, CM: camion, CMT: camionnette, AA: autocar-autobus, TR: tracteur routier et enfin TA: tracteur agricole.

? Les individus sont les wilayas (n=48).

Les tableaux de données sont à trois entrées, ils se présentent sous la forme suivante : Année 2000

Wilaya	VT	CM	CMT	AA	TR	TA
Adrar
. . .
Alger
. . .
Relizane

.

.

Année 2009

Wilaya	VT	CM	CMT	AA	TR	TA
Adrar
. . .
Alger
. . .
Relizane

Chapitre III Application de la DACP

USTHB Page 22

Traitement des données

La DACP, que nous allons appliquer sur des données concernant le parc automobile Algérien, comporte trois phases:

1- Une analyse en composantes principales des centres de gravité des tableaux.

2- Les 10 ACP de chacun des 10 tableaux.

3- La sélection d'un système d'axes dans lequel s'effectuera la représentation des trajectoires.

I. Phase1: Etude de l'interstructure Analyse des nuages du centre de gravité

Ici, nous avons étudié l'évolution des tableaux (genre /wilaya) par l'intermédiaire de leur centre de gravité.

On a d'abord transformé les tableaux bruts en tableaux de fréquences (tableau de taux), ensuite on a centré chaque tableau, ainsi nous avons obtenu le vecteur centre de gravité de chacun des dix tableaux genre/wilaya

Afin d'obtenir le tableau des centres de gravité, nous avons regroupé les vecteurs des centres de gravités dans un seul tableau que voici :

(Les programmes utilisés pour obtenir ces résultats sont présent au niveau de l'annexe c)

Tableau des centres de gravités :

	VT	CM	CMT	AA	TR	TA
2000	-1,43045	0,850652	-0,80273	0,817806	0,069007	1,565093
2001	0,40346	0,850652	-0,07298	0,817806	0,069007	-0,59366
2002	1,137025	-0,49248	0,656781	-0,99954	0,069007	-0,05397
2003	0,036678	0,40294	-0,07298	0,817806	0,069007	-0,05397
2004	1,137025	-0,04477	-2,26224	0,817806	-1,31112	0,485718
2005	0,770243	0,850652	-0,07298	-0,99954	0,759072	0,485718
2006	-0,69689	0,40294	0,656781	-0,09087	0,069007	-0,59366
2007	-1,43045	-2,28333	-0,07298	-0,09087	-1,31112	-2,21272
2008	-0,69689	-0,94019	0,656781	-1,90821	-0,62106	0,485718
2009	0,770243	0,40294	1,386537	0,817806	2,139203	0,485718

L'analyse en composantes principales du tableau des centres de gravités centré et réduit fournit les valeurs propres suivantes :

Chapitre III Application de la DACP

USTHB Page 23

Valeurs propres et variabilité de l'inter-structure :

	Axe1	Axe2	Axe3	Axe4	Axe5	Axe6
Valeurs propres	2.39	1.62	0.92	0.81	0.22	0.05
% d'inertie	39.76	27.06	15.33	13.42	3.59	0.81
% cumulé	39.76	66.83	82.16	95.59	99.19	100

Graphique des valeurs propres :

Les deux premiers axes factoriels expliquent 66.83 % d'inertie, une représentation des variables et des années dans le premier plan factoriel suffit.

Matrice de corrélation:

Variables	VT	CM	CMT	AA	TR	TA
VT	1	0,348	-0,057	0,041	0,335	0,222
CM	0,348	1	-0,076	0,402	0,587	0,642
CMT	-0,057	-0,076	1	-0,376	0,621	-0,179
AA	0,041	0,402	-0,376	1	0,146	0,049
TR	0,335	0,587	0,621	0,146	1	0,377
TA	0,222	0,642	-0,179	0,049	0,377	1

Chapitre III Application de la DACP

USTHB Page 24

Chapitre III Application de la DACP

Le cercle de corrélation des variables dans le plan (inter-structure de la DACP)

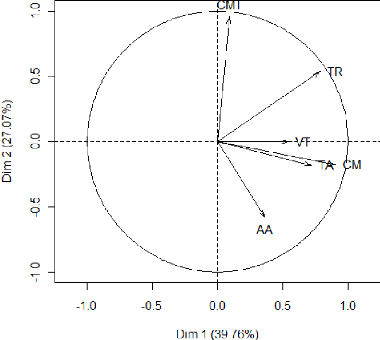
Interprétation de l'inter-structure

Le premier axe s'interprète comme un facteur temps, nous constatons une évolution temporelle quasi-linéaire des années de long du premier axe. Cela signifie que la demande associée aux tracteurs routiers, aux véhicules touristiques, tracteurs agricoles et camions, qui eux sont fortement corrélées avec cet axe, varie de façon linéaire par rapport au temps, en d'autres termes que la demande en ces véhicules augmente sur le marché Algérien. Tant-dit que les autocar-autobus et camionnettes sont les seules à ne pas varier de façon quasi-linéaire avec le temps, cela signifie que la demande en ces véhicules n'est pas en progression sur la période étudiée.

Camionnette et autocar-autobus sont en opposition dans le cercle de corrélation, cela signifie que lorsqu'il y a augmentation de la demande en camionnettes, il y'a chute de la demande en autocar-autobus, et que lorsqu'il y'a augmentation d'autocar-autobus, la demande en camionnettes est en chute, ils varient de façon opposée sur la période qui va de 2000-2009.

USTHB Page 25

Évolution des variables VT CM TA et TR en Algérie

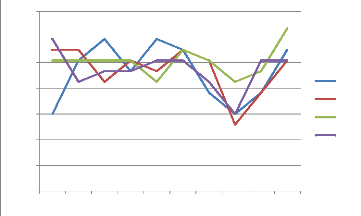
2,095

2,085

2,075

2,065

2,09

2,08

2,07

2,06

2000 2001 2002 2003 2004 2005 2006 2007 2008 2009

VT CM TR TA

Pendant le début de la période étudiée, de 2000 à 2001, la demande en camions et en tracteurs routiers est constante sur le marché Algérien, alors que nous pouvons constater une très nette augmentation en véhicules touristiques et une chute quasi-brutale de la demande en tracteurs agricoles qui néanmoins ne durera pas, puisque à partir de 2001 elle connaitra une augmentation régulière jusqu'en 2005, en ce qui concerne les tracteurs routiers, la demande en ces véhicules demeurera constante jusqu'en 2003 date à laquelle elle connaitra une chute puis à nouveau une augmentation de 2004 à 2005, pour les véhicules touristiques, la demande continuera à augmenter jusqu'en 2002 où là, elle connaitra une baisse mais de courte durée puisqu'en 2003 la demande en ces véhicule fera de nouveau un bond, quant aux camions, la stabilité donc jouissait le marché de 2000 à 2001 fut brève, car on constate effectivement que tout au long de la période qui va de 2001 à 2005, la demande en ces véhicules sur le marché commencera par baisser pour à nouveau augmenter, pour à nouveau baisser et ensuite augmenter et ce, année par année, cela reflète l'instabilité de la demande en camions, chose dont est caractérisée aussi les véhicules touristiques dans cette même période de 2001 à 2005. A partir de 2005 et jusqu'en 2007, nous constatons que la demande sur le marché, pour les quatre genres de véhicules connait une chute quasi-brutale, dont la plus importante sera celle en camion, chose toute aussi remarquable, à partir de 2007, et ce pour les quatre genres de véhicules et pratiquement de la même manière, il y'a rétablissement de la demande d'une façon très nette et continue, mise à part les tracteurs agricoles, où il y'a stabilité de 2008 à 2009.

Chapitre III Application de la DACP

USTHB Page 26

Évolution des variables CMT et AA en Algérie

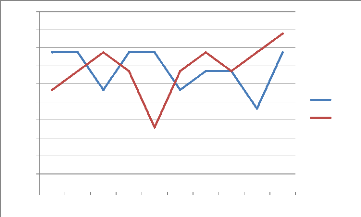
2,092

2,088

2,086

2,084

2,082

2,078

2,076

2,074

2,072

2,09

2,08

1 2 3 4 5 6 7 8 9 10

AA CMT

De 2000 à 2002, on peut constater que la demande en autocar-autobus est constante alors que celle en camionnettes est en augmentation jusqu'en 2003, il est remarquable de voire qu'à partir de 2002, la demande associée aux camionnettes et aux autocar-autobus est en opposition, lorsqu'il y'a augmentation de l'un, il y'a baisse de l'autre avec un pic pour les camionnettes en 2005 et un pic pour les autocars-autobus en 2009, date à laquelle il y'a une augmentation de la demande pour les deux genres de véhicules et de manière très nette et visible.

Coordonnées des variables

variables	F1	F2
VT	0.539	-0,003
CM	0,903	-0,180
CMT	0,089	0,962
AA	0,362	-0,584
TR	0,787	0,537
TA	0,720	-0,184

Contribution et cosinus carrés des variables

	Contributions		Cos2
variables	F1	F2	F1	F2
VT	12,219	0,001	0,291	0,000
CM	34,204	2,003	0,815	0,033
CMT	0,337	57,048	0,008	0,926
AA	5,508	21,033	0,131	0,341
TR	25,988	17,810	0,619	0,289
TA	21,741	2,103	0,518	0,034

Chapitre III Application de la DACP

USTHB Page 27

Représentation des tableaux dans le plan (inter-structure)

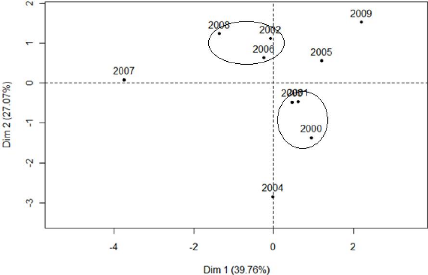
La représentation de l'inter-structure sur cette figure fait apparaitre des groupes d'années qui se ressemblent ; nous avons matérialisé ces groupes par des cercles. Les tableaux qui se situent dans un même cercle présentent des caractéristiques communes tel que 2001 et 2000 ainsi que 2002, 2006 et 2008, cela signifie que le parc auto est resté pratiquement le même sur ces années, en d'autres termes, il n'y'a pas eu de modification de la structure du parc automobile national pendant ces année-là.

Chapitre III Application de la DACP

Résultats des individus de l'inter-structure

	Coordonnées		Contributions		Cos2
Observation	F1	F2	F1	F2	F1	F2
2000	0,957	-1,366	3,838	11,487	0,126	0,257
2001	0,616	-0,460	1,592	1,303	0,178	0,099
2002	-0,081	1,115	0,028	7,659	0,002	0,377
2003	0,470	-0,475	0,927	1,388	0,235	0,240
2004	-0,011	-2,851	0,000	50,029	0,000	0,809
2005	1,203	0,559	6,068	1,927	0,416	0,090
2006	-0,245	0,630	0,252	2,445	0,038	0,247
2007	-3,754	0,086	59,071	0,045	0,913	0,000
2008	-1,363	1,237	7,792	9,423	0,276	0,227
2009	2,208	1,524	20,432	14,293	0,538	0,256

II. Phase2: Analyse des 10 nuages d'individus

Dans cette seconde phase, nous avons effectué une analyse en composantes principales sur chacun des dix tableaux, ces 10 ACP nous ont fournis 10 systèmes de facteurs principaux et 10 systèmes de composantes principales, c'est avec ces systèmes d'axe que l'on va rechercher un espace de représentation commun des wilayas.

Nous ne détaillerons pas dans cette partie les résultats issue des dix analyses en composantes principales car ce n'est pas l'objectif principal de la DACP. Les résultats sont affichés si dessous :

Coordonnées des observations :

	2000		2001		2002		2003		2004
Observation	F1	F2	F1	F2	F1	F2	F1	F2	F1	F2
Adrar	-2,030	-0,836	-1,034	-0,902	-1,556	-0,451	-1,028	-0,897	-1,014	-0,902
Chlef	2,901	2,352	0,374	1,361	1,114	0,242	0,355	1,360	0,340	1,362
Laghoua	-0,799	0,340	-1,025	-0,864	-1,400	-0,460	-1,029	-0,856	-1,028	-0,858
OumElBo	-1,179	0,026	-0,958	-0,686	-0,819	-0,049	-0,952	-0,682	-0,941	-0,687
Batna	1,335	0,674	0,904	0,902	0,254	-0,097	0,867	0,902	0,853	0,909
Bejaia	2,286	-0,036	1,008	0,310	1,586	1,217	1,012	0,382	1,011	0,382
Biskra	0,568	0,511	-0,437	-0,397	-1,068	-0,193	-0,434	-0,396	-0,426	-0,398
Bechar	-1,684	-0,853	-0,985	-1,229	-1,380	-0,499	-0,982	-1,224	-0,970	-1,228
Blida	5,305	-1,006	2,277	0,292	11,735	-4,144	2,358	0,254	2,287	0,255
Bouira	-0,563	0,153	0,092	0,996	-0,616	-0,232	0,083	0,993	0,075	0,996
Tamanra	-1,687	-0,894	-1,144	-1,353	-1,354	-0,392	-1,139	-1,347	-1,124	-1,352
Tebessa	-0,085	1,022	-0,680	-0,556	-0,914	-0,263	-0,689	-0,552	-0,691	-0,553
Tlemcen	-0,726	-0,325	0,617	2,146	0,388	0,523	0,634	2,134	0,599	2,137
Tiaret	-0,905	0,587	-0,033	1,017	0,217	-0,067	-0,048	1,020	-0,072	1,018
TiziOuz	2,492	0,382	0,341	0,002	1,807	2,068	0,363	-0,003	0,407	0,060
Alger	9,866	-2,518	13,850	-1,438	5,732	4,551	13,885	-1,437	13,951	-1,424

USTHB Page 28

Chapitre III Application de la DACP

Djelfa	-1,440	-0,096		-0,773		0,067		-1,421		-0,469		-0,775		0,072		-0,747		0,069
Jijel	-0,402	-0,683		-0,532		-0,636		-0,524		-0,043		-0,536		-0,637		-0,530		-0,641
Setif	3,618	0,788		-0,316		0,752		1,082		0,360		-0,288		0,744		-0,274		0,738
Saida	-1,728	-0,705		-0,600		0,757		-0,981		-0,256		-0,590		0,756		-0,593		0,755
Skikda	-0,600	0,315		-0,264		1,207		-0,793		-0,334		-0,273		1,200		-0,272		1,197
SidiBel	-1,169	-0,390		-0,370		1,348		-0,111		-0,070		-0,355		1,267		-0,374		1,268
Annaba	-0,886	-0,497		0,199		0,143		-1,112		-0,073		0,168		0,139		0,152		0,140
Guelma	-0,592	0,753		-0,986		0,223		-0,845		-0,103		-0,976		0,225		-0,949		0,223
Contant	-0,365	-0,533		0,953		0,746		-0,578		0,093		0,893		0,744		0,855		0,745
Médéa	1,126	1,393		0,226		2,404		-0,800		-0,246		0,241		2,397		0,243		2,398
Mostaga	-0,538	0,406		0,359		1,494		0,848		0,372		0,370		1,563		0,367		1,562
M'sila	0,084	0,559		0,533		0,009		-0,172		-0,467		0,518		0,014		0,510		0,104
Mascara	-0,617	0,566		0,141		1,757		0,765		0,123		0,138		1,754		0,128		1,754
Ouargla	-0,738	-0,635		-0,135		-1,170		-0,442		-0,361		-0,134		-1,167		-0,166		-1,162
Oran	0,526	-0,604		2,052		-0,496		2,507		1,995		1,982		-0,494		1,915		-0,487
ElBayad	-1,679	-0,561		-1,185		-0,743		-1,293		-0,396		-1,177		-0,738		-1,162		-0,743
Illizi	-2,136	-0,889		-1,409		-1,423		-1,818		-0,605		-1,404		-1,416		-1,387		-1,422
BordjBo	2,238	1,252		-0,305		0,512		0,481		0,442		-0,299		0,510		-0,323		0,509
Boumerd	0,150	-0,766		1,055		0,233		-0,243		-0,080		1,060		0,225		1,037		0,230
ElTarf	-1,147	0,503		-0,932		0,225		-1,711		-0,486		-0,933		0,229		-0,923		0,225
Tindouf	-2,252	-0,939		-1,484		-1,495		-1,761		-0,558		-1,478		-1,487		-1,460		-1,494
Tissem	-1,878	-0,440		-1,079		-0,433		-1,007		-0,343		-1,088		-0,432		-1,075		-0,438
ElOued	0,734	-0,154		-1,306		-1,200		0,262		0,165		-1,300		-1,194		-1,284		-1,200
Khenche	-0,962	-0,015		-0,997		-0,452		-1,125		-0,190		-0,990		-0,448		-0,990		-0,451
SoukAhr	-0,266	2,141		-1,313		-0,670		-1,013		-0,423		-1,311		-0,740		-1,296		-0,746
Tipaza	0,545	-0,603		0,112		-0,834		-0,273		0,702		0,081		-0,830		0,088		-0,836
Mila	0,337	0,644		-0,732		-0,465		0,171		0,270		-0,718		-0,467		-0,709		-0,471
AinDefl	0,622	1,788		-0,515		0,527		-0,779		-0,065		-0,520		0,528		-0,491		0,520
Naama	-1,821	-0,787		-1,187		-1,353		-1,495		-0,559		-1,183		-1,346		-1,167		-1,352
AinTemo	-1,580	-0,669		-0,801		-0,009		-0,491		-0,307		-0,806		-0,006		-0,824		-0,010
Ghardai	-0,752	-0,667		-0,920		-1,226		0,514		0,421		-0,917		-1,220		-0,904		-1,224
Relizan	-1,527	-0,054		-0,654		0,602		0,432		-0,260		-0,656		0,604		-0,654		0,525
	2005				2006				2007				2008				2009
Observation	F1		F2		F1		F2		F1		F2		F1		F2		F1		F2
Adrar	-1,016		-0,904		-1,010		-0,904		-1,661		-0,464		-2,006		-0,397		-1,010		-0,911
Chlef	0,296		1,368		0,307		1,380		2,751		1,171		2,409		0,498		0,457		1,367
Laghoua	-1,007		-0,863		-0,984		-0,859		-1,373		-0,269		-1,452		-0,422		-1,029		-0,853
OumElBo	-0,934		-0,691		-0,939		-0,688		-0,795		0,081		-0,169		0,320		-0,906		-0,618
Batna	0,849		0,918		0,769		0,860		-0,269		0,079		-1,191		-0,281		0,705		0,889
Bejaia	1,023		0,382		1,114		0,299		2,807		-0,233		2,437		-0,345		1,314		0,264
Biskra	-0,456		-0,476		-0,493		-0,472		-1,128		-0,380		-1,254		-0,137		-0,475		-0,401
Bechar	-0,996		-1,227		-0,991		-1,228		-2,246		-0,476		-2,315		-0,412		-1,086		-1,233
Blida	2,200		0,249		2,144		0,235		4,435		-0,885		3,689		-0,954		2,018		0,182

USTHB Page 29

Chapitre III Application de la DACP

Bouira	0,062	1,002	0,051	0,940	1,886	1,836	0,951	0,884	0,036	1,034
Tamanra	-1,114	-1,359	-1,126	-1,362	-1,797	-0,496	-1,462	-0,440	-1,132	-1,376
Tebessa	-0,686	-0,556	-0,704	-0,551	-0,668	0,301	-0,680	0,230	-0,699	-0,555
Tlemcen	0,561	2,141	0,556	2,312	-0,252	-0,008	-1,312	-0,173	0,503	2,265
Tiaret	-0,096	0,945	-0,094	0,961	-2,123	-0,230	-1,620	0,072	-0,226	0,987
TiziOuz	0,497	0,047	0,682	0,022	3,465	-0,729	3,212	-1,033	0,977	0,058
Alger	14,000	-1,397	14,024	-1,362	8,248	-2,568	9,174	-2,033	14,050	-1,345
Djelfa	-0,725	0,070	-0,710	0,154	1,122	2,223	3,043	3,801	-0,581	0,242
Jijel	-0,500	-0,646	-0,525	-0,645	-0,173	-0,353	-0,610	-0,406	-0,515	-0,655
Setif	-0,242	0,741	-0,242	0,746	3,471	0,601	1,902	0,242	-0,060	0,740
Saida	-0,591	0,755	-0,587	0,843	-2,090	-0,297	-1,283	0,296	-0,627	0,785
Skikda	-0,264	1,194	-0,259	1,203	1,487	0,835	0,641	0,532	-0,103	1,276
SidiBel	-0,373	1,270	-0,365	1,282	-1,024	-0,105	-1,501	-0,089	-0,343	1,225
Annaba	0,119	0,141	0,051	0,073	1,988	-1,165	1,457	-1,158	0,179	0,055
Guelma	-0,933	0,219	-0,923	0,226	-0,847	0,240	-0,821	0,430	-0,914	0,237
Contant	0,853	0,743	0,798	0,671	1,558	-0,993	0,870	-0,909	0,771	0,672
Médéa	0,215	2,408	0,203	2,347	-0,738	-0,129	-0,531	0,651	0,180	2,378
Mostaga	0,347	1,566	0,305	1,501	-1,351	0,048	-1,435	-0,100	0,175	1,441
M'sila	0,483	0,121	0,425	0,132	4,130	3,124	2,699	1,314	0,329	0,241
Mascara	0,106	1,753	0,100	1,694	-1,222	-0,019	-0,606	0,546	0,002	1,636
Ouargla	-0,147	-1,162	-0,106	-1,167	-0,276	-0,558	-0,206	-0,737	-0,121	-1,183
Oran	1,861	-0,476	1,929	-0,411	1,630	-0,306	-0,121	-0,651	1,876	-0,433
ElBayad	-1,153	-0,748	-1,145	-0,745	-1,865	-0,332	-2,063	-0,333	-1,117	-0,749
Illizi	-1,376	-1,429	-1,370	-1,432	-2,353	-0,429	-2,124	-0,369	-1,406	-1,442
BordjBo	-0,323	0,508	-0,317	0,514	0,645	0,641	0,917	0,473	-0,352	0,440
Boumerd	1,061	0,310	1,052	0,318	0,098	-0,217	0,001	-0,114	1,024	0,322
ElTarf	-0,918	0,223	-0,909	0,230	-1,632	-0,226	-1,730	-0,360	-0,963	0,164
Tindouf	-1,448	-1,501	-1,430	-1,507	-2,313	-0,391	-2,373	-0,390	-1,457	-1,519
Tissem	-1,068	-0,442	-1,062	-0,440	-1,663	0,022	-2,014	-0,226	-1,113	-0,439
ElOued	-1,239	-1,129	-1,222	-1,133	-0,840	1,066	2,599	0,100	-1,119	-1,074
Khenche	-0,983	-0,455	-1,004	-0,453	-1,747	-0,090	-0,129	0,627	-1,029	-0,451
SoukAhr	-1,287	-0,751	-1,279	-0,750	-1,246	0,395	-1,404	0,367	-1,264	-0,749
Tipaza	0,089	-0,838	0,034	-0,835	-0,450	-0,765	-0,491	-0,597	-0,022	-0,766
Mila	-0,704	-0,475	-0,711	-0,471	0,548	0,209	3,081	1,278	-0,663	-0,479
AinDefl	-0,500	0,521	-0,495	0,528	-0,860	0,551	-0,318	0,857	-0,640	0,469
Naama	-1,157	-1,358	-1,151	-1,358	-1,888	-0,427	-2,029	-0,370	-1,191	-1,371
AinTemo	-0,830	-0,010	-0,812	-0,007	-1,459	-0,029	-1,658	-0,030	-0,865	0,002
Ghardai	-0,895	-1,229	-0,901	-1,228	-0,955	-0,550	-0,699	-0,399	-0,846	-1,244
Relizan	-0,661	0,527	-0,680	0,535	-0,964	0,700	-1,474	0,351	-0,722	0,472

USTHB Page 30

Chapitre III Application de la DACP

Variabilités des individus :

	2000		2001		2002		2003		2004
	Axe1	Axe2	Axe1	Axe2	Axe1	Axe2	Axe1	Axe2	Axe1	Axe2
Valeur propre	4,550	0,807	4,813	0,998	4,648	1,103	4,829	0,994	4,840	0,995
Variabilité (%)	75,831	13,452	80,219	16,628	77,465	18,376	80,484	16,565	80,665	16,581
% cumulé	75,831	89,283	80,219	96,848	77,465	95,841	80,484	97,049	80,665	97,246
	2005		2006		2007		2008		2009
	Axe1	Axe2	Axe1	Axe2	Axe1	Axe2	Axe1	Axe2	Axe1	Axe2
Valeur propre	4,848	0,994	4,861	0,991	4,680	0,765	4,661	0,699	4,883	0,979
Variabilité (%)	80,795	16,573	81,014	16,519	78,001	12,756	77,691	11,657	81,383	16,313
% cumulé	80,795	97,369	81,014	97,533	78,001	90,758	77,691	89,348	81,383	97,696

III. Phase3 : Étude de l'intrastructure Représentation des trajectoires des wilayas

Nous avons choisi d'utiliser le second critère proposé par J-M Bouroche pour déterminer le système d'axes dans lequel nous représenterons les trajectoires des wilayas.

Le critère 2 consiste à chercher un système d'axe tel que l'inertie des nuages de points associé à chacun des tableaux projetés sur ce système d'axe soit maximale.

Détermination du compromis et des axes :

? REMARQUE : On a représenté le critère 1 et son programme sous le langage R mais sans travailler avec, le programme est présenté dans l'annexe.

Le système d'axe recherché est constitué des vecteurs propres de la matrice variance-

covariance V telle que V=? V_t ou V_t est la matrice variance-covariance de chaque

tableau (t)

(le programme utilisé pour obtenir la matrice compromis est présent au niveau de l'annexe c)

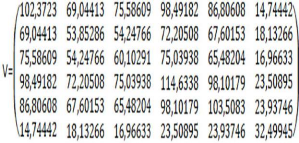
USTHB Page 31

Chapitre III Application de la DACP

Cette matrice V est considérée comme une matrice de variance-covariance « compromis » des variables sur notre période d'étude, les résultats de la diagonalisation de cette matrice V sont les suivants :

Valeurs propres et variabilité de l'intra-structure :

	Axe1	Axe2	Axe3	Axe4	Axe5
Valeurs propres	5.346	0.610	0.038	0.004	0.000
% d'inertie	89.102	10.173	0.639	0.073	0.010
% cumulé	89.102	99.276	99.916	99.989	100.000

Graphique des valeurs propres :

USTHB Page 32

Les deux premiers axes factoriels expliquent 99.27 % d'inertie car nous avons appliqué une ACP sur les composantes principales.

Chapitre III Application de la DACP

USTHB Page 33

Le cercle de corrélation des variables dans le plan :

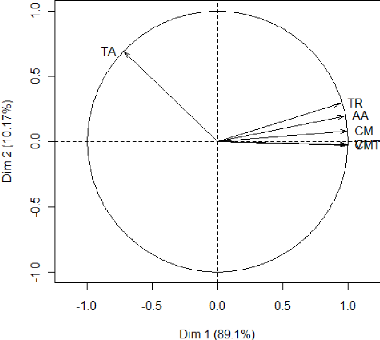
Interprétation des axes :

L'interprétation des axes se fait grâce à l'examen de leurs corrélations avec les « variables-compromis ». Les corrélations correspondent à des corrélations moyennes de nos dix variables sur la période de temps qui va de 2000 à 2009.

L'axe 1 explique 89.1 % d'inertie, nous nous limiterons à son examen et à son interprétation.

Le premier axe caractérise un effet d'opposition, en effet, nous pouvons observer depuis le cercle de corrélation que le groupe de droite, formé par les véhicules touristiques, les tracteurs routiers, les autocar-autobus, les camionnettes ainsi que les camions (qui eux sont fortement corrélés avec l'axe 1) est en opposition aux tracteurs agricoles.

La première composante principale définit donc un « facteur opposition »

Ainsi, l'axe 1 permet de distinguer les wilayas qui se caractérisent par un nombre de véhicules touristiques, tracteurs routiers, autocar-autobus, camions et camionnettes élevé de celles qui se caractérisent par un nombre de tracteurs agricoles élevé.

Chapitre III Application de la DACP

USTHB Page 34

A. Représentation des individus (les wilayas) :

On projette les individus définis par chaque tableau sur le système d'axes.

(Les coordonnées avec lesquelles on a représenté les trajectoires de chaque wilaya sont dans le tableau des coordonnées des observations issu de la deuxième phase de la DACP).Nous présentant les trajectoires des wilayas suivantes: Alger, Adrar, Chlef, Oran, Blida, Constantine, Skikda, Biskra, Annaba, Tlemcen, Jijel, Ghardaïa. (Le programme utilisé pour représenter les trajectoires sur le plan est présent dans l'annexe c).

Graph des trajectoires des wilayas (Alger, Adrar et Chlef)

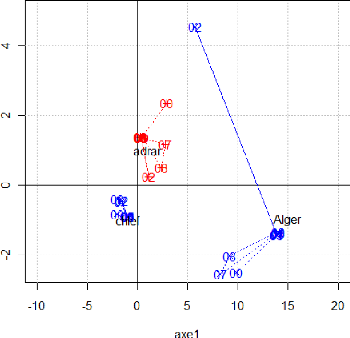
ALGER :

La trajectoire d'Alger se situe dans le coin inferieur droit du plan principal.

Les coordonnées de la trajectoire sur l'axe 1 sont toujours positives. Cela signifie que les valeurs des variables corrélées avec le premier axe, qui sont les véhicules touristiques, les tracteurs routiers, les autocar-autobus, les camionnettes ainsi que les camions, sont supérieures à la moyenne nationale pendant toute la période.

Chapitre III Application de la DACP

USTHB Page 35

De plus, les coordonnées sur le premier axe augmentent au cours du temps ; la trajectoire a tendance à aller vers la droite (avec tout-de -même un recul pour les années 2002, 2007, 2008). Ce phénomène est dû au fait que les valeurs des variables corrélées avec l'axe 1, en particulier les véhicules touristiques, augmente plus que les valeurs de ces mêmes variables pour l'Algérie.

Les coordonnées sur l'axe 2 sont toujours négatives, excepté en 2002. Cela signifie qu'Alger présente un taux de tracteurs agricoles inférieur au taux observé en Algérie pendant toute la période étudiée. La remonté de la trajectoire en 2002 montre que le niveau de la variable tracteur agricole rattrape le niveau national, en cette année.

Nous remarquons que la trajectoire est très étendue, cela se traduit par le fait que la structure du parc automobile pour la wilaya d'Alger a connu beaucoup de modification.

ADRAR :

La trajectoire de Adrar se situe dans le coin supérieur droit du plan principal.

A Adrar, les coordonnées de la trajectoire sur l'axe 1 sont toujours positives, comme ce fut le cas pour la wilaya d'Alger, cela signifie que les valeurs des variables corrélés avec le premier axe sont supérieures à la moyenne nationale.

Toujours sur le même axe, on peut remarquer que les coordonnées de la trajectoire augmentent avec le temps à un degré moindre qu'à Alger, cela se traduit parc le fait que l'augmentation à Adrar des véhicules touristiques, des tracteurs routiers, des autocar-autobus, des camionnettes et camions est moins importante qu'à Alger.

Quant au second axe, les coordonnées de la trajectoire sont toujours positives. Cela signifie que le taux de tracteurs agricoles dans cette wilaya est toujours supérieur à celui observé en Algérie.

CHLEF :

La trajectoire de la wilaya de Chlef se situe dans le coin inferieur gauche du plan factoriel.

La trajectoire est beaucoup moins étendue que celle d'Alger et de Adrar, ce qui signifie qu'il n'y a pas ou peu de modification de la structure du parc automobile dans la wilaya de Chlef sur la période étudiée.

Contrairement à Alger et à Adrar, les coordonnées de la trajectoire sur l'axe 1 sont toujours négatives, ce qui veut dire que le nombre de véhicules touristiques, de tracteurs routiers, d'autocar-autobus, de camions et de camionnettes est inférieur à la moyenne national.

Toujours sur le premier axe, nous pouvons remarquer que les coordonnées de la trajectoire augmentent beaucoup moins vite à Chlef qu'à Alger et à Adrar, cela signifie que l'augmentation des variables corrélées avec l'axe1 est beaucoup moins importante dans cette wilaya. De plus, ces variables présentent des valeurs très inférieures à celles observées à Alger.

Chapitre III Application de la DACP

USTHB Page 36

Quant au second axe, les coordonnées de la trajectoire sont toujours négatives. Cela signifie, comme ce fut le cas pour la wilaya d'Alger, que le nombre de tracteurs agricoles est toujours inférieur à celui observé en Algérie.

Graphe des trajectoires des wilaya (Oran, Blida, constantine)

Chapitre III Application de la DACP

Graphe des trajectoires des wilayas (Skikda, Biskra, Annaba)

USTHB Page 37

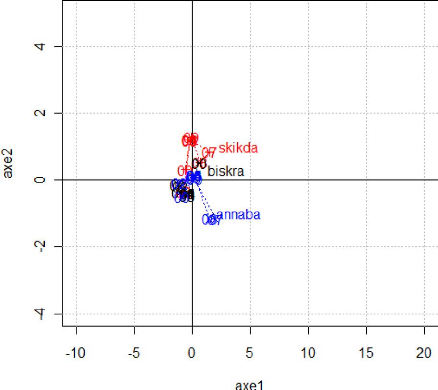
Chapitre III Application de la DACP

Graphe des trajectoires des wilaya (Telimcen, Jijel, Ghardaia)

USTHB Page 38

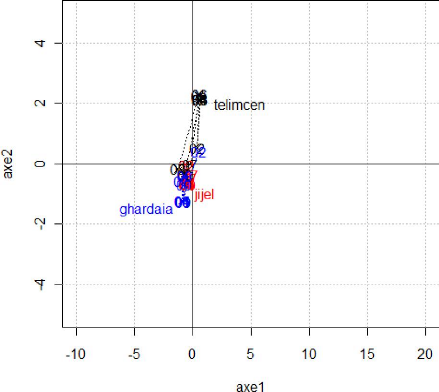
hapitre I

	r~

ai se fsctorielle

des

rresp nd nixes

Chapitre Iii Analyse des correspondances

USTHB Page 40

Analyse factorielle des correspondances

I. Définition :

L'analyse Factorielle des Correspondances ou AFC constitue une technique d'analyse

statistique d'un ou de plusieurs tableaux de contingences permettant une représentation graphique des attractions et des distances entre les modalités des variables choisies.

L'analyse factorielle des correspondances (AFC) peut être considérée comme une extension de l'analyse en composantes principales (ACP). Elle est adaptée au traitement de données qualitatives sans restrictions fortes, son but répond à tout essai d'analyse d'un tableau formé par des observations qualitatives sur des individus ou des catégories.

L'analyse des correspondances va effectuer l'analyse générale d'un nuage de points pondérés

dans un espace muni de la métrique . Donc on se référera donc à l'analyse générale avec des métriques et des critères quelconques.

II. Eléments de base de l'analyse

- Tableau de données, distances, géométrie des nuages

A. Tableau de contingence :

Le tableau de contingence (ou tableau croisé) est obtenu en ventilant une population selon deux variables nominales. L'ensemble des colonnes du tableau désigne les modalités d'une variable et l'ensemble des lignes correspond à celles de l'autre variable. De ce fait, les lignes et les colonnes, qui désignent deux partitions d'une population, jouent des rôles symétriques et sont traitées de façon analogue.

Considérons le tableau de contingence K à n lignes et p colonnes.

A l'intersection d'une ligne et d'une colonne, nous avons le nombre d'individus ayant

simultanément la modalité i de la variable ligne et la modalité j de la variable colonne.

kj .

_ki.

Le total est le nombre d'individus ayant la modalité i de la variable ligne.

Le total est le nombre d'individus ayant la modalité j de la variable colonne.
On a les relations suivantes :

Chapitre Iii Analyse des correspondances

Qui, en termes de fréquences relatives, donnent lieu aux relations :

Transformation du tableau de contingence :

Pour analyser un tableau de contingence, ce n'est pas le tableau d'effectifs bruts qui nous intéresse mais les tableaux des profils-lignes et celui des profils-colonnes c'est-à-dire les répartitions en pourcentages à l'intérieur d'une ligne ou d'une colonne.

Contrairement à l'analyse en composantes principales, le tableau de données subit deux transformations, l'une en profils-lignes, l'autre en profils-colonnes, à partir desquelles vont

^j

^kij

ⁱ

être construits les nuages des points dans et dans

^ki.

^{Tableau de contingence K}

^k

^k.j

^{Fréquences relatives F}

^j

^fi.

^{Profils-colonnes}

^fi.

ⁱ

^fij

^f.j

ⁱ

^j

^{Profils-lignes}

^j

ⁱ

¹

^fij

^fi.

^fij ^f.j

^1

^1

^1

*

*

*

*

*

* *

R n

*

^dans R p

^{nuage des p points}

^dans R n

·

·
·

·

·

·

·

·

^{nuage des n points}

·
·

·

·

·

·

R p

·

·

USTHB Page 41

Transformation du tableau de contingence

Chapitre Iii Analyse des correspondances

Les transformations opérées sur le tableau des données peuvent s'écrire à partir des trois

matrices F, et qui définissent les éléments de base de l'analyse. F d'ordre (n,p) désigne

le tableau des fréquences relatives ; d'ordre (n,n) est la matrice diagonale dont les

éléments diagonaux sont les marges en lignes ; est la matrice diagonale d'ordre (p,p)
des marges en colonnes .

^Fréquences

^{relatives F}

^{f.j 0}

⁰

ⁱ

^j

^fij

^{Marges-lignes} D n

^{Profils-lignes D F}

^-1

ⁿ

^{fi. 0}

{ }(j)

^fij

^fi.

⁰

^p

^{Profils-colonnes D F} '

^-1

^p

{ }(i)

^{Marges-colonnes Dp}

^f.j

ⁿ

Fréquences, marges, profils

^fij

B. Construction des nuages :

Pour l'analyse d'un tableau de contingence, nous raisonnerons en termes de profils, ce qui

permet de rendre comparables les modalités d'une même variable. Les proximités entre les

points s'interpréteront en termes de similitude.

? _f ?

? Nuage des n lignes :

L'ensemble des profils-lignes forme un nuage de n points dans l'espace des p colonnes et représente le nuage des n modalités de la variable ligne.

Chaque point i a pour coordonnées dans :

? ?

ij ; _{j 1,2,..., p} ?

? f _i . ?

Il est affecté d'une masse qui est sa fréquence relative.

^p f

? =

^ij 1

_{j i}

= f

₁

Puisque

, les n points du nuage sont situés dans un sous-espace à p-1 dimensions.

.

USTHB Page 42

Chapitre Iii Analyse des correspondances

USTHB Page 43

Le centre de gravité de ce nuage est la moyenne des profils-lignes affectés de leurs masses et correspond au profil moyen. Sa ^jième composante vaut :

C'est la fréquence marginale des colonnes.

? Nuage des p colonnes :

De la même façon, l'ensemble des p profils-colonnes constitue un nuage de p points dans l'espace des n lignes et représente le nuage des p modalités de la variable colonne.

Les coordonnées dans du point j sont données par :

(Références bibliographiques: Ouvrages, [1])

bspitre

"pile Ho* de

P F

Chapitre V Application AFC

USTHB Page 45

Application de l'analyse factorielle des correspondances

I. Répartition : genre véhicule/ tranche d'âge

Dans le but d'examiner comment sont repartis les genres de véhicule du parc national selon les tranches d'âge, nous effectuons une analyse factorielle des correspondances sur un tableau de contingence qui croise deux variables : « tranche d'âge et genre du véhicule », les données ont été récoltées au courant de l'année 2009.

Nous avons appliqué la méthode statistique appelé AFC car nos données dont de type qualitatives.

? Présentation des variables :

Variable n°1 : Genre de véhicule à 9 modalités.

Variable n°2 : Tranche d'âge à 5 modalités (M5, 5à9, 10à14, 15à19, P20).

M5: Véhicules de moins de 5ans, 5à9: Véhicules de 5à9ans, 10à14: Véhicules de 10à14ans, 15à19: Véhicules de 15à19ans, P20: Véhicules de plus de 20ans.

1. Tableau de contingence : hypothèse d'indépendance

Soit le tableau de contingence K, à n lignes (n=9) et p colonnes (p=5), pour une population total de 33.841.162 correspondants aux véhicules recensés en 2009 sur l'ensemble du territoire national.

Tableau croisant genre véhicule avec tranche d'âge correspondant à l'année 2009.

	M5	5à9	10à14	15à19	P20
VT	.	.	.	.	.
CT	.	.	.	.	.
C	.	.	.	.	.
TA	.	.	.	.	.
R	.	.	.	.	.
TR	.	.	.	.	.
AA	.	.	.	.	.
M	.	.	.	.	.
VS	.	.	.	.	.

) :

2

2. Teste d'indépendance (x

Test :

H0 : Les variables X et Y sont indépendantes H1 : Les variables X et Y sont liées entre elles

Chapitre V Application AFC

USTHB Page 46

Khi^2 (valeur observée)	855851,070
Khi^2 (valeur critique)	46,194
ddl	32
p-value unilatérale	< 0,0001
Alpha	0,05

CONCLUSION :

Au seuil de signification =0.05 on rejette l'hypothèse nulle d'indépendance entre les lignes et les colonnes.

Autrement dit, la dépendance entre les lignes et les colonnes est significative

3. Valeurs-propres et pourcentages d'inertie :

	F1	F2	F3	F4
Valeur propre	0,015	0,009	0,001	0,000
% variance	60,326	34,818	3,973	0,883
% cumulé	60,326	95,145	99,117	100,000

4. Coordonnées, contributions et cosinus carrés :

LIGNES	Coordonnées				Contributions		Cos2
genres	F1		F2		F1	F2	F1	F2
VT	0,078		0,012		24,13	0,92	0,977	0,022
CT	-0,041		-0,181		1,45	47,83	0,048	0,916
C	-0,200		0,013		44,13	0,33	0,972	0,004
TA	0,145		-0,026		2,81	0,16	0,450	0,014
R	-0,207		-0,009		5,47	0,02	0,827	0,001
TR	-0,177		0,156		6,53	8,82	0,539	0,421
AA	0,516		0,328		10,17	7,14	0,707	0,286
M	-0,152		0,365		3,41	34,23	0,142	0,825
VS	-0,353		-0,145		1,90	0,56	0,854	0,144
COLONNES		Coordonnées			Contributions		Cos2
Tranches d'âge		F1		F2	F1	F2	F1	F2
M5		0,259		-0,050	53,92	3,53	0,955	0,036
5à9		0,119		0,183	6,81	28,07	0,266	0,632
10à14		0,034		0,192	0,73	40,12	0,027	0,854
15à19		-0,182		0,047	36,44	4,30	0,907	0,062
P20		-0,024		-0,063	2,10	23,97	0,128	0,845

Chapitre V Application AFC

5. Nuage des points lignes :

USTHB Page 47

6. Nuage des points colonnes :

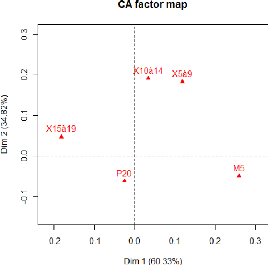
Chapitre V Application AFC

USTHB Page 48

7. Nuage des points (représentation quasi-barycentrique) :

8. Inteprétation :

Les coordonnées sur le premier axe montre que les genres véhicule touristique, tracteur

agricole et autocar-autobus s'opposent aux genres moto, tracteur routier, camion, remorque, camionnette et véhicule spécial.

Avec une contribution de 24.13 % et un cosinus carré de 0.97, le genre véhicule touristique se trouve pratiquement sur l'axe1 et ne pourra donc pas caractériser les axes ultérieurs.

Le second axe est essentiellement construit par le genre camionnette avec une contribution 47.83 %, il s'oppose simultanément aux genres véhicule touristique, autocar-autobus, camion, tracteur routier et moto, avec un cosinus carré de 0.91.

Chapitre V Application AFC

USTHB Page 49

Pour les points colonnes (tranche d'âge), le premier axe est construit presque exclusivement par la tranche d'âge de moins de 5ans et celle qui va de 15 à 19 ans (avec des contributions de 53.92 % et 36.44 %) cela signifie que ces deux modalités se situent pratiquement sur l'axe1 (cosinus carrés 0.95 et 0.90), le second axe (profil colonne) est surtout lié au tranches d'âges plus de 20ans (23.97%) et 10 à 14ans (40.12%).

L'axe 1

Cet axe oppose les vehicules du genre véhicule de tourisme, tracteur agricole et autocar-autobus dont la tranche d'âge est moin de 5 ans avec les véhicules du genre remorque, camion, véhicule speciale, tracteur routier et moto dont la tranche d'âge varie entre 15 et 19 ans. Autrement dit, le parc national automobile a connu en 2009 un renouveau beaucoup plus important dans les véhicules de transport et les véhicule de tourisme.

L'axe 2

Cet axe oppose essentiellement les vehicules du genre moto et autocar-autobus dont les tranches d'âges sont 5à 9 et10 à 14 ans, aux véhicules du genre véhicule spéciale et camionnette dont la tranche d'âge est de plus de 20ans, par consequent, les véhicules speciaux et les camionnettes sont les genres les plus anciens circulant en Algérie.

Chapitre V Application AFC

II. Répartition : genre véhicule/ tranche de puissance

Dans le but d'examiner comment sont repartis les genres de véhicule du parc national selon les tranches de puissance, nous effectuons une analyse factorielle des correspondances sur un tableau de contingence qui croise deux variables : « tranche de puissance et genre du véhicule », les données ont été récoltées au courant de l'année 2009.

Nous avons appliqué la méthode statistique appelé AFC car nos données dont de type qualitatives.

? Présentation des variables :

Variable n°1 : Genre de véhicule à 8 modalités.

Variable n°2 : Tranche de puissance à 8 modalités (1à2, 3à5, 6à7, 8à10, 11à16, 17à20, 21à25, Plus de 25) : correspondant au différentes tranches de puissances exprimées en Chevaux.

1. Tableau de contingence : hypothèse d'indépendance :

Soit le tableau de contingence K, à n lignes (n=8) et p colonnes (p=8) pour une population total de 24.557.981 correspondants aux véhicules recensés en 2009 sur l'ensemble du territoire national.

Tableau croisant genre véhicule avec tranche de puissance correspondant à l'année 2009

	VT	CM	CMT	AA	TR	TA	VS	M
1 à 2	.	.	.	.	.	.	.	.
3 à 5	.	.	.	.	.	.	.	.
6 à 7	.	.	.	.	.	.	.	.
8 à 10	.	.	.	.	.	.	.	.
11 à 16	.	.	.	.	.	.	.	.
17 à 20	.	.	.	.	.	.	.	.
21 à 25	.	.	.	.	.	.	.	.
PLUS 25	.	.	.	.	.	.	.	.

) :

2

2. Teste d'indépendance (x

Test :

H0 : Les variables X et Y sont indépendantes H1 : Les variables X et Y sont liées entre elles

Khi^2(valeur observée)	18827624,602
Khi^2(valeur critique)	66,339
ddl	49
p-value unilatérale	< 0,0001
Alpha	0,05

USTHB Page 50

Chapitre V Application AFC

CONCLUSION :

Au seuil de signification =0.05 on rejette l'hypothèse nulle d'indépendance entre les lignes et les colonnes.

Autrement dit, la dépendance entre les lignes et les colonnes est significative

3. Valeurs-propres et pourcentages d'inertie :

	F1	F2	F3	F4	F5	F6	F7
Valeur propre	0,482	0,148	0,102	0,028	0,005	0,002	0,000
% variance	62,864	19,254	13,352	3,698	0,613	0,220	0,000
% cumulé	62,864	82,118	95,469	99,167	99,780	100,000	100,000

4. Coordonnées, contributions et cosinus carrés :

LIGNES	Coordonnées				Contributions			Cos2
tranche de puissance	F1			F2	F1		F2	F1		F2
1 à 2	-0,730			-0,171	0,48		0,03	0,066		0,001
3 à 5	-0,668			-0,161	7,06		0,41	0,688		0,012
6 à 7	-0,644			-0,159	11,25		0,68	0,732		0,014
8 à 10	-0,443			-0,056	5,86		0,09	0,307		0,001
11 à 16	2,106			-1,229	60,58		20,62	0,905		0,094
17 à 20	1,266			-0,804	1,70		0,69	0,641		0,079
21 à 25	0,450			-0,116	0,49		0,03	0,456		0,009
PLUS 25	1,174			2,913	12,59		77,45	0,346		0,651
COLONNES		Coordonnées				Contributions			Cos2
genres		F1	F2			F1	F2		F1		F2
VT		-0,331	-0,030			14,01	0,38		0,744		0,006
CM		1,542	-0,135			48,47	1,22		0,984		0,008
CMT		-0,249	0,019			2,69	0,05		0,147		0,001
AA		1,026	0,462			3,60	2,38		0,751		0,152
TR		1,172	2,761			4,64	84,00		0,152		0,841
TA		1,814	-0,666			26,09	11,49		0,864		0,117
VS		1,268	0,870			0,32	0,49		0,569		0,267
M		-0,534	0,018			0,18	0,00		0,027		0,000

USTHB Page 51

Chapitre V Application AFC

5. Nuage des points lignes :

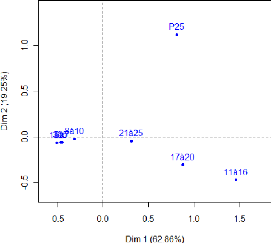
USTHB Page 52

6. Nuage des points colonnes :

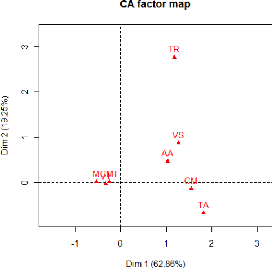
Chapitre V Application AFC

USTHB Page 53

7. Nuage des points (représentation quasi-barycentrique) :

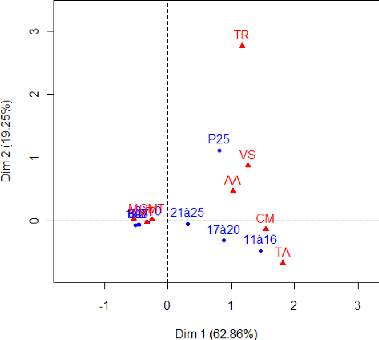
8. Interprétation :

Les coordonnées sur le premier axe montrent que les genres véhicule de tourisme, moto et

camionnette s'opposent aux genres camion, tracteur agricole, tracteur routier, véhicule spécial et autocar-autobus ; surtout le genre camion avec une contribution de 48.47% et un cosinus carré de 0.98.

Le second axe est essentiellement construit par le genre tracteur routier (contribution 84 %), il est le seul à être bien représentée sur le deuxième axe avec un cosinus carré de 0.84.

Pour les points lignes (tranche de puissance), le premier axe oppose deux groupes ; ce sont les tranches de puissances (1 à 2, 3 à 5 ,6 à 7 et 8 à 10) avec les tranches de puissances (11à 16,17 à20, 20 à25), l'axe1 est construit pratiquement par la tranche de puissance qui va de 11 à 16 chevaux avec une contribution de 60.58% et cos2 de 0.90.

Chapitre V Application AFC

Le second axe étant lié à la tranche de puissance p20 chevaux (77.45 %) avec cos2 (0.65)

Axe1

Le premier axe oppose les genres moto, véhicule touristique et camionnette dont les tranches de puissances sont 1à2, 3à5, 6à7 et 8à10 aux genres camion et tracteur agricole caractérisés par les puissances qui vont de 11à16 et 17à20 autrement dit les véhicules les plus puissants circulant en Algérie pendant l'année 2009 sont les camions et les tracteurs agricoles.

Axe2

Le second axe oppose les tracteurs routiers avec les tracteurs agricoles dont la tranche de puissance est 11à16 chevaux et 17à20 chevaux.

USTHB Page 54

F'ré				hi		D)		Et
	h	s	pitre

c^-v^-ith d I le de

)3o Jen,kkne

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 57

I. Définitions sur les séries chronologiques:

1. Qu'appelle-t-on série chronologique ?

Une série chronologique (chronique) ou encore temporelle est une succession

d'observations au cours du temps représentant un phénomène économique (prix, vente...) ; par hypothèse, le pas du temps des observations est considéré constant (heure, jour, mois, trimestre, année). La valeur courante en de la chronique est notée , où le temps est compris entre 1 et avecle nombre total d'observations.

2. Représentation graphique:

L'examen graphique de la chronique étudiée permet de dégager

lorsqu'on envisage une période de temps suffisamment longue, un certain nombre de composantes fondamentales de l'évolution de la grandeur étudiée.

Il est utile d'analyser ces composantes, en les dissociant les unes des autres, c'est-à-dire que l'on suppose que la structure de la chronique peut être décomposée en éléments simples (modélisables), et donc plus facilement prévisibles, pour ensuite être reconstituée pour donner la prévision de la chronique.

On isole habituellement quatre composantes :

A. La tendance :

Elle représente l'évolution à long terme de la grandeur étudiée, et traduit l'aspect général de la série, en outre la tendance est une caractéristique d'un phénomène stable de croissance ou de décroissance dans le temps.

B. Les variations saisonnières :

Les variations saisonnières décrivent un mouvement plus au moins régulier d'amplitude presque constante et qui se répète à des intervalles égaux.

Elles sont liées au rythme imposé par les saisons météorologiques (production agricole, consommation de gaz,...), ou encore par des activités économiques et sociales (fêtes, Vacances, solde,...).

C. Le cycle : noté

Regroupe les variations autour de la tendance avec des alternances de phases d'expansion et de récession. Ces phases durent généralement plusieurs années, mais n'ont pas de durée fixe. Cette composante est généralement traitée concomitamment avec la tendance ; car il est très difficile de les dissocier.

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 58

d. La composante résiduelle (aléatoire) : notée

Elle rassemble tout ce que les autres composantes n'ont pu expliquer du phénomène observé. Elle contient de nombreuses fluctuations, en particulier accidentelles, dont le caractère est exceptionnel et imprévisible (catastrophes naturelles, grèves, guerres) Le résidu présente en général une allure aléatoire plus au moins stable autour de sa moyenne.

La technique de décomposition recomposition repose bien évidemment, sur un modèle qui l'autorise. Ce modèle porte le nom de schéma de décomposition.

3. Schéma de décomposition d'une chronique:

Il en existe essentiellement deux grands types de schémas de décomposition :

A. I.3.1 Le schéma additif : Il s'écrit :

Dans ce schéma la saisonnalité est rigide en amplitude et en période.

B. I.3.2 Le schéma multiplicatif :

Il s'écrit : Il est le plus utilisé en économie.

L'identification du type de schéma se fait selon la procédure de la bande.

4. La procédure de la bande :

La procédure de la bande consiste à partir de l'examen visuel du graphique de

l'évolution de la série brute à relier, par une ligne brisée, toutes les valeurs hautes locales et toutes les valeurs basses locales de la chronique.

Si les deux lignes sont parallèles, la décomposition de la chronique peut se faire selon un schéma additif ; dans le cas contraire, le schéma multiplicatif semble plus adapté.

Unité Unité

Temps Temps

Schéma additif Schéma multiplicatif

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 59

Chapitre VI Méthodologie de Box & Jenkins

5. Prévision:

A. I.5.1 Qu'est-ce que la prévision ?

La prévision est une activité préalable à toute prise de décision.

Tout comme les besoins, les méthodes sont multiples et d'inspirations très différentes.

Trois critères permettent de distinguer les types de prévision :

L'horizon : le court, le moyen ou le long terme;

La finesse : micro-économique (firme, marché), ou macro-économique (grands

agrégats de la comptabilité nationale) ;

La technique : qualitative (appel au jugement humain) ou quantitative (formalisation

et estimation statistique)

Les critères sont indépendants les uns des autres : il est possible d'élaborer une

prévision à court terme à l'aide d'une technique qualitative ou bien une prévision à long

terme de données micro-économiques par une technique quantitative.

? _Xt , _t ? _T?

? _{E, P?}

B. I.5.2 Prévision d'une série chronologique :

La prévision d'une chronique consiste à évaluer les valeurs futures ;

d'une variable à partir de l'observation de ses valeurs passées . Or

la valeur que la variable prendra à l'instant sera plus au moins égale à la valeur
prédite ; pour cette raison, on construit un intervalle de prévision susceptible de contenir la valeur inconnue. La qualité de la prévision dépend d'une part de l'évolution de la série, d'autre part de l'horizon h ; en d'autres termes, la qualité de la prévision est meilleure lorsque la série évolue d'une façon régulière dans le temps et / ou lorsque l'horizon est petit.

_T ? _Z

II. Processus stochastique:

1. Définition:

Soit un espace probabilisé et soit un espace probabilisable.

Un processus stochastique (aléatoire) noté est une famille de variables

aléatoires indicées par le temps, définies sur le même espace , et à valeur dans

l'espace , appelé espace d'états du processus stochastique.
t est l'instant d'observation, est l'espace des indices.

Si est dénombrable ( ou ou ), le processus est dit à temps discret.

USTHB Page 60

Si est non dénombrable (par exemple T = ), le processus est dit à temps continu.

_{(t,s)-*8(t,s)= cov(Xt,Xs} )= _{E? (Xt --pt)(Xs --ps} )]

a. Caractéristiques d'un processus stochastique : La moyenne :

La moyenne d'un processus est définie par l'application suivante :

6 ^2x

La variance :

La variance d'un processus est définie par l'application suivante :

T-*IR

₆₂

_x

_t-*

_{(t). E(Xt} -- _pt)2

La fonction d'autocovariance :

La fonction d'autocovariance d'un processus est définie par l'application suivante :

_8:TxT-*IR

La fonction d'autocorrélation :

La fonction d'autocorrélation d'un processus est définie par l'application suivante :

_p:TxT-*IR

_{(t,s)-*p(t,s)}

2. Processus stationnaire

Dans une acceptation générale, on dit qu'un processus est stationnaire si sa distribution de probabilité est la même par translation au cours du temps. On distingue deux types de stationnarité :

(Xt ₁ , , Xtn)

a. Stationnarité stricte : (forte)

Un processus est dit strictement stationnaire si

_{V nE IN*} ,(t ₁ , _t2 , ?,t _{n )E} Z ⁿ , _{V hE} Z , la suite ^(Xtl+h ,.......X_tn+h) a la même

probabilité que la suite . Autrement dit :

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 61

La stationnarité stricte implique que tous les moments, s'ils existent, soient indépendants du temps.

b. Stationnarité faible :

Le processus est dit stationnaire au sens faible, ou stationnaire au second

ordre si les premiers (moyenne ou espérance mathématique) et second (variance et autocovariance) moments du processus existent et sont indépendants de t :

(indépendante de t)

? _X1 , ₁ ? _T?

(indépendant de t)

: ? _k ? _{ou si n} ? ₁₅₀

_{6 3 5}

Remarque :

Si le processus est du second ordre ( ) alors la stationnarité stricte

implique la stationnarité faible.

3. Caractéristiques d'un processus stationnaire

_{n n n}

A. Corrélation, autocorrélation, corrélogramme :

La corrélation est un moyen utilisé pour comparer l'évolution de deux ou plusieurs phénomènes. L'autocorrélation est un concept lié à celui de la corrélation, il s'agit d'une corrélation entre les composantes du processus à différents décalages dans le temps. En pratique, les coefficients d'autocorrélation sont calculés pour des ordres allant de 0 à k,

k étant le décalage maximum tel que .

Le corrélogramme est une représentation graphique des coefficients d'autocorrélation de retards successifs d'une série chronologique.

B. Fonction d'autocovariance :

La fonction d'autocovariance mesure la covariance entre deux composantes du

processus séparées par un certain délai. Elle fournit des informations sur
l'évolution et sur les liaisons temporelles pouvant exister entre les différentes composantes de la série.

Chapitre VI Méthodologie de Box Z Jenkins

La fonction d'autocovariance d'un processus stationnaire est définie comme

suit :

Propriétés :

(L'inégalité de cauchy-schwartz)

(Symétrique, fonction paire).

C. Fonction d'autocorrélation simple d'un processus stationnaire : (FAC) Elle permet de mesurer les liaisons temporelles entre les différentes composantes

du processus générateur de la série. Elle est définie par :

Elle vérifie les propriétés suivantes :

(la parité)

D. Fonction d'autocorrélation partielle d'un processus stationnaire (FAP) :

Elle mesure la corrélation entre , l'influence des variables

ayant été retirée. Etant donnée la matrice des corrélations symétrique formée des (k-1) premières autocorrélations.

^?1

¹

.

¹

.

? ?

^k ? ^{1 k} ? ²

^1	^?1				. ? ^k

¹

²

.?

P k

?

^k

?

?

¹ ? ? ? ? ??

?

?

?

?

?k	?	P * k P k

USTHB Page 62

La fonction d'autocorrélation partielle est donnée par :

Chapitre VI Méthodologie de Box Z Jenkins

_B ? _F

_{B X} B ^j _{c c j Z}

j ? ? ? ?

Où	est le déterminant de la matrice obtenu à partir de , en remplaçant la

dernière colonne de celle-ci par le vecteur

?

?

¹

= = X _{t i} j ( _i , _j ) _Z

^p . ^p

¹

¹

^p 1. ^p ^1 ^2

?

.

.

^{p p}

^{k?1 k}
? ? ? ? ? ??

? i ? ? _{V E}

X _t i _{i Z}

_{t t} ? ?

Ainsi

_{B B X B X}

P k

* ?

_{i j i} ? _j

Vu la complexité des calculs, on utilise plutôt l'écriture récurrente de tel que :

_{B X}

¹

?

_{i j i j}

+ t = t + = + _{V i j E} Z ²

?

¹

^j

?

¹

^{si i}

?

ⁱ

¹

? ? ? ? ?

^{i i} ? ¹ , ^{j i} ? ^j

¹

^j

?

ⁱ

¹

? ?

ⁱ ? ¹ , ^{j j}

^?ii

? ? ???

^{i?2, ,k}

Où

Cet algorithme résolvant les équations de Yule-Walker de manière récursive est appelé algorithme de Durbin (1960).

_{V E}

_{t t} ? _{i t} ? _j

4. Les opérateurs:

a. Opérateur de retard (Backward):

On considère un processus stochastique , l'opérateur de retard noté B,

_?1

_t

₂

_t

est défini par : cet opérateur permet ainsi de définir une application qui à

toute variable associe la variable .
Il a les propriétés suivantes :

, en particulier

si (c IR) :

; avec (l'opérateur d'avance)

l'opérateur de retard permet d'écrire un polynôme :

? _{a X} ? ? _{a B} X t ? _n ? _IN

( ) ,

_{i t} ? _{i i}

_{n n}

_i

?

i ?

i ?

USTHB Page 63

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 64

b. Opérateur de différence ordinaire:

On note l'opérateur de différence première ordinaire associé au processus tel que :

? _X1 ? ₁ ? _Z

.

Et par construction, on obtient l'opérateur de la d^eme différence, noté

b. Opérateur de différence saisonnière:

Soit un processus auquel on associe l'opérateur de différence

_X = _{qS X} + _{qS X} + ? + _{qS X} + _{s où} { _{s t E Z}}

_{t 1 t} ? _{1 2 t} ? _{2 p t} ? _{p t} t ,

saisonnière d'ordre, noté , par construction nous

obtenons l'opérateur de la D^eme différence saisonnière d'ordre noté

5. Processus bruit blanc:

Un processus bruit blanc, noté est une suite de variables aléatoires
non corrélées telles que :

? ? _B ? _Xt ? ? t

5. Classes des modèles ARMA: _p

_{D B} = ₁ _ _{Ø B} _ _Ø B ²

( ) _ ? _ _{Ø B Ø E IR} , _{V i} = _1, ? ,

1 p

_{2 p i}

a. Modèle autorégressif AR d'ordre p: 1) Définition :

Un processus est dit autorégressif d'ordre p, noté AR (p) s'il admet la
représentation suivante :

est un bruit blanc de variance .

En utilisant l'opérateur de retard , on obtient :

avec :

2) Chapitre VI Méthodologie de Box & Jenkins

Condition nécessaire et suffisante de causalité et d'inversibilité d'un AR

(p)

:

Une condition nécessaire et suffisante pour que le modèle autorégressif

soit causal (annexe 1) est que les

racines de la fonction caractéristique : soient en

valeurs absolues supérieurs à 1 c'est-à-dire

.

D'après la définition d'inversibilité (annexe 1), un modèle autorégressif d'ordre fini est toujours inversible.

3) Les caractéristiques des processus AR (p) :

· Fonction d'autocovariance :

La fonction d'autocovariance d'un processus AR (p) satisfait une
relation de récurrence de la forme :

_{I ?1?1} ? _?2?2 ? ? _S ? ?£ _k ? ₀

? ? ,/ ,/ _p p avec :

^k 0

1?k?1 ? _028k?2 ?
·
·
· + ? _s

pk _{k 0}

_p

?

?

· Fonction d'autocorrélation simple :(FAC)

La fonction d'autocorrélation, notée ou p_k , d'un processus AR (p)
Satisfait une relation de récurrence de la forme :

₀

?

_{1 k=0}

_0:1)(B)P(k) = _{0 =Pk} = b'kE Z'

₀

_?

_{1Pk-1 +}

_{2Pk-2 +}

_+0pPk-p

USTHB Page 65

Ces relations sont connues sous le nom d'équation de Yule-Walker.

La FAC est une exponentielle et /ou une sinusoïde amortie (lorsque le processus est causal).

· Fonction d'autocorrélation partielle :(FAP)

Les autocorrélations partielles, notées d'un processus AR (p)

_{Xt =c} + 01 _{Xt_1} +02 _{Xt_2} +
·
·
· _+0p Xt _p +Et sont nulles pour tout ordre supérieur à p

_(Pk ? _{0,? k?} p) et non nulles pour tout ordre inférieur à p. De plus on a = .

Seuls les p premiers termes de la FAP sont significativement différents de 0.

Chapitre VI Méthodologie de Box Z Jenkins

b. Modèle moyenne mobile d'ordre q MA (q):

1) Définition:

On appelle un processus moyenne mobile d'ordre q, noté MA (q) s'il

admet la représentation suivante :

Avec : est un bruit blanc de variance

2) Condition nécessaire et suffisante d'inversibilité et de causalité d'un MA (q):

Une condition nécessaire et suffisante pour que le modèle moyenne mobile

soit inversible est que les racines de la fonction

caractéristique soient en valeurs absolues

supérieures à 1

.

D'après la définition de causalité (annexe 1), un modèle moyenne mobile d'ordre fini

est toujours causal, car c'est une combinaison linéaire finie de processus stationnaire

.

3) Les caractéristiques des processus MA (q):

? Fonction d'autocovariance :

_{2 2}

₍₁ ? ? ? ? ? ?

₂ 2 ? ? ? _k?
q )

_{1 2} ?

La fonction d'autocovariance d'un processus MA (q) est donnée par la relation :

( ? ? ? ? ? ? ? ? ? ? ? ? _k ?

?

?

?

?

?

?

? k

₀

_q

_{k k} ? _{q k} q ) ₀

_{1 1} ? ?

₂

_E(? ? ) ? _{0 si j} ? ₀

_{t t} ? _j

0

k

?

q

_E ( ² ) 2

? ? ?

_t ? _j ?

_?j

Avec :

? ? ? ?? et

USTHB Page 66

? Fonction d'autocorrélation simple : (FAC)

La fonction d'autocorrélation d'un processus MA (q) est donnée par la relation :

Chapitre VI Méthodologie de Box Z Jenkins

_?k

?

?k ?

? ? ₁ ? ? ? ? ? ?

_{0 1 2 q}

? ₁

? ? ? ? ? ? ? ? ? ? ?

_{k 1 k} ? _{1 q} ? _{k q}

? _{2 2}

2 ? ?

? ? 0

? Soit sous la forme MA (?) :

a? avec

x: ? i=1

<x: et

a0

1

_k ? ₀

? q

q

_0?

_k

_k

?

La fonction d'autocorrélation simple d'un MA (q) s'annule à partir de l'ordre q+1. c. Fonction d'autocorrélation partielle : (FAP)

La fonction d'autocorrélation partielle d'un processus MA (q)

défini par se comporte comme une exponentielle ou une sinusoïdale

amortie.

c. Processus autorégressif moyenne mobile d'ordre (p, q) ARMA(p,q):

Les processus ARMA se définissent par l'adjonction d'une composante

autorégressive AR et d'une composante moyenne mobile MA.

1) Définition:

On appelle un processus autorégressif moyenne mobile d'ordre (p, q)

noté ARMA (p, q) s'il s'écrit sous la forme suivante :

avec: : est un bruit blanc de variance .

.

.

Nous avons : ARMA (p, 0) = AR (p) et ARMA (0, q) = MA (q).

2) Condition d'inversibilité et de causalité d'un ARMA (p, q):

Une condition nécessaire et suffisante pour que le modèle autorégressif moyenne

mobile soit inversible est que les racines de l'équation

caractéristique soient à l'extérieur du cercle unitaire.

De même, il est causal si et seulement si les racines de l'équation caractéristique

soient à l'extérieur du cercle unitaire.

? ( _B )

X t ? ? ( ) ? ? 0

B _i ?

_{i t} ? _i

a i

Remarque : Siet ont leurs racines à l'extérieur du disque unité, on peut écrire

un modèle ARMA (p, q) :

USTHB Page 67

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 68

Soit sous la forme AR (?) : avec

? ? ₀ : _Xt

: X t ? X _t ?1 ? ? t

3) Les caractéristiques des corrélogrammes des modèles ARMA (p, q):

Les corrélogrammes simple et partiel d'un processus ARMA (p, q) synthétisent ceux des processus AR (p) et MA (q), ils sont un mélange de fonctions exponentielles et sinusoïdales amorties.

7. Processus non stationnaires:

Ces processus sont représentatifs de la plupart des phénomènes aléatoires dans la mesure où d'autres facteurs ne sont pas pris en compte en dépit de leur importance ou de leur imprévisibilité (grève, catastrophe,...). Les cas de non stationnarité sont représentés par :

? ? ₀

X t

=X _t ?1 _+fl +s t

a. Processus TS:

Les processus TS représentent une non stationnarité de type déterministe et s'écrivent comme suit :

Où:est une fonction du temps, linéaire ou non est un processus stationnaire.
Soit le processus TS :

dépend du temps, ce qui implique qu'il n'est pas stationnaire.

Pour le stationnariser, on soustrait de la valeur de en t la valeur estimée en
utilisant la méthode des moindres carrés ordinaires (MCO).

b. Processus DS:

Les processus DS représentent les processus non stationnaires aléatoires

(Differency Stationnary). Ils s'expriment par l'équation suivante :

Où un processus stationnaire.

On distingue deux types de processus :

Pour s'écrit .

Le processus DS est dit sans dérive, il est appelé aussi marche aléatoire (Random walk). Il s'agit d'un processus autorégressif d'ordre 1.

.

Pour : s'écrit

Le processus DS est dit avec dérive, il s'agit d'un processus autorégressif d'ordre 1 avec constante.

Pour stationnariser ces deux processus, on utilise le filtre aux différences.

USTHB Page 69

Chapitre VI Méthodologie de Box Z Jenkins

_{1 2 q}

? _B ? ? ? _B ? ? _B ? ? ? ?

( ) 1 ₁ 2 qB

Pour :

Pour : Avec d l'ordre de différenciation ou d'intégration.

_{2 Qs}

® ( ) 1 1

B s = - ₀ - ₀ - - ₀

_s s B ¹ s _B ? Qs B

c. Processus autorégressif moyenne mobile intégré d'ordre (p, d,q):

Ce sont des modèles ARMA intégrés notés ARIMA. Ils sont issus des séries stationnarisées par l'application du filtre aux différences et ceci, bien entendu dans le cas des processus DS détectés par le test de Dickey-Fuller (défini dans le chapitre 3).

Le processus suit un ARIMA (p, d, q), c'est-à-dire qu'il est solution d'une

équation aux différences stochastiques du type .
₍₁ ? _B )

d. Processus autorégressif moyenne mobile intégré saisonnier:

Il est possible de trouver que certaines séries chronologiques peuvent être caractérisées par une allure graphique périodique, pour cela il est important de les analyser en tenant compte de l'effet saisonnier. Box et Jenkins (1970) ont proposé une classe de modèles particulière appelée : classe de modèles ARIMA saisonniers.

? t ? _BB ??

1) Modèles saisonniers mixtes : SARIMA

Ce sont des extensions des modèles ARMA et ARIMA. Ils représentent généralement des séries marquées par une saisonnalité comme c'est le plus souvent le cas pour des séries économiques voire financières. Ces séries peuvent mieux s'ajuster par des modèles saisonniers. Ce sont les modèles SARIMA (p, d, q) (P, D, Q) qui répondent au modèle:

₍₁ ? _B)d

_{S D}

où

:polynôme autorégressif non saisonnier d'ordre p.

: polynôme autorégressif saisonnier d'ordre P.

: polynôme moyenne mobile non saisonnier d'ordre q.

( 0, ² )

₂

: polynôme moyenne mobile saisonnier d'ordre Q.

: opérateur de différence d'ordre d.

: opérateur de différence saisonnière d'ordre D.

, s correspond à la saisonnalité.

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 70

2) Modèles saisonniers purs : (SARMA)

Un processus stochastique est dit processus autorégressif moyenne

mobile intégré saisonnier pur d'ordre , si son évolution satisfait la forme

suivante :

, s correspond à la saisonnalité.

III. Méthodologie de Box & Jenkins:

1. Définition :

Box & Jenkins (1976) ont conçu une méthodologie consistant à modéliser les séries temporelles au moyen des modèles ARMA.

Pourquoi les modèles ARMA ?

L'idée de base est le concept de parcimonie, ou de la minimisation du nombre de paramètres.

En pratique, ces derniers étant inconnus, ils sont donc remplacés par leur valeur estimée : plus il y a de paramètres, plus nombreuses sont les chances de se tromper.

Les modèles ARMA modélisent très bien l'historique des données afin de prévoir le futur ; il s'agit donc d'une méthode de prévision extrapolative.

L'information permettant de mettre en évidence le processus est contenue dans la série chronologique elle-même, sans apport externe, d'où le nom de prévision endogène.

La méthode de Box & Jenkins s'applique sur des séries stationnaires, or les chroniques économiques sont rarement des réalisations de processus aléatoires stationnaires. La non stationnarité des processus peut concerner aussi bien le moment du premier ordre (espérance mathématique) que celui du second ordre (variance et covariance). Cette non stationnarité peut être repérée graphiquement (tendance, saisonnalité). Pour avoir une certitude, il existe des tests pour confirmer les déductions tirées du graphique.

Chapitre VI Méthodologie de Box Z Jenkins

T ? _{A P R}

3. Test de la saisonnalité et de la tendance :

a. Test de la saisonnalité :

Il existe plusieurs méthodes pour détecter l'existence d'une composante saisonnière, dont :

La méthode graphique :

Elle consiste à comparer les observations des différentes années et de voir s'il existe un certain aspect qui se répète à chaque période, ou à l'aide des fonctions d'autocorrélations : elle consiste à analyser le corrélogramme simple : s'il laisse apparaître des pics très marqués aux retards S, 2S, 3S, ..., on en déduit une saisonnalité de périodicité S (S=4, 6, 12,...).

Remarque :

L'examen du graphique ne suffit pas très souvent pour mettre en évidence une saisonnalité, donc il est nécessaire d'utiliser le test de Fisher à partir de l'analyse de la variance (test d'ANOVA).

Test de Fisher :

On considère n: Le nombre d'années. P: Le nombre d'observations dans l'année : La valeur de la série pour la i^ème année et la j^ème période.

_p ( _{X X} )

_i .

?? . . _i ? ₁

_VAR ?

^A _n ? ₁

^P _p -- ₁

v 1 ? ? _P ? _1? v 2 ? ? _n ? ₁ ?? _P ? _1?

La moyenne générale , la moyenne de l'année i , la moyenne de la période j

La variance année et la variance période sont définies respectivement par :

_VAR =

_{n p}

_{i=1 j=1}

_{(X-X- X} - _X

_i . . _j . . )

_{i j}

₂

_n

₂

,
_{n p} ? _{j=1 (X.j--X..)}

_-1)(p-

₁₎

_(n

=

??

_R

VAR P

La variance résiduelle :

_VAR

_F0 ?

Fv 1 v 2

₂

_{n p}

_{i=1 j=1}

L'équation de la variance totale :

F 0 ?

_(X ? _X )

_i j ..

₂

??

=

₁

_n

?

L'hypothèse est : « pas de saisonnalité » contre : « il existe une saisonnalité

que l'on compare à la valeur tabulée

La valeur calculée

USTHB Page 71

?

avec , degré de liberté

Si on rejette, la série est saisonnière.

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 72

Soient les hypothèses : : « La série n'est pas affectée d'une tendance »

Contre : « La série est affectée d'une tendance »

On calcule que l'on compare avec

Avec , degré de liberté

Si > on rejette l'hypothèse nulle, la série est affectée d'une tendance.

Concernant l'existence de la tendance, le test de Fisher s'avère faible, il convient d'effectuer un autre test.

b. Test de la tendance : (Dickey-Fuller)

Dans l'analyse d'une série affectée d'une tendance, il convient d'étudier ces caractéristiques selon le test de Dickey-Fuller.

A présent nous allons présenter une stratégie de tests de Dickey-Fuller permettant de tester la non stationnarité conditionnellement à la spécification du modèle utilisé.

On considère trois modèles définis comme suit :

Modèle (1) : Modèle (2) : Modèle (3) :

Avec .

On cherche à tester l'hypothèse de racine unitaire :

H0 : « » H1 : « »

On présente ci-dessous un organigramme qui résume les différentes étapes du test de Dickey-Fuller :

Chapitre VI Méthodologie de Box Z Jenkins

Estimation du modèle (3)

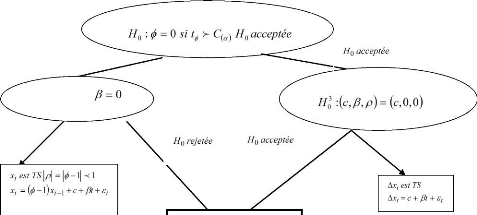
Test de Student :

Test

Test

Estimation modèle (2)

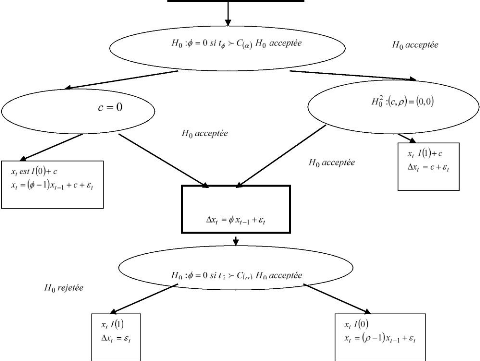
Test de Student :

Test

Estimation modèle (1)

Test

Test

USTHB Page 73

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 74

3. Principe de la méthode : Il s'agit de procéder en six étapes.

A. Stationnarisation de la série :

L'analyse des séries chronologiques est basée sur l'hypothèse de stationnarité.

Effectivement, nous ne pouvons identifier clairement les caractéristiques d'une chronique que si elle est stationnaire.

Pour cela, on commence tout d'abord par la détection de la saisonnalité (à l'aide du test graphique et/ou du test d'ANOVA). Dans le cas où il s'avère que la série est affectée de celle-ci, il convient (d'après Box & Jenkins) de l'enlever. Vient ensuite la détection de la tendance. Si les tests de stationnarité de Dickey-fuller augurent que la série est déjà stationnaire, on entamera dans ce cas la phase d'identification. Sinon, notre série est affectée d'une tendance de type DS ou TS. Dans ce cas, on doit la stationnariser.

Une fois la série stationnaire, on passe à la deuxième étape.

B. Identification du modèle :

On détermine une valeur plausible pour l'ordre des parties AR et MA, ainsi SAR et

SMA s'il existe une composante saisonnière, cette phase est fondée sur l'étude des fonctions d'autocorrélation simple et partielle.

C. Estimation des paramètres du modèle : Pour cela, les méthodes les plus utilisées sont :

méthode du maximum de vraisemblance méthode des moindres carrés ordinaires

d. Validation du modèle :

Afin de s'assurer de la robustesse et la pertinence du modèle, on vérifie ses qualités prédictives au moyen de tests :

1) Test concernant les paramètres : (test de Student)

Afin que le modèle soit valide, il faut que tous les coefficients soient significativement différent de zéro (leurs probabilités critiques soient inférieures à 0,05). Pour vérifier cela, on applique le test de Student. Si un coefficient n'est pas significativement différent de zéro, on envisage une nouvelle spécification du modèle en supprimant l'ordre AR ou MA qui n'est pas valide et en vérifiant à chaque fois les conditions de stationnarité et d'invérsibilité.

Chapitre VI Méthodologie de Box & Jenkins

? i ; = _2(n ? 2) ; _{=16 n} ? ₂₉

La règle de décision :

Si (au seuil = ), on acceptera l'hypothèse , tel que

var( p )

H 1 : « Les paramètres significativements déférents de zéro »

2) Tests concernant les résidus :

· Test de points de retournement :

Il teste la nature aléatoire des résidus, on dira que la suite des données

,,..., présente un point de retournement à la date i si :

où

Soit la variable aléatoire tel que :

?

?

=

S'il présente un point de retournement à la date S'il présente un point de retournement à la date t ? ??

inn Sinon

La variable aléatoire suit la loi Bernoulli de paramètre 2/3.

Si T désigne le nombre total des points de retournement alors on a :

_{3 90}

.

₁

_n

T=

₂

_i?

Sous l'hypothèse que () forment une suite de variables aléatoires Indépendantes et identiquement distribuées :

_T ? _E(T)

La statistique U=

_var(T

N (0,1) , pour n>50

Donc on accepte l'hypothèse : « les sont non corrélés» si U 1.96 et cela au

?

Soit

?_{E(? )?m} seuil

· Test de nullité de la moyenne :

_var(?t)??

_{2 et} ? _{:la moyenne calculée des résidus}

?

_t

.

USTHB Page 75

L'hypothèse à tester est :

Chapitre VI Méthodologie de Box Z Jenkins

Pour n suffisamment grand ce qui implique que :

? _tn ? ₁

	: si :	à
Et comme est inconnue, on l'estime par
D'où :
On accepte l'hypothèse au seuil
S n ?				1

? Test de Box Ljung :

Ce test est basé sur la statistique définie par :

_5%

?

Où : n : la taille de la série

h : l'écart entre les résidus

L'autocorrélation empirique d'écart h entre les résidus.

Avec Q suit asymptotiquement une loi Khi-deux à (h-p-q) degré de Liberté où : ( ? ??) ( ? ? ? )

_{t t?h}

_n?h

(? ? ? )

_H :" _F ? _F " _{contre H} :" _F ? _F "

_{0 0 1 0}

_n?h

?

_t

?

à

? ?

₁

_(h)

?

USTHB Page 76

?

t

₁

_t

?

Ce test concerne les K premières autocorrélations , où K est égale au quart de la taille de la sérier (K=n/4) , un modèle est cohérent si ces résidus se comportent comme une réalisation d'un bruit blanc , il s'agit de tester l'hypothèse nulle :

: " Les résidus sont un bruit blanc "

Contre : " les résidus ne forment pas un bruit blanc ".

On accepte au seuil si Q X (K-p-q-P-Q)

? Test de normalité : (test de Kolmogorov-Smirnov)

Pour calculer des intervalles de confiance prévisionnels et aussi pour effectuer les tests de Student sur les paramètres, il convient de vérifier la normalité des erreurs.

On veut tester , où est la fonction de répartition de la

Loi normale.

Chapitre VI Méthodologie de Box Z Jenkins

?

D ? ? _max ? F ₀ ( x _i ) ?

n i ?

_i ? ? _n ?

Soit l'écart maximum entre la fonction de répartition empirique et la fonction de

Répartition . Où :

^0

^si x ^<x

^(1)

^{si x}

⁽¹

^{si x}

(

~ ^x < ^x

) ⁽²⁾

~ ^x < ^x

ⁱ ) ( ⁱ ~ ¹⁾

¹

ⁿ

^{F X}

n ( )

^I ? ^{I I I}

¹

ⁱ

ⁿ

^{si x}

? ^x

⁽ⁿ⁾

USTHB Page 77

Etape du test :

Ranger les n observations par ordre croissant soit :

On calcule la fonction de répartition empirique .

.

Calculer

Déterminer à partir de la table, la valeur critique C en fonction de n et du risque. Règle de décision :

Si

Et si

? Test de Von-Neuman : (indépendance)

C'est un test valide dans le cas où les résidus sont gaussiens, sous les hypothèses : H0 : « les résidus sont indépendants et identiquement distribués » contre

H1 : « au moins deux observations successives tendent à être corrélées » Il est fondé sur les deux estimateurs suivants :

1 _n ? _{1 n}

_{2 2 2}

? ?? 1 ?

_D ? ( ) ²

( ? ? _S

) ? ? ?

_t ? _{1 t t t}

_n ? _{1 n} ? ₁

_t ? _{1 t} ? ₁

? _D ?

_E ? ? ? ₁

? 2 ²

S ?

_{(D2 n-2}

_{2 2}

? ₂ S ) _n - ₁

,

2 Sous H0 :

var 1=

Chapitre VI Méthodologie de Box Z Jenkins

La statistique utilisée est :		D ^2 ? ? ? ? ? 1 2 I 2 S ? asymptotiquement suit une VN ?
n				?	2
n			2 ?			1
Si	< avec on accepte H0.

? Test de Durbin et Watson :

Les modèles ajustés à des séries chronologiques manifestent parfois un certain degré de corrélation entre les valeurs successives des erreurs. En terme probabiliste, cela signifie que les erreurs sont autocorrélées, ou encore qu'une erreur produite en t-1 à une influence sur l'erreur en t. Le test de Durbin et Watson (1951) permet de détecter

l'autocorrélation des résidus pour un ordre un (corrélation entre et ) sous la forme :

où on teste

H0 : « » (absence d'autocorrélation à l'ordre 1 des résidus).Contre

H1 : « » (présence d'autocorrélation à l'ordre 1 des résidus).

La statistique de Durbin et Watson, notée DW, est donnée par :

avec : sont les résidus de l'estimation du modèle.

_(S ? _S

_{t t} ? 1)

₂

?

_t

?

₂

_DW

_n

₂

_t

₁

_n

?

_S

_t

?

USTHB Page 78

De par sa construction, cette statistique varie entre 0 et 4 et nous avons DW=2 lorsque (est l'estimateur de) on a :

, il existe une autocorrélation positive ;

, il existe une autocorrélation négative ;

, indique l'absence d'autocorrélation.

? Test d'hétéroscédasticité : (l'existence d'effet ARCH)

Pour ce faire, on utilise les corrélogrammes des carrés des résidus, si un ou plusieurs termes sont significativement différents de zéro, on déduit qu'il y a effet ARCH qui est détecté par la statistique de Box et Ljung, ceci est confirmé par la statistique du Multiplicateur de Lagrange LM=n R² avec n = le nombre d'observations servant au calcul de la régression.

R²= le coefficient de détermination.

Soit une spécification de type ARCH pour les erreurs tel que :

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 79

avec et Soit

l'hypothèse H0 : « » contre H1 : « non tous nul »

Si LM < on accepte H0, la variance de l'erreur est constante

Dans le cas contraire LM > à p degrés de libertés compris entre 1 et 3, on rejette

H0 et le processus est justifiable d'un modèle ARCH (p).

Si p >3 le modèle sera justifié d'un modèle de type GARCH.

4. Choix du modèle :

On fait appel à des critères d'information afin de choisir le modèle optimal parmi tous les modèles repérés :

Le critère AIC introduit par Akaike :

AIC (p, q) = log [?²] +

Le critère BIC de Schwartz :

BIC (p, q) = log [?²] + (p+q) *

Le modèle optimal est celui qui minimise ces deux critères.

5. Prévision :

A. Transformation de la série :

Lorsque on a appliqué différentes transformations (exemple différenciation dans le cas d'une série I (1)) afin d'identifier le modèle ARMA, il est nécessaire lors de la phase de prévision de prendre en compte la transformation retenue et de recolorer la prévision. Plusieurs cas sont possibles :

Si le processus contient une tendance déterministe, on extrait cette dernière par régression afin d'obtenir une série stationnaire lors de la phase de prévision, on adjoint aux prévisions réalisées sur la composante ARMA stationnaire, la projection de la tendance.

Si la transformation résulte de l'application d'un filtre linéaire (de type par exemple différence premières), on réalise les prévisions sur la série filtrée stationnaire e l'on reconstruit ensuite par inversion du filtre les prévisions sur la série initiale.

B. Prédicteur pour un modèle ARMA :

On considère un modèle ARMA tel que :

Chapitre VI Méthodologie de Box Z Jenkins

Avec : .

Appliquons le théorème de Wold au processus et considérons la forme

MA (?) correspondante :

Il s'ensuit que la meilleure prévision que l'on peut faire de compte tenu de toute

l'information disponible jusqu'à la date t, notée , est donnée par :

Dès lors, l'erreur de prévision est donnée par la réalisation en de l'innovation qui

en n'est pas connue :

Plus généralement pour une prévision à un horizon on a :

_X _ X à ( _k ) l

_t + _k t --~ _N(0,1)

₁

_var [ à ( ) ] 2 _T ??

_{X X k}

_t k _

+ _t

et

Déterminons un intervalle de confiance sur la prévision sous l'hypothèse de

normalité des résidus. On montre alors que : _E X _t k X à t ( _k )

? ? ? ?

_k ? _{1 k} ? ₁

? ? ? ? _{2 2}

? _E ? ?? ? ? ? ? ? ? ? ?

_{j t} ? _k ? _{j j} ?

_j ? _{0 j} ? ₀

? ? ??

2 ?

_{X X} k l

_t k ? _{N (0,1)}

? Or on sait que : ? t ( ) 1 ? ? ? ? ? k ? 1 2 2 T ?? ? j j ? 0

2

_IC

₂

à

_?e ? ? ? _J

à

?

D'où

r ? _k ? 1 ?

? 2

X à ( ) ^a a

On peut donc construire un intervalle de confiance sous la forme :

_k t 2 ? ?

_?

_{t j}
? _j ? ₀ ?
? ? ?

USTHB Page 80

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 81

L'étude des séries temporelles, correspond à l'analyse statistique d'observations régulièrement espacées dans le temps. Leur domaine d'application est très vaste et s'étend de l'astronomie à l'économie en passant par la biologie. Elles ont donc suscité un très vif intérêt, ce qui a eu pour conséquences le développement de nombreux modèles : AR, ARMA, ARIMA...s'appliquant particulièrement à la compréhension des processus à mémoire courte, c'est-à-dire ceux pour lesquels il n'y a pas de persistance des chocs. Pour tenir compte de la persistance à long terme des chocs dans certaines séries, phénomène appelé « mémoire longue », d'autres modèles ont été développés dont les modèles ARFIMA au début des années 1980.

IV. Analyse spectrale :

1. Introduction:

L'objet de l'étude précédente d'une série temporelle a été la détermination de ses composantes et de leurs importances respectives. Pour cela, on a principalement utilisé la fonction d'autocorrélation. Cette fonction, a comme inconvénient majeur d'être un indicateur sommaire de détection des différentes composantes.

En effet, quand les influences saisonnières se combinent, la fonction d'autocorrélation reflète ces deux phénomènes. De plus sa précision dépend directement de la taille de la série qui diminue quand le nombre de retards tend vers le nombre total d'observation.

Pour vérifier cette imprécision, les statisticiens ont voulu transposer l'idée générale de l'autocorrélation de l'espace des temps à l'espace des fréquences.

2. Le périodogramme:

Le spectre principale fonction d'intérêt dans le domaine des fréquences, est

essentiellement une décomposition harmonique de la variance. Pour découvrir les périodicités cachées de la série des taches solaires, Shuster a proposé pour estimer le spectre la méthode du périodogramme qui est une transformation du corrélogramme (ou fonction d'autocorrélation) dans le domaine des fréquences. Bartlett a suggéré une approche basée sur l'utilisation d'une fonction d'autocovariance pondérée cette approche est appelée : analyse spectrale.

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 82

3. Objectif de l'analyse spectrale:

L'analyse spectrale est une opération de moyenne sur le périodogramme,elle détermine l'évolution de la variance d'un processus stochastique aux différentes fréquences, elle décompose d'une façon différente l'information contenu dans la fonction d'autocovariance, et permet d'identifier distinctement les influences qui gouvernent le comportement de chaque série, pour ensuite adopter une spécification correspondante aux phénomènes cycliques et la recherche des composantes périodiques d'une série, plus particulièrement de composante périodique la plus importante.

L'objectif premier de l'analyse spectrale est donc l'identification d'une série temporelle aux principales fréquences, l'application de cette analyse se fait sur les séries stationnaires.

4. Concepts de l'analyse harmonique de Fourier:

Soit un vecteur F dans le plan complexe, qui s'écrit où a et b sont des

réels, a étant la partie réelle et ib la partie imaginaire, avec la convention i² = -1. Pour

définir les paramètres et , oùest l'argument, phase ou angle de phase, et est

le module ou amplitude.

Si on multiplie F par i, on a iF = ia - b, c'est un nouveau vecteur de coordonnées (-b,

a), donc faisant un angle de avec le vecteur original. En général en suppose que

l'amplitude est constante et que la phaseest une fonction linéaire du temps :

où est la fréquence angulaire constante exprimée en radians etest l'angle de

la phase initiale au temps zéro.

La fréquence angulairepeut être exprimée en fréquence circulaire v par la relation : , ou v est exprimée en cycle par unité de temps. La

fréquence v est donc l'inverse de la période T. la phase peut être exprimée en fonction de

la fréquence circulaire : .

A la base de l'analyse harmonique de Fourier se trouve une opération appelée transformation de Fourier, qui prend des formes distinctes en fonction du type de série analysée. Ces différentes formes ont en commun de supposer que chaque série est constituée d'un ensemble de composantes sinusoïdales à différentes fréquences, chacune ayant une certaine amplitude et une phase initiale.

USTHB Page 83

Chapitre VI Méthodologie de Box Z Jenkins

= _{1/ 2 a} + ? _{a w fl w}

_{t t}

_cos + _sin )

_{j j j j}

? j _et ? j

A titre d'exemple, on peut représenter une composante sinusoïdale typique

d'amplitude A, de phase initiale et de fréquence v.

_j = ₁

La projection dans le plan complexe représente la position des vecteurs au temps zéro d'amplitude (A/2) qui trouvent en sens opposé l'un de l'autre, de phase et -. La somme vectorielle est toujours réelle et retrace la courbe sinusoïdale. L'amplitude A est la valeur maximale de l'oscillation, la période T d'une série temporelle sera l'intervalle de temps a partir duquel l'observation se répète.

Enfin la phase, précise l'intervalle de temps entre l'origine des temps et le moment où l'oscillation est nulle. Ainsi une série temporelle assimilée à une oscillation peut s'écrie :

_{X t}

( ) ₀ (

( _{W E} [ _{0, r} ] ) en utilisant

= _{1/ 2 a} + ? _{a co fl co}
II vient :

_j = ₁

Où

En généralisant cette relation, on obtient pour une fonction de période

_{X t}

_t

_cos + _sin )

_{j j j j}

= _2rj / _T

?

( ) 0 (

L'expression définissant X(t) est appelée fonction trigonométrique polynomiale de

degré infini et de période T. est appelée fréquence fondamentale. Les

fréquences (j >1) sont appelées harmoniques d'ordre j.

Les harmoniques sont des multiples de la fréquence

?

t fondamentale. La série :

est appelée

série de Fourier, et les coefficients coefficients de Fourier.

La densité spectrale d'un processus stationnaire décrit la répartition de la variance suivant différentes fréquences angulaires

L'intérêt des représentations spectrales est la mise en évidence de cycles et/ou de fluctuations d'une série.

Chapitre VI Méthodologie de Box Z Jenkins

USTHB Page 84

En effet, les variances associées aux différentes fréquences ont des amplitudes décroissantes au fur et à mesure que l'on passe des basses fréquences aux hautes fréquences. Pour interpréter la densité spectrale, en termes de cycles, on s'intéresse aux pics les plus importants. Si la densité spectrale est parallèle à l'axe des abscisses, il n'y a aucun pic, et donc il n'existe pas de cycle : c'est le cas du bruit blanc.

Donc si on observe un pic proche des hautes fréquences, il peut exister un cycle de court terme, et si on observe un pic proche des basses fréquences ; il peut exister un cycle de long terme.

Un pic sera considéré comme significatif si, dans l'intervalle de confiance, on ne peut pas tracer une droite parallèle à l'axe des fréquences. On peut également considérer les valeurs spectrales multiple de.

		hapitre =I pp icat a de In mithode de
			Jenk			US

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 86

Application de la Méthodologie de Box - Jenkins

I. Série annuelle d'importation des véhicules touristiques (VT) mis en circulation dans le parc automobile national

Soit la série VT (véhicule touristique) représentant le nombre de véhicules de genre touristique, importés et mis en circulation pour la premier fois au niveau national sur la période allant de 1963 à 2009, donc un total de 47 observations.

On va utiliser, pour la série VT, la méthodologie de Box Jenkins (Identification, Estimation et Validation).

1. Analyse préliminaire de la série VT (véhicules tourismes) Diagramme séquentiel de la série brute VT

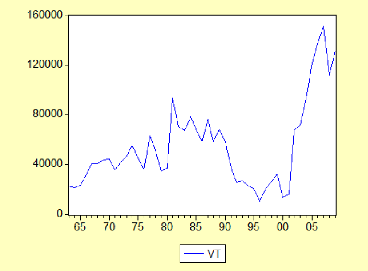
Le diagramme séquentiel de la série brute VT représente une variabilité dans le temps, ceci est un indicateur de non stationnarité de la série.

Chapitre VII Application de la méthode de Box & Jenkins

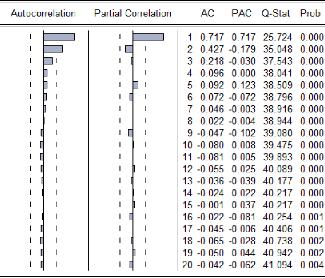
USTHB Page 87

Corrélogramme de la série brute

2. Test de la racine unitaire (Dickey-Fuller) sur la série VT On teste les hypothèses suivantes :

Modèle [3] : H'0 : "le coefficient de la tendance est nul f = 0" contre H'1: "f ? 0 "

Modèle [2] : H»0 : "la constante est nulle C = 0" contre H»1 :"C ? 0"

Modèle [1] : H0 : "l'existence d'une racine unitaire 4i= 0" contre H1 :" 4i ?0"

Tout d'abord, on sélectionne le nombre de retards p, de sorte à minimiser le critère d'information d'AKAIKE et Schwartz. Dans notre cas p= 1.Puis on estime le modèle avec constante et tendance déterministe, c'est-à-dire le modèle trois.

Modèle [3] : modèle avec constante et tendance déterministe

Où Et est un bruit blanc

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 88

On commence par tester la significativité de la tendance.

On remarque que la tendance n'est pas significativement différente de zéro, puisque sa t-statistique |1.27| est inférieure à la valeur critique 2.78 (donnée par la table de Dickey-Fuller) au seuil 5%. On le confirme par la proba = 0.21 qui est supérieure à 0.05

Modèle [2] : modèle avec constante

(p=1) est le retard qui minimise le critère d'informations d'Akaike et Schwarz

Où Et est un bruit blanc.

On remarque que la constante n'est pas significativement différente de zéro, puisque sa t-statistique |1.47| est inférieure à la valeur critique 2.52 (donnée par la table de Dickey-Fuller) au seuil 5%. On le confirme par la proba = 0.14 qui est supérieure à 0.05, donc on passe au modèle [1]

Modèle [1] : modèle ni constante ni tendance

Où Et est un bruit blanc.

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 89

On remarque que la valeur estimée de la statistique ADF est égale à -1.58. Cette valeur est supérieure à la valeur critique -3.51 au seuil 5%. On accepte par conséquent l'hypothèse nulle de racine unitaire : la série VT possède une racine unitaire ; la série est générée par un processus de type non stationnaire de type DS.

3. Etude de la série RVT

RVTt = VTt - VTt-1

Diagramme séquentiel de la série brute RVT

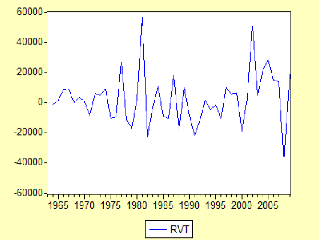
Chapitre VII Application de la méthode de Box & Jenkins

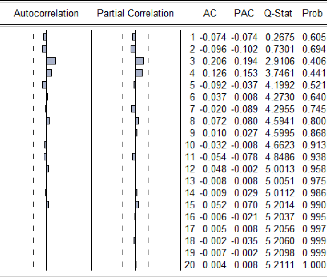
Corrélogramme de la série RVT

On teste à nouveau la non stationnarité de la série RVT par un test de Dickey Fuller.

4. Test de la racine unitaire (Dickey-Fuller) sur la série RVT :

Tout d'abord, on sélectionne le nombre de retards p, de sorte à minimiser le critère d'information d'AKAIKE et Schwartz. Dans notre cas p= 0.Puis on estime le modèle avec constante et tendance déterministe, c'est-à-dire le modèle trois.

Modèle [3] : modèle avec constante et tendance déterministe

RVTt= 1 RVTt-1+ ât+c+

Où est un bruit blanc.

On commence par tester la significativité de la tendance

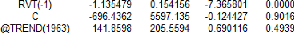
USTHB Page 90

On remarque que la tendance n'est pas significativement différente de zéro, puisque sa t-statistique |0.69| est inférieure à la valeur critique 2.78 (donnée par la table de Dickey-Fuller) au seuil 5%. On le confirme par la proba = 0.49 qui est supérieure à 0.05

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 91

Modèle [2] : modèle avec constant RVTt= ₁ RVTt + c +

Où est un bruit blanc.

On remarque que la constante n'est pas significativement différente de zéro, puisque sa t-statistique |1.01| est inférieure à la valeur critique 2.52 (donnée par la table de Dickey-Fuller) au seuil 5%. On le confirme par la proba = 0.31 qui est supérieure à 0.05, donc on passe au modèle [1]

Modèle [1] : modèle ni constante ni tendance

RVTt= ₁ RVTt +

Où est un bruit blanc

On remarque que la valeur estimée de la statistique ADF est égale à -7.38, Cette valeur est inférieure à la valeur critique -1.92 au seuil 5%. On rejette par conséquent l'hypothèse nulle de racine unitaire : la série RVT ne possède pas une racine unitaire.

Chapitre VII Application de la méthode de Box & Jenkins

5. analyse spectrale Périodogramme

Périodogramme

500000000

2,5E+09

1,5E+09

2E+09

1E+09

0

0 0,5 1 Fréquence [0,Pi]

1,5 2 2,5 3 3,5

On remarque, par le graphe de fréquence, que le 1^ere pic significatif est égale à f=1.536 On a f=2ð/w donc w=4.09

6. Désaisonnaliser la série RVT

SRVTt=RVTt - RVTt-4

Diagramme séquentiel de la série brute SRVT

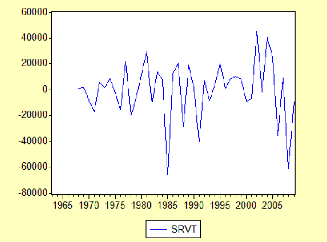
USTHB Page 92

Chapitre VII Application de la méthode de Box & Jenkins

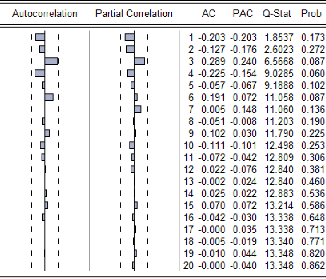
USTHB Page 93

Corrélogramme de la série SRVT

7. Identification et estimation du modèle a priori

Il convient à présent d'estimer le modèle susceptible de représenter notre série SRVT

L'observation des corrélogrammes nous permet d'avoir plusieurs modèles candidats , par conséquent nous avons choisi le modèle qui minimise les deux critères AIC et SC qui est le modèle: SARIMA(3.1.0)(0.1.1)4

On constate que les coefficients des variables explicatives sont significativement différents de zéro, car la valeur absolue de t-statistic > 1.96, ce qui est confirmé par les probabilités de nullité des coefficients qui sont tous inférieures à 0.05.

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 94

8. Test de validation

Graphique et table des inverses des racines

AR Root(s) Modulus Cycle

0.633023 #177; 0.633023i 0.895230 8.000000

-0.633023 #177; 0.633023i 0.895230 2.666667

No root lies outside the unit circle. ARMA model is stationary.

MA Root(s) Modulus Cycle

-0.731765 0.731765

0.365882 #177; 0.633727i 0.731765 6.000000

No root lies outside the unit circle. ARMA model is invertible.

A partir de la représentation graphique des inverses des racines des polynômes de retards moyen mobile et autorégressif, nous constatons qu'ils sont tous à l'intérieur du cercle unité (les racines sont à l'extérieur du cercle unité).

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 95

9. Test sur les résidus

Autocorrélations simples et partielles des résidus

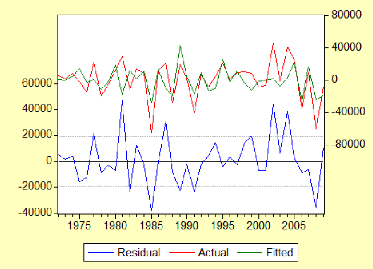
Corrélogramme des résidus

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 96

Le corrélogramme des résidus du modèle montre que les résidus forment un bruit blanc puisque toutes les Autocorrélations et les Autocorrélations partielles sont significativement nulles.

? Test des points de retournements

Il s'agit de tester : l'hypothèse nulle H0 : «les åi sont aléatoires» contre H1 « il existe une corrélation entre les åi i=1,..., n ».

Le nombre de points de retournements égale à p= ? = 27
On a n=38 et on a calculé E(p), Var(p) et S

E(p)= (n-2) =24 Var(p)= = 6.43 |T | = v = 1.18

? _t

_T?

? ?

|T| =1.18< 1.96 donc on accepte H0 au seuil 0.05. C'est-à-dire que les résidus sont non corrélés.

? Test de nullité de la moyenne des résidus

L'hypothèse H0 : « m=0 » contre H1 : « m ? 0 », nous utilisons le test de Student basé sur la

statistique :

_n?1

La moyenne de la série : åt = -0.027023

L'écart type : ót =2.110572

La statistique t=0.094953 qui suit asymptotiquement une loi de Student. Au seuil á=0.05 on a: |t|<1.96, on accepte H0, alors m=0.

? 2

K i

= #177; ?=

_{Q n n}

( 2) _{1 =1 1.903431}

ⁱ _n - _i

? Test de Ljung -Box

Nous calculons la statistique de Ljung-Box avec MATLAB

au seuil

0,05

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 97

H0 : « les Autocorrélations ne sont pas significativement différentes de zéro

Jusqu'au pas k = N/ 4 »

Contre H1 : « Pi, i=1,2..., K / Pi?0 ».

L'ordre de retard K= [N/4]= [47/4]=12

Au seuil á= 0.05 on a la valeur critique d'une

? 2 (2)

₀ . _{9 5}

=11.903431< 24.995790

alors les autocorrélations ne sont pas significatives jusqu'au pas K=15 I.e. les résidus forment un bruit blanc.

? Test de Jaque -Bera

On test H0 :" accepter la normalité des résidus au seuil 0.05" Contre H1 :"il n'y a pas de normalité des résidus".

On accepte l'hypothèse nulle H0 si JB <

On a la statistique JB= 1.58 <5.99 donc on accepte l'hypothèse de normalité des résidus.

? Test de Skewness (asymétrie) et de Kurtosis (aplatissement) :

On test : « =0 et =0" contre : " 0 ou 0"

/

? Test de Skewness : = I 1

s₁ - 0 où : S₁^1/2 est le coefficient de Skewness
1 6/n

(l'indicateur d'asymétrie des résidus).

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 98

La statistique de SKEWNESS = 1.12 qui est asymptotiquement N(0,1)

Au seuil á= 0.05 on a:1.12 <1.96, alors on accepte que la distribution des résidus ne sont pas asymétriques.

? Test de Kurtosis : = v où s2 est le coefficient de Kurtosis (degré

d'aplatissement de la loi des résidus).

La statistique de KURTOSIS = 0.56 qui est asymptotiquement N(0,1)

Au seuil á = 0.05.

On a: 0.56 <1.96, alors on accepte l'hypothèse des queues de la distribution des résidus non chargées.

Les résidus forment un bruit blanc gaussien (suit une loi Normal). ? Test de Kolmogorov - Smirnov

Nous testons H0 : « F=F0 » vs H1 : « F?F0 » où F0 est la fonction de répartition de la loi normal.

La statistique de Kolmogorov - Smirnov notée Dn =SUP (|Dn+|, |Dn-|)=0.10.le seuil critique pour ce test est dc=0.22. On a Dn< 0.22 au seuil 0.05. Donc, on accepte l'hypothèse que les résidus sont gaussiens.

? Test d'indépendance de Von - Newman

L'hypothèse à tester est :

H0 : « les résidus sont indépendants et identiquement distribués ».

H1 : « au moins deux observations successives tendent à être corrélées positivement ».

S2?	1 ? ? ? ? ? 47 2 2 2 ? ? D ? 1 ?? 46 ? ? ? ? ? i 1 i n ? 1 1 ? 1 ? i i i n 1

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 99

La variance corrigé S²= 352009710.494254.

La statistique D² = 779221306.474829.

La statistique de Von_Neumann |?|= 0.676279 <1,96, nous acceptons l'hypothèse H0. Les résidus sont indépendants et identiquement distribués.

Test de Durbin -Watson (test de détection d'autocorrélation d'ordre 1)

Nous testons H0 : « ñ=0 » vs H1 : « ñ?0 ».

On a la statistique de Durbin - Watson : DW=2,206 d'après le tableau ci-dessus. Avec du, á/2<DW<4-du,á/2 et du,á/2 =1,69 c.-à-d. on accepte H0 :« les résidus sont non corrélés ».

Conclusion

Nous pouvons conclure d'après ces tests que les résidus forment bien un bruit blanc gaussien. Finalement le modèle qui ajuste le mieux la série VT (véhicule touristique) est SARIMA (0, 1,3) (1, 1,0) qui s'écrit sous la forme suivante :

(1-B⁴)(1+0.642 B⁴)VTt= (1-0.391 B³)åt

Chapitre VII Application de la méthode de Box & Jenkins

10. Prévision

Les prévisions sont calculées pour la période allant de 2010 à 2013.

année	PREVISION
2010	116708
2011	194566
2012	142172
2013	117398

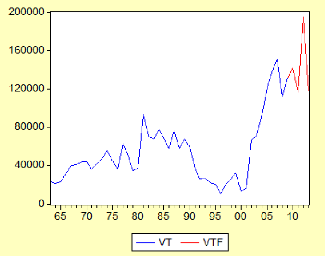
USTHB Page 100

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 101

II. Série annuelle d'importation des autocar-autobus(AA) mis en circulation dans le parc automobile national:

Soit la série AA (autocar autobus) représentant le nombre de véhicules de genre autocar et autobus importés et mis en circulation pour la premier fois au niveau national sur la période allant de 1963 à 2009, soit donc un total de 47 observations.

On va utiliser la méthodologie de Box Jenkins (Identification, Estimation et Validation)

1. Analyse préliminaire de la série AA Diagramme séquentiel de la série brute AA

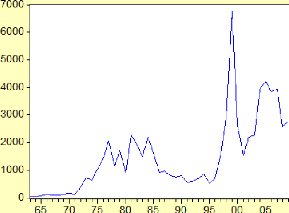
Le diagramme séquentiel de la série brute AA présente une variabilité dans le temps, ceci est un indicateur de non stationnarité de la série.

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 102

Corrélogramme de la série brute

2. Test de la racine unitaire (Dickey-Fuller) sur la série AA On teste les hypothèses suivantes :

Modèle [3] : H'0 : "le coefficient de la tendance est nul f = 0" contre H'1: "f ? 0 "

Modèle [2] : H»0 : "la constante est nulle C = 0" contre H»1 :"C ? 0"

Modèle [1] : H0 : "l'existence d'une racine unitaire 4i= 0" contre H1 :" 4i ?0"

Tout d'abord, on sélectionne le nombre de retards p, de sorte à minimiser le critère d'information d'AKAIKE et Schwartz. Dans notre cas p= 1.Puis on estime le modèle avec constante et tendance déterministe, c'est-à-dire le modèle trois.

Modèle [3] : modèle avec constante et tendance déterministe

Où Et est un bruit blanc.

Chapitre VII Application de la méthode de Box & Jenkins

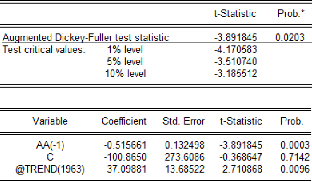
USTHB Page 103

On commence par tester la significativité de la tendance.

On remarque que la tendance est significativement différente de zéro, puisque la probabilité qui est égale à 0.0096 est inférieure à 0.05

La statistique de Student =-3.891 est inférieur à la valeur critique -3,510, donc la série ne

possède pas de racine unitaire (on rejette l'hypothèse nulle « «).

D'où la série est non stationnaire de type TS.

Pour la stationnariser, nous allons faire un ajustement de la forme :

TAA=AA-y(t)

Estimation de la tendance linéaire :

Estimons l'équation d'ajustement qui est donnée par la formule suivante:

À l'aide du logiciel EVIEWS, nous obtenons le résultat donné dans le tableau suivant :

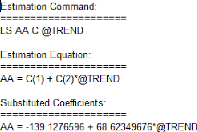
Donc y(t)= -139.1276596 + 68.6234967*t

Chapitre VII Application de la méthode de Box & Jenkins

Diagramme séquentiel de la série ajustée TAA

Diagramme séquentiel de la série brute AA avec ajustement

USTHB Page 104

Chapitre VII Application de la méthode de Box & Jenkins

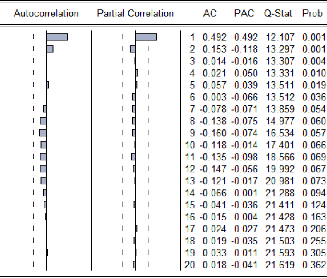
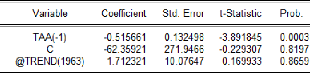
USTHB Page 105

Corrélogramme de la série ajustée TAA

On teste à nouveau la non stationnarité de la série TAA par un test de Dickey Fuller

Application de la Méthodologie de Box - Jenkins à la série AA (autocar-autobus) sans tendance.

3. Test de la racine unitaire (Dickey-Fuller) sur la série TAA

Tout d'abord, on sélectionne le nombre de retards p, de sorte à minimiser le critère d'information d'Akaike et Schwartz. Dans notre cas p= 1.Puis on estime le modèle avec constante et tendance déterministe, c'est-à-dire le modèle [3].

Modèle [3] : modèle avec constante et tendance déterministe

TAAt= TAAt-1+ ât +c+ _1TAAt-1 +

Où est un bruit blanc.

On commence par tester la significativité de la tendance

On remarque que la tendance n'est pas significativement différente de zéro, puisque sa t-statistique |0.1699| est inférieure à la valeur critique 2.78 (donnée par la table de Dickey-Fuller) au seuil 5%. On le confirme par la probabilité égale à 0.86 qui est supérieure à 0.05

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 106

Modèle [2] : modèle avec constante

TAAt= TAAt-1 + C+ _1TAAt-1 + Où est un bruit blanc.

On remarque que la constante n'est pas significativement différente de zéro, puisque sa t-statistique -0.167 est inférieure à la valeur critique 2.52 (donnée par la table de Dickey-Fuller) au seuil 5%. On le confirme par la probabilité égale à 0.86 qui est supérieure à 0.05, donc en passe au modèle [1]

Modèle [1] : modèle sans constante ni tendance

TAAt= TAAt-1 + _1TAAt-1 +

Où est un bruit blanc

On remarque que la valeur estimée de la statistique ADF est égale à -3.97. Cette valeur est inférieure à la valeur critique -1.94 au seuil 5%. Par conséquent, on rejette l'hypothèse nulle de racine unitaire : la série TAA ne possède pas une racine unitaire.

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 107

4. analyse spectrale

Périodogramme

14000000

12000000

10000000

4000000

8000000

6000000

2000000

0

0 0,5 1 1,5 2 2,5 3 3,5

Fréquence [0,Pi]

Périodogramme (804,1276596)

On remarque à partir du graphe de fréquence que le pic significatif est égale à w =0,273 On a T=2ð/w donc T =23

Donc la série TAA n'est pas affectée d'une saisonnalité.

5. Identification et estimation du modèle a priori

Il convient à présent d'estimer le modèle susceptible de représenter notre série TAA. L'observation des corrélogrammes nous permet d'avoir plusieurs modèles candidats, par conséquent nous avons choisi le modèle qui minimise les deux critères AIC et SC qui est le modèle: AR (1)

Variable	Coefficient	Std. Error t-Statistic	Prob.
AR(1)	0.331481	0.144959 2.286719	0.0271
MA(12)	-0.794373	0.045930 -17.29534	0.0000
R-squared	0.385340	Mean dependent var	-17.48104
Adjusted R-squared	0.371370	S.D. dependent var	1015.745
S.E. of regression	805.3458	Akaike info criterion	16.26293
Sum squared resid	28537600	Schwarz criterion	16.34243
Log likelihood	-372.0473	Durbin-Watson stat	1.801552
Inverted AR Roots	.33
Inverted MA Roots	.98	.85+.49i .85-.49i	.49-.85i
	.49+.85i	.00+.98i -.00-.98i	-.49-.85i
	-.49+.85i	-.85+.49i -.85-.49i	-.98

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 108

Chapitre VII Application de la méthode de Box & Jenkins

On constate que les coefficients des variables explicatives sont significativements différents de zéro car la valeur absolu de t-statistic > 1.96 ce qui est confirmé par les probabilités de nullités des coefficients qui sont tous inférieures à 0.05.

6. Test de validation

Graphique et table des inverses des racines

AR Root(s) Modulus Cycle

0.331481 0.331481

No root lies outside the unit circle. ARMA model is stationary.

MA Root(s)	Modulus	Cycle
-0.849570 #177; 0.490500i	0.980999	2.400000
0.000000 #177; 0.980999i	0.980999	4.000000
0.490500 #177; 0.849570i	0.980999	6.000000
0.849570 #177; 0.490500i	0.980999	12.00000
0.980999	0.980999
-0.490500 #177; 0.849570i	0.980999	3.000000
-0.980999	0.980999

No root lies outside the unit circle. ARMA model is invertible.

USTHB Page 109

7. Test sur les résidus

Autocorrélations simples et partielles des résidus

Corrélogramme des résidus

Le corrélogramme des résidus du modèle montre que les résidus forment un bruit blanc puisque toutes les Autocorrélations et les Autocorrélations partielles sont significativement nulles.

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 110

? Test des points de retournements

Il s'agit de tester : l'hypothèse nulle H0 : «les åi sont aléatoires» contre H1 « il existe une corrélation entre les åi i=1,..., n ».

Le nombre de points de retournements égale à p= ? = 28
On a n=38 et on a calculé E(p), Var(p) et S

E(p)= (n-2) =29.333 Var(p)= = 7.855 |T | = v = 29.333

? _t

? ?

P ²

K i

= #177; ?=

_{Q n n}

( 2) 1 = _8.933

ⁱ _n - _i

|T| =1.546< 1.96 donc on rejette H0 au seuil 0.05. C'est-à-dire que les résidus sont non

corrélés.

_T?

? Test de nullité de la moyenne des résidus

L'hypothèse H0 : « m=0 » contre H1 : « m ? 0 », nous utilisons le test de Student basé sur la

statistique :

_n?1

La moyenne de la série : åt = -53.169 L'écart type : ót =794.530

La statistique t=0.448 qui suit asymptotiquement une loi de Student., Au seuil á=0.05 on a: |t|<1.96, on accepte H0, alors m=0.

? Test de Ljung -Box

Nous calculons la statistique de Ljung-Box avec MATLAB

au seuil 0,05

2 21.026

H0 : « les Autocorrélations ne sont pas significativement différentes de zéro

Jusqu'au pas k = N/ 4 » Contre H1 : « Pi, i=1,2..., K / Pi?0 ».

? ₀ . ₉ 5 _{(1 1)} ?

L'ordre de retard K= [N/4]= [47/4]=12

Au seuil á= 0.05 on a la valeur critique d'une

=9.215 < 21.026 alors les autocorrélations ne sont pas significatives jusqu'au pas

K=12

I.e. les résidus forment un bruit blanc.

? Test de Jaque -Bera

On test H0 :" accepter la normalité des résidus au seuil 0.05" Contre H1 :"il n'y a pas de normalité des résidus".

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 111

On accepte l'hypothèse nulle H0 si JB <

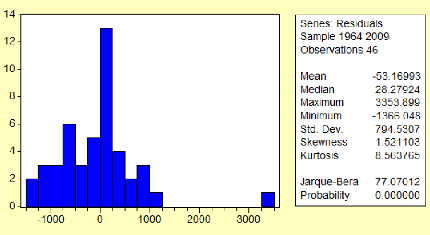
On a la statistique JB= 77.070 >5.99 donc on rejette l'hypothèse de normalité des résidus.

? Test de Skewness (asymétrie) et de Kurtosis (aplatissement)

On test : « =0 et =0" contre : " 0 ou 0"

? Test de Skewness : = où : est le coefficient de Skewness

v

(l'indicateur d'asymétrie des résidus).

La statistique de SKEWNESS = 4.211 qui est asymptotiquement N(0,1)

Au seuil á= 0.05 on a: 4.211 > 1.96, Donc on rejette, la distribution des résidus n'est pas asymétriques.

Test de Kurtosis : = v où s2 est le coefficient de Kurtosis (degré

d'aplatissement de la loi des résidus).

La statistique de KURTOSIS = 7.702 qui est asymptotiquement N(0,1)

Au seuil á = 0.05

7.702 >1.96, alors on rejette l'hypothèse des queues de la distribution des résidus non chargées. Les résidus forment un bruit blanc non gaussien

REMARQUE Nous ne pouvons pas appliquer le test de Durbin-Waston et le test d'indépendance de Von-neumann puisque les résidus ne sont pas gaussiens

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 112

? Test d'homoscédasticité des résidus

Soit les hypothèses :H0 :« les résidus sont homoscédastique »contre

H1 : « les résidus sont hétéroscédastique »

L'hypothèse nulle à tester est celle d'homoscédasticité H0 : « á1= á2=...= á_p=0 » .

Si H0 est acceptée, la variance conditionnelle de l'erreur est constante = á0.
Sinon les résidus suivent un processus ARCH(p) dont l'ordre p est à déterminer.

Corrélogramme simple et partielle des résidus au carrée

L'analyse du corrélogramme des résidus au carrée, montre que tous les termes sont significativement différents de zéro car les probabilités sont toutes supérieur à 0,05, cela veut dire qu'il n'ya pas un effet ARCH. Pour confirmer, nous sommes passées au test d'homoscédasticité dont le résultat est donné par Eviews5.

ARCH Test:

F-statistic 0.155699 Probability 0.695098

Obs*R-squared 0.162352 Probability 0.687000

Test Equation:

Dependent Variable: RESID^2

Method: Least Squares

Date: 05/09/11 Time: 13:30

Sample (adjusted): 1965 2009

Included observations: 45 after adjustments

USTHB Page 113

Chapitre VII

		Application de la méthode de Box & Jenkins
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	556019.8	269442.0 2.063597	0.0451
RESID^2(-1)	0.059703	0.151305 0.394587	0.6951
R-squared	0.003608	Mean dependent var	592700.3
Adjusted R-squared	-0.019564	S.D. dependent var	1680138.
S.E. of regression	1696493.	Akaike info criterion	31.56945
Sum squared resid	1.24E+14	Schwarz criterion	31.64975
Log likelihood	-708.3127	F-statistic	0.155699
Durbin-Watson stat	1.984068	Prob(F-statistic)	0.695098

Rappelons que, sous l'hypothèse nulle d'homoscédasticité, la statistique du multiplicateur de Lagrange (n* R²) au seuil 5% suit une loi de khi-deux à p degrés de liberté. Dans notre cas p = 1.Nous avons (n* R²) = 0.155 est inférieure à ÷²(1) = 3.84, donc nous acceptons l'hypothèse nulle d'homoscédasticité en faveur de l'hypothèse alternative d'hétéroscédasticité conditionnelle (il n'y a pas effet ARCH).

Conclusion

Nous pouvons conclure d'après ces tests que les résidus forment bien un bruit blanc gaussien. Finalement le modèle qui ajuste le mieux la série TAA est AR (1) qui s'écrit sous la forme suivante :

(TAAt -y(t))(1-0.313B)= (1+0.806B¹⁰) Et

8. Prévision

Les prévisions sont calculées pour la période allant de 2010 au 2011.

année	PREVISION
2010	3722
2011	2473

	n

C 13 n dust

énér le

USTHB Page 115

Conclusion générale

Nous avons, tout au long de ce mémoire intitulé « Application des méthodes de l'analyse des données sur l'évolution du parc automobile national », essayé d'atteindre l'objectif fixé, à savoir, trouver des méthodes d'analyses statistiques adéquates afin d'interpréter les données récoltées.

Notre travail est scindé en deux parties. La première porte sur l'utilisation des méthodes de l'analyse des données sur des statistiques représentant les véhicules en circulation sur le territoire national. La deuxième partie est consacrée à l'analyse de séries chronologiques représentant l'importation des véhicules neufs ; dont l'objectif sera de prévoir à court terme le nombre futur de véhicule mis en circulation.

Dans un premier temps, nous nous sommes intéressés à l'évolution des différents genres de véhicules au niveau national à travers le temps, et ce, en appliquant la méthode d'analyse des données appelée DACP ou double analyse en composants principales, ensuite, afin d'étudier la répartition genre par ancienneté ainsi que genre par puissance de véhicule, l'analyse factorielle des correspondances a été utilisée.

Les résultats obtenus par la DACP nous ont amené à la conclusion que le parc automobile Algérien a évolué de façon homogène sur la période de temps allant de 2000 à 2009.

Les resultats obtenus par l'AFC nous ont amené à la conclusion que l'Algérie a connu, en l'année 2009, un renouveau beaucoup plus important dans les véhicules de transport et les véhicules de tourisme, quant aux plus anciens véhicules en circulation; ce sont les camionnettes et les véhicules speciaux. nous somme aussi arrivé à la conclusion que les véhicules les plus puissants en circulation pendant l'année 2009 sont les camions et les tracteurs agricoles.

En seconde lieu, nous avons réalisé une étude prévisionnelle univariée, par le moyen de séries chronologiques. Nous avons appliqué le plan de modélisation suivant : la méthode de Box & Jenkins.

L'application de Box & Jenkins nous a permis de modéliser le phénomène étudié pour certains genres de véhicules. Dans cette méthode l'obtention des valeurs futures d'une série temporelle se fait par extrapolation des observations passées de la série en question.

Nous espérons que les résultats obtenus sauront répondre à l'attente de l'office national des statistiques ainsi qu'à tous les utilisateurs.

Le tableau des données brutes `a partir duquel on va faire l'analyse est noté X et a la forme suivante :

Analyse en composantes principales

I. Définition :

L'analyse en composantes principale « ACP », est une méthode statistique

multidimensionnelle qui permet de synthétiser un ensemble de données en identifiant la redondance dans celles-ci et consiste à rechercher les directions de l'espace qui représentent le mieux les corrélations entre n variables aléatoires, donc elle permet de :

Résumer les grands ensembles de données

ce et les corrélations.

L'ACP n'est pas une fin en soi. Elle servira à mieux connaître les données sur lesquelles on travaille, à détecter éventuellement des valeurs suspectes, et aidera à formuler des hypothèses qu'il faudra étudier à l'aide de modèles et d'études statistiques inférentielles.

Tableau de données :

Les données sont les mesures effectuées sur n unités {u1, u2, ..., ui, ...u_n}(en ligne). Les p variables quantitatives qui représentent ces mesures sont {v1, v2, ..., vi , ...v_p}(en colonne).

?

X=

^xij

?

?

?

^xi

¹

^xi

²

?

?

?

?

?

^xn

¹

^xn

²

^xnj

?

^{x x}

^{11 12}

?

^{x x}

^{21 22}

?

^j

^x1

^{x x}

j ?

^{2 2 p}
? ^{x1 p} ? ? ?

?

^xip

?

^xnp ? ? ? ? ? J

^xi

¹

?

?

?

^xi

²

?

^ui

?

^xij

^xip ? ? ? ? ? ??

On peut représenter chaque unité par le vecteur de ses mesures sur les p variables :

ce qui donne

Alors est un vecteur de .

De façon analogue, on peut représenter chaque variable par un vecteur de dont les

composantes sont les valeurs de la variable pour les n unités :

?

?

^x1

^j

^x2

^j

^v

^j

?

^xij

?

^xnj ? ? ? ? ? J

?

?

Pour avoir une image de l'ensemble des unités, on se place dans un espace affine en

choisissant comme origine un vecteur particulier de , par exemple le vecteur dont toutes

les coordonnées sont nulles. Alors, chaque unité sera représentée par un point dans cet espace. L'ensemble des points qui représentent les unités est appelé traditionnellement «nuage des individus».

En faisant de même dans , chaque variable pourra être représentée par un point de l'espace

affine correspondant. L'ensemble des points qui représentent les variables est appelé «nuage des variables».

_sj

L'idée générale des méthodes factorielles est de trouver un système d'axes et de plans tels que les projections de ces nuages de points sur ces axes et ces plans permettent de reconstituer les positions des points les uns par rapport aux autres, c'est-à-dire avoir des images les moins déformées possible.

II. Individus et variables : A. Distance entre individus :

La distance entre deux individus i et i' est la distance euclidienne usuelle donnée par la formule 3-1-1.

Il peut exister des valeurs de j pour lesquelles les variables correspondantes sont d'échelles très diverses, on veut que la distance entre deux points soit indépendante des unités sur les variables. On peut parfois désirer, surtout lorsque les unités de mesures ne sont pas les mêmes, faire jouer à chaque variable un rôle identique dans la définition des proximités entre individus : on parle alors d'analyse en composantes principales normée. Pour cela on corrige les échelles en adoptant la distance :

p ? ?

_{r r} ?

_{ij i? j}

_{d i i}

² ( , ? ) ? ?? ?

? _s n ?

_j ? 1 ? j ?

_s = ( )

^j n j=1

2 1 ⁿ r _jj r j ₂

désignant l'écart-type empirique de la variable j dont le carré (variance empirique) vaut :

_ ₂

Finalement, nous retiendrons que l'analyse normée dans du tableau brute est l'analyse

générale de X , de terme général :

_jj ?

? ?

x _ij x ij

Toutes les variables ainsi transformées sont « comparables » et ont même dispersion : _c ? _cor ? _j , _j ? ?

_jj ?

Les variables sont centrées réduites. On mesure l'écart à la moyenne en nombre d'écarts-types de la variable j.

_cjj ?

B. Matrice à diagonaliser :

En résumé, l'analyse du nuage des points-individus dans nous a amené à effectuer une
translation de l'origine au centre de gravité de ce nuage et à changer, dans le cas de l'analyse normée, les échelles sur les différents axes.

_c

?

_?r ? _r ?? _r ? _r ?

_jj ? _{n s s}

_{i j j} ?

L'analyse du tableau transformé X nous conduit à diagonaliser la matrice

.Le terme général de cette matrice s'écrit :

_{ij j ij} ? _j ?

_n

_c ?

_i

Soit :

₁

_n

C'est-à-dire :

n'est autre que le coefficient de corrélation empirique entre les variables et. A matrice à diagonaliser est donc la matrice de corrélation C

C. Axes factoriels :

Les coordonnées des n points-individus sur l'axe factoriel normé ( vecteur propre de

la matrice C associé à la valeur propre) sont les n composantes du vecteur :

Le vecteur est une combinaison linéaire des variables initiales.

^p _r ?

_?a = _{U X} = _U

_{i a j ij a jS}

_j = 1 j

r j

Puisque le nuage des individus est centré sur le centre de gravité (les masses affectées aux

individus étant égales à ), la moyenne du facteur est nulle :

Et sa variance vaut :

La coordonnée du point-individu sur cet axe s'écrit explicitement :

_j

_p

₁

_n

III. Analyse du nuage des variables : ? distance entre points-variables :

La distance entre variables découle de l'analyse dans .

Calculant la distance euclidienne usuelle entre deux variables et :

Soit :

² ( ) ? ? ?

_{d j j} x ij

, ₂

_n

₂

? = + x ²

? - _{x x}

_{ij ij ij} ?

_{n n}

_{i=1 i=1}

i=1

Remplaçant par sa valeur tirée précédemment et tenant compte du fait que

On obtient : et également :

D'où la relation liant la distance dans entre deux points-variables et et le coefficient de

corrélation entre ces variables :

Dans l'espace de, le cosinus de l'angle de deux vecteurs-variables est le coefficient de

corrélation entre ces deux variables .

-Deux variables centrées réduites fortement corrélées sont très proches l'une de l'autre

ou au contraire les plus éloignées possible .

-Deux variables orthogonales sont linéairement indépendantes.

_v ? _Xu

IV. Axes factoriels ou composantes principales :

Une fois connus les vecteurs propres et les valeurs propresde la matrice C=X'X d'ordre

(p, p), il est inutile de procéder à la diagonalisation de la matrice XX' d'ordre (n, n).

a ? a

1 a Le vecteur

est en effet un vecteur propre unitaire de XX', relativement à la ? ? X? V ? 1 X? XU ? U ?

même valeur propre . Le facteur dans s'écrit :

? ? ? ? ?

? ?

Comme , on a :

Alors les coordonnées factorielles des points-variables sur l'axe sont les composantes de

soit encore de :

Et l'on a :

(Références bibliographiques: Ouvrages, [1])

Tableau croisant genre véhicule avec tranche d'âge correspondant à l'année 2009

	M5	5à9	10à14	15à19	P20
VT	2883367	1630851	2046311	3053306	10681365
CT	527242	174860	292236	684852	2684467
C	399067	384648	494212	1265222	3164961
TA	115410	73902	41861	104741	357897
R	58238	31723	58057	160361	353925
TR	65307	86147	140993	231340	554507
AA	44313	32581	33801	11637	74907
M	43945	78848	137105	174711	329378
VS	3006	2367	4510	18896	49781

Tableau croisant genre véhicule avec tranche de puissance correspondant à l'année 2009

	VT	CM	CMT	AA	TR	TA	VS	M
1 à 2	196881	0	0	0	0	0	0	22946
3 à 5	3387463	0	478774	0	0	0	319	23025
6 à 7	5672018	21562	933678	1644	1294	6972	602	13476
8 à 10	3939884	214963	3043181	102946	1222	32990	717	9978
11 à 16	754700	1464512	266907	132363	7500	721736	7107	257
17 à 20	102806	50570	30260	18201	1885	54901	1630	200
21 à 25	325428	130560	94194	21335	5007	15389	2395	16
PLUS 25	785878	530109	293820	127853	382633	106562	10577	4155

les tableaux bruts (genre/wilaya) :	les taux des tableaux bruts :
p0=read.table("nom du tableau 1.txt")	t00=round(t(t(p0)/apply(t(p0),1,sum)),3)*100
p1=read.table("nom du tableau 2.txt")	t01=round(t(t(p1)/apply(t(p1),1,sum)),3)*100
p2=read.table("nom du tableau 3.txt")	t02=round(t(t(p2)/apply(t(p2),1,sum)),3)*100
p3=read.table("nom du tableau 4.txt")	t03=round(t(t(p3)/apply(t(p3),1,sum)),3)*100
p4=read.table("nom du tableau 5.txt")	t04=round(t(t(p4)/apply(t(p4),1,sum)),3)*100
p5=read.table("nom du tableau 6.txt")	t05=round(t(t(p5)/apply(t(p5),1,sum)),3)*100
p6=read.table("nom du tableau 7.txt")	t06=round(t(t(p6)/apply(t(p6),1,sum)),3)*100
p7=read.table("nom du tableau 8.txt")	t07=round(t(t(p7)/apply(t(p7),1,sum)),3)*100
p8=read.table("nom du tableau 9.txt")	t08=round(t(t(p8)/apply(t(p8),1,sum)),3)*100
p9=read.table("nom du tableau 10.txt")	t09=round(t(t(p9)/apply(t(p9),1,sum)),3)*100
Les centres de gravités :	Centrage des tableaux de taux :
CG0=colMeans(t00)	tc0=scale(t00,center=T,scal=F)
CG1=colMeans(t01)	tc1=scale(t01,center=T,scal=F)
CG2=colMeans(t02)	tc2=scale(t02,center=T,scal=F)
CG3<-colMeans(t03)	tc3=scale(t03,center=T,scal=F)
CG4<-colMeans(t04)	tc4=scale(t04,center=T,scal=F)
CG5<-colMeans(t05)	tc5=scale(t05,center=T,scal=F)
CG6<-colMeans(t06)	tc6=scale(t06,center=T,scal=F)
CG7<-colMeans(t07)	tc7=scale(t07,center=T,scal=F)
CG8<-colMeans(t08)	tc8=scale(t08,center=T,scal=F)
CG9<-colMeans(t09)	tc9=scale(t09,center=T,scal=F)

Le tableau des centres de gravité :

g<-matrix(c(CG0,CG1,CG2,CG3,CG4,CG5,CG6,CG7,CG8,CG9),nrow=10, ncol=6, byrow=T)

Transformations les tableaux centrés en matrices :	Les matrices variance-covariance :
tc0=as.matrix(tc0)	v0<- (1/48)*(t(tc0)%*%tc0)
tc01<-as.matrix(tc1)	v1<- (1/48)*(t(tc01)%*%tc01)
tc02<-as.matrix(tc2)	v2<- (1/48)*(t(tc02)%*%tc02)
tc03<-as.matrix(tc3)	v3<- (1/48)*(t(tc03)%*%tc03)
tc04<-as.matrix(tc4)	v4<- (1/48)*(t(tc04)%*%tc04)
tc05<-as.matrix(tc5)	v5<- (1/48)*(t(tc05)%*%tc05)
tc06<-as.matrix(tc6)	v6<- (1/48)*(t(tc06)%*%tc06)
tc07<-as.matrix(tc7)	v7<- (1/48)*(t(tc07)%*%tc07)
tc08<-as.matrix(tc8)	v8<-(1/48)*(t(tc08)%*%tc08)
tc09<-as.matrix(tc9)	v9<- (1/48)*(t(tc09)%*%tc09)

La matrice du compromis v=v0+v1+v2+v3+4+v5+v6+v7+v8+v9

Programmation du premier critère

Les vecteurs propres

uij tel que i=2000,..., 2009 et j=1,2

u01=c(-0.513,-0.397,-0.531,-0.44,-0.29,-0.137) u02=c(-0.248,0.165,-0.252,-0.171,0.622,0.657) u11=c(0.479,0.352,0.36,0.521,0.495,0.022) u12=c(-0.176,-0.118,-0.371,0.007,0.548,-0.719) u21=c(-0.186,-0.261,-0.186,-0.569,-0.551,-0.484) u22=c(0.811,0.181,0.441,-0.174,-0.084,-0.279) u31=c(-0.488,-0.35,-0.358,-0.524,-0.485,-0.023) u32=c(-0.143,-0.122,-0.362,0.013,0.521,-0.749) u41=c(-0.493,-0.346,-0.353,-0.532,-0.478,-0.022) u42=c(0.115,0.134,0.35,-0.072,-0.431,0.809) u51=c(-0.5,-0.344,-0.354,-0.533,-0.47,-0.022) u52=c(-0.082,-0.136,-0.335,0.089,0.377,-0.844) u61=c(-0.509,-0.341,-0.358,-0.529,-0.465,-0.022) u62=c(0.049,0.15,0.311,-0.111,-0.319,0.874) u71=c(-0.505,-0.341,-0.405,-0.438,-0.461,-0.246) u72=c(0.456,-0.102,0.135,0.308,-0.483,-0.66) u81=c(-0.474,-0.394,-0.375,-0.456,-0.451,-0.261) u82=c(-0.416,0.219,-0.033,-0.339,0.152,0.8) u91=c(-0.531,-0.345,-0.365,-0.499,-0.465,-0.026) u92=c(-0.021,0.155,0.237,-0.109,-0.213,0.929)

U1 <- matrix(c(u01,u11,u21,u31,u41,u51,u61,u71,u81,u91),6)

U2 <- matrix(c(u02,u12,u22,u32,u42,u52,u62,u72,u82,u92),6)

Les valeurs propres

lambda1 <- c(24.525,55.029,43.607,56.313,58.14,59.328,60.408,20.795,20.801,58.401)

lambda2 <- c(2.242,2.128,6.451,2.083,2.031,1.974,1.918,3.118,2.743,1.756)

k <- 1 ## pour 2000

Q0 <- vector()

for (j in 1:10){

Q0[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v0 %*% U1[,j]) -

(t(U2[,j]) %*% v0 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2)

I

k <- 2 ## pour 2001

Q1 <- vector()

for (j in 1:10){

Q1[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v1 %*% U1[,j]) -

(t(U2[,j]) %*% v1 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2)

I

k <- 3 ## pour 2002

Q2 <- vector()

for (j in 1:10){

Q2[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v2 %*% U1[,j]) - (t(U2[,j]) %*% v2 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

k <- 4 ## pour 2003

Q3 <- vector()

for (j in 1:10){

Q3[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v3 %*% U1[,j]) -

(t(U2[,j]) %*% v3 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2)

I

k <- 5 ## pour 2004

Q4 <- vector()

for (j in 1:10){

Q4[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v4 %*% U1[,j]) - (t(U2[,j]) %*% v4 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

k <- 6 ## pour 2005

Q5 <- vector()

for (j in 1:10){

Q5[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v5 %*% U1[,j]) - (t(U2[,j]) %*% v5 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

k <- 7 ## pour 2006

Q6 <- vector()

for (j in 1:10){

Q6[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v6 %*% U1[,j]) - (t(U2[,j]) %*% v6 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

k <- 8 ## pour 2007

Q7 <- vector()

for (j in 1:10){

Q7[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v7 %*% U1[,j]) - (t(U2[,j]) %*% v7 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

k <- 9 ## pour 2008

Q8 <- vector()

for (j in 1:10){

Q8[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v8 %*% U1[,j]) - (t(U2[,j]) %*% v8 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

k <- 10 ## pour 2009

Q9 <- vector()

for (j in 1:10){

Q9[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v9 %*% U1[,j]) - (t(U2[,j]) %*% v9 %*% U2[,j]) )) * (lambda1[k]+lambda2[k])^(-1),2) I

MQ0 <- mean(Q0)

MQ1 <- mean(Q1)

MQ2 <- mean(Q2)

MQ3 <- mean(Q3)

MQ4 <- mean(Q4)

MQ5 <- mean(Q5)

MQ6 <- mean(Q6)

MQ7 <- mean(Q7)

MQ8 <- mean(Q8)

MQ9 <- mean(Q9)

minimum<-min(MQ0,MQ1,MQ2,MQ3,MQ4,MQ5,MQ6,MQ7,MQ8,MQ9)

Résultats :

Ö(00,00)= 0	Ö(01,00)=0.09	Ö(02,00)=0.17	Ö(03,00)=0.09	Ö(04,00)=0.09
Ö(00,01)=0.05	Ö(01,01)= 0	Ö(02,01)=0.32	Ö(03, 01)=0.00	Ö(04,01)=0.00
Ö(00,02)=0.08	Ö(01,02)= 0.11	Ö(02,02)= 0	Ö(03, 02)=0.11	Ö(04,02)=0.11
Ö(00,03)=0.06	Ö(01,03)=0	Ö(02, 03)=0.32	Ö(03, 03)= 0	Ö(04, 03)=0
Ö(00,04)=0.06	Ö(01,04)=0	Ö(02,04)= 0.31	Ö(03, 04)=0	Ö(04, 04)= 0
Ö(00,05)=0.06	Ö(01,05)=0	Ö(02, 05)=0.30	Ö(03, 05)=0	Ö(04, 05)=0
Ö(00,06)=0.06	Ö(01,06)=0	Ö(02, 06)=0.29	Ö(03, 06)=0	Ö(04, 06)=0
Ö(00,07)=0.03	Ö(01,07)=0.05	Ö(02, 07)=0.15	Ö(03,07)=0.05	Ö(04,07)=0.04
Ö(00,08)=0.06	Ö(01,08)= 0.03	Ö(02, 08)=0.18	Ö(03, 08)=0.02	Ö(04,08)=0.02
Ö(00,09)=0.06	Ö(01,09)= 0.01	Ö(02, 09)=0.27	Ö(03, 09)=0.00	Ö(04,09)=0.00
D(., 00)=0.052	D(.,01)=0.029	D(., 02)= 0.231	D(., 03)=0.027	D(.,04)= 0.026
Ö(05,00)=0.09	Ö(06,00)=0.09	Ö(07,00)=0.02	Ö(08,00)=0.03	Ö(09,00)=0.08
Ö(05,01)=0.00	Ö(06,01)=0.00	Ö(07, 01)=0.10	Ö(08,01=0.06	Ö(09,01)=0.01
Ö(05,02)=0.11	Ö(06,02)=0.10	Ö(07,02)=0.06	Ö(08,02)=0.07	Ö(09,02)=0.09
Ö(05,03)=0	Ö(06,03)=0.00	Ö(07,03)=0.10	Ö(08,03)=0.06	Ö(09,03)=0.01
Ö(05,04)=0	Ö(06,04)=0.00	Ö(07,04)=0.09	Ö(08,04)=0.05	Ö(09,04)=0.00
Ö(05,05)= 0	Ö(06,05)=0.00	Ö(07,05)=0.08	Ö(08,05)=0.04	Ö(09,05)=0.00
Ö(05,06)=0	Ö(06,06)= 0	Ö(07,06)=0.08	Ö(08,06)=0.04	Ö(09,06)=0.00
Ö(05,07)=0.04	Ö(06,07)=0.04	Ö(07,07)= 0	Ö(08,07)=0.01	Ö(09,07)=0.03
Ö(05,08)=0.02	Ö(06,08)=0.01	Ö(07,08)=0.02	Ö(08,08)= 0	Ö(09,08)=0.01
Ö(05,09)=0.00	Ö(06,09)=0.00	Ö(07,09)=0.06	Ö(08,09)=0.02	Ö(09,09)= 0
D(.,05)=0.026	D(.,06)=0.024	D(., 07)=0.061	D(., 08)=0.038	D(.,09)=0.023

les trajectoires : (Alger, Adrar, Chlef)

chlef=read.table("nom du tableau des coordonnées chlef.txt")

attach(chlef)

ard=read.table("nom du tableau des coordonnées de Adrar.txt")

attach(ard)

alger=read.table("nom du tableau des coordonnées de Alger.txt")

attach(alger)

plot(axe1,axe2,type="p",pch=3,xlim=c(-10,20),ylim=c(-2.5,5),col="red")

lines(axe1,axe2,lty=3,col="red")

abline(v=0,h=0,panel.first=grid(col="gray"))

text(chlef,labels =c("00","01","02","03","04","05","06","07","08","09"),cex =1, col =

"red")

points(ax1,ax2,pch=4,col="blue")

lines(ax1,ax2,lty=3,col="blue")

text(adrar,labels =c("00","01","02","03","04","05","06","07","08","09"),cex =1, col

= "blue")

points(a1,a2,pch=4,col="blue")

lines(a1,a2,lty=3,col="blue")

text(alger,labels =c("00","01","02","03","04","05","06","07","08","09"),cex =1, col

= "blue")

text(15,-1,"Alger")

text(1,1,"adrar")

text(-1,-1,"chlef")

Références bibliographiques

:

? Ouvrages :

[1] Ludovic Lebart Marie Piron Alain Morineau :

« Statistique exploratoire multidimensionnelle » Dunod 3^e (18 août 2000)

[2] Gilbert Saporta :

« L'Analyse des données évolutives: Méthodes et applications » Technip (3 mai 2000)

? Mémoires :

[1] Zitouni Kamel - Imoudache Farouk

« Analyse et prévision du budget en matières d'explorations bancaires » Mémoire d'ingéniorat. Promotion 2010-2011. USTHB.

[2] Haddadou Fouad - Maloum Aghiles

« Modélisation et prévision de la part de marché d'Air Algérie sur les différentes réseaux internationaux affectés par la concurrence »

Mémoire d'ingéniorat. Promotion 2008-2009. USTHB.

[3] Merieme Bensalloua - Nora cherfi

« Modélisation et prévision des paramètres du marché pétrolier algérien » Mémoire d'ingéniorat. Promotion 2004-2005. USTHB.