
REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET
POPULAIRE
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA RECHERCHE
SCIENTIFIQUE
Université MENTEURI Constantine
Faculté des
Sciences De L'ingénieur
Département De Génie
Mécanique

Mémoire de Fin d'Etude pour l'Obtention du
Diplôme de MASTER en Génie Mécanique
OPTION : Génie Thermique Et
Energétique
THEME :
SIMULATION NUMERIQUE DU TRANSFERT
THERMIQUE CONJUGUE
DANS DES MICRO-CANAUX
Proposé et dirigé par :
Réalisé par :
Pr: KADJA Mahfoud - HAMLA Ilyes
-CHOUCHENE Youcef
Promotion : juin 2012

Je dédie ce modeste travail à :
mon dieu.
mes très chers parents.
mes frères et soeurs.
toute ma famille.
tous mes amis.
Ilyes

Je dédie ce modeste travail à :
mon dieu.
mes très chers parents.
mes frères et soeurs.
toute ma famille.
tous mes amis.
youcef

Nous remercions en premier lieu Dieu tout puissant pour nous
avoir accordés la puissance et la volonté de terminer ce travail,
puis...
Nous remercions vivement et chaleureusement Monsieur
M.KADJA, Professeur à l'Université Mentouri
Constantine, encadreur de ce mémoire, pour nous avoir soutenus et
guidés tout au long de ce travail. Nous le remercions
particulièrement pour la confiance qu'il nous a accordée, pour sa
rigueur scientifique, pour sa patience et pour ses conseils judicieux qui ont
contribué à l'accomplissement de ce travail.
Nous tenons à exprimer nos remerciements à
Monsieur R .BESSAIH, professeur à l'Université
Mentouri-Constantine, responsable de la spécialité. Qu'il trouve
ici l'expression de notre profonde gratitude pour l'aide qu'il nous a fournie
tout au long de la formation.
Aussi, nous remercions l'ensemble des enseignants du
département de génie
mécanique pour la bonne formation et les conseils que
nous avons reçus de leur part.
Tous nos remerciements à nos amis et collègues
pour leur soutien et leur gentillesse.
Nous remercions toutes personnes, qui, de près ou de
loin, ont contribué à l'aboutissement de ce modeste
travail.
A tous, nous tenons à exprimer nos sincères
remerciements.
Ilyes et Youcef
Résumé :
En électronique de puissance, la gestion thermique est
un processus indispensable pour évacuer la chaleur
générée par les composants électroniques et alors
mieux fonctionner dans des conditions adéquates. Laquelle est l'un des
sujets de la recherche le plus avancé technologiquement. La taille
réduite des nouvelles générations de microprocesseurs
exige des systèmes de refroidissement très modernes. Les
échangeurs de chaleur à micro-canaux ont des substrats en
silicone qui est l'une des méthodes qui attire une attention
considérable à nos jours : ce sont des micro-canaux très
fins donnant un très grand taux d'échange de chaleur convectif et
offrant la possibilité de couvrir le besoin du refroidissement des
microprocesseurs dans le futur. Dans notre projet nous avons
étudié un écoulement laminaire (R=51, 84, et 169) à
l'intérieur d'un micro-canal de section rectangulaire de diamètre
hydraulique égal à (86um) pour une seule phase de
l'écoulement du liquide. Le modèle du micro-canal en question est
constitué d'un substrat en silicone (puits de chaleur) de (10mm=10000um)
de longueur, (57um) de largeur, et (180um) de profondeur usiné sur la
longueur entière. L'eau à (293K) s'écoule à
l'intérieur comme fluide de refroidissement. Le coefficient local du
transfert de chaleur, le nombre de NUSSELT moyen sont calculés et
tracés avec des nombre de Reynolds égaux à (51, 84 et
169). Les résultats sont obtenus pour les flux suivants
(50W/cm2, 90W/cm2, et 150W/cm2). A partir de
ces résultats, nous avons tiré les conclusions suivantes :
· Le transfert thermique combiné
convection-conduction dans le micro-canal est bien simulé d'après
l'analyse des profils de températures traversant en même temps le
solide et le fluide. La chaleur diffusée par conduction dans le solide
avant d'atteindre le fluide par convection, qui la véhicule vers
l'extérieur.
· L'examen des nombres de Nusselt montre que le fluide
reçoit la plus grande partie de sa chaleur dans la région
d'entrée du micro-canal et plus celui-ci avance dans le micro-canal,
plus il s'échauffe, donc la différence entre sa
température et celle des parois du micro-canal diminue.
· Les pertes de charge calculées sont en
très bon accord avec les formules théoriques classiques.
Mots clés: transfert de chaleur
conjugué, la dissipation visqueuse, micro-canaux, simulation
numérique.
ABSTRACT:
In electronic equipments, thermal management is indispensable
for its longevity and hence, it is one of the important topics of current
research. The dissipation of heat is necessary for the proper functioning of
these instruments. The heat is generated by the resistance encountered by
electric current. This has been further hastened by the continued
miniaturization of electronic systems which causes increase in the amount of
heat generation per unit volume by many folds. Unless proper cooling
arrangement is designed, the operating temperature exceeds permissible limit.
As a consequence, chances of failure get increased.
Increasing circuit density is driving advanced cooling systems
for the next generation microprocessors. Micro-Channel heat exchangers (MITE)
in silicon substrates are one method that is receiving considerable attention.
These very fine channels in the heat exchanger provide greatly enhanced
convective heat transfer rate and have been shown to be able to meet the
demands of the cooling challenge for the microprocessors for many generations
to come.
This work focused on laminar flow (Re=51, 84, 169) within
rectangular micro-channel with hydraulic diameter (86um) for single-phase
liquid flow. The influence of the thermo-physical -properties of the fluid on
the flow and heat transfer is investigated by evaluating thermo-physical
properties at a reference bulk temperature. The micro-heat sink model consists
of a (10 mm=10000um) long silicon substrate, with rectangular micro-channels,
(57um) wide and (180um) deep, fabricated along the entire length. Water at
(293k) is taken as working fluid. The results indicate that thermo-physical
properties of the liquid can significantly influence both the flow and heat
transfer in the micro-channel. The local heat transfer coefficient and averaged
NUSSELT number is calculated and plotted for Reynolds number (51, 84, and 169).
The results are verified for heat flux (50w/cm2, 90w/cm2,
and 150w/cm2). From these results we have taken the next
conclusions:
· A combined heat transfer convection-conduction within
the micro-channel is simulated according from the analyses of the temperature
profiles crossing in the same time the solid and the fluid. The diffuse heat
per conduction in the solid before attains the fluid per convection that is
vehicular to the exterior.
· The analyses of the Nusselt number show that the fluid
receives the big part of its heat in the inlet region of micro-channel, and if
the fluid advance in this channel; it heated. So, the difference between its
temperature and walls temperature decreased.
· The pressure drops calculated are agreed with the
theoretical and classical formulas.
Key words: conjugated heat transfer, viscous
dissipation, micro-channels, numerical simulation.
Nomenclature
Nomenclature :
Notations latines
Symboles Dénominations Unités
Dh
Cp Chaleur spécifique à p=cte J/Kg
4????
Diamètre hydraulique????h = m
????
2
????? Accélération gravitationnelle m/s
h Coefficient d'échange moyen W/m2 .K
m
2
q0 Densité De Flux Dégagée Par Le
Microprocesseur w/cm
T Température de fluide caloporteur k
U, V, W Composantes du vecteur de la vitesse d'écoulement
m/s
suivant x, y et z
|
~?
????
|
Vecteur de vitesse
|
x Largeur du micro-canal m
y Hauteur du micro-canal m
z Longueur du micro-canal m
Notations grecques
a diffusivité thermique m2/s
B coefficient de dilatation thermique du fluide 1/ k
K conductivité thermique du fluide W/m.K
3
ñ masse volumique du fluide Kg/m
u Viscosité dynamique du fluide kg/m.s
í Viscosité Cinématique du fluide
m2/s
???? La dissipation visqueuse J/m3.s
s-1
? Opérateur de vecteur Nabla
?2 Opérateur laplacien s-2
p pression N/m2
2
A surface m
t Temps s
Nombres adimensionnelles
Br Nombre de Brinkman
???????? Coefficient de frottement
Gr Nombre de grashof
Nu Nombre de Nusselt moyen
Ra
Re
Pr Nombre de Prandtl
Nombre de Rayleigt Nombre de Reynolds
Ri Nombre de Richardson
Indices
f Fluide
i interface
in Entrée
o Sortie
s Solide
Sommaire
Sommaire :
Remerciements. i
Dédicaces. ii
Nomenclatures. iii
Liste des figures et des tableaux. v
Introduction générale. 1
Chapitre 01
Revue bibliographique
1.1. Introduction. 4
1.2. Problèmes de composants électroniques. 5
1.2.1. L'influence de la température sur les circuits
électroniques. 5
1.3. Mécanismes de transfert de chaleur dans les
systèmes à refroidir. 7
1.3.1. Évacuation de la chaleur par convection. 7
1.3.2. Convection naturelle et mixte. 8
Conclusion. 10
Chapitre 02
Généralités sur le transfert de
chaleur
2.1. Introduction. 11
2.2. Modélisation des liquides. 12
2.2.1. Équation de continuité. 12
2.2.2. Équation de quantité de mouvement. 13
2.2.3. Équation de l'énergie. 13
2.3. Conditions aux limites. 14
2.4. La dissipation visqueuse. 14
2.5. Conduction dans le solide. 15
2.6. Équations simplifiées. 16
2.6.1. Équation de continuité. 16
2.6.2. Équation de quantité de mouvement. 16
2.6.3. Équation de l'énergie. 17
2.7. Conditions aux limites du domaine étudié.
17
2.7.1. Conditions aux limites hydrodynamiques. 17
2.7.2. Conditions aux limites thermiques. 18
Conclusion. 19
Chapitre 03
Description de l'outil informatique
3.1. Introduction. 20
3.2. Les principales étapes pour définir un
problème de CFD. 20
3.3. Quelques instructions qui concernent GAMBIT. 20
3.4. Préprocesseur GAMBIT. 21
3.5. Maillage. 24
3.5.1. Qualité du maillage. 25
3.5.2. Conditions aux limites en GAMBIT. 25
3.6. Présentation du logiciel FLUENT. 25
3.6.1. Méthode des volumes finis. 25
3.6.2. Schémas de discrétisations. 26
3.6.3. Choix du solveur. 27
3.6.4. Spécifications du fluide et des matériaux
utilisés. 27
3.7. Domaine d'étude. 28
3.7.1. Maillage du domaine d'étude. 29
3.8. Critère de convergence. 31
Conclusion. 31
Chapitre 04
Résultats et Discussions
4.1. Introduction. 32
4.2. Résultats. 32
1ier cas : un seul canal. 32
2mecas : double canal. 40
4.3. Discussions. 41
Conclusion. 43
Conclusion générale. 44
Références bibliographiques. 46
Annexes 47
Liste des figures et de tableaux
Liste des figures :
Chapitre 01
Revue Bibliographique
Fig. I-1 : Echauffement d'un microprocesseur dans son milieu de
fonctionnement. 6
Fig. I-2 : Evolution de la puissance thermique dissipée
pour un transistor (FETS et IGBTS) et
un conducteur Smart. 7
Fig. I-3 : Différentes géométries des
micro-canaux. 9
Chapitre 02
Généralités sur le transfert de
chaleur
Fig. 2.1 : Micro échangeur de chaleur. 11
Fig. 2.2 : Ecoulement entre deux plaques parallèles. 16
Chapitre 03
Description de l'outil informatique
Fig. 3.1 : La fenêtre ci-dessous est une
présentation importante pour la définition d'un
problème. 21
Fig. 3.2 : Représentation graphique d'un maillage
structuré (a) et non structuré (b) généré
par
Gambit en 2D. 21
Fig. 3.3 : Opérations fondamentales en GAMBIT. 22
Fig. 3.4 : Elaboration des vertex. 22
Fig. 3.5 : Création de la géométrie. 23
Fig. 3.6 : Commandes de fichier en FLUENT. 24
Fig. 3.7 : Domaine d'étude. 28
Fig. 3.8.a : Maillage des parois droite et gauche du puits
thermique (NYxNZ=150x20). 29
Fig. 3.8.b : Maillage de la paroi d'entrée du puits
thermique (NYxNX=150x20). 30
Fig. 3.8.c : Maillage des sections d'entrée et sortie du
micro-canal (NYxNX=30x20). 30
Chapitre 04
Résultats et discussions
Fig. 4.1 : Diagramme schématique d'un seul micro-canal par
GAMBIT. 32
Fig. 4.2 : Température à la sortie (q=50
W/cm2, Re=84). 33
Fig. 4.3 : Température à la sortie (q=90
W/cm2, Re=84). 33
Fig. 4.4 : Température à la sortie (q=150
W/cm2, Re=84). 34
Fig. 4.5 : Profil de température au milieu de la
configuration (canal + puits de chaleur). 34
Fig. 4.6 : Variation de la température du fluide le
long de l'axe du micro-canal pour (q=150
W/cm2, Re=169). 35
Fig. 4.7 : Vitesse à la sortie (q=50 W/cm2,
Re=84). 35
Fig. 4.8 : Vitesse à la sortie (q=150 W/cm2,
Re=84). 36
Fig. 4.9 : Profil de vitesse à la sortie du canal,
(q=50W/cm2, Re=84). 36
Fig. 4.10 : Variation du nombre de Nusselt en fonction de Z (q=50
W/cm2, Re=84). 37
|
Fig. 4.11 : Nombre de Nusselt en fonction du Nombre de Reynolds
(q=150 W/cm2
|
). 37
|
Fig. 4.12 : Perte de pression en fonction de la distance de
l'entrée du canal. 38
Fig. 4.13 : Température à la sortie (q=50
W/cm2, Re=51). 38
Fig. 4.14 : Température à la sortie (q=90
W/cm2, Re=51). 39
Fig. 4.15 : Température à la sortie (q=150
W/cm2, Re=51). 39
Fig. 4.16 : Température à la sortie (q=50
W/cm2, Re=169). 40
Fig. 4.17 : Diagramme schématique de deux micro-canaux par
GAMBIT. 40
Fig. 4.18 : Les isothermes obtenus avec une configuration
à deux micro-canaux (q=50 /cm2,
Re=84). 41
Liste des tableaux :
Chapitre 01
Revue
Bibliographique
Chapitre 02
Généralités sur
le transfert de chaleur
Tab. 2.1 : Classification des canaux. 12
Chapitre 03
Description de l'outil informatique
Tab. 3.1 : propriétés du silicium et du quartz.
28
Chapitre 04
Résultats et discussions
Introduction générale
Page 1
Introduction générale
Introduction générale :
Les avancées des techniques de gravure des circuits
intégrés et l'évolution de l'électronique de
puissance permettent d'avoir des composants de plus en plus petits. Depuis 20
ans, l'ensemble de ces technologies a été développé
ouvrant la voie à des nouveaux champs d'application qui vont de la
physique fondamentale à la micromécanique en passant par la
biologie et la chimie. Bien que récents, ces domaines comptent
déjà des
réalisations impressionnantes.
Cette course vers la miniaturisation entraîne de
sévères contraintes de fonctionnement sur les composants
électroniques, et notamment le niveau de leur température
critique. Pour travailler dans des conditions adéquates, ces composants
doivent fonctionner à une température de jonction
inférieure à celle spécifiée par le
constructeur.

Figure 1 Photos des micro-canaux prises au microscope
électronique.
L'étude du comportement thermique des composants
électroniques et des assemblages de puissance tient aujourd'hui une
place capitale dans la conception des fonctions électroniques soumises
à environnement sévère. Un échauffement excessif
dégrade les performances du composant, réduit sa durée de
vie et peut provoquer la défaillance. L'étude du comportement
thermique de tel composant aidera donc à prévoir sa
fiabilité, sa durée de vie et l'évolution de ses
performances dans le temps.
En effet, de nos jours, les composants de puissance
(microprocesseurs, disques durs, barrettes mémoires, convertisseur de
tension, ...) peuvent dissiper plusieurs centaines de watts par
centimètre carré. Ainsi, l'évacuation de la chaleur est
devenue le problème majeur à résoudre pour
développer les composants miniaturisés et augmenter leur
fréquence d'utilisation. Il est donc primordial de concevoir des
systèmes énergétiques efficaces pour le refroidissement de
ces composants afin d'éviter des surchauffes locales ou globales.
Plusieurs méthodes de refroidissement ont
été étudiées dans le but d'améliorer le
transfert de chaleur et augmenter l'efficacité des systèmes de
refroidissement. Parmi ces méthodes, on trouve les méthodes
classiques de refroidissement par convection naturelle et forcée avec
des écoulements gazeux et liquides. Il est à noter que la
convection naturelle est utilisée pour les systèmes de faible
puissance et de densités de flux réduite. Le refroidissement des
systèmes de forte puissance et à grande échelle
nécessite une dissipation thermique plus élevée, raison
pour laquelle la convection forcée est la plus
Page 2
Introduction générale
appropriée dans la plupart des cas.
Le refroidissement par un liquide peut être soit
monophasique (la température du fluide reste inférieure à
celle de saturation), soit accompagné d'un échange thermique par
ébullition. Toutefois, dans les deux cas on utilise un circuit
hydraulique dans lequel circule un liquide caloporteur entraîné
par une pompe qui emmagasine la chaleur au niveau du système à
refroidir et la redistribue à un dissipateur.
Quoique le refroidissement de certains composants de forte
puissance (microprocesseurs, diodes laser...) se fasse de plus en plus avec
écoulement d'un liquide ou avec changement de phase, le refroidissement
par écoulement d'air demeure encore très utilisé. En
effet, ce type de refroidissement est approprié pour des composants de
moyenne et de faible puissance tels que le processeur des cartes graphiques,
les disques durs, les racks de serveur, de réseau ou de
télécommunication. Il constitue l'une des solutions
énergétiques les plus économiques.
Différentes solutions ont été
adoptées pour augmenter l'efficacité d'un système de
refroidissement à air :
La première consiste à greffer des ailettes
offrant une plus grande surface de contact. En électronique de
puissance, les dimensions des panneaux à ailettes sont en
général proportionnelles aux capacités des modules
chauffants. Cela conduit à concevoir des ailettes jusqu'à 100 mm
de longueur et 5 mm d'épaisseur. Bien qu'il soit très
répandu en micro-électronique, le principe est toujours
utilisé en électronique de puissance. Le principal
inconvénient de cette technique est l'encombrement qu'elle introduit.
La deuxième solution pour augmenter l'efficacité
d'un système de refroidissement à air, en particulier quand il
n'y a pas assez de place pour installer un radiateur à ailettes ou un
ventilateur sur le composant, consiste à implanter des
déflecteurs qui jouent le rôle de dirigeants de
l'écoulement d'air dans les boîtiers contenant les composants. Ces
déflecteurs guident le flux d'air circulant dans le boîtier vers
les zones les plus critiques sur les cartes. Ces solutions sont aussi
préconisées lorsqu'il s'agit de refroidir des convertisseurs de
courant ou de tension. Ces derniers peuvent générer des champs
magnétiques qui perturbent le fonctionnement des pompes ou des
ventilateurs s'ils étaient placés à proximité des
composants.
C'est dans ce contexte que nous allons mener notre
étude. L'objectif de ce travail de mémoire consiste donc à
étudier numériquement le transfert de chaleur dans un micro-canal
contenant un fluide caloporteur (l'eau) consiste à améliorer les
techniques de refroidissement d'un microprocesseur.
Le présent manuscrit s'articule autour de quatre
chapitres et une conclusion générale :
?Faisant suite à cette introduction, le premier
chapitre est consacré à une synthèse bibliographique
concernant les problèmes d'évacuation de chaleur dus à la
miniaturisation.
?Le deuxième chapitre aborde essentiellement des
généralités sur le transfert de chaleur. Cette partie est
suivie d'un rappel des équations qui régissent
l'écoulement incompressible en régime laminaire.
Page 3
Introduction générale
?Le troisième chapitre présente le domaine
d'étude et la description de l'outil informatique
utilisé(logiciels FLUENT et GAMBIT).
?Le quatrième chapitre propose une étude
numérique sur le transfert de chaleur conjugué à
l'intérieur d'nu micro-canal dans les processus de refroidissement
inclues dans l'électronique de puissance.
Nous terminons ce mémoire par une conclusion
générale et des recommandations.
Chapitre 01
Revue bibliographique
Page 4
REVUE BIBLIOGRAPHIQUE
1.1. Introduction.
Suite aux progrès technologiques récents en
électronique, les composants deviennent de plus en plus puissants et de
plus en plus petits. En conséquence, la chaleur à évacuer
devient très importante dans le domaine de l'électronique. En
effet, de nos jours, les composants de puissance (microprocesseurs, disques
durs, barrettes mémoires, convertisseur de tension, ...) peuvent
dissiper plusieurs centaines de watts par centimètre carré. La
surchauffe des composants réduit leur durée de vie et peut
provoquer des contraintes de fonctionnement. Une bonne évacuation de la
chaleur est donc primordiale pour assurer le bon fonctionnement et la
fiabilité de ces dispositifs [1, 2].
Le besoin d'améliorer les techniques de refroidissement
des composants électroniques à faible et à forte puissance
a élargi le champ de la recherche concernant le transfert thermique au
niveau de ces derniers, en particulier sur :
· la température maximale de jonction (au
delà de laquelle il y a destruction du composant ou non
fonctionnement),
· la résistance thermique de contact
(exprimée en °C/W) qui quantifie la facilité
d'évacuation du flux thermique du composant vers le boîtier ou le
substrat, la capacité thermique qui chiffre "l'inertie" thermique d'un
composant soumis à un régime transitoire.
Les technologies de la microélectronique
développées depuis plusieurs décennies ont permis de
réduire la taille des composants, et d'augmenter leur densité
dans les circuits intégrés. Si, en 1958, il n'y avait qu'un seul
transistor par circuit intégré, de nos jours, il y'en a des
millions. Au début des années 80 et après avoir
considérablement diminué les dimensions des composants, les
électroniciens ont intégré sur une même plaque en
silicium, les capteurs, les actionneurs, les éléments
mécaniques, engrenages et moteurs.
Cet ensemble appelé MEMS (Micro Electro-Mechanical
System) fait appel pour sa fabrication aux micro-technologies [3], qui
permettent une production à grande échelle. Les années 90
ont été marquées par l'émergence des MEMS sur des
marchés industriels de grands volumes comme l'automobile ou la
péri-informatique. Des usines de semiconducteurs dédiés
à la production de MEMS furent construites par des entreprises telles
que Bosch ou Motorola. Aujourd'hui, l'offre des MEMS concerne des domaines
aussi variés que la défense, le médical,
l'électronique, les communications et l'automobile, ...
Il est à noter, qu'en 20 ans, l'évolution des
MEMS a été extrêmement importante sur deux points
essentiellement :
- Les niveaux d'intégration sont de plus en plus
poussés et les systèmes sont de plus en plus complexes. La
frontière entre micro-électronique et microsystèmes tend
à s'estomper, l'industrie microélectronique s'enrichi par des
fonctions initialement dévolues aux microsystèmes.
- Les MEMS sont partout. 90% des marchés des MEMS sont
dans l'automobile (les capteurs de pression pour l'injection de carburant dans
les cylindres d'un moteur, et également dans les roues pour
détecter les crevaisons), les têtes d'injection d'imprimantes, la
domotique... Mais d'autres secteurs très prometteurs pour les
Page 5
REVUE BIBLIOGRAPHIQUE
MEMS sont en cours d'émergence. Il faut citer la
biologie où les MEMS révolutionneront très probablement
l'analyse biologique en permettant des millions de tests unitaires en moins
d'une seconde. En optique, les micro-gyromètres équipent les
caméras vidéo qui détectent les tremblements du
cinéaste et commandent la correction automatique.
Depuis la naissance de ces dispositifs miniaturisés,
disposer d'une source d'énergie suffisante est un challenge permanent.
L'urgence et l'intérêt ont encore grandi dans les années
90-95 avec le développement des microsystèmes embarqués
[4, 5], des microsystèmes répartis [6, 7], des
systèmes de surveillance...
I-2 Problèmes de température des
composants électroniques.
L'augmentation de la fréquence de fonctionnement et
l'explosion de projets de miniaturisation a engendré plusieurs
problèmes dus à l'augmentation considérable du flux de
chaleur généré par les composants électroniques. Si
la chaleur n'est pas dissipée en temps voulu, la température de
jonction sera supérieur à la température de fonctionnement
maximale mentionnée par le constructeur, le contrôle thermique
devient donc de plus en plus complexe.
M. REBAY et al. [8] ont montré par thermographie
infrarouge que la température globale d'un microprocesseur ne
reflète pas la topographie thermique réelle de la puce
intégrée. Comme le montre la figure I-1, une partie dégage
plus de chaleur que les autres. C'est ce que l'on appelle un point chaud
("hotspot"), représenté en rouge sur cette figure. J.
Donald et M. Martonosi [9] parlent d'une différence de
température de l'ordre de 5 à 25°C, entre la
température moyenne et le point le plus chaud. Ces pics de
température risquent de causer de graves dégâts sur une
zone précise du processeur.
1.2.1. L'influence de la température sur les
circuits électroniques.
- Les performances électriques : la température
peut être une valeur limite au-delà de laquelle le fonctionnement
n'est plus garanti, des dérivées des paramètres provoquent
une diminution des performances pouvant aller jusqu'à la
défaillance.
- Le packaging soumis à des gradients de
température très importants. Il existe des températures
critiques pour lesquelles se produisent des changements d'état, de
structure physique. Le fluage et le relâchement des contraintes dans les
matériaux sont accélérées par la température
et peuvent conduire à des ruptures d'éléments.
- Les cycles thermiques, auxquels sont soumis des
matériaux reliés entre eux et de coefficient de dilatation
différent, induisent des forces très importantes qui peuvent
conduire à une rupture instantanée ou créer une fatigue
qui provoque une rupture à long terme.
Page 6
REVUE BIBLIOGRAPHIQUE
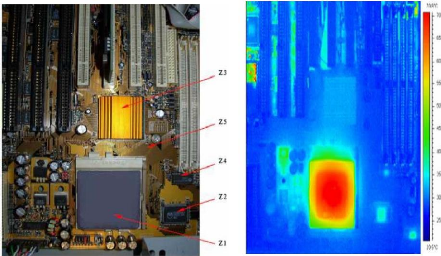
(1) : Image d'une carte mère (2) : Thermographie
infrarouge
Fig. I-1 : Echauffement d'un microprocesseur dans son
milieu de fonctionnement [8]
Le packaging et la gestion thermique dans les
équipements électroniques sont devenus des enjeux importants en
raison de l'augmentation des niveaux de puissance et de la miniaturisation des
dispositifs. Avec l'arrivée de conditionnements plus denses et des
fréquences de fonctionnement plus élevées, le coût,
la fiabilité et la taille ont été améliorés,
mais, la gestion thermique n'a pas suivi suffisamment cette
évolution.
L'évolution des techniques de refroidissement est
étroitement liée à l'augmentation de la puissance
thermique et de la complexité des circuits électroniques. La
tendance de l'industrie électronique de dissiper plus de puissance dans
de plus petits modules a créé des défis de gestion
thermique croissants. La densité de flux atteint les 50 W/cm2
dans les nouvelles générations de microprocesseurs, quant aux
convertisseurs d'électronique de puissance leur volume s'est vu
réduire d'une manière importante.
En effet, depuis l'apparition des IGBT (Insulated Gate
Bipolar Transistors), les convertisseurs sont capables de fonctionner à
haute fréquence avec des densités de flux pouvant atteindre 400
W/cm2 (un IGBT de taille 12 x 12 mm2 peut dissiper 680W)
tout en conservant des valeurs élevées de courant et de tension.
Les diodes laser quant à elles dissipent 500 W/cm2 et plus.
De nos jours, les futures exigences thermiques sont soigneusement
étudiées.
La figure I-2 présente l'évolution de
la puissance thermique dissipée pour un transistor (FETS et IGBTS) et un
conducteur Smart. Nous notons une augmentation considérable de la
puissance thermique dissipée par les transistors. Nous remarquons
également, une complexité de plus en plus importante de
systèmes embarqués.
Page 7
REVUE BIBLIOGRAPHIQUE
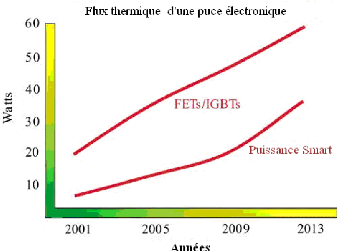
Fig. I-2 : Evolution de la puissance thermique
dissipée pour un transistor (FETS et IGBTS) et un conducteur Smart [26,
27, 28].
1.3. Mécanismes de transfert de chaleur dans
les systèmes.
Afin de maintenir sa température dans des limites
où la performance et le fonctionnement ne sont pas compromis, le
refroidissement d'un composant générant de la chaleur est
essentiel. D'une manière générale, un transfert de chaleur
a lieu par trois mécanismes qui sont la conduction, la convection et le
rayonnement. En matière d'évacuation de chaleur par conduction,
la technique des plaques de fibres de carbone orientées (conduction
anisotrope) est incontestablement la plus performante, mais à ce jour
réservée à l'aéronautique et au spatial pour une
question de coût. Plus usuellement, la chaleur est transmise à
l'air ambiant par des radiateurs et des ventilateurs.
Si la charge thermique imposée à l'air ambiant
est trop importante, on confine cette chaleur directement dans un fluide
caloporteur par l'intermédiaire d'un échangeur de chaleur. Le
transfert de chaleur au fluide réfrigérant peut alors fonctionner
soit en mode monophasique en utilisant un liquide ou un gaz (eau simple, eau +
glycol, CO2...), soit en mode diphasique (C4 F10, glace binaire
(mélange d'eau, méthanol et glace)...)
1.3.1. Evacuation de chaleur par convection.
En 1994, Kakaç, Yurucu et Hijikata [1] ont
étudié différentes méthodes de refroidissement dans
le but d'améliorer le transfert de chaleur. Parmi ces méthodes,
on trouve les méthodes traditionnelles de refroidissement par convection
naturelle et forcée.
Page 8
REVUE BIBLIOGRAPHIQUE
Il est à noter que la convection naturelle est
utilisée pour les systèmes de faible puissance et de
densités de flux réduite [10]. Le refroidissement des
systèmes de forte puissance et à grande échelle
nécessite une dissipation thermique plus élevée, raison
pour laquelle la convection forcée est la plus appropriée dans la
plupart des cas.
1.3.2. Convection naturelle et mixte.
Parmi les travaux réalisés dans ce domaine, on
peut citer l'étude menée par Icoz et Jaluria [11] qui ont fait
une simulation numérique de la convection naturelle bidimensionnelle
dans un canal rectangulaire ouvert et contenant des sources de chaleur. Leurs
résultats montrent que les dimensions du canal et la présence des
ouvertures ont des effets considérables sur l'écoulement mais
très peu d'effet sur le transfert de chaleur.
D'autres études numériques ont
été faites sur des géométries
élémentaires (canal vertical) pour déterminer le transfert
de chaleur par convection naturelle [12, 13, 14].
Récemment, Desrayaud [15] a réalisé une
étude paramétrique sur un système en 2D constitué
de canaux parallèles avec une seule source de chaleur. Le système
simule le refroidissement d'un ensemble de circuits imprimés (PCB) avec
des modules chauffés placés à la surface des circuits. La
solution a été calculée simultanément dans le
solide (module et substrat) et dans les régions de fluide en tenant
compte de la continuité de la température et du flux de chaleur
aux interfaces solide-liquide.
Par la suite, Icoz et Jaluria [16] ont élaboré
une méthodologie pour la conception et l'optimisation des
systèmes de refroidissement des équipements électroniques.
Dans cette approche, les données expérimentales ou de simulation
numérique, notamment le nombre de Reynolds et la taille des composants,
ont été utilisées pour obtenir une conception thermique
acceptable et optimale.
Le concept de micro-canaux a été introduit
depuis les années 80 par Tuckerman et Pease [17]. Pour déterminer
les performances de refroidissement des composants électroniques
à l'aide d'un écoulement liquide à travers des
micro-canaux sans changement de phase, ils ont fabriqué un
échangeur de 1cm2 en silicium, composé de canaux et
d'ailettes de 0,05mm de largeur et de hauteur 0,3mm, soit 50 canaux en tout.
Ces micro-canaux permettent une dissipation thermique de l'ordre de 800
W/cm2. Ces résultats ont montré que le coefficient de
transfert thermique d'un écoulement laminaire à travers les
micro-canaux est plus important que le coefficient de transfert thermique
à travers les canaux de taille conventionnelle.
Plusieurs recherches ont été menées afin
d'étudier le transfert thermique convectif monophasique en utilisant
l'eau [18, 19, 20], l'eau ionisée [21, 22] et le méthanol comme
fluide de fonctionnement.
Récemment, Wu et Cheng [23] ont effectué des
recherches expérimentales sur le transfert thermique convectif et sur la
chute de pression de l'eau dé-ionisée dans plusieurs micro-canaux
de forme trapézoïdale en silicium ayant différents
paramètres géométriques, rugosité de surface et des
propriétés hydrophiles de paroi. Ils ont montré que le
nombre de Nusselt et le coefficient de frottement dépendent
considérablement des différents paramètres
géométriques : ils augmentent avec la rugosité de la paroi
et ils
Page 9
REVUE BIBLIOGRAPHIQUE
diminuent corrélativement les propriétés
hydrophiles de la paroi. De ce fait, le nombre de Nusselt et le coefficient de
frottement, dans des micro-canaux ayant des parois hydrophiles dures (parois en
oxyde thermique) sont plus importants que ceux des micro-canaux ayant des
parois fragiles (parois en silicium). Wu et Cheng ont montré aussi que
le nombre de Nusselt augmente quasi- linéairement pour de faibles
valeurs du nombre de Reynolds (Re<100) et augmente plus lentement avec des
valeurs du nombre de Reynolds comprises entre 100 et 1000.
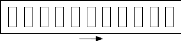

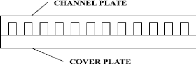
Fig. I-3 : Différentes géométries
des micro-canaux [23]
Par ailleurs, plusieurs chercheurs se sont
intéressés aux analyses numériques. Parmi eux, nous citons
Morini [24]. Il a étudié numériquement le rôle du
transfert visqueux d'un écoulement liquide dans des micro-canaux. Un
modèle basé sur la théorie conventionnelle est
développé pour prédire l'effet de la dissipation visqueuse
dans les micro-canaux avec le changement de la section de ces derniers.
Particulièrement Morini a analysé le rôle des
propriétés thermo-physiques et de la géométrie des
micro-canaux sur la dissipation visqueuse.
Qu et Mudawar [27] se sont intéressés aussi aux
écoulements liquides à travers les
micro-tubes. Ils ont analysé numériquement un
écoulement
tridimensionnel et les performances liées au transfert
thermique dans un micro-
échangeur rectangulaire formé par des
couches de 1 cm2 de silicium et utilisant l'eau comme fluide de
fonctionnement. Les micro-canaux utilisés ont une largeur de 57 um et
une hauteur de 180 um et sont séparés par une paroi de 43 um
d'épaisseur. Le code numérique basé sur la méthode
des différences finies est validé en comparant les
résultats trouvés avec les solutions analytiques et les
données expérimentales disponibles dans la littérature.
Pour les micro-échangeurs étudiés, ils ont constaté
que l'élévation de la température dans le sens de
l'écoulement à l'interface fluide-solide peut être
supposée linéaire.
Page 10
REVUE BIBLIOGRAPHIQUE
Les auteurs ont montré que l'augmentation de la
conductivité thermique dans le matériau réduit la
température à la surface de la base de l'échangeur,
particulièrement à la sortie du canal. Il a été
noté que la méthode des différences finies classique a
apporté des simplifications pour modéliser le transfert thermique
à l'intérieur des micro-échangeurs.
Conclusion.
Dans ce chapitre, plusieurs méthodes de
refroidissement ont été étudiées dans le but
d'améliorer le transfert de chaleur et augmenter l'efficacité des
systèmes de refroidissement. Parmi ces méthodes, on trouve les
méthodes traditionnelles de refroidissement par convection naturelle et
forcée avec des écoulements liquides.
Les chercheurs ont mené des études analytiques,
numériques et expérimentales pour mieux comprendre les
caractéristiques de l'écoulement et du transfert thermique. Les
résultats de leurs recherches sont parfois très dispersés,
voir même contradictoires aussi bien pour les caractéristiques de
l'écoulement que pour le transfert thermique. Certaines études
mettent en évidence une augmentation des transferts thermiques.
Plusieurs chercheurs attribuent cette augmentation à la réduction
de la viscosité du liquide, d'autres la concèdent à la
miniaturisation des dimensions
Différentes interprétations ont
été détaillés pour expliquer certains changement de
comportement et différentes questions ont été
posées afin d'éclaircir ces contradictions à savoir les
limite de validité d'utilisation des systèmes de plus en plus
complexes.
Parmi les solutions qui ont été
élaborées, nous citons l'utilisation des micro-canaux. C'est dans
ce contexte que va être menée notre étude. En effet, en
particulier quand il n'y a pas assez de place pour installer un radiateur
à ailettes ou un ventilateur sur le composant, consiste à
implanter un micro-canal qui joue le rôle d'un refroidisseur dans les
boîtiers contenant les composants.
Chapitre 02
Généralités sur le transfert
thermique
Page 11
Généralités sur le Transfert de Chaleur
2.1. Introduction.
Durant les 20 dernières années, le
développement considérable qu'ont connu les industries
électronique et informatique, surtout en miniaturisation des
équipements, n'était possible que par une bonne évacuation
de la chaleur générer par le fonctionnement des composants
électroniques. On cite la technologie des semi-conducteurs (ITRS),
où la puissance thermique dégagée pas les micros
processeurs était de moins de 50 w avant l'an 2000, cette puissance a
pratiquement doublée au bout de 10 ans.
Plusieurs techniques d'évacuation du flux de chaleur
généré par les composants électroniques sont
adoptées et continuellement améliorer. L'une des approches les
plus prometteuses étant le refroidissement au moyen d'écoulements
simples ou diphasiques dans des micro-canaux. Ces derniers forment des
échangeurs de chaleur de hautes performances comme le montre la figure
(2.1) qui représente une pile d'échangeurs de chaleur à
flux croisés de dimensions 14 mm x14mmx14mm capables de
transférer 10 kilowatts avec une différence de
températures entrée/sortie de 80 K malgré leurs faibles
dimensions.

Fig. 2.1 : Micro échangeur de chaleur
[35].
Les micro-canaux peuvent être définis comme des
canaux dont les dimensions sont comprises entre un micron et un
millimètre Tableau (2.1). Au-delà d'un millimètre le
comportement de l'écoulement est identique à celui
présenté dans l'analyse macro-échelles.
Généralités sur le Transfert de
Chaleur
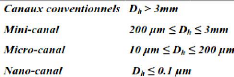
Tab. 2.1 : Classification des canaux
Actuellement, les micro-canaux ont des dimensions de l'ordre
des microns, ils sont fabriqués à partir de plusieurs
matériaux tels que le verre, les polymères, le silicium.... en
utilisant différentes techniques d'usinage telles que la
micro-gravure.
L'un des avantages que présente les micros-canaux est
leur rapport élevé de surface/volume ainsi que leur faible
encombrement. En effet, lorsque la taille du canal devient très petite
le rapport de la surface au volume devient plus grand. Si on considère
un tube de diamètre D et de longueur L. Le rapport de
la surface A au volume V0 est :
A V0
|
=
|
mDZ
mD2Z/4 =
|
4 (2.1)
D
|
|
????????
+?.????V
????????
= 0 (2.2)
~?
L'équation (2.1) montre que lorsque le diamètre
D est très petit, le rapport A/V0 devient très grand, en
conséquence les forces de surface deviennent plus dominantes et donc les
conditions aux frontières peuvent s'écarter du comportement des
milieux continus et prendre différentes formes. Cela a des implications
importantes dans l'analyse des problèmes de micro-canaux.
2.2. Modélisation des liquides.
2.2.1. Equation de continuité [32].
Le principe de conservation de masse peut être
formulé comme suit : L'accumulation de la masse dans un volume
donné par unité de temps est égale à la
différence entre les masses qui entrent et celles qui sortent du volume
infini. Il est exprimé par l'équation de continuité comme
suit :
Page 12
Page 13
Généralités sur le Transfert de
Chaleur
2.2.2. Equation des quantités de mouvement.
Les équations de Navier-Stockes s'expriment par la
deuxième loi fondamentale de la dynamique.
????????~?
???? = ???????? ~?-?p~? +1 3 ????? (?????~?) +
?????2????~? (2.3)
????????
Où :
????= ???? ????
+ ????
???????? ???????? ????????
|
???? ????
+ ???? + ???? (2.4)
???????? ????????
|
|
Représente l'expression de la dérivée
particulaire.
2.2.3. Equation de l'énergie.
L'équation de l'énergie traduite par le premier
principe de la thermodynamique s'écrit comme suit :
????????
???????????? = ?. (?????????) + ????0 + ???????? (2.5)
????????
L'expression de la dissipation visqueuse en coordonnées
cartésiennes est la suivante :
????= 2???? ~(????????
???????? )2 + (????????????? ???)2 +
(???????? 2 (????????
???????? )2 + 2 1 (????????
???????? + ????????
????????)2 + 2 1 (????????
???????? + ????????????? ??? )2 + 1 ???????? + ????????
???????? )2~ +
2
???? ~????????
???????? + ????????????? ??? + ????????????? ??? ~ (2.6)
Dans le solide
On a la relation suivante :
????????
???????????? = ?. (?????????) + ????0 + ????????
(2.7)
????????
Page 14
Généralités sur le Transfert de
Chaleur
2.3. Conditions aux limites.
Dans le cas des liquides nous avons vu que leur
modélisation par le modèle continu nécessite les
conditions d'adhérence à la paroi, c'est-à-dire que la
vitesse du fluide la plus proche de la paroi va prendre la valeur de cette
dernière (paroi mobile, ou fixe).
Par contre pour la modélisation des gaz on introduit
des conditions aux limites de glissement pour la vitesse et de saut de
température à la paroi.
2.4. La dissipation visqueuse.
Les effets de la dissipation visqueuse sur les
écoulements avec transfert de chaleur à l'intérieur d'une
conduite sont souvent négligés. Cependant, lorsque le
diamètre hydraulique est très petit, la production de chaleur
interne en raison des forces visqueuses peut entraîner une hausse de
température même si les parois sont adiabatiques. La variation de
température en raison de la dissipation visqueuse change les valeurs des
propriétés thermo-physique du fluide entre l'admission et la
sortie et peuvent remarquablement influencer sur le transfert chaleur.
Nombre de Reynolds :
Le nombre de Reynolds est donné par la relation suivante
:
Re = u.Dh (2.8)
v
Nombre de Nusselt :
C'est un nombre adimensionnel qui mesure la valeur du taux de
transfert de chaleur d'une surface chauffante. Généralement, il
compare le transfert de chaleur seulement s'il la conduction doit apparaitre.
Il est donné par la relation suivante :
h .Z
Nu = (2.9)
????
Nombre de Prandtl :
C'est le rapport entre la diffusivité dynamique et la
diffusivité thermique, sa relation est donnée comme suit :
Pr = v (2.10)
a
Nombre de Grashof :
C'est le rapport de la force de Buoyancy à la force
visqueuse régissant sur un fluide :
Gr = 913 (Ts
-T8)Z3 (2.11)
v2
Page 15
Généralités sur le Transfert de
Chaleur
Nombre de Rayleigt :
C'est le produit du nombre de Grashof et le nombre de
Prandtl, il est un nombre adimensionnel associe avec la force de Buoyancy qui
dirige l'écoulement. Quand le nombre de Rayleigt est au dessous de la
valeur critique (Ra=10 3 ou Ra=105) ; le transfert de
chaleur est complètement par conduction, et s'il monte au dessus de
cette valeur critique ; alors, le transfert thermique est totalement sous forme
de convection.
Ra = Gr. Pr = ???????? (TS-T8).
Z3 (2.12)
????.????
Nombre de Richardson :
Ri = Gr/Re2 (2.12.a)
Chen [37] a montré que sous l'effet de la dissipation
visqueuse, le nombre de Nusselt local subit un saut à une certaine
position axiale puis se stabilise pour tendre vers sa valeur finale. Tunc et
Bayazitoglu [25] ont constaté que, lorsqu'une température
constante est imposée à la paroi et pour le cas où le
fluide est refroidi, le nombre de Nusselt en régime
développé augmente indépendamment des valeurs de Br et
reste supérieur au cas où Br = 0. Lorsque la chaleur est
uniformément fournie au fluide par les parois, une diminution du nombre
de Nusselt en régime établi a été constatée,
ce qui est en bon accord avec les résultats présentés par
Jeong et Jeong [26].
Morini [34] a montré que l'échauffement
dû à la dissipation visqueuse est inversement proportionnel au
diamètre hydraulique élevé à la puissance trois ;
par conséquent, il pourrait être très significatif dans les
micro-canaux. Il a proposé la condition suivante pour tenir compte des
effets de la dissipation visqueuse :
Br <
|
????lim dh
(2.13)
2A cfRe
|
|
lim Rapport maximal permit ente l'augmentation de la
température due à la dissipation visqueuse sur l'augmentation de
température due au flux de chaleur à la paroi
2.5. Conduction dans le solide.
Maranzana et al [38] ont analysé ce type de
problème à partir d'une étude numérique sur le
transfert de chaleur d'un écoulement entre deux plaques
parallèles. La géométrie utilisée dans leur
simulation est montrée dans la figure (2.2)
Page 16
Généralités sur le Transfert de Chaleur
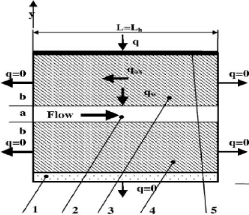
Fig. 2.2 : Ecoulement entre deux plaques
parallèles [38]
1 : couvercle ; 2 : micro-canal ; 3 et 4 : bloc en
silicone ; 5 : plaque chauffée.
2.6. Equations simplifiées.
Hypothèses.
· Ecoulement tridimensionnel.
· Fluide incompressible (????= constante et????? = 0)
· Fluide à propriétés physiques
constantes
· Ecoulement avec dissipation visqueuse.
En tenant compte des hypothèses citées ci-dessus,
les équations simplifiées s'écrivent comme suit :
2.6.1. Equation de continuité.
???????? + ???????? + ????????= 0 (2.14)
???????? ???????? ????????
2.6.2. Equations des quantités de Mouvement.
???? ~????????????? ??? + ???? ????????????? ??? + ????
????????????? ??? + ???? ????????????? ??? ~ = ????????
???????? + ????????? ??? ~???? ????????
???????? ~ + ???? ???????? ~???? ????????
????????~ + ???? ???????? ~???? ????????
???????? ~ (2.15)
Page 17
Généralités sur le Transfert de
Chaleur
???? ~????????
???????? + ???? ????????????? ??? + ???? ????????????? ??? +
???? ????????????? ???~ = - ????????
???????? + ????????? ??? ~???? ????????
????????~ + ???? ???????? ~???? ????????
????????~ + ???? ???????? ~???? ????????
????????~ (2.16)
???? ~????????????? ??? +???? ????????????? ??? +????
????????????? ??? +???? ????????????? ??? ~ = - ????????
???????? + ????????? ??? ~???? ????????????? ??? ~ +????
???????? ~???? ????????????? ??? ~ +???? ???????? ~???? ????????????? ??? ~
(2.17)
2.6.3. Equation d'énergie.
-dans le fluide :
2
???????????? ~???????? ???????? ???????? ????????
???????? + ???? ????????????? ??? + ???? ????????????? ??? +
???? ????????
????????~ = ????????? ??? ~???????? ????????~ + ???? ????????
~???????? ????????~ + ???? ???????? ~???????? ????????~ + 2???? ~~????????
????????~ +
2 2 2 2 2
~???????? + ~???????? + 2 1 ~????????
????????~ ???????? ~ ???????? + ???????? + 2 1 ~????????
2 ~????????
????????~ ???????? + ???????? + 1
????????~ ???????? + ????????
???????? ~ ~ (2.18)
-dans le solide :
????????????~???????? ???????? ???????? ????????
????????~ = ???? ???????? ~???????? ????????~ + ????????????
~???????? ????????~ + ???????????? ~???????? ????????~ (2.19)
2.7. Conditions aux limites.
La résolution de ces équations aux
dérivées partielles nécessite des conditions aux limites
(hydrodynamiques et thermiques) aux quatre frontières du domaine
d'étude.
2.7.1. Conditions aux limites hydrodynamiques.
A l'entrée du micro-canal z = 0
???? = ???????????? (2.20)
???? = ???? = 0 (2.21)
A la sortie du micro-canal z= 10000
???????? ???????? ????????
= = = 0 (2.22)
????????
???????? ????????
A la paroi supérieure y = 180
????= ????= ????= 0 (2.23)
Page 18
Généralités sur le Transfert de Chaleur
A la paroi inferieure y = -180
????= ????= ????= 0 (2.24)
A la
paroi latérale droite x = +28.5
????= ????= ????= 0 (2.25)
A la
paroi latérale gauche x = -28.5
????= ????= ????= 0 (2.26)
2.7.2. Conditions aux limites thermiques. A
l'entrée : z = 0
???? = ???????????? (2.27)
A la Sortie z = 10000 (Régime établi)
????????
???????? ~????=1???????????????? = 0 (2.28)
Pour les parois du puits de chaleur en silicium x=-50,
x=+50, y=+450, z=0, z=L
????????
???????? ~????????????????????
|
= 0 (Paroi thermiquement isolée) (2.29)
|
|
Et à la paroi inferieure du puits de chaleur
????????
-???? ???????? ~????=-450 = ????0
(Flux imposé) (2.30)
A l'interface fluide/solide
????????= ???????? (2.31)
Et :
???????? ~????????????
???????? ~???? = ???????? ~????????????
???????? ~???? (2.32)
Page 19
Généralités sur le Transfert de Chaleur
Conclusion.
Une étude générale sur les notions du
transfert de chaleur et les écoulements à l'échelle
microscopique est présentée dans ce chapitre, lorsque le fluide
de fonctionnement est à l'état liquide le régime est
continu, l'écoulement est modélisé par les
équations de Navier-Stokes associées aux conditions classiques de
continuité comme à l'échelle macroscopique.
De plus, de l'analyse bibliographique les grandeurs sans
dimensions fondamentales obtenues par l'analyse à la micro
échelles et ceux rapporter dans la littérature à la macro
échelles présentaient des déviations plus au moins
important. Les auteurs suggèrent dans plusieurs études de tenir
compte des effets qui étaient généralement
négligés à la macro échelle comme : la dissipation
visqueuse, la conduction axiale,... pour expliquer les écarts obtenus
entre les deux analyses. En plus de cela nous allons prendre en
considération l'effet de la dissipation visqueuse sur le nombre de
Nusselt.
Chapitre 03
Description de l'outil
informatique
Page 20
Description de l'Outil Informatique
3.1. Introduction.
La complexité de la résolution numérique
des problèmes de transfert de chaleur, et de l'écoulement de
fluide est reflétée par la complexité des équations
qui gouvernent les phénomènes physiques. C'est pourquoi, ces
équations doivent être discrétisées.
Il existe plusieurs méthodes de discrétisation
des équations différentielles aux dérivées
partielles telles que : la méthode des volumes finis, la méthode
des différences finies....
Dans la présente étude, on utilisera la
méthode des volumes finis qui consiste à diviser le domaine de
calcul en un nombre de volumes de contrôles entourant les noeuds du
maillage, les équations aux dérivées partielles sont alors
intégrées sur chaque volume de contrôle. Le résultat
de la discrétisation en un point est une équation
algébrique liant sa valeur de la variable ???? aux valeurs des variables
des points adjacents.
3.2. Les principales étapes pour définir
un problème de CFD.
Les étapes suivantes constituent la procédure
à suivre pour simuler les écoulements à l'aide du logiciel
FLUENT et de son mailleur GAMBIT
· Lancer gambit
· Définition du modèle (la
géométrie)
· Charger son fichier du maillage
· Vérifier son maillage
· Choix des conditions aux limites
· Exporter le fichier au FLUENT
· Lancer FLUENT
· Choix du modèle physique
· Contrôle de la convergence
· Afficher les résultats
3.3.Quelques instructions qui concernent GAMBIT.
On va présenter dans cette partie les principaux outils
existant dans GAMBIT.
Description de l'Outil Informatique
Fig. 3.1 : La fenêtre ci-dessus est une
présentation importante pour la définition d'un
problème
3.4. Le préprocesseur GAMBIT.
GAMBIT permet à l'utilisateur de réaliser ou
d'importer une géométrie, de générer des maillages
plus ou moins complexes selon la géométrie adoptée. Le
préprocesseur permet aussi de définir les conditions aux limites
appropriées aux frontières du domaine de calcul. Afin
d'intégrer le domaine fluide dans le micro-canal.
GAMBIT peut utiliser différents types de maillages,
à savoir : des maillages structurés, non structurés et
hybrides (combinaison géométrique d'éléments de
différentes natures). Un maillage structuré est
généralement composé de cellules quadrilatérales en
deux dimensions (2D ou maillage surfacique) et hexaédriques en trois
dimensions (3D ou maillage volumique), tandis qu'un maillage
non-structuré peut être composé de mailles
quadrilatérales ou triangulaires en 2D et hexaédriques ou
tétraédriques en 3D.
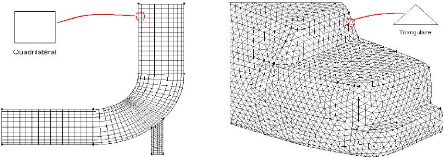
Page 21
(a) (b)
Fig.3.2 : Représentation graphique d'un
maillage structuré (a) et non structuré
(b)
généré par Gambit en 2D [29]
Description de l'Outil Informatique
Cette fenètre illustre quelques operations fait par
GAMBIT
Symbole indique
la création
d'une
géométrie
Symbole indique la
création d'un
maillage
Symbole implique
la détermination
des
conditions
aux limites
Symbole désigné
pour
des
opérations
spécialisées
Page 22
Fig. 3.3 : Opérations fondamentales en
GAMBIT
Cette fenêtre constitue la barre essentielle dans GAMBIT
pour La création des géométries
Fig. 3.4 : Elaboration des vortex
Description de l'Outil Informatique
En cliquant sur la touche cube foncé, elle va
paraître la barre suivante :
La création d'une face
La création d'un point
La création d'une ligne
Page 23
Fig. 3.5 : Création de la
géométrie
Quelque option jointive pour définir la
géométrie
GLOBAL CONTROLE contient 15 boutons de
commande actifs. L'ensemble supérieur de cinq boutons de commande permet
d'activer et neutraliser différents quarts de cercle de fenêtre de
graphique. L'ensemble inferieur de boutons de commande permet de
contrôler l'apparence du graphique.
Page 24
Description de l'Outil Informatique
Quelques commandes de fichier
Le menu de commande des fichiers de GAMBIT
inclut les commandes suivantes : En cliquent sur FILE
:
(Nouveau)Ouvrir une nouvelle session
sessions
|
|
(Ouvrir) ouvrir une session précédemment
sauvegardée
|
|
(Enregistrement) enregistré la session
courante
(Enregistrement comme) enregistré la session
courante sous un nouveau nom
|
|
(Importation) des géométries et des
données des mailles
(Exportation) des géométries et des
données des mailles
Fig. 3.6 : Commandes de fichier en FLUENT
3.5. Maillage.
Dans un maillage hybride, les mailles proches des parois sont
des quadrilatères en 2D et des hexaèdres en 3D. Les mailles du
reste du domaine sont des triangles en 2D et des tétraèdres en
3D. Les cellules qui font les liaisons entre les hexaèdres et les
tétraèdres sont des prismes ou des pyramides.
Afin d'optimiser le nombre de cellules, la qualité du
maillage et le temps de calcul. Cette opération permet de réduire
les erreurs d'approximations engendrées par la discrétisation des
équations de transport.
Il existe deux méthodes possibles pour réaliser le
maillage sur GAMBIT: ? Soit avoir un volume et le mailler
régulièrement sans avoir maillé les arêtes,
? Soit mailler partie par partie, c'est-à-dire
utiliser le maillage défini sur les lignes pour mailler les surfaces et
par la suite les volumes.
C'est le premier type de maillage que nous avons choisi.
Page 25
Description de l'Outil Informatique
3.5.1. Qualité du maillage.
Avant d'entreprendre la simulation numérique de
l'écoulement, il est nécessaire de vérifier les
étapes suivantes :
- Assurer une bonne résolution dans les régions
à fort gradient - Maintenir une bonne qualité des
éléments
- Minimiser le nombre total des éléments
(temps de calcul) 3.5.2. Conditions aux limites.
Une fois que la géométrie et le maillage du
domaine physique étudié sont définis, nous
spécifierons les zones géométriques sur lesquelles nous
allons appliquer les conditions aux limites.
Le logiciel GAMBIT propose différents types de
conditions aux limites. Nous aurons quatre : vitesse, conditions de parois,
condition à la sortie et conditions de symétrie.
3.6. Présentation du logiciel Fluent.
Le calcul numérique a été
effectué à l'aide du code "Fluent" 6.3.26. Le logiciel Fluent est
un code CFD (anonyme de : Computational Fluid Dynamics) qui permet la
prédiction des écoulements fluides par résolution des
équations de bilan en se basant sur la méthode des volumes finis
et des schémas de discrétisation existant dans sa banque de
données.
Fluent permet de simuler tous les écoulements fluides,
incompressibles ou compressibles, impliquant des phénomènes
physiques complexes tels que les écoulements multiphasiques, la
turbulence, le transfert thermique, les réactions chimiques... etc.
3.6.1. Méthode des volumes finis.
La méthode des volumes finis utilise des
approximations d'intégrales. Toutefois, elle consiste à
discrétiser le domaine de l'écoulement en une multitude de
volumes de contrôle (hexaèdres, tétraèdres, prismes
...) qu'on appelle aussi cellules ou mailles.
Ensuite, cette méthode permet d'effectuer des bilans
de masse, de quantité de mouvement et d'énergie sur tous les
volumes ainsi que dans tout le domaine de calcul. Son avantage est qu'elle est
conservative : tout ce qui sort d'un volume de contrôle entre dans le
volume voisin [33].
En Fluent, toutes les variables sont stockées au
centre des cellules. Ce procédé est appelé
"collocalisé".
Page 26
Description de l'Outil Informatique
La méthode des volumes finis, applicable à
toutes les géométries (simples ou complexes), aussi facilite la
linéarisation des termes dans les équations de conservation. Pour
cela, il faut suivre des étapes primordiales pour la
détermination du champ des variables dépendantes4), à
savoir :
· Définition du domaine d'étude et maillage
des volumes correspondants,
· Intégration des équations de conservation
sur chaque volume de contrôle,
· Discrétisation des différents termes de
l'équation de transport,
· Affectation des conditions aux limites,
· Linéarisation des équations
discrétisées,
· Résolution du système final par l'une
des méthodes de résolution itérative comme la
méthode itérative de Gauss-Seidel, semi itérative ou
directe.
· Présentation du champ approché de 4) dans
les points discrets du domaine étudié. 3.6.2.
Schémas de discrétisation.
Les termes des équations de transport de la variable
4) sont discrétisés de manières différentes. Pour
les termes convectifs, Fluent propose plusieurs schémas de
discrétisation, parmi lesquels nous citons :
· Le schéma amont du premier ordre : ce
schéma permet une certaine stabilité dans les calculs. La valeur
stockée au centre d'une cellule est égale à la moyenne de
toutes les valeurs de la même cellule. Les valeurs aux niveaux des faces
sont égales à celles des cellules se trouvant en amont. Il est
à noter qu'un raffinement du maillage est nécessaire pour pouvoir
utiliser ce schéma.
· Le schéma amont du second ordre : l'utilisation
de cette méthode permet de minimiser la diffusion numérique. Le
développement des calculs des valeurs aux centres des cellules est
effectué en série de Taylor afin de calculer les valeurs aux
faces. La valeur approchée d'une variable au niveau de la face
dépend dans ce cas de la valeur au sein du volume des deux autres
cellules en amont.
· Le schéma QUICK est un schéma d'ordre
supérieur disponible dans Fluent. Il prend en compte le flux aux
interfaces. Ce schéma est plus précis dans le cas d'un maillage
structuré aligné avec le sens de l'écoulement.
Néanmoins, il peut être utilisé avec des maillages bien
raffinés, non structurés ou hybrides, dans les zones à
forts gradients.
Page 27
Description de l'Outil Informatique
3.6.3. Choix du solveur.
Deux types de solveurs existent dans Fluent :
? Le solveur découplé (Segregated) est le plus
approprié pour les écoulements incompressibles, il résout
les équations de continuité, de quantité de mouvement et
de l'énergie séparément.
? Le solveur couplé implicite ou explicite
est plutôt réservé aux écoulements compressibles
à grande vitesse ce qui lui donne un avantage pour le traitement des
écoulements à forte interdépendance entre la pression, la
densité et la température. Le solveur couplé permet la
résolution simultanée des équations gouvernantes. Dans le
cas des écoulements in-stationnaires, il est judicieux d'utiliser le
solveur implicite.
Le choix de l'un des solveurs est basé sur la nature
du problème étudié. La différence entre les deux
réside dans la manière de résoudre les équations
régissant l'écoulement.
Nous avons choisi le solveur découplé pour la
simulation numérique pour notre domaine physique que nous allons
étudier (fig. 3.7).
3.6.4. Spécification du fluide et des
matériaux utilisés.
Dans le module " Define " de Fluent, on peut choisir le type
du fluide (gaz ou liquide), les conditions d'opération (effet de la
gravité et de la pression), les conditions aux limites...etc.
· Les matériaux et le fluide utilisés pour
notre étude sont choisis à partir de la banque de données
dans Fluent.
· Le fluide de fonctionnement à
l'intérieure du domaine d'étude c'est de l'eau, nous avons
précisé sa masse volumique et sa viscosité
cinématique à une température de 293 °C.
· Le matériau utilisé pour le micro-canal
et le puits thermique est le silicium, nous avons ajouté ce
matériau et ses propriétés physiques dans la base de
données de Fluent.
Les propriétés thermo-physiques et
mécaniques du silicium et du quartz :
Le quartz et le silicium sont supposés
élastiques isotropes (compte tenu de la rareté des données
relatives à l'anisotropie du silicium, en particulier dans un
environnement cryogénique). Les propriétés correspondantes
sont énumérées dans le tableau 1 pour les
températures 293K et 473K.
Page 28
Description de l'Outil Informatique
|
Température (k)
|
Coefficient de dilatation thermique (k -1)
|
Conductivité thermique (W/m.k)
|
Module d'Young (GPa)
|
Chaleur spécifique
(J.Kg -1.K - 1
)
|
Coefficient de poisson
|
|
Quartz
|
293
|
4.6 E - 007
|
1.4
|
72.6
|
698.6
|
0.16899
|
|
473
|
6.3 E -007
|
1.6
|
74.8
|
939.6
|
0.17601
|
|
Silicium
|
293
|
2.6 E -6
|
154.8
|
163
|
704.4
|
0.2204
|
|
473
|
3.6 E -6
|
81.5
|
161
|
825.4
|
0.21994
|
Tab. 3.1 : propriétés du silicium et du
quartz
3.7. Domaine d'étude.
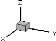
Fig. 3.7 : Domaine d'étude.
La figure (3.7) montre le schéma d'un micro-canal
usiné dans un puits de chaleur en silicium.
Page 29
Description de l'Outil Informatique
3.7.1. Maillage du domaine d'étude.
Le choix du maillage est une étape cruciale de la
simulation numérique. Il est donc important de bien choisir un maillage
s'adaptant au mieux aux problèmes considérés.
Le domaine d'étude est divisé en un certain
nombre de volumes de contrôle de telle façon qu'il soit
entièrement recouvert par eux (Figure 3.8.a, 3.8.b, et 3.8.c). Chaque
volume de contrôle de dimension ÄX.ÄY.ÄZ, doit conserver
la grandeur scalaire T dans le noeud du maillage (P) qui se situe au centre du
volume de contrôle et les grandeurs vectorielles U ,V, et W au milieu des
segments reliant les deux noeuds adjacents. Ces quatre faces sont
repérées à l'aide des quatre points, cardinaux e, w, n, s
et les centres des volumes adjacents par E,W, N, S.
Cette configuration a été maillée avec
GAMBIT utilisant (20x150x20 volumes de contrôle).
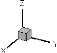
Fig. 3.8.a : Maillage des parois droite et gauche du
puits thermique (NYxNZ=150x20)
Page 30
Description de l'Outil Informatique
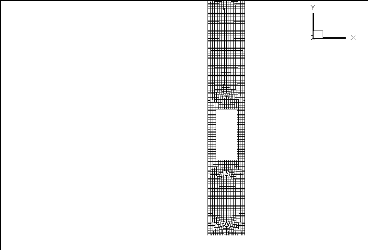
Fig. 3.8.b : Maillage de la paroi d'entrée du
puits thermique (NYxNX=150x20)
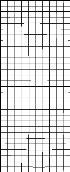
Fig. 3.8.c : Maillage des sections d'entrée et
sortie du micro-canal (NYxNX=30x20)
Page 31
Description de l'Outil Informatique
3.8. Critère de convergence.
Le critère de convergence utilisé dans le code
de calcul est basé sur le résidu Ro donné pour
tout le domaine d'étude comme suit
Emailles~Enb anb
????nb + S0 - ap????p ~
???????? = < 10-6
quantité de
mouvement ou débit à l'entréedu domaine de
calcul
A chaque itération, Fluent permet de juger de
l'état de la convergence par le biais du calcul des résidus
Ro pour chaque variable (pression, composantes de vitesse...etc.).
Conclusion.
Dans ce chapitre, le but était de présenter la
formulation du problème en commençant par détailler les
méthodes utilisées dans la création et la
génération du maillage du domaine physique. Par la suite, nous
avons présenté le logiciel Fluent. Enfin, nous avons
établi le domaine physique propre à notre cas d'étude.
Chapitre 04
Résultats et discussions
Page 32
Résultats et Discussions
4.1. Introduction.
L'objectif de ce travail est d'étudier le transfert de
chaleur conjugué convection-conduction dans les micro-canaux avec
l'effet de la dissipation visqueuse. Le but est d'appréhender
l'évolution du coefficient de transfert de chaleur à
l'échelle microscopique où ces effets ne peuvent plus être
négligés, comme c'est souvent le cas à l'échelle
macroscopique.
4.2. Résultats.
1ier cas : Un seul canal
Avant de réaliser les simulations numériques,
nous avons crée le modèle géométrique à
l'aide du logiciel GAMBIT. Nous avons aussi choisi une modélisation en
3D dans le but d'étudier le transfert de chaleur conjugué dans un
micro-canal où il circule l'eau comme fluide de travail en régime
laminaire, lequel est implanté dans un puits de chaleur situé au
dessus d'un composant électronique pour le refroidir.
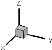
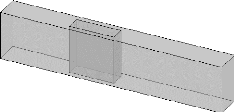
Fig. 4.1 : Diagramme schématique d'un seul
micro-canal par GAMBIT
Page 33
Résultats et Discussions
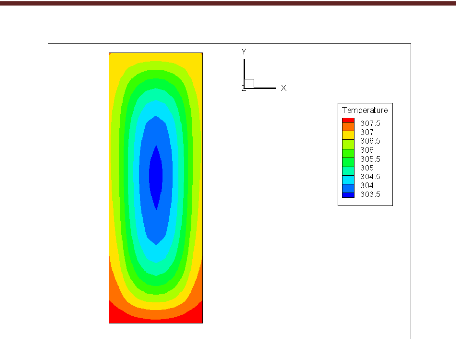
Fig. 4.2 : Température à la sortie (q=50
W/cm2, Re=84)
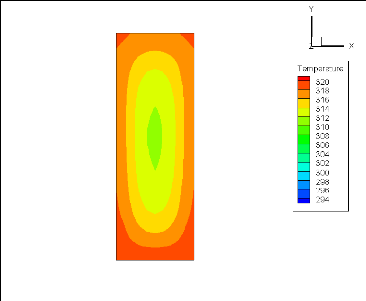
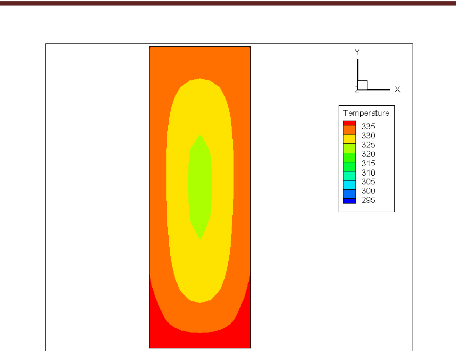
Fig. 4.3 : Température à la sortie (q=90
W/cm2, Re=84)
Page 34
Résultats et Discussions
Fig. 4.4 : Température à la sortie (q=150
W/cm2, Re=84)
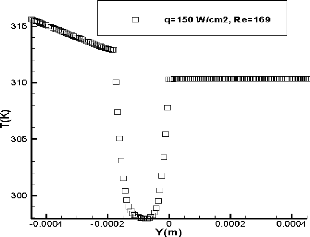
Fig. 4.5 : Profil de température au milieu de la
configuration (canal + puits de chaleur)
Page 35
Résultats et Discussions
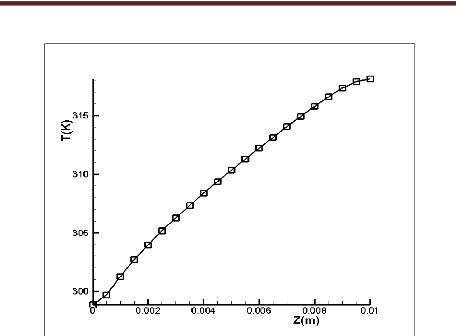
Fig. 4.6 : Variation de la température du fluide
le long de l'axe du micro-canal pour
(q=150 W/cm2,
Re=169)
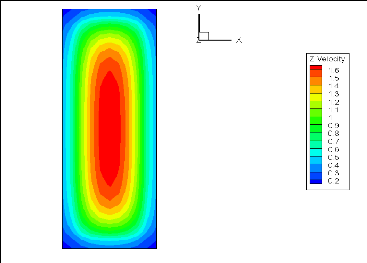
Fig. 4.7 : Vitesse à la sortie (q=50
W/cm2, Re=84)
Page 36
Résultats et Discussions
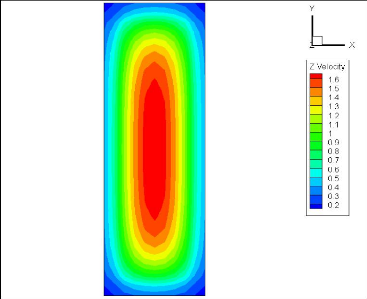
Fig. 4.8 : Vitesse à la sortie (q=150
W/cm2, Re=84)
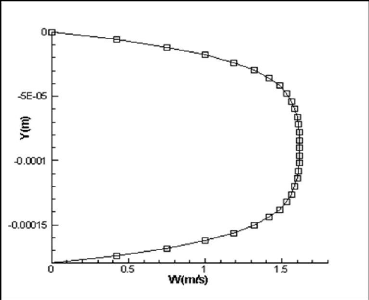
Fig. 4.9 : Profil de vitesse à la sortie du
canal, (q=50W/cm2, Re=84)
Page 37
Résultats et Discussions
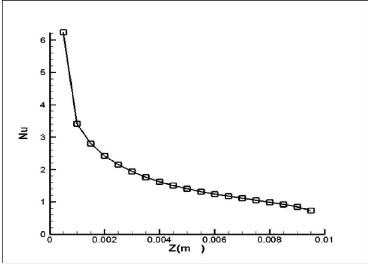
Fig. 4.10 : Variation du nombre de Nusselt en fonction
de Z (q=50 W/cm2, Re=84)
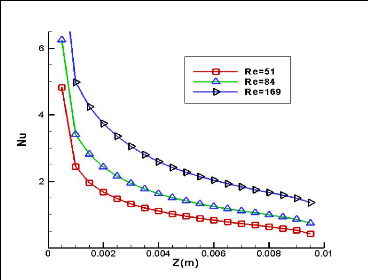
Fig. 4.11 : Nombre de Nusselt en fonction du Nombre de
Reynolds (q=150 W/cm2)
Page 38
Résultats et Discussions
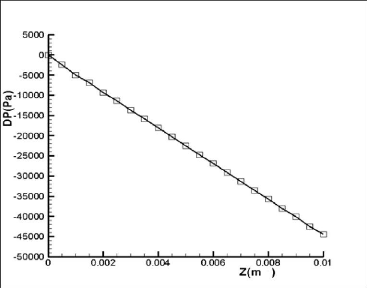
Fig. 4.12 : Perte de pression en fonction de la
distance de l'entrée du canal
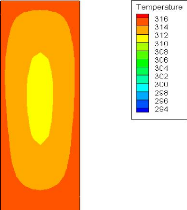
Fig. 4.13 : Température à la sortie (q=50
W/cm2, Re=51)
Page 39
Résultats et Discussions
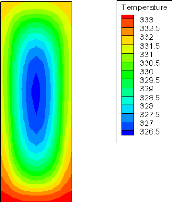
Fig. 4.14 : Température à la sortie (q=90
W/cm2, Re=51)
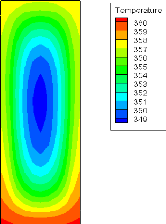
Fig. 4.15 : Température à la sortie
(q=150 W/cm2, Re=51)
Page 40
Résultats et Discussions
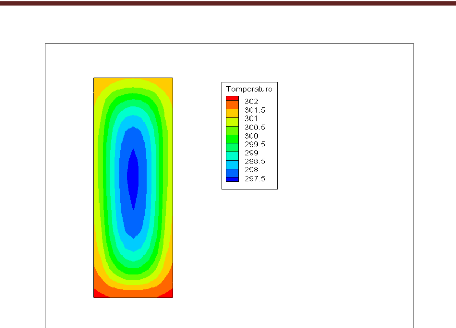
Fig. 4.16 : Température à la sortie (q=50
W/cm2, Re=169)
2me cas : Double canal
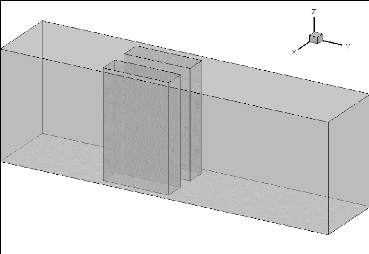
Fig. 4.17 : Diagramme schématique de deux
micro-canaux par GAMBIT
Page 41
Résultats et Discussions
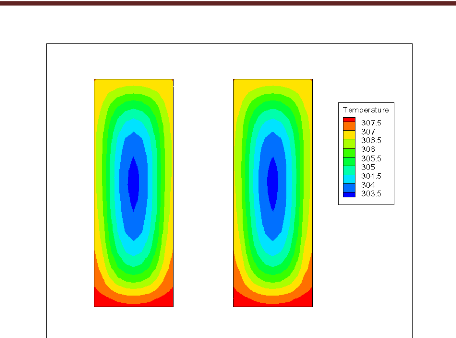
Fig. 4.18 : Les isothermes obtenus avec une configuration
à deux micro-canaux (q=50
/cm2, Re=84)
4.3. Discussions.
Maillage.
Les figures (4.1 et 4.17) montrent les diagrammes
schématiques d'un seul canal et le cas d'un double canal respectivement
par GAMBIT. La modélisation a été faite selon les
dimensions données, le maillage illustre le flux massique entrant,
sortant, en plus la conduction dans les parois du puits de chaleur et les
micro-canaux.
Isothermes pour un nombre de Reynolds de 84 :
Les figures (4.2, 4.3, et 4.4) montrent les isothermes
à la sortie du micro-canal correspondantes à des flux thermiques
de 50, 90 et 150 W/cm2 et un nombre de Reynolds constant égal
à 84. Lorsque le flux thermique augmente la température de sortie
de l'eau augmente parce que le fluide reçoit une quantité assez
grande de chaleur à travers les parois du micro-canal. La chaleur passe
par conduction à travers les parois en silicium du « puits
thermique » puis elle passe au fluide par convection mixte.
Page 42
Résultats et Discussions
Isothermes pour un flux thermique de 50
W/cm2 :
La variation de la température en fonction du nombre de
Reynolds pour un flux thermique donné est montrée dans les
figures (4.2) et (4.13) pour Re=84 et 51 respectivement. On peut remarquer que
l'augmentation du nombre de Reynolds entraine un mauvais refroidissement, car
la chaleur générée par frottement augmente avec Re.
Distribution de température dans la section
médiane (Z=0.005 m) :
La figure (4.5) montre une température maximale au
niveau de la paroi inférieure du puits thermique, paroi à travers
laquelle la chaleur rentre. Il y a une variation linéaire de la
température au sein du puits thermique. Dans le fluide, le profil de
température est parabolique, mais la température à la
paroi inférieure du canal est supérieure à celle à
la paroi supérieure. Dans la partie supérieure du puits
thermique, la température est presque constante.
Variation de la température du fluide le long
du plan de symétrie du micro-canal :
La Figure (4.6) montre la distribution de la
température le long du plan de symétrie du micro-canal. On peut
constater facilement d'après cette figure l'échauffement
progressif du fluide quand il avance dans le micro-canal. La température
s'élève de 293 K à l'entrée jusqu'à 317 K
environ quand le fluide quitte le micro-canal.
Iso-vitesses :
Pour le même nombre de Reynolds à
l'entrée, les figures (4.7 et 4.8) montrent les lignes d'égale
vitesse à la sortie du micro-canal. La distribution des vitesses n'est
pas affectée d'une manière significative par le transfert
thermique puisque le fluide est incompressible.
Distribution de la vitesse au plan médian (x=0)
la section de sortie :
On voit d'après la figure (4.9) que le profil de
vitesse est presque parabolique, c'est-à-dire on n'arrive pas au
régime pleinement développé et on a besoin d'une longueur
largement suffisante pour atteindre ce régime à la sortie du
micro-canal (18000 à 20000um environ).
Nombre de Nusselt (q=50 W/cm2, Re=84) :
La figure (4.10) montre une diminution du nombre de Nusselt
local en fonction de la distance Z(m).
Nombre de Nusselt en fonction de Re :
Plus que Re augmente, plus le Nusselt local,
c'est-à-dire une meilleure prise de la chaleur par le fluide. Ceci peut
être observé dans la figure (4.11).
Page 43
Résultats et Discussions
La chute de pression du fluide tout le long du
micro-canal :
La perte de pression en fonction de la distance de
l'entrée du micro-canal est linéaire comme il est montré
dans la figure (4.12). Ceci est en bon accord avec les résultats obtenus
des formules classiques de ?P.
Refroidissement avec deux micro-canaux :
La figure (4.18) montre les isothermes obtenues avec une
configuration à deux micro-canaux avec (q=50 W/cm2, Re=84).
En comparant les résultats avec ceux correspondant à un seul
canal (la figure 4.16) mais avec (Re=169). On peut conclure que le
refroidissement est meilleur avec deux micro-canaux car le fluide sort à
une température supérieure à celle dans le cas d'un seul
micro-canal.
Conclusion.
Dans ce chapitre, nous avons présenté les
résultats associés avec des discussions concernant la simulation
numérique du transfert thermique conjugué d'un écoulement
monophasique, tridimensionnel, et laminaire dans un micro-canal.
Chapitre 05
Conclusion générale et
recommandations
Page 44
Conclusion générale et
recommandations
Conclusion générale et recommandations :
Le travail rapporté dans ce mémoire a
été consacré à l'étude du refroidissement
d'un microprocesseur à l'aide d'un fluide caloporteur s'écoulant
dans un micro-canal.
Une analyse bibliographique a permis d'établir un bilan
des résultats numériques concernant les problèmes
liés à la surchauffe de certains composants de puissance et nous
a aidés à répertorier les différentes
méthodes de refroidissement de tels composants ainsi que leurs limites
d'utilisation.
Ce travail a permis de mieux cerner les aptitudes de l'outil
numérique à reproduire les phénomènes physiques
intervenant (zones où le transfert de chaleur est très
important).
Le deuxième volet de cette étude
numérique a été consacré à la
détermination de la variation du nombre de Nusselt en fonction du nombre
de Reynolds dans le but de caractériser le transfert thermique
conjugué.
L'analyse effectuée fournit une compréhension
fondamentale de la combinaison de l'écoulement et du transfert thermique
conjugué convection-conduction dans un puits thermique à
micro-canal tridimensionnel. La formulation du modèle est
générale et seulement quelques hypothèses simplificatrices
ont été faites. Donc les résultats de l'analyse sont assez
généraux et applicables à tous les problèmes
tridimensionnels de transfert de chaleur conjugués.
Un modèle mathématique tridimensionnel,
développé en utilisant les équations de quantité de
mouvement de Navier-Stokes incompressibles et laminaires, est capable de
prédire correctement l'écoulement et le transfert de chaleur
conjugué dans le puits thermique à micro-canaux. Les
résultats des pertes de charge sont en bon accord avec les formules
classiques obtenues expérimentalement, ce qui a permis de valider ce
modèle.
Le transfert thermique combiné convection-conduction
dans le micro-canal apparait bien en utilisant des profils de
températures traversant en même temps le solide et le fluide. On
constate alors que la chaleur est distribuée par conduction dans le
solide avant d'atteindre le fluide par convection.
L'examen des nombres de Nusselt montre que le fluide
reçoit ou apporte la plus grande partie de sa chaleur dans la
région d'entrée du micro-canal et plus que le fluide avance
Page 45
Conclusion générale et
recommandations
dans le micro-canal, plus il s'échauffe, donc la
différence entre sa température et celle des parois du
micro-canal diminue.
Plusieurs travaux futurs, concernant la simulation
numérique des écoulements tridimensionnels dans des micro-canaux,
sont à envisager en perspectives de ce mémoire.
Comme perspective immédiate, Il est à envisager de
poursuivre la simulation en faisant une étude qui prend en
considération les autres phénomènes intervenant comme le
changement de phase à l'intérieur des micro-canaux.
Bibliographie
Page 46
Références
Références:
[1] S. Kakaç, H. Yurucu, and K.A. Hijikata, Cooling of
Electronic Systems, Kluwer Academic Publishers, Massachusetts, 1994.
[2] M.M. Mohammed, Air cooling characteristics of uniform
square modules array for electronic device heat sink, J. App. Thermal
Engineering, 26, pages: 486-493, 2006.
[3] A.A. Berlin, K.J. Gabriel, Distributed MEMS: New
Challenges for Computations, IEEE Computationnal Sciences & Engineering,
pages :12-16, 1997.
[4] G. Poulin, E. Sarraute, F. Costa, Generation of
electrical energy for portable devices: Comparative study of an electromagnetic
and a piezoelectric system, Sensors and Actuators A: Physical, Volume 116, 3,
29, pages 461-471, 2004.
[5] L. Cao, S. Mantell, D. Polla, Design and simulation of an
implantable medical drug
delivery system using microelectromechanical
systems technology, Sensors and
Actuators A: Physical, Volume 94, 1-2, pages: 117-125, 31,
2001.
[6] Distributed Micro-Electro-Mechanical Systems Processing
Environment,
http://www.darpa.mil/mto/mems/summaries/Projects/The_13.html.
[7] J. Hill, R. Szewczyk, et al, System Architecture
Directions for Networked Sensors, ACM 9th Int. Conf on Architectural Support
for Programming Language, ACM
Sigplan Notices, vol 35, pages : 93-105, 2000.
[8] M. Rebay, S. Kakaç , R. Ben Maad , J. Padet,
Experimental Evaluation of the Heat Transfer Coefficient in Electronic
Air-Cooling, Int. Journal of Transport
Phenomena, Vol. 11, pages :185-196, 2009.
[9] J. Donald et M. Martonosi. Temperature-aware design
issues for SMT and CPM architectures.
[10] M. K.Subha, R. M. John, Optimization of Elliptical Fin
Heat sink Design in Forced Convection: Single and Multiple Heat Sink,
Interpack, pages : 350-369, 2003.
[11] T. Icoz and Y. Jaluria, Numerical simulation of boundary
conditions and the onset of instability in natural convection due to protruding
thermal sources in an open rectangular channel, Numerical Heat Transfer, Part A
48, pages: 831-847, 2005.
[12] W. Aung, Heat transfer in a electronic systems with
emphasis on asymmetric heating, Bell Syst. Tech. J. 52, pages: 907-925,
1973.
[13] J.R. Bodoia, J.F. Osterle, The development of free
convection between heated vertical plates, J. Heat Transfer 84, pages: 40-44,
1962.
[14] H.H. Chu, W.S.Churchill, The development and testing of
a numerical method for computation of laminar natural convection in enclosures,
Comuters and Chimical Eng., Vol.1, pages: 101-102, 1977.
Page 47
Références
[15] G. Desrayaud, A. Fichera and G. Lauriat, Natural convection
air-cooling of a substrate-mounted protruding heat source in a stack of
parallel boards, Int. J. Heat and Fluid Flow, Vol.28., pages: 469-482, 2007.
[16] T. Icoz and Y. Jaluria, Design of cooling system for
electronic equipment using both experimental and numerical inputs, Journal of
Electronic Packaging 126, pages: 465-470, 2004.
[17] D. B. Tuckerman and R. F. W. Pease, High-performance heat
sinking for VLSI, IEEE Electron Device Letters, vol. EDL- 2, pages: 126-129,
1981.
[18] M. Richter, R. Linnemann and P. Wolas, Robust design of gas
and liquid micropumps, Sensors and Actuators A, vol. 68, pages: 480-486,
1998.
[19] T. Fujiwara, O. Kitoh et T. Tsuda, Original Effect of
applied parallel Electric Field on Electroosmotic Flow in donut channel,
Chromatography, Vol.23, pages: 25-31, 2002.
[20] M. Stehr, S. Messner, H. Sandmaier and R. Zengerlle, The
VAMP - a new device for handling liquid or gases, Sensors and Actuators A, vol.
57, pages: 153-157, 1996.
[21] G. M. Mala and D. Li, Flow characteristics of water in
micro-tubes, International Journal of Heat and Fluid Flow, vol. 20, pages:
142-148, 1999.
[22] Q. Weilin, G. M. Mala and L. Dongqing, Pressure-driven
water flows in trapezoidal silicon micro-channels, International Journal of
Heat and Mass Transfer, vol. 43, pages: 353364, 2000.
[23] H. Y. Wu et P. Cheng, Friction factors in smooth
trapezoidal silicon micro-channels with different aspect ratios, Int. J. Heat
and Mass Transfer 46, pages: 2519- 2525, 2003.
[24] Morini G.L., Laminar liquid flow through silicon
microchannels, Journal of fluids engineering, Vol. 126, pages 485-489, 2004.
[25] Tunc, G. and Bayazitoglu, Y., Heat transfer in microtubes
with viscous dissipation, International Journal of Heat and Mass Transfer,
Vol. 4, pp 2395- 2403, 2001.
[26] Jeong, H.-E., Jeong, J.-T., Extended Graetz problem
including streamwise conduction and viscous dissipation in microchannel,
International Journal of Heat and Mass Transfer, Vol. 49, pp
2151-2157, 2006.
[27] W. Qu, I. Mudawar, Analysis of three-dimensional heat
transfer in micro-channel heat sinks, International Journal of Heat and Mass
Transfer, Vol. 45, pages 3973-3985, 2002.
[28] I. Md. Didarul, O. Kenyu, Y. Minoru, S. Izuru, Study on
heat transfer and fluid flow
characteristics with short rectangular plate fin of different
pattern, Experimental Thermal
and Fluid Science, Volume 31, pages 367-379 ,
2007.
[29] Fluent User's Guide, Release 6.1. Fluent Inc, 2003.
Page 48
Références
[30] Gambit 2.2.30 User's Guide (2006).
[31] Bessaih, R., Effet thermique d'un craque
mécanique dans un micro processeur, Thèse de Magister
Université Mentouri Constantine Algérie, 1994.
[32] Kabar, Y., Kadja, M., Rebay, M., Padet, C., Numerical
Resolution of
Conjugate Heat Transfer Problem in a Parallel-Plate
Micro-Channel, Heat Transfer Research, Vol. 41, No. 3, pp 247-263,
2010.
[33] Li, J., Peterson, G. P., Cheng, P., Three-dimensional
analysis of heat transfer in a micro-heat sink with single phase flow,
International Journal of Heat and Mass Transfer, Vol. 47, pp
4215-4231, 2004.
[34] Morini G.L., Scaling effects for liquid flows in
microchannels, Heat Transfer Eng, Vol. 27, No. 4, pp 64-73, 2006.
[35] Gad-el-Hak, M., MEMS introduction and
fundamentals, Taylor & Francis Group, 2002.
[36] Koo, J. and Kleinstreuer, C., Viscous
dissipation effects in microtubes and
microchannels, International
Journal of Heat and Mass Transfer, Vol. 47, pp
31593169, 2004.
[37] Chen C.-H., Slip-flow heat transfer in a microchannel
with viscous dissipation, Heat Mass Transfer , Vol. 42 , pp 853-860,
2006.
[38] Maranzana, G., Perry, I., Maillet, D.,
Mini- and micro-channels: influence of axial conduction in the walls,
International Journal of Heat and Mass Transfer, Vol. 47,
pp 39934004, 2004.
Annexes
Page 49
Annexes
Annexe 01 : calcul du nombre de
Richardson (Ri)
????????
On a : ???????? = ????????2
Avec :???????? = ????????
(?????)????2????3
????2
????????h
Et :???????? = ???? , pour (51, 84, et 169)
|
Sachant que :???? = 0,18
|
* 10-3 [1/????]
|
|
???? =
|
1,379
|
10-3
[???????? .
*
|
????-1]
|
|
|
=
|
????????
838,4
|
[????????/????3 ]
|
|
????
????= 9,81 [????2]
?????= 7 [???? ]
???? = 10000 [????????] = 0,01[????] Donc ; on trouve que :
???????? = 1,76 >> 1
On constate que la convection naturelle est dominante par
rapport à la convection forcée, parce que la différence de
température entre fluide et paroi est significative.



