|
EBS BUSINESS SCHOOL
EBS UNIVERSITÄT FÜR WIRTSCHAFT UND RECHT
Thesis
Spring Term 2020
to obtain the academic degree
Master of Science
Strategic Behavior in Sport Contests: Application to
Middle-Distance Races From the 2010-2019 Decade
Name: Nicolas Herbin
Addresse: 42, rue des Ardoisières
50000 Saint-Lô France
Submitted to: Dr Elena Jarocinska
Submission Date: April
21st 2020
Strategic Behavior in Sport Contests i
Table of Content
List of Abbreviations iii
List of Figures iv
List of Tables v
1 Introduction 1
1.1 Problem Definition and Objectives 1
1.2 Course of the Investigation 4
2 Theoretical Background 6
2.1 Why sport is a good field to study economics? 6
2.1.1 Tournament Theory 6
2.1.2 Equilibria in Mixed Strategies 8
2.1.3 Contract Theory 13
2.1.4 Behavioral economics 13
2.1.4.1 Social pressure and favouritism 14
2.1.4.2 The role of emotions 14
2.2 Theory of Contests 17
2.2.1 Contests Modelling Framework 17
2.2.1.1 All-pay Auctions 18
2.2.1.2 Rank-Order Tournaments With Additive Noise 18
2.2.1.3 Contests With Ratio-Form Success Function 19
2.2.2 Contests Models in Various Framework 20
2.2.2.1 Sequential Moves in Contests 20
2.2.2.2 Contests With Budget Constraints 21
2.2.2.3 Contests With Non-Risk-Neutral Players 21
2.2.2.4 Asymmetric Contests 22
2.3 Strategic Behavior in Contests 23
2.3.1 Theoretical Background 23
2.3.2 Empirical Studies 27
2.3.3 Application to the Field Events of 1992 Olympic Games 29
2.3.3.1 Context and Presentation of the Experiment 29
Strategic Behavior in Sport Contests ii
2.3.3.2 Empirical Model 30
2.3.3.3 Results... 31
2.3.3.4 Observations on this Experiment 34
3 Methodology 36
3.1 Delimitation of the Frame of the Study 37
3.2 Underdog-Favorite Variable Implementation 40
3.3 Empirical Model 45
4 Results 47
4.1 Validation of the Favorite Index 47
4.2 800m Races Results 48
4.3 1500m Races Results 50
4.4 5000m Races Results 51
4.5 Aggregated Results 52
4.6 Analysis of Strategic Behavior in Middle-Distance Races 53
4.6.1 Impact of Gender on Strategic Behavior in Contests 54
4.6.2 Impact of Gender on Strategic Behavior in Contests 54
4.6.3 Impact of Gender on Strategic Behavior in Contests 56
5 Discussion 57
5.1 General Implications for Management 57
5.2 What the Analysis on Gender, Culture and Density Implies?
58
5.3 Why is 800m Still Not Working? 61
5.4 What Could Have Been Improved in This Study? 62
6 Conclusion 63
References 66
Strategic Behavior in Sport Contests iii
List of Abbreviations
AME America
AMO Africa and Middle Orient
APA American Psychological Association
ASO Asia and Oceania
EUR Europe
HDR High-Density Races
HRM Human Resources Management
LDR Low-Density Races
PB Personal Best
PGA Professional Golfers Association
NBA National Basketball Association
R&D Research and Development
SB Season Best
SME Small and Medium Enterprises
Strategic Behavior in Sport Contests iv
List of Figures
Figure 1. Return and marginal return for
player 1 24
Figure 2. Reaction functions in a two-player
case 25
Figure 3. Reaction functions when the player
1 is the favorite 26
Figure 4. Hypothesized relative race
positions over time 29
Strategic Behavior in Sport Contests v
List of Tables
Table 1. Results of Walker and Wooders 9
Table 2. Gain Distribution 11
Table 3. Observation Versus Theoretical
Predictions 11
Table 4. Regression Results for Men's and
Women's running events 32
Table 5. Regression Results for Men's and
Women's Distance Field Events 33
Table 6. Comparison Between Position and
Ranking Over the Lap 35
Table 7. Available Level of Detail for Data
for Each Event 39
Table 8. Rules for Estimation of the Missing
Data 41
Table 9. Honors Multiplier Settings 43
Table 10. Results of Underdog-Favorite
Parameter Regression 48
Table 11. Results of the 800m Races 49
Table 12. Results of the 1500m Races 50
Table 13. Results of the 5000m Races 51
Table 14. Aggregated Results 52
Table 15. Gender and Strategic Behavior 54
Table 16. Culture and Strategic Behavior
55
Table 17. Density of Competition and
Strategic Behavior 56
Strategic Behavior in Sport Contests 1
1 Introduction
1.1 Problem Definition and Objectives
Lots of economic and social interactions consists in a
competition where the players expend their effort in order to increase their
probability to win a prize. These situation can be research and development
(R&D) rivalry between firms or countries to get a lucrative or strategic
innovation, bribery to assure a profitable license, patent or contract from the
government, the war for a new global market that has been created by a new
innovative product, a political election where candidates fight during long
campaigns in order to get elected, or candidates who compete for a job, or to
win a promotion.
Example of contests can also be found in sport competition.
These competitions can take shape in three different forms. Championships,
where each player plays against each other and the ranking of the competition
is determined by the results of the players against all the players of the
championship. Famous examples of championships are the English Premier League
or the Bundesliga in football, the Six Nations Tournament in Rugby. Another
type of competition is the tournament. Tournaments is a form of competition
which takes the shape of a direct elimination competition. The competitors
compete pair by pair and the winner can play against the winner of another pair
until only one winner remains and win the prize. Famous examples of tournaments
are Grand Slam Tournaments in Tennis, or the play-offs of the National
Basketball Association (NBA). Eventually, another type of sport competition
takes the form of a race. A race is a competition where the prize is given to
the first competitor to cross the finish line. This type of competition is
different from a tournament or a championship since in a race, the competitors
are competing against one another at the same time. They are not challenging
each other by pairs like in a game of football or tennis. Therefore, they are
the most interesting competition in order to analyze the behavior of agents in
a situation where they are faced to many competitors. Races are therefore in
regard of their nature more interesting to analyze agents' behaviors in order
to find beginning of answers on the behavior of agents in a R&D rivalry
between firms or country because a lot of countries or firms are involved at
the same time to develop the same technology and the first one to be able to
create it will gain an economic or strategic advantage upon the others that can
be seen as the prize.
Strategic Behavior in Sport Contests 2
Some models of the tournament theory take an interest in the
strategic behaviors of the players in a case where the intrinsic capacities of
the agents are heterogenous, which means in a case where there is a favorite
and an underdog. Dixit (1987), shows with a model of game theory that if he
plays first, the favorite has always an interest to engage a high level of
effort, while the underdog has the opposite incentive. Baik and Shogren (1992)
extended Dixit's model considering an endogenous choice for the order of
intervention of the agents. They show that the underdog has always an interest
to play first while the favorite's best interest is to wait and play in
second.
The theoretical models on the strategic behaviors of the
favorite and the underdog haven't been much studied empirically. The reason why
is quite obvious, it is very difficult to find economic situations where the
status of favorite and underdog is clearly established and defined and the
strategies of the favorites and underdogs are directly observable, especially
the order in which they are engaging their effort. This is particularly true in
the economic context used by Dixit (1987) and Baik and Shogren (1992) which is
the race to innovation.
Boyd and Boyd (1995) avoid this difficulty by analyzing the
strategic behaviors of the athletes during athletics competitions (from 800
meters (m) to 10 000 m) at the Olympic Games of 1992. As part of an athletics
race, the model of Baik and Shogren (1992) predicts clearly the following
course: underdogs tend to start the fastest, then are caught back before being
usually passed by the favorite.
Boyd and Boyd used data coming from the races of the 1992
Olympic Games in Barcelona to test this theory. They only looked at the races
for which distance were superior or equal to 800 m, which are the distances for
which the tactics have a real role to play and where runners run inside a
peloton (and not in lanes). For each distance, they visualized the video
recordings of the semi-finals and the final. For the short distances (such as
800 m or 1500 m, they recorded the positions of the runners every 200 m while
for the longer distances (3000 m women, 5000 m men and 10 000 m), they recorded
the position of the runner every 400 m. At the end, their database contains
more than 2300 observations spread over 14 races. Concerning the key variable
of the study, which is the measure of the runner status before the race,
favorite or underdog, Boyd and Boyd used as a proxy the ranking of the runner
in the previous race, which means in the semi-finals if the race studied is a
final, or the heats if the race studied is a semi-final.
Strategic Behavior in Sport Contests 3
From a general perspective, the results of Boyd and Boyd are
clear and coherent with the theory of Baik and Shogren: the course of races see
the relative position of the underdog decline during the race. On the contrary,
the favorites improve progressively and end up winning most of the time. Boyd
and Boyd also notice that the results are clearer for the men than for the
women since for men, all races (semi-finals and finals) confirm the theory,
except the 800m final.
However, when I read the article of Boyd and Boyd, I noticed
some details that was posing me some problems regarding the model's
veracity.
First, the proxy that Boyd and Boyd used to determine who was
favorite before the race and who was not, which is the ranking of the runner in
the previous round, do not seem to me the best way to measure a runner's
chances to win a race. I am myself a French athlete running 800 m at the
national level since 10 years, I participated to 12 French National
Championships, and I never looked at the ranking of a rival in the previous
round in order to determine if his chances where greater than mine to win.
Indeed, heats or semi-finals are an unreliable information since they runners
who are in my race do not come from the same race. I usually make a complex
calculation based on his personal best (PB), his ability to finish quickly his
races, his recent shape, the races he has won before, his weather preferences,
etc. This way I am able to assess what are the odds for me to beat him and what
is the best strategy to apply, or at least try to apply, in order to beat him.
One of the goals of this thesis is therefore to create a calculated index based
on the different data that can be gathered today for a runner. This way the
proxy will be calculated the same way for all runners of all races and will
give homogeneity to the analyzed races.
My second observation is about the use of the position of the
runner as the parameter which determines the level of effort of the runner over
the lap. I do not think it is the most accurate measure we can have today of
the level of effort for a runner. Indeed, with the race reports that have been
given for the last four World Championships races, we are able to determine who
has run the fastest and the slowest on each lap because we have the split times
for each runner from every kilometers to every hundred meters. This way if a
runner did his first interval much faster than others, then his second interval
slower but he had taken such an advantage over the first interval that he has
not be caught up by others, he will not be any more considered as the one who
has given the greatest effort on the interval. This change is, in my opinion
very important if the purpose of the study is to
Strategic Behavior in Sport Contests 4
measure correctly when runners put their highest level of
effort in regard of the pre-race status.
The third observation is that they only try to verify if there
is a difference in the strategic behavior of men and women. Not only do I
believe there should not be a big difference in the strategic behavior of men
and women, but I also believe that there are other parameters about the runners
or the race that could explain a different behavior, such as the culture of the
runner, or the density of the race. These parameters would be, in my opinion,
very interesting to test in order to see if one of them changes the strategies
of the runners.
The objective of this thesis is to replicate the experiment of
Boyd and Boyd with the data of the last world championships and to apply all
the modifications that I mentioned above. Moreover, I will be studying the
other potential factors of strategic behavioral change in order to see if Baik
and Shogren results are still coherent with this new methodology. Therefore, we
will be trying to give an answer to the question: how effort is expended
over time by a runner in athletics events depending on the pre-race status of
the same runner and what other parameters may affect the runner behavior?
This question is almost the same that the one Boyd and Boyd asked
themselves and the purpose of this study will be to see if we can find similar
results when applying a more efficient methodology.
1.2 Course of the Investigation
The thesis design will take the shape of an empirical study.
It will therefore analyze through collected data the phenomenon observed by
Boyd and Boyd over the 1992 Olympic Games in Barcelona.
It will start with an overview of the relevant literature
review over the field of sports as an application to economic theory and over
the field of strategic behavior in contests. This theoretical background will
help me to justify why sport and athletics are a relevant application in order
to prove Baik and Shogren results in R&D rivalry and to have a better
understanding of Boyd and Boyd model in order to be able to modify it correctly
and improve it. After that, I will define a methodology that would try to
improve Boyd and Boyd model. Most of the articles come from EBSco Host database
and some others I took on Google scholar, especially for the scientific
articles that are not economic science or game theory related.
Strategic Behavior in Sport Contests 5
I will try first to improve it by changing the proxy variable,
which is the key variable of the study since the purpose of the study is to
measure in what way the behavior of a runner is affected by his pre-race
status. I will change it by implementing a calculated methodology for the
parameter which consider several data such as the PB, the season best (SB), the
honors. All the data concerning the different runners background, honors and
level, which will determine the index that will inputs the proxy of who is
favorite of the race and who is an underdog will be collected from the database
of World Athletics, (ex-International Association of Athletics Federations)
which is the international federation of athletics.
Then I will analyze all the race reports of the World
Championships finals from 2013 to 2019, which makes 4 world championships for
the distances of 800 m to 5 000 m (data was not available for 3000m
steeplechase and too complicated to collect for 10 000 m) in order to collect
data which will enable me to determine the level of effort for each athlete for
each interval studied. Only middle-distance races will be analyzed since they
are the only track and field event on which a strategic component is
involved.
After the compilation of all this data, I will analyze the way
the level of effort for a runner was influenced by the pre-race status of the
runner and by the place of the interval in the race, or in other words, is it
the beginning or the end of the race? However, I will also aggregate the data
coming from all the races much more than Boyd and Boyd did in order to be able
to find out if my observations are true in particular for specific cases of
race taken individually only or a more general phenomenon. I will also study
the model separating the population studied under different parameters such as
gender of the runners, cultures of the runners and density of the race.
Once the results of these regression will have been obtained,
I will be able to verify if my method observe the same phenomenon that Boyd and
Boyd did and find similar results to them. I will be also able to discuss the
results found and explain why some differences between my method and Boyd and
Boyd's method could be found. I will also try to find answers to the possible
differences I will find inside the population studied when I will have looked
at the variations inside the population looking at the different parameters
that I mentioned above.
Once all this will have been done, I hope I will be able to
give an answer to the research question I asked myself and be able to assess
Baik and Shogren results and Boyd and Boyd results or not. I hope also to find
other interesting results that will create something
Strategic Behavior in Sport Contests 6
Boyd and Boyd did not notice when they did their experiment
and that these findings will bring new insights in the field of strategic
behavior.
2 Theoretical Background
2.1 Why sport is a good field to study economics?
First, I would like to present examples where the study of
sport cases helped the economists to better understand economic theories. My
goal is here to prove that the study of sport is a relevant case in order to
understand economic, strategic, or behavioral phenomenon.
Sport economics strongly developed recently (Andreff &
Szymanski, 2006). People generally think of it as the use of economic analysis
tools to study the sports industry. However, this thinking forgets a second
face of sport economics: when sport helps better understand economics. (Eber,
2008) Eber wrote in 2008 an article whose topic was this second face of sport
economics. He explains that the observation of high-level athletes can give
interesting leads to economists since sport competition delivers a frame
particularly fit to the verification of some economic theories as it is a
highly competitive context, with actors very motivated and gifted (i.e.
rational), clear and stables rules for the game, and perfectly objective
results or performances measured without any ambiguity by a score, a distance
or a time.
The next part is going to be a bunch of examples where sport
have helped verifying economic theories that are very difficult to observe in
the economic world due to the complexity to get some data on the level of
effort of the agents, their level of skills, their final performance, etc.
2.1.1 Tournament Theory
Economic theory took a lot of interest starting from the
eighties and the articles of Lazear and Rosen (1981) and Rosen (1986), at the
type of competition which are tournaments, i.e. highly competitive situation
characterized by the fact that the prize of an individual depends only of his
ranking compared to the others. Tournaments models describe very well the
reward systems used for the corporation management, for sales team members
Strategic Behavior in Sport Contests 7
or in academical environment (bonuses, promotion, etc.). Under
hypotheses, the tournament system present interesting normative properties
since it is based on an efficient incentives structure. (Lazear and Rosen,
1981).
Few empirical studies have been led on the incentive effects
of tournaments. Econo-metrical studies on «real» data turn to be
delicate since it is very difficult to identify precisely, within an
organization, what are the tournaments set in place, what are these tournaments
rules, what are these tournaments prizes, etc. Moreover, it is very difficult
to measure the level of effort of the agents. From an experimental point of
view, Bull, Schot-ter and Weigelt (1987) found relatively inconclusive
results.
In front of this lack of empirical elements, Ehrenberg and
Bognanno (1990a) used the results of great tournaments of American golf
(tournaments from the Professional Golfers Association (PGA) Tour) that took
place in 1984.
It is here important to point out that tournament theory is in
opposition to the fair-wage theory based on equity. Indeed, when tournament
theory insists on the dispersion of the revenues, the hypothesis of group
cohesion proposed (Levine, 1991) insists on the perverse effects (jealousy,
mistrust, disincentive) of a very unequal salary structure, especially in the
case of teamwork. Therefore, tournament theory applies better to individual
sport than collective sport. That's why empirical test on tournament theory are
mostly based on individual sports (golf, tennis, running) while those of
fair-wage theory are based on team sports (baseball, basketball, hockey,
football).
To test the hypothesis that states that tournaments have
positive incentive effects Ehrenberg and Bognanno estimate a simple
econometrical model with the following structure:
sly = ac, + a1TPRIZEi + a2xi +
a3yi + a4zi + eLi
where sly is the final
score of the golfer ] in the tournament
i, TPRIZEL the prize money of the
tournament i, xi a vector
of variables on the difficulty of the tournament, the weather conditions, etc.
y, is a vector of proxies for the quality of the
player] (average score over the season, etc.),
zi is a vector of control variable on the quality of
the competition in the tournament i, and
eu the error term.
Tournament theory predicts that al <
0. All other things being equal, higher prize money should give
an incentive for a bigger effort from participants, and this bigger effort from
participants should lead to better performances, which means lower and lower
scores. (In golf, the lower is your score, the best you are). The estimations
of Ehrenberg
Strategic Behavior in Sport Contests 8
and Bognanno (1990a) lead as predicted to a coefficient
??? significantly negative. More precisely, they find that a
raise by a 100,000 $ of the global prize money leads to an average diminution
of the number of strokes. In average, every player plays 1,1 strike less during
the entire tournament than before the raise of the global prize money which
proves that players have an incentive to play better with a raise of the global
prize money. Ehrenberg and Bognanno (1990b) replicated their test on the
results of the great Europeans tournaments of 1987 and found similar results.
However different results were found in a study on the PGA data for the year
1992 (Orszag, 1994).
Other empirical studies based on data coming from sport seem
to confirm this result since the positive link between incentives and
performances stated in the tournament theory has also been observed in other
sport competition such as running in road races (Frick, 1998; Maloney and
McCormick, 2000), and tennis (Barget, Llorca, & Teste, 2011) either that
you take a population of men (Sunde, 2003) or women (Lallemand, Plasman, &
Rycx, 2008). However, it is important to note that concerning the road races in
running, more qualified results have been found (Frick & Prinz, 2007) and
Lynch and Zax (2000) couldn't find a strong relation between performance and
revenues, once the quality of the participants at the beginning of the race was
controlled.
2.1.2 Equilibria in mixed strategies
A large number of experimental studies have been made in
laboratories in order to test the empirical validity of the equilibrium in
mixed strategies. The result of these studies is on average not really
positive. Usually, except for perfectly symmetric games, observations are very
far from the theoretical predictions (Camerer, 2003, Chapter 3). Therefore, the
conclusion of experimental works is usually to invalidate the mixed strategies
theory. The only cases in which the empirical observations match the
equilibrium are the studies of cases lead in the field of professional sport,
tennis and football.
The first study mobilizing observations coming from sport in
order to evaluate the accurateness of the concept of mixed strategies
equilibrium has been done by Walker and Wooders (2001). In this study, Walker
and Wooders interest themselves to the case of tennis, and more precisely, to
the strategic game which consists in service. Indeed, during a service, two
players, the server and the returner, are engaged in a game in the sense of a
strategic interaction. The gain issued from the game for each player is the
probability to win the point. The server has to choose between two strategies:
to serve on the right (R) of the returner or to serve on the left (L) of the
returner. As the speed of the serving ball
Strategic Behavior in Sport Contests 9
is very high, often above 200 km/h, the returner has to
anticipate the choice of the server. It brings him to play either
«Right» if he anticipates that the server is going to serve on his
right, or «Left», if he anticipates that the server is going to serve
on his left. That way, we can consider that both players play simultaneously
and not one after the other.
This makes clearly a constant-sum game since the probability
to win the game for a player is the probability to lose it for the other. This
game, in which it is essential for the players to be unpredictable, admits a
unique Nash equilibrium in which the server and the returner decide both to
take a mixed strategy.
What predictions can we make starting from the theoretical
analysis of the game? By the definition of an equilibrium in mixed strategies,
both pure strategies (L and R) have to, at the equilibrium, bring the exact
same Esperance of win to the server. This way, for the server, the percentage
of success (i.e. the rate of won points) has to be the same when he serves on
the right of the returner that when he serves on his left. Walker and Wooders
studied ten finals of Grand Slam Tournaments or Masters. The Table 1 gives the
aggregated results for all ten games.
|
Services
|
L
|
1622
|
|
R
|
1404
|
|
Total
|
3026
|
|
Services (in %)
|
L
|
54
|
|
R
|
46
|
|
Won points
|
L
|
1040
|
|
R
|
918
|
|
Won points rate (in %)
|
L
|
64
|
|
R
|
65
|
Table 1. Results of Walker & Wooders (Walker
& Wooders, 2001, p. 1526)
This table is really impressive. On the all set of ten games
studied, which represent in total 3026 services, the rate of points won are
almost identical for both strategies (64% for L, 65% for R). This agrees to the
theoretical prediction of mixed strategies equilibrium.
Another characteristic of the Nash equilibrium in mixed
strategies is that players have to choose randomly. This way, there should not
be a correlation between the present choices and the past choices. This
characteristic is nevertheless not verified by the study
Strategic Behavior in Sport Contests 10
of Walker and Wooders. Indeed, players modify their choice too
frequently in comparison to a random decision, which means, like in the other
experiments made in laboratory, that there is no independence between the
present actions and the past actions. This result come to balance a little bit
the conclusion of Walker and Wooders in favor of the mixed strategies
theory.
A replication of Walker and Wooders' study was done on another
set of games (Hsu, Huang, & Tang, 2007). They find even clearer results in
favor of mixed strategies theory since both properties of the mixed strategies
equilibrium, i.e. an identical rate of success on both pure strategies and a
random choice between strategies, are verified on this replication study.
The same type of study has been made on penalties in football
(Chiappori, Levitt, & Groseclose, 2002, Palacios-Huerta, 2003). Like for
the service in tennis, the penalty in football is a simple situation of
strategic interaction between two players, the striker and the goalkeeper with
the characteristics of a constant-sum game. They consider that both players
have two pure strategies. The striker can choose to shoot on his right (R) or
the shoot on his left (L). To simplify, they suppose that the striker does not
have the possibility to shoot in the middle, however the analysis would be
exactly the same if we included this third pure strategy. Like the ball only
takes 0,3 seconds to reach the goal line because of the strength of the strike,
the goalkeeper has to anticipate a strike on his right (R) or on his left (L)
before the striker has even touched the ball. Here again, they do not consider
the possibility for the goalkeeper not to dive, which means to stay put in the
middle of the goal. To support this choice, observations have been made that a
psychological bias exists in favor of action that pushes goalkeepers to dive
too systematically compared to strikes distribution. (Bar-Eli, Azar, Ritov,
Keidar-Levin, & Schein, 2007). In other words, this situation is a
simultaneous game, both players ignoring the choice of the other at the moment
they make their decision.
In this constant-sum game, the gain of the striker is the
probability for him to score a goal while the gain for the goalkeeper is the
probability for the striker to fail. On the basis of the 1417 penalty strikes
analyzed by Palacios-Huerta (2003), the values of gains are presented in the
following table:
Strategic Behavior in Sport Contests 11
|
Goalkeeper
|
|
L
|
R
|
|
Striker
|
L
|
(58.30, 41.70)
|
(94.97, 5.03)
|
|
R
|
(92.91, 7.09)
|
(69.92, 30.08)
|
Table 2. Gain Distribution (Palacios-Huerta, 2003)
In every cell of the table, the first number is the gain of
the striker, i.e. the probability, in percentage that he scores, and in second
the gain of the goalkeeper, which is the complementary probability.
They name ??? the probability at the
equilibrium that the striker shoots on the left, ??? the
probability that, at the equilibrium, the striker shoots on the right,
??? the probability at the equilibrium for the goalkeeper to
dive on the left and ??? the probability that, at the
equilibrium, the goalkeeper dive on the right. It is very easy to verify that
the unique equilibrium in mixed strategies is characterized by:
??? = 0.39,??? = 0.61,??? = 0.42,??? =
0.58
The data of Palacios-Huerta concerning 1417 penalties shot in
games of the English, Spanish or Italian league. The following table compares,
at the aggregated level, the observed strategies with the theoretical
predictions.
|
Striker
|
Goalkeeper
|
|
L (%)
|
R (%)
|
L (%)
|
R (%)
|
|
Nash Equilibrium
|
38.54
|
61.46
|
41.99
|
58.01
|
|
Observations
|
39.98
|
60.02
|
42.31
|
57.69
|
Table 3. Observation versus theoretical predictions
(Palacios-Huerta, 2003)
The observations are very close to the theoretical
predictions. This way, the mixed strategy equilibrium turns out to be a good
predictive model of the strategies actually adopted by the strikers and the
goalkeepers.
For a given player, the concept of mixed strategies implies
that he has to have the same success rate on both pure strategies. Let's be
French a little and take the case of Zinédine Zidane, one of the best
football players ever and one of the players studied by Palacios-Huerta. On 40
observed penalties, he shot 19 times on the left (48%) and 21 times on the
right (52%) with success rates almost identical of 74% and 76% respectively.
This way Zinédine Zidane, aside of being a great football player, is a
pretty good game theorist too!
Strategic Behavior in Sport Contests 12
However, the strategic choices of penalty strikers or
goalkeepers can be largely unconscious, but their huge expertise of the game
drive them to take naturally the optimal strategies (Palacios-Huerta, 2003,
p.406).
Palacios-Huerta also shows that the decisions of the players
are random, as a consequence, the present choices available are independent
from the past choices. This way, the second implication of Nash equilibrium in
mixed strategies, which is that the decisions are taken randomly, is also
verified by this experiment on the way strikers and goalkeepers act
strategically in the penalty game.
From a methodological point of view, it is important to note
that a major difficulty comes from the heterogeneity of the strikers and the
goalkeepers. Indeed, the basic characteristic, the equality of probabilities to
score for each of both pure strategies) is not preserved by the aggregation of
heterogenous players. Thanks to about forty observations for each player,
Palacios-Huerta is able to realize individual tests (i.e. by players). He
proposes also aggregated tests that make it possible to evaluate if, on the
global study, the probabilities to score are the same on the right and on the
left for each player of the sample, even if they can be potentially different
between the players.
Very similar results to those of Palacios-Huerta were found
(Chiappori et al., 2002; Coloma, 2007) and we can therefore affirm that players
choose optimal mixed strategies and their decisions are random. Another study,
which is this time studying another typical phase of the game, when the striker
is at the beginning of the penalty area (Moschini, 2004). This study also finds
results that match the theoretical predictions by the Nash equilibrium in mixed
strategies.
What conclusion can be taken from all these studies based on
data coming from sport competition? Classical experiment done in laboratory
show that beginners in a game that just started to play this game do not adopt
the optimal strategies in games with a mixed strategies equilibrium. However,
the studies considering the case of tennis or football show that professional
athletes find the equilibrium strategy. On the spectrum of expertise, we find
at one extremity the beginners without a lot of experience, for whom theory
does not work very well, and at the other extremity, we have professional
athletes, for whom theory seems to apply correctly. Of course, the majority of
«real» constant-sum game happen in an intermediary context between
these two extreme cases, however, this intermediary level has not been much
studied and not a lot of things is known about it in the scientific world.
Strategic Behavior in Sport Contests 13
2.1.3 Contract Theory
In the contract theory, the employer (the principal) has to
conceive an incentive contract in order to assure that the employee (the agent)
will give the desired level of effort. This theory stipulates that the
assurance to keep his job thanks to a long-term contract can create a classical
problem of moral hazard giving an incentive for the employee to reduce his
efforts, i.e. shirking. The evaluation of this theory turns out to be complex,
because it is difficult to estimate in a reliable way the individual
performances of the employees. Once again, the interest of data coming from
sport comes from the fact that the individual performances, so the contribution
of the employee (the player) to the company (the team) can be measured without
any ambiguity. Some studies have mobilized the data on professional American
team sports to test the hypothesis of a disincentive effect of long-term
contracts. The purpose of the study is simply to see if, as the hypothesis of a
disengagement of the effort after the signing of a long-term contract states,
the performances of the players diminish just after the signing of such a
contract.
The results of the studies are rather inconclusive. Some
authors observe a modification of performances in the expected way, with a
diminution of the performances of baseball players (Woolway, 1997; Marburger,
2003) and NBA basketball players (Stiroh, 2007). But other researchers do not
find a significative difference in the performances before and after the
signing of the new long-term contract for baseball players (Krautmann, 1990;
Maxcy, Fort, & Krautmann, 2002). In fact, in the case of baseball
(Scoggins, 1993) and NBA basketball (Berri & Krautmann, 2006), it is shown
that the conclusion depends in a crucial manner in the way the performance
measure is done. Another observation can also be made by saying that in team
sports, the performance and influence of a player is not always perfectly
measurable. Indeed, some players have a style of play based on moves without
the ball that are going to draw the opponent's defense to him, giving space for
his teammates to go to the goal or basket and score more easily. His presence
is therefore absolutely essential to the team, but it will not be measured in
statistics.
2.1.4 Behavioral economics
Behavioral economics consist in finding stronger psychological
foundations to the standard economic theory. This leads to take into
consideration the judgements bias of individuals, the social norms or the
social pressure. A few studies have worked from the sport field to measure
empirically the impact of social pressure on favoritism (2.1.4.1), or more
generally, the role of emotions on the behaviors and the performances
(2.1.4.2).
Strategic Behavior in Sport Contests 14
2.1.4.1 Social pressure and favoritism.
Social pressure plays an important role in a large number of
economic contexts. In the wave of the new behavioral economics, it is today
clear that social pressure impacts the individual behaviors and can lead to the
shape of implicit corruption that is favoritism. (Prendergast & Topel,
1996) While many experimental results observe a decisive impact of social
pressure on the individual behaviors, econometrical verifications on real case
are very rare, because it is very difficult to find reliable data. Sport
competition have made possible to test in a real-life environment the effect of
social pressure.
Three studies considering the case of professional football
refereeing analyze the behavior of referees in order to verify the role of
social pressure on favoritism (Garicano, Palacios-Huerta, & Prendergast,
2005; Sutter & Kocher, 2004; Dohmen, 2008a). The idea to study if referees,
surely pushed by the pressure of the stadium crowd, really have a tendency to
favorize the home team (home bias). The problem is of course to be able to find
an objective measure of the referees' behavior. However, there exists one
decision that fits quite well to such a measure. It is the extra-time that the
referees grant at the end of the game in order to compensate the stops that
happened during the regular time for injuries, substitutions, unsporting,
etc.). Indeed, if the law is fixed concerning the general principles guiding
the management of this extra time, the field referee remains free to decide
when to blow the end-of-the-game whistle.
A study (Garicano et al., 2005) use a database on refereeing
int the Spanish league in order to see if the referee are not more in a hurry
to blow the end-of-the-game whistle if the home team is leading with a weak
margin, which means with a one goal advantage, and less in a hurry to blow the
whistle when the home team is lead by one goal. The results are very clear. For
example, in the case where the home team is lead by one goal, the extra-time is
around 35% longer than on average, and when the home team leads by one goal, it
is 29% shorter than on average. Similar studies have been made (Sutter &
Kocher, 2004; Dohmen, 2008) on the German Bundesliga. Their results confirm
largely those of Garicano et al. in favor of the hypothesis of favoritism for
the team playing at home.
2.1.4.2 The role of emotions
One of the great contributions of behavioral economics is to
show the fundamental role of emotions in the behaviors of individuals. Here
again, the observation of the world of sport can turn out to be very
informative.
Strategic Behavior in Sport Contests 15
A study on missed penalties on German Bundesliga (Dohmen,
2008b) confirms that emotion and social pressure have a major role in
individual performances, even for high level athletes. In particular,
individuals can «crack under the pressure», an effect much studied in
social psychology, but neglected by economists. However, like Dohmen notes:
«There are plenty of situations in which pressure arises in the workplace.
Knowing how individuals perform under pressure conditions is crucial because it
has implications for the design of the workplace and the design of incentive
schemes» (Dohmen, 2008b, p. 636). It is clear that it is very difficult to
obtain in the world of enterprise the kind of data necessary to the evaluation
of an eventual perverse effect of the pressure on the performances. Dohmen
(2008b) goes around this difficulty by studying the missed penalties of German
footballer since the foundation in 1963 of the German professional football
league, the Bundesliga. He chooses to give a strict definition of what is
«cracking under the pressure» in the case of a penalty since he
considers that it returns to an off-target strike (or on the posts), i.e. a
situation of complete failure without any interference of the goalkeeper. He
observes then that the proportion of missed penalties «under the
pressure» is higher for team that are playing at home (7.54% against 5.57%
for teams playing away from home), but that it does not depend significantly of
what is in stake with the success of this penalty's importance (score at the
penalty's time, decisive game at the end of the season). This way, the players
seem more sensitive and fragilized by the pressure of the public than by the
context of the game. This could have very interesting development in the
enterprise field as pointed out Dohmen: «The empirical result of this
paper implies, for example, that workers who might feel they are being
observed, especially by well disposed co-workers or spectators, perform worse
than they otherwise would» (Dohmen, 2008b, p.652)
Besides, it has been noticed on the basis of a thorough
analysis of professional tennis games (Paserman, 2007) that men and women do
not behave in the same way under the pressure. More precisely, his data on the
speed of the service, the percentage of first service or the length of the
exchanges for the points suggests that men maintain the same strategy and the
same level of performance in key moments of the game, while women turn to a
less aggressive strategy (slower services, longer exchanges) for important
points. This result that there is a difference between men and women in the
manner to manage the pressure in a highly competitive context confirms a whole
set of experimental results. (Gneezy, Niederle, & Rustichini, 2003; Gneezy
& Rustichini, 2004)
Strategic Behavior in Sport Contests 16
Another study based on data coming from sport have brought
forward the role of emotions in the performances. (Palomino, Rigotti, &
Rustichini, 1998) They estimate, on the basis of 2885 professional football
games, the probability to score a goal at the different moment of the game.
They study how this probability is linked to three founding determinants of the
performance of a football team:
- the abilities, measured by indicators such as the
number of scored goals or conceded goals over the whole season.
- the strategy, defined by the choice to attack or to
defend in reaction to the score of the game depending on the time remaining of
the game (beginning, last fifteen minutes). This is measured by the way the
probability to score a goal depends of the score and the time remaining for a
team.
- the emotions, that regroup an entire set of
emotional and psychological factors about the game, with the advantage of
playing at home.
The results show clearly that the three factors intervene
simultaneously and interact in the determination of the performance, i.e. the
probability to score. In detail the results show that:
- A better ability than the opposite team multiplies the
probability to score by a factor between 2.1 and 2.4
- Different strategic situations make the probability to score
vary following a factor between 1.4 and 2.2
- To play at home (emotion factor) multiplies the probability
to score by a factor between 1 and 2
In total, these results show that the three forces have
equivalent importance in the determination of the performance, which is the
probability to score.
Palomino et al. (1998) think their results could have
important implications in economics since they clearly show that psychology and
rationality occur simultaneously in the behavior of actors and the result of
the game. This type of phenomenon is possibly also existing in the economic
world. Very general factors occurring in the behavior and performances of a
football team is most probably also occurring in other type of organizations
that are living in a highly competitive environment, such as enterprises.
Palomino et al. (1998) even note that:
«Soccer teams are examples of economic organizations who
face each other in a very standardized, repeated, situation (a soccer match),
which is therefore easy to study. Their behavior can provide insights on the
way an economic organization
Strategic Behavior in Sport Contests 17
works and in particular on the way strategic and emotional
factors interact in its life» (Palomino et al., 1998, p.30)
This way, they hope that their results to stimulate a new axis
in economic theoretical research with the building of new models able to take
explicitly into account the interactions between reason and emotions.
2.2 Theory of Contests
Contests are a fact of life that can be witnessed everywhere,
even in the non-human spheres. Knight (1935, p. 301) saw contests as games as
an essential part of economic life:
«The activity which we call economic, whether of
production or of consumption or of the two together, is also, if we look below
the surface, to be interpreted largely by the motives of the competitive
contest or game, rather than those of mechanical utility functions to be
maximized.»
They are defined as: «a situation in which players
compete with one another by expending effort to win a prize» (Baik, 1994).
This part reviews the literature on theory of contests. The literature on
theory of contest is very large and diverse and there is not the place in this
Master Thesis to cover it entirely, however I will try to present the most
basic models alongside models that have been useful in the study of sports.
This literature has been remarkably reviewed by Corchón (2007), Konrad
(2009), and Fu and Wu (2019). Besides, and inside the scope of my particular
topic, Szymanski (2003) made a survey that study the application of contests in
sporting events. The following part 2.2 is largely inspired by the recent
review of Fu and Wu (2019) that gives a large and efficient vision of the
current scientific knowledge. They begin with a summary of important contest
modelling frameworks which differ in the mechanisms of selection of the winner,
these frameworks will be presented in the 2.2.1 part. They continue by
presenting a large range of various contest models in different contexts. Some
of these models, the most relevant for this master thesis, will be presented in
the part 2.2.2
2.2.1 Contest Modelling Frameworks
Fu and Wu (2019) start their review by considering three types
of models: perfectly discriminatory contest models, where one secures a win
when he outperforms, and which are named as all-pay auctions, rank-order
Tournaments (Lazear & Rosen, 1981; Green &
Strategic Behavior in Sport Contests 18
Stokey,1983) and contests with ratio-form contest success
functions (Tullock, 1967; Tullock 1980)
2.2.1.1 All pay Auctions
Fu and Wu start by present ting all-pay auctions, which are
models applied to a large number of contexts like R&D races (Dasgupta,
1986), litigation (Baye, Kovenock, & de Vries, 2005), lobbying (Hillman
& Samet, 1987; Hillman & Riley, 1989), etc. In the case of a classical
winner-take-all all-pay auction (Hillman & Riley, 1989; Baye, Kovenock,
& de Vries, 1996). Then, for an effort profile x = (x?, ... ,
x?), a player ?? wins a contest with a
probability equal to:
1, if x?? > max{x?, ... , xi??, xi??, ... ,
x?};
1
??i = ? ?? , if xiis among the ?? highest of x with a
tie;
0, if x?? < max{x?, ... , xi??, xi??,
... , x?}.
This type of contest has no pure strategy equilibrium and
gives a mixed strategy equilibrium. Baye et al. (1996) gave a general
determination of the equilibria in a ??-person all-pay auction
where the information is complete. For the case of an incomplete information
auction, then the bids of the contestants are distributed above zero, therefore
a tie is an event with a zero probability.
A framework of large contests was developed that enables for
many heterogeneous players and prizes (Olszewski & Siegel, 2016) with
complete or incomplete information. Olszewski and Siegel (2020) also show by
continuing the research designed by Moldo-vanu and Sela (2001) that many
heterogeneous prizes are possibly optimal in a large contest framework where
contestants are risk averse with convex costs. Olszewski and Siegel (2019)
applied the framework to model college admissions.
2.2.1.2 Rank-Order Tournaments With Additive Noise
Fu and Wu (2019) explain that the result of an all-pay auction
is determined easily, as a small difference secures the win of the auction for
a contestant. However, the result of a `real life' contest often depends not
only on the effort of the contestants but also on perturbations that happen in
a random manner. There exists two ways to model contest with a mechanism of
selection of the winner with noise.
Lazear and Rosen (1981) proposed a rank-order tournament. If
each contestant ?? exert an effort xi which
produces an output ??i with:
??i = ??i (xi) + ??i
where the output function ???(???) is usually
an increasing function of effort ???.It is also called by
convention the impact function.
Strategic Behavior in Sport Contests 19
The function ??? (???) is a settled output
and increases with the contestant's effort, ??? is a random
effect, which is usually identically and independently distributed among the
contestants. Contestants are ordered by their respective output
???, and the contestant with the highest ???
wins. If two players are involved in the contest, the condition for
the player 1 to win can be written as:
|
???(???)
|
+ ???
|
> ???(???)
|
+ ???
|
|
? ??? -
|
??? <
|
???(???) -
|
???(???)
|
If the noise term (??? - ???) is distributed
with a cumulative distribution function ??(·). The
probability that contestant 1 wins is then given by:
??? = ??(??? - ???)
= ??(???(???) - ???(???))
which is the probit winning probability specification that we
are going to see later. (Dixit, 1987)
This framework has been applied in many studies in order to
explore the optimal prize structure in small tournaments (Krishna and Morgan,
1998) and demonstrate that optimal tournaments do not necessarily induce
first-best outcome, contestant's incentive for risk taking in tournaments
(Hvide, 2002), dynamic versions of the model to investigate optimal interim
feedback policies in this framework (Aoyagi, 2010). There is also a study
(Balafoutas, Dutcher, Linder, & Ryvkin, 2017) that investigated the optimal
prize allocation in tournaments of heterogenous contestants. They observe that
a loser-prize tournament that gives as a reward a low prize to bottom
performances can be optimal.
2.2.1.3 Contests With Ratio-Form Success Functions
However, Fu and Wu (2019) note that the most adopted modeling
approach that permits a noisy mechanism for the selection of the winner is the
one that takes a ratio-form contest success function. The Tullock (1980)
contest model is the most popular case of this modeling form. For the case of a
winner-take-all contest with a ratio-form contest success function, the
probability that a contestant ?? wins, ???,
is given by the ration of the output of his effort to the total output supplied
by the entire group of contestants such as:
??? =
? ???(???) ?
if ? ???(???) > 0;
? ? ???(???)
?
??? ???
1 ?
? ? ?? if? ???????? < 0,
? ???
Strategic Behavior in Sport Contests 20
Under the assumption that all the contestants follow a linear
effort cost function ??(x?) = x?. Then this framework
gives a measurement for the winning probability as a function of effort in a
winner-take-all imperfectly discriminatory contest. Tullock (1980) adopts
???(x?) = x?? with r>
0. He then applies this model to the rent-seeking contest. These
types of model are called Tullock contests. If r is
large, the marginal pay back for effort will be higher and other factors that
have an influence on the winner's selection will count less. As a consequence,
if for the case of a symmetric contest, contestants tend to increase their bids
when r increases. In a traditional symmetric Tullock
contest game, there is a unique Nash Equilibrium in pure strategy only if the
contest is not very discrim-
inatory, i.e. if r < ? .
???
2.2.2 Contests Models in Various Contexts
In this part are presented a few of the many models on which
Fu and Wu (2019) reviewed the existing literature. The choice of these models
is set on the applicability of these models to the case of this thesis: running
races.
2.2.2.1 Sequential Moves in Contests
The model studied in this Thesis is a model which works in
sequential moves. Therefore, it is important to see where it is coming from. Fu
and Wu (2019) point out that the first to bring the structure of Stackelberg is
Dixit (1987). He identifies the conditions under which a contestant benefits
from being the first mover, as he can strategically impact the late mover
behaviour by his action. It has been shown many things about these types of
contests. First, that only the contestant with the lowest costs has a positive
payoff in return (Konrad & Leininger, 2007), that a head start given to the
first mover can have an impact of the contest's performance (Segev and Sela,
2014), or that sequential moves lead to a higher rent dissipation if more than
two players are involved in the auction. (Klunover, 2018)
Fu and Wu (2019) also note that there has been a continuous
research trying to en-dogenize the timing of moves of contestants with for
example a three-period model. (Baik and Shogren, 1992a; Leininger, 1993). In
this model, the contestants can furnish their efforts in either period 1 or 2,
and a winner is selected after both contestants have completed their entire
effort. They decide the timing to commit their effort simultaneously before the
game. It is shown that in the case where contestants are asymmetric in regard
of their capacities, the underdog always choose to commit effort earlier while
the favorite
Strategic Behavior in Sport Contests 21
chooses to commit effort later. In a model with settings of an
all-pay action (Konrad & Leininger, 2007), it is also shown that the
strongest contestant always chooses to move later. This theory is very
important for the following master thesis because it is the one we are trying
to verify.
2.2.2.2 Contests With Budget Constraints
Contests with budget constraints are highly relevant in regard
of a running race. Indeed, every athlete knows that his capacities are not
unlimited and that if he goes too fast for too long, then he is going to be
biologically forced to slow down by the rise of the lactic acid in his muscles
which is going to tetanize him.
Fu and Wu (2019) enumerate a large number of models that take
the assumption that «contenders have budget constraints and have to
allocate their resources among parallel battles to maximize the sum of the
expected rent they can receive from the whole set of battlefields» (Fu
& Wu, 2019) These types of model are called a Colonel Blotto game of
duopoly conflicts in multiple battlefields. This game was proposed by Borel
(1921) and analyzed in the case of three markets (Borel & Ville, 1938). The
analysis was generalized to a certain number of markets for symmetric players,
with one asymmetric case being solved by Gross and Wagner (1950). Kovenock and
Roberson (2012) investigated a Colonel Blotto game in which two players make an
alliance and compete against a common rival, where allied players can transfer
resources to each other. This situation is interesting for sport because it can
model the situation of a race where two runners are going to unite their forces
to beat the favorite. This happens a lot in cycling for example where leaders
from different teams can command their whole teams to work together in order to
beat the leader of the general ranking or the favorite.
These studies take as an assumption that the contestants
allocate their budgets simultaneously. A study about a two-stage tournament
with each player effort being constraint by a limit show that the underdog
tends to behave more aggressively in the first period (Harbaugh and Klumpp,
2005) which agrees with Baik and Shogren (1992a). Therefore, it is really
interesting in order to affirm that theoretically, underdogs over commit their
effort in races because it brings the idea of the limitation of the resources
of the runner.
2.2.2.3 Contests With Non-Risk-Neutral Players
Fu and Wu (2019) remark in their review that most modeling
frameworks of contests have been assumed with risk-neutral contestants.
However, the result of a contest is most of the time. Even if Real Madrid will
in 99% of the cases crush a fifth division team, there
Strategic Behavior in Sport Contests 22
may be a chance they might get beaten. This can also be
observed in cycling races where there are some cyclists who are very cautious
in their strategy, waiting for the last hundred meters to attack, and cyclists
who launch attacks 200km from the finish line even though they know their
chances of success is very poor because this strategy is very much riskier.
A way to bring risk in a model is to take the assumption that
contestants are risk averse. Hillman and Katz (1984) investigated contenders'
incentive with the presence of risk aversion. The contestants' utility function
u(·) is assumed to be strictly increasing and
concave, which is different from models with risk-neutral players who have a
linear utility. For a given award w, with a personal
valuation of the prize by the contestant v? the
expected payoff of contestant j in the contest game
is calculated by:
???(x) = ???(x) × u(w+ v? - x?) + [1 -
???(x)] × u(w- x?)
In a two-player contest, this model admits a pure strategy
Nash equilibrium if both contestants are constantly absolute averse. (Skaperdas
& Gan, 1995) Moreover, Cornes and Hartley (2012) generalized this result in
order to prove the existence of a unique equilibrium in the case of an
asymmetric contest.
Fu and Wu (2019) also explain that the impact of risk aversion
on the effort of contestants is ambiguous. Indeed, Skaperdas and Gan (1995)
pointed out that a more risk-averse contestant has an incentive to exert less
effort in the contest because he reduces his safe payment by doing so but a
contestant becomes also at the same time more risk averse, which gives him an
incentive to increase his level of effort because he reduces the probability of
losing this game that way. This is called the self-protection effect.
2.2.2.4 Asymmetric Contests
Fu and Wu (2019) explain that the competitive balance between
contenders is key in the performance of a contest. If there is a too large
difference between contestants, then the underdog is discouraged while the
favorite will be allowed to slack off. Baye, Kovenock, and de Vries (1993)
illustrate this logic with a multiplayer all-pay auction model with complete
information. In the case where the favorite possesses an excessive advantage,
the context is paradoxically generating a higher revenue by excluding him.
While keeping only the underdogs in the contest. This can be assimilated once
again to cycling races, where if a rider is considered too strong by others,
nobody will want to take him a relay, then the favorite will be forced to slow
down because he would be beaten if he was pushing forward. This way the average
speed of the group is reduced. An experiment using
Strategic Behavior in Sport Contests 23
data from professional golf tournaments demonstrates
empirically that the presence of a superstar in a competition tends to lead to
a lower general performance.
Fu and Wu (2019) note this has inspired research efforts to
study the incentive effects of identity-dependent rules and research for the
model that exploits the heterogeneity of the ability of contestants optimally
and manipulate the balance of the playing field to make desirable equilibrium
behaviors. An all-pay auction model considering two players and complete
information showed that a contestant can be favored in two ways: by having his
bid being scaled up by a fixed percentage to simulate a handicap or by the
addition of a fixed constant from his bid. (Konrad, 2002). Other studies
(Siegel, 2009; 2014) describe more general settings enabling for discriminatory
rules for the contests.
2.3 Strategic Behavior in Contests
The purpose of this part is to remember the key theoretical
background and the surrounding empirical studies about the experiment of Boyd
and Boyd (1995), which is the key experiment of this study, and around which
this whole thesis is built. I will therefore in a first part remember the
findings of Dixit (1987) and Baik and Shogren (1992a) on which the experiment
of Boyd and Boyd (1995) is built. Then I will present other empirical studies
about the strategic behavior in contests. After that, I will present thoroughly
Boyd and Boyd's experiment that will be replicated in this thesis.
2.3.1 Theoretical Background
The first to consider the case where one of the players is
given a chance to pre-commit strategically his effort is Dixit (1987). He is
the first to impose an order of moves based on a Stackelberg leadership which
brings sequential moves in the contest. In his paper, he studies two models. A
model with two players, and a model with several contestants. For the model
with two players, he finds that the player which is the favorite is the player
who has an incentive to overexert. He explains it by the Figure 1 coming from
Dixit (1987) paper. In the panel (a) of Figure 1, The curve TT
shows the total growth return for player 2, [1 -
p(x1, x2)]K, where p(x1, x2) is the
probability for the player 1 to win and K is the
prize to win, as a function of his effort
x2 for a fixed level of
x1. In the part (b) of the graph, the
curve MM is the corresponding marginal. Dixit (1987)
explains that a slight increase in x1 shifts these
curves to T'T'and M'M' respectively and the marginals
cross at the point P. If there is an increase to its
left in xlreduces the marginal return
in
Strategic Behavior in Sport Contests 24
x2, which leads the player 2 to
reduce x2 if x? is pre-committed. If the
player 1 is the favorite, then (1 - p) is low and
x2 lies to the left of P.
Therefore, it is in player 1 strategic interest to commit to overexertion.
Dixit (1987) notes however that the opposite holds if the player 1 is the
underdog.
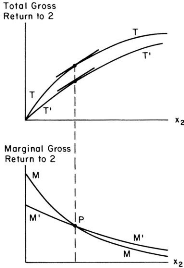
Figure 1. Return and marginal return for player 1 (Dixit, 1987,
p. 894).
Dixit also develops the corresponding intuition with the
Figure 2 using reaction or best response functions. In the case where player 1
is the favorite, in the neighborhood of the Nash equilibrium
N, the favorite's best response function (R?)
is sloping upward and the one of the underdog (R2) is sloping
downward. In this case, the player 1 has an incentive to make a strategic
pre-commitment to ma higher x?, which moves the outcome from
N to S?. Player 2 wins he can commit to a
lower x2, which will move the outcome from N
to S2. When the pre-commitment is made by the means
of a separate variable Y?(respec-tively Y2),
then the effect is to push the best response functions R? to the left
to R? ? and R2 downward
to R2 ? . If you compare the position of
these curves compared to the p =
1
? line which represents the line where both players have the
same probability of win-2 ning, we can see that at the Nash
equilibrium, the outcome of the favorite (player 1) gets
higher if he increases his level of effort x?
while the underdog (player 2) sees his outcome increase if he lowers
his level of effort x2.
Strategic Behavior in Sport Contests 25
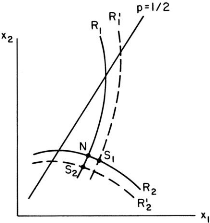
Figure 2. Reaction functions in a two-player
case (Dixit, 1987, p. 894).
This result support the idea that in a situation where there
is a favorite and an underdog, the favorite has to overexert his effort
compared to the underdog, Dixit (1987) explains it with the phenomenon that can
be seen in sport where the manager of the team declares that «since he is
expected to win, he mut try all the harder» while the underdog says to be
«under no pressure, and is just going to enjoy the occasion».
However, Baik and Shogren (1992a) demonstrates in a comment of
Dixit's model that the favorite will never overcommit effort if you extend
Dixit's model to allow for endogenous order of moves. They take an endogenous
order of moves, in this case, the favorite will tend to find it advantageous to
wait until the underdog moves while the underdog's best strategy is to make the
first move and not to wait.
For this, they consider a situation in which two risk neutral
players (1 and 2) compete against each other to a K
prize. If xland x2
are the players' effort levels and p(xl, x2)
the probability that player 1 wins. For this situation the
players' expected payoffs are:
11-l = Kp(xl, x2) - xl
(11-2 = K[1 - p(xl,x2)] - x2
Following Dixit, they assume that p(xl,
x2) takes either the logit form
p(xl, x2) = fl(xl)/[fl(xl) + f2(x2)]
or the probit form p(xl,x2) = G[fl(xl) -
f2(x2)]. They also assume that f?(0) > 0
for i = 1, 2 and that
fl,
f2, and G
[fl(xl) - f2(x2)] are
increasing functions.
Strategic Behavior in Sport Contests 26
They then draw the Figure 3 by defining QQ as
the locus of points that satisfy f1(x1) =
f2(x2). Since
f1(x1) and
f2(x2) are increasing functions, the
curve QQ is sloping upwards. Moreover, f1(x1) <
f2(x2) above the curve, and f1(x1) > f2(x2) below
the curve. Given the assumptions, they find that the reaction function of
player 1 r1(x2) is increasing in x2, reaches
the maximum on the curve QQ and then decreases, while the
reaction function of player 2 r2(x1) is increasing in
x1, reaches the maximum on the curve QQ and
then decreases. They assume finally that f1(x1) > f2(x2) at
the Nash equilibrium, which is equivalent to saying that the player 1 is the
favorite and the player 2 is the underdog.
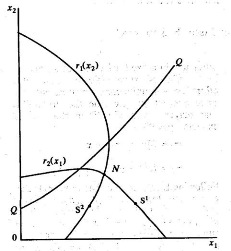
Figure 3. Reaction functions when player 1 is
the favorite (Baik & Shogren, 1992, p. 360).
This graph allows them to say that Player 1's expected payoff
is decreasing when
one moves up along his own reaction function while the Player
2's expected payoff is decreasing when one moves right along his own reaction
function.
Then Baik and Shogren (1992a) consider the following game: The
players decide in a first time and announce simultaneously publicly the periods
in which they will choose their level of effort. The players then choose
simultaneously their effort level knowing when the opponent will choose his
level of effort. In the case where both players announce the same period, the
subgame would be a simultaneous-move game.
If the favorite announces the first period and the underdog
announces the second, then the favorite is the Stackelberg leader and the
underdog the Stackelberg follower. Baik and Shogren call this subgame the
favorite-leader subgame. In this subgame, the underdog
Strategic Behavior in Sport Contests 27
chooses his own level of effort after having observed the
favorite's level of effort. The opposite game is the underdog-leader subgame.
Baik and Shogren note that the simultaneous move subgame payoffs are
(????, ??? ?), those of the favorite-leader subgame are
(?????, ??? ??), and those of the
underdog-leader subgame are ???? ??, ??? ???. From the
analysis
of the graph, they obtain that ????? < ??? ? <
??? ?? for the underdog. Therefore, they demonstrate that in the
announcement stage of the game, the underdog will choose the first period
without caring at what strategy is the favorite taking. They explain that the
underdog has no incentive to wait for the favorite's choice as this strategy of
selecting effort in the second period is a dominated strategy. And since the
underdog chooses the first period,
the favorite chooses the second since ??? ? <
?????. The unique subgame-perfect equilibrium shows that the underdog
will choose to move first in the announcement stage and the favorite will
choose to move second. This demonstration enables them to make the following
proposition:
«In the equilibrium, the favorite moves after the
underdog. Endogenous order of moves results in both players expending less
effort compared with the Nash equilibrium. Consequently, strategic behavior
leads to under-commitment of effort associated with a contest over a fixed
reward.» (Baik and Shogren, 1992a, p. 360)
This result is very interesting in the theory of contests
because this suggests that in a situation with endogenous order of plays will
lead to see the underdog acting as a leader in terms of strategic behavior.
They explain it by taking an R&D analogy where two firms are trying to
develop a product based on their relative power derived from the research
stage. The firm that has an advantage in the research is considered the
favorite while the other is considered the underdog. Then if their model
prediction is true, the underdog will lead research and the favorite will
follow. They note however that they do no eliminate the potential for
industrial sabotage (Hirschleifer, 1988) with the example of a firm that
decides to aim for a «victory at all costs» and which will be putting
all its effort to disabling its rival.
2.3.2 Empirical studies
If strategic behavior in contests is used a lot in R&D,
innovation, academic publishing and sports (Vojnovic, 2016), they are however
much better understood in principle that in practice (Carpenter, Matthews,
& Schirm, 2010). Besides, strategic behaviors of contestants that are
unintended like self-promotion or sabotage are not often studied. Indeed, it is
difficult to study such behaviors since contestants usually try to hide these
behaviors
Strategic Behavior in Sport Contests 28
because they are usually associated with the idea of being
illegal or immoral (Charness & Levine, 2004). Because of this, the studies
investigating strategic behavior are usually restricted to laboratory
experiments or formal models of behavior. (Harbring & Irlen-busch, 2011;
Lazear, 1989; Münster, 2007).
However, a few empirical studies exist that try to investigate
the «real» strategic behaviors of individuals in «real
situations».
Concerning the behavior in an asymmetric contest, Baik and
Shogren (1992b) study in a laboratory experimental design the model of
strategic behavior proposed by Dixit (1987). For this, they designed an
experiment as follows: the subjects enter a room and are divided in two groups,
favorite and underdogs. Each subject read the experimental instructions
concerning their group without being able to communicate in any possible
manner. The instructions told the subjects that they would be in competition
against an opponent to try winning 360 tokens, with each token being worth
$0.0025. The probability that a contestant will win depends on the number,
which represents the expenditure, he selected and the number the opponent
selected in an expected payoff matrix. Therefore, the higher number a
contestant selects, the more chances he gets to win, but his cost would
increase accordingly. If a player loses, his number is subtracted from his
opportunity cost of participating in the experiment ($5/hr.) To represent the
asymmetry, favorites and underdogs are given distinct payoff matrices but both
players have both payoff matrices at their disposal. Then the two players chose
a number from their payoff sheets simultaneously in order to test the Nash
benchmark game. To test the favorite first-mover game, the favorites were told
to select their number first while the underdog had to wait the favorite's
choice before selecting his level of effort. 20 games were done in the
experiment. Their results are that the support to Dixit's model where the
favorite will expend more effort in the Stackelberg case is only partial. They
found indeed in this experiments that in some cases, the underdog tries harder
because probably he has nothing to lose.
Concerning the unintended behaviors such as sabotage, Riedl,
Grad, and Lettl (2019) made an experiment made on the digital environment,
which is really interesting nowadays since many contests take place in these
environments. The particularity of this environment is that the barriers of
entry are very low (Boudreau, 2018) which means that even low skilled
contestant can enter the competition, which increases the heterogeneity between
contestants. This phenomenon is called the «rise of the amateur»
(Howe, 2008). Moreover, this environment enables large number of contestants in
the contests thanks to
Figure 4. Hypothesized relative race positions
over time (Boyd & Boyd, 1995, p. 1039).
Strategic Behavior in Sport Contests 29
the internet compared to prior research. Riedl et al. (2019)
major findings are that self-promotion decreases as the contest size increases
and that the contestants that have the higher ability are less likely to
self-promote compared to contestants who have a lower ability. Moreover, they
found that the contestants with the higher ability are the most likely to
choose the strategy of sabotage.
2.3.3 Application to the Field Events of 1992 Olympics Games
2.3.3.1 Context and Presentation of the Experiment
Boyd and Boyd (1995) observe the opposite theoretical findings
of Dixit (1987) and Baik and Shogren (1992a) and try to find an empirical
verification to these theory by finding a real situation in which to observe
the behavior of agents. But this cannot be easily done in situations involving
strategy, where the economic actors are loath to reveal any information
concerning their strategic intention because of competitive reason. They decide
therefore to apply these theoretical results to the field events of the Olympic
Games of 1992 in Barcelona. They choose this example because in athletics,
athletes have the freedom to make decisions on how to strategically expend or
conserve effort during the event, which makes it possible to apply Baik and
Shogren (1992a) findings because this incorporates the endogenous order of
moves. Therefore, it will be the findings of Baik and Shogren that they will be
trying to prove, which are, when applied to running events, the pre-race
favorite being conservative at the beginning of the race, then increasing his
effort as the race develops while the underdog will start quickly before being
caught up by the favorites at the end of the race.
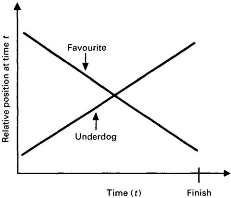
Strategic Behavior in Sport Contests 30
The figure 4 present these predictions graphically showing the
evolution of the position of the favorite and the underdog as the race progress
towards the finish line. Their analysis carries of the running distance from
800m to 10 000m and the distance field events which are the long jump, triple
jump, shot put, discus throw, javelin throw, and hammer throw.
2.3.3.2 Empirical Model
Boyd and Boyd (1995) empirical model is built the following
way: they consider a race with T successive
intervals, or laps. They define Pit as the
relative position of the runner i at the end of lap
t, with t = 1, 2, ... , T.
Their interest is to analyze the manner in which Pit
evolves over the course of the race. This is modelized with the
relationship:
(1) Pit = 13it + ai + uit
where aicaptures unmeasured runner
specific effects that might influence the strategy of a runner and which are
individual, uit the error terms, which
also change over individuals and laps, are independent and identically
distributed, and the 13i coefficient which measures
how the runner's position evolves during the race. Although 13i
is different for each runner i, Boyd
and Boyd define it such as it is a function of each individual runner's
foreshadowed measurement of race favorite or underdog. This enable them to
conjecture the following relationship for 13i:
(2) 13i = 13o + 131UFi
where UFi is a proxy for the
runner's status as a pre-race favorite or underdog. UF
settings are such as it is positive, integer valued, and the
bigger is this proxy, the more the athlete is considered as a pre-race
underdog.
By substituting the equation 2 into the equation 1, they
generate an equation where the relative race position of each
runner i at the lap t is a
function of the current lap position t and the
interaction term t
· UFi:
(3) Pit = 13ot + 131tUFi + ai
+ uit
Partially differentiating the equation 3 with respect to
t, they obtain:
/ aPit aa
(4) at = No + 131UFi =
13i
If the theoretical results of Baik and Shogren are correct,
underdogs have an incentive to overexert effort early in a race whereas
favorites have an incentive to let them do, saving energy for the end of the
race. In this case, 13o is negative, 131
is positive, and both are statistically significant.
Strategic Behavior in Sport Contests 31
Boyd and Boyd (1995) also note that the way a runner choose to
exert effort rationally and strategically depends in part on his physical
attributes. For example, some runners choose strategically to use their
superior foot speed by waiting the final hundreds meters to unleash their final
kick to the finish, but tall runners may choose to go to the front of the
peloton to minimize the risk of being jostled by the other runners with their
long legs. These unobservable individual characteristics may be a form of
misspecification of the model and is potentially a bias for the estimates
??? and ???. Boyd and Boyd use therefore
fixed effects (Mundlak, 1978; Greene, 1993) to separate individual
characteristics that affect the relative position over time (???)
from lap-to-lap strategic behavior stemming from the individual status
as a pre-race favorite or underdog (???). Each ???
is unobservable, but constant over time, therefore its effect can be
removed by taking deviations from the mean. Furthermore, they observe that by
specifying ??? as a function of pre-race status as given in
equation 2, what seemed to be individual-specific slope characteristics in
equation 1 are estimated by ??? and ???. This
way, Boyd and Boyd (1995) are able to obtain unbiased estimators for equation
(3) using fixed effects model:
(5) ???? - ??? = ???(??- ??) + ???(??- ??)????? +
????
where ??? = 1 /?? ? ????
? ??? is the average position of the
??th runner over the ?? laps of the
event, ?? is the mean lap of the event and
the error terms ????are again independent and
identically distributed. They eventually pool data for each athlete within an
event which enables them to estimate equation 5 using ordinary least squares,
which provide them consistent estimates of ??? and ???
for each race.
2.3.3.3 Results
For the running events, they analyzed the races by observing
the videotapes in order to record the position of each athlete at the end of
the lap. Positions were recorded every 200m for the 800 and 1500m while it was
recorded every 400m for the longer distances which are 3000m for women, 3000m
steeplechase for men, 5000m, and 10 000m. They did this for the semi-finals and
the final of the competition which spread out over 14 races. The proxy for the
underdog-favorite variable (?????) was the runner's finishing
position in the previous race of the competition, i.e. the semi-finals if the
analyzed race was the final, or the heats if the analyzed race was a
semi-final. The regression for 14 men and women races is shown in the table
3.
Strategic Behavior in Sport Contests 32
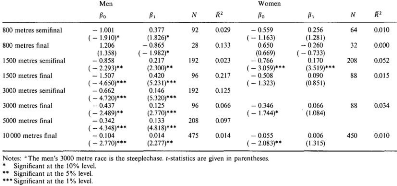
Table 4. Regression Results for Men's and
Women's Running Event. (Boyd & Boyd, 1995, p. 1041)
They find that the signs of 85% of the estimates are
consistent with Baik and Shogren's hypothesis that underdogs tend to overexert
effort early in races with 75% of the estimates being statistically significant
at the level of at least 10%. This is shown by the fact that 85% of the
estimates have a negative ??? and a positive
???. They also note that the magnitude in the ???
coefficients in absolute value is inversely proportional with the
distance of the race. Which means that pre-race favorites move to the front of
the peloton much faster in short races, which can be explained by the fewer
number of laps of short events. In a similar manner, the ???
coefficient varies inversely with the race distance in absolute value.
Boyd and Boyd explain it again by the greater number of laps but also by the
greater number of participant to the races (8 participants for an 800m against
15 for a 5000m) which increase the likely range of the underdog-favorite
proxy.
For the distance field events, Boyd and Boyd bring a slight
modification to the equation 5 to estimate the following model:
(6) ???? - ??? = ???(?? - ????) + ???(?? - ????)????? +
????
where ???? is the distance of the
??th athlete's throw or jump on her ??th
attempt, ??? =
1 /?? ? ????
? ??? is the ??th athlete
average distance over her ??? throws or jumps ????
is the ??th
athlete's mean number of non-foul attempts, and the error
terms are again independent and identically distributed. For the events they
took for the underdog-favorite variable the distance of the athlete best
attempt in the qualifying round. This way the hypothesis of Baik and Shogren
are the same for ??? and ??? than for the
running races. They obtained for the distance field events the following
results:
Strategic Behavior in Sport Contests 33

Table 5. Regression Results for Men's and
Women's Field Distance Events. (Boyd & Boyd, 1995, p. 1042)
The regression results show that the coefficients are
consistent with Baik and Shogren hypothesis for three of the events (men's
discus and hammer, women long jump). But from a general perspective, the
distance fields events results are more ambiguous than the running events
results. They give for an explanation that they do not take in the analysis the
weather since in a race, the runners face the same weather since they are
running simultaneously. However, in distance field events, competitors are
jumping or throwing one after another, so the weather conditions are not always
exactly the same for every athletes. They explain also this ambiguity by the
fact that in qualifications of a field event there is a distance of direct
qualification to the final. If an athlete reaches this distance, he gets
automatically directly qualified, therefore the ?????
may get biased since the athlete who reaches this distance at his
first attempt in qualification will not try to do better afterwards since he
will be willing to save energy for the final.
2.3.3.4 Observations on This Experiment
This thesis is born by reading the paper of Boyd and Boyd
(1995) and observing some methodological details that could be improved in
order to prove Baik and Shogren theoretical hypothesis.
The first observation I could make is about the idea to
analyze the semi-finals in the paper. In my opinion, semi-finals are not as
interesting to study as finals since, for starters, it is not the final race of
the competition. Therefore, there is a bias created by the fact that runners
that are a little bit above others in terms of level may try to save some
energy in order to qualify for the final. In a middle-distance international
championship, there are two ways to qualify for the next round. Either you get
your «qualification through the
Strategic Behavior in Sport Contests 34
place» by finishing in the first positions of your race,
(2 for the 800m, 4 for the 1500m, 5 for the 5000m) or you hope to be in the
best times of all the semi-final in order to get your «qualification
through the time» in order to get the last places remaining for the final.
If we take the example of the 800m there are usually three semi-finals of eight
runners at an international level for eight tickets for the final. In order to
get to the final, a runner has the choice between finishing in the first two
places of his semi final or to finish third or fourth and hope to have a time
sufficient to be in the eight best runners. This disposition completely biases
the analysis of semi-finals since usually the runners of the third semifinal
have a huge advantage compared to others since they know what time they have to
do in order to qualify through the time. Therefore, we can observe frequently
much faster races in the last semi-final because runners are incented to do so
since if they succeed to be faster than other semi-finals runners (which often
happen because these runners do not have this incentive) they have more chances
to qualify. If by allying themselves, the race is fast, they will have a
probability to get to the final of 0.5 (4 places out of 8) instead of 0.25 (2
places out of 8). Their chances to qualify have been doubled! Therefore, only
finals will be taken into account in the races that I will analyze in my
study.
This phenomenon creates another problem in Boyd and Boyd
model, but this time about the UF1 variable. Indeed,
the settings of the UF1 variable are such that it is
the place of the runner in the previous turn that is taken into account.
However, how the races are not the same because a semi-final can be fast and
the other slow, therefore, biases are created since for example the best runner
can win the slowest race and be nevertheless ranked behind a runner who
finished fourth of the fastest race in the settings of the underdog-favorite
variable proxy. The best way to determine the favorite of a race prior to the
race is to analyze loads of data such as the PBs, the races the runner has run
recently, the weather conditions, his results against the opponents, his final
kick, the previous races he has won, etc. This is what I'm going to try
achieving in this thesis by creating a method to determine the
underdog-favorite variable proxy by an aggregation of different and various
data.
The third observation is about the fact to choose the place of
a runner at the end of an interval or lap is not the perfect way to measure the
level of effort of an individual during an interval. Indeed, if we take the
example of two competitors A and B on an 800m, the runner A starts quickly and
run his first 200m in 24.0 seconds. The competitor B starts slower his race and
cover the first 200m in 25.5 seconds. At the 400m, the competitor A passes the
line in 50.5 seconds which means he has run the second 200m in 26.5 seconds.
Strategic Behavior in Sport Contests 35
The competitor B is still behind him in 51 seconds but has
closed the gap since he has run his second 200m in 25.5 seconds. The following
table represents the respective rankings of both runners if we take into
account the place at the end of the lap or the ranking of the runner over the
lap.
|
|
|
|
Position Method
|
Ranking Method
|
|
0-200m
|
200-400
|
400m
|
200m
|
400m
|
0-200m
|
200-400m
|
|
Runner A
|
24.0
|
26.5
|
50.5
|
1
|
1
|
1
|
2
|
|
Runner B
|
25.5
|
25.5
|
51.0
|
2
|
2
|
2
|
1
|
Table 6. Comparison Between Position and Ranking
Over the Lap.
We can see from this table that if we follow Boyd and Boyd
methodology to determine who has exerted the greatest effort on the second lap,
the runner A will be designated as the runner who will have done so. However,
we see with this concrete example that he was not the fastest runner over this
interval. Therefore, it is more relevant to my opinion to take into account the
ranking of the runner over the interval rather than the position of the runner
at the end of the lap because we can see with this example that the runner who
has run the fastest, i.e. who has committed the greatest effort is the runner
B. I will therefore take the ranking of the runner over the interval rather
than his position. Of course, at the time Boyd and Boyd did their experiment it
was impossible to analyze the times over all the laps of every runner since the
data was not available. But now the data is partially available for the last
world championships and I think it is a good occasion to test Baik and
Shogren's hypothesis using more precise data.
This change is important and has major impacts. First by
taking the ranking over the lap, the volatility of the positions of the runners
will be increased, especially for the longer distances. Indeed, for long
distances, the races start usually very slowly, and the runners run in pack.
Therefore, the difference between the fastest runner over the lap and the
slowest is usually very slow (sometimes less than a second) and a runner
ranking over different laps can be second on the lap 2 but fourteenth on the
lap 3 because he has run 0.15 seconds slower than the other runners before
getting back to fourth place over lap 4 because he has run 0.22 seconds faster
than others. The ranking of this runner is too unstable to be able to find a
significant regression. In order to get results, I will have to reduce the
number of laps for longer races to gain in stability of the regression. But
this decision makes sense, indeed the time over a longer interval will be more
representative of the effort of the runner than the time over a shorter
interval which will be almost the
Strategic Behavior in Sport Contests 36
same for every runner of the race at the beginning. This
decision is also taken from a practical point of view since the data collected
if we take the example of the 5000m gives only the times for every 1000m for
every runner. There is another advantage of reducing the number of laps which
is we will be able to see if the variation in absolute value of the estimates
in function of the distance in Boyd and Boyd experiment was real or simply
caused by the greater number of laps since all races will have a similar number
of laps.
Eventually, my last observation is upon the choice to analyze
distance field events in order to verify Baik and Shogren hypothesis. I think
this choice to be not a very good one. Indeed, if middle-distance races are a
highly relevant example to test strategic behavior in contests. It is because
these races are not done with a maximum effort during the whole event. Indeed,
over this distances, it is not possible to start in pure sprint and finish the
race. Therefore, runners have to strategically decide when to exert their
effort and when to save energy. Distance fields events on the contrary are pure
explosive efforts where the effort lasts a few seconds or even a fraction of a
second for throws. Athletes are therefore giving a hundred percent of their
energy on each jump or throw and do not calculate if they have to save some
energy for the next ones. Therefore, there is no strategic choice in trying to
exert effort at the best timing, they are trying their best every time. They
may improve their distance a bit along the event since they can better their
technique are adapting their marks to the weather condition. But there is no
strategic choice to overexert at the beginning of the event. This is, in my
opinion, why Boyd and Boyd have ambiguous result for these types of event. This
makes me say that the study of distance fields event is irrelevant in order to
determine if an underdog overexerts his effort at the beginning of a contest.
Therefore, these events will not be studied in this thesis.
3 Methodology
The objective of this thesis is to improve Boyd & Boyd
(1995) in order to verify if Baik and Shogren hypothesis can still be verified
after these changes. As a reminder, these changes would be: defining the events
most relevant in order to prove Baik and Shogren hypothesis the calculation of
the underdog-favorite variable proxy via a combination of data, and to build an
empirical model based on the ranking of the runner on the interval rather than
on the place of the runner at the end of the interval. The methodology of this
thesis will consist therefore in delimiting the frame of the study in a first
time, defining what data to collect and how. Then in a second time to determine
what data to collect and
Strategic Behavior in Sport Contests 37
how to combine it in order to build an underdog-favorite
variable proxy only with data available prior to the race that will be a good
predictor of the issue of the race. Eventually, it will be to build an
empirical model that will make it possible to verify Baik and Shogren
hypothesis that the underdog overexerts his level of effort at the beginning of
a contest.
3.1 Delimitation of the Frame of the Study
The first task to be able to improve Boyd and Boyd empirical
model is to determine precisely what data is relevant for the study and what is
not. The events in track and field that will be considered will be middle
distance races. These races are the most interesting to study in order to
analyze strategic behavior of contestants since strategic choices are key in
determining who will win in these races. Moreover, these races are not event
that are realized in a purely explosive effort, such as 100m, long jump, hammer
throw. The athletes do have to choose when to exert their effort in the race
and therefore make a strategic choice. Therefore, it is a perfect situation to
verify Baik and Shogren hypothesis that underdogs tend to overexert their
effort level in the first stages of a sequential contest. The other events are
less interesting to study since they are mainly based on the explosive
qualities of the contestants and their technical qualities. There is no choice
on how much effort you should exert for this try or this sprint in these events
since these events are competed with full energy delivered all race or try
long. This important delimitation will make me study only the race that will be
longer than 800m included. However, I decided not to include the 10 000m since
this race is not really considered as a middle-distance race but a
long-distance race.
The fact that I want to use the ranking of a runner over an
interval as the endogenous variable rather than his position at the end of the
interval like Boyd and Boyd had done gave me constraints. Indeed, in order to
be able to collect this type of data, you need to have electronic cells such as
the ones over the finish line at every 100m if you want the splits for every
100m. However, this technology is very expensive therefore it is usually only
available for the major events of the athletics season such as World
Championships or Diamond League meetings, which is the circuit with all the
greatest athletics meetings in the World. However, to study the strategies of
runners in meetings is to my opinion not particularly relevant. Indeed, this
races do not happen exactly the same way than the championships since a runner,
the pacemaker is paid by the organization in order to sacrifice himself and to
make the race start quickly by overexerting his level of effort on
Strategic Behavior in Sport Contests 38
purpose at the beginning of the race. This is done in order to
give an opportunity to the runners to beat their PBs, to qualify for the great
championships, or beat the World Record. Every other runner know that he will
be doing so and therefore try to place themselves behind him. Usually, this
pacemaker does not finish the race since he has overexerted so much effort at
the beginning of the race that he is too tired to finish it with the hope to
get a good time. This changes also completely the chances for the favorite and
the underdog to win. Indeed, usually the faster is the race, the less chances
have the underdogs to beat the favorite. Therefore, as meeting races are
usually fast races, underdogs incentive to try to beat the favorites are
usually low, since they know they have really small chances to do so. Instead,
they will try to remain behind the favorites for as long as they can hoping to
beat their PBs with the aspiration, motivation and pace provided by the
favorites. With these observations, I believe that only championships races are
relevant to study strategic behavior in order to prove Baik and Shogren
hypothesis. Therefore, the studied race will be the races from 800m to 5000m
from the world championships between 2013 and 2019, which makes 4 events, world
championships being biannual events. The world championships of 2011 were not
studied since the technology giving the split times of every runner along the
event did not exist at the time.
Besides, and as explained in the part 2.3.3.4, I decided that
only races that are finals of the championships are going to be studied in
reason of the strategic biases that are created by semi-finals because of the
qualification procedures to the final.
Moreover, the choice to use ranking over the interval rather
than the position at the end of it limits me because in order to be able to
assess which runner has run the fastest on an interval, I need to have the
split times of every runner for every interval. This means, if I want to
replicate the exact methodology of Boyd and Boyd every 200m for the 800m and
1500m and every 400m for the 3000m steeplechase and the 5000m. However, the
collection of this data was not always possible homogenously. Indeed, the race
analysis reports, coming from the World Athletics (i.e. the international
federation of athletics) website that were analyzed in order to collect the
data were not splited in a homogenous way. For 2013 and 2019 world
championships for example the detail of split times was given for every 100m
for every runner while for 2015 and 2017 world championships, they were only
given every 400m for the 1500m (splits being 400-800-1200-1500) and every 1000m
for the 5000m. Table 7 present the different split levels that were available
for each races over the studied period. The table shows that if for the 800m,
there are not problems about the availability and the homogeneity of the data
for split times of runners,
Strategic Behavior in Sport Contests 39
it is quite different for 1500m and 5000m. Moreover, it shows
also that the data was not available for the 3000m steeplechase. Indeed, this
event is a 3000m over which runners have to pass 4 barriers of 91.4 cm for men
and 76.2 cm for women and a river made by a barrier and after that barrier a
pit of 2m deep filled this water. The problem is that this «river» is
usually situated inside of the track in the second turn of the lap. Therefore,
runners have to «cut» the lap in order to pass over that river. Their
lap is therefore shorter than 400m and to compensate it, the starting line of
the 3000m steeple chase is 25m farther from the finish line than the 3000m flat
starting line. Therefore, every turn, runners catch up 3.57m which makes it
impossible to measure the split times every 400m since every lap the line of
the 400m is virtually moving. Therefore, the international federation do not
release the data concerning the split times of each runner for the steeplechase
events and I am forced to rule it out of the study for this reason.
|
Level of
|
800
|
800
|
800
|
800
|
1500
|
1500
|
1500
|
1500
|
5000
|
5000
|
5000
|
5000
|
|
Detail
|
2013
|
2015
|
2017
|
2019
|
2013
|
2015
|
2017
|
2019
|
2013
|
2015
|
2017
|
2019
|
|
Split 100
|
X
|
X
|
X
|
X
|
X
|
|
|
X
|
X
|
|
|
X
|
|
Split 400
|
|
|
|
|
|
X
|
X
|
|
|
|
|
|
|
Split 1000
|
|
|
|
|
|
|
|
|
|
X
|
X
|
|
Table 7. Available Level of Detail for Data for
Each Event
We face here a situation where we have to choose what level of
number of laps we want to study. In order to get comparable and homogenous data
for every race, I decided to study races with the minimum number of laps
possible. This choice has many advantages. First, it will give me homogenous
data that will make all 800m, 1500m, and 5000m comparable between each other
since all races of a same event will be comparable. I will be therefore able to
aggregate the data from all 800m together, all 1500m together, and all 5000m
together. Second, it will improve the volatility of the data. Indeed, by
choosing the ranking over the interval over the place at the end of the lap,
the volatility of the place of runners has increased a lot. As explained in the
2.3.3.4, the reduction of the number of laps is going to help to get a
statistically significant regression since it is going to reduce the number of
laps which are potentially subject to the increase of volatility of the ranking
of runners over laps. Eventually, this choice is interesting because races are
going to be more comparable in terms of number of intervals. Therefore, we will
be able to assess if the variation of the estimates in absolute value in
function of the distance is a real thing or just a statistical phenomenon due
to the bigger number of laps.
Strategic Behavior in Sport Contests 40
Because of these practical but also methodological reasons,
the number of studied intervals for 800m races will be of 4, e.g. each 200m
interval, the number of studied intervals for 1500m will also be of 4,
following the splits of the race analysis reports (400-8001200-1500), and for
5000m the number of studied intervals will be of 5, e.g. each 1000m.
This frame delimitation will, I hope, enable me to measure as
accurately as possible the strategic behavior of contestants in the case of
middle-distance running depending on their pre-race status. This pre-race
status, which is based on the place of the runners in the previous round in
Boyd and Boyd's experiment, will be for this study defined by a combination of
data available prior to the race. The methodology used to determine this proxy
will be discussed in the following part.
3.2 Underdog-Favorite Variable Implementation
The game of predicting who is going to win a race is very
popular among observant of athletics competitions. In order to predict
correctly the outcome of a race, a lot of parameters is usually taken into
account by the persons who play it. The interesting fact about this game is
that it can be assimilated to the pre-race favorite variable since this
variable is a perception of who is going to win the race, which is the same
process than when someone is predicting it.
To predict who is favorite of a race and who is not, the
relevant and easily collectable data are, to my opinion, the following:
- The personal best of the runner, this is the most
obvious data to collect. Indeed, the first thing that runners look about their
opponents is their respective PBs since it is the best measure they can have on
how fast the opponent can run the distance in the case the race is fast, and
what margin they have between their PBs pace and the race pace if the race is
slow.
- The season best of the runner, which is the best
time the runner has run the distance during the year. This data is interesting
for the same reason than the PBs. Moreover, it brings information on the
current shape of the runner, indeed by taking SB into account in the parameter,
we are able to ponder the PB of the runner if his PB has been done 10 years ago
for example. For example, in 2019, if a runner A who has a PB of 3'28»53
at 1500m done in 2009 and a SB of 3'34»45, he will be probably ranked
behind a runner B who has run 3'30»32 in 2019 since the «real»
level of runner A in 2019 is much closer to 3'34»45 than 3'28»53.
Strategic Behavior in Sport Contests 41
There are other data that are highly relevant in my opinion to
take into consideration but that are note easily collectable even though they
can be estimated by other data easier to collect:
- the final kick of the runner. In middle distance
races, and especially for championships races, one key asset to have in order
to be able to win the races is to be able to have a high finishing speed. This
can be also seen in championships by the fact that, often, runners from the
below distances try their chance on the superior distance to try to get
something thanks to their superior speed. Indeed, tactical races, which are
usually the rule of finals, are races that are usually ran slowly in the first
two thirds of the race, with a strong acceleration in the last third to the
last quarter of the race. This slow pace does not tire off completely the
runners from shorter distances such as would have done the pace in a meeting.
Therefore, they are still «fresh enough» to use with full capacity
their final kick in the last part of the race and this kind of effort is much
closer to the distance they are used to run which gives them a significant
advantage. To represent this aspect of championships races, I decided to take
the PB of the runner on the distance just below the studied distance. This PB
was taken in an area of 3 years before and after the studied race because the
idea is not to get the level of the runner on the distance but his potential to
run fast, which is generally constant over time. When the data was not
available, I used the following rules to fill the gaps:
Distance Men Women
800m 47.5 for all runners without data 55 for all runners without
data
1500m PB on 1500m divided by 2 PB on 1500m divided by 2
5000m PB on 3000m speed + 6.5% PB on 3000m speed + 6.5%
Table 8. Rules for Estimation of the Missing
Data
For the explanations on the estimation of the PB on the
shorter distance, I need to explain a concept first. For every distance there
are two profile of runners, the short profile and the long profile. The short
profile is the runner who has abilities on the distance and the shorter
distance. The long profile is the runner who has abilities on the distance and
the distance above. The problem with long profile runners is that they often do
not run on the distance below, therefore their PB on the shorter distance has
to be estimated. The estimation of the final speed of the runner in a race for
the 800m is the trickiest one. Indeed, the 800m is the distance that is at the
limit between the sprint and the middle-distance race. Therefore, to estimate
the final speed of an 800m with his level on 400m is
Strategic Behavior in Sport Contests 42
probably less relevant compared to 1500m and 5000m. therefore,
and to limit the impact of the 400m on the results, I decided to take the same
value of PB for every runner with lacking data, which are runners that have a
long profile rather than a short profile or that have an insufficient PB on the
distance because they do not run 400m at their best shape or often enough have
been given a time on 400m which is the minimum level they need to have in order
to qualify for a world class competition. For the men for example, the minimum
level to get into a world final is of 1'45»50 on 800m. To do this time,
runners need to pass at least 51» at the 400m because 800m is a positive
split race, i.e. a race where the second part of the race is slower than the
first part, because of the energetic sector that is used in this event (lactic
anaerobia). Therefore, to be able to pass in 51sec-onds at the 400 with
sufficient margin on their 400m PB to finish the race correctly, this margin
needs to be of 3.5 seconds, which gives an estimated PB on 400m of 47.5 seconds
for men. The same calculation was made for women and gave the estimated PB on
400m of 55.0 seconds. For the 1500m, the calculation method is based on a very
popular model in the world of athletics that stipulates that a 1500m runner
with a longer profile can run his 1500m in a time which is twice is time on
800m. This method of calculation of is usually very accurate and I decided to
use it. Moreover, there is no risk that a 1500m runner with a short profile
might get this estimation because these runners usually run 800m in reality
since the two races are quite close and do not necessitate different
preparations in the training. For the 5000m, I took the 3000m into
consideration since if a 5000m runner has not run a 1500m, it is because he has
a long profile and the short distance for 5000m long profile is 3000m. Then I
used the fact that an elite athlete can run a 3000m at his maximum aerobic
speed (MAS). Then as it has been proven that an elite runner can run 1500m at
106.5% of his MAS (Scherrer & Monod, 1960; Ettema, 1966), I estimated this
way the PB of the 5000m runner over 1500m.
- the experience and the tactical sense of
the runner, for every contests, it seems an evidence that the experience of a
runner is a substantial help to his claim for victory. Indeed, it will help him
to deal with pressure, to feel when to make his effort, etc. Moreover, and as
the parameter that we try to determinate in this part is the perception of how
favorite a runner is and how this parameter influences his strategy but also
the relative strategy of other runners, it is important to note that a runner
who has a lot of experience and who has one titles in the past is usually
perceived as favorite by other runners. Indeed, even if every runner in a World
final is a fierce competitor, it is easier to frighten your opponents if you
are the reigning world champion and world record holder than if you
Strategic Behavior in Sport Contests 43
are a runner who has never won anything in his life and for
who this race is the first final in an international championship. Therefore,
the champion has more chances to influence the strategies of the other runners,
because being afraid, they will try to surprise him in order to have a chance
to beat him, while the newbie will not be calculated. In order to represent
this impact, I will take the previous honors that the runner has won in his
career to represent his experience. The advantage of taking the previous honors
of a runner is that it will also be a good representation of the tactical
intelligence of the runner. Indeed, to be able to win or to finish in the first
places of a world championships or a continental championship is a good
indicator of the tactical intelligence of a runner, since without tactical
sense, it is very complicated to get in these places, unless you are much
stronger than other, but this will be compensated by the PB and SB data in the
frame of my underdog-favorite variable proxy. To represent the effect of the
experience over a runner I decided to use the system of a multiplier. Each
level of experience will be given a coefficient that will multiply the score
that the runners will have obtained with the other gathered data. The
multipliers follow the rule in the Table 9:
Honor Coefficient
World Champion or Olympic Champion 0.10
World Podium or Olympic Podium 0.08
World Indoor Champion or Continental Champion 0.06
World Indoor Podium, Continental Podium, Diamond League Winner in
the last 0.04
2 years, or World Championships Top 5
Continental Indoor Champion, Continental Championships Top 5,
World Cham 0.02
pionships Top 8
Continental Indoor Podium or Continental Championships Top 8
0.01
|
Bonuses and maluses:
- World Record Holder
- Last Winner of Global Championship
- Running at Home
- Last big performance is more than 2 years old
- Honor obtained on another distance
|
+0.05
+0.02
+0.02
-0.01/year
-0.02
|
Table 9. Honors Multiplier Settings
The logic of this settings is the following, a World
Championships honor is superior to a Continental honor but also to a World
Indoor Championships honor because usually, the indoor season is not as dense
as the summer season, because a lot of middle distance
Strategic Behavior in Sport Contests 44
runners prefer either to run in cross-country running or to
train a lot in order to be better in the summer. Therefore, the level of these
indoor competition is not as high as the outdoor competition and are therefore
similar to an outdoor continental level. The bonuses and maluses are here to
affine the analysis. Indeed, in the perception of a lot of runners, to be the
world record holder makes of you a kind of a legend of your sport, therefore, a
big bonus is given to the runner who is the holder of this record on this race.
Anyway, the case happens just once in the study for the Kenyan David Lekuta
Rudisha on the men 800m, so its impact is not very significant. A more
significant bonus is the last global championships winner. In terms of
perception of who is a favorite of the race, the memory of runners who have
usually witnessed or participated to last final of a global championships
reminds them a lot of who won the last race and therefore they usually adapt
their strategy to this parameter. Eventually, I added the running at home bonus
to represent the fact that some runners are inspired by the fact of running in
his country in front of his friend and family and this inspiration can lead to
big surprises since it helps these runners to surpass themselves. The maluses
are here to represent the fact that the relevance of honors diminish rapidly
with the time passing, and that an honor obtained on another distance is not as
good a predictor as an honor on the same distance for.
Eventually there are some other data that are relevant such as
the weather preferences, the previous results of runners in
direct confrontation. But this kind of data is too complex to be collected and
will be therefore let out of the model.
Now that all the data that need to be required has been
defined it is time to build our underdog-favorite parameter. Note that all the
data concerning athletes have been collected from the respective athlete
profile on the website of World Athletics. If we define ?? as
the year of the race, ???? the year in which the runner
realized his PB. If ???? is the PB of the runner over the
distance and ???? his SB over the distance. Then we can do a
weighted average of the PB and the SB of the runner. This way, the older is the
PB of a runner the less its influence will be strong on the time that will be
implemented in the variable. We therefore define the estimated time over the
distance ?????? as:
(?? - ????)???? + ????
?????? = (??- ???? + 1)
Once this variable representing the estimated time is
obtained, we want to incorporate into it the variable that represent the final
kick of the runner, which is his time over the distance just below,
???????. The problem is that this two data are times that
represent
Strategic Behavior in Sport Contests 45
different distances; therefore, it is difficult to aggregate
them simply by adding the times or by combining them.
Luckily we have a very practical tool in the world of
athletics that help us to compare the level of performance of athletes in
events that have nothing in common such as the hammer throw and 50km Walk Race:
the Scoring Table of Athletics (Spiriev & Spiriev, 2017). This table
enables the comparison between all events of athletics by scoring the possible
performances for each event on a 1400 points table. This table is built
statistically from the World Record and the global level of performance over
the years. This table is modified every 3 years and I took the latest version
(2017) for my study. In this table, a World Record is usually around 1300
points, an international level runner is around 1200 points, a continental
level runner is around 1100 points, and a national level runner is around 1000
points in France. This way, if we take the barrier of the 1200 points, we can
say that 20»13 on Men 200m is equivalent to 13'02»56 on Men 5000m,
17.33m in Men Triple Jump but also 66.55 m for Women Javelin Throw since the
table is built with the same method for women. Thanks to this table, it is
possible to combine the estimated time on the distance and the time on the
shorter distance by converting the times of each distance in the scoring table.
In order to represent the fact that, the time of the runner on the distance is
still more important that his final kick, I decided to put a 2/3; 1/3 balance
in favor of TDist. Then to implement the
experience and the tactical sense of the runner, I combine the raw score
obtained by the combination of the two times with the relative multiplier
m calculated by the analysis of the athlete profile
on World Athletics Database. I obtain this way the
Favoriteindex which is:
2 1
Favoriteindex = (1 + m)
·
(3TDist + 3 Tshort)
This index is built such as the greater is
Favoriteindex, the more chances
he will have to be considered as a favorite of the race in the empirical model.
This way I hope to have built a variable relying on data that will give a
strong indication of who is perceived as the favorite before the race when
applied to the empirical model, and therefore, that I will have improved Boyd
and Boyd experiment.
The empirical model that I am going to use is largely inspired
by the empirical model used by Boyd and Boyd (1995) but with the slight
modifications explained in the 3.1 and
3.3 Empirical Model
Strategic Behavior in Sport Contests 46
3.2. For a race with T successive
intervals. Let's Rtt be the ranking of the
runner i over the interval
t, with t = 1, 2, ..., T.
My interest is to analyze the manner in which Rtt
evolves over the course of the race. As for Boyd and Boyd, this
is modelized with the relationship:
((~~
(1) Rtt = flit + at +
utt
Where, as for Boyd and Boyd,
atcaptures unmeasured runner specific effects that
might influence the strategy of a runner and which are individual,
utt the error terms, which also change
over individuals and intervals, are independent and identically distributed,
and the fit
coefficient which measures how the runner's position evolves
during the race. fit
is different for each runner i, I also
classify it such as it is a function of each individual runner's predicted
measurement of race favorite or underdog. This enable them to conjecture the
following relationship for fit:
(2) fit = fio + fi1UFt
where UFt is a proxy for the
runner's status as a pre-race favorite or underdog. UF
settings are such as it is positive, integer valued, and the
bigger is this proxy, the more the athlete is considered as a pre-race
underdog. UFt is given for each runner
i by ranking them with
Favoriteindex developed in the part 3.2.
The runner who has the greatest Favoriteindex gets
for UFt value 1 the second runner who has the biggest
Favoriteindex is given the UFt
value 2 and so on until all runners have a value for their
UFt with the runner with the lowest
Favoriteindex being given as
UFt the number of participants in the race.
By substituting the Equation 2 into the Equation 1, I
generate just as Boyd and Boyd did an Equation where the relative ranking of
each runner i over the interval t
is a function of the current interval ranking t
and the interaction term t
·
UFt:
(3) Rtt = fiot + fi1tUFt + at
+ utt
Partially differentiating the Equation 3 like Boyd and Boyd
with respect to t, I obtain therefore:
ôRtt
(4) et = fio + fi1UFt = fit
Like for Boyd and Boyd experiment if the theoretical results
of Baik and Shogren are correct, underdogs have an incentive to overexert
effort early in a race whereas favorites have an incentive to let them do,
saving energy for the end of the race. In this case,
fio is negative,
fi1 is positive, and both are
statistically significant.
Like Boyd and Boyd, I use fixed effects (Mundlak, 1978;
Greene, 1993) to separate individual characteristics that affect the relative
position over time (at) from interval-to-
Strategic Behavior in Sport Contests 47
interval strategic behavior stemming from the individual
status as a pre-race favorite or underdog (Ni) and
which represents unobservable individual characteristics such as physical
attributes that may be a form of misspecification of the model and may bias the
estimates No
and Ni. Each
ai is unobservable, but constant over time, therefore its effect
can be removed by taking into consideration deviations from the mean.
Furthermore, by specifying Ni as a function of
pre-race status as given in Equation 2, what seemed to be individual-specific
slope characteristics in Equation 1 is estimated by
No and
N1. This way, I am able to obtain unbiased estimators
for Equation 3 using fixed effects model, just like Boyd and Boyd did in their
experiment:
(5) Rit - Ri = No(t- t) + Ni(t- t)UFi +
vit
where Ri = 1 /T E Ri?
? ??? is the average position of the
ith runner over the T
intervals of
the event, f is the mean interval of
the event and the error terms vitare again
independent and identically distributed. I pooled the data for each athlete
like Boyd and Boyd did within an event which enables me to estimate Equation 5
using ordinary least squares, which provides me consistent estimates of
No and
Ni for each race.
4 Results
The result section will be organised in the following way: in
a first time, I will verify that my perception of who is favorite of the race
has a good correlation with the final result. Then, in a second time will be
presented the results of regression race by race classified by event. The only
aggregation of data that will be done at this stage will be done by event and
by sex. In a third time, I will present the general results of the regression
by aggregating both sexes. Eventually, I will present the results obtained by
dividing the studied population in order to study the difference in strategic
behavior in function of the characteristics of this population. The results
analyzed are the Student statistics (T-Stat), the critical probability (Crit-P)
and the R2 since they were the results analyzed by Boyd and Boyd.
4.1 Validation of the Favorite Index
Of primary concern for this study is to know if the favorite
index is a good one. In order to verify it, the solution, in my opinion, is to
verify if the expected result of runners that is predicted by the
Favoriteindex is a good explainer of the
final result. For this, I did a
Strategic Behavior in Sport Contests 48
regression of the final result by the proxy that is given for
each race by the ?????????????????????. Therefore, I tried to
explain the final result with the predicted position of the proxy. For example,
if a runner had the third best ????????????????????? of his
race, his proxy value was 3. I tried to figure out with this regression how far
is the final result for runners from this proxy value. If the
?????????????????????. model is a good estimator of the
underdog-favorite variable, then the coefficient ??? of the
regression should be close to 1, for a model, of regression such as:
??? = ??? · ???? + ??
where ??? is the final position of the runner
?? at the end of the race, ??? ? is the
predicted final position calculated thanks to the favorite index, and
?? is the error term. The results for this regression are the
following Table 10:
??? T-Stat Sign. Crit-P N R2
???? 0.931 42.67 *** 4,81E-124 279 0.868
Table 10. Results of Underdog-Favorite Parameter
Regression
The number of runners studied is of 279, this means that we
compared the final ranking with the predicted ranking built with the
????????????????????? 279 times. As expected, the coefficient
of the regression ??? is close to 1. Moreover, it is highly
significant and the R2 is of 0.862. These observations enable us to
assert that the ranking predicted with the use of the
????????????????????? is a good explainer of the final result
of the race. This result validates the use of the ?????????????????????
as a method to determine who is the pre-race favorite.
4.2 800m Races Results
Concerning the 800m, the results of Boyd and Boyd were
interesting in the way that it was the distance for which their results had
been the least significant. For the 800m, four women finals and four men finals
were studied. Each of these finals had 8 runners that contested over a race
sliced in four intervals which gives 32 estimations of ????
for these events. The results are presented in the following Table 11.
Every time, before the detailed results for each race, which is the equivalent
of the result presented by Boyd and Boyd, I aggregated the results for all the
races below. This way, I am able to evaluate the general behavior on 800m races
for women and for men and see if there is a significative difference. Moreover,
by aggregating the data, I improve the significance of my regressions since the
number of position ???? is greater, as the compilation of all
the aggregate
Strategic Behavior in Sport Contests 49
races studied is analyzing the evolution of ????
on 128 different positions. The results for the 800m event are the
following:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
Women
|
-0.238
|
-0.695
|
|
0.489
|
0.053
|
0.779
|
|
0.437
|
128
|
0.005
|
|
2013 W
|
-0.300
|
-0.749
|
|
0.692
|
0.067
|
0.449
|
|
0.657
|
32
|
0.007
|
|
2015 W
|
-0.311
|
-0.407
|
|
0.687
|
0.069
|
0.457
|
|
0.651
|
32
|
0.007
|
|
2017 W
|
-0.654
|
-1.136
|
|
0.265
|
0.145
|
1.275
|
|
0.213
|
32
|
0.053
|
|
2019 W
|
0.311
|
0.476
|
|
0.674
|
-0.069
|
-0.476
|
|
0.637
|
32
|
0.008
|
|
Men
|
-0.541
|
-1.547
|
|
0.124
|
0.126
|
1.826
|
*
|
0.070
|
128
|
0.026
|
|
2013 M
|
-0.921
|
-1.236
|
|
0.226
|
0.205
|
1.387
|
|
0.176
|
32
|
0.062
|
|
2015 M
|
-1.596
|
-2.559
|
**
|
0.016
|
0.380
|
3.074
|
***
|
0.005
|
32
|
0.249
|
|
2017 M
|
-0.782
|
-1.005
|
|
0.323
|
0.174
|
1.128
|
|
0.269
|
32
|
0.042
|
|
2019 M
|
1.135
|
1.875
|
*
|
0.071
|
-0.252
|
-2.104
|
**
|
0.044
|
32
|
0.132
|
* Significant at the level of 10% ** Significant at the level of
5% *** Significant at the level of 1%
Table 11. Results of the 800m Races
As for Boyd and Boyd experiment, the results for the 800m are
not very significant and are rather ambiguous. For women, no race has
significant estimates of ??? and ??? at the
critical probability of 10% and the aggregation is not significant. However, we
can note that for the women races, at the exception of the 2019 final, the
signs are such that they validate the Baik and Shogren hypothesis, which is
that ??? is negative and ??? is positive. The
estimates for ??? and ??? for the aggregation
of women races is not significant either, but their signs seem to confirm Baik
and Shogren hypothesis. For men the results are a little bit better but more
ambiguous, the estimates of the races from 2013 to 2017 have signs that confirm
the hypothesis of Baik and Shogren and the race of 2015 is even significant at
the level of 5%. But the 2019 final estimates are significant at the level of
10% with signs that are opposite to Baik and Shogren hypothesis. Despite this
data opposite to the expected result, the aggregation of the men 800m races
data gives estimates with a small significance at the level of 10% for
??? and with a critical probability of 12,4% for
???. This means that if the 2019 race was ejected out from the
sample, the results would be probably significant for the aggregated races. As
a conclusion of these results, we can say that the results for the 800m are as
ambiguous as the results of Boyd and Boyd experiment and it is complicated to
validate Baik and Shogren hypothesis.
Strategic Behavior in Sport Contests 50
4.3 1500m Races Results
Concerning the 1500m, the results of Boyd and Boyd results had
been for the validation of Baik and Shogren hypothesis with significant
estimates for men's races and non-significant estimates for women races. As for
the 800m, four women finals and four men finals were studied. Each of these
finals had 12 runners that contested over a race sliced in four intervals which
gives 48 estimations of ???? for each of these events. The
results are presented in the following Table 12. As for 800m, before the
detailed results for each race, I aggregated the results for all the races
below. This way, I am able to evaluate the general behavior on 1500m races for
women and for men and see if there is a significative difference. Moreover, by
aggregating the data, I improve the significance of my regressions since the
number of position ???? is greater, as the compilation of all
the aggregate races studied is analyzing the evolution of ????
on 192 different positions. The results for the 1500m event are the
following:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
Women
|
-0.468
|
-1.192
|
|
0.235
|
0.072
|
1.349
|
|
0.179
|
192
|
0.010
|
|
2013 W
|
-0.936
|
-1.189
|
|
0.241
|
0.144
|
1.346
|
|
0.185
|
48
|
0.039
|
|
2015 W
|
0.514
|
0.586
|
|
0.561
|
-0.079
|
-0.663
|
|
0.511
|
48
|
0.010
|
|
2017 W
|
-1.009
|
-1.175
|
|
0.246
|
0.155
|
1.331
|
|
0.190
|
48
|
0.038
|
|
2019 W
|
-0.441
|
-0.676
|
|
0.503
|
0.068
|
0.765
|
|
0.448
|
48
|
0.013
|
|
Men
|
-0.656
|
-1.643
|
|
0.102
|
0.101
|
1.86
|
*
|
0.064
|
192
|
0.018
|
|
2013 M
|
-0.441
|
-0.512
|
|
0.611
|
0.068
|
0.580
|
|
0.565
|
48
|
0.007
|
|
2015 M
|
-1.845
|
-2.366
|
**
|
0.022
|
0.284
|
2.679
|
**
|
0.010
|
48
|
0.138
|
|
2017 M
|
0.218
|
0.279
|
|
0.782
|
-0.034
|
-0.316
|
|
0.754
|
48
|
0.002
|
|
2019 M
|
-0.554
|
-0.687
|
|
0.496
|
0.085
|
0.778
|
|
0.441
|
48
|
0.013
|
Table 12. Results of the 1500m Races
For women, no race has significant estimates of ???
and ??? at the critical probability of 10% and the
aggregation is not significant. However, we can note that for the women races,
at the exception of the 2015 final, the signs are such that they validate the
Baik and Shogren hypothesis, which is that ??? is negative and
??? is positive. The estimates for ??? and
??? for the aggregation of women races is not significant
either, but their signs seem to confirm Baik and Shogren hypothesis. For men
the results are a little bit better, at the exception of the 2017 final, the
estimates of the races have signs that confirm the hypothesis of Baik and
Shogren and the race of 2015 is even significant at the level of 5%. The
Table 13. Results of the 5000m Races
Strategic Behavior in Sport Contests 51
aggregation of the men 1500m races data gives estimates with a
small significance at the level of 10% for ??? and with a
critical probability of 10,2% for ??? which is very close of
being significant. Therefore, we can conclude from this that Baik and Shogren
hypothesis on strategic behavior are somewhat validated by the results of the
men races.
4.4 5000m Races Results
Concerning the 5000m, the results of Boyd and Boyd results had
been for the validation of Baik and Shogren hypothesis with significant
estimates for men's races and no results for women since in 1992, women were
not allowed to run this distance, and were running the 3000m. As for 800m and
1500m, four women finals and four men finals were studied. Each of these finals
had 15 runners that contested over a race sliced in five intervals which gives
75 estimations of ???? for each of these events. However, for
the 2017 men final, a runner did not start the race and was therefore not
accounted in the results. The results are presented in the following Table 13.
As for 800m and 1500m, before the detailed results for each race, I aggregated
the results for all the races below. This way, I am able to evaluate the
general behavior on 1500m races for women and for men and see if there is a
significative difference. Moreover, by aggregating the data, I improve the
significance of my regressions since the number of position ????
is greater, as the compilation of all the aggregate races studied is
analyzing the evolution of ???? on 300 different positions for
women and 295 positions for men . The results for the 5000m event are the
following:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
Women
|
-1.049
|
-4.305
|
***
|
0.001
|
0.131
|
4.571
|
***
|
0.001
|
300
|
0.066
|
|
2013 W
|
-1.583
|
-3.041
|
***
|
0.003
|
0.198
|
3.456
|
***
|
0.001
|
75
|
0.142
|
|
2015 W
|
-1.414
|
-2.421
|
**
|
0.018
|
0.177
|
2.752
|
***
|
0.008
|
75
|
0.095
|
|
2017 W
|
-1.222
|
-2.322
|
**
|
0.023
|
0.151
|
2.610
|
**
|
0.011
|
75
|
0.086
|
|
2019 W
|
0.023
|
0.051
|
|
0.959
|
-0.003
|
-0.058
|
|
0.9591
|
75
|
0.000
|
|
Men
|
-0.815
|
-2.537
|
**
|
0.012
|
0.105
|
2.932
|
***
|
0.004
|
295
|
0.029
|
|
2013 M
|
-0.863
|
-1.217
|
|
0.228
|
0.108
|
1.383
|
|
0.171
|
75
|
0.026
|
|
2015 M
|
-1.991
|
-3.159
|
**
|
0.002
|
0.249
|
2.752
|
***
|
0.001
|
75
|
0.152
|
|
2017 M
|
-0.388
|
-0.592
|
|
0.556
|
0.059
|
0.771
|
|
0.443
|
70
|
0.009
|
|
2019 M
|
0.017
|
0.030
|
|
0.977
|
-0.002
|
-0.034
|
|
0.973
|
75
|
0.000
|
Strategic Behavior in Sport Contests 52
For women, the results are globally very significant. The
estimates of ??? and ??? for the finals of
2013, 2015 and 2017 are significant at the 5% level, and their signs validate
the hypothesis of Baik and Shogren. The only contradictory result is for the
2019 final for which the signs of the estimates are opposite to Baik and
Shogren hypothesis, but this result is not significant and therefore can be not
overlooked at. The estimates for ??? and ???
for the aggregation of women races is very significant in the
validation of Baik and Shogren hypothesis since their critical probabilities
are at the level of 1%. For men the results are a little bit shallower, the
estimates of the races have signs that confirm the hypothesis of Baik and
Shogren but not at the significant level of 10% at the exception of the final
of 2015 which is significant at the 5% level. As for women, the 2019 final is
not validating Baik and Shogren hypothesis but as the estimates are pretty
insignificant, the result does not have much impact on the results of the
study. The aggregation of the men 5000m races data gives however significant
estimates at the level of 5% for both estimates. Therefore, we can conclude
from this that Baik and Shogren hypothesis on strategic behavior are validated
by the results of the 5000m races.
4.5 Aggregated Results
For this part, I did something that Boyd and Boyd did not do
in their experiment, which is to aggregate all the data of both sexes for each
event in order to see if the behavior is different from one race to another.
Moreover, I have aggregated the data of all races in order to see if there is a
general strategic behavior that is significant and verifiable for all
middle-distance races. The results are presented in the following Table 14:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
800m
|
-0.390
|
-1.598
|
|
0.111
|
0.090
|
1.858
|
*
|
0.064
|
256
|
0.014
|
|
1500m
|
-0.562
|
-2.014
|
**
|
0.045
|
0.086
|
2.281
|
**
|
0.023
|
384
|
0.013
|
|
5000m
|
-0.933
|
-4.535
|
***
|
0.001
|
0.118
|
5.182
|
***
|
0.001
|
595
|
0.043
|
|
General
|
-0.570
|
-4.240
|
***
|
0.001
|
0.081
|
4.914
|
***
|
0.001
|
1235
|
0.019
|
Table 14. Aggregated Results
The results of the aggregated data are really interesting;
indeed, it increases the significance of the estimates for every event. For
example, once the data of men and women are aggregated for 800m, the estimates
are almost significant while it was very difficult to obtain any significance
for this distance. The estimate of ??? is significant at the
10%
Strategic Behavior in Sport Contests 53
level and the estimate of f.??
is almost significant at the 10% level since its critical
probability. And the interesting point is that the signs of the estimates agree
with the hypothesis of Baik and Shogren which enables to affirm that on 800m,
if by taking the case of a particular race, it is not possible to assert that
underdogs overexert their effort in the first stages of the race. But if a
sufficiently big number of races is aggregated in the database, then it can be
affirmed that this tendency of underdog's behavior is real, even for 800m. This
conclusion is strengthened by the results obtained by the 1500m and the 5000m.
Indeed, the 1500m estimates are significant at the level of 5% and the 5000m
estimates are significant at the level of 1%. The signs of the estimates for
1500m and 5000m all confirm the hypothesis of Baik and Shogren. Eventually, if
the data for all races is aggregated, the results are highly significant and in
the sense of Baik and Shogren hypothesis since the signs of the estimates
support their hypothesis and that they are significant at the level of 1%.
Since the races are different, we can therefore conclude with a small margin of
possible error, that in the context of middle-distance races, the hypothesis of
Baik and Shogren are correct. This mean that in a situation of a competition
where there is a clear favorite to the race, the more a runner is an underdog,
the more is level of effort will be high at the beginning of the race, while
the more a runner is a favorite, the more is level of effort will be high at
the end of the race.
Another interesting point observation is that the magnitude of
the f.?? coefficients is proportional to
the race distance and it seems, even if the progression is not perfect, that
the magnitude of the f.?? coefficients is
also proportional to the race distance. This is opposite to what Baik and
Shogren had found in their results, and as this time, there is no bias due to
the greater number of laps. This mean that the gradient of runners is much
steeper in the long-distance races than in the short races, therefore, this
means that the pre-race favourites tend to move to the front of the peloton
much faster in the longer races. This can be explained by the facts that in
longer races, favorites may have an incentive to start tiring off the runners
from shorter distance with a medium intensity pace.
4.6 Analysis of Strategic Behavior in Middle-Distance
Races
This part will be consisting in the analysis of the possible
variations of strategic behavior in contests by analysis of the population
through its characteristics. The analyzed characteristics will be the gender of
participants, the cultural background of the participants, and the density of
the races.
Strategic Behavior in Sport Contests 54
4.6.1 Impact of Gender on Strategic Behavior in Contests
The first and most obvious impact to be tested is the impact
of gender on the strategic behavior. Boyd and Boyd had found that the results
for men were slightly more significant than the results for women. I divided
therefore my population in two based on their gender and did the regression for
men and the regression for women in order to see if there is a significant
difference in the result. There are 139 men and 140 women in the sample which
gives 615 rankings ???? to study for men and 620 for women.
The results are the following:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
Men
|
-0.406
|
-1.992
|
**
|
0.046
|
0.059
|
2.341
|
**
|
0.019
|
615
|
0.020
|
|
Women
|
-0.731
|
-4.144
|
***
|
0.001
|
0.103
|
4.766
|
***
|
0.001
|
620
|
0.035
|
|
General
|
-0.570
|
-4.240
|
***
|
0.001
|
0.081
|
4.914
|
***
|
0.001
|
1235
|
0.019
|
Table 15. Gender and Strategic Behavior
What we can say on a first basis is that results for women are
more significant than the results for men. The estimates of women are also
bigger than the estimates of men in absolute value with a ???
of -0.731 for women versus -0.406 for men, and a
???of 0.103 for women versus 0.059 for men. This means that
their gradient is steeper, therefore that women tend to move to the front of
the pack sooner than men in races. To see if the estimates are significantly
different for men and women, I realised a test of Chow (Chow, 1960), which is a
statistical and econometrical test in order to determine if the coefficients
established by a linear regression of two linear series are equal. This test is
based on the Fisher's law. This test realised with the software Gretl gives a
F-Stat of 0.588 which gives a critical probability of 62%. Therefore, we can
conclude that there is no significant difference in the strategic behavior of
men and women in middle distance races.
4.6.2 Impact of Culture on Strategic Behavior in Contests
Another impact that I would like to test is the impact of
culture on strategic behavior. Indeed, it seems interesting to see in the
cultural background of contestants can have an influence on their strategic
behavior, since most of our intellectual constructions and way of thinking are
actually based on our cultural background. Therefore, I believe there should be
an impact between culture and strategic behavior. To test this hypothesis, I
divided my population by nationality in four groups. Africa & Middle
Orient, America, Europe, Asia and Oceania. The nationality taken was the
nationality at the birth of the
Strategic Behavior in Sport Contests 55
runner and not the country they represent during the
competition. Indeed, a lot of African runners are paid by countries in order to
win medal for them in exchange of their nationality, these runners are
considered as African & Middle Orient, not Asian or European. The
population studied had 132 Africa & Middle Orient (AMO) runners, 59 America
(AME) runners, 76 Europe (EUR) runners, and 12 Asia and Oceania (ASO) runners.
The results are the following:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
AMO
|
-0.774
|
-4.252
|
***
|
0.001
|
0.135
|
5.021
|
***
|
0.001
|
590
|
0.041
|
|
AME
|
0.731
|
2.524
|
**
|
0.012
|
-0.075
|
-2.451
|
**
|
0.015
|
258
|
0.025
|
|
ASO
|
-2.879
|
-1.616
|
|
0.112
|
0.256
|
1.834
|
*
|
0.072
|
57
|
0.071
|
|
EUR
|
-1.251
|
-4.201
|
***
|
0.001
|
0.155
|
4.228
|
***
|
0.001
|
330
|
0.054
|
|
General
|
-0.570
|
-4.240
|
***
|
0.001
|
0.081
|
4.914
|
***
|
0.001
|
1235
|
0.019
|
Table 16. Culture and Strategic Behavior
The results of this analysis are very interesting. Indeed, and
to the exception of Asia & Oceania runners (but that can be explained by
the small number of observations for this culture, and it is very close to
significance, since the estimate for ??? is significant at the
10% level and the estimate for ??? has a critical probability
of 11.2%), all cultures have significant estimates for ??? and
??? at the level of 5% which means that they all have a
tendency in strategic behavior. However, we can notice that if Africa &
Middle Orient runners and Europe runners estimates signs confirm the hypothesis
of Baik and Shogren, the signs of the estimates for the America runners are
opposite to this hypothesis, since ??? is positive and
??? is negative. This means that in a situation of contest
where there is a favorite and an underdog, American runners who are pre-race
favorites tend to overexert their level of effort at the beginning of the race,
while underdogs tend to wait until the end of the race in order to exert their
effort. By aggregating the three other populations, (AMO, ASO, EUR) in order to
have two subset of the general regression, I realised a Chow test in order to
see if the difference between the estimates for American runners is
significantly different to the estimates for runners from other part of the
World. The F-Stat for this test realised with Gretl is equal to 8.250 which
gives a critical probability of 0%. We can therefore affirm that there is a
significant difference in the strategic behavior in contests between Americans
and the rest of the word.
Strategic Behavior in Sport Contests 56
4.6.3 Impact of Density on Strategic Behavior in Contests
The last phenomenon impact that I would like to analyze in
this study is the impact of the density of competition on the strategic
behavior in contests. Indeed, if we look at races from the point of view of the
favorite, then we can think that the less dense are the races, the more
interest the favorite has to exert his effort early in the race. For example,
if we take the example of a runner who is 2 seconds ahead of any other runner
on 800m, then why would I remain inside of the peloton with the risk of being
jostled, the risk to fall, to be surprised by an unexpected attack while I am
blocked by other runners, etc.? We can imagine that in such cases their may be
an incentive for the favorite to overexert his level of effort in the first
stages of the race, since he knows that he has such a margin over other runners
that for whatever his margin may be, there is still a chance for him to win.
This reasoning can be reproduced for the second and third biggest favorites who
might want to eliminate potential rivals for the race to the podium. In order
to represent this phenomenon, I decided to divide the 24 races that I studied
in two classes, the low-density races and the high-density races. For this, I
studied for each races the difference in percentage between the runner with the
highest estimated time ?????? (see 3.2 for the explanations on
the calculation of this variable) with the eighth runner with the highest
estimated in order to avoid the bias of the number of runners in the races.
Indeed, there is only 8 runners in an 800 m final while there are 15 of them in
a 5000m final. This means that the probability of having the fifteenth runner
of a 5000m final with a ??????being farther from the best one
than the eighth runner in an 800m final is pretty high. Moreover, runners that
are ranked ninth are farther have usually but a marginal influence on a race,
therefore their impact on the density of the race can be considered as
negligible. Once the density was determined for each race, I ranked them by
level of density and separated the sample of race in two subsets: one with the
races for which the density was above 2.5% and are categorized as Low-Density
Races (LDR), one with the races for which the density was below 2.5% that I
categorized as High-Density Races. There are 13 HDR in the studied sample and
11 LDR. The results of the regressions for the two subsets are the
following:
|
Race
|
???
|
t-stat
|
Sign.
|
Crit-P
|
???
|
t-stat
|
Sign.
|
Crit-P
|
N
|
R2
|
|
LDR
|
-0.394
|
-2.056
|
**
|
0.040
|
0.059
|
2.429
|
**
|
0.015
|
631
|
0.009
|
|
HDR
|
-0.759
|
-4.016
|
***
|
0.001
|
0.104
|
4.595
|
***
|
0.001
|
604
|
0.034
|
|
General
|
-0.570
|
-4.240
|
***
|
0.001
|
0.081
|
4.914
|
***
|
0.001
|
1235
|
0.019
|
Table 17. Density of Competition and Strategic
Behavior
Strategic Behavior in Sport Contests 57
The results show that the two subsets follow the hypothesis of
Baik and Shogren. However, we can notice that the estimates for
f? and f?
are more significant for the high-density races than for
the low-density races which means that there is a bigger chance that the
favorites do wait the end of the race to exert their effort in races with a
high density than in races with a low density. Moreover, the absolute values of
the estimates are bigger for low-density races than for high-density races
which means that the gradient is steeper for the high-density races. This means
that in high-density races, favorites tend to move to the front of the pack
much later than in low-density races. However, we cannot say that the estimates
of the low-density and high-density races have a significant difference, since
if we realise the test of Chow for these two subsets, we obtain a F-Stat of
0.663 which gives a critical probability of 57.5%. We cannot therefore assert
that there is a significant difference between the races with a high density
and the races with a low density. This can be explained by the fact that we
took only races which are world championships finals in the study. Therefore,
the level of density is usually constant for all of these races. If we had
taken races from a lower level, like a regional level, the runners would have
been much more heterogenous in terms of level of performance, and we would have
witnessed probably a much more significant result.
5 Discussion
5.1 General Implications for Management
From a general perspective, the results are in favor and Baik
and Shogren hypothesis that in a situation of contest where there is
heterogeneity among the contestants with underdogs and a favorite, the
underdogs have an incentive to overexert their level of effort in the first
stages of the contest. Indeed, if the analysis of races taken individually may
show cases of races that have contradictory results, as soon as a certain
number of races are compiled in order to have enough data, the results follow
the predictions of Baik and Shogren and are highly significant.
These results are highly interesting because if these
strategic behaviors are applicable to athletic competition, it is a strong
possibility that they also apply in other contests which happen in different
contests such as R&D rivalry between corporations to get a lucrative or
strategic innovation, bribery to assure a profitable license, patent or
contract from the
Strategic Behavior in Sport Contests 58
government, war for a new global market that has been created
by a new innovative product, a political election where candidates fights
during long campaigns in order to get elected, or candidates who compete for a
job or to win a promotion. This could represent the fact that the underdog in
these situation, in order to have a chance to beat the favorite, is trying to
anticipate the effort of the favorite in order to have a competitive advantage
that might shake the balance of the game. This business strategy has been used
for example by Microsoft (i.e. the underdog) with the release of the Xbox 360
in 2005 that anticipated the release of its rival the PlayStation 3 of Sony by
one year. This strategy has enabled Microsoft to build the biggest possible
installed base option for players (To-maselli, Di Serio, & De Oliveira,
2008) and therefore a strategic advantage that enabled Microsoft to catch up
Sony in terms of sold home video game consoles. Another example can be the
strategy of Small and Medium Enterprises (SME) that can have a more aggressive
strategic behavior in their Human Resources Management (HRM) in their
recruitment in order to get a chance to get the best candidates. (Brand &
Bax, 2002) By overexerting their level of efforts in the early stage of the job
research of the ideal candidate, with the promise of an higher pay, the fact
that they contact the candidate instead of waiting the candidate to come to
them, they indeed increase their chances to recruit a better candidate than if
they had waited the candidate to come to them. As these results are complicated
to find in the economic environment, we have obtained them by using the example
of athletics and the result of the study seems to approve this hypothesis, at
least for sports. However, there are still some little oddities that can be
remarked in the results and that is not yet answered.
5.2 What the Analysis on Gender, Culture, and Density
Implies?
The results of this study about the impact of Gender, Culture
and Density are also very interesting. Concerning gender, the results are a
little bit different from what Boyd and Boyd had found in their study. Indeed,
they had found that the results were more significant for men than for women,
and in our experiment, it seems that the aggregated results are more
significant for women than for men. However, the differences are very narrow
and there is no significant difference between the estimates of the two subsets
men and women, even if we can notice that the gradient of the women is higher,
which means that women who are favorite of a race tend to make their move in
the latest stages of the race. This result can be in part explained by the men
can usually be more confident than women
Strategic Behavior in Sport Contests 59
in situations of competition (Gneezy et al., 2003; Gneezy
& Rustichini, 2004). If a favorite has more confidence in his capacities,
then his incentive will be to exert his effort soon in the first stages of the
race to eliminate as many opponents as possible with an elevated pace. This
observation is really interesting from a managerial point of view, because it
would mean that a managerial environment based on competition could be more
interesting for men in order to improve the immediate performance of employees.
However, this observation is I believe in this study by the fact that the
population studied is an elite that evolves in a very competitive environment,
therefore, women in a world championships final are fierce competitors and
maybe this is why this phenomenon is complicated to observe in this study.
Maybe if we had observed a population with more «amateur» athletes,
there would have been a stronger difference between men's and women's
difference.
Concerning the impact of culture, the result have been quite
surprising to me because if I expected the Africans to run differently from the
rest of the World, eventually they had the same strategic behavior than others
and it is the Americans who act differently. Not a lot of studies have studied
the association between the dimensions of culture and strategic behavior. Some
studies have studied the link between national culture and entrepreneurship
characteristics and traits (Hayton, George, & Zahra, 2002; Müller
& Thomas, 2000; Shane, Kolvereid, & Westhead, 1991) and some of these
findings may explain the fact that American still overexert their level of
effort at the beginning of races since it has been proved that entrepreneurial
traits such as risk taking and high energy levels decrease as cultural distance
from the US increases (Thomas & Müller, 2000). If risk taking and high
energy levels are cultural traits closer to American culture, then it can
explain why favorites may decide to overexert their level of effort at the
beginning of races. This difference in behavior could be a possible explanation
of why American corporations usually enter more easily foreign markets than
corporation from other country do, because from the moment they enter in the
competition, they set the level of effort required for the home compagnies at a
level that the foreign companies can never reach. However, there is another
explanation in the fact that the university athletics system is highly
developed in the US and Canada. This means that almost all young American
runners between 18 and 23 go through this systems of competitions which work
only on a championships basis. While young Europeans and young Africans run in
meetings where there are pacemakers, the Americans of the same age run in
championships. Therefore, young Americans have learned from the beginning how
to run fast in championships
Strategic Behavior in Sport Contests 60
races because they still have minimum time required in order
to qualify for International championships. They have to do these minimum time
required in the university competition where there are no pacemakers and
therefore favorites are learned to start with a higher level of effort compared
to the level of effort that favorites of middle distance races exert at the
beginning of races, because if they still try to win the race, there is still a
time to do for them, while in Europe, as soon as you have qualified for the
championship, time doesn't matter any more at all. I believe this is the most
plausible explanations of why Americans favorites have an opposite strategic
behavior compared to the rest of the world. However, we can note that this
behavior is also true for central and south American runners, even if these
runners usually go to study in American or Canadian universities and therefore
learn the same strategic patterns.
The last finding that could have interesting impact from a
managerial point of view is the fact that it seems (even if results on this
study are not significant because of the homogeneity of the population of
races) that the more a race is dense, the more favorites wait before exerting
their level of efforts. If we accept the fact that we do not obtain a
significant result because of the homogeneity of the races which gives only
races with a high level of density, this could explain for example why in the
fight for innovation, the enterprises that deposit the patent first are rarely
the ones that do the first macro-scale commercialization. (Golder, Shacham;
Mitra, 2009). However, I fear that it is the only example that we may find an
explanation in the economic world. Indeed, in the digitalized market world, the
forces in high density contests have more incentive to overexert rapidly all
their possible effort because these markets work in a fashion of «first
mover wins» and «first wins all» (Liebowitz, 2002) and the
strategy to let the underdogs do their first move is probably not the good one
since by letting underdogs grow, you may end-up with a rival bigger than you
that will make of you tomorrow's underdog. This logic can also be applied for
example in politics, where if a favorite candidate, for example the mayor
elected in the last election, has no real rival for the next election, he will
start his campaign at the last moment because he will not have the need to
campaign early and he will prefer to implement his policies as mayor instead.
On the contrary, if his election is hanging by a thread, he will start his
campaign much sooner and will exert his effort months before the election. This
is why I believe the strategic impact of density in the way that a higher
density leads to a lower exertion of effort at the beginning of the competition
is only valid for the situations like athletics.
Strategic Behavior in Sport Contests 61
5.3 Why is 800m Still not Working?
The results are not as significant for the aggregation of the
800m races than for the other studied events. Indeed, they are almost the only
aggregated results with more than four races compiled that is not significant.
But I believe an explanation to this insignificance can be found in the
characteristics of this race.
800m races are the only one that are run in positive split in
international championships, this means that the first half of an 800m final is
usually faster that the second half of the 800m. A study by Hanon, Choffin,
Descoux, Dupont, Gajer, Lacroix, Lamare, Ma-rajo, Mossant, Stéphan,
Viale, and Vollmer (2015) who analyzed all the split times in all international
finals since the Olympic Games of 1960 in Rome. He observes that on the 28
analyzed finals, 57% of them are run with a faster first half of the race. This
means that on the contrary to 1500m and 5000m, the 800m in championships is a
race that is run at a pace closer to the meeting pace in his first part than
1500m or 5000m. This can explain why favorites tend to be in front of the race
much sooner in 800m than 1500m, because the pace is high enough during the
race, therefore the chances for the favorite to be surprised by the underdog is
much lower. The fact that the 800m in championships is run closer to its pace
in meetings can also be explained by the fact that 800m is run with an
intensity around 120% of the MAS of the runner (Spencer, Gastin, & Payne,
1996; Thomas, Hanon, Le Chevalier, Couturier, & Vandewalle, 2003), this is
much higher than the value for 1500m which is 106.5% and 5000m which is 97%
(Scherrer & Monod, 1960; Ettema, 1966). This means that even, when they are
slow in the first half of the race, 800m runners run at a level that is already
much above their MAS and production of lactic acid is high even with a slow
start, which explains why it is possible to run a 800m in 1'44» with a
first lap in 51 seconds and a second lap in 53 seconds, but it is not possible
to do it with a first lap in 53 seconds and a second lap in 51 seconds. Indeed,
to run 53 seconds on 400m for 800m elite runners, it is required a speed that
is already much above their MAS. Therefore, they are usually not able to
accelerate in the last stages of the race because their muscles are completely
tetanized by the lactic acid produced by the muscles when he produces an effort
above his MAS and the last 200m of an 800 meters in championships is often the
slowest of the race while it is the fastest for 1500m and 5000m. Hanon et al.
(2015) also show this phenomenon in their study and even show that the first
and third 200m are usually the fastest ones in championships 800m because it is
the moment where runners want to place themselves in the peloton for the first
one, and
Strategic Behavior in Sport Contests 62
because it is the moment every runner accelerates to get the
best position in the final «sprint» for the third one. In fact, the
repositioning in the third 200m of 800m is more a question of getting a spot in
the peloton where I have less chances to be jostled in the last 200m where
runners know they will not be able to accelerate any more if they ever lose
speed in a hustle because of the tetanizing effect of lactic acid.
This effects means that it is a little bit more an advantage
in 800m to be in front of the pack a little bit sooner since you have less
chances to be jostled in the last 200m, and therefore lose crucial km/h, if you
are in front of the pack. It is as a consequence crucial to be able to run a
strong third 200m without exploding in the last 200m in order to win a 800m
race, this overexertion of the level of effort a bit sooner than in other
events is for me a reasonable explanation of why the study does not work as
well for 800m than for the other events.
5.4 What Could Have Been Improved in This
Study?
As explained many times in this study, the main thing that
could have been improved is the heterogeneity of the population of races.
Indeed, because of the nature of the collected data, the split times for every
runners for a number of intervals during the race, it was impossible to gather
for me data of this quality on second-tier events such as national
championships, or even continental championships because of the costs implied
by such a technology. It was of course not available either for competitions of
even lower importance such as regional races. However, such a data would be
highly interesting in order to study the difference in behavior between elite
athlete and more amateur ones, between genders, because amateur women may be
less competitive than amateur men compared to elite women versus elite men.
Therefore, a higher difference in competitive mindset may give a higher
difference of impact concerning the gender. Such a data would be also
interesting in order to see the strategic behavior in races where the density
level is above 10% or even 20%. In such a case we could well imagine that
favorites are absolutely not going to wait for the slowest underdogs and
therefore exert their level of effort according their own level from the
beginning of the race. Of course, those races would need to be championships
races, i.e. races without a pacemaker.
Another amelioration that we could make is to insert other
variables in the study, by taking into account the biological characteristics
of the runner such as his height. Indeed, a tall runner may have an incentive
to run either more in front of the peloton because his
Strategic Behavior in Sport Contests 63
long legs need more place and he wants to avoid to trip over
someone, and therefore lose energy, or at the back of it behind everybody to be
like a tower guard watching the peloton and waiting his moment to attack from
behind, surprising everybody. Therefore, if we succeeded to implement these
variables in the model, it would be very interesting the impact they can have
on the effort expenditure over the race. More variables would be needed in
order to improve the R2 of the aggregated data which is, I must
admit it a little bit low. It could be the weather preferences, or the cultural
background, since it seems to have an impact from what this studied have found.
Maybe even the density of the race could be implemented in it.
However, I believe that it will always be complicated to have
a strong R2 for this model since if there can be found patterns
based on quantitative and qualitative data, the problem of the level of effort
during a middle-distance race is that the choice of exerting the level of
effort is dynamic. Indeed, if a runner may choose before the race to take such
or such a strategy, in reality all of them adapt their strategy to the living
moment, except from the runner who chooses to go from the start and exert his
level of effort from the beginning. The decisions have to be taken so quickly
in these moments that they do not always really have the time to think their
strategy during the race, they rather react by instinct and by experience to
the behavior of other runners. It would be interesting I believe to measure the
way runners react to other runners' actions and analyze it in terms of
strategic choices in the context of a game. However, I must admit that my
mathematics level is not sufficient to apply this theory to the model.
6 Conclusion
Overall, sport has proved once again that it is a very
interesting field of study to test economics theories. The results of this
study agree with Baik and Shogren hypothesis that in a contest with sequential
moves and with heterogenous participants, the favorite has an incentive at the
beginning of the race to let the underdog overexert his level of effort. If the
fact to use the ranking of a runner over the interval instead of his position
at the end of the interval like Boyd and Boyd had done in their experiment has
reduced the significance of each race individually because of the increase of
the volatility of the runners positions on the intervals, the aggregated
results validate the hypothesis of Baik and Sho-gren with a strong level of
significance.
Strategic Behavior in Sport Contests 64
This result seems to be true also for all distances, at least
with the aggregated results, and for all sexes and cultures, to the exception
of American runners who seem to choose an opposite strategy when they are
favorite of the races. Moreover, the results do not show significant
differences in the results of men and women and in terms of density even if the
homogeneity of the sample (races of elite competitors with a very close level
one to another) may have biased the observation of these phenomenon. We also
found that it seems that the longer are the races, the sooner the favorite make
their effort. This result is contradictory with the results of Boyd and Boyd.
However, it is complicated to make real comparisons between my results and
theirs results because they had not aggregated their data and they had not
studied the races the way I did, therefore the difference of results probably
comes from the different methodology. We obtain moreover strong level of
significance for most of the results obtain and at least with one of the
estimates with a significance at the level of 10% for all the results.
I also believe that the fact that American have an opposite
strategic behavior compared to other runners is the most surprising result but
also the most exciting one. Indeed, this result shows that there is a
significant difference between Americans and other cultures and may be this
should need further research in the future in order to see if it is just a
particular case in athletics races or a more general result applicable to other
types of contests, and possibly economic ones.
I believe that the fact that I found the same results than
Boyd and Boyd despite of the fact that I changed two major important
methodologies in their study, with the creation of a favorite index and the
change from position to ranking, gives a strong support to Baik and Shogren
hypothesis, because I believe these two changes are a considerable improvement
of Boyd and Boyd experiment and makes the experiment of this study much more
supportive for Baik and Shogren hypothesis.
These results are very interesting because if the hypothesis
that underdogs usually overexert their level of efforts at the beginning of
contests, then it could have implications for the numerous other situation
where contests happen. This could apply to contests such as R&D rivalry for
a lucrative or strategic innovation, bribery to assure a profitable patent or
contract from the government, competition for a new global market that has been
created by a new innovative product, a political election, or candidates who
compete for a job or to win a promotion.
The biggest limitation of this study is I believe the low
level of R2 for all the results that I found, which means that the
model that I used is not that good an explanation of the
Strategic Behavior in Sport Contests 65
evolution of effort in a race. However, the R2
scores for each race are in the same dimension than the ones that Boyd and Boyd
obtained in their study. Therefore, maybe this is just a characteristic of the
model and this is not too relevant. Other limitations are that the data is not
as various as it could have been, it would have been indeed interesting to
study races from a lower level that a world championship final, for example a
regional races. Moreover, the splits available were not always sufficient and
it could have been interesting to study 1500 and 5000m with more intervals
available in the data. Even if this narrowing of the number of laps have helped
me getting results because of the increase of volatility of the positions due
to the use of ranking over interval rather than position at the end of the
interval.
Further research possible could be done by analyzing with a
similar methodology races from a more heterogeneous sample, indeed, by only
analyzing world championships finals, I analyzed only races with high-level
competitors, i.e. people with extreme competitive mindset compared to other
populations. Therefore, it would be really interesting to replicate the same
study on more «amateur» races. Moreover, such a study could also help
to observe differences in strategic behavior impacted by the gender of the
runners or by the density of competition inside of the race. Therefore, further
research may try to look in the direction of the differences of strategic
behavior between genders and also between different contexts of competition
density. Another possible way of further research that could improve this study
would be to analyze the impact of the actions of runners on the runner actions.
Such a study could possibly increase the level of R2 for this
particular case which is middle-distance races.
Eventually, I believe that the case of semi-finals could be
really interesting in order to study the behavior of economic agents when they
have secured their maximum utility. Indeed, the case of semi finals could be
used to analyze the level of effort of an agent when he has already attained
his objective. In general, a runner who knows that he will not be caught up and
has therefore secured his position in the direct qualifying places for the
final may have an incentive to save some energy and therefore reduce his level
of effort. It could prove once again that sport is a relevant empirical
background to study the behavior of economic agents, since this behavior, and
the reduction of the level of effort of a employee for example that would have
already reached his yearly objective before the end of the year.
Boudreau K. J. (2018). Amateur Crowds & Professional
Entrepreuners as Platform Com-plementors. Working paper
Strategic Behavior in Sport Contests 66
References
Andreff, W., & Szymanski, S. (2006). Handbook on the
Economics of Sport. Elgar Original Reference series.
Aoyagi, M. (2010). Information feedback in a dynamic
tournament. Games and Economic Behavior,70(2), 242-260
Baik, K. H. (1994). Effort levels in contests with two
asymmetric players. Southern Economic Journal, 61(2), 367.
https://doi-org.library.myebs.de/10.2307/1059984
Baik, K. H., & Shogren, J. F. (1992a). Strategic behavior
in contests: Comment. American Economic Review,82(1), 359-362.
Shogren, J.F., Baik, K.H. (1992b) Favorites and underdogs:
Strategic behavior in an experimental contest. Public Choice 74,
191-205.
https://doi.org/10.1007/BF00140767
Balafoutas, L., Dutcher, E. G., Lindner, F., & Ryvkin, D.
(2017). The optimal allocation of prizes in tournaments of heterogeneous
agents. Economic Inquiry,55(1), 461-478.
Bar-Eli M., Azar O., Ritov I., Keidar-Levin Y., & Schein
G. (2007). Action Bias Among Elite Soccer Goalkeepers: The Case of Penalty
Kicks. Journal of Economic Psychology, 28, p. 606-621.
Barget, E., Llorca, M., & Teste, T. (2011). La
théorie des tournois appliquée aux joueurs de tennis
professionnels : Peut-on encore parler d'incitations à la performance
? Revue D'économie Politique, 121(3), 347-370.
Baye, M. R., Kovenock, D., & de Vries, C.G. (1993).
Rigging the lobbying process: An application of the all-pay auction.
American Economic Review,83(1), 289-294.
Baye, M. R., Kovenock, D., & de Vries, C. G. (2005).
Comparative analysis of litigation systems: An auction-theoretic approach.
Economic Journal,115(505), 583-601.
Brand, M. J., & Bax, E. H. (2002). Strategic HRM for SMEs:
Implications for firms and policy. Education+ Training.
Berri D., & Krautmann A. (2006). Shirking on the Court:
Testing for the Incentive Effects of Guaranteed Pay. Economic Inquiry,
44, p. 536-546.
Borel, E. (1921). La théorie du jeu les
équations intégrales à noyau symétrique.
Comptes-Rendus de l'Académie,173, 1304-1308; The theory of play and
integral equations with skew symmetric kernels. Econometrica, 21(1),
97-100.
Borel, E., & Ville, J. (1938). Application de la
théorie des probabilités aux jeux de hasard. Paris, France:
Gauthier-Villars
Ehrenberg R., & Bognanno M. (1990a). Do Tournaments Have
Incentive Effects? Journal of Political Economy, 98, p. 1307-1324.
Strategic Behavior in Sport Contests 67
Boyd, D. W., & Boyd, L. A. (1995). Strategic behaviour in
contests: Evidence from the 1992 Barcelona Olympic games. Applied
Economics, 27(11), 1037.
https://doi-org.li-brary.myebs.de/10.1080/00036849500000086
Bull C., Schotter A., & Weigelt K. (1987). Tournaments and
Piece Rates: An Experimental Study. Journal of Political Economy, 95,
p. 1-33.
Camerer C. (2003). Behavioral Game Theory: Experiments in
Strategic Interaction, Princeton University Press.
Carpenter, J.P., Matthews, P.H., & Schirm, J. (2010).
Tournaments and Office Politics: Evidence from a Real Effort Experiment.
Conference
Charness G. & Levine, D. (2004). The Road to Hell: An
Experimental Study of Intentions. Working paper
Chiappori P.-A., Levitt S., & Groseclose T. (2002).
Testing Mixed-Strategy Equilibria When Players Are Heterogeneous: The Case of
Penalty Kicks in Soccer. American Economic Review, 92, p.
1138-1151.
Chow G. C. (1960). Tests of Equality Between Sets of
Coefficients in Two Linear Regressions. Econometrica.28(3), p.
591-605.
Coloma G. (2007). Penalty Kicks in Soccer: An Alternative
Methodology for Testing Mixed-Strategy Equilibria. Journal of Sports
Economics, 8, p. 530-545.
Corchón, L. C. (2007). The theory of contests: A
survey. Review of Economic De-sign,11(2), 69-100.
Cornes, R., & Hartley, R. (2012). Risk aversion in
symmetric and asymmetric contests. Economic Theory,51(2), 247-275.
Dasgupta, P. (1986). The theory of technological competition.
New developments in the analysis of market structure p. 519-549.
London, U.K.: Palgrave Macmillan.
Dixit, A. (1987). Strategic Behavior in Contests. American
Economic Review, 77(5), 891.
Dohmen T. (2008a). The Influence of Social Forces: Evidence
from the Behavior of Football Referees, Economic Inquiry, 46, p.
411-424
Dohmen T. (2008b), Do Professionals Choke under Pressure?
Journal of Economic Behavior and Organization, 65, p. 636-653.
Eber, N. (2008). Ce que les sportifs ont appris aux
économistes. (What Athletes Have Taught Economists. With English
summary.). Revue d'Economie Politique, 118(3), 341-374.
https://doi-org.library.myebs.de/http://www.cairn.info/revue-d-economie-politique.htm
Hayton, J. C., George, G., & Zahra, S. A. (2002). National
culture and entrepreneurship: A review of behavioral research.
Entrepreneurship theory and practice, 26(4), 33-52.
Strategic Behavior in Sport Contests 68
Ehrenberg R., & Bognanno M. (1990b). The Incentive Effects of
Tournaments Revisited: Evidence from the European PGA Tour, Industrial and
Labor Relations Review, 43, p. S74-S88.
Ettema, J. H. (1966). Limits of human performance and
energy-production. Internationale Zeitschrift Für Angewandte
Physiologie Einschließlich Arbeitsphysiologie, 22(1), 45-54.
Frick B. (1998). Lohn und Leistung im professionellen Sport: Das
Beispiel Stadt-Mara-thon. Konjunkturpolitik, 44, p. 114-140.
Frick B., & Prinz J. (2007). Pay and Performance in
Professional Road Running: The Case of City Marathons. International
Journal of Sport Finance, 2, p. 25-35.
Fu Q., & Wu Z. (2019). Contests: Theory and Topics.
Oxford Research Encyclopedia.
https://oxfordre.com/economics/view/10.1093/acre-fore/9780190625979.001.0001/acrefore-9780190625979-e-440
Garicano L., Palacios-Huerta I. & Prendergast C. (2005).
Favoritism Under Social Pressure. Review of Economics and Statistics,
87, p. 208-216.
Green, J. R., & Stokey, N. L. (1983). A comparison of
tournaments and contracts. Journal of Political Economy,91(3),
349-364.
Green W.H. (1993) Econometric Analysis, p. 466-469.
Macmillan, New York
Gneezy U., Niederle M., & Rustichini A. (2003) Performance in
Competitive Environments: Gender Differences. Quarterly Journal of
Economics, 118, p.1049-1074.
Gneezy U., & Rustichini A. (2004). Gender and Competition at
a Young Age. American Economic Review, 94, p. 377-381.
Golder, P. N., Shacham, R., & Mitra, D. (2009). Innovations'
Origins: When, By Whom, and How Are Radical Innovations Developed?
Marketing Science, 28(1), 166-179.
https://doi-org.library.myebs.de/10.1287/mksc.1080.0384
Gross, O., & Wagner, R. (1950). A continuous Colonel
Blotto game. RM-408. Santa Monica, CA: RAND Corporation.
Hanon C., Choffin T., Descoux R., Dupont P., Gajer B, Lacroix G.,
Lamare D., Marajo J., Mossant G., Stéphan H., Viale C., Vollmer J.-C.
(2015). Le 800 mètres. Analyse Descriptive et Entraînement.
INSEP-Editions
Harbaugh, R., & Klumpp, T. (2005). Early round upsets and
championship blowouts. Economic Inquiry,43(2), 316-329
Krautmann A. (1990). Shirking or Stochastic Productivity
in Major League Baseball? Southern Economic Journal, 57, p.
961-968.
Strategic Behavior in Sport Contests 69
Hillman, A. L., & Katz, E. (1984). Risk-averse
rent seekers and the social cost of monopoly power. Economic
Journal,94(373), 104-110.
Hillman, A. L., & Riley, J. G. (1989).
Politically contestable rents and transfers. Economics &
Politics,1(1), 17-39.
Hillman, A. L., & Samet, D. (1987). Dissipation
of contestable rents by small numbers of contenders. Public Choice,54(1),
63-82
Hirschleifer, J. (1988). The analytics of Continuing
Conflict. Synthese, August 1988, 76, p. 201-233
Howe, D. (2008). The Emotionally Intelligent Social
Worker. Macmilllan International Higher Education.
Hsu S.-H., Huang C.-Y., & Tang C.-T. (2007).
Minimax Play at Wimbledon: Comment. American Economic Review, 97, p.
517-523.
Hvide, H. K. (2002). Tournament rewards and risk
taking. Journal of Labor Econom-ics,20(4), 877-898.
Harbring, C., & Irlenbusch, B. (2011). Sabotage
in Tournaments: Evidence from a Laboratory Experiment. Management Science,
57, 4, p. 611-627
Jensen M. C., & Meckling. W. H. (1976). Theory of
the firm: Managerial behavior, agency costs and ownership structure.
Journal of Financial Economics, Volume 3, Issue 4,
Pages 305-360
Klunover, D. (2018). A note on rent dissipation in
lottery contests. Economics Letters, 168, 90-93.
Knight F.H. (1935). The Ethics of Competition and Other
Essays. Harper and Brothers, New York NY
Konrad, K. A. (2002). Investment in the absence of
property rights: The role of incumbency advantages. European Economic
Review,46(8), 1521-1537.
Konrad, K. A. (2009). Strategy and dynamics in contests.
Oxford, U.K.: Oxford University Press.
Konrad, K. A., & Leininger, W. (2007). The
generalized Stackelberg equilibrium of the all-pay auction with complete
information. Review of Economic Design,11(2), 165- 174.
Kovenock, D., & Roberson, B. (2012). Coalitional
Colonel Blotto games with application to the economics of alliances.
Journal of Public Economic Theory,14(4), 653-676.
Münster J. (2007). Selection Tournament, Sabotage, and
Participation. Wiley Online library.
https://doi.org/10.1111/j.1530-9134.2007.00163.x
Strategic Behavior in Sport Contests 70
Krishna, V., & Morgan, J. (1998). The winner-take-all
principle in small tournaments. Advances in Applied Microeconomics,7,
61-74.
Lallemand T., Plasman R., & Rycx F. (2008). Women and
Competition in Elimination Tournaments: Evidence from Professional Tennis Data.
Journal of Sports Economics, 9, p. 3-19.
Lazear, E. P. (1989). Pay Equality and Industrial Politics.
Journal of Political Economy, 97, p. 561-580.
Lazear, E. P., & Rosen, S. (1981). Rank-Order Tournaments as
Optimum Labor Contracts. Journal of Political Economy, 89(5), 841-864.
https://doi-org.li-brary.myebs.de/http://www.journals.uchicago.edu/loi/jpe
Leininger, W. (1993). More efficient rent-seeking - a
Münchhausen solution. Public Choice,75(1), 43-62.
Levine D. (1991). Cohesiveness, Productivity, and Wage
Dispersion. Journal of Economic Behavior and Organization, 15, p.
237-255.
Liebowitz, S. (2002). Rethinking the networked economy: The true
forces driving the digital marketplace. AMACOM Div. American Management
Association, Dallas.
Lynch J., & Zax J. (2000). The Rewards to Running: Prize
Structure and Performance in Professional Road Racing. Journal of Sports
Economics, 1, p. 323-340.
Maloney M. & McCormick R. (2000). The Response of Workers to
Wages in Tournaments: Evidence from Foot Races. Journal of Sports
Economics, 1, p. 99-123.
Marburger D. (2003). Does the Assignment of Property Rights
Encourage or Discourage Shirking? Evidence from Major League Baseball.
Journal of Sports Economics, 4, p. 19-34.
Maxcy J., Fort R., & Krautmann A. (2002). The Effectiveness
of Incentive Mechanisms in Major League Baseball. Journal of Sports
Economics, 3, p. 246-255.
Moldovanu, B., & Sela, A. (2001). The optimal allocation of
prizes in contests. American Economic Review,91(3), 542-558.
Moschini G. (2004). Nash Equilibrium in Strictly Competitive
Games: Live Play in Soccer. Economics Letters, 85, p. 365-371.
Müller, S. L., & Thomas, A. S. (2000). Culture and
entrepreneurial potential: A nine country study of locus of control and
innovativeness. Journal of Business Venturing, 16, 51-75
Mundlak, Y (1978). On the pooling of time series and cross
section data. Econometrica, 46, p. 69-85
Strategic Behavior in Sport Contests 71
Olszewski, W., & Siegel, R. (2016). Large contests.
Econometrica,84(2), 835-854
Olszewski, W., & Siegel, R. (2019). Pareto improvements in
the contest for college admissions. Working Paper
Olszewski, W., & Siegel, R. (2020). Performance-maximizing
contests. Theoretical Economics, 15, p.57-88
Orszag J. (1994). A New Look at Incentive Effects and Golf
Tournaments. Economics Letters, 46, p. 77-88.
Palacios-Huerta I. (2003). Professionals Play Minimax.
Review of Economic Studies, 70, p. 395-415.
Paserman D. (2007). Gender Differences in Performance in
Competitive Environments: Evidence from Professional Tennis Players. CEPR
Discussion Paper n°6335.
Palomino F., Rigotti L., & Rustichini. A. (1998). Skill,
Strategy and Passion: an Empirical Analysis of Soccer, Working
paper
Prendergast C., & Topel R. (1996). Favoritism in
Organizations. Journal of Political Economy, 104, p. 958-979.
Riedl, C., Grad, T., & Lettl, C. (2019). Strategic
Behavior in Contests with Heterogeneous Agents: Evidence from the Field.
Academy of Management Annual Meeting Proceedings, 2019(1), 396-401.
https://doi-org.library.myebs.de/10.5465/AMBPP.2019.71
Rosen S. (1986). Prizes and Incentives in Elimination
Tournaments. American Economic Review, 76, p. 701-715.
Scoggins J. (1993). Shirking or Stochastic Productivity in
Major League Baseball: Comment. Southern Economic Journal, 60, p.
239-240.
Scherrer, J., & Monod, H. (1960). Le travail musculaire local
et la fatigue chez l'homme. Presse Médicale, 68(46),
1717-1717.
Segev, E., & Sela, A. (2014). Multi-stage sequential
all-pay auctions. European Economic Review,70, 371-382.
Shane, S., Kolvereid, L., & Westhead, P. (1991). An
exploratory examination of the reasons leading to new firm formation across
country and gender. Journal of Business Venturing, 6, 431-446
Shogren, J.F., & Baik, K.H. (1992). Favorites and
underdogs: Strategic behavior in an experimental contest. Public Choice
74, 191-205
Siegel, R. (2009). All-pay contests. Econometrica,77(1),
71-92.
Strategic Behavior in Sport Contests 72
Siegel, R. (2014). Asymmetric contests with head starts and
nonmonotonic costs. American Economic Journal: Microeconomics,6(3),
59-105
Skaperdas, S., & Gan, L. (1995). Risk aversion in
contests. Economic Journal,105(431), 951-962.
Spencer, M. R., Gastin, P. B., & Payne, W. (1996). Energy
system contribution during 400 to 1500 metres running. New Studies in
Athletics, 11(4), 59-66.
Spiriev B, & Spiriev A. (2017), IAAF Scoring Tables of
Athletics, IAAF
Stiroh K. (2007). Playing for Keeps: Pay and Performance in
the NBA. Economic Inquiry, 45, p. 145-161.
Sunde U. (2003). Potential, Prizes and Performance: Testing
Tournament Theory with Professional Tennis Data. IZA Discussion Paper
n° 947
Sutter M., & Kocher M. (2004). Favoritism of Agents - The
Case of Referees' Home Bias. Journal of Economic Psychology, 25, p.
461-469.
Szymanski, S. (2003). The economic design of sporting
contests. Journal of Economic Literature,41(4), 1137-1187.
Thomas, C., Hanon, C., Le Chevalier, J. M., Couturier, A.,
& Vandewalle, H. (2003). Estimation de la contribution
énergétique d'origine aérobie et anaérobie et de sa
répartition au cours d'un 800 m couru sur le mode compétition.
Science & sports, 18(1), 3233
Thomas, A. S., & Müller, S. L. (2000). A case for
comparative entrepreneurship: Assessing the relevance of culture. Journal
of International Business Studies, 31, 287-301
Tomaselli, F. C., Di Serio, L. C., & de Oliveira, L. H.
(2008). Value chain management and competitive strategy in the home video game
industry. In 19th Annual Conference POMS.
Tullock, G. (1967). The welfare costs of tariffs, monopolies,
and theft. Economic Inquiry, 5(3), 224-232.
Tullock, G. (1980). Efficient rent seeking. In Toward a
theory of the rent-seeking society. College Station, TX: Texas A&M
University Press.
Vojnovic, M. (2017). Contest Theory. Communications of the
ACM, 60(5), 70-80.
https://doi-org.library.myebs.de/10.1145/3012008
Walker M., & Wooders J. (2001). Minimax Play at Wimbledon,
American Economic Review, 91, p. 1521-1538.
Woolway M. (1997). Using an Empirically Estimated Production
Function for Major League Baseball to Examine Worker Disincentives Associated
with Multi-Year Contracts. The American Economist, 41, p. 77-83.
Strategic Behavior in Sport Contests 73
EBS E Business School
For the digital version of the thesis this document has been
signed by the author and added as the last page of the PDF file.
Honourable Declaration
I certify that:
(a) the thesis being submitted for examination is created by my
own account.
(b) my research has been conducted ethically,
(c) the data and results presented are the genuine data and
results actually obtained by me during the conduct of the research.
(d) where I have drawn on the work, ideas and results of others
this has been appropriately acknowledged in the thesis.
(e) where any collaboration has taken place with other
researchers, I have clearly stated in the thesis my own personal share in the
investigation.
(f) the thesis has not been presented to any other examination
committee before. (An exception applies only to dual degree programmes in which
a joint thesis has to be submitted to both the EBS Business School and the
partner university.)
(g) the thesis has not been published before.
Oestrich-Winkel 2-A / OLI 1 20 L
0

(date: day / month I year)
(signature)
CLAS
(first name in BLOCK LETTERS)
(last name in BLOCK LETTERS)
| 


