Essai de modélisation de l'inflation en Algerie

Chapitre III

PRESENTATION DES METHODES

SECTION 1 : METHODOL OGIE DE BOX & JENKINS Introduction :

Box & Jenkins (1976) ont proposé une méthode qui permet en plusieurs étapes de trouver un modèle ARMA susceptible de représenter une série chronologique. Elle est en fait, l'application de la méthode scientifique afin d'obtenir un modèle de la réalité (que constitue la série chronologique).

Rappelons que la méthode scientifique consiste à formuler les suppositions sous forme d'un modèle à mettre à l'épreuve et à réviser le modèle en conséquence, ces étapes étant répétées autant de fois que nécessaire.

Une fois le modèle connu, on peut déterminer mécaniquement les prévisions à court terme des valeurs futures du processus, comme il faut encore pouvoir représenter la tendance et la saisonnalité, on étend la classe de modèle aux modèles ARIMA et SARIMA.

Il apparaît que la méthode, simple dans son principe de base, est complexe dans sa mise en oeuvre. Il s'agit néanmoins d'une méthode de prévision d'extrapolation puisque seul le passé des variables est utilisé à cette fin, sans apport d'informations extérieures.

La méthode de Box & Jenkins est constituée des étapes qui sont généralement répétées jusqu'à la satisfaction ; ces étapes sont illustrées par l'organigramme suivant :

Familiarisation avec les données

Analyse préliminaire des données

Stationnarisation et dessaisonalisation
de la série

Identification du modèle

Estimation des paramètres

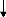
Prévision ou contrôle

Non Oui

Adéquation du modèle

Dans ce qui suit, nous allons décrire les quatre principales étapes de la méthode : stationnarisation, identification, estimation et vérification (adéquation) :

1.1 STATIONNARISATION DE LA SERIE :

En pratique si la fonction d'autocorrélation estimée reste proche de 1 pour un assez grand nombre de retard, on a une racine et la série n'est pas stationnaire. Le test de Dickey-fuller nous permet de voir si cette série est de type TS ou DS.

Si la série est de type TS on peut la rendre stationnaire en modélisant cette tendance par une régression sur le temps, et on retranche cette modélisation à la série d'origine ; sinon si cette chronique est DS, il suffit de la différencier pour la rendre stationnaire.

1.2 IDENTIFICATION :

Cette méthode est fondée sur la comparaison des moments empiriques de la série considérée aux moments théoriques associés aux différentes représentations potentielles. On se concentre ici sur les moments d'ordre deux résumés par la fonction d'autocorrélation simple (FAC) et la fonction d'autocorrélation partielle (PACF).

Les propriétés de ces fonctions sont résumées dans le tableau suivant :

Processus	FAC	PACF
AR (p)	Décroissance exponentielle et/ou sinusoïde.	Pics significatifs pour les p premiers retards.
MA (q)	Pics significatifs pour les q premiers retards.	Décroissance exponentielle et/ou sinusoïde.
ARMA (p, q)	Décroissance exponentielle ou sinusoïde amortie tronquée après (q-p) retards.	Décroissance exponentielle ou sinusoïde amortie tronquée après (p-q) retards.

1.3 ESTIMATION DES PARAMETRES :

L'estimation des paramètres d'un modèle ARMA (p, q) lorsque les ordres p et q sont supposés connus peut se réaliser par différentes méthodes dans le domaine temporel :

· Moindres Carrés Ordinaires (modèle sans composante MA, q = 0). Dans ce cas, on retrouve les équations de Yule Walker. En remplaçant les autocorrélations théoriques par leurs estimateurs, on peut retrouver les estimateurs des MCO des paramètres du modèle par la résolution des équations de Yule Walker.

· Maximum de Vraisemblance. Cette maximisation est réalise à l'aide d'algorithme d'optimisation non linéaire (Newton-Raphson, méthode du simplex).

1.4 VALIDATION DU MODELE :

Au début de cette étape on dispose de plusieurs processus ARMA dont on a estimé les paramètres. Il faut maintenant valider ces models afin de les départagés. Pour cela, on applique des tests sur les paramètres et les résidus.

Si plusieurs models sont validés, l'étape de validation doit se poursuivre par une comparaison des qualités de ces derniers.

1.4.1 Tests sur les paramètres :

> Test de Student : les coefficients non significatifs sont supprimés.

> Test de redondance : les racines des composantes AR et MA d'un ARMA en communs sont exclus.

> Coefficient de détermination : il donne une information sur la part de la variance de la variable endogène qui peut être expliquée par le modèle estimé.

1.4.2 Tests de bruit blanc des résidus :

Lorsque le processus est bien estimé, les résidus entre les valeurs observées et les valeurs estimées par le modèle doivent se comporter comme un bruit blanc.

> Test de nullité de la moyenne des résidus : car un bruit blanc est d'espérance mathématique nulle.

> Tests d'autocorrelation des résidus :

Si les résidus obéissent à un bruit blanc, il ne doit pas exister d'autocorrelation dans la série. Les tests suivant peuvent être utilisés :

1. Test de Durbin-Watson :(DW)

Le test de Durbin-Watson (1950,1951) permet de tester la présence d'autocorrélation à l'ordre 1 des résidus (c'est-à-dire, le résidu en t dépend du résidu en t-1, mais pas du résidu t-2, t-3,...). On considère le processus suivant décrivant une autocorrélation à l'ordre 1 des résidus :

å à t =ñå à t-1^+ít

où í_t est un bruit blanc et åà_t désigne les résidus estimés. Le test DW a pour objet de tester l'hypothèse nulle ñ = 0 (absence d'autocorrélation à l'ordre 1 des résidus) contre l'hypothèse alternative ñ ? 0 (présence d'autocorrélation à l'ordre 1 des résidus). La statistique de Durbin-Watson, notée DW, est donnée par :

?

(àà)² å å - t t -1

	t	=	2
=

DW

2

T

?

à

^å_t

t =

1

Cette statistique varie entre 0 et 4 et vaut 2 en l'absence d'autocorrélation à l'ordre 1 des résidus. Durbin et Watson ont tabulé les valeurs critiques de la statistique DW en fonction de la taille de l'échantillon T et du nombre de variables explicatives.

Il est important de noter que ce test n'est plus valable dès lors que le modèle estimé comprend une variable endogène retardée parmi les variables explicatives, ce qui est le cas lorsqu'on estime un processus avec une composante autorégressive.

Dans ce cas, on calcule la statistique h de Durbin (1970) :

T

1à -

T ö _ó²

1

h

=

à ñ

où ñà est l'estimateur MCO de ñ dans la relation åà _t = ñå à _t-1+ í _t et 1

óàö désigne la

2

variance estimée du coefficient de Xt - ₁. Sous l'hypothèse nulle, ñ = 0 tatistique h suit

la s

ö < 1 .

2

1

une loi normale centrée réduite. Le test h d Durbin est relativement peu puissant et ne peut être appliqué que si T ó à

2. Etude de la FAC et de la FAP : on doit vérifier qu'il n'existe aucune autocorrélation ou autocorrélation partielle significativement non nulle pour le processus étudié. Cette étude est prolongé par les tests du »porte-manteau».

3. Tests du »porte-manteau» ou tests d'adéquation globale du modèle. Ces tests reposent sur l'idée que la FAC d'un bruit blanc ne doit pas révéler d'autocorrélations non nulles. En pratique, on utilise deux tests :

a) Le test de Box-Pierce :

Ce test a pour objet de tester le caractère non autocorrélé des résidus. La statistique du test s'écrit :

2

k( à )

å t

K

= ?

BP

() à
KTñ

k

=

1

où ñà _k ( å à t ) est le coefficient d'autocorrélation d'ordre k des résidus estimés et K est le nombre maximal de retards.

Sous l'hypothèse nulle d'absence d'autocorrélation :

0

=

à à à
ñ_å= ñ_å= = ñ k å t

2(à) ...

1(à) ( à )

t t

La statistique BP (K) suit une loi du Khi-deux à (K-p-q) degrés de liberté.

Remarque : Si la variance des résidus varie au cours du temps (résidus hétéroscédastiques), il est possible de calculer la statistique de Box-Pierce corrigée de l 'hétéroscédasticité, notée BP_c et définie par :

() à()
KVK

= ????

1 2
K

?

ñ_å

à t

k(à)

k=1

BP _c

K

à où V(K) est une estimation de la variance de

ñå 2 ? à t k(à)

:

k= 1

K

VK ä j

à () à ( )

= ?

j 1

T

?

()() 2 2
åå k k j
-

^kj⁼+ 1

? ?

? ?

? ?

? ( )

k = 1 T

å k 2 2

à

ä () j

avec :

Sous l'hypothèse nulle d'absence d'autocorrélation, la statistique suit une loi de

BP_c (K)

Khi-deux à (K-p-q) degrés de liberté.

b) Le test de Ljung et Box :

Ce test est à appliquer, de préférence au test de Box-Pierce, lorsque l'échantillon est de petite taille. La distribution de la statistique du test de Ljung-Box est en effet plus proche de celle du Khi-deux en petit échantillon que ne l'est celle du test de Box-Pierce. La statistique du test s'écrit :

K

= + ?

LB ()(2) KTT k 1

ñåà ² k(à) t

Tk-

Sous l'hypothèse nulle d'absence d'autocorrélation : 2 2 2

ñ _å =ñå==ñk å t =

à 1( à ) à 2(à)^... à ( à ) 0

t t

La statistique LB (K) suit une loi de Khi-deux à (K-p-q) degrés de liberté. > Tests d'homoscédasticité :

Un bruit blanc est, par définition, homoscédastique. Tous les tests d'hétéroscédasticité peuvent être employés pour vérifier cette hypothèse.

1. Le test de White (1980) :

Ce test général d'homoscédasticité est fondé sur l'existence d'une relation entre le carré du résidu et une ou plusieurs variables explicatives (endogènes retardées, dans notre cas) en niveau et au carré :

å p t

à 0 1 1 11 22 22

t a aX _t bX _t aX _t bX _t ... a _p X t p b _p X t 2

2 = + - + - + - + - + + - + - +í

2 2

Si au moins un des coefficients de régression est significatif, on rejette l'hypothèse nulle d'homoscédasticité en faveur de l'hypothèse alternative d'hétéroscédasticité. Pour effectuer ce test, on utilise la statistique du multiplicateur de Lagrange , ou T est le

TR²

nombre d'observation et est le coefficient de détermination associé à la régression ci-

R2

dessus. Cette statistique suit une loi de Khi-deux à 2p degrés de liberté sous l'hypothèse

2 2

nulle. En conséquence, si TR<÷_p , on accepte l'hypothèse nulle d'homoscédasticité. Si

2

TR> ÷ 2p , on conclut en faveur de l'hypothèse alternative d'hétéroscédasticité.

2 2

2. Le test ARCH de Engle (1982) :

Ce test, très fréquemment employé en économétrie des séries temporelles financières, a pour objet de tester l'hypothèse nulle d'homoscédasticité contre l'hypothèse alternative d'hétéroscédasticité conditionnelle. On effectue la régression suivante :

l

å ááå _t - i

à à

2 2

t i

=+ ?

0

i =

1

à

où å t sont les résidus issus de l'estimation du processus de type ARMA (p, q).

On calcule la statistique où T est le nombre d'observations de la série

TR²åàt et est

_R2

le coefficient de détermination associé à l'équation ci-dessus. Sous l'hypothèse nulle

2

d'homoscédasticité (á_i = 0, ? i = 1,..., l), la statistique suit une loi de Khi-deux à l

TR

degrés de liberté. La règle de décision est alors :

- Si 2 2

TR< ÷ l , on accepte l'hypothèse nulle d'homoscédasticité

- Si 2 2

TR>÷ _l , on rejette l'hypothèse nulle en faveur de l'hypothèse alternative d'hétéroscédasticité conditionnelle.

En conclusion, à l'issue de l'application de ces différents tests, plusieurs modèles peuvent encore paraître adéquats. Il reste alors à les comparer entre eux pour tenter de retenir le modèle « le plus adéquat ». A cette fin, divers critères de choix de modèles peuvent être utilisés.

> Le test de normalité de Jarque et Bera :

Pour une loi normale, le coefficient de skewness (S) -ou coefficient d'asymétrie- est nul, et le coefficient de kurtosis (K) -ou coefficient d'aplatissement- vaut 3, cette loi étant caractérisée par sa symétrie par rapport à la moyenne ainsi que par la faible probabilité des points extrêmes. Le test de normalité de Jarque et Bera (1980) est basé sur la définition des coefficients d'asymétrie et d'aplatissement :

S

2

??
¹()

T

3

? ?

?XX

-

t 2

??

T ì

t =1 3

=

3 3

ì₂

? ?

1 ( )

T

2

? ?

? X X

-

t

? ?

T t = 1

K

¹()

?XX

t -

T ì

t=1 4

=

2 2

??

2 2 ì

1 ()

T

??

? XX

t -

? ?

T t = 1

où X est la moyenne de la série X_t , t=1 ... T et les ì_i sont des moments centrés d'ordre i.

Pour une loi normale, on a :

2 ?? ???= = ìì 3 4 2 ì0 3

La statistique de Jarque et Bera est donnée par :

Tk

-? ?

JBS K

=+-

¹(3)²

64 ? ?

? ?
où k est le nombre de paramètres estimés (dans le cas d'un test sur les résidus, sinon k=0).

Sous l'hypothèse nulle de normalité, la statistique JB suit une loi de Khi-deux à deux degrés de liberté.

1.5 LES CRITERES DE CHOIX DE MODELES :

1.5.1 Les critères standards :

Ils sont fondés sur le calcul de l'erreur de prévision que l'on cherche à minimiser. On rappelle ici l'expression des trois critères les plus fréquemment utilisés.

- Erreur absolue moyenne (Mean Absolute Error) : =1 à

MAE

t

t ? ^å

t

- Racine de l'erreur quadratique moyenne (Root Mean Squared Error) :

-

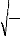
T ? å

1 à_t

=

t

RMSE

^2

Ecart absolu moyen en pourcentage (Mean Absolute Percent Error):

= ?

T

MAPE

à

å_t

X_t

t

où T est le nombre d'observations de la série X_t étudiée et åà_t désigne les résidus estimés.

Plus la valeur de ces critères est faible, plus le modèle estimé est proche des observations. D'autres critères, basés sur la théorie de l'information, ont été développés et sont donnés ci-après.

1.5.2 Les critères d'in formation :

L'idée sous-jacente consiste à choisir un modèle sur la base d'une mesure de l'écart entre la vraie loi inconnue et le modèle estimé. Cette mesure peut être fournie par la quantité d'information de Kullback. Les différents critères ont alors pour objet d'estimer cette quantité d'information. Parmi les plus fréquemment utilisés :

- Le critère d'information d'Akaike (1969) :

₂2(p q)

AIC ó å +

= +
logà_à

T

- Le critère d'information bayésien d'Akaike (1977) ou de Schwartz (1978) :

2 log

SIC=ó_à+p+q logà()^T

å T

Remarque: On cherche à minimiser ces différents critères. Leurs applications nous permet de retenir un modèle parmi les divers processus ARMA validés. Ainsi s'achève l'étape de validation. La dernière étape de la méthodologie de Box-Jenkins est celle de la prévision.

1 :

.6 PREVISION

Transformation de la série :

Lorsque pour identifier le processus étudié à un processus ARMA, on a appliqué différentes transformations (exemple différenciation dans le cas d'une série I (1)), il est nécessaire lors de la phase de prévision de prendre en compte la transformation retenue et de »recolorer la prévision». Plusieurs cas sont possibles :

· Si le processus contient une tendance déterministe, on extrait cette dernière par régression afin d'obtenir une série stationnaire lors de la phase d'estimation. Ensuite, lors de la phase de prévision, on adjoint aux prévisions réalisées sur la composante ARMA stationnaire, la projection de la tendance.

· Si la transformation résulte de l'application d'un filtre linéaire (de type par exemple différences premières), on réalise les prévisions sur la série filtrée stationnaire et l'on reconstruit ensuite par inversion du filtre les prévisions sur la série initiale.

Prédicteur pour un processus ARMA :

On considère un processus ARMA (p, q) tel que :

x=öx- + ..+öx-+å+è1å- 1+ +èå-

t tptptt ...qt q
11

avec IC = 2* et

(öp,èq)? R 2

åti.i.d.(0,ó _å ). Appliquons le théorème de Wald au processus {xt, t ? Z} et considérons la forme MA (8) correspondante

xt =

t j
-

? ð å , ð0= 1

j

j = 0

Il s'ensuit que la meilleure prévision que l'on peut faire de xt + 1 compte tenu de toute l'information disponible jusqu'à la date t, notéex^&&(1) , est donnée par :

xà(1)=E(xt+1/xt,xt-1,...,x0)

= E ( x t +1/åt,åt-1,..., å 0)

8

=? ð j=0

åt j +- 1 j

Des lors, l'erreur de prévision est donnée par la réalisation en t+1 de l'innovation qui en t n'est pas connue :

xt + 1 - x à t (1) = åt + 1

Plus généralement pour une prévision à l'horizon k on a :

8

xk

t+-

kj

à() ð å
t= ? j j^k=

k

-

1

xxk

tkttkj + à ()ðå+-
-= ? j

j

=

0

Déterminons un intervalle de confiance sur la prévision xà t (k), sous l'hypothèse de normalité des résidus. On montre alors que :

xt k

+ -

x k à ( )

t

1/2 T?8

N(0, 1)

var(à()) xxk

tk

+-

Or on sait que :

k 1

E{( xt +k-x à t (k))} =E

2

k

(())

2

tkj

+ -

? ðå

j

j

=?

ðó _å

2 2 j

j 0

1

-

0

=

1/2

x x k

tk t

+- à ( )

k

-

ó_å(ð)

j

1 2

?=0 ^j

T?8 N(0,1)

On peut construire un intervalle de confiance sous la forme :

? k - 1

IC xkt

à() ( )

á/2 2 2

=#177; ? ð ó å

? j

? j = 0