|
 
INTRODUCTION
GENERALE

Théorie et principe
de la spectroscopie
Raman
I. 1) Introduction :
Il existe de nombreuses techniques d'investigation des oeuvres
d'art dont il est important de connaître les caractéristiques et
les possibilités pour en faire une utilisation judicieuse. Les unes et
les autres présentent des avantages et des inconvénients ;
deux critères nous paraissent importants pour guider le choix :
- la quantité de matière nécessaire et le
caractère non destructif de leur utilisation
- le type d'information atteint, analyse
élémentaire ou moléculaire, structure cristalline,
composition s'il y a mélange ...
Dans l'optique, la spectrométrie RAMAN présente
une spécificité intéressante qui en fait un outil
analytique bien adapté à l'étude des matériaux des
ouvres d'art.
I. 2) Bref historique de la spectroscopie Raman
:
En 1928, en Inde, Sir C. V. Raman a été le
premier à s'intéresser au phénomène
d'émission lumineuse inélastique. Le rayonnement émis par
des molécules bombardées contient des photons de même
fréquence que ceux du rayonnement incident, mais aussi des photons de
fréquences différentes. Cet effet est très faible.
A la fin des années 1930, la spectroscopie Raman
était devenue la principale méthode non destructive d'analyse
chimique.
Malgré le développement des lasers dans les
années 60, la spectroscopie Raman resta largement confinée dans
les laboratoires, car nécessitant toujours des gens très
qualifiés pour obtenir des spectres très simples. De plus, la
spectroscopie Raman souffrit fortement du phénomène de
fluorescence.
En 1986, un interféromètre commercial infrarouge /
transformée de Fourier et une source d'excitation proche de l'infrarouge
ont été combinés pour obtenir un spectre Raman. Ceci a
donné beaucoup de points positifs :
- L'excitation laser proche de l'infrarouge réduit
considérablement le nombre d'échantillons susceptibles de donner
lieu à la fluorescence et permet d'utiliser des lasers plus puissants
sans photo décomposition.
- La possibilité d'analyser rapidement une large gamme
d'échantillons et la capacité de collecter un grand nombre de
spectre avec une haute résolution en une seule mesure ont rendu la
technique Raman accessible à un nombre beaucoup plus grand de
scientifiques.
I-3) Théorie de la spectrométrie
Raman :
Le phénomène de diffusion
Raman concerne des photons,
c'est pourquoi on a besoin de l'aide de la mécanique classique et de
celle de la mécanique quantique pour comprendre correctement le
phénomène.
a) APPORT DE LA MECANIQUE CLASSIQUE :
On sait que le phénomène de diffusion est
lié à la polarisabilité de la molécule, mais
qu'est- ce que la polarisabilité ?
La polarisabilité 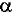 caractéristique moléculaire qui caractérise la
faculté du nuage électronique à acquérir un moment
dipolaire induit P sous l'effet d'un champ électrique
E, elle se met sous la forme suivante:
caractéristique moléculaire qui caractérise la
faculté du nuage électronique à acquérir un moment
dipolaire induit P sous l'effet d'un champ électrique
E, elle se met sous la forme suivante:
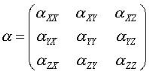
Où 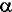 ij
sont les composantes de ij
sont les composantes de 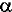 dans
le repère (Oxyz). dans
le repère (Oxyz).
L'application d'un champ électrique E
(V/m) peut induire la création d'un dipôle P
(V/m).Le moment dipolaire P sera alors défini
par l'expression:
P =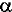 *E *E
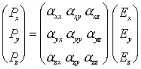
où E est le champ électrique
appliqué
De manière simple, on peut rappeler que la
polarisabilité représente la facilité avec laquelle le
nuage électronique peut se déformer sous l'effet d'un champ
électrique appliqué.
Une radiation lumineuse peut être associée
à un champ électrique oscillant à la fréquence 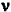 0 : 0 :
E = E0*cos(2 ð 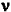 0t) (équation 1) 0t) (équation 1)
Ainsi la polarisabilité peut s'exprimer:
P = á E0 cos(2ð í0
t) (équation 2)
Maintenant si on suppose que la molécule vibre à
la fréquence 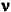 vib et si q représente la variation
de la position du centre de masse de la molécule par rapport à la
position d'équilibre, on a: vib et si q représente la variation
de la position du centre de masse de la molécule par rapport à la
position d'équilibre, on a:
q = q0 cos(2 ð ívib t)
(équation 3)
Si les mouvements de la molécule entraîne une
variation de la polarisabilité et si on suppose que ces variations sont
de faible amplitude, on admet que:
á = á0 +
(äá?äq)0 q (équation
4)
Ainsi en combinant les équations (3)
et (4) on obtient:
á = á0 +
(äá?äq)0 q0 cos(2 ð ívib
t) (équation 5)
Enfin si on exprime la polarisabilité grâce
à l'équation (5) dans l'équation
(2):
P = á0 E0 cos(2ð
í0 t)+ (äá?äq)0 q0
cos(2 ð ívib t) cos(2ð í0 t)
(équation 6)
Or on sait que
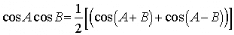
Donc on peut réécrire l'équation 6:
P = á0 E0 cos(2ð
í0 t)+1/2 (äá?äq)
q0{cos(2ð[í0+ívib]t)+cos2ð[í0-ívib])}
(éq 7)
L'équation (7) est constituée de
deux termes:
* Le premier terme de l'équation 7 (terme en 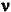 0) correspond à la diffusion
Rayleigh (processus élastique qui se produit
pour 1 photon incident sur 10 000). On aura alors une émission de
lumière qui se fera à la même fréquence que celle de
l'onde incidente. 0) correspond à la diffusion
Rayleigh (processus élastique qui se produit
pour 1 photon incident sur 10 000). On aura alors une émission de
lumière qui se fera à la même fréquence que celle de
l'onde incidente.
* Le deuxième terme correspond à la diffusion
Raman (processus inélastique) qui est beaucoup
plus faible que le terme de diffusion élastique. On estime
en effet que 1 photon sur 100 000 000 est diffusé
inélastiquement, soit 10 000 fois moins probable que la diffusion
Rayleigh. Comme il s'agit d'un processus
intrinsèquement très faible, des sources de lumière
intense telles que les lasers sont nécessaires.
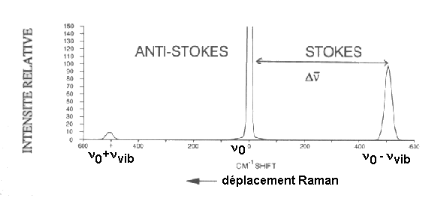
Il est également à noter que la diffusion
Raman n'existe que si la polarisabilité varie
avec q. La lumière diffusée à la
fréquence (í0 +ívib
) est connue sous le nom de diffusion Raman
Anti-Stokes alors que celle diffusée à
(í0 - ívib ) est connue
sous le nom de diffusion Raman Stokes. Les raies
Stokes et Anti-Stokes se situent de part et d'autre
de la raie Rayleigh. De plus on remarque
expérimentalement que les raies Stokes sont
plus intenses que les raies Anti-Stokes.
L'aspect classique de la diffusion
Raman reproduit bien l'expérience en ce qui
concerne l'existence ou non des raies (règles de sélection) de
part et d'autre du pic de diffusion Rayleigh dont
l'écart avec ce pic central est égal aux fréquences de
vibration de la molécule. Par contre, ce modèle ne reproduit pas
les intensités relatives des raies Stokes et
Anti-Stokes que seul le traitement par la mécanique
quantique permet d'obtenir.
b) APPORT DE LA MECANIQUE QUANTIQUE:
Comme l'indique la figure ci-dessous, l'interaction entre la
lumière incidente caractérisée par un
photon d'énergie
hí0 et une molécule se trouvant dans
un état d'énergie donné (différentes valeurs de V
où les niveaux d'énergie sont séparés par un
même écart d'énergie correspondante à
hívib ) peut engendrer différents
phénomènes:

· Si la fréquence de la lumière incidente
est proche d'une fréquence de vibration de la molécule, on
observe un phénomène d'absorption, c'est le cas de la
spectroscopie infrarouge.
· Si cette fois la fréquence de la lumière
incidente est très grande par rapport aux fréquences de
vibrations de la molécule (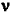 0 >> 0 >> 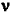 vib), le phénomène le plus probable est une
diffusion dont on peut décrire le mécanisme de manière
très schématique de la façon suivante : vib), le phénomène le plus probable est une
diffusion dont on peut décrire le mécanisme de manière
très schématique de la façon suivante :
Lors de l'excitation par le photon incident d'énergie
hí0, la molécule transite dans un
état virtuel car l'énergie du photon est très importante.
Puis redescend sur un niveau réel. On peut montrer que
seuls les niveaux V-1, V et
V+1 sont possibles. On retrouve ainsi les trois types de
diffusions rencontrées dans la description classique de la
spectroscopie Raman.
ü On remarque que la diffusion
Rayleigh est la plus probable alors que les
diffusions Stokes et
Anti-Stokes sont très peu favorisés.
De plus, à une température donnée, le
remplissage des niveaux d'énergie est donné par une loi de
Maxwell-Blotzmann qui prédit que les niveaux
excités (V+1, V+2...) sont très peu
peuplé par rapport aux niveaux d'énergie fondamental
(V). Or la diffusion Anti-Stokes ne concerne
que les molécules se trouvant dans un état excité
(transition V+1 > V) ce qui explique sa
faible intensité par rapport à la diffusion Stockes.
I-4) Domaines d'applications de la spectroscopie
Raman.
Les domaines d'application de la spectrométrie Raman sont
nombreux, parmis lesquels on trouve :
* Détermination de la structure chimique (C=O, C=C, O-H,
C-O, C-C, C-S, ... etc).
* Configuration (cis, trans.) tacticité pour les
polymères.
* Conformation (arrangement planaire, en hélice
á, â, ... etc en feuillets) :
domaine biologie.
* Détermination de la cristallinité et de
l'épaisseur lamellaire (modes à basses fréquences) pour
les polymères.
* Etude des forces intra et intermoléculaires (liaison
hydrogène).
* Etude de l'orientation des molécules (polarisation).
* Analyses de traces (police scientifique : drogues, explosifs,
sang, peinture dans les oeuvres d'art).
I-5) Principaux avantages de la spectroscopie
Raman. :
Par rapports aux techniques d'analyse la spectroscopie Raman
apporte certains avantages qu'on peut citer ci-dessous :
* Pas de préparation de l'échantillon avant
analyse.
* Analyse non destructive.
* Etude de solutions aqueuses possible (l'eau diffuse peu en
Raman), cellule liquide en verre utilisable.
* Résolution spatiale meilleure en microscopie (1 à
5 um suivant la longueur d'onde ë du laser utilisée).
I-6) Principaux
inconvénients :
* Echantillon fluorescent (même si excitation dans le
proche infrarouge) effet Raman masqué.
* Echantillon au moins épais de 100 um.
* Bibliothèque de spectres encore très
incomplète.
* Analyse quantitative : avec précaution.
* Sensibilité moins bonne qu'en infrarouge (FT
Raman).
I-7)
CONCLUSION :
La spectrométrie Raman est une technique bien
adaptée à l'analyse des composants des oeuvres d'art, son
évolution bénéficie des développements
technologiques les plus récents, on peut espérer :
Améliorer la détection.
Adapter une fibre optique sur l'appareil, ce qui devrait
faciliter l'étude d'objets pour lesquels le prélèvement
est impossible, ou éviter le recours symétrique au
prélèvement.
| 


