|
Remerciements
Ce mémoire a été financé par le
projet OUEME-2025, préparé conjointement au Laboratoire de
Physique du Rayonnement (LPR/UAC) et au
Laboratoire des Transferts en Hydrologie et Environnement
(LTHE/Grenoble).
4 J'exprime ma gratitude tout d'abord au
directeur du LPR, le Professeur Cossi Norbert Awanou et au directeur du LTHE Mr
Thierry Lebel qui m'ont accueilli et permis de
réaliser ce travail dans leurs laboratoires respectifs.
4 Mes sincères remerciements vont a l'endroit de
Arnaud Zannou, Coordonateur du Projet Ouémé-2025 pour la
confiance qu'il a placé en moi en m'offrant ce
stage dans son projet.
4 Je tiens a remercier particulièrement Basile
Kounouhéwa, Sylvie Galle et Jean-Martial Cohard avec
qui j'ai fait mes premiers pas dans la recherche et qui
ont su parfaitement encadrer mes travaux malgré mes
cheminements parfois tortueux. Vos critiques et conseils m'ont
permis d'améliorer la qualité de ce document.
4 A toute l'équipe de l'Ecole
doctorale qui a assuré notre formation, je dis infiniment
merci.
4 Merci a Léandro Suarez pour m'avoir appris
EdiRe le fameux logiciel de traitement de flux;
Stéphanie Leroux pour ses nombreuses explications sur la circulation
atmosphérique a grande échelle;
Franck Houénou pour son initiation au Latex et grace a
qui vous trouvez la beauté dans ce document; Jules
Sogba-Goh qui est souvent sur le terrain pour ramener les
données. Que Jean-Bosco Voudounou, Maurille Agoua et Armelle
Dossou-Yovo trouvent ici l'expression de notre profonde reconnaissance pour le
précieux concours apporté maintes fois pour les tracas
administratifs.

4 L'ensemble de mes camarades, je veux nommer Gabin
Koto N'gobi; Richard Agbokpanzo;
Eric Cojo; Tahirou Djarra; Ouzel Oumarou;
Armand Djossou et Didier Boko-Haya pour leur amitié et leur
bonne humeur permanente.
4 Je remercie aussi mes parents qui m'ont
accompagné tous les jours bien au delà de mon travail
et à qui je dédie ce mémoire.
4 Enfin, merci à Djouma!
Résumé
Cette étude est focalisée sur la
variabilité saisonnière des termes du bilan
d'énergie sur deux végétations
contrastées de la Donga/Bénin : une jachère
herbacée (Nalohou : 974484N, 160457E, 449 m) et une forêt claire
(Bellefoungou : 979115N, 171800E, 414 m).
Pour caractériser cette variabilité, trois
périodes de quinze (15) jours ont été
identifiées. La première pendant la saison sèche, la
seconde pendant la saison des pluies et la dernière se situe dans la
période de transition de la saison humide a la saison sèche. Dans
un premier temps, nous comparons sur les 3 périodes les
paramètres météorologiques des deux
stations. Nous analysons ensuite la fermeture du bilan
énergétique. Les coefficients de
détermination obtenus sur le site de Nalohou entre H+LE et Rn-G sur les
périodes sont assez satisfaisants et confirment la
qualité des mesures d'eddy corrélation
effectuées dans la région soudanienne. Les
séries temporelles des flux moyennées sur
chaque heure pour les différentes périodes sont
comparées entre elles. Les flux de chaleur sensible et de chaleur a la
surface du sol sont les termes majoritaires du bilan en Janvier et en Novembre.
Les maxima observés a Nalohou sont de 315W.m-2 et
170W.m-2 en Janvier et 271W.m-2 et
115W.m-2 en Novembre respectivement pour les flux de
chaleur sensible et de chaleur a la surface du sol. Quant au flux de chaleur
latente, il représente environ 70% du rayonnement net en
Juillet, reste faible en Novembre (20% du rayonnement net) et est
inférieur a 5% en Janvier. A Bellefoungou, les
résultats sont similaires mais en Juillet les flux de chaleur latente et
de chaleur sensible sont plus grands que ceux obtenus sur
la jachère de Nalohou.
Mots dles : bilan d'énergie, eddy
corrélation, qualité des données,
variabilité, climat soudanien, AMMA-CATCH, OUEME-2025 .
Abstract
This study focuses on the seasonal
variability of energy budget terms on two
contrasted vegetations of Donga/Benin a fallow bush
(Nalohou 974484N, 160457E, 449 m) and a clear forest (Bellefoungou
979115N, 171800E, 414 m).
To characterize the variability, three 15
days periods have been identified. The first one concerns the
dry season, the second one concerns the wet season and the last one
the transition period from wet to dry season. We compare first the
weather parameters during the 3 periods at the two stations. We
analyze then the energy budget closure. The
determination coefficients obtained on the site of Nalohou between H+LE and
Rn-G over the periods are rather satisfactory and confirm the
quality of flux measurements carried out in the sudanian
area. The hourly time series of fluxes realised for the various
periods are compared. The sensible and ground heat flux are the main
terms of the budget in January and November. The maxima
observed in Nalohou are respectively for the sensible heat flux and
ground heat flux 315W.m-2 and
170W.m-2 in January and
271W.m-2 and 115W.m-2 in November. The
latent heat flux accounts for approximately 70% of the Net radiation
in July, but remains weak in November (20% of the Net radiation) and
is lower than 5% in January. For the forest site, the results are
similar in July but the latent and ground heat flux are
large than those of the fallow bush site.
Keywords energy budget,
eddy correlation, quality of data,
variability, soudanian climate , AMMA-CATCH, OUEME-2025.
Table des matières
Remerciements i
Résumé iii
Abstract v
Introduction générale 1
1 Mesure des termes du bilan d'énergie 5
1.1 Le bilan d'énergie dans la Couche Limite
Atmosphérique (C.L.A) 5
1.2 Le rayonnement net Rn 6
1.3 Le flux de chaleur a la surface du sol G 7
1.3.1 Estimation théorique de G méthode
des harmoniques 8
1.3.2 Formulation de la FAO-56 pour l'obtention de G 11
1.4 Flux turbulents de chaleur le flux de chaleur sensible H et
de chaleur latente
LE 11
1.4.1 Principe de l'eddy covariance et
mesure des flux turbulents de chaleur 12
1.4.2 Présentation du logiciel EdiRe
16
1.4.3 Algorithmes associés aux calculs des flux de
chaleur sensible H et de
chaleur latente LE dans EdiRe 18
1.5 Critères de vérification de la
qualité des données
d'eddy corrélation 19
1.5.1 Test des Caractéristiques
Intégrales de Turbulence (ITC) 19
1.5.2 Classification globale des données
20
1.6 Conclusion 22
2 Description de la zone d'étude et caractérisation
météorologique des sous périodes
d'étude 23
2.1 Situation
géographique de la zone d'étude
23
2.2 Dynamique saisonnière de la
surface du sol sur les deux stations 25
2.3 Description de l'année 2007 - 2008 cas de la station
de Nalohou (Aoüt 07 -
Juillet 08) 26
2.3.1 Le rayonnement net 26
2.3.2 La température de l'air 28
2.3.3 La tension de vapeur réelle 29
2.3.4 La vitesse et la direction du vent 30
2.4 Conditions climatiques locales Comparaison de la
météo de Nalohou et celle
de Bellefoungou 34
2.4.1 Sous période sèche (16 au 30 Janvier 2008)
34
2.4.2 Sous période humide (16 au 30 Juillet 2008) 36
2.4.3 Sous période intermédiaire (16 au 30 Novembre
2007) 37
2.5 Conclusion 39
3 Exploitation des résultats 41
3.1 Le flux de chaleur a la surface du sol 41
3.1.1
Comparaison de la température de surface et de la température
infra-
rouge 42
3.1.2 Comparaison des flux de chaleur a
la surface du sol calculés avec la
méthode des harmoniques et la formulation de la
FAO 47
3.1.3 Comparaison des flux de chaleur a la surface a Nalohou et a
Bellefoungou 48
|
3.2
|
Les flux turbulents de chaleur H et LE
3.2.1 ContrOle de qualité
|
51
51
|
|
3.2.2
|
Analyse de la qualité des
données
|
53
|
|
3.3
|
Calcul du bilan d'énergie
|
57
|
|
3.3.1
|
Variabilité temporelle du bilan
d'énergie a Nalohou
|
58
|
|
3.3.2
|
Fermeture du bilan d'énergie a Nalohou
|
61
|
|
3.4
|
Variabilité spatiale des flux turbulents de chaleur
|
64
|
3.4.1 Cas du flux de chaleur sensible 64
3.4.2 Cas du flux de chaleur latente 65
3.5 Conclusion 66
Conclusion generale 69
.1 Références
Bibliographiques 72
.2 Annexe1 Proclist de Nalohou 76
.3 Annexe 2 Description des installations 84
Liste des tableaux
|
1.1
|
Valeurs des constantes C1 et C2
d'après 1311.
|
20
|
|
1.2
|
Différents tests appliqués sur les
flux H et LE
|
21
|
|
1.3
|
Classification globale d'après 1321.
|
21
|
|
3.1
|
Classification des données de flux : sous période
sèche
|
52
|
|
3.2
|
Classification des données de flux : sous période
humide
|
52
|
|
3.3
|
Classification des données de flux : sous période
intermédiaire . . .
|
53
|
LISTE DES TABLEAUX xii
Table des figures
1.1 Schéma montrant les différentes parties de la
couche limite atmosphérique 6
1.2 L'anémomètre sonique
(gauche) et le Licor (droite) effectuant des mesures sur la
forêt claire de Bellefoungou. 13
2.1 Carte de localisation des stations de mesure dans la
Donga 24
2.2 Couverture du sol à Nalohou en Novembre (a) et en
Juillet (b) 25
2.3 Couverture du sol à Bellefoungou en Juillet
(a) et vue de dessus de la végétation de
Bellefoungou (b) 26
2.4 Evolution temporelle des moyennes
journalières du rayonnement net à Nalohou. . 27
2.5 Evolution temporelle des moyennes
journalières du rayonnement incident courte
(Swin) et grande (Lwin) longueur d'onde
à Nalohou. 27
2.6 Evolution temporelle des moyennes
journalières, des valeurs minimale et maximale
de la température de l'air à Nalohou. 28
2.7
Ecart entre les températures moyennes journalières
maximales et minimales au cours
de la période Aoüt 07-Juillet 08 à Nalohou.
29
2.8 Evolution temporelle de la moyenne journalière de
la tension de vapeur réelle sur la
période Aoüt 07-Juillet 08 à Nalohou.
29
2.9 Evolution temporelle des moyennes journalières ,
des valeurs minimale et maximale
de la vitesse du vent 30
2.10 Cycle journalier du vent sur la période
Aoüt 2007-Juillet 2008 à Nalohou 31
2.11 Station de Nalohou, rose des vents Aoüt 07-Juillet 08
(pour des vents supérieurs à 1m.s-1) 33
2.12 Cycle journalier du rayonnement
incident(a), rayonnement réfléchi(b),
température de l'air (c), humidité relative(f), vitesse du vent
(d) et tension de vapeur réelle (e)à Nalohou et à
Bellefoungou (sous période sèche) 35
2.13 Cycle journalier du rayonnement
incident( a), rayonnement réfléchi(b),
température de l'air (c), humidité relative (f), vitesse du vent
(d) et tension de vapeur réelle (e) a Nalohou et a
Bellefoungou (sous période humide) 37
2.14 Cycle journalier du rayonnement
incident (a), rayonnement réfléchi(b),
température de l'air (c), humidité relative (f), vitesse du vent
(d) et tension de vapeur réelle (e) a Nalohou et a
Bellefoungou (sous période intermédiaire) 39
3.1 Evolution temporelle de la température
infrarouge et des températures de surface calculées a
partir des mesures aux profondeurs z1= 9 et 10cm a Nalohou en Janvier (haut) et
en Juillet (bas). 44
3.2 Evolution temporelle de la température
infrarouge et des températures de surface calculées a
partir des mesures aux profondeurs z1= 9 et 10cm a Nalohou (Novembre). 45
3.3 Evolution du rayonnement net et du flux de chaleur
a la surface du sol a Nalohou pendant trois jours en Janvier 45
3.4 Evolution du rayonnement net et du flux de chaleur
a la surface du sol a Bellefoungou pendant trois jours en Janvier
46
3.5 Evolution du rayonnement net et du flux de chaleur
a la surface du sol a Nalohou pendant trois jours en Novembre (haut) et en
Juillet (bas). 47
3.6 Evolution temporelle des flux de chaleur a la surface du 20
au 23 Janvier 2008 sur
la station de Nalohou 47
3.7 Cycle journalier moyen de G
harmonique a Nalohou et a Bellefoungou (sous
période sèche). 49
3.8 Cycle journalier moyen de G
harmonique a Nalohou et a Bellefoungou (sous
période humide). 49
3.9 Cycle journalier moyen de G
harmonique a Nalohou et a Bellefoungou (sous
période intermédiaire). 50
3.10 Cycle journalier et qualité de
LE et de H durant les sous périodes sèche (a et b), humide (c et
d)et intermédiaire (e et f) a Nalohou. 56
3.11 Cycle journalier et qualité de
LE et de H durant les sous périodes sèche (c) et humide
(a et b) a Bellefoungou. 57
3.12 Cycle journalier horaire moyen de Rn,
H, LE et G en Janvier (a), en Novembre (b)
et en Juillet (c) a Nalohou 59
3.13 Pourcentage de
H, LE et G par rapport a Rn en Janvier (a), Juillet (b) et en
Novembre (c) a Nalohou 61
3.14 H+LE en fonction de Rn-G en
Janvier (a), Juillet (b) et en Novembre (c) a Nalohou. 63
3.15 Cycle journalier de H a Nalohou et a
Bellefoungou (sous période sèche). 64
3.16 Cycle journalier de H a Nalohou et a
Bellefoungou (sous période humide) 65
3.17 Cycle journalier de H a Nalohou et a
Bellefoungou (sous période humide) 66
Introduction générale
La question de la ressource en eau est d'une
importance capitale en Afrique de l'Ouest. En effet, les
économies de la plupart de ces pays reposent sur
l'agriculture et sont donc tributaires des pluies. Deux
épisodes de sécheresse (en 1972-1973 et en 1984-1985) au Sahel
ont eu un impact sur la ressource en eau a l'échelle de la
région Ouest-Africaine et des conséquences
dramatiques pour les populations. Les observations montrent en effet
qu'une baisse du régime
pluviométrique entraIne une chute deux a trois fois plus
importante [1; 2; 31 du débit des fleuves et
asséche certains cours d'eau. Pour tenter de comprendre de tels
épisodes climatiques et leurs impacts, il importe de bien
connaItre le cycle de l'eau, a toutes les échelles spatiales
et temporelles. Dans ce contexte, la communauté scientifique
soutenue par les organismes internationaux a mis en place un
ambitieux programme trans-disciplinaire et multi-échelles le
programme AMMA (Analyse Multidisciplinaire de la Mousson
Africaine). Il vise a documenter la variabilité climatique
associée a la mousson Ouest-Africaine en vue de comprendre les
interactions océan-atmosphère-continent. Trois sites de
méso-échelle échantillonnent le gradient
éco-climatique en climat semi-aride (Mali, 300 mm),
sahélien (Niger, 600 mm) et soudanien (Bénin, 1200 mm)
depuis 2001.
Les flux d'évapotranspiration interviennent a la fois
dans les bilans d'eau et d'énergie. Ils sont un
élément incontournable pour l'étude des
échanges entre l'atmosphère et le cycle
hydrologique mais encore très peu
documentés. C'est pourquoi, au Bénin, l'observatoire
AMMA-CATCH en collaboration avec le projet Ouémé-2025 ont
décidé de s'associer afin de mieux comprendre le fonctionnement
de l'interface surface - atmosphère en zone soudanienne ainsi
que, pour documenter les flux d'évapotranspiration. Des
stations de mesure de flux ont été donc installées sur
trois couverts végétatifs dans la Donga
(586km2) représentatifs de la zone [41. La première
est située sur une jachère herbeuse a Nalohou, la seconde, a
Belle-
foungou est située sur une forêt
claire a isoberlinia et la dernière a Bira, est située dans une
savanne arbustive. Ce réseau de mesure va permettre une
quantification plus fiable du bilan
hydrologique dont les flux
d'évapotranspiration sont le terme principal [5;
6; 7].
Nos travaux de DEA ont porté sur deux de ces stations
Nalohou et Bellefoungou et se sont déroulés dans le
cadre du projet Ouémé-2025.
Au cours de ces dernières années, les
méthodes de mesure des flux turbulents ont été beau-coup
développées. Aujourd'hui, la méthode d'eddy
covariance est considérée comme la méthode standard de
mesure de flux de surface [81. Dans cette méthode, les flux turbulents
sont calculés directement comme la covariance entre les fluctuations de
la composante verticale de la vitesse du vent et les fluctuations d'un terme
scalaire (température, humidité, concentration de CO2) [91. Il
s'agit donc de mesures directes de la turbulence utilisées
pour obtenir les flux de surface. Cette méthode permet de mesurer a
l'échelle de quelques dizaines a
quelques centaines de m2, le flux de chaleur
latente en W.m-2 qui est lié a
l'évapotranspiration réelle (ETR) en
mm.j-1.
Notre travail consiste donc a utiliser cette méthode pour
estimer l'ETR.
L'objectif visé dans cette étude est de
caractériser la variabilité du bilan d'énergie
de ces deux types de végétation durant
trois périodes clefs de leur cycle annuel la saison
sèche en Janvier, la saison des pluies en Juillet et la période
de transition entre saison des pluies et la saison sèche en Novembre.
Pour cela, nous présentons d'abord dans le chapitre 1 les
méthodes d'obtention des flux d'énergie a la surface.
Il développe aussi les corrections appliquées aux
données d'eddy corrélation ainsi que les
critères de validation de ces données.
Le deuxième chapitre situe la zone d'étude et
caractérise les périodes d'étude. Cette
caractérisation s'appuie sur une année complète de
données météorologiques issues de la
station de Nalohou. Nous comparerons ensuite dans ce chapitre, les
cycles journaliers des deux stations entre elles durant les trois
(3) périodes définies plus haut.
Le chapitre 3 expose les résultats. On y
compare d'abord les résultats des méthodes de calcul du flux de
chaleur a la surface du sol. Ensuite, la qualité des
données d'eddy corrélation
est validée selon 2 approches (a) la
détermination des critères des caractéristiques
intégrales de turbulence développés dans le
chapitre 1 et (b) la fermeture du bilan d'énergie. Un
regard sera porté sur le cycle journalier
(variation temporelle) des flux de chaleur sensible et de chaleur latente sur
les deux sites (variation spatiale) et la corrélation entre ces flux
sera dégagée.
Ce travail sera conclu par un chapitre de
synthèse dans lequel les perspectives
envisagées seront présentées.
CHAPITRE 1
MEsuRE DEs TERMEs Du BiLAN
D'ÉNERGiE
Le climat détermine la structure et le fonctionnement
des écosystèmes essentiellement à travers les
variations de température, des pluies et de rayonnement
solaire. Il influence aussi l'état hydrique et
thermique du sol. Le sol et l'atmosphère forment ainsi un
système couplé : chaque composante
influence l'état et l'évolution des autres composantes a travers
différents mécanismes. Ces interactions ont lieu a des
échelles de temps allant de quelques secondes a
des millions d'années. Dans la suite de ce document, on
s'intéresse particulièrement aux interactions entre la surface du
sol et l'atmosphère sur une superficie de quelques
hectares et a leurs variabilités saisonnières.
1.1 Le bilan d'energie dans la Couche Limite
Atmospherique (C.L.A)
Le terme de couche limite a été introduit par
Prandtl [10], qui étudiait les propriétés
d'écoulements fluides de faible viscosité a proximité
d'une limite solide. Dans le contexte atmosphérique, la
couche limite est la couche d'air directement en contact avec la surface de la
terre, et au sein de laquelle les effets de la surface (frottement,
réchauffement et refroidissement) sont ressentis a des échelles
de temps inférieures a la journée, et dans laquelle
d'importants flux de quantité de mouvement, de chaleur et de
matière sont entretenus par des mouvements turbulents. Elle se subdivise
en deux couches : la couche d'Ekman et la couche limite de surface
(Figure 1.1). C'est la couche limite de surface située dans
les premiers mètres au dessus de la surface du sol qui nous
intéresse dans notre étude. Cette couche
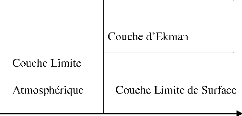
est la partie de la CLA qui est directement en
contact avec la surface terrestre. Elle est encore appelée sous couche a
flux constants car c'est la couche dans laquelle les variations des
flux selon z sont inférieures a 10%.
FIG. 1.1 Schéma montrant les différentes parties de
la couche limite atmosphérique.
L'énergie qui parvient au sol
provient du soleil sous forme de rayonnement. Le bilan
d'énergie au travers de la surface du sol exprime
que la somme des flux est nulle au niveau de cette surface
(Eq 1.1).
Rn -- G -- H -- LE = 0 (1.1)
oi Rn est le rayonnement net, G le flux de chaleur
dans le sol, H le flux de chaleur sensible et LE le flux de chaleur latente.
Dans les sections suivantes, chaque terme du bilan
d'énergie est défini.
1.2 Le rayonnement net Rn
Le rayonnement net Rn est la
quantité d'énergie radiative disponible a
la surface terrestre. Il représente le bilan des rayonnements
incident et réfléchi de courtes longueurs d'onde et
des rayonnements grandes longueurs d'onde
incident et réfléchi ou émis par la surface [111. Les
courtes longueurs d'ondes appartiennent au domaine du visible et du
proche infrarouge tandis que les grandes
longueurs d'ondes sont celles de l'infrarouge
thermique. Le bilan radiatif de la surface terrestre s'écrit
alors :
Rn = Swin - Swout + Lwin - Lwout
(1.2)
oii Swin est le rayonnement incident de
courtes longueurs d'onde, Swout est le
rayonnement réfléchi de courtes longueurs
d'onde, Lwin le rayonnement incident de grandes
longueurs d'onde (venant des nuages et de
l'atmosphère) et Lwout le rayonnement
réfléchi et émis par la terre en grandes
longueurs d'onde.
Sur les stations de mesure, les flux radiatifs sont
mesurés a l'aide de capteurs hémisphériques
(qui mesurent le rayonnement provenant de tout
l'hémisphère). Les quatre composantes du
rayonnement net sont directement mesurées a l'aide d'un
bilanmètre CNR1 de la marque Kipp & Zonen qui
est composé de 2 pyranomètres CM3 (courtes
longueurs d'onde 0.3um < A < 3um)
et de 2 pyrgéomètres CG3
(grandes longueurs d'onde 5um < A <
50um). Les spécificités des capteurs sont
décrites dans un tableau en annexe 2.
1.3 Le flux de chaleur a la surface du sol G
Les transferts thermiques dans le sol sont
gouvernés par des échanges de chaleur par
conduction. D'après l'équation de Fourier, le flux de
chaleur G est proportionnel au gradient vertical de
température et a la conductivité thermique du sol
k (W.m-1.K-1). Il est
donné par l'expression
C = -k?T ?t |z= 0
(1.3)
Le flux de chaleur dans le sol G peut être mesuré
soit par des plaques a flux qui doivent être
placées très proches de la surface du sol [121; soit
modélisé a partir des mesures de température et
d'humidité du sol réalisées a différentes
profondeurs. Plusieurs modélisations peuvent être
employées méthode du bilan ou méthode des
harmoniques. La deuxième per-met une meilleure estimation des
flux sans biais et sans décalage temporel [131. En l'absence
de mesures spécifiques, la FAO propose des relations
empiriques le flux G est considéré comme nul au pas de
temps journalier, il peut être estimé au pas de temps horaire
comme une fraction du rayonnement net [141.
A partir des mesures des profils de températures a
différentes profondeurs et d'humidité du sol, nous avons
calculé le flux de chaleur a la surface du sol par la méthode des
harmoniques. Une comparaison entre le flux de chaleur calculé
a partir de la méthode des harmoniques et la formulation de
la FAO est présentée au chapitre 3.
1.3.1 Estimation théorique de G :
méthode des harmoniques
La méthode des harmoniques peut être
utilisée pour calculer le flux de chaleur a la surface du sol a partir
des profils verticaux de températures et d'humidité dans le sol
[151. En supposant que le sol est homogène et
que les transferts de chaleur dans le sol sont unidirectionnels, la
température a la profondeur z est obtenue en résolvant
l'équation de chaleur suivante :
?T
?t = á
?2T (1.4)
?2z
oi á est la diffusivité
thermique du sol en (m2.s-1).
a)- solution de l'equation de la chaleur
Qn va résoudre cette équation par la
méthode de séparation des variables. Qn souhaite avoir une
variation périodique du signal suivant t,
posons :
|
T(z,t) = C +
|
X8
n=1
|
Zn(z)Hn(t)
|
avec C constante, Zn(z) et
Hn(t) sont respectivement des suites de fonction
de z et de
t.
Pour chaque n, l'équation
devient en prenant inw comme constante de séparation ou
d'intégration :
|
H0 n(t)
Hn(t)
|
= á
|
Z00
n(z)
Zn(z)
|
= inw (1.5)
|
Qn résoud d'abord l'équation en
t
|
H0 n(t)
Hn(t)
|
= inw = Hn(t) =
C1
n(t)expi(nwt) (1.6)
|
Résolvons ensuite l'équation en z :
inw
Z00 n(z) -
Zn(z) = 0
á
Posons
v
i
r r mw
a a
r2 = imw imw
= r = #177; a = #177;
avec i nombre imaginaire complexe.
or
v2 v2
v rmw
i = 2 + i 2 = r1,2 =
#177; 2a (1 + i)
on a donc :
rmw rmw
Zn(z) =
C2 n(z) exp(-
2a (1 + i)z) +
C3 n(z) exp(
2a (1 + i)z) (1.7)
La solution générale de
l'équation (1.3) s'écrit :
|
T(z,t) = C +
|
X8
n=1
|
Vmw
[C4 n(z, t)
exp(imwt) exp(- 2a (1 +
i)z)
|
rmw
+ C5 n(z, t)
exp(imwt) exp( 2a (1 + i)z)]
(1.8)
oi C4 n(z,t) =
C1
n(t).C2
n(z) et C5
n(z,t) = C1
n(t).C3
n(z)
La première condition aux limites (T(z -?
8, t) = Tm), Tm étant la
température moyenne a la profondeur z. Cette condition impose
de prendre la constante d'intégration C =
Tm et de prendre la constante
C5 n(z,t) = 0.
L'équation (1.8) devient :
|
T(z,t) = Tm +
|
X8
n=1
|
rmw
C4 n(z, t)
exp(imwt) exp(- 2a (1 +
i)z) (1.9)
|
En décomposant la partie complexe on a :
|
T(z,t) = Tm +
|
X8
n=1
|
rmw rmw
C4'
n (z, t) exp(-
2a z) cos(mwt - 2a
|
z)
|
+ i X8
n=1
rmw rmw
C4''
n (z, t) exp(-
2a z) sin(mwt - 2a z)
(1.10)
La seconde condition aux limites
T(z = 0, t) = Tm +
P8 n=1 An sin(mwt +
?n) (conditions aux limites en surface) impose :
C4'
n (z, t) = 0
Et on retrouve la solution suivante :
00
n=1
nw
T (z, t) = Tm +
i
nw "
Cn 4 (z, t)
exp(-2á
z) sin(nwt + ?n -
2á z)
(1.11)
b)- modelisation du champ de temperature du sol a partir d'une
serie temporelle a 2 profondeurs
En utilisant la transformée de Fourier directe, la
série de température a la profondeur z peut etre exprimée
en fonction de ses caractéristiques
fréquentielles Cj :
N-1
1 X Tk exp i(2ðj
Cj = v Nj )k (1.12)
N
k=0
avec T k les mesures de température
disponibles, N leur nombre. La température a la profondeur
z peut etre exprimée comme :
|
T (z, t) = Tm +
|
n=1
|
An exp(- z)sin(nwt +
?n nw z)
2á 2á (1.13)
|
oil n est le nombre d'harmoniques,
Tm la température moyenne a la profondeur
z, w la fréquence radiale
(2ðN) , M étant
la plus grande harmonique du domaine Cj et
An la longueur du vecteur de Fourier :
An = |Cn| (1.14)
an
et ?n, l'argument du vecteur de
Fourier
(1.15)
bn
avec an et bn,
respectivement la partie réelle et imaginaire de
Cn. En prenant la dérivée
(?T?z ) de l'équation on a :
?n = arctan(
)
|
?T(z, t)
?z
|
|
n=1
|
vnwá rnw v2 rnw
An exp(-
2á z) 2 [sin(nwt
+ ?n - 2á z)
á
|
+ cos(nwt + ?n -
\/n2wá
z)] (1.16)
on sait que :
ð ð ð
2 [cos a + sin a] = cos 4 cos a
+ sin 4 sin a = sin(a + 4 )
2
=(1.16) devient :
|
?T(z,t)
?z
|
|
n=1
|
An vnwá exp(
\/nw 2á 4
2á
z) sin(nwt + ?n +
ð- \/nwz) (1.17)
á
|
En remplaçant l'équation
(1.17) dans l'équation (1.3) on a :
|
G(z,t) = k
|
XM
n=1
|
vnwá rnw
rnw
An exp(-
2á z) sin(nwt +
?n + ð 4 -
2á z) (1.18)
á
|
avec k = ñCpá.
ñCp peut être calculé
comme une combinaison linéaire entre les
caractéristiques d'un sol sec et celles de l'eau [131 soit
ñCp = ñdCpd +
èñwCpw oi è est
l'humidité volumique mesurée in situ;
ñwCpw les caractéristiques de l'eau et
ñdCpd celles du sol sec. En considérant un sol
homogène, la diffusivité á peut
être estimée a partir des amplitudes journalières
(ÄTz1, ÄTz2) de deux
séries de températures a deux profondeurs différentes :
wÄz2
á =
(1.19)
2[ln(ÄTz1
ÄTz2 )]2
oi ÄTz1 et ÄTz2
représentent les variations journalières des températures
aux profondeurs z1 et z2.
1.3.2 Formulation de la FAO-56 pour l'obtention de G
Le flux de chaleur dans le sol peut être estimé au
pas de temps horaire ou inférieur a partir de la formule de la FAO-56
[141. Cette formulation stipule que :
- G O.1*Rn durant la journée (pour Rn >
OW.m-2)
G O.5*Rn durant la nuit (pour Rn OW.m-2)
1.4 Flux turbulents de chaleur le flux de chaleur sensible H et
de chaleur latente LE
Dans cette section, nous nous penchons sur les flux turbulents
de chaleur latente LE et sensible H. Nous abordons ensuite le principe de
l'eddy covariance et les calculs des flux H et LE.
Définition
Le flux de chaleur latente LE est l'énergie
utilisée pour faire passer les molécules d'eau
de
l'état liquide a l'état gazeux a
température constante. Le flux de chaleur latente
entre la surface et
l'atmosphère est associé a la quantité de
vapeur d'eau introduite
dans l'atmosphère par évaporation du sol ou /et
par transpiration des végétaux
(évapotranspiration). Le flux de chaleur sensible est le flux de chaleur
issu de la convection entre la surface du sol et l'air. La chaleur sensible est
la chaleur, qui contrairement a la chaleur latente, entraIne une
modification de la température lorsqu'on l'ajoute ou la
soustrait.
1.4.1 Principe de l'eddy covariance et mesure des
flux turbulents de chaleur
La méthode de l'eddy covariance utilise des
mesures de la turbulence pour obtenir les flux de surface, qui sont
calculés comme la covariance entre les fluctuations de la vitesse du
vent vertical et les fluctuations d'un terme scalaire.
Théorie de l'eddy covariance
La majeure partie du transport de chaleur, d'humidité
et des gaz dans l'atmosphère est due a la turbulence. En
effet, lorsque l'on introduit la décomposition de
Reynolds Eq.(1.20), les flux turbulents de chaleur FX
Eq.(1.21) peuvent être calculés comme la
covariance entre les fluctuations de la variable X' et les
fluctuations de la vitesse de vent verticale w'.
X = X + X' (1.20)
Dans l'Eq.(1.20), X est la valeur
instantanée d'une variable (u, w, T, q), X est la
moyenne sur une période Lt
(typiquement 10 - 60 minutes), et
X' est la partie fluctuante de la variable X.
FX = w'X' (1.21)
avec X T (température pour le flux de chaleur
sensible), q (humidité pour le flux de
chaleur latente), u (vitesse du vent pour le flux de
quantité de mouvement). Si on dispose de mesures a une
fréquence suffisamment haute (20 Hz), obtenues par des
instruments avec un temps de réponse rapide, ces flux peuvent être
calculés directement. Malheureusement, les instruments disponibles ne
permettent pas d'échantillonner toutes les échelles de la
turbulence et les mesures directes nécessitent des corrections pour
prendre en compte les erreurs causées par le dispositif
expérimental, les capteurs, l'installation et les conditions
atmosphé-
riques.
Mesure des flux turbulents de chaleur
Dans cette étude, nous avons utilisé les capteurs
suivants pour la mesure des paramètres turbulents
- Humidité de l'air q LI-7500 C02/q
open path gaz Analyser (LI-COR Biosciences Inc.) Le
licor-7500 est un analyseur de gaz à
infrarouge qui permet de mesurer la concentration de C02
et de vapeur d'eau dans l'air. Deux types existent le licor à
circuit ouvert et le licor à circuit fermé. Ici nous utilisons le
licor à circuit ouvert (Figure 1.2) c'est-à-dire
que l'air passe librement entre une source d'infrarouge
et un détecteur, la mesure étant réalisée in
situ.
- Vitesse du vent tridimensionnelle (u,v,w),
température du sonique (T5) CSAT3
Anémomètre Sonique tridimensionnel (Campbell
Scientific Ltd.)
Le CSAT3 est un anémomètre
ultrasonique (Figure 1.2) qui mesure la
vitesse du vent dans les trois dimensions de l'espace. Il utilise trois paires
de transducteurs orientées de manière non-orthogonale
par rapport à la composante horizontale du vent. Chaque paire
de transducteurs transmet et reçoit un signal
ultrasonique. Le temps de transmission entre les paires de
transducteurs est directement relié à la vitesse du vent le
long de l'axe des transducteurs. La vitesse du son est directement
liée à la densité de l'air, elle dépend par exemple
de la température et de l'humidité.

FIG. 1.2 L'anémomètre sonique
(gauche) et le Licor (droite) effectuant des mesures sur la
forêt claire de Bellefoungou.
Théorie de mesure du CSAT3
a)- Vitesse du vent
Chaque paire de transducteurs du CSAT3 envoie deux
impulsions ultrasoniques de direction opposée qui
se propagent a la célérité c. Le temps de vol
t0 pour le premier signal (aller) est donné par :
et le temps de vol du second signal (retour) est
donné par :
oi t0 est le temps de vol aller le long de
l'axe du transducteur, tb le temps de vol retour du second
signal, dans la direction opposée, ua est
la vitesse du vent le long de l'axe des transducteurs
supposée constante pendant les deux impulsions, d est la
distance entre transducteurs et c la vitesse du son.
La vitesse du vent, ua d'un axe donné
peut être trouvée en inversant les relations
précédentes, puis en soustrayant l'Eq
(1.23) de l'Eq (1.22) et on a :
ua =
d 2[ 1 - 1 ]
(1.24)
t0 tb
La vitesse du vent est mesurée selon les trois axes non
orthogonaux pour donner ua, ub et
uc oi les indices a, b et c se
réfèrent aux trois axes soniques non
orthogonaux. Les composantes non orthogonales de vitesse
de vent sont transformées en composantes orthogonales de
vitesse de vent, u, v et w a partir de
l'équation ci-dessous :
?
????
ua
ub
= A
?
????
uc
? ?
u
? ?
? ?
? v ?
? ?
w
oi A est une matrice (3*3) de transformation de
coordonnées, qui est unique pour chaque
CSAT3, stockée dans sa mémoire ROM. u , v et
w représentent les vitesses du vent dans la direction
horizontale, latérale et verticale.
b)-Température de l'anémomètre
sonique
La vitesse du son c (calculée en faisant la somme
de 1/t0 et 1/tb) est liée a la température
du sonique par la relation suivante :
c2
Ts = ãdRd
273, 15 (1.25)
oi c est la vitesse du son; ãd
est le rapport de chaleur spécifique de l'air sec a une
pression constante, sur celui a volume constant
[16;17;18;191.
ãd 1,4 et Rd est la constante des
gaz pour l'air sec et est égal a
287,04J.K-1.kg-1.
Les mesures sont faites a 20 Hz sur une centrale
d'acquisition Campbell Scientific Ltd. CR3000 avec une carte PCMCIA
(Personal Computer Memory Card International Association) de 1Go
pour le stockage des données brutes. Les flux turbulents sont
ensuite calculés hors-ligne en tenant compte des corrections
suivantes :
La correction de vent en travers l'anémomètre
sonique [201
La méthode de la double rotation [211 qui
annule la composante de la vitesse verticale du vent et ramène le
système tridimensionnel a un système
bidimensionnel. Deux rotations sont effectuées pour annuler la
composante verticale w du vent.
1ère rotation
v = 0; tan ã = ( vm
)
um
2ème rotation
w = 0; tan u = (wm )
um
Correction de la sensibilité du licor a
l'oxygène
Le licor est employé pour mesurer la teneur
en vapeur d'eau contenue dans l'air par absorption des molécules d'eau
dans le spectre infrarouge. En raison de la longueur
d'onde utilisée, le licor est influencé par les molécules
d'oxygène. Une correction recommandée par [221
s'applique donc aux mesures de vapeur d'eau.
w'q' =
w'Kq' + Ck0(ñd T
)w'T0
|
o'
|
Ck0 =
|
C0M0
Ma
|
= 0,23 k0
kw
|
kw, k0 et K sont des
constantes spécifiques au Licor-7500, Co est la
concentration en % de l'oxygène dans l'atmosphère
(Co = 0,21 ) , M0 = 32 et Ma =
28,97 sont les poids moléculaires de
l'oxygène et de l'air sec, et ñd est la
densité d'air sec.
Conversion de la température sonique
(virtuelle) en température de l'air
Les anémomètres soniques ne mesurent
pas vraiment la température mais la vitesse du son. La vitesse du son
dépend de la température de l'air et également
de la teneur en vapeur d'eau de l'air. Pour obtenir les fluctuations de la
température réelle au lieu des fluctuations de la
température du sonique, l'effet d'humidité de l'air
doit être corrigé [181.
Ts
T = (1.26)
1 + 0, 51q
Ts est la température du
sonique qui est en fait une estimation de la
température virtuelle car les effets de l'humidité ne sont pas
pris en compte dans l'Eq(1.25), q la
quantité de vapeur d'eau et T la température
de l'air.
Correction pour des fluctuations de densité
(WPL-correction)
Pour déterminer les flux turbulents des constituants
d'air comme la vapeur d'eau, la correction d'après [231 est
nécessaire. Elle corrige deux aspects. Le premier est relatif
au contenu en eau de l'air. Le deuxième aspect est la correction de
l'écoulement de la masse d'air selon l'altitude, parce que
les vitesses verticales ascendantes sont différentes de celles
descendantes effet du aux différences de la densité de l'air
[24; 25; 26 ].
w'T'
Fv = (1 +
uó)(w'ñv + ñv
) (1.27)
T
|
avec
|
ma
u =
mv
|
= 1, 6 et ó = ñv
ña
|
~ Des corrections sont effectuées pour enlever tous les
types d'erreurs de réponse en fréquence
(par exemple, réponse en fréquence limitée des
capteurs et centrales d'acquisition, séparation des capteurs
ou l'intégration sur le trajet de mesure)[27;
281.
Toutes les corrections, sauf les deux premières sont
réalisées itérativement.
1.4.2 Presentation du logiciel EdiRe
L'outil utilisé ici pour le traitement des données
est le logiciel EdiRe. Il a été
développé par l'Université d'Edinburgh (GB) et
est dédié au traitement des mesures d'eddy
corrélation.
Il peut être téléchargé
gratuitement sur le site
www.geos.ed.ac.uk/abs/
research/micromet/EdiRe. C'est un logiciel dans lequel
les données brutes de flux sont traitées en utilisant des
routines configurées par l'utilisateur. Le choix et l'ordre
de traitement des routines sont définis par l'utilisateur dans une
'proclist'. Ce fichier proclist appelle diverses fonctions permettant (1) la
conversion des unités, (2) le filtrage des valeurs
aberrantes, (3) la prise en compte des caractéristiques de
l'appareil (calibration, angle d'attaque, temps de
réponse), (4) celles du climat (densité et stabilité de
l'air) et (5) l'analyse statistique et spectrale des
données haute fréquence. EdiRe offre ainsi la
possibilité de calculer les flux de chaleur latente et /ou chaleur
sensible. Les choix que nous avons fait sont décrits
ci-dessous, la proclist correspondante se trouve en annexe 1.
Préparation des données
-Calcul de la variance et de la covariance des composantes des
flux sur un intervalle de temps de 30mn.
-Suppression des pics isolés [29; 301.
-Détection du temps de latence du licor et du CSAT.
Conversions et corrections
-Correction du vent au travers de la température du
sonique pour le CSAT [201. -Double rotation [211.
-Corrections spectrales [271.
-Conversion de la température du sonique en
température réelle [181.
-Correction pour les fluctuations de la densité du Licor
[261.
ContrOle de la qualité des données.
- Test de qualité d'après la description
de [311 Foken et Wichura (1996), classification des données en 3 classes
selon leur qualité [321.
1.4.3 Algorithmes associes aux calculs des flux de
chaleur sensible H et de chaleur latente LE dans EdiRe
a)- Algorithme de H dans EdiRe
Le flux de chaleur sensible est obtenu par la formule suivante
:
H =
ñCp(w'T0s) (1.28)
avec :
ñCp = Cp-humideñv +
Cp-sec(ña ñv)
Cp-humide = 1859 + 0, 13Hr
+ T(0, 193 + 0, 00569Hr) +
T2(0, 001 + 0, 00005Hr)
Cp-sec = 10005 + T + 23, 12 = 29, 002(P --
0, 3780e)
ña
3364 Rd(T + 273,16)
= 100e
18P 17, 502T
ñv Rd(T + 273, 16)
es
· Hr = et es =
0, 61121 exp( T + 240, 97)
oil : ña est la masse
volumique de l'air sec
en(Kg.m-3);
ñv la masse volumique de la vapeur d'eau
(Kg.m-3); Cp-humide et
Cp-sec chaleur massique a pression constante de l'air humide et
de l'air sec en
(J.kg-1.K-1);
T la température de l'air (SC);
Ts0 la fluctuation de la température de
l'anémometre sonique (°K); e tension
de vapeur réelle (kPa); es tension de
vapeur saturante (kPa); Hr humidité
relative de l'air (%); P pression de l'air (kPa);
Rd constante des gaz pour l'air sec qui vaut :
287,04 J.K-1.kg-1.
b)- Algorithme de LE dans EdiRe
Le flux de chaleur latente est défini par :
LE = L(w'q') (1.29)
oil
240, 97ln( 617121)
L = 2500, 25 -- 2,
365117, 502ln( 61)
21
avec : L la chaleur latente d'évaporation de l'eau en
(J.g-1); w0 la fluctuation de la vitesse du vent
dans la direction verticale mesurée par le CSAT3; q0
la fluctuation de la quantité de vapeur d'eau présente
dans l'atmosphére en (g.m-3)
mesurée par le licor et es la tension de vapeur
saturante.
Si on ne dispose pas d'appareil spécifique,
le flux de chaleur latente est déduit de l'équation du
bilan d'énergie Eq(1.1). L'incertitude sur
l'estimation de LE est alors la somme de celle sur tous les autres termes du
bilan.
LE = Rn -- G -- H (1.30)
1.5 Critères de vérification de la
qualité des données d'eddy
corrélation
Pour estimer la qualité des données
de flux calculés, différents tests statistiques sont
effectués sur les sorties semi-horaires de EdiRe en suivant le
schéma de [321. Ces tests sont basés sur les vérifications
des caractéristiques intégrales de
turbulences (ITC), la stabilité de
Monin-Obukhov et la stationnarité des flux turbulents
w'q' et w'T
0s. Ils permettent de vérifier la
stationnarité des données et le développement de la
turbulence nécessaire a la théorie des eddy
corrélation. On les synthétise dans un label de
qualité a trois niveaux attribué a chaque
donnée et a chaque pas de temps.
1.5.1 Test des Caractéristiques
Intégrales de Turbulence (ITC)
Ce test a été développé pour
qualifier les conditions de développement de la turbulence de
l'atmosphère par rapport aux flux turbulents. Les tests sur les
caractéristiques intégrales permettent de
vérifier si les conditions de la théorie des similitudes sont
remplies. Cette théorie permet de relier les différentes
grandeurs de la Couche Limite Atmosphérique
(écarttype de T par exemple) a une échelle
caractéristique (T* pour la
température) et a une fonction d'une seule variable (la
stabilité). Si les données collent au modèle alors, on est
dans les conditions de la théorie et les transferts sont verticaux (le
bilan des flux turbulents horizontaux est nul), sinon d'autres processus sont
en jeu et des termes supplémentaires peuvent s'ajouter dans
l'Eq (1.20) (gradients horizontaux non nuls par exemple).
Les modèles de similitude reliant la variance d'une variable X
a son échelle caractéristique X* ont
été documentés [31; 21] et s'expriment comme
des lois puissances de la stabilité (Eq.1.31).
( ax )modele = c1(
z L)c2 (1.31)
X*
On calcule ensuite le ratio de la différence entre le
modèle et la mesure par rapport au modèle Eq(1.31).
( X* óx )modele - ( X*
óx )mesure
IT Có =| | (1.32)
( X* óx)modele
oi (z L) est la
stabilité de Monin-Obukhov, X* le paramètre turbulent
qui peut être la température T, la vitesse du
vent verticale w ou horizontale u,
óx est l'écart-type du
paramètre X*, c1 et c2 sont des
constantes dont les valeurs sont représentées dans le tableau
ci-dessous. Si le paramètre ITCó est
inférieur à 30% une turbulence bien développée peut
être supposée. Pour une atmosphère stable ou neutre,
c'est-à-dire pour des valeurs de flux de chaleur sensible
inférieures à 10W.m-2, le test ne peut
être appliqué.
TAB. 1.1 - Valeurs des constantes c1 et c2
d'après 1311.
|
Paramètre
|
z/L
|
c1
|
c2
|
|
óu
|
0 > z/L > -0,032
-0,032 > z/L
0 > z/L
> -0,032
-0,032 > z/L
0,02
< z/L < 1
0,02 > z/L >
-0,062
-0,062 > z/L >
-1
-1 > z/L
|
2,7
4,15
1,3
2
1,4
0,5
1,0
1,0
|
0
1/8
0
1/8
-1/4
-1/2
-1/4
-1/3
|
|
u*
ów
|
|
u*
óT
|
|
T*
|
1.5.2 Classification globale des données
Les caractéristiques
intégrales de turbulences sont calculées pour
w, u et Ts. La
qualité
d'un flux est composée du résultat du test sur
les paramètres turbulents
w'Ts' et
w'q' et de celui du " Test des
Caractéristiques Intégrales de Turbulence"
des deux séries chronologiques dont la covariance
est calculée. Le tableau ci-dessous montre le test qui est
appliqué pour chaque flux de chaleur.
TAB. 1.2 - Différents tests appliqués
sur les flux H et LE
|
Test flux
|
Tests paramètres turbulents
|
Test ITCów
|
Test ITCóTs
|
|
u*
|
T s *
|
|
H
LE
|
|
*
*
|
*
|
|
w0T s0
|
|
w'q'
|
Le résultat combiné des tests
appliqués est récapitulé suivant trois classes
:
TAB. 1.3 - Classification globale d'après
1321.
|
Test paramètres turbulents(%)
|
Test ITC (%)
|
Classe finale des flux
|
|
<
|
30
|
<
|
30
|
0
|
|
<
|
100
|
<
|
100
|
1
|
|
>
|
100
|
>
|
100
|
2
|
Ces tests sont appliqués aux données
semi-horaires issues des calculs de EdiRe et sont ensuite classées selon
l'approche suivante :
Hypothèse de base Pour des valeurs de flux
de chaleur sensible inférieures a 10W.m-2, nous ne
disposons pas de critères pour classer ces données. Nous leur
affectons une classe supplémentaire qui est '-1'.
Classes de H
- Si les trois paramètres w'T
0s, ITCów u* et
ITC óTs
s sont chacun inférieurs a 30% alors
nous
T *
attribuons a la donnée semi-horaire la classe '0'.
- S'ils sont tous compris entre 30 et 100% alors nous avons
classe '1'. - Et s'ils sont chacun supérieurs a 100% alors nous avons
classe '2'.
Classes de LE
- Si les paramètres w'q' et
ITCów u* sont chacun inférieurs a 30%
alors nous attribuons a la
donnée semi-horaire la classe '0'.
- S'ils sont compris entre 30 et 100% alors nous lui attribuons
la classe '1'. - Et s'ils sont chacun supérieurs a 100% alors nous avons
classe '2'.
Description des classes
Classe -1 : données inclassables
Classe 0 : données de très bonne
qualité haute, utilisables pour une recherche fondamentale.
Classe 1 : données a qualité modérée
utilisables pour des études de bilan.
Classe 2 : données de mauvaise
qualité.
1.6 Conclusion
Dans ce chapitre, nous avons développé les
différentes méthodes d'obtention des flux notamment le flux de
chaleur dans le sol et les flux de chaleurs sensible et de chaleur latente. Les
critères pour vérifier la qualité des
données des flux turbulents de chaleur ont été
également exposés. Dans la suite de ce document, nous
décrivons la zone d'étude puis procédons a une
analyse météorologique des
différentes périodes retenues.
CHAPITRE 2
DEscRipTioN DE LA zoNE D'ETuDE ET
cARAcTERisATioN METEoRoLoGiQuE DEs
sous pERioDEs D'ETuDE
Ce chapitre présente dans un premier temps la zone
d'étude ainsi que les données utilisées. A
partir des moyennes journalières du rayonnement
net, de la température de l'air, la tension de vapeur réelle, la
vitesse et la direction du vent issues des mesures de la station de Nalohou,
nous décrivons les traits caractéristiques d'une
année en climat soudanien (Aoilt 07- Juillet 08). Nous comparons ensuite
les paramètres météorologiques des
deux stations entre elles pendant les différentes sous périodes
choisies : la saison sèche en Janvier, la saison des pluies en Juillet
et la période de transition entre saison des pluies et la saison
sèche en Novembre.
2.1 Situation geographique de la
zone d'etude
Nos stations d'étude sont localisées dans la
Donga (Nord Bénin) qui est
caractérisé par un climat soudanien. La première 'Nalohou'
(latitude 9°74484 N, longitude 1°60457 E, altitude 449m)
est située a environ 11km du centre ville de Djougou. Cette
station se trouve dans une zone anthropisée oil les arbres sont rares.
La deuxième 'Bellefoungou' (latitude 9°7915N,
longitude 1°718 E, altitude 414m) est localisée dans une
forêt claire a isoberlinia située à 17km de
Djougou. La hauteur de la végétation
présente sur celle-ci est d'environ 14m. La station de Nalohou a
été installée en Juillet 2007 tandis que celle
de Bellefoungou a vu le jour un peu plus tardivement en Septembre
2007 et complétée en Juin 2008. Sur ces stations sont
installés des capteurs de mesures
météorologiques et des flux de chaleur
sensible et de
chaleur latente. Tous les capteurs (météo +
flux) ont été ré-installés a Nalohou en Juillet
2007. Alors que ce n'est qu'en Juin 2008 que
celle de Bellefoungou a bénéficié du capteur de
mesure du flux de chaleur latente. Notons que ces deux stations sont
distantes de 20km environ (Figure 2.1).
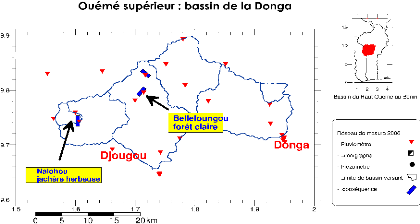
FIG. 2.1 Carte de localisation des stations de mesure dans la
Donga.
Données
météorologiques
On dispose des capteurs placés a 2m (Nalohou) et a 5.5m
(Bellefoungou) du sol qui enregistrent toutes
les quinze minutes, la vitesse et la direction du vent, la
température de l'air, la pression atmosphérique,
l'humidité relative, le rayonnement (incident et
réfléchi) courtes longueurs d'onde, le
rayonnement(incident et réfléchi) grandes
longueurs d'onde, le rayonnement net, la pression de
vapeur saturante et réelle, la température du sol a -10, -20 et
-40 cm et le flux de chaleur dans le sol. Le tableau en annexe 2
récapitule toutes les variables mesurées avec leurs
précisons.
Données flux
Les flux sont calculés par eddy correlation
(Chapitre 1) a partir des mesures a haute
fréquence
(20Hz). Elles englobent les mesures issues d'un
anémomètre sonique 3D
(CSAT3, Campbell Scientific Ltd.) pour la vitesse et la
température et d'un analyseur de gaz (Li7500,
Licor) pour les concentrations en H20 et C02 présentent dans
l'atmosphere. A Bellefoungou, les capteurs de flux sont
disposés au dessus de la végétation (18m) et a
Nalohou a 4m du sol.
2.2 Dynamique saisonnière de la
surface du sol sur les deux stations
Les photos de la figure (2.2) illustrent l'état
de la surface de Nalohou en Novembre et en Juillet.
a) b)

FIG. 2.2 Couverture du sol a Nalohou en Novembre (a) et en
Juillet (b).
Le site de Nalohou est trCs influencé par les
activités économiques (agriculture,
passage des baufs pour pãturer dans cette zone). En Novembre,
on tend vers la fin des saisons pluvieuses. La jachCre herbeuse est trCs sCche,
touffue et couvre partiellement le sol. Elle empêche l'air qui
circule au-dessus de la jachCre d'atteindre directement la surface même
du sol et atténue par conséquent la
quantité d'énergie qui doit
servir a chauffer la surface. Non seulement, cette quantité
est atténuée mais aussi elle met également plus
de temps avant de parvenir au sol. En saison pluvieuse (Juillet), nous avons de
la jachCre humide. Par contre en Janvier, le sol est nu car les brülis et
le sarclage (enlCvement des herbes) s'effectuent souvent en
Décembre.
La station de Bellefoungou n'est pas
influencée par les activités anthropiques. La surface
du sol est plus ou moins homogène. En saison humide, la
surface du sol est couverte d'herbacées.
a) b)

FIG. 2.3 Couverture du sol a Bellefoungou en Juillet
(a) et vue de dessus de la vegetation de Bellefoungou
(b).
2.3 Description de l'année 2007 - 2008 cas de la station
de Nalohou (Aoflt 07 - Juillet 08)
Le rayonnement net, la température de l'air,
le vent et la tension de vapeur constituent les paramètres
climatiques déterminants sur lesquels on se base
pour caractériser la météo d'une région.
La description de ces principaux paramètres
météorologiques nous permettra de
souligner les grands traits de la
dynamique intra-saisonnière de la zone
d'étude.
2.3.1 Le rayonnement net
La figure (2.4) montre l'évolution des
moyennes journalières du rayonnement net entre le
01/08/07 et le 31/07/08 a Nalohou.
Le maximum observé est de 190W.m-2
en Septembre et en Juin. Des valeurs élevées du
rayonnement net s'observent durant toute la saison des pluies
(Mars-Octobre). On remarque que durant cette
période, le rayonnement fluctue beaucoup d'un jour a l'autre
alors qu'en saison sèche il garde une valeur plus
ou moins stable (Figure 2.4). Cependant, nous constatons
que la période qui s'étale de Novembre a
Décembre est aussi marquée par une diminution
notable du rayonnement net par rapport à celle
humide.
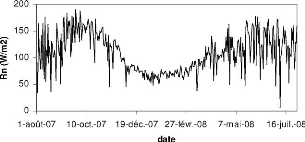
FIG. 2.4 Evolution temporelle des moyennes
journalières du rayonnement net a Nalohou.
Les fluctuations relevées en saison des pluies sont
dues à la présence des nuages. Pendant cette
même période on a une atmosphere propre c'est-à-dire
dépourvue d'aérosols; ce qui
explique le fort taux de rayonnement observé en
absence de nuages. La venue de l'harmattan en Novembre se traduit
par la baisse du taux de rayonnement causée par un
réchauffement du sol et un rayonnement émis par la
surface qui est plus important. Ces différences
relevées au cours de l'évolution saisonniCre du
rayonnement net s'expliquent également
par la baisse du rayonnement incident grande
longueur d'onde observée des mi-novembre et qui
demeure faible jusqu'à la fin Janvier (Figure
2.5).
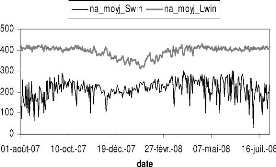
FIG. 2.5 Evolution temporelle des moyennes
journalières du rayonnement incident courte (Swin) et
grande (Lwin) longueur d'onde a Nalohou.
2.3.2 La temperature de l'air
La température moyenne sur l'année est
de 25,3CC.
Cette moyenne cache d'importantes fluctuations
journalières qui peuvent atteindre 20CC dans une
journée de saison sèche. Sur la période Aoüt
07-Juillet 08, les températures extremes enregistrées
sont 38CC en Mars et 13CC en Janvier (Figure 2.6 ).
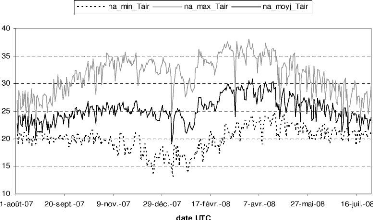
FIG. 2.6 Evolution temporelle des moyennes
journalières, des valeurs minimale et maximale de la temperature de
l'air a Nalohou.
Les températures les plus élevées
s'observent en Mars-Avril et en Novembre, les plus basses en Décembre et
en Juillet. En Décembre, la baisse des températures est due a la
baisse du rayonnement et au vent (l'harmattan) qui soufle
plus fort (voir figure 2.9). En Juillet, la baisse des
températures est causée par le flux de mousson. En
général, les températures moyennes
maximales sont élevées sur toute l'année et varient entre
22CC et 38CC. En revanche, les minima s'échelonnent entre 13CC et 25CC.
La montée observée des températures en début
d'année (Mars-Avril) correspond a l'augmentation du
rayonnement solaire dont l'action va Ctre ensuite
contrecarrée par l'arrivée des flux de mousson provenant du sud .
Il s'ensuit une baisse des températures qui débute
avec la mousson, qui atteignent un minimum au mois
d'Aoüt (22,5CC). La fin de la saison des pluies entraIne une
augmentation de la température qui va Ctre
très rapidement contrariée par la baisse du
rayonnement net
amorcée des Novembre. L'amplitude thermique
journaliCre est maximale durant le mois sec de Décembre, 20,9CC, et se
réduit progressivement pour être minimale au mois
d'Aoüt 6-7C en moyenne glissante sur 10 jours
(Figure 2.7).
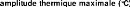
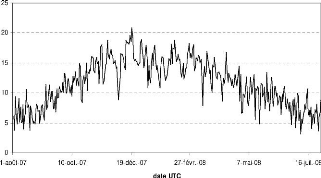
FIG. 2.7 Ecart entre les températures moyennes
journalières maximales et minimales au cours de la période
Aoüt 07-Juillet 08 a Nalohou.
2.3.3 La tension de vapeur réelle
La figure (2.8) montre l'évolution temporelle
de la moyenne journaliCre de la tension de vapeur réelle.
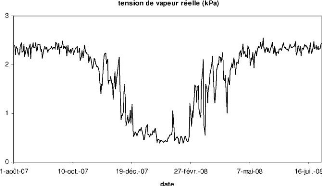
FIG. 2.8 Evolution temporelle de la moyenne
journalière de la tension de vapeur réelle sur la période
Aoüt 07-Juillet 08 a Nalohou.
A Nalohou, le minimum de tension de vapeur a lieu en
Février avec une valeur de 0,38 kPa. Sur la période Aoüt 07
- Juillet 08, le maximum de tension de vapeur s'observe en Mai (2,54 kPa).
Pendant la mousson (Mai-Octobre), on observe des valeurs élevées
plus ou moins constantes de la tension de vapeur. Elle chute ensuite en
Novembre pour atteindre sa valeur la plus faible en Février. En saison
humide, l'atmosphère contient une forte quantité de
vapeur d'eau, celle-ci chute en Novembre avec l'arrivée de l'harmattan
et devient faible en saison sèche.
2.3.4 La vitesse et la direction du vent
- La vitesse du vent
L'examen des vitesses moyennes journalières
(figure 2.9) montre que la variation annuelle des
vitesses moyennes du vent est assez faible. La vitesse la plus forte
enregistrée sur un quart d'heure est de
8m.s-1. Les vitesses moyennes
journalières varient entre un maximum en Janvier
(3,1m.s-1) vers un minimum en Octobre
(0,61m.s-1). Les maxima sont observés pendant la
période de l'harmattan et induisent une baisse des
températures.
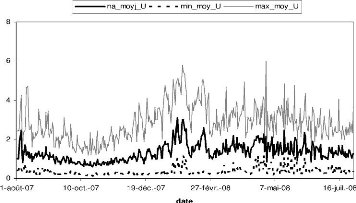
FIG. 2.9 Evolution temporelle des moyennes
journalières , des valeurs minimale et maximale de la vitesse du
vent.
On observe toujours un maximum du vent aux heures diurnes
(figure 2.10) mais sa valeur, relativement a celle des heures
nocturnes, évolue considérablement. Ce maximum horaire se
situe généralement entre 9h et 11
heures. Les vents nocturnes sont plus faibles. Le cycle
diurne
fait penser à la mise en place de vents thermiques locaux
qui sont générés par
des
gradients de température et /ou de pression en surface
(différence de couvert, d'altitude).
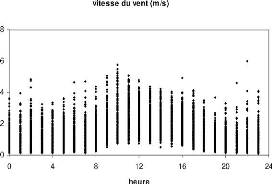
FIG. 2.10 Cycle journalier du vent sur la
période Aoüt 2007-Juillet 2008 a Nalohou.
- La direction du vent
La figure (2.11) indique les
orientations moyennes mensuelles correspondant à une rose des
vents divisée en seize (16) parts. Seuls les vents supérieurs
à 1m.s-1 ont été
considérés dans cette analyse. L'étude
comparative des mois de l'année montre que la
répartition mensuelle des directions n'est pas constante. On observe
successivement :
- Janvier-Février La direction
privilégiée est NE. On a la direction principale la
mieux établie en Janvier 49,7%. On note l'apparition des vents du
NNE.
- Mars Ce mois est assez particulier, il n'y a pas
de direction privilégiée. On a des vents humides du
SSW, et une infirme partie du NE et NW. C'est le passage de la
saison sèche à la saison humide.
- Avril-Aoüt Durant cette période, la direction
principale du vent varie entre 180 et 230. C'est-à-dire que
la zone d'étude est sous l'influence des vents humides venant de la
cOte.
- Septembre-Octobre Ces deux mois se ressemblent; mis
a part l'apparition des vents de E observée en Octobre. La direction
privilégiée est le SE.
- Novembre-Décembre la prédominance des vents du
NEE et du NE s'affirme. On note la persistance des vents du SW en Novembre.
On remarque que la direction du vent
suit une évolution au cours de la période de l'année.
Pendant la saison sèche, la zone d'étude est sous l'influence des
vents forts et secs provenant du Sahara, l'harmattan (NE). Cette direction
change progressivement avec l'arrivée de la
mousson. En saison pluvieuse, la vitesse des vents fluctue beaucoup plus
qu'en saison sèche, la direction
privilégiée est imposée par la mousson
(SSW).
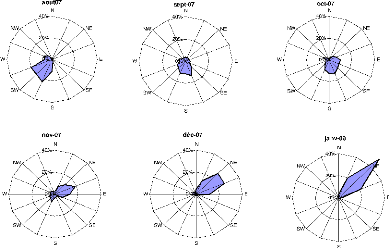
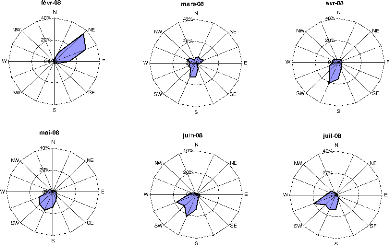
FIG. 2.11 Station de Nalohou, rose des vents Aoüt 07-Juillet
08 (pour des vents supérieurs a
1m.s-1)
Conditions climatiques locales : Comparaison de la
météo de Nalohou et celle de Bellefoungou 34
2.4 Conditions climatiques locales Comparaison de
la météo de Nalohou et celle de Bellefoungou
Les conditions climatiques sont
analysées a partir des mesures
météorologiques des deux stations sur
lesquelles s'effectue cette étude. Afin de
caractériser la variabilité des paramètres
climatiques, trois sous périodes de quinze (15)
jours chacune ont été choisies a partir des analyses
précédentes. La première située entre le 16 au 30
Janvier 2008 est qualifiée de 'sous période
sèche'. Durant celle-ci l'air est très sec. La seconde sous
période (sous période humide) se trouve en pleine saison des
pluies 16 au 30 Juillet 2008. La dernière du 16 au 30 Novembre 2007 est
dénommée ' sous période intermédiaire '. Cette
période est marquée par la fin de la saison des
pluies, on a remarqué que durant celle-ci
l'atmosphère est encore sous l'influence des vents humides venant du
Sud-Ouest.
Pour comparer la météo des deux stations, nous
avons effectué la moyenne sur chaque heure des 15
jours pour les différentes sous périodes définies
précédemment afin d'avoir des journées types
représentatives de chaque sous période.
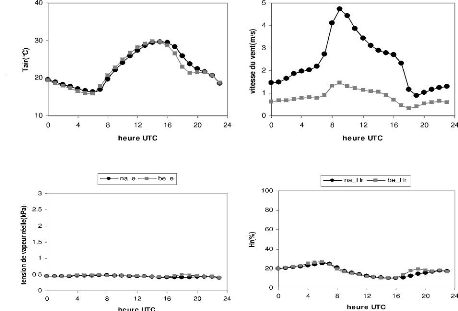
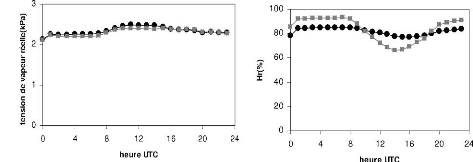
2.4.1 Sous période sèche (16 au 30 Janvier 2008)
Le rayonnement solaire incident courte
longueur d'onde a Bellefoungou est plus fort
que le rayonnement solaire incident de Nalohou
889W.m-2 et 812 W.m-2. Il en est de
même pour le rayonnement solaire réfléchi courte
longueur d'onde (173 W.m-2 et 145
W.m-2). Quant a la température et l'humidité
relative des deux stations, elles varient très peu durant cette sous
période. On note un coefficeint de détermination
(R2) de 95% et 88% respectivement pour la
température et l'humidité. On relève pour la
température un maximum de 29,7C au niveau des deux stations et des
minimums de 15,8CC a Bellefoungou et 16,3CC a Nalohou. Les
variations de l'humidité relative sont de 26,9 % et 10,45 % en
forêt; 25% et 10% sur la jachère . Les nuits a
Bellefoungou sont nettement plus froides. Ce qui se
traduit par l'écart de 0,08kPa observé au niveau de la tension de
vapeur réelle sur les deux stations. Notons que pendant cette
période, l'air est très sec de jour comme de nuit. Le pic
observé en soirée a Bellefoungou est certainement
dü a la végétation qui
dégage de la vapeur d'eau.
Conditions climatiques locales : Comparaison de la
météo de Nalohou et celle de Bellefoungou 35
Le vent est très faible sur le site de la forêt.
Cette mesure est certainement sous estimée a cause de la position du
capteur dans la canopée. Sa valeur quelle que soit
la période est pratiquement le 1/3 de celle de Nalohou. Le
maximum observé a Nalohou est de 4,7m.s-1 pour un
minimum de 0,89m.s-1.
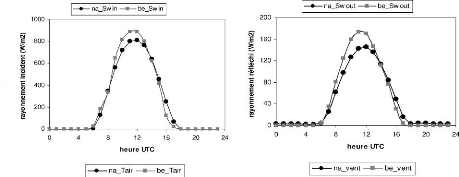
a)
c)
e)
FIG. 2.12 Cycle journalier du rayonnement
incident(a), rayonnement réfléchi(b),
température
de l'air (c), humidité relative(f), vitesse du vent (d) et
tension de vapeur réelle (e)à Nalohou et à
Bellefoungou (sous période sèche).

Conditions climatiques locales : Comparaison de la
météo de Nalohou et celle de Bellefoungou 36
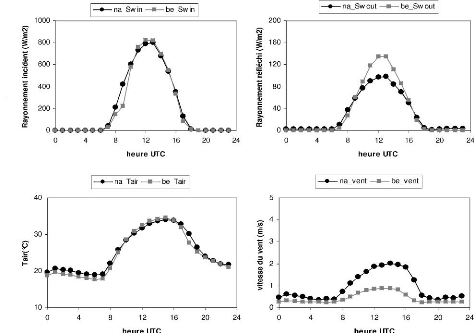
2.4.2 Sous période humide (16 au 30 Juillet 2008)
Ici on note une forte variation de tous les paramètres.
Il existe toujours une différence entre les maxima des
rayonnements solaires incidents courte longueur d'onde
des deux stations, mais elle est plus faible que celle
observée au cours de la sous période sèche (645
W.m-2 et 631W.m-2) pour
Bellefoungou et Nalohou. Les rayonnements solaires
réfléchis sont les mêmes. Le site de
Bellefoungou connaIt une amplitude plus grande (8CC) pour
la température comparée au site de Nalohou (3CC). Dans la
journée, les fortes températures s'observent a
Bellefoungou et dans la nuit a Nalohou. On a les valeurs de 27,3 et
19,5CC a Bellefoungou; 24,6 et 21C a Nalohou. La station
de Bellefoungou est toujours plus froide les nuits que
celle de Naholou ce qui fait qu'on obtient les fortes
valeurs d'humidité relative sur cette dernière (93 et 66%) contre
(85 et 77%) a Nalohou. Par contre la tension de vapeur réelle a Nalohou
dépasse quelques fois celle de
Bellefoungou durant tout le cycle. Le vent est
moyen, la valeur maximale observée est de
2,5m.s-1 a Nalohou. Notons que cette sous
période est située en saison pluvieuse. On remarque
pendant cette période de multiples passages
nuageux entre 12h et 13h; ce qui se traduit
par les sauts brusques de rayonnements qui
s'observent a ces moments précis de la journée (Figure
2.13).
Conditions climatiques locales : Comparaison de la
météo de Nalohou et celle de Bellefoungou 37

e)
FIG. 2.13 Cycle journalier du
rayonnement incident( a), rayonnement
réfléchi(b), température de l'air (c), humidité
relative (f), vitesse du vent (d) et tension de vapeur réelle (e) a
Nalohou et a Bellefoungou (sous période humide).
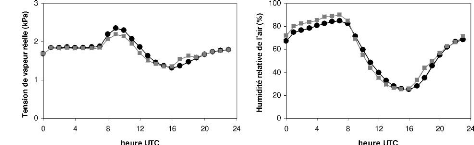
2.4.3 Sous période intermédiaire (16 au 30 Novembre
2007)
On remarque également durant
cette sous période que les rayonnements solaires
(incident et réfléchi) a Bellefoungou sont
élevés par rapport a ceux de Nalohou 825
W.m-2 et 134 W.m-2 pour le site de la
foret; et 799 W.m-2 et 98
W.m-2 pour celui de la jachère. Les deux extremes
d'humidité relative s'observent a Bellefoungou 89,99 et
24,92%. Le maximum de température sur les deux stations avoisine 34CC.
Bellefoungou est toujours plus froide. La tension de vapeur diurne
de Nalohou est supérieure a celle de Bellefoungou;
néanmoins
a)
c)
Conditions climatiques locales : Comparaison de la
météo de Nalohou et celle de Bellefoungou 38
on remarque une variation brusque de celle
de Bellefoungou entre 17h et 18h. La vitesse du vent observée
est pratiquement la même qu'en période
humide (Figure 2.14).
Le capteur de rayonnement est situé
très bas. Il y a certainement des problèmes düs
à la position du capteur en particulier au lever et au coucher du soleil
(effet d'ombrage). La différence entre la vitesse du vent
s'explique par le fait qu'à
Bellefoungou, les capteurs qui mesurent le vent sont
situés à 5,5m du sol. Or on a une hauteur de
végétation qui est de 14m, par
conséquent le vent mesuré est celui relatif à
la circulation au sein de la canopée. Nous prenons dans la suite le vent
et sa direction mesurés à Nalohou comme
référence.

e)
FIG. 2.14 Cycle journalier du
rayonnement incident (a), rayonnement
réfléchi(b), température de l'air (c), humidité
relative (f), vitesse du vent (d) et tension de vapeur réelle (e) a
Nalohou et a Bellefoungou (sous période
intermédiaire).
Remarques
Nous avons remarqué que les
rayonnements solaires réfléchis sont des variables
stationnelles. Le couvert végétal, la texture du sol,
les activités anthropiques (défrichage du
sol, brülure des herbes, etc) sont des facteurs agissant
directement sur l'atmosphère et influencent le rayonnement
solaire réfléchi mesuré a l'échelle de la station.
Les autres paramètres a savoir l'humidité relative, la
température de l'air et la tension de vapeur réelle étant
tous liés au rayonnement solaire connaissent
également une variabilité a l'échelle de la
station.
2.5 Conclusion
Dans ce chapitre, nous avons décrit la zone
d'étude et fait l'inventaire des données utilisées dans
cette étude. La température, le rayonnement net, la
vitesse et la direction du vent connaissent une saisonnalité
marquée. La saison sèche se caractérise par un
renforcement important des flux du Nord Nord Est et la saison humide par ceux
du Sud Sud Quest. Les vents secs coIncident avec une diminution de
l'humidité relative de l'air. Nous retenons a travers ce chapitre
que les paramètres tels que la tension de vapeur,
l'humidité relative de l'air sont des paramètres qui
varient a l'échelle de la station donc en fonction du type de
végétation.
CHAPITRE 3
EXpLoiTATioN DEs REsuLTATs
Les résultats des différentes méthodes
d'obtention des flux turbulents de chaleur (chaleur sensible et latente) et
dans le sol sont exposés dans ce chapitre. Dans un premier temps, nous
avons comparé les résultats des deux méthodes d'obtention
du flux de chaleur a la surface du sol (G) entre elles. Nous avons ensuite
étudié l'évolution intra-saisonnière et l'influence
du couvert végétal sur ce paramètre. La
qualité des données recueillies par le
système d'eddy covariance sera
évaluée a la fois par le test de classification selon la
procédure proposée par [32] ainsi que par
l'analyse du bilan
énergétique.
A partir de ces réflexions sur la
qualité des données, nous pourrons discuter de la
comparaison des flux d'évapotranspiration mesurés sur les deux
types de couverts végétaux.
3.1 Le flux de chaleur a la surface du sol
Le flux de chaleur a la surface du sol G, est une composante
du bilan d'énergie que l'on ne peut pas
négliger en climat tropical. En zone semi-aride
par exemple sur un sol nu, il représente plus de 40% du
rayonnement net [12]. Il est donc nécessaire de
l'évaluer avec précision pour garantir une bonne
estimation de la différence Rn-G. Le problème principal
réside dans son estimation a la surface. Généralement, les
mesures disponibles ne sont pas faites a la surface, par
conséquent on observe souvent une sous estimation et un
décalage temporel des maxima de G du a la diffusion dans la
terre [13].
Sur nos stations d'étude, nous disposons de
capteurs qui mesurent la température du sol aux profondeurs
10, 20 et 40cm. Une bonne connaissance de ces profondeurs s'avère
nécessaire pour pallier aux problèmes de
décalage temporel et de sous estimation du flux de chaleur
à la surface. Le décalage temporel est très
pénalisant pour la fermeture du bilan d'énergie car
celui-ci amène au lever et au coucher du soleil des
pics irréalistes de G de plusieurs dizaines de
W.m-2. Toutefois, il n'est pas évident de
définir la position de la surface de façon
précise le sol réel n'est pas strictement plat et une
érosion peut se faire au cours du temps. La planéIté de la
surface, le couvert végétal etc... peuvent induire des
erreurs dans le calcul du coefficient de diffusion. D'autre part, le calcul des
grandeurs en surface dépendent des gradients
verticaux de température et donc de la distance entre les capteurs et la
surface. Enfin, il faut noter que l'estimation de la distance entre
deux capteurs est a priori plus précise que l'estimation de
la profondeur absolue de chaque capteur. Pour tenir compte de ces
incertitudes sans dégrader les résultats, nous avons
essayé d'estimer les profondeurs des capteurs a partir des
séries de mesures de températures dans le sol. Deux
critères sont utilisés pour estimer la profondeur des deux
capteurs z1 et z2 :
1) Nous vérifions le calage temporel entre
la température estimée en surface par la méthode des
harmoniques et la 'température infrarouge'
calculée a partir des mesures des rayonnements incident et
réfléchi grandes longueurs d'onde
(Eq 3.4) . Ce critère permet d'estimer z1, la profondeur du
premier capteur et donc de corriger les défauts
d'installation, de tassement du sol, de processus de changement
d'état du sol non pris en compte dans l'équation de
chaleur. La conséquence de ce calage temporel
entre la température de surface et la température
infrarouge est que le rayonnement net et le
flux de chaleur a la surface seront aussi phasés.
2) Une fois G et Rn phasés temporellement, nous
faisons varier la profondeur relative des deux capteurs en conservant le
rapport z1/Liz avec (Liz = z2 - z1) de
sorte que le flux de chaleur a la surface du sol garde le
même phasage et que durant la nuit, il soit
approximativement égal au rayonnement net
nocturne. Cette procédure est appliquée sur la
période sèche pendant laquelle, la nuit les flux
turbulents sont nuls.
3.1.1 Comparaison de la temperature de surface et de la
temperature infrarouge
Les émissions radiatives des corps terrestres et
atmosphériques appartiennent au domaine des
grandes longueurs d'onde. Le flux radiatif total
émis par un corps noir correspond a l'intégrale de la
loi de Planck (Eq 3.1) pour l'ensemble des longueurs
d'onde.
Flux radiatifs emis = óT4
(3.1)
Oi ó est la constante de Stefan - Boltzmann
(5,67.10-8W.m-2K-4)
et T est la température du corps en degré Kelvin.
L'énergie totale émise par tout corps, proportionnelle
a celle d'un corps noir, est fonction de son facteur d'émission (ou
émissivité)c. Pour un corps
quelconque, l'équation (3.1)
s'écrit alors :
Flux radiatifs emis = cóT4
(3.2)
Le rayonnement JR qui arrive au sol est
absorbé, a proportion du facteur d'absorption (î) de la
surface. Selon la loi de Kirchhoff, les corps d'absorption élevée
sont aussi de bons émetteurs, et (î = c) [331.
La plupart des corps terrestres se comportent quasiment comme des
corps noirs. Une part du rayonnement de grandes
longueurs d'onde incident (Lwin) est réfléchie par le
sol. Ainsi, si cs est l'émissivité de la
surface, le rayonnement de grandes longueurs
d'onde partant de la surface (Lwout), mesuré sur le terrain,
est la somme des rayonnements émis et réfléchis
par la surface :
Lwout = ócsT 4 IR + (1 -
cs)Lwin (3.3)
TIR est la température de surface
déterminée a partir des mesures de Lwin et Lwout
et nommée 'Température infrarouge '.
cs = 0, 95 [341. La température
infrarouge TIR est égale a
:
|
TIR = (Lwout - (1 -
cs)Lwin
ócs
|
)1/4 (3.4)
|
Nous rappelons qu'en raison de l'incertitude sur
les valeurs de cs et de celle des mesures des
pyrgéomètres, cette méthode
d'évaluation de la température infrarouge n'est pas
d'une très grande précision pour la valeur de la
température, mais renseigne bien sur la
dynamique du cycle journalier.
La figure (3.1) montre l'évolution
temporelle des températures de surface calculées en prenant pour
profondeurs z1 9 et 10cm avec z2 contante et égale a 20cm et
la température infrarouge calculée a partir de la
formule définie ci-dessus.
On voit bien que la température de surface
Ts (z1 10cm et z2=20cm) est mieux phasée avec la température
infrarouge que Ts(z1=9cm et z2=20cm). Bien
qu'en fin de journée Ts (z1=10cm et z2=20cm) décroit
plus rapidement que TIR. L'objectif poursuivi
étant d'arriver a caler temporellement Tsurface et TIR, nous ne
nous attardons pas sur les différences entre
les variations des deux températures . z1 = 10
cm est confirmée a travers ce calage sur les données
de Janvier. En Juillet, le cycle de rayonnement
grandes longueurs d'onde est très affecté
par les pluies et les nuages et la comparaison a moins de sens. Pour
le mois de Novembre, il semble que le modèle retenu de sol
homogène ne soit pas correct. En effet a cette
période, les herbes sont brülées sauf a l'endroit de la
station oii elles sont simplement coupées. Malheureusement celles-ci
n'ont pas été ramassées et elles créent une couche
d'herbe sèche qui maintient le sol a l'ombre. Ainsi, les
températures et les flux calculés ont une amplitude faible et
déphasée par rapport aux mesures de TIR et aux flux de
rayonnement.
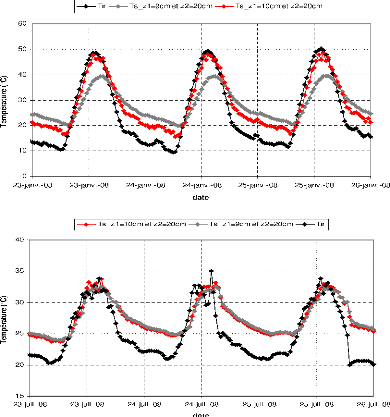
FIG. 3.1 Evolution temporelle de la temperature
infrarouge et des temperatures de surface calculees a partir des
mesures aux profondeurs z1= 9 et 10cm a Nalohou en Janvier (haut) et en Juillet
(bas).
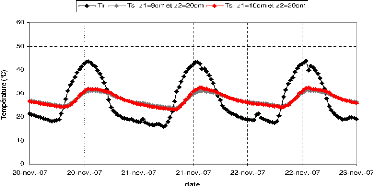
FIG. 3.2 Evolution temporelle de la température
infrarouge et des températures de surface calculées a
partir des mesures aux profondeurs z1= 9 et 10cm a Nalohou (Novembre).
Quant au calage de Rn et G, nous avons
procédé de la même façon mais cette fois
en conservant z1/Äz. Nous avons finalement
retenu z2 17cm pour l'égalité entre Rn et G la nuit.
La même méthode a été exploitée sur la
station de Bellefoungou. Notons que sur cette station,
nous ne disposons pas de pyrgéomètres (pas
de mesures de Lwin et Lwout). Nous avons pris les mesures de
Lwin de la station de flux (Bira) située aux environs (5km) de
celle de Bellefoungou en faisant l'hypothèse
que le rayonnement solaire incident est
pratiquement le même sur les deux stations.
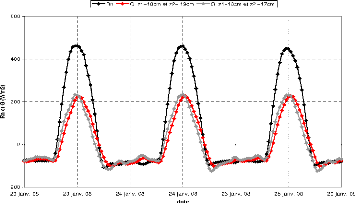
FIG. 3.3 Evolution du rayonnement net et du flux de
chaleur a la surface du sol a Nalohou pendant trois jours en Janvier.
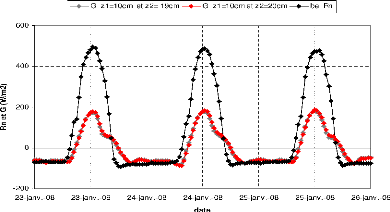
FIG. 3.4 Evolution du rayonnement net et du flux de
chaleur a la surface du sol a Bellefoungou pendant trois jours en
Janvier.
On a constaté que le
décalage temporel entre Rn et G évolue au cours de
l'année. En Novembre, G met plus de temps a décoller. La surface
du sol commence par se chauffer vers 10h au moment oi le rayonnement
avoisine les 400W.m-2. En Juillet, le même constat
est fait mais cette fois-ci en fin de journée oi le sol se refroidit
très lentement. Par contre en Janvier, le pic du rayonnement
net et le flux de chaleur a la surface du sol s'observent a la même heure
(figure 3.3 et 3.4). z2 17cm.
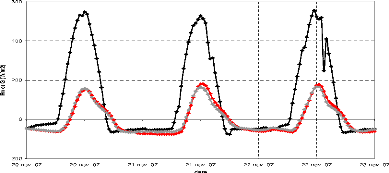
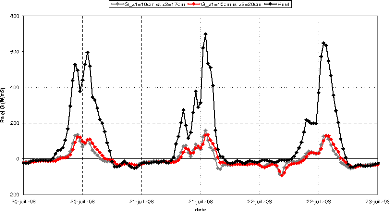
FIG. 3.5 Evolution du rayonnement net et du flux de
chaleur a la surface du sol a Nalohou pendant trois jours en Novembre (haut) et
en Juillet (bas).
3.1.2 Comparaison des flux de chaleur a la surface du sol
calculés avec la méthode des harmoniques et la
formulation de la FAO
- Station de Nalohou
Nous allons comparer le flux de chaleur a la surface du sol en
Janvier oi la surface de Nalohou est nue, calculé a partir de la
méthode des harmoniques avec la formulation de la FAO
(section 1.3.2).
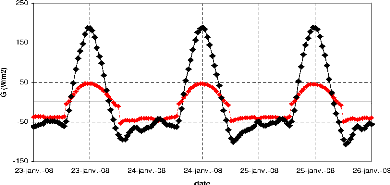
FIG. 3.6 Evolution temporelle des flux de chaleur a la surface du
20 au 23 Janvier 2008 sur la station de Nalohou
Nous remarquons que les flux de chaleur
harmonique et de la FAO sont très bien phasés avec Rn
de part sa formulation. Le problème majeur réside dans le fait
que le flux de chaleur calculé avec la formulation de la FAO
soit toujours pratiquement la moitié de celui estimé
par la méthode des harmoniques. On note un écart de
100W.m-2 entre les maxima de ces deux grandeurs.
La nuit, le flux de chaleur de la FAO est plus important que
G(harmonique), mais la différence observée entre les
valeurs minimales nocturnes est relativement faible . La nuit, la surface du
sol restitue toute la chaleur qu'elle a accumulée dans la
journée; c'est elle qui joue le rOle de
'pourvoyeur' d'énergie. Nous tirons de la
comparaison entre G(FAO) et G(harmonique) que la
formulation empirique de la FAO sous estime les flux diurnes pour
les sols chauds et secs de moitié. Dans la suite du document, nous
n'utiliserons plus que la méthode harmonique pour
estimer G.
3.1.3 Comparaison des flux de chaleur a la surface a Nalohou et a
Bellefoungou
Dans cette section, nous comparons les cycles diurnes
moyens de G (harmonique) a Nalohou et a
Bellefoungou pour les 3 sous périodes.
- Sous pen ode sèche
La figure (3.7) montre pour la sous période
sèche que le flux de chaleur a la surface a une allure en
cloche avec des valeurs positives le jour et négatives la
nuit. Les valeurs positives désignent un gain pour
la surface et les valeurs négatives une perte pour la
surface. G a Nalohou atteint son maximum 170W.m-2 a 13h
alors que la surface de Bellefoungou se réchauffe
plus rapidement et atteint un maximum très voisin
(172W.m-2) mais, une heure plus tOt 12h (figure
3.7).
Dans l'après midi, la quantité
d'énergie reçue par la surface de
Bellefoungou décroIt plus rapidement que celle de
Nalohou, et ses valeurs nocturnes sont plus basses entre 0h et 7h
(Bellefoungou). On note une très faible différence des
flux de surface sur ces deux stations durant cette sous
période; le coefficient de corrélation est de 93%.On
peut enfin noter un léger infléchissement du
cycle diurne en matinée et en soirée a
Bellefoungou dü a un effet
d'ombrage sur le capteur qui est
situé en-dessous de la cime des arbres avoisinants.

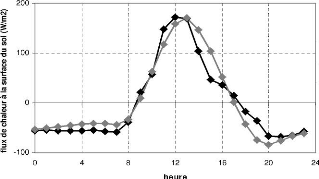
FIG. 3.7 Cycle journalier moyen de G
harmonique a Nalohou et a Bellefoungou (sous
période sèche).
- Sous période humide

Durant cette période, le flux de chaleur à
Nalohou est plus faible qu'à Bellefoungou. La
surface du sol de Bellefoungou se refroidit toujours plus vite
que celle de Nalohou, la nuit la jachère humide (Nalohou)
dégage plus de chaleur que la
forêt claire de Bellefoungou. Le maximum observé en
forêt est de 168W.m-2 et 89W.m-2
sur la jachère. On note une corrélation de 91,7% entre les deux
flux.
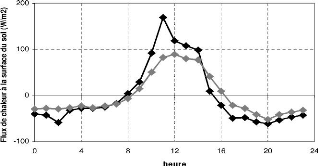
FIG. 3.8 Cycle journalier moyen de G
harmonique a Nalohou et a Bellefoungou (sous
période humide).
- Sous peniode iritenmCdiaine
La figure (3.9) montre le cycle journalier
moyen du flux de chaleur a la surface du sol a Nalohou et a
Bellefoungou.
On observe un décalage d'environ 2h entre les 2
maxima.
Le flux de chaleur observé a Nalohou est beaucoup plus
tardif que celui de Bellefoungou, ce qui se
traduit par la faible corrélation obtenue entre les deux stations 60%.
L'écart observé pendant cette sous période est plus de
100W.m-2 269 W.m-2 a
Bellefoungou et 115W.m-2 a Nalohou. Le
décalage temporel et la différence obtenue sont
liés notamment a la couverture végétale de
Nalohou pendant cette période. En Novembre, nous avons de la
jachère herbeuse sèche coupée qui recouvre la
surface du sol. Elle empeche le rayonnement solaire d'atteindre
directement la surface du sol et atténue donc la
quantité de chaleur qui servirait a chauffer la
surface du sol. Le signal obtenu a la surface du sol est
retardé et par conséquent la réponse du sol
(flux de chaleur a la surface du sol) est aussi retardée. Ce
qui explique le faible taux de corrélation obtenu.
La jachère herbeuse sèche joue donc le rOle d'amortisseur entre
la surface du sol et l'atmosphère. Par conséquent, la
valeur de G obtenue a Nalohou pendant cette sous période est donc sous
estimée par rapport a un sol oi les pailles auraient été
brülées.
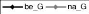
FIG. 3.9 Cycle journalier moyen de G
harmonique a Nalohou et a Bellefoungou (sous
période intermédiaire).
Conclusion : On retient de cette comparaison que la
formulation de la FAO est bien phasée mais sous estime nettement G pour
les sols chauds et secs. La couverture végétale
influence le flux de chaleur a la surface du sol, elle joue le rOle
d'amortisseur entre l'atmosphère et la surface du sol. On a
remarqué que le flux de chaleur a la surface du
sol (G) varie beaucoup. La surface de Bellefoungou
dégage plus la chaleur la nuit que
celle de Nalohou. Ceci est lié a la forte réflexion du sol
observée sur cette dernière.
3.2 Les flux turbulents de chaleur H et LE
Dans cette partie, nous présentons les résultats
des tests statistiques effectués sur les flux eux
mêmes. Les résultats des sous périodes définies
précédemment sont d'abord présentés pour
chaque station. Ensuite, nous procédons a une
analyse de la qualité des données.
3.2.1 Contrôle de qualité
La qualité des données de flux est
vérifiée afin de s'assurer de la validité de la
théorie utilisée pour le dépouillement des données
d'eddy corrélation dans la zone soudanienne. Pour ce faire,
des seuils sont établis pour chacun des tests utilisés (voir
chapitre 1). Foken et al. (2004) ont décrit les principaux tests pouvant
être utilisés pour le contrOle de qualité [301.
Les tableaux suivants illustrent les résultats obtenus (pour
chaque sous période) pour les tests de
vérification.
Nous rappelons que :
Classe 0 : données de très bonne
qualité haute, utilisables pour une recherche fondamentale.
Classe 1 : données a qualité modérée
utilisables pour une étude du bilan.
Classe 2 : données de mauvaise
qualité.
A Nalohou, plus des deux tiers des données
qualifiables (289 pour H et 313 pour LE) appartiennent a la classe
0; seulement 11% de H et 7% de LE sont de mauvaise
qualité.
A Bellefoungou, au contraire, sur un total de 268
données qualifiables c'est-a-dire les données pour
lesquelles H >10W.m-2, 70% sont de mauvaise
qualité (tableau 3.1).
TAB. 3.1 - Classification des données de flux: sous
période sèche
|
Nalohou
H % LE %
|
Bellefoungou
H %
|
|
Classe 0
|
66 74
|
10
|
|
Classe 1
|
22 18
|
19
|
|
Classe 2
|
11 7
|
70
|
|
Total données qualifiables
|
289 313
|
268
|
En saison humide (tableau 3.2), la qualité des
données de Bellefoungou est meilleure par rapport a celle
observée en saison sèche (tableau 3.1). On note :
- 45% (H) et 50% (LE) appartiennent a la classe 0.
- 27 % (H) et 18% (LE) appartiennent a la classe 1.
Plus de 80% (H) et environ 68% (LE) des données
qualifiables sont de bonne qualité.
Par contre a Nalohou, on note une baisse du taux des
données de la classe 0.
- 50% (H) et 53% (LE) pour la classe 0.
- 24% (H) et 13%
(LE) pour la classe 1.
TAB. 3.2 - Classification des données de flux: sous
période humide
|
Nalohou
H % LE %
|
Bellefoungou
H % LE %
|
|
Classe 0
|
50
|
53
|
45
|
50
|
|
Classe 1
|
34
|
13
|
27
|
18
|
|
Classe 2
|
15
|
32
|
26
|
31
|
|
Total données qualifiables
|
294
|
390
|
233
|
276
|
En Novembre, la qualité est plus ou moins bonne
pour LE. Environ 86% de H et 63% de LE sont de qualité haute
et modérée.
TAB. 3.3 - Classification des données de flux: sous
période intermédiaire
|
Nalohou
H % LE %
|
|
Classe 0
|
63
|
32
|
|
Classe 1
|
22
|
31
|
|
Classe 2
|
13
|
36
|
|
Total données qualifiables
|
305
|
432
|
Récapitulatif
Sur les trois sous périodes, on a constaté
que sur la jachère herbeuse les 2/3 des données sont
de bonne qualité (classes 0 et 1). En saison sèche
c'est-à-dire en Janvier la qualité est très
bonne, environ 90% pour H et 93% pour LE. En Novembre la
qualité des données de LE est très
partagée, 1/3 pour chaque classe. Pendant cette
période, on a obtenu le taux le plus élevé (36%) des
données de mauvaise qualité pour LE.
A Bellefoungou, en saison humide, la
qualité est meilleure par rapport à la saison
sèche. La mauvaise qualité obtenue en Janvier est
liée principalement à la hauteur du mat sur lequel
sont installés les capteurs de mesures d'eddy
corrélation. En effet, au cours la période de Septembre 2007
jusqu'en Juin 2008, l'anémomètre sonique
était placé au sein de la canopée (17m du sol), toutes les
mesures étaient donc relatives à la canopée . La
végétation empêche la turbulence de l'air de
bien se développer. Mais depuis l'installation du Licor en Juin 2008, le
mat reliant l'anémomètre sonique + Licor a
été placé à 18m du sol.
3.2.2 Analyse de la qualité des
données
Les figures 3.10 et 3.11 illustrent le
cycle journalier et la qualité des flux de chaleur
sensible et latente au cours des trois sous périodes à Nalohou et
à Bellefoungou.
La nuit, les flux de chaleur sensible sont très faibles
(inférieurs à 10 W.m-2), les flags
de qualités ne peuvent être attribués.
Lorsqu'ils le sont, ils sont de mauvaise qualité
car l'atmosphère est très proche de la neutralité.
On distingue trois périodes dans la
journée le matin (7h-8h30) oi la qualité est
moyenne
ou mauvaise (30% des données de bonne
qualité), le restant de la journée (8h30-17h) oi
les
flux sont de bonne qualité (80%), puis un
déclin en fin de journée (17h-18h) mais avec une
qualité légèrement meilleure
que celle du matin (50% de haute qualité). Le
matin et le soir sont des périodes de transition entre une
atmosphère turbulente la journée et stable la nuit, les
performances des capteurs en sont affectées. On constate
également une qualité globale
meilleure pour H que pour LE. Comme on l'aperçoit
sur les figures ci-dessous , les données de LE sont de bonne
qualité en milieu de journée quand les flux
de H sont les plus importants et la couche limite est bien
développée. Remarquons qu'à
Bellefoungou, en saison sèche entre 11h et 17h on a
que 20% de flux de bonne qualité.
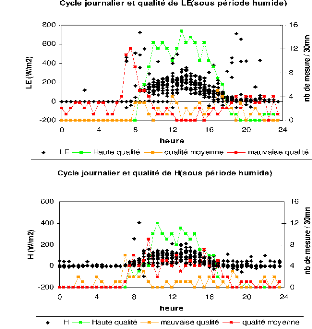
c)
e)
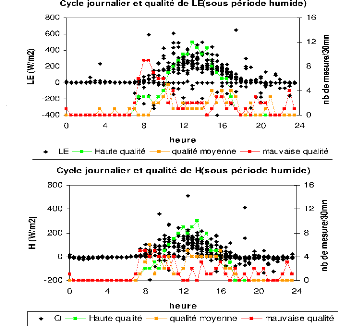
a)
c)
FIG. 3.10 Cycle journalier et
qualité de LE et de H durant les sous périodes
sèche (a et b), humide (c et d)et intermédiaire (e et 1) a
Nalohou.
FIG. 3.11 Cycle journalier et
qualité de LE et de H durant les sous périodes
sèche (c) et humide (a et b) a Bellefoungou.
3.3 Calcul du bilan d'énergie
La qualité des données de flux peut
être aussi vérifiée par l'analyse du bilan
énergétique [35; 361. Le test de
la fermeture du bilan énergétique
implique la comparaison des flux d'énergie
mesurés par le système de covariance de turbulences a
des flux mesurés indépendamment (rayonnement net et le
flux de chaleur ala surface du sol). Pour vérifier le
degré de fermeture, il suffit de vérifier
l'égalité entre les deux membres de
l'équation du bilan
énergétique soit :
Rn -- G = H + LE
oi H est le flux de chaleur sensible et LE celui de chaleur
latente, tous deux mesurés par le système de
covariance de turbulences, Rn le rayonnement net et G le flux de
chaleur a la surface du sol.
- Elimination des données douteuses
Les données utilisées présentent
quelques aberrations dues au mauvais fonctionnement des
appareils (par exemple faible tension de batterie) en Novembre et en Juillet.
Ces défauts de fonctionnement affectent considérablement les
mesures d'eddy corrélation notamment en début de
journée - entre 8h et 10h, en fin de journée - entre 17h et 18h
et quelques fois la nuit entre 1h et 3h. En Janvier, on
relève a Nalohou une période (14 au 17 janvier 2008)
oi la vitesse du vent a dépassé
30m.s-1. Toutes ces valeurs ont été
supprimées. Remarquons
aussi que nous n'avons
pas tenu compte des données obtenues les moments oi il y a eu
pluie.
3.3.1 Variabilité temporelle du bilan
d'énergie a Nalohou
Les figures 3.12 a, b et c illustrent le
comportement moyen horaire des termes du bilan
d'énergie sur les 3 sous périodes d'étude. Le
rayonnement net impose son allure a H, G et LE. Elle est
caractéristique d'un ciel sans nuage. Toutefois,
le rayonnement net moyen maximal est assez faible
(450W.m-2 en saison sèche) qui est
caractéristique d'une surface chaude qui perd
beaucoup d'énergie par rayonnement
infrarouge.
- En saison sèche, le flux de chaleur latente
(évapotranspiration) est extrêmement faible . Le maximum
observé est de 5W.m-2. Quant au flux de chaleur
sensible, il est pratiquement égal au double du
flux de chaleur dans le sol. Le maximum observé est de
450W.m-2, 315W.m-2 et
170W.m-2 respectivement pour Rn, H et G.
- En saison des pluies (figure 3.12.c), le
rayonnement net fluctue beaucoup avec l'ennuagement.
Toutefois, le maximum observé est supérieur a celui
observé en saison sèche. Le ciel plus clair, le sol plus froid et
l'albédo plus faible produisent un Rn plus important. Enfin, le 'retard'
observé au niveau du maxima du rayonnement net montre
que les nuages sont présents plutOt en
matinée. Le maximum (560W.m-2) est atteint entre 13h
et 14h. La chaleur latente est importante durant cette période
(233W.m-2); H et G sont presque du
même ordre de grandeur. Leur maxima est de
111W.m-2 et 89W.m-2.
- En Novembre (figure 3.12.b), un mois après
la dernière pluie, le rayonnement net est du même ordre
de grandeur qu'en saison des pluies
(569W.m-2). Par contre, le flux de chaleur latente a
beaucoup diminué (63W.m-2) au profit du flux de
chaleur sensible (271W.m-2). Le flux de chaleur a la
surface du sol augmente bien plus lentement (115
W.m-2).
FIG. 3.12 Cycle journalier horaire moyen de
Rn, H, LE et G en Janvier (a), en Novembre (b) et en Juillet (c) a Nalohou.
Pour comparer les différents flux sur les
différentes sous périodes, nous avons exprimé
chaque terme du bilan en % du rayonnement net
(Figure 3.13). On constate donc a Nalohou :
- En Janvier (figure 3.13.a), G représente
pratiquement 80% du bilan la nuit, LE est toujours faible
inférieur a 5%. Pendant la journée, le pourcentage de
H augmente de 40 a 80% tandis que celui de G diminue de
40 a 10%.
- En Juillet (figure 3.13.b), H varie peu durant le
cycle nycthéméral, environ 20 a 25% de Rn.
LE dans la journée passe de 60 a 80% et la nuit il reste
inférieur a 10%. G est de 25% dans la journée.
- En Novembre (figure 3.13.c), dans la
journée le pourcentage de H augmente de 30 a 70%
tandis que celui de LE diminue de 30 a 10%. G est sous estimé
pour cause de mauvaise estimation pendant cette période (herbes
couchées ).
FIG. 3.13 Pourcentage de H, LE et G par rapport a
Rn en Janvier (a), Juillet (b) et en Novembre (c) a Nalohou.
Les périodes sèche et intermédiaire sont
marquées par un dégagement
nocturne important de la chaleur par le sol. Au cours des mêmes
périodes, le flux de chaleur sensible est le terme
prépondérant du bilan, quant à la chaleur
latente elle passe de sa haute valeur en saison pluvieuse à une
moyenne en Novembre et devient extrêmement faible en saison
sèche.
Il est à noter enfin le bon phasage temporel
entre Rn et G obtenu en Janvier et en Juillet. Ce n'est pas le cas en Novembre
pour cause de mauvaise estimation de G (voir figure 3.9). A
contrario, les flux turbulents (H et LE) perdurent plus longtemps en
soirée et causent des rapports H/Rn et LE/Rn divergents
lorsque le rayonnement net s'annule le soir. C'est
également le cas pour LE/Rn le matin ce qui
signifie que la végétation
commence à fonctionner dès que le soleil se
lève. A ce moment de la journée, le rayonnement
courtes longueurs d'onde est disponible alors que le
rayonnement net passe des valeurs négatives
à des valeurs positives.
3.3.2 Fermeture du bilan d'energie a Nalohou
Nous avons comparé la répartition de la fraction
d'énergie disponible à la surface du sol
c'est-à-dire Rn-G et celle ayant servi à la convection
et à l'évaporation (H+LE). Pour cela, nous avons tracé le
nuage de corrélation et calculé le coefficient de
détermination entre Rn-G et H+LE à partir des moyennes
de chaque heure sur les quinze (15) jours de
chaque sous
période (Figure 3.14).
Dans les trois cas, la comparaison a mis en évidence
une relation très peu dispersée et linéaire entre Rn-G et
LE + H.
En Janvier et Juillet, plus de 98% de la variance de (H+LE)
est expliquée par (Rn-G). En Novembre, on note une dispersion
plus accentuée autour de la première bissectrice, le coefficient
de détermination (R2) de 94%. La pente obtenue en
Novembre était prévisible. Ce pourcentage est
lié a la qualité des données de flux turbulents
de chaleur observée pendant cette période et
également a la répartition des flux de chaleur a la
surface du sol. En effet, nous avons montré dans la section (3.1),
que le flux de chaleur a la surface du sol réel est sous
estimé dans la zone de mesure de G oi l'herbe n'est pas
brülée mais coupée. Aussi on constate qu'en
Janvier, on obtient une bonne fermeture du bilan d'énergie
avec une pente de 1,07 et une légère surestimation des
flux turbulents. En Juillet, la pente de la droite de
régression est 0,77. La différence entre les deux
saisons étant essentiellement le flux de chaleur latente, il est
probable que l'estimation de ce terme soit sous estimé en
Juillet. En Novembre, la pente de la droite de régression est
0,68. Cette mauvaise fermeture est causée d'une part par un flux dans le
sol sous estimé et déphasé et d'autre part au flux de
chaleur latente qui est également sous
estimé. La sous estimation du flux de chaleur latente provient du fait
que les mesures de w' et de
q' sont réalisées par 2 capteurs
qui ne sont pas parfaitement colocalisés.
Dans la littérature, plusieurs auteurs ont fait cas de
cette situation. Foken et al. (2006) ont montré que la non
fermeture du bilan d'énergie est liée aux erreurs de
mesure, particulièrement celle de la technique
d'eddy corrélation qui cause une sous estimation
des flux turbulents [371. Egalement, Kukharets et al. (2000) ont
montré que cette non fermeture est liée au
stockage d'énergie qui s'effectue entre
la surface du sol et les différents capteurs de mesure qui ne
se trouvent pas a la même hauteur du sol [381. Panin et al. (1998)
pensent que cette non fermeture est liée a
l'hétérogénéIté de la surface du
sol [391. D'autres auteurs ont supposé que les
hétérogénéItés du sol produisent
des turbulences a de plus grandes échelles de temps
que les turbulences mesurées par le système
d'eddy corrélation. Les causes de non fermeture du bilan pour
nos données sont certainement une combinaison de ces trois raisons.
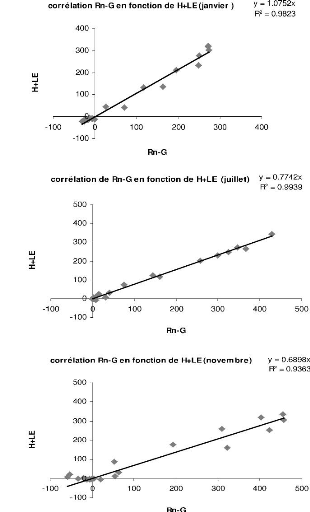
a)
c)
e)
FIG. 3.14 HH-LE en fonction de Rn-G en Janvier (a), Juillet (b)
et en Novembre (c) a Nalohou.
3.4 Variabilité spatiale des flux turbulents de chaleur
3.4.1 Gas du flux de chaleur sensible
La comparaison des flux de chaleur sensible en saison
sèche montre un écart de 44W.m-2 entre les
flux de chaleur sensible à Nalohou et à Bellefoungou.
Cet écart est certainement du au gradient
thermique en surface c'est-à-dire la différence entre
la température de surface et la température de l'air ambiant
qui serait plus importante sur la jachère qu'en
forêt. En particulier, la température de la canopée de
Bellefoungou est certainement plus faible que la
température du sol à Nalohou à cause des processus de
transpiration. La différence relevée entre ces flux
s'explique aussi par le fait que l'air est plus humide et
plus dense en forêt ce qui influe sur le développement
de la turbulence. Cela est confirmé par la figure (3.15) oi
les flux de chaleur sensible la nuit sont nettement négatifs
à Bellefoungou, ce qui est
caractéristique d'une couche de surface stable. Le couvert
arboré réduit la convection au-dessus de la surface du sol, elle
se fait au-dessus de la canopée sur une épaisseur bien plus
importante qu'au dessus des herbacées de la
jachère.
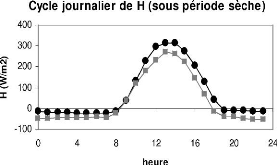
FIG. 3.15 Cycle journalier de H a Nalohou et a
Bellefoungou (sous période sèche).
En saison humide (figure 3.16), le flux de chaleur
sensible diurne est plus important en forêt. Cela est causé par un
effet de rugosité plus fort à Bellefoungou
alors que les températures de couvert sont sensiblement
identiques en cette saison. Le sol reste frais (pas de
gradient de température entre la surface du
sol et l'air ) sur les deux sites, on n'a donc pas de flux nocturne. La forme
du flux obtenue a Nalohou entre 12h et 14h traduit l'effet de
passage des nuages qui est très
marqué sur la jachère. Une comparaison sur une
durée plus longue nous permettra de mieux apprécier la
variabilité de ce paramètre. En Novembre 2007, la station de flux
de Bellefoungou avait un problème de batterie, ce
qui fait qu'on ne dispose pas de données sur cette
période pour comparaison avec Nalohou.
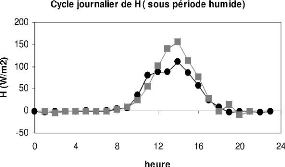
FIG. 3.16 Cycle journalier de H a Nalohou et a
Bellefoungou (sous période humide).
3.4.2 Gas du flux de chaleur latente
La figure 3.17 traduit le cycle
journalier horaire moyen du flux de chaleur latente a Nalohou et a
Bellefoungou en Juillet. On constate que
l'évapotranspiration est plus importante en forêt que
sur la jachère pendant la journée. Dans la nuit,
l'évaporation est pratiquement nulle sur les deux
stations.
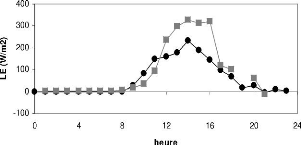

FIG. 3.17 Cycle journalier de H a Nalohou et a
Bellefoungou (sous période humide).
La jachère commence plus tot son évaporation le
matin. Les herbacés semblent être plus réactifs a
l'éclairement que la végétation
haute. Pour la forêt la mise en route est plus lente mais la
dynamique est plus importante. En Janvier 2008, le Licor
(qui mesure le flux de chaleur latente) n'était pas encore
installé, nous n'avons donc pas de mesure de LE sur cette période
ni en Novembre.
3.5 Conclusion
Nous avons étudié précisément
chaque terme de l'équation du bilan
d'énergie de surface. Le calcul des flux turbulents est celui
qui demande le plus d'attention. Le flux de chaleur a la surface du
sol a été réalisé par la méthode des
harmoniques a partir des mesures de températures du sol en
prenant un soin particulier aux profondeurs de mesures. Nous avons
montré a travers la comparaison du flux de chaleur harmonique
et celui de la FAO que la formulation de [141 n'est pas
adaptée aux sols chauds et secs. L'influence du couvert
végétal sur ce paramètre est aussi a noter. La
couverture du sol joue un rOle d'amortisseur entre la surface du sol et
l'atmosphère.
Les flux turbulents de chaleur sont calculés par la
méthode d'eddy corrélation. La
qualité
de ces données a été
vérifiée selon deux approches le schéma de [321 et la
fermeture du bilan d'énergie. La qualité
des données est relativement bonne pendant les trois sous
périodes. Le test de fermeture du bilan d'énergie est
aussi correct pour la sous période sèche. Pour la sous
période humide, les flux de chaleurs latentes sont probablement sous
estimés, et pour la sous période intermédiaire le flux a
la surface du sol est faussé par le fait qu'une
litière a été laissée sur le sol a l'endroit des
capteurs. Les différents coefficients de détermination obtenus
entre la quantité d'énergie disponible et
celle ayant servi a la convection et a l'évaporation a
Nalohou sont satisfaisants lorsque les données aberrantes
sont filtrées.
Conclusion générale et perspectives
Ce mémoire qui s'inscrit dans le cadre du
programme AMMA (Analyse Multidisciplinaire de la Mousson
Africaine) et du projet Ouémé-2025, vise a comprendre le
fonctionnement de l'interface surface - atmosphère. L'objectif est de
réaliser une première estimation des flux
d'énergie et de documenter les flux
d'évapotranspiration en climat soudanien.
Les interactions surface - atmosphère sont complexes.
L'analyse détaillée des processus des
différents échanges qui s'effectuent dans
la couche limite atmosphérique est indispensable a leur
compréhension. Dans cette optique, l'analyse du
bilan d'énergie a la surface est une étape
incontournable. Comprendre cette relation en zone soudanienne est
particulièrement intéressant en raison du lien étroit
observé entre condition atmosphérique et
variabilité climatique, ainsi que le rOle
important que joue l'évapotranspiration dans le bilan
hydrologique.
Ce travail constitue une première analyse du
bilan d'énergie en zone soudanienne. Notre étude a
porté sur deux stations situées dans la
Donga/Bénin une jachère herbacée (Nalohou
974484N, 160457E, 449 m) et une forêt claire (Bellefoungou
979115N, 171800E, 414 m).
L'analyse
météorologique sur une année faite
(chapitre 2) a partir des données de Nalohou montre une
saisonnalité notable des paramètres climatiques. De
cette analyse, trois périodes de quinze (15) jours
chacune ont été identifiées. Les principaux termes du
bilan d'énergie de méso-échelle ont
été évalués et leur variabilité
caractérisée sur ces différentes périodes. Le
calcul des flux turbulents de chaleur est celui qui nécessite
le plus d'attention. Le flux de chaleur a la surface du sol a été
calculé par deux méthodes la méthode des
harmoniques et la formulation empirique de la FAO.
Dans un premier temps, nous avons comparé le flux de
chaleur harmonique calculé a Nalohou en janvier oi le sol est
nu et aucune pluie n'est tombée depuis des mois, avec celui
calculé a partir de la formulation de la FAO. On a
remarqué a travers cette comparaison que le flux
de chaleur calculé a partir de la formulation de FAO sous estime le flux
de chaleur a la surface du sol quand le sol est sec et chaud de
presque 50%. La conclusion tirée de cette comparaison est
que la formulation de la FAO est mise a défaut pour les sols
chauds et secs. D'autre part, on a constaté a partir de la comparaison
des cycles journaliers de G au niveau des deux sites et sur les
trois périodes que ce paramètre est plus important a
Bellefoungou qu'a Nalohou. Le déphasage
temporel et la faible amplitude observés en Novembre a Nalohou sont
liés a la couverture du sol (litière) qui diminue et
retarde la quantité d'énergie devant
parvenir a la surface du sol. Elle joue donc le rOle d'amortisseur entre la
surface du sol et l'atmosphère.
Les flux turbulents de chaleur ont été
mesurés par eddy corrélation. L'analyse de
leur qualité a permis de vérifier la fiabilité
des ces données. Plus des 75 % des données
qualifiables sont de qualité haute c'est-a-dire
qu'elles sont utilisables pour une recherche fondamentale. Aussi,
l'analyse des tracés des cycles journaliers de H
et de LE ainsi que de leurs qualités
associées a montré que les données sont de
très bonne qualité dans la journée
lorsque l'atmosphère est instable. On a
remarqué également que la
qualité de LE est liée a celle de H. Plus
l'atmosphère est turbulente et plus l'eau arrive a s'évaporer
rapidement au sein de celle-ci. On a remarqué enfin
que, les flux d'évapotranspiration mesurés sur la
forêt de Bellefoungou étaient de mauvaise
qualité avant la construction d'un pilOnne pour supporter les
appareils. L'ancien mat téléscopique était trop
court et surtout trop instable pour permettre des mesures de
qualité bonne.
Les résultats du calcul du bilan
d'énergie (Nalohou) sur les trois périodes ont
montré une saisonnalité très marquée des
flux d'énergie. La saison sèche est
caractérisée par un taux élevé du flux de chaleur
sensible et du flux de chaleur a la surface du sol; le flux de
chaleur latente est faible pendant cette période. En saison humide, le
flux de chaleur latente est prépondérant. En Novembre oii le
rayonnement net est plus élevé que ce
qui est observé en
saison sèche et en saison humide, H et G
représentent aussi les termes majoritaires du bilan. Mais, ils demeurent
plus faibles que ceux observés en Janvier. Le flux de chaleur
latente est moyen durant cette période. La variabilité
spatiale des flux de chaleur sensible et de chaleur latente a été
montrée a travers la comparaison de ces paramètres au niveau des
deux sites en saison sèche et humide. Nous pouvons a partir de cette
première analyse du bilan d'énergie donner
une dynamique de l'évapotranspiration
réelle au pas de temps mensuel, journalier et voir même de la
demi-heure.
Les travaux réalisés dans le cadre de cette
étude nous ont permis de quantifier chacune des composantes
du bilan d'énergie sur trois périodes de 15 jours
chacune dans la Donga/Bénin. Une analyse plus
poussée reste nécessaire pour l'estimation du flux de chaleur
latente au vu des résultats qui montrent une sous estimation
systématique de ce terme. D'autre part, une
attention particulière sera portée au calcul du flux a la surface
du sol aux inter-saisons en raison de la couche de litière
laissée sur le site de mesure en Novembre.
La poursuite de cette étude sur une durée plus
longue permettra de mieux caractériser les
variabilités intra et inter saisonnières des différentes
composantes du bilan. Elle permettra également
d'acquérir une meilleure compréhension du
fonctionnement de l'interface surface - atmosphère en vue de la
documentation des flux d'évapotranspiration. Il est aussi a noter
que cette étude menée sur une période plus
longue contribuera a bien identifier les paramètres
qui influencent le bilan d'énergie en zone
soudanienne. Enfin, il s'agira également de
vérifier la fermeture du bilan de masse
hydrologique a partir des mesures de
l'évapotranspiration réelle. Une comparaison entre
l'évapotranspiration réelle et l'évapotranspiration
potentielle est envisagée afin de tester le réalisme
des paramétrisations couramment utilisées en
hydrologie et qui estiment
l'évapotranspiration réelle a partir de
l'évapotranspiration potentielle.
.1 Références
Bibliographiques
[11 Descroix, L., Mahé, G., Lebel, T., Favreau, G.,
Galle, S, Gautier, E., Olivry, J-C., Albergel, J.,
Amogu, 0., Cappelaere, B., Dessouassi, R., Diedhiou, A., Le Breton,
E., Mamadou, I., Sighomnou, D., 2009. Spatio-Temporal
Variability of Hydrological Regimes
Around the Boundaries between Sahelian and Sudanian Areas of West Africa: A
Synthesis. Journal of Hydrology, AMMA special
issue, in press. doi :10.1016/j.jhydrol.2008.12.012.
[21 Andersen, I., Dione, O., Jarosewich-Holder, M.,
Olivry, J.C., 2005. The Niger River Basin : a vision for
sustainable management.. The World Bank, Washington, DC,
the USA; Directions in development, K.G. Golitzen Ed.145 p.
[31 Mahé, G., Olivry, J. C., Dessouassi, R.,
Orange, D., Bamba, F. and Servat, E. 2000. Relations eaux de surface
- eaux souterraines d'une rivière tropicale au Mali. Comptes Rendus de
l'Académie des Sciences, Serie IIa, 330, 689-692.
[41 Zin, I., Zribi, M., Ottlé, C., Hiernaux, P.,
Lacaze, R., Le Hégarat-Mascle, S., Sanou, B., André,
C., Guibert, S., Saux-Picard, S., Dessay, N., Boulain, N.,
Cappelaere, B., Descroix, L., Galle, S., Peugeot, C.,
Seghieri, J., Séguis, L., 2009. Land cover
assessment on the three AMMA experimental sites from SPOT/HRVIR data. Soumis a
International Journal of Applied Earth Observation and Geoinformation.
[51 Galle S., Séguis L., Arjounin M., Bariac
T., Bouchez J.-M., Braud I., Cohard J.-M., Descloitres M., Favreau G.,
Kamagaté B., Laurent J.-P., Le Lay M., Malinur F.,
Peugeot C., Robain H., Seghieri J., Seidel J.-L., Varado
N., Zin I. and Zribi M., 2005. Evaluation des termes du bilan
hydrologique de la Donga par mesure
et modélisation. In : "Premier colloque de restitution
scientifique Ecosphère Continentale", Toulouse. ECCO-PNRH :
411-416.
[61 Varado N., Braud I., Galle S., Le Lay M.,
Séguis L., Kamagaté B. and Depraetere C.,
2006. Multicriteria assessment of the Representative Elementary
Watershed approach on the Donga catchment (Benin) using a
downward approach of model complexity.
Hydrology and Earth System Sciences, 10 :
427-442.
[71 Le Lay M., Saulnier G.-M., Galle S.,
Séguis L., Métadier M. and Peugeot C.,
2008. Model representation of the Sudanian hydrological
water cycle. Application on the Donga catchment
(Bénin). Journal of Hydrology, 363(1-4) :
32-41.
[8lFoken.,T., 2006. "50 Years of the Monin-Obukhov
Theory ". Boundary-Layer
Meteorology 119(3) : 431-447.
[91 Van Dijk, A., Moene, A.F., De Bruin, H.A.R, 2004. The
principles of surface flux physics : theory, practice and
description of the ECPACK library.Meteorology and Air
Quality Group Wageningen University
Duivendaal 2 6701 AP Wageningen The Netherlands.
[101 Prandtl, L., 1904. Uber,
Flussibkeitsbewegung bei sehr kleiner Reibung,
Verhandl. III, Internat. Math.- Kong., Heidelberg,
Teubner, Leipzig pp.484-491.
[111 Brutsaert, W., 1982. Evaporation in the Atmosphere,
theory History, And Applications, 1st ed., 299pp.,
Dordrecht, Kluwer Academic Publishers, 1982.
[121 Heusinkveld, B.G., Jacobs A.F.G., Holtslag,
A.A.M., Berkowicz, S.M., 2003. Surface energy balance closure in an
arid region : role of soil heat flux. Agricultural and
Forest Meteorology 122 (2004) 21-37.
[131 Guyot, A., Cohard, J-M., Anquetin,
S., Galle, S., 2008. Combined analysis of energy and
water budgets to consolidate latent heat fux estimation
using an infrared scintillometer. Agricultural and Forest
Meteorology, this issue.
[141 Allen, R.G., Pereira, L.S., Raes, D., Smith, M., 1998.
Crop Evapotranspiration : Guidelines for Computing Crop Water
Requirements. United Nations Food and Agriculture
Organization, Irrigation and Drainage Paper
56. Rome, Italy, 300 pp.
[151 Van Wijk, W. et De Vries, D., 1963. Periodic temperature
variations in a homogeneous soil. Physics of Plant
Environment : 103-143.
[161 Kaimal, J. C. et Businger, J. A., 1963. A
Continuous Wave Sonic Anemometer-Thermometer, J. Applied Meteorol., 2,
156-164.
[171 Fleagle, R. G., Businger, J. A., 1980.
An Introduction to Atmospheric Physics, Academic Press, Inc., New
York.
[181 Schotanus, P., Nieuwstadt, F. T. M., De Bruin, H. A. R.,
1983. Temperature Measurement with a Sonic Anemometer and its Application to
Heat and Moisture Fluxes, Boundary-Layer Meteorol., 26,
81-93.
[191 Kaimal, J. C. et Gaynor, J. E., 1991. Another
Look at Sonic Thermometry, Boundary-Layer
Meteorol., 56, 401-410.
[201 Liu, H., Peters, G., Foken, T., 2001. New
Equations for Sonic Temperature Variance and
Buoyancy Heat Flux with an Omnidirectional Sonic
Anemometer, Boundary-Layer Meteorol., 100, 459-468.
[211 Kaimal, J.C. et Finnigan, J.J., 1994. Atmospheric
boundary layer flows : Their structure and measurement.
Oxford University Press, New York, NY, 289 pp.
[221 Tanner, B.D., Swiatek, E. et Greene, J.P., 1993.
Density fluctuations and use of the krypton
hygrometer in surface flux measurements. In : R.G. Allen (Editor),
Management of irrigation and drainage
systems : integrated perspectives. American
Society of Civil Engineers, New York, NY, pp. 945-952.
[231 Webb, E.K., Pearman, G.I. et Leuning, R.,
1980. Correction of the flux measurements for density effects due to
heat and water vapour transfer. Quarterly Journal of The
Royal Meteorological Society, 106 : 85-100.
[241 Liebethal, C. et Foken, T., 2004. On the
significance of the Webb correction to fluxes.
Corrigendum. Boundary-Layer
Meteorology, 113 : 301.
[251 Liebethal, C. et Foken, T., 2003. On the
significance of the Webb correction to fluxes.
Boundary-Layer Meteorology, 109
: 99-106.
[261 Fuehrer, P.L. et Friehe, C.H., 2002. Flux corrections
revisited. Boundary-Layer Meteorology, 102 :
415-457.
[271 Moore, C.J., 1986. Frequency response
corrections for eddy correlation systems.
Boundary-Layer Meteorology, 37 : 17-35.
[281 Horst, T.W., 2003. Corrections to Sensible and Latent Heat
Flux Measurements.
[291 Vickers, D. et Mahrt, L., 1997. Quality control
and flux sampling problems for tower and aircraft data. Journal of
Atmospheric and Oceanic Technology, 14 : 512-526.
[301 Højstrup, J., 1993. A statistical data
screening procedure. Measuring Science
Technology, 4 : 153-157.
[311 Foken, T. et Wichura, B., 1996. Tools for
quality assessment of surface-based flux measurements.
Agricultural and Forest Meteorology, 78 : 83-105.
[321 Foken, T., et Mauder, M., 2004. Documentation and
Instruction Manual of the Eddy Covariance Software
Package TK2. Department of Micrometeorology, Univ of
Bayreuth, Germany.
[331 Favier,V., 2004. Etude du bilan
d'énergie de surface et de la production des
écoulements de fonte d'un glacier des Andes
d'Equateur; relation glacier-climat en zone
tropicale. These de doctorat de l'Université Montpellier II, 248 pp.
[341 Rubio, E., Caselles, V., Coll, C., Valour, E. et
Sospedra, F., 2003. Thermal-infrared emissivities of natural surfaces :
improvements on the experimental set-up and new measurements, International
Journal of Remote Sensing,24 :24, 5379 - 5390.
[351 Aubinet, M., Grelle, A., Ibrom, A., Rannik, U.,
Moncrieff, J., Foken, T., Kowalski, A.S., Martin, P.H., Berbigier,
P., Bernhofer, C., Clement, R., Elbers, J., Granier, A., Grünwald, T.,
Morgenstern, K., Pilegaard, K., Rebmann, C., Snijders,
W., Valentini, R. et Vesala, T., 2000. Estimates of the annual net carbon and
water exchange of forests : The EUROFLUX methodology.
Andvances in Ecological Research, 30 : 113-175.
[361 Aubinet, M., Chermanne, B., Vandenhaute, M.,
Longdoz, B., Yernaux, M., Lai-tat, E., 2001. Long term
carbon dioxide exchange above a mixed forest in the
Belgian Ardennes. Agric. For. Meteorol. 108, 293-315.
[371 Foken, T., Wimmer, F., Mauder, M., Thomas, C.,
Liebethalal, C., 2006. Some aspects of the energy balance closure
problem. Department of Micrometeorology, Univ of
Bayreuth, Germany.
[381 Kukharets, V. P., Nalbandyan, H. G., et Foken,
T., 2000. Thermal Interactions between the underlying
surface and a nonstationary radiation flux, Izv., Atmos. Ocenanic
Phys., 36, 318-325.
[391 Panin, G. N., Tetzlaff, G., et Raabe, A., 1998.
Inhomogeneity of the land surface and
problems in the 10 parameterization of surface fluxes in natural
conditions,Theor. Appl. Climat., 60, 163-178.
.2 Annexe1 Proclist de Nalohou
Comments
Comment = Station Campbell
Comment = Nalohou Csat + Licor
Comment = 20/10/2008
Comments
Comment = Actions effectuees
Comment = Extraction des donnees du fichier meteo,
Comment = Despike, Calculs Statistiques, Pression
partielle
Comments
Comment = Direction et vitesses du vent, Rotations
Comment = Comment = Comments
Comment = Correction temperature sonique, Covariance
wT, wq et wco2
Comment = Correction Webb LE et Fco2
Comment = Flux de chaleur sensible corrige
Comments
Comment = variable d'installation
Comment = Comment = Set Values From Time =
To Time =
Number of Variables = 3
Storage Label = hauteur-sonic
Assignment value = 4.95
Storage Label = ecart-nord
Assignment value = 0
Storage Label = ang-sonic-licor
Assignment value = 0
Comments
Comment = Variable de configuration sonic licor
Comment = pour le calcul des corrections
frequentielles
Set Values From Time =
To Time =
Number of Variables = 10
Storage Label = Csat-samplefreq
Assignment value = 20
Storage Label = Licor7500-samplefreq
Assignment value = 20
Storage Label = Csat-path
Assignment value = 0.116
Storage Label = Licor7500-path
Assignment value = 0.125
Storage Label = wT-ver-path-sep
Assignment value = 0
Storage Label = wT-hor-path-sep
Assignment value = 0
Storage Label = wx-ver-path-sep
Assignment value = 0.1
Storage Label = wx-hor-path-sep
Assignment value = 0.3
Storage Label = Csat-TimeConStant
Assignment value = 0.05
Storage Label = Licor7500-TimeConStant
Assignment value = 0.05
Comments
Comment = Valeur dynamiques alternatives
Comment = T en(c)c, P en kPa, Rh en %
Set Values From Time =
To Time =
Number of Variables = 3
Storage Label = T-alt
Assignment value = 30
Storage Label = P-alt
Assignment value = 100
Storage Label = Rh-alt
Assignment value = 70
Comments
Comment = rhoCp en J/m3/K
Comment = L en J/g
Comment = ecart nord en degre
Set Values From Time =
To Time =
Number of Variables = 2
Storage Label = rhoCp-cst
Assignment value = 1130
Storage Label = L-cst
Assignment value = 2450
Comments
Comment = Extraction des variables
Comment = du fichier meteo
Comment = Preprocessed Files
File <0>=C \Documents and
Settings\mamadou\Bureau\traitementedire
\na\na-met-090707-040908-EdiRe-heure
locale-rugosite.csv
File <1> = File
<2> = Set Values From Time =
To Time =
Number of Variables = 7
Storage Label = offsetc
Assignment value = <0>
offsetc
Storage Label = gainc
Assignment value = <0>
gainc
Storage Label = offsetq
Assignment value = <0>
offsetq
Storage Label = gainq
Assignment value = <0>
gainq
Storage Label = h-veg
Assignment value = <0>
h
Storage Label = disp-height
Assignment value = <0> d
Storage Label = Z0
Assignment value = <0> Z0
Set Values
From Time = To Time =
Number of Variables = 3
Storage Label = T-meteo
Assignment value = <0>
Ta-meteo
Storage Label = Rh-meteo
Assignment value = <0>
Rh
Storage Label = P-meteo
Assignment value = <0>
Patm
Comments
Comment = Conversion de la pression meteo
Comment = unite d'entree hPa
Comment = unite de sortie kPa
User defined From Time = To Time =
Storage Label = P-meteo
Apply to =
Apply by =
Equation = P-meteo*0.1
Variable = P-meteo
Comments
Comment = Extraction des variables du fichier brut Comment =
Vitesse en m/S, Co2 en mg/m3, H20 en g/m3 Comment =
Pression en kpa, T en~C
Extract
From Time = To Time =
Channel = 1
Label for Signal = SECONDS
Extract
From Time = To Time =
Channel = 2
Label for Signal = NANOSECONDS
Extract
From Time = To Time =
Channel = 3
Label for Signal = RECORD
Extract
From Time = To Time =
Channel = 4
Label for Signal = u-sonic
Extract
From Time = To Time =
Channel = 5
Label for Signal = v-sonic
Extract
From Time = To Time =
Channel = 6
Label for Signal = w-sonic
Extract
From Time = To Time =
Channel = 7
Label for Signal = T-sonic
Extract
From Time = To Time =
Channel = 8
Label for Signal = diag-csat
Extract
From Time = To Time =
Channel = 9
Label for Signal = co2-licor
Extract
From Time = To Time =
Channel = 10
Label for Signal = q-licor
Extract
From Time =
To Time =
Channel = 11
Label for Signal = P-licor
Comments
Comment = Changement d'unité
Comment = CO2 en mmol/m3
Comment = h2O en g/m3
Linear
From Time = To Time =
Signal = co2-licor
1st Offset = 0
1st Gain = 0.0227273
1st Curvature = 0
2nd Offset = 0 2nd Gain = 1 2nd Curvature = 0
Linear
From Time = To Time =
Signal = q-licor 1st Offset = 0 1st Gain
= 1 1st Curvature = 0
2nd Offset = 0 2nd Gain = 1 2nd Curvature = 0
Comments
Comment = Despike
Comment = 3 fois l'écart-type
Comment = Si plus de 4 spike de suite, on ne les compte pas
Despike
From Time = To Time =
Signal = u-sonic Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-U
Despike
From Time = To Time =
Signal = v-sonic Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-V
Despike
From Time = To Time =
Signal = w-sonic
Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-W
Despike
From Time = To Time =
Signal = co2-licor
Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-co2
Despike
From Time = To Time =
Signal = q-licor Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-q
Despike
From Time = To Time =
Signal = T-sonic
Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-T
Despike
From Time = To Time =
Signal = P-licor Standard Deviations = 3
Spike width = 4
Spike % consistency = 50
Replace spikes = x
Storage Label spike count = spike-P
Comments
Comment = Calcul Stat
Comment = moyenne et écart-types
Comment = sur U, V, W, co2, q, T, P 1 chn statistics
From Time =
To Time =
Signal = u-sonic
Storage Label Mean = u-sonic-mean
Storage Label Std Dev = u-sonic-std Storage Label
Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity = Alt
Turbulent Intensity Denominator = 1 chn statistics
From Time =
To Time =
Signal = v-sonic
Storage Label Mean = v-sonic-mean
Storage Label Std Dev = v-sonic-std Storage Label
Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity = Alt
Turbulent Intensity Denominator = 1 chn statistics
From Time =
To Time =
Signal = w-sonic
Storage Label Mean = w-sonic-mean
Storage Label Std Dev = w-sonic-std Storage Label
Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity = Alt
Turbulent Intensity Denominator = 1 chn statistics
From Time =
To Time =
Signal = T-sonic
Storage Label Mean = T-sonic-mean
Storage Label Std Dev = T-sonic-std Storage Label
Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity = Alt
Turbulent Intensity Denominator = 1 chn statistics
From Time =
To Time =
Signal = co2-licor
Storage Label Mean = co2-licor-mean
Storage Label Std Dev = co2-licor-std Storage Label
Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity = Alt
Turbulent Intensity Denominator = 1 chn statistics
From Time =
To Time =
Signal = q-licor
Storage Label Mean = q-licor-mean
Storage Label Std Dev = q-licor-std Storage
Label Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity = Alt
Turbulent Intensity Denominator = 1 chn statistics
From Time =
To Time =
Signal = P-licor
Storage Label Mean = P-licor-mean
Storage Label Std Dev = P-licor-std Storage Label
Skewness =
Storage Label Kurtosis = Storage Label
Maximum = Storage Label Minimum = Storage Label Variance
=
Storage Label Turbulent Intensity =
Alt Turbulent Intensity Denominator =
Spectra
From Time = 18/01/2008 12 :00 :00
To Time = 18/01/2008 16 :00 :00
Signal = T-sonic
Window = Hamming Kaiser/Bell coef = Output Spectra =
spec-T Sort Output =
Detrend data = None Comments
Comment = Direction du vent
Comment = se fait avant rotation
Comment =
Wind direction
From Time =
To Time =
Signal (u) = u-sonic Signal (v) = v-sonic
Orientation = ecart-nord
Wind Direction Components = U-fS-V-fE
Wind Direction Output = N-0-deg-E-90-deg
Storage Label Wind Direction = Wind-sonic-Direction
Storage Label Wind Dir Std Dev = Wind-sonic-Direction-std
Comments
Comment = Rotation (double rotation)
Comment = Vitesse du vent
Comment = dans sys orthogonal
Rotation coefficients From Time =
To Time =
Signal (u) = u-sonic Signal (v) =
v-sonic Signal (w) = w-sonic Storage Label Alpha =
Alpha
Storage Label Beta = Beta
Storage Label Gamma = Gamma
Optional mean u = Optional mean v = Optional mean w =
Rotation
From Time =
To Time =
Signal (u) = u-sonic Signal (v) =
v-sonic Signal (w) = w-sonic Alpha = Alpha
Beta = Beta
Gamma = Gamma Do 1st Rot = x
Do 2nd Rot = x
Do 3rd Rot = x
Comments
Comment = Les variables de vent sont
Comment = dans un repére instantané fonction
Comment = du vent (v-sonic-mean = 0)
1 chn statistics
From Time =
To Time =
Signal = u-sonic
Storage Label Mean = wind-sonic-speed-mean
Storage Label Std Dev = wind-sonic-speed-std
Storage Label Skewness =
Storage Label Kurtosis =
Storage Label Maximum = wind-sonic-speed-max
Storage Label Minimum =
Comments
Comment = Calcul et Retrait du Lag
Comment = pour le Licor Openpath
Comment =
Cross Correlate
From Time =
To Time =
Signal = w-sonic
Signal which lags = q-licor
Correlation type = Covariance
Output Correlation curve = 10
Storage Label Peak Time =
time-lag-wq
Storage Label Peak Value =
Cross Correlate
From Time =
To Time =
Signal = w-sonic
Signal which lags = co2-licor
Correlation type = Covariance
Output Correlation curve = 10
Storage Label Peak Time = time-lag-wco2
Storage Label Peak Value =
Cross Correlate
From Time =
To Time =
Signal = w-sonic
Signal which lags = P-licor
Correlation type = Covariance
Output Correlation curve = 10
Storage Label Peak Time = time-lag-wp
Storage Label Peak Value =
Remove Lag From Time = To Time =
Signal = co2-licor
Min Lag (sec) = -2
Lag (sec) = time-lag-wco2
Max Lag (sec) = 2
Below Min default (sec) = 0
Above Max default (sec) = 0
Remove Lag From Time = To Time =
Signal = q-licor Min Lag (sec) =
-2
Lag (sec) = time-lag-wq
Max Lag (sec) = 2
Below Min default (sec) = 0
Above Max default (sec) = 0
Remove Lag From Time = To Time =
Signal = P-licor Min Lag (sec) = -2
Lag (sec) = time-lag-wp
Max Lag (sec) = 2
Below Min default (sec) = 0
Above Max default (sec) = 0
Comments
Comment = Calcul de la pression partielle
Comment = directement en kPa
Comment = Partial pressure From Time = To Time =
Storage Label = e-vapor-licor
Apply to =
Apply by =
Variable type = Absolute density
Measured variable = q-licor-mean
Min or QC = 0.001
Max or QC = 40
Temperature (C) = T-sonic-mean
Min or QC = Max or QC = Pressure (Kpa) = P-licor-mean
Min or QC = 0 Max or QC = 105
Molecular weight (g/mole) = 18.0
Conc conv factor = 1000
Partial pressure From Time = To Time =
Storage Label = e-vapor-meteo
Apply to =
Apply by =
Variable type = Relative humidity
Measured variable = Rh-meteo
Min or QC = Max or QC = Temperature (C) = T-meteo
Min or QC = Max or QC = Pressure (Kpa) = P-meteo
Min or QC = Max or QC = Molecular weight
(g/mole) = 18.0
Conc conv factor = 1000
Comments
Comment = Calcul de q-meteo
Comment = en g/m3
Comment = User defined From Time = To Time =
Storage Label = q-meteo
Apply to =
Apply by =
Equation =
18*e-vapor-meteo*1000/(8.32*(273.15fT-meteo)) Variable = e-vapor-meteo
Variable = T-meteo
Comments
Comment = Application du gain
q-licor-mean/q-meteo a q-licor-mean Comment =
pour rephasage de q-licor sur q-meteo
Comment = On reste en g/m3
User defined From Time = To Time =
Storage Label =
gain-q-licor-mean
Apply to =
Apply by =
Equation =
q-meteo/q-licor-mean
Variable = q-licor-mean
Variable = q-meteo
Linear
From Time = To Time =
Signal = q-licor 1st Offset = 0
1st Gain = gain-q-licor-mean
1st Curvature = 0
2nd Offset = 0 2nd Gain = 1 2nd Curvature = 0
Comments
Comment = Correction température sonique
Comment = Schotanus et al. 1983; Manuel Csat Campbell
Scientifique Comment =
T-sonic-cor=T-sonic(1-f0.51q-licor)
User defined From Time = To Time =
Storage Label = T-sonic-cor
Apply to =
Apply by =
Equation = ((T-sonic-mean--273.15)/(1
f.32*e-vapor-meteo/P-meteo))- 273.15
Variable = P-meteo
Variable = e-vapor-meteo
Variable = T-sonic-mean
Density of moist air
From Time = To Time =
Storage Label = rho-licor
Apply to =
Apply by =
Vapour pressure (Kpa) = e-vapor-licor
Min or QC = Max or QC = Temperature (C) = T-sonic-cor
Min or QC = Max or QC = Pressure (Kpa) = P-licor-mean
Min or QC = Max or QC = Density of moist air
From Time = To Time =
Storage Label = rho-meteo
Apply to =
Apply by =
Vapour pressure (Kpa) = e-vapor-meteo
Min or QC = Max or QC = Temperature (C) = T-meteo
Min or QC = Max or QC = Pressure (Kpa) = P-meteo
Min or QC = Max or QC = Comments
Comment = Changement d'unité de la masse
volumique de l'air humide Comment = entrée en :
Comment = sortie en :
User defined From Time = To Time =
Storage Label = rho-licor
Apply to =
Apply by =
Equation = rho-licor/1000
Variable = rho-licor
Variable =
Variable =
Variable =
Variable =
User defined From Time = To Time =
Storage Label = rho-meteo
Apply to =
Apply by =
Equation = rho-meteo/1000
Variable = rho-meteo
Variable =
Variable =
Variable =
Variable =
Comments
Comment = Calcul de rhocp
Comment = en j/g
Comment =
Sensible heat flux coefficient
From Time = To Time =
Storage Label = rhoCp-licor
Apply to =
Apply by =
Vapour pressure (Kpa) = e-vapor-licor
Min or QC = Max or QC = Temperature (C) = T-sonic-cor
Min or QC = Max or QC = Pressure (Kpa) = P-licor-mean
Min or QC = Max or QC = Alternate rhoCp = 1100
Sensible heat flux coefficient
From Time = To Time =
Storage Label = rhoCp-meteo
Apply to =
Apply by =
Vapour pressure (Kpa) = e-vapor-meteo
Min or QC = Max or QC = Temperature (C) = T-meteo
Min or QC = Max or QC = Pressure (Kpa) = P-meteo
Min or QC = Max or QC = Alternate rhoCp = 1100
Comments
Comment = flux de chaleur sensible sonique
Comment = calcul covariance
Comment = 2 chn statistics From Time = To Time =
Signal = w-sonic Signal = T-sonic
Storage Label Covariance = wT-cov
Storage Label Correlation =
Storage Label Flux = H-sonic-tmp
Flux coefficient = rhoCp-meteo
Comments
Comment = Flux de chaleur latente
Comment = Calcul covariance
Comment = 2 chn statistics From Time = To Time =
Signal = w-sonic Signal =
q-licor Storage Label Covariance = wq-cov
Storage Label Correlation =
Storage Label Flux = E-licor-tmp
Flux coefficient =
Comments
Comment = Calcul de la chaleur latente de vaporisation de l'eau
Comment = J/g
Comment =
Latent heat of evaporation
From Time = To Time =
Storage Label = L-meteo
Apply to =
Apply by =
Temperature (C) = T-meteo
Min or QC = Max or QC = Pressure (KPa) = P-meteo
Min or QC = Max or QC = LE flux coef, L = L-cst
Latent heat of evaporation
From Time = To Time =
Storage Label = L-licor
Apply to =
Apply by =
Temperature (C) = T-sonic-cor
Min or QC = Max or QC = Pressure (KPa) = P-licor-mean
Min or QC = Max or QC = LE flux coef, L = L-cst
Comments
Comment = Calcul du flux
Comment = Comment = User defined From Time = To Time =
Storage Label = LE-licor-tmp
Apply to =
Apply by =
Equation = E-licor-tmp*L-licor
Variable = E-licor-tmp
Variable = L-licor
Comments
Comment = Flux de carbone Fco2-licor-tmp
Comment = unité mmol/m2/s
Comment = 2 chn statistics From Time = To Time =
Signal = w-sonic Signal = co2-licor
Storage Label Covariance = wco2-cov
Storage Label Correlation =
Storage Label Flux = Fco2-licor-tmp
Flux coefficient = 1
Comments
Comment = Conversion de Fco2-licor-tmp
Comment = entree mmol/m3
Comment = sortie umol/m3
User defined From Time = To Time =
Storage Label = Fco2-licor-tmp2
Apply to =
Apply by =
Equation = 1000*Fco2-licor-tmp
Variable = Fco2-licor-tmp
Comments
Comment = Calcul du flux de quantité de
mouvement Comment =
Comment =
2 chn statistics From Time = To Time =
Signal = w-sonic Signal = u-sonic
Storage Label Covariance = uw-cov
Storage Label Correlation =
Storage Label Flux = momentum-sonic
Flux coefficient = rho-meteo
Comments
Comment = u-sonic* Vitesse de frottement
Comment = Comment = U star
From Time = To Time =
Storage Label = U-star
Apply to =
Apply by =
uw covariance (m2/s2) = uw-cov
Min or QC = Max or QC = Virtual temperature
From Time = To Time =
Storage Label = T-virtual
Apply to =
Apply by =
Vapour pressure (Kpa) = e-vapor-meteo
Min or QC = Max or QC = Temperature (C) = T-meteo
Min or QC = Max or QC = Pressure (Kpa) = P-meteo
Min or QC = Max or QC = Comments
Comment = Calcul Lo
Comment = hauteur du sonique 4,95m
Comment = hauteur végétation selon
relevé Omar Stability - Monin Obhukov
From Time = To Time =
Storage Label = stability
Apply to =
Apply by =
Measurement height (m) = hauteur-sonic
Zero plane displacement (m) = disp-height
Virtual Temperature (C) = T-virtual
Min or QC = Max or QC = H flux (W/m2) = H-sonic-tmp
Min or QC = Max or QC = H flux coef, RhoCp = rhoCp-meteo
Min or QC = Max or QC = Scaling velocity
(m/s) = U-star
Min or QC = Max or QC = Comments
Comment = Corrections spectrales
Comment =
Comment =
Frequency response
From Time =
To Time =
Storage Label = freq-corr-uw
Apply to =
Apply by =
Correction type = UW
Measurement height (m) = hauteur-sonic Zero plane
displacement (m) = disp-height Boundary layer
height (m) =
Stability Z/L = stability
Wind speed (m/s) = wind-sonic-speed-mean
Sensor 1 Flow velocity (m/s) =
wind-sonic-speed-mean Sensor 1 Sampling
frequency (Hz) = Csat-sampleFreq Sensor 1 Low
pass filter type = Recursive
Sensor 1 Low pass filter time conStant = 0.02 Sensor 1
High pass filter type = Recursive Sensor 1
High pass filter time conStant = 600 Sensor 1 path length
(m) = Csat-path
Sensor 1 Time conStant (s) = Csat-TimeConStant Sensor 1 Tube
attenuation coef =
Sensor 2 Flow velocity (m/s) =
wind-sonic-speed-mean Sensor 2 Sampling
frequency (Hz) = Csat-SampleFreq Sensor 2 Low
pass filter type = Recursive
Sensor 2 Low pass filter time conStant = 0.02 Sensor 2
High pass filter type = Recursive Sensor 2
High pass filter time conStant = 600 Sensor 2 path length
(m) = Csat-path
Sensor 2 Time conStant (s) = Csat-TimeConStant Sensor 2 Tube
attenuation coef =
path separation (m) = wT-hor-path-sep Get spectral data
type = Model
Get response function from = model
Reference tag =
Reference response condition =
Sensor 1 subsampled =
Sensor 2 subsampled =
Apply velocity distribution adjustment =
Use calculated distribution =
Velocity distribution std dev=
Stability distribution std dev=
Frequency response
From Time =
To Time =
Storage Label = freq-corr-tw
Apply to =
Apply by =
Correction type = WX
Measurement height (m) = hauteur-sonic Zero plane
displacement (m) = disp-height Boundary layer
height (m) =
Stability Z/L = stability
Wind speed (m/s) = wind-sonic-speed-mean
Sensor 1 Flow velocity (m/s) =
wind-sonic-speed-mean Sensor 1 Sampling
frequency (Hz) = Csat-SampleFreq Sensor 1 Low
pass filter type = Recursive
Sensor 1 Low pass filter time conStant = 0.02 Sensor 1
High pass filter type = Recursive Sensor 1
High pass filter time conStant = 600 Sensor 1 path length
(m) = Csat-path
Sensor 1 Time conStant (s) = Csat-TimeConStant Sensor 1 Tube
attenuation coef =
Sensor 2 Flow velocity (m/s) =
wind-sonic-speed-mean Sensor 2 Sampling
frequency (Hz) = Csat-SampleFreq Sensor 2 Low
pass filter type = Recursive
Sensor 2 Low pass filter time conStant = 0.02 Sensor 2
High pass filter type = Recursive Sensor 2
High pass filter time conStant = 600 Sensor 2 path length
(m) = Csat-path
Sensor 2 Time conStant (s) = Csat-TimeConStant Sensor 2 Tube
attenuation coef =
path separation (m) = wT-hor-path-sep Get spectral data
type = Model
Get response function from = model
Reference tag =
Reference response condition =
Sensor 1 subsampled =
Sensor 2 subsampled =
Apply velocity distribution adjustment =
Use calculated distribution =
Velocity distribution std dev=
Stability distribution std dev=
Comments
Comment = Calcul de la séparation latérale Comment
=
Comment =
User defined
From Time =
To Time =
Storage Label = lat-path-sep
Apply to =
Apply by =
Equation =
SQRT((wx-hor-path-sep*sin(Wind-sonic-Direction-ang-soniclicor))*
(wx-hor-path-sep*sin(Wind-sonic-Direction-ang-sonic-licor))-Fwxver-path-sep*wx-ver-path-sep)
Variable = wx-hor-path-sep Variable = Wind-sonic-Direction
Variable = ang-sonic-licor Variable =
wx-ver-path-sep Frequency response
From Time =
To Time =
Storage Label = freq-corr-7500
Apply to =
Apply by =
Correction type = WX
Measurement height (m) = hauteur-sonic
Zero plane displacement (m) = disp-height
Boundary layer height (m) =
Stability Z/L = stability
Wind speed (m/s) = wind-sonic-speed-mean
Sensor 1 Flow velocity (m/s) =
wind-sonic-speed-mean
Sensor 1 Sampling frequency (Hz)
= Csat-SampleFreq
Sensor 1 Low pass filter type = Recursive
Sensor 1 Low pass filter time conStant = 0.02
Sensor 1 High pass filter type =
Recursive
Sensor 1 High pass filter time conStant = 600
Sensor 1 path length (m) = Csat-path
Sensor 1 Time conStant (s) = Csat-TimeConStant
Sensor 1 Tube attenuation coef =
Sensor 2 Flow velocity (m/s) =
wind-sonic-speed-mean
Sensor 2 Sampling frequency (Hz)
= Licor7500-SampleFreq
Sensor 2 Low pass filter type = Recursive
Sensor 2 Low pass filter time conStant = 0.02
Sensor 2 High pass filter type =
Recursive
Sensor 2 High pass filter time conStant = 600
Sensor 2 path length (m) = Licor7500-path
Sensor 2 Time conStant (s) = Licor7500-TimeConStant
Sensor 2 Tube attenuation coef =
path separation (m) = lat-path-sep
Get spectral data type = Model
Get response function from = model
Reference tag =
Reference response condition =
Sensor 1 subsampled = Sensor 2 subsampled = Apply
velocity distribution adjustment =
Use calculated distribution = Velocity distribution
std dev=
Stability distribution std dev=
Mathematical operation From Time =
To Time =
Storage Label = uw-cov-fc Apply to =
Apply by =
Measured variable A = uw-cov
Operation = *
Measured variable B = freq-corr-uw
Mathematical operation From Time =
To Time =
Storage Label = U-star-fc Apply to =
Apply by =
Measured variable A = U-star
Operation = *
Measured variable B = freq-corr-uw
Mathematical operation From Time =
To Time =
Storage Label = Fco2-licor-fc Apply to =
Apply by =
Measured variable A = Fco2-licor-tmp
Operation = *
Measured variable B = freq-corr-7500
Mathematical operation From Time =
To Time =
Storage Label = H-sonic-fc Apply to =
Apply by =
Measured variable A = H-sonic-tmp
Operation = *
Measured variable B = freq-corr-tw
Mathematical operation From Time =
To Time =
Storage Label = E-licor-fc Apply to =
Apply by =
Measured variable A = E-licor-tmp
Operation = *
Measured variable B = freq-corr-7500
Mathematical operation
From Time = To Time =
Storage Label = LE-licor-fc
Apply to =
Apply by =
Measured variable A = LE-licor-tmp
Operation = *
Measured variable B = freq-corr-7500
Comments
Comment = Correction de Webb pour la vapeur d'eau Comment =
Comment = Webb correction From Time = To Time =
Storage Label = LE-licor-webb
Apply to =
Apply by =
Scalar value type = Density
(g/m3)
Scalar value = q-meteo
Min or QC = Max or QC =
Water vapour value type = partial Pressure (kpa) Water
vapour value = e-vapor-meteo
Min or QC = Max or QC = Temperature (C) = T-sonic-cor
Min or QC = Max or QC = Pressure (Kpa) = P-meteo
Min or QC = Max or QC = H flux (W/m2) = H-sonic-fc
Min or QC = Max or QC = LE flux (W/m2) = LE-licor-fc
Min or QC = Max or QC = H flux coef, RhoCp = rhoCp-meteo
Min or QC = Max or QC = LE flux coef, L = L-licor
Min or QC = Max or QC = Scalar molecular wt. = 18
Scalar flux type = LE (W/m2)
Scalar flux coefficient = 1
Min or QC = Max or QC = Alternate water vapour pressure (kpa)
=
Alternate temperature (C) =
Alternate pressure (kpa) =
User defined From Time = To Time =
Storage Label = LE-licor-Q0
Apply to =
Apply by =
Equation = LE-licor-tmp-fLE-licor-webb
Variable = LE-licor-tmp
Variable = LE-licor-webb
Variable =
Variable =
Variable =
Comments
Comment = Correction de Webb pour le co2 Comment = entrée
en mmol/m2/s
Comment = sortie en umol/m2/s
Webb correction From Time = To Time =
Storage Label = Fco2-licor-webb
Apply to =
Apply by =
Scalar value type = Density
(mg/m3)
Scalar value = co2-licor-mean
Min or QC = Max or QC =
Water vapour value type = partial Pressure (kpa) Water
vapour value = e-vapor-meteo
Min or QC = Max or QC = Temperature (C) = T-sonic-cor
Min or QC = Max or QC = Pressure (Kpa) = P-meteo
Min or QC = Max or QC = H flux (W/m2) = H-sonic-fc
Min or QC = Max or QC = LE flux (W/m2) = LE-licor-Q0
Min or QC =
Max or QC =
From Time =
To Time =
Left Axis Value = H-sonic-Q0 Right Axis Value =
H-sonic-tmp
Left Axis Minimum = -100 Left Axis Maximum = 500
Right Axis Minimum = -100 Right Axis Maximum = 500 Match
Left/Right Axes = Plot Value
From Time =
To Time =
Left Axis Value = LE-licor-Q0 Right Axis Value =
LE-licor-tmp
Left Axis Minimum = -200 Left Axis Maximum = 800
Right Axis Minimum = -200 Right Axis Maximum = 800 Match
Left/Right Axes = Plot Value
From Time =
To Time =
Left Axis Value = Fco2-licor-Q0
Right Axis Value = Fco2-licor-tmp2
Left Axis Minimum = -20 Left Axis Maximum = 20
Right Axis Minimum = -20 Right Axis Maximum = 20 Match
Left/Right Axes = Plot Value
From Time =
To Time =
Left Axis Value = q-licor-mean Right
Axis Value = T-sonic-cor Left Axis Minimum = 0
Left Axis Maximum = 25
Axis Minimum = 10
Right Axis Maximum = 50 Match Left/Right
Axes = Plot Value
From Time =
To Time =
Left Axis Value = beta Right Axis Value =
gamma Left Axis Minimum =
Left Axis Maximum = Right Axis Minimum =
Right Axis Maximum = Match Left/Right Axes = Plot
Value
From Time =
To Time =
Left Axis Value = spike-T Right Axis Value =
spike-q Left Axis Minimum =
Left Axis Maximum = Right Axis Minimum =
Right Axis Maximum = Match Left/Right Axes =
H flux coef, RhoCp = rhoCp-meteo
Min or QC =
Max or QC =
LE flux coef, L = L-meteo
Min or QC =
Max or QC =
Scalar molecular wt. = 44
Scalar flux type = Fx (umol/m2/s)
Scalar flux coefficient = 1
Min or QC =
Max or QC =
Alternate water vapour pressure (kpa) =
Alternate temperature (C) =
Alternate pressure (kpa) =
User defined From Time =
To Time =
Storage Label = Fco2-licor-Q0
Apply to = Apply by =
Equation = Fco2-licor-tmp2-f-Fco2-licor-webb Variable
= Fco2-licor-tmp2
Variable = Fco2-licor-webb
Variable = Variable = Variable = Comments
Comment = Calcul du flux de chaleur sensible corrige
Comment =
Comment = User defined From Time =
To Time =
Storage Label = H-sonic-Q0
Apply to = Apply by =
Equation =
H-sonic-fc-(0.32*rhoCp-meteo*LE-licor-Q0*(T-sonic-mean+273.15)*
Right
(T-sonic-cor--273.15))/(216.5*P-meteo*10*L-meteo) Variable =
H-sonic-fc
Variable = rhoCp-meteo
Variable = LE-licor-Q0
Variable = T-sonic-mean
Variable = T-sonic-cor
Variable = P-meteo
Variable = L-meteo
Comments
Comment = Test de Stationarite
Comment = Critère de qualite
Comment =
Stationarity
From Time =
To Time =
Signal (A) = u-sonic
Signal (B) = w-sonic
Storage Label A StdDev Stationarity =
u-stat Storage Label B StdDev Stationarity = w-stat
Storage Label AB Covariance Stationarity = uw-stat
Segment length, minutes = 5
Linear detrend segments =
Linear detrend run =
Stationarity
From Time =
To Time =
Signal (A) = co2-licor
Signal (B) = w-sonic
Storage Label A StdDev Stationarity =
Storage Label B StdDev Stationarity =
Storage Label AB Covariance Stationarity =
co2w-stat Segment length, minutes = 5
Linear detrend segments =
Linear detrend run =
Stationarity
From Time =
To Time =
Signal (A) = q-licor
Signal (B) = w-sonic
Storage Label A StdDev Stationarity =
Storage Label B StdDev Stationarity =
Storage Label AB Covariance Stationarity =
qw-Stat Segment length, minutes = 5
Linear detrend segments =
Linear detrend run =
Stationarity
From Time =
To Time =
Signal (A) = T-sonic
Signal (B) = w-sonic
Storage Label A StdDev Stationarity =
Storage Label B StdDev Stationarity =
Storage Label AB Covariance Stationarity =
tsw-Stat Segment length, minutes = 5
Linear detrend segments =
Linear detrend run =
Plot Value
.3 Annexe 2 Description des installations
| 


