3.4. NEURONES ARTIFICIELS (OU FORMELS)
Le neurone formel de Mc Cullogh et Pitts (1974) est la cellule
élémentaire de calcul dans un réseau de neurones formels.
Il consiste en une unité d'addition et une fonction neurone ou fonction
d'activation :
|
m
i. l'unité d'addition i
W ij X
i=1
|
effectue une somme pondérée des entrées Xi
par les poids
|
des connexions (Wij, i=1, m). Wij est le
poids de la connexion qui lie l'entrée Xi au neurone nj. Wij
est positif, si la série Xi doit augmenter la sortie du neurone nj et
Wij est négatif, si Xi doit la diminuer ;
ii. la fonction neurone (fj) sert à limiter la sortie du
neurone nj dans un intervalle
prédéfini et/ou augmenter la non
linéarité du neurone.
Le modèle du neurone peut inclure une valeur limite
appelée Seuil (S). Dans la littérature le mot seuil est souvent
remplacé par le terme biais.
Lorsque le niveau d'activation, (la somme
pondérée WijXi) atteint ou dépasse ce biais,
alors l'argument de la fonction d'activation devient positif ou nul ; sinon, il
est négatif (Parizeau, 2004). L'équation de la sortie
calculée est donnée par la relation (1).
Outj = fj(In j )
(1)
Inj = WijXi-Si (2)
Avec : Inj : l'entrée de la fonction d'activation du
neurone j ; Outj : la sortie de la fonction d'activation du neurone j ; Xi :
l'entrée i connectée au neurone j ; Wij : le poids de la
connexion entre l'entrée Xi et le neurone j ; Sj : le seuil du neurone j
; m : le nombre d'entrées connectées au neurone j ; f : la
fonction d'activation du neurone j.
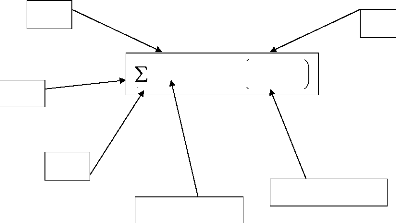
Le schéma d'un neurone formel adapté des travaux
d'Awadallah (1999) est présenté à la figure
19.
S
Xi
Xi+1
i
m
=
1
W X
ij i / Out f W X S
= ij i i
-
m
i = 1
Xm
Unité d'addition
Unité d'activation
Figure 19 : Schéma d'un
neurone formel
La modélisation pluie-débit, objectif de ce travail
de recherche ne s'intéresse pas aux neurones pris individuellement mais
plutôt à leurs différentes combinaisons en
réseaux.
3.5. ORGANISATION DES NEURONES EN RÉSEAUX
Un réseau de neurones est un maillage de plusieurs
neurones, généralement organisés en couches. Les
connexions entre les neurones, définies précédemment, qui
composent le réseau décrivent la topologie ou l'architecture du
modèle. Elle peut être quelconque, mais le plus souvent, dans la
littérature, il est possible de distinguer une certaine
régularité, (Touzet ,1992). Selon le chemin suivi par
l'information dans le réseau on peut classer les réseaux de
neurones en deux grandes catégories : les réseaux
«feed-forward» et les réseaux «feed-back».
3.5.1. Réseaux «feed-forward»
Les réseaux «feed-forward» ou réseaux
«nourrir en avant» appelés aussi «réseaux de type
Perceptron», sont des réseaux dans lesquels l'information se
propage de couche en couche, sans retour possible en arrière. Nous
pouvons citer parmi ces réseaux les Perceptrons (objet de cette
étude) et les réseaux à fonction radiale.
3.5.1.1. Modèle perceptrons
Il existe deux modèles Perceptrons : les modèles
Perceptrons Monocouches et les modèles Perceptrons Multicouches
(PMC).
Le Perceptron Monocouche est historiquement le premier
réseau de neurones, c'est le Perceptron de Rosenblatt. C'est un
réseau simple, puisqu'il ne se compose que d'une couche d'entrée
et d'une couche de sortie. Il est calqué, à la base, sur le
système visuel et de ce fait a été conçu dans un
but premier de reconnaissance des formes. Cependant, il peut aussi être
utilisé pour faire de la classification et/ou pour résoudre des
opérations logiques simples («ET» ou «OU»). Sa
principale limite est qu'il ne peut résoudre que des problèmes
linéairement séparables, ce qui diffère de la relation
pluie-débit qui est non-linéaire. Il suit
généralement un apprentissage de type supervisé selon la
règle de correction de l'erreur (ou selon la règle de Hebb
(Parizeau, 2004)). La typologie des apprentissages sera détaillée
dans la suite de cette étude. La figure 20
représente un Perceptron Multicouches simplifié avec une seule
couche de neurones cachés. Les variables d'entrée sont la pluie
et la température et la variable cible est le débit.
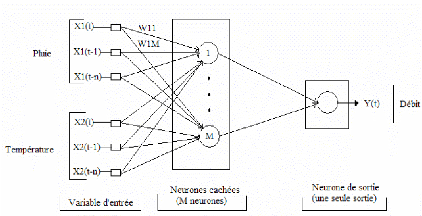
Figure 20 : Perceptron Multicouche
simplifié avec une seule couche de neurones cachés
Le Perceptron Multicouches (PMC) est une extension du
précédent, avec une ou plusieurs couches cachées entre
l'entrée et la sortie. Chaque neurone dans une couche est
connecté à tous les neurones de la couche
précédente et de la couche suivante (excepté pour les
couches d'entrée et de sortie) et il n'y a pas de connexions entre les
cellules d'une même couche. Ce type de réseaux a été
récemment classé comme outil de prévision et de simulation
des débits (Fortin et al., 1997). Cependant, ces applications
se sont largement diversifiées et les fonctions d'activation
utilisées dans ce type de réseaux sont principalement les
fonctions à seuil ou sigmoïdes. Il peut résoudre des
problèmes non-linéairement séparables et des
problèmes logiques plus compliqués comme la relation
pluie-débit. Il suit aussi un apprentissage supervisé selon la
règle de correction de l'erreur.
Le Perceptron Multicouches est le Réseau de neurones le
plus utilisé en modélisation hydrologique (Coulibaly et
al., 1999). Plusieurs auteurs considèrent que ce type de
réseau comprend trois groupes de neurones. Par exemple, Awadallah,
(1999) identifie trois groupes de neurones : un groupe d'entrée, un
groupe intermédiaire et un groupe de sortie. Cette considération,
faite notamment par plusieurs auteurs, paraît «impropre» ; car,
d'après Dreyfus et al. (2004), la couche des entrées
n'effectue aucune modification de l'information donc ne fait aucun calcul.
L'équation générale d'un réseau de neurones formels
de type Perceptron Multicouches, avec une seule couche cachée et une
seule sortie scalaire, est formulée comme suit :
m n
(3)
Y f Wo f Wh X b b
= * + +
2 j * 1 ij i 1 2
j= 1 i = 1
Où :
Y : est la sortie calculée par
le réseau,
f2 : est la fonction
d'activation du neurone de la couche de sortie,
m : est le nombre de neurones
cachés,
n : est le nombre de variables d'entrée
Woj : est le poids de la
connexion entre la jième neurone sur la couche cachée
et le neurone de sortie,
f1 : est la fonction
d'activation du neurone de la couche cachée,
Whij : est le poids entre la
iième entrée et le jième neurone sur
la couche cachée,
Xi : est la matrice
d'entrée,
b1 : est le biais de la
fonction d'activation du jième neurone caché,
b2 : est le biais de la
fonction d'activation du neurone de sortie.
Pour la classification des Perceptrons Multicouches deux
critères peuvent être considérés :
i) le comportement dynamique des réseaux, qui
dépend de la présence ou non de bouclages et ;
ii) ii) la complexité des opérations
effectuées par le réseau, qui est liée à la
présence de neurones cachés (Johannet, 2006).
| 


