Les fractals et leur géométrie

République Algérienne Démocratique et Populaire
Ministere de l'Enseignement Supérieure et de la Recherche Scientifique
??????????
UNIVERSIT'E DR. YAHIA FAR`ES DE M'ED'EA
FACuLT'E DES SCIENCES ET DE LA TECHNOLOGIE

M'EMOIRE

présentéen vue de l'obtention du

DIPL ^àOME DE MASTER EN MATH'EMATIQUES

Spécialité: Analyse et Modélisation Mathématique
par

BELL L bderrahmane & BENTERKI bdessalem

Titre:

Les fractals et leur géométrie

Date de soutenance : 30 Juin 2011

Composition du Jury :
Président :	KOuADIK Smain	Maître de Conférences	UYFM
Rapporteur :	ALLECHE Boualem	Maître de Conférences	UYFM
Examinateur :	DEKAR Lies	Maître de Conférences	UYFM
Examinateur :	OuKIL Walid	Maître Assistant	UYFM
Invité:	ABDELLAH EL-HADJ Abdellah	Maître de Conférences	UYFM

«Je
dédie ce tra-
vail a` ma mere, a`
mon pere, a` mon frere
et a` mes soeurs et
a` tous mes
amis.»

BELLAL Abiterrahmane

«Je dédie ce travail
a` mes parents qui m'ont
fait confiance et m'ont
soutenu tout au long
de mes études.»

?

BENTERKI Abitessalem

Remerciements

Le docteur ALLECHE Boualem a acceptéd'être notre directeur de th`ese et nous a <sup>dirigé</sup>avec passion et enthousiasme. Il nous a initiéa` la recherche et nous a soutenu pendant toute la durée de ce travail. Qu'il soit assuréde trouver ici notre profonde reconnaissance.

?

Le docteur KOuADIK Smain nous a fait l'honneur et le plaisir de présider notre jury de soutenance. Nous lui exprimons toute notre gratitude.

?

Nos vifs remerciements vont au docteur DEKAR Li`es et a` M. OuKIL Walid d'avoir acceptéde lire notre travail et au docteur ABDELLAH EL-HADJ Abdellah, directeur du laboratoire

«Mécanique, Physique et Modélisation Mathématique» d'avoir mis a` notre disposition les moyens du laboratoire et d'avoir acceptéde faire partie de ce jury.

?

Nous tenons a` exprimer aussi notre profonde reconnaissance a` tous nos enseignants qui nous ont accompagnétout au long de nos études. Sans eux, ce travail n'aurait certainement jamais pu voir le jour.

Nous remercions également tous nos amis et en particulier Hamza, Rachid, Madjid, Mustapha, ... qui nous ont aidé, chacun a` sa mani`ere, dans un cadre mathématique ou autre.

Enfin, merci a` toutes nos familles pour leur amour et leur soutien constant.

R'esum'e

La question de construire les fractales interesse les chercheurs depuis plusieurs annees, et la methode des systemes des fonctions iterees (IFS) est actuellement tres utilisee.

Le but de notre travail est de presenter les fractals et leur geometrie et d'introduire les methodes de construction basees sur la notion des systemes de fonctions iterees (IFS) et en particulier ceux des multifonctions. Nous avons eteamenes, dans cette these, a` donner les notions de base de topologie et de theorie de la mesure de l'espace euclidien IV necessaires a` l'etude des fractals. Nous avons ensuite introduit les notions de dimension de Hausdorff et la dimension topologique pour bien cerner la definition mathematique des fractals et nous avons presentela geometrie des fractales ainsi que quelques exemples celebres et leur programmation sous Matlab®.

Enfin, nous nous sommes interesses aux systemes de fonctions iterees (IFS) qui permettent de construire aisement les objets fractals et nous avons presentela technique des IFS sur les multifonctions.

Mots-clefs

Fractal, dimension de Hausdorff, dimension topologique, mesures de Hausdorff, systeme de fonctions iterees, les multifonctions, mesure exterieure.

Abstract

The questions of fractal's constructions interest the researchers since many years and the method of iterated functions systems is currently very used.

Our work is in order to present the fractals and their geometry and to introduce the method of construction based on iterated functions systems (IFS) and in particular, those on multifunctions. To do this, we have given in this thesis some notions on topology and on measure theory of the Euclidien space IV necessary to the study of fractals. We have then introduced the notions of Hausdorff dimension and that of topological dimension to give the mathematical definition of fractals. The geometry of fractals and some well known examples and their program in Matlab® have been also presented.

In the last part of this thesis, we were interested in the IFS technics and in particular those on multifunctions.

Keywords

Fractal, Hausdorff dimension, topological dimension, Hausdorff measure, iterated functions systems, multifunctions, outer measure.

Table des matières

Remerciements iii

Résuméiii

Notations et symboles ix

Introduction xi

1	Mesures et structures boréliennes 1.1 Mesure positive 1.2 Mesure extérieure		1 1 5
		1.2.1 Prolongement d'une mesure	7
		1.2.2 Exemples de mesures extérieures	9
2	Dimension et mesures de Hausdorff		11
	2.1	Mesures de Hausdorff	11
	2.2	Dimension de Hausdorff	19
	2.3	Calculs des dimensions	23
3	Dimension topologique		33
4	La géométrie des fractals		37
	4.1	Système de fonctions itérées	38
		4.1.1 Dimensions des ensembles auto-similaires	47
		4.1.2 Système de fonctions itérées affines dans R^2 50
	4.2	Système de fonctions itérées complexes	54

4.2.1 Les ensembles de Julia 55

4.2.2 L'ensemble de Mandelbrot 61

4.3 Systeme de fonctions it'er'ees sur les multifonctions 65

Conclusion et perspectives 71

Programmes sur les fractals 72

.1 L'ensemble de Cantor 72

.2 Courbe de von Koch 73

.3 Triangle de Sierpenski 74

.4 Fougere de Barnsley 76

.5 Poussiere de Cantor 77

.6 Tapis de Sierpenski 78

.7 L'ensemble de Julia 80

.8 L'ensemble de Mandelbort 81

R'ef'erences bibliographiques 82

Table des figures

2.1 Graphe de 7(⁸(F) 20

2.2 L'ensemble triadique de Cantor 23

2.3 La courbe de von Koch 25

2.4 La courbe de Koch quadratique de type 1 26

2.5 La courbe de Koch quadratique de type 2 27

2.6 Le flocon de von Koch 28

2.7 Le triangle de Sierpinski 28

2.8 Recouvrements du triangle de Sierpinski 29

2.9 Le tapis de Sierpinski 30

2.10 L'éponge de Menger 30

2.11 La courbe de Peano 31

3.1 Poussière de Cantor 36

4.1 Exemple d'auto-similarité 38

4.2 La courbe de Koch quadratique modifié 49

4.3 La fougère de Barnsley 54

4.4 Ensemble de Mandelbrot 62

Notations et symboles

Symboles Description

Ø L'ensemble vide.

:= Par définition

volⁿ Le volume n-dimensionelle.

diam Diamètre

P(E) L'ensemble des parties de E.

A L'adhérence de A.

?A La frontière de A.

Gä L'itersection dénombrable des ouverts.

F_ó L'union dénombrable des fermés.

u|A La restriction de u sur M.

B Une tribu.

B(E) La tribu borélienne de E.

u Une mesure positive.

u* La mesure extérieure.

M = {A E P(E) : A est u^*-mesurable}.

L1 La mesure extérieure de Lebesgue dans R¹.

Ln La mesure extérieure de Lebesgue dans Rⁿ.

Hs La mesure de recouvrement s-dimensionnelle.

ä

Hs La mesure de Hausdorff s-dimensionnelle.

dimT La dimension topologique.

dimH La dimension de Hausdorff.

(x) La fonction gamma d'Euler.

K(E) L'ensemble des compacts de E.

Symtholes Description

dH Distance de Hausdorff dans /C(E).

J(f) L'ensemble de Julia de fonction f.

CHAPITRE 0

INTRODUCTION

P

lUSIEURS personnes ont une idée de la signification du mot «fractal» mais peu savent vraiment de quoi il s'agit. Inventépar Benoàýt Mandelbrot, ce mot signifie a` la fois «brisé» et «irrégulier» et sert a` représenter géométriquement des objets dont la forme est extrêmement irrégulière.

Dans les années 70, le champ d'action des mathématiques a pris une nouvelle dimension par l'ajout de la géométrie fractale. Depuis, il a étédémontréque les fractals peuvent servir de modèle pour représenter la géométrie de la nature et ont des applications dans plusieurs domaines (théorie des nombres, système dynamique, mécanique, mouvement Brownien, applications physiques, ... etc [voir [8, 9]]).

Cette thèse, qui se veut être une introduction et une modeste contribution a` la compréhension de la complexitédes fractals, consiste a` présenter les fractals et leur manière de construction par une méthode simple due a` J. E. Hutchinson et perfectionnée par Michael Barnsley.

Notre travail se subdivise en quatre chapitres.

Le premier présente les outils mathématiques de base qui seront utilisés tout au long de ce travail. Il sera consacréau rappel de quelques notions de topologie, de mesures et de mesures extérieures.

Le second est dédiéaux mesures de Hausdorff qui sont des mesures extérieures et a` leurs principales propriétés. La notion de mesure de Hausdorff est plus générale que celle de Lebesgue, et malgréla difficultéde calculer la mesure de Hausdorff d'un objet fractal, on peut

xii

connaitre sa dimension de Hausdorff beaucoup plus facilement.

Le troisieme chapitre est consacr'e a` l''etude de la dimension topologique qui est primordiale pour la d'efinition math'ematique des objets fractals. Nous y avons pr'esent'e la dimension topologique pour un espace topologique quelconque, et comme tous les fractals 'etudi'es sont exclusivement dans Rⁿ, nous avons pr'esent'e «la forme simplifi'ee» de la dimension topologique sur les espaces m'etrisables.

Le quatrieme chapitre a` servi pour d'efinir les objets factals qui sont des objets dont la dimension de Hausdorff est strictement sup'erieure a` la dimension topologique. Ce chapitre est subdivis'e en trois parties.

- La premiere sert a` pr'esenter les systemes de fonctions it'er'ees (IFS) qui constituent une facon de construire les fractals. Et pour le faire, nous avons 'et'e amen'es a` pr'esenter quelques rappels sur les espaces m'etriques complets, la distance de Hausdorff et le th'eoreme de point fixe de Banach. Nous avons donn'e la dimension de certains ensembles auto-similaires et la m'ethode num'erique pour la d'eterminer ainsi que les algorithmes pour d'eterminer les attracteurs de ces IFS.

- La deuxieme partie est consacr'ee a` deux ensembles fractals sur C (les ensembles de Julia et l'ensemble de Mandelbrot) et a` leurs propri'et'es topologiques et g'eom'etriques.

- La troisieme partie traite des questions plus r'ecentes et de la g'en'eralisation des IFS a` l'espace des multifonctions.

A la fin du document et en utilisant les systemes de fonctions it'er'es (IFS), nous avons pr'esent'e des programmes permettant de visualiser la construction des fractals sous Matlab®.

CHAPITRE 1

MESURES ET STRUCTURES BOR'ELIENNES

n

iEI

Dans ce chapitre, nous donnons quelques notions de base qui serons utilisées tout au long de cette th`ese. Nous commencons tout d'abord par un rappel sur la théorie de la mesure qui joue un ràole important dans l'étude des fractals.

Section 1.1

Mesure positive

Soit E un ensemble quelconque (généralement, nous travaillons sur un espace euclidien n-dimensionnel, Rⁿ).

Une collection non vide A de parties de E est dite :

- algèbre sur E si elle contient 0 et E, stable par passage au complémentaire et par union finie (i.e. pour tout A, B ? A, on a : A^c ? A et A ? B ? A).

- ó-algèbre ou bien tribu sur E si elle contient 0 et E, stable par passage au complémentaire et par union dénombrable.

Si B est une tribu sur E, le couple (E, B) est appeléespace mesurable. Les parties de E
qui sont ( resp. ne sont pas) des 'el'ements de B sont dites mesurables (resp. non mesurables).
Soient E et I deux ensembles. Pour tout i ? I, on se donne une tribu Bi sur E. Alors
Bi = {A ? E : A ? Bi, ?i ? I} est encore une tribu sur E. Cette stabilitépar intersection

des tribus permet de définir la notion de tribu engendr'ee par une partie C ? P(E) comme la plus petite tribu contenant C. On la note óE(C) ou ó(C).

On rappelle qu'une «topologie» sur E est la donnée d'une famille de parties de E, appelées
«ouverts de E», contenant 0 et E, stable par union (quelconque) et stable par intersection
finie. L'ensemble E, muni de cette famille de parties, est alors appeléun «espace topologique».
On appelle tribu bor'elienne (ou tribu de Borel) sur un espace topologique E, la tribu

engendr'ee par l'ensemble des ouverts de E, cette tribu sera not'e B(E). Les 'el'ements de
B(E) sont appel'es les boréliens de E. Dans le cas E = Rⁿ, cette tribu est donc not'e B(Rⁿ).

Il est clair (Rudin [29, p. 11]) que les ferm'es de E sont des bor'eliens puisque par d'efinition ce sont les compl'ementaires des ouverts de E. De màeme, les r'eunions d'enombrables de ferm'es et les intersections d'enombrables d'ouverts constituent des bor'eliens fort importants, auxquels on a respectivement donn'e a` la suite de Hausdorff le nom de F<sub>a</sub> et G8. Les lettres F et G sont utilis'es pour d'esigner respectivement les ferm'es et les ouverts ; ó se rapporte a` la r'eunion, ä se rapporte a` l'intersection. Par exemple, tout intervalle semi-ouvert [a, b[ est un G8 mais 'egalement un F_a dans R.

Soit C une partie de P(E) contenant 0. Une mesure positive sur C est une application u : C ? R+ v'erifiant :

? u(0) = 0.

? u est ó-additive, c'est-`a-dire que pour toute famille (A<sub>n</sub>)<sub>nE</sub>N ? C de parties deux a` deux

disjointes, (i.e. An n Am = 0, si n =6 m) et telle que U nEN			An ? C, on ait
u( U nEN	X An) = nEN	u(An). (1.1)

Si B est une tribu sur E et si u est une mesure positive sur B, le triplet (E, B, u) est appel'e espace mesur'e.

Proposition 1.1.1 (Propri'et'es des mesures) Soit (E, B, u) un espace mesuré. La mesure u vérifiéles quatres propriétés suivantes

? Monotonie : Soit A, B ? B, A ? B, alors

u(A) .<, u(B). (1.2)

? ó-sous-additivité: Soit (A_n)_nEN ? B, alors

u( U nEN

An) ... E nEN

u(An). (1.3)

? Continuitécroissante : Soit (A_n)_nEN ? B, tel que A_n ? An+1, pour tout n ? N, alors

u(U nEN

An) = lim n-+oo

u(An) = sup nEN

u(An). (1.4)

T Continuitedecroissante : Soit (An)n?N ? B, tel que A_n+1 ? An, pour tout n ? N, et tel qu'il existe n0 ? N, u(A_n0) < 8, alors

\ u( n?N

An) = lim n?8

u(An) = inf u(An). (1.5) n?N

D'EMONSTRATION :

1. Monotonie. Soit A, B ? B, A ? B. On a B = A ? (B\A) et A n (B\A) = Ø. Comme A ? B et B\A = BnA^c ? B, l'additivitede u (voir 1.1) donne u(B) = u(A)+u(B\A) > u(A), car u prend ses valeurs dans R+.

Noter aussi que u(B\A) = u(B) - u(A) si 0 6 u(A) 6 u(B) < 8 (mais cette relation n'a pas de sens si u(A) = u(B) = 8).

2. ó-sous additivite. Soit (An)n?N ? B. On veut montrer que _u(?n?NAn) 6 E u(A_n).

n?N

On pose B0 = A0 et, par recurrence sur n, B_n = A_n \(?_i^n-₀ ¹Bi) pour n > 1. Par recurrence sur n on montre que B_n ? B pour tout n en remarquant que, pour n > 1, B_n = A_n n (nin0 ¹B). La construction des B_n assure que B_n n B_m = Ø si n =6 m et ?n?NAn = ?n?NBn. Pour verifier cette derni`ere propriete, on remarque que B_n ? A_n donc ?n?NBn ? ?n?NAn. Puis, si x ? A_n et x ?/ ?in-0 1 Bi, on a alors x ? Ann(ni^n-0 ¹B) =

B_n. Ceci prouve que ?n?NAn ? ?n?NBn et donc, finalement,?_n?NA_n = ?n?NBn.

On utilise maintenant la ó-additivitede u et la monotonie de u (car B_n ? A_n) pour

ecrire u(?n?NAn) = u(?n?NBn) = E u(B_n) 6 E u(A_n).

n?N n?N

3. Continuitecroissante. Soit (An)n?N ? B, tel que A_n ? An+1, pour tout n ? N. Par

monotonie de u, on a u(An+1) > u(An), pour tout n ? N, et donc lim n?8

u(An) =

sup u(A_n) ? R+. On pose A = ?n?NAn et on definit la suite _(Bn)n?N par B0 = A0 et

n?N

B_n = An\An-1 pour tout n > 1 (noter que An-1 ? A_n). On a A = ?n?NAn = ?n?NBn, B_n ? B pour tout n ? N et B_n n B_m = Ø si n =6 m.

La ó-additivitede u nous donne

u(A) = u(U n?N			X Bn) = n?N	u(Bn) = lim n?8		Xn p=0	u(Bp)
donne	Pn p=0	u(Bp) = u(An) et donc u(A) = lim n?8			u(An).

Puis, comme A_n = ?ⁿp=0Bp, l'additivitede u (qui se deduit de la ó-additivite) nous

4. Continuitédécroissante. Soit (An)n?N ? B, tel que A_n+1 ? An, pour tout n ? N, et telle qu'il existe n0 ? N, u(A_n0) < 8.

Par monotonie, on a u(An+1) 6 u(An) pour tout n ? N et donc lim n?8

u(An) =

inf u(A_n) ? R+. On a aussi, par monotonie, u(A) 6 u(A_n), pour tout n ? N, avec

n?N

A = nn?NAn. Comme u(A_n0) < 8, on a aussi u(A_n) < 8 pour tout n > n0 et u(A) < 8. _On pose Bn = An0\An = An0nA^c_n ? B, pour tout n > n0. La suite (Bn)n>n0 est croissante (B_n ? Bn+1 pour tout n n0) et B = ?n.0Bn = ?n?n0An0\An = An0\ nn>n0 A_n = A_n0\A.

La continuitecroissante donne

u(An0\A) = u(B) = lim n?8 u(Bn) = lim n?8

u(An0\An) (1.6)

Comme A ? An0, on a u(A_n0\A) = u(A_n0) -u(A) _(car u(A) 6 u(A_n0) < 8, on utilise
ici la remarque a` la fin de la preuve de la monotonie). De màeme, comme A_n ? An0
(pour n n0), on a u(An0\An) = u(A_n0) - u(A_n) _(car u(A_n) 6 u(A_n0) < 8). En

utilisant une nouvelle fois que u(An0) < 8, on deduit de (1.6) que u(A) = lim n?8

u(An). 111

Une mesure u sur B est dite finie si u(E) < +8. Une probabilitésur B est une mesure sur B telle que u(E) = 1.

Soit (E, B,u) un espace mesure. On dit que A est négligeable s'il existe un ensemble B ? B tel que A ? B et u(B) = 0. Si toutes les parties negligeables sont mesurables, on dit que u est complete ou que (E, B, u) est complet.

Soit E un espace topologique, une mesure u sur B(E) est dite mesure borélienne sur E si elle est localement finie, c'est-`a-dire ; chaque x ? E admet un voisinage ouvert U_x tel que u(U_x) < +8. (voir [1, 5, 13] pour plus de details)

Soit u une mesure borelienne sur un espace topologique E. On dit que u est une mesure réguliere si pour tout B ? B(E) on a :

sup{u(F) : F ? B, F fermede E} = u(B)

= inf{u(O) : B ? O,O ouvert de E}

On peut consulter (Rudin [28, p. 303]) pour voir qu'une mesure u sur E est reguli`ere si et seulement si pour tout B ? B(E) et tout å > 0, il existe un ouvert O et un fermeF tels que F ? B ? O et

u(O) - å 6 u(B) 6 u(F) + å. (1.7)

Section 1.2

Mesure ext'erieure

D'efinition 1.2.1 On appelle mesure exterieure sur E, une application u* : P(E) -? R+ verifiant :

X u*(Ø) = 0. ® (ó-sous-additivite) u*( U nEN

An) 6 E nEN

u^*(An) pour tout {An}nEN ? P(E).

(c) (monotonie) A ? B u^*(A) 6 u^*(B).

Une partie A ? E sera dite u^*-mesurable (au sens de Caratheodory) si

VX ? P(E), u^*(X) = u^*(X n A) + u^*(X n A^c) (1.8)

En vertu de ®, A est u^*-mesurable si et seulement si

VX ? P(E), u^*(X) > u^*(X n A) + u^*(X n A^c) (1.9)

Th'eor`eme 1.2.2

Soit u* une mesure exterieure sur E. La collection M des parties u^*-mesurables forme une tribu sur E et la restriction de u* sur M est une mesure positive. De plus, l'espace mesure(E, M, _u*|M) est complet.

D'EMONSTRATION :

- Il est claire que Ø ? M et que A^c ? M, VA ? M.

- Soit A1, A2 ? M. Montrons que A1 n A2 ? M

Soit X ? M. En utilisant la u^*-mesurabilitede A1 et A2 et la ó-sous-additiviteon obtient :

u^*(X) = u^*(X n A1) + u^*(X n A^c₁)

= u^*(X n A1 n A2) + u^*(X n A1 n A^c ₂) + u^*(X n Ac 1 n A2) + u^*(X n Ac 1 n A^c ₂)

> u^e(X n A1 n A2) + u^*(X n [(A1 n A^c ₂) ? (A^c₁ n A2) ? (A^c₁ n A^c₂)])

> u^*(X n (A1 n A2)) + u^*(X n (A1 n A2)^c)

Alors A1 n A2 ? M. On conclut que M est stable par reunion finie et par intersection finie.

- Soit (An) une suite dans M deux a` deux disjoint. Posons A = U nEN		An. Montrons que
A ? M et u^*(A) = E nEN	u^*(An).

Soit X ? P(E). Comme A1 ? M, on a

u^*(X n (A1 ? A2)) = u^*((X n (A1 ? A2)) n A1) + u^*((X n (A1 ? A2)) n A^c₁) = u^*(X n A1) + u^*(X n A2)

Par recurrence, on obtient pour tout n :

u* X n

Ai) = u^*(X n Ai) (1.10)

ni=1

_[n
i=1

Donc, pour tout n :

>

_Pn
i=1

u*(X) > u^*(X n Sni=1 Ai) + u^*(X n (Uni=1 Ai)c) u^*(X n Ai) + u^*(X n A^c)

00

D'o`u u^*(X) > i=1 u* (X n Ai) + u* (X n A^c) > u* (X n A) + u* (X n A^c) d'après la ó-sous-

additivite de u*. Donc A ? M.

Il s'en suite que u* (X) = u* (X n A) + u^*(X n A^c). En prenant X = A, on obtient

00

u^*(A) = i=1 u^*(Ai). (1.11)

On vient donc de demontrer que M est stable par reunion denombrable disjointe et que u* est un mesure positive sur M.

- Reste a` demontrer que M est une tribu. Soit maintenant (B_n) une suite dans M. On pose A_n = B_n\ ?n¹ Bi. Alors ?nENAn = ?nENBn et donc ?nENBn ? M. On conclut donc que M est une tribu.

On vient de demontrer que M est une tribu et que u = ur_M est une mesure positive sur M.

- Montrons maintenant que (E, M, u) est complet. Pour cela, il suffit de montrer que pour tout A ? P(E) si u^*(A) = 0, alors A ? M.

Soit A ? P(E) tel que u^*(A) = 0. On a pour tout B ? P(E) :

u^*(B n A) + u^*(B n A^c) = u^*(B n A^c) 6 u^*(B)

d'o`u A ? M.

111

1.2.1 Prolongement d'une mesure

Le theorème de prolongement le plus celèbre et le plus utilisea etedemontrevers 1914 par Caratheodory, qui a` cette occasion a developpele concept important de mesure exterieure ou mesure de Caratheodory.

Th'eor`eme 1.2.3 (Carath'eodory)

Soient E un ensemble, A une alg`ebre sur E et u une mesure positve sur A. Soit u* : P(E) ? R+ definie par

8u^*(A) := inf { E u(A_n) : (A_n) suite dans A avec A ? U A_n (1.12)

n=1 n?N

Alors

1. u* est une mesure exterieure sur E avec u^*_|4 = u,

2. ó(A) ? M,

3. _u*|ó(A) est un prolongement de u en une mesure positive sur ó(A) (not'ee ue et appelee extension de Caratheodory de la mesure u).

D'EMONSTRATION : 1. Montrons que u* est une mesure exterieure. En effet : - u*(Ø) = u(Ø) = 0. - Si A ? A' clairement u^*(A) 6 u^*(A'). - Soit (An) une suite de partie de E. Posons A = U

An. Montrons que u^*(A) 6

n?N

E n?N

u^*(An).

Si pour un n, u^*(A_n) = +8, la formule est verifie. Supposons que pour tout n,
u^*(A_n) < +8. Soit 6 > 0 et pour chaque n, soit (B_n^k)k dans A tel que A_n ? U B_n^k

k

et E u(B^k_n) < u^*(A_n) + 6/2ⁿ. On a A ? U U B_n^k et donc

k n k

u* (A) 6 E E u(B^k_n)6E (* (A_n) + 6/2ⁿ) 6 E u^*(A_n) + 6.

n k n n

D'o`u u^*(A) 6 E n	u^*(An). Il est aisede voir que u^*|4 = u.
2. Montrons que A ? M. Soit A ? A et B ? P(E). A-t-on u^*(B) ?-. u^*(B n A) + u^*(B n A^c) ? Si u^*(B) = +Do, c'est 'evident. Supposons que u^*(B) < +Do. Soit å > 0 et (An)n dans A telle que B ? U n		An avec

E u(A_n) 6 u^*(B) + å. On a B n A ? U (A_n n A) et B n A^c ? U (A_n n A^c) donc

n n n

u^*(B n A) + u^*(B n A^c) 6 _En u(A_n n A) + En u(A_n n A^c)

= E_n(u(A_n n A) + u(A_n n A^c))

= E_n u(An)
6 u^*(B) + å

D'o`u u^*(B) > u^*(B n A) + u^*(B n A^c). Donc A ? M.

3. Comme M est une tribu qui contient A, on a ó(A) ? M. Comme u^*_|M est une mesure sur M (d'apr`es 1.2.2), ue = u*|:(A) est une mesure sur ó(A) qui est un prolongement de u en une mesure sur ó(A).

111

Comme nous l'avons vu, le th'eor`eme de prolongement de Carath'eodory et la Proposition 1.2.2 permettent de construire une tribu M sur laquelle la mesure ext'erieure u* est automatiquement ó-additive. Le crit`ere de Carath'eodory que nous allons voir plus loin, est une condition d'apparence relativement simple qui entraine que M contient la tribu bor'elienne. C'est le crit`ere que l'on utilise traditionnellement pour construire les mesures de Hausdorff dans 1[Iⁿ, que nous 'etudierons plus tard.

Soit E un ensemble quelconque. Une m'etrique d sur E est une application d : E×E ? IR+ v'erifiant pour tout x, y, z ? E :

0 d(x, y) = 0 ? x = y. 0 d(x, y) = d(y, x). 0 d(x, z) 6 d(x, y) + d(y, z).

Un espace m'etrique est un couple (E, d) o`u E est un ensemble muni d'une m'etrique d. S'il existe un hom'eomorphisme de E sur un espace m'etrique on dit que E est un espace m'etrisable.

D'efinition 1.2.4 Soit u* une mesure ext'erieure sur un espace m'etrique (E, d) :

- On dit que u* est une mesure ext'erieure bor'elienne si tout bor'elien est u^*-mesurable, i.e. B(E) ? M.

- Une mesure ext'erieure u* est de type m'etrique si pour tous A, B ? E tels que d(A, B) := inf{d(x, y)/x ? A et y ? B} > 0

on ait u^*(A U B) = u^*(A) + u^*(B).

Th'eor`eme 1.2.5 (Crit`ere de Carath'eodory)

Soit u* une mesure ext'erieure sur un espace m'etrique (E, d). Si u* est de type m'etrique, alors u* est bor'elienne.

D'EMONSTRATION :

Il suffit de prouver que tout fermeF C E est u^*-mesurable, i.e. verifie

VX E P(E), u^*(X) > u^*(X n F) + u^*(X n F^c)

On peut supposer u^*(X) < +cc. Posons X0 := {x E X : d(x, F) > 1} et

1 1

Xk := {x E X : k +1 d(x, F)

} k

Il est clair que d(Xk, Xk+2) > 0, pour tout k, par consequent

Xm j=0	m u^*(X2j) = u^*(U j=0		X2j) 6 u^*(X) < +cc,
ce qui entraine en particulier que la serie		P8 j=0		u^*(X2j) converge. De même	P8 j=0	u^*(X2j+1)

converge. Notons P_m := U²k^m4¹Xk = (U^mj=0X2j) U (U^mj=0X2j+1). Observons que X n F^c = P_m U _(U8k=2m+2Xk) puisque F est ferme.

Donc u^*(X n F^c) 6 u^*(Pm) +

P8 k=2m+2

u^*(Xk), et comme u^*(Xk) converge, on a

u^*(X n F^c) 6 lim u* (P_m).

m?+8

D'autre part, comme d(P_m, X n F) > 0 on a

u^*(X n F) + u^*(P_m) = u^*((X n F) U P_m) 6 u^*(X). Ces deux inegalites entrainent

u^*(X n F) + u^*(X n F^c) 6 u^*(X n F) + lim u* (P_m) 6 u* (X).

m?+8

111

1.2.2 Exemples de mesures ext'erieures

Voici quelques exemples de mesures et de mesures exterieures qui seront utilises dans la suite du document :

Exemple 1.2.6 Mesure de comptage :

irg. Elle est aussi une mesure ext'erieure

Pour tout sous-ensemble A de Rⁿ, La mesure de comptage n'est autre que la fonction «cardinal» de A, a` valeurs dans N ? {+8}.

Exemple 1.2.7 Mesure ext'erieure de Lebesgue dans R :

La mesure ext'erieure de Lebesgue, ou longueur, d'une partie A de R est d'efinie comme l'infimum des sommes des longueurs des intervalles recouvrant A :

i=1 i=1

L¹(A) := inf {E(bi - ai) : A ? U]ai, bi[ (1.13)

Pour les intervalles ferm'es ou ouverts, on a L^1(]a, b[) = L^1([a, b]) = b-a. Si A =U i		[ai, bi]
des intervalles finies (d'enombrables) disjoints, on a L^1(A) = E i	(bi - ai).

Exemple 1.2.8 Mesure ext'erieure de Lebesgue dans Rⁿ :

Si A = {(x1, . . . ,x_n) ? Rⁿ : ai 6 xi 6 bi}, le n-dimensionelle volume de A est donn'e par

volⁿ(A) = (b1 - a1)(b2 - a2)
·
·
· (bn - an). On d'efinit alors la mesure ext'erieure de Lebesgue dans Rⁿ par

{ L^n(A) = inf vol^n(Ai) : A ? U Ai i=1 i=1

(1.14)

Exemple 1.2.9 Restriction d'une mesure :

Soit u une mesure dans Rⁿ et E un sous-ensemble bor'elienne de Rⁿ. On d'efini une mesure í dans Rⁿ s'appelle la restriction de u sur E, par í(A) = u(E n A) pour tout ensemble A.

Nous verrons dans le chapitre suivant les mesure de Hausdorff qui sont essentielles dans l''etude des fractals.

CHAPITRE 2

DIMENSION ET MESURES DE HAUSDORFF

Dans ce chapitre, nous etudions les mesures de Hausdorff et leurs proprietes pour introduire la dimension de Hausdorff qui s'appellera plus tard la dimension des fractals.

Section 2.1

Mesures de Hausdorff

Pour un sous-ensemble non vide U de l'espace euclidien Rⁿ de dimension n, on definit le diamètre de U, notediam(U), par : diam(U) := sup{|x - y| : x, y ? U} o`u | · | est la distance euclidienne usuelle.

Si un ensemble F est recouvert par une collection denombrable d'ouverts {Ui} de diamètre

00

au plus 8, c'est-`a-dire F ? Ui avec 0 < diam(Ui) 68pour tout i, on dit que {Ui} est un

i=1

8-recouvrement de F.

Soit F un sous-ensemble de Rⁿ et soit s un reel positif. Pour tout 8 > 0, on definit

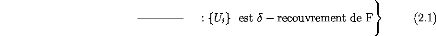
00

H;^s5(F) := inf {á(s) · E (diam(Ui)) s

vol^s(B_r)

i=1

2

o`u á(s) := _rs

_ðs/2

= (s ₂ +1) (voir [3, p. 327]) avec (t) =

+00_f

0

}: {Ui} est 8 - recouvrement de F (2.1)

e^-xx^t-1dx verifie

(1) = 1, (¹₂) = vð, (t + 1) = t(t)

et vol^s(B_r) signifie le volume de la boule de rayon r en dimension s.¹

1. Cette formule est pour s ? N, mais si l'on cherche a` d'efinir des dimensions s non enti`eres, il est naturel d'utiliser la màeme formule pour á(s).

D'efinition 2.1.1 Soient F ? Rⁿ, 0 -<, s < +8 et 0 < 8 < +8. On d'efinit la mesure de Hausdorff s-dimensionnelle H^s de F par

H^s(F) := lim ä--0

H^sä(F) = sup ä>0

H^sä(F) (2.2)

avec la convention H^s(F) = +8 pour s < 0.

Remarque 2.1.2

- Comme H^s_ä(F) est clairement une fonction decroissante de 8, l'existence de lim H^s_ä(F)

ä--0

est assuree, et cette limite est un supremum et peut àetre egal a` 0 ou a` +8.

- Cette mesure est appelee aussi la mesure de Hausdorff spherique (Falconer [8, 9]).

Les propositions suivantes donnent les premi`eres proprietes des mesures de Hausdorff.

Proposition 2.1.3 Pour tout s ?-. 0 et tout n ? N, la fonction F 7? H^s(F) est une mesure ext'erieure sur Rⁿ et d'efinit une mesure sur la tribu bor'elienne B(Rⁿ).

D'EMONSTRATION :

Il est clair que H^s(Ø) = 0 et que H^s est une fonction croissante d'ensembles. On verifie facilement que

H^sä(U kEN

Ak) ,<..E kEN

H^sä(Ak)

En passant a` la limite 8 ? 0 dans le terme de gauche, et en utilisant l'inegaliteH^s_ä ,<.. Hs dans le terme de droite, on trouve

H^s(U kEN

Ak) ,<..E kEN

H^s(Ak) (2.3)

La fonction H^s est donc sous-additive : c'est bien une mesure exterieure, definie sur l'ensemble de toutes les parties de Rⁿ.

Soit M la tribu des ensembles H^s-mesurables, au sens de l'enoncedu Theor`eme 1.2.2 ; on sait que H<sup>s</sup> definit une mesure sur M. Pour verifier que M contient toutes les parties boreliennes, on utilise le crit`ere de Caratheodory presenteau Theor`eme 1.2.5. Soient donc A et B deux parties de R<sup>n</sup> verifiant d(A, B) > 0, on cherche a` montrer que

H^s(A ? B) = H^s(A) + H^s(B). (2.4)

Pour tout 8 < d(A, B)/2, un ensemble de diam`etre 8 ne peut couper a` la fois A et B. Si l'on se
donne un recouvrement de A?B par des ensembles de diam`etre au plus 8, on pourra donc en

extraire des sous-recouvrements disjoints de A et B en considérant d'une part les ensembles qui coupent A, d'autre part ceux qui coupent B. On déduit que H^s_ä(A?B) = H^s_ä(A)+H^s_ä(B), et la conclusion en découle par passage a` la limite.

111

Proposition 2.1.4 Si F ? 118ⁿ et ë > 0, alors

H^s(ëF) = ë^sH^s(F) o`u ëF = {ëx : x ? F} (2.5)

D'EMONSTRATION :

Si {Ui} est un ä-recouvrement de F, alors {ëUi} est un ëä-recouvrement de ëF. D'o`u

H^sëä(ëF) 6 á(s)

(diam(2 ëUi) )s ës á(s) ^cE^° (diam(Ui))^s Hëä(ëF) 6 ë^sH^sä(F) ) 2 ) i=1 i=1

comme l'inégalitéest valable pour tout ä-recouvrement {Ui}, en faisant tendre ä ? 0, on obtient

H^s(ëF) = lim ä--0

H^sä(ëF) = lim ä--0

H^sëä(ëF) 6 ë^s lim ä--0

H^sä(F) = ë^sH^s(F).

En remplacant ë par 1/ë et F par ëF on obtient l'autre inégalité, d'o`u le résultat.

111

Un raisonnement similaire donne une estimation de la mesure de Hausdorff sur l'effet de transformations sur les ensembles.

Proposition 2.1.5 Soit F ? 118ⁿ et soit f : F ? 118^m une application lipschitzienne, i.e. |f(x) - f(y)| 6 c|x - y|, ?x,y ? F (2.6)
pour une constante c > 0. Alors, pour tout s > 0

H^s(f(F)) 6 c^sH^s(F) (2.7)

D'EMONSTRATION :

Si {Ui} est un ä-recouvrement de F, comme |f(F n Ui)| 6 c|F n Ui| 6 c|Ui|, on a que {f(F n Ui)} est un å-recouvrement de f(F), o`u å = cä.

Donc á(s) Ei

(diam(f(F n Ui)))s cs á(s) Ei 2 (diam(Ui))^s 2 . . , anis]. en prenant d'abord

(diam(Ui))^s

l'infinimum sur les 6-recouvrements, on a H^s_å(f (F)) < c^s · á(s) Ei 2 , ensuite,
comme l'in'egalit'e est vraie pour tout 8-recouvrement, en prenant l'infinimum sur ceux-ci, on

obtient H^s_å(f(F)) < c^sH^s_ä(F). Quand 8 ? 0 on a 6 ? 0 aussi, d'o`u le r'esultat. El

Si f est une isom'etrie, i.e. |f(x) - f(y)| = |x - y|, alors H^s(f(F)) = H^s(F). Donc, la mesure de Hausdorff est invariante par translation (i.e. H^s(F + z) = H^s(F) o`u F + z = {x + z : x ? F}).

Rappellons qu'une mesure ext'erieure est dite r'eguli`ere si, pour tout ensemble A, il existe un ensemble u^*-mesurable X tel que A ? X et u^*(A) = u^*(X).

Le lemme suivant est utile pour la suite. Voir Falconer[8, p. 4] pour la d'emonstration. Lemme 2.1.6 Si u* est une mesure exterieure r'eguli`ere et si {Ai}i est une suite croissante d'ensembles, alors

lim _k8u^*(Ai) = u^*(limAi). (2.8)

i--

i?8

Th'eor`eme 2.1.7 (R'egularit'e de la mesure de Hausdorff)

Soit s > 0 et soit A ? Illⁿ une partie quelconque. Alors

1. Il existe un ensemble Gä not'e G avec A ? G et tel que

H^s(G) = H^s(A) (2.9)

2. Si A est H^s-mesurable et H^s(A) < +8, alors il existe un ensemble F_ó not'e H avec H ? A et tel que

H^s(H) = H^s(A). (2.10)

D'EMONSTRATION :

1. Si H^s(A) = +8 alors Illⁿ est l'ensemble ouvert de Mesure (de Hausdorff) infinie. Supposons que H^s(A) < +8. Pour tout k, on a Hs1/k(A) < H^s(A) < +8, et on choisit {Ui,k}i un 2/k-recouvrement de A, ouverts, telle que

X8 i=1

~diam(Ui,k) ~s '31 s ( ) + < k'^A / k1 á(s) 2

On pose alors

[Ok := Ui,k, G := n Ok.

iEN k>1

Il est clair que G contient A, et d'autre part pour tout k on a

7-1^s2/k(G) 6

00 i=1

~diam(Ui,k) ~s '31 s ( A 6 1/k k') + k1 á(s) 2

Il s'ensuit que 7-1^s(G) 6 7-1^s(A), d'o`u la conclusion.

2. Soit A est 7-1^s-mesurable et 7-1^s(A) < +Do. Par la partie 1 du theor`eme on definit des

ouverts Ok avec A ?

00 k=1

00 Ok telle que 7-1s( n k=1

Ok \A) = 7-1s( n k=1

Ok)-7-1^s(A) = 0. Comme

00

tout ouvert de Rⁿ est un F_ó, on suppose que Ok = Fi_,k pour tout k, avec {Fi,k}k

i=1

suite de fermes croissante. Gràace au Lemme 2.1.6 ci-dessus

lim i-00

7-1^s(A n Fi,k) = 7-1^s(A n Ok) = 7-1^s(A).

Pour tout E > 0 et k > 1 on choisit ik tel que

7-1^s(A\Fik,k) < 2^-kE.

On pose F :=

00 k=1

Fik,k ; on a alors

00

7-1^s(F) > 7-1^s(A n F) > 7-1^s(A) - 7-1^s(A\Fik,k) > 7-1^s(A) - E.

k=1

Comme F ?

00 k=1

00 Ok, alors 7-1^s(F\A) 6 7-1s( n k=1

Ok\A) = 0. Par la partie 1, il existe un

ensemble G, intersection denombrable d'ouverts, de mesure nulle, tel que F\A ? G.
Alors F_å := F\G est contenu dans A, c'est une intersection denombrable de fermes, et

7-1^s(F_å) > 7-1^s(F) - 7-1^s(G) = 7-1^s(F) > 7-1^s(A) - E.

On conclut en posant H := _S00 F1/k.

k=1

111

Soit A ? Rⁿ de demi-diam`etre r. Il est clair que le volume de A est 'egal a` á(n)rⁿ si A est une boule, mais que peut-on dire dans le cas g'en'eral? On est tent'e de penser que A est inclus dans une boule de rayon r ou r + 6 avec 6 > 0 arbitrairement petit, mais ce n'est pas forc'ement le cas, comme le montre l'exemple d'un triangle de càot'e 1 dans R² et de diam`etre 1. Cependant, l'in'egalit'e isodiam'etrique ci-dessous assure que le volume d'un tel ensemble est inf'erieur ou 'egal a` celui d'une boule de màeme rayon.

Th'eor`eme 2.1.8 (In'egalit'e isodiam'etrique)

Soit A ? Rⁿ un ensemble Lebesgue-mesurable, et r son demi-diam`etre. Alors

volⁿ(A) 6 á(n)rⁿ. (2.11)

Lemme 2.1.9 'Etant donneun cube Q et 6 > 0, on peut ecrire

[ Q = j>1

Bj ? N (2.12)

o`u les Bj sont des boules fermees de rayon au plus 6, disjointes, et N est un ensemble Lebesgue-negligeable.

Th'eor`eme 2.1.10 (Propri'et'es des mesures de Hausdorff) X H⁰ est la mesure de comptage, i.e. H⁰(A) = E

1.

pEA

® H¹(A) = L¹(A), ?A ? R.

(c) H^s(A) = 0, ?A ? Rⁿ si s > n. T Hⁿ(A) = Lⁿ(A), ?A ? Rⁿ.

D'EMONSTRATION :

X Soit p ? Rⁿ. Pour tout 8 > 0, par d'efinition, on a H⁰({p}) = 1.

® Soient A ? R et 8 > 0. On va montrer que L¹(A) > H¹ä(A) et puis L¹(A) 6 H¹ä(A). On a

L¹(A) = inf {E(bi - ai) : A ? ]ai, bi[

i=1 i=1

00

{ 00

= inf E(b_i -- a_i) : A c U]ai, bi[, 0 < bi - ai 6 8

i=1 i=1

> H¹_ä(A)

Pour l'autre in'egalit'e, supposons A ? U iEN

Ui, ai:= inf Ui et bi := sup Ui. On obtient

diam(Ui) = bi - ai et donc

00 00

H¹ä (A) = infá(1) Vbi - 2 ai : A ? U[ai, bi], 0 < bi - ai 6 ä {

L--^,

i=1 i=1

00 00

( _X [

i=1 i=1

= inf (bi - ai) : A ? [ai, bi], 0 < bi - ai 6 ä

Soit å > 0 et supposons que {Ui} soit un ä-recouvrement de A satisfaisant

00

]ai, bi[

i=1

00

_P
i=1

et

(bi-ai) < H¹ä(A)+å. Soient ai := ai- 2i^å+1 , et bi := bi+ å

2i+1 . Alors, on a A ?

L^1(A) 6

00 i=1

(bi - ai) 6

00 i=1

(bi - ai) +

00 i=1

2i < H1 å ä(A) + 2å

. Pour

m m

(c) On va recouvrir le cube unit'e n-dimensionnelle Q = [0, 1]ⁿ ? Rⁿ par mⁿ petits cubes Qm,k(1 6 k 1 mⁿ) avec des cotes de longueur (m ? N^* et de diamètre) vn

> 0, on choisit m tel que n m

< ä. Pour s > n, on a

H^s_ä(Q) 6 á(s)

X mⁿ_{~vn ~s}

2m

k=1

= á(s)

_vn s

2s_ms-n

Pour m ? +8, on obtient H^sä(Q) = 0 pour tout ä > 0. Alors H^s(Q) = 0. Comme Rn est un r'eunion d'enombrable des translations du cube unit'e, alors H^s(Rⁿ) = 0.

T Soit {Ui} un ä-recouvrement de A. Gràace a` l'in'egalit'e isodiam'etrique 2.1.8, on a

L^n(A) 6

00 i=1

vol^n(Ui) 6 á(n)

X00 ~diam(Ui) ~n 2 i=1

En passant a` l'infinimum, on voit que L<sup>n</sup>(A) 6 H<sup>n</sup><sub>ä</sub>(A), et donc L<sup>n</sup>(A) 6 H<sup>n</sup>(A). Il nous reste a` montrer l'in'egalit'e inverse.

Soit maintenant A un ensemble Lebesgue-mesurable, on choisit une famille {Ui} de cubes Qi recouvrant A telle que

00

i=1 volⁿ(Qi) 6 Lⁿ(A) + ä,

o`u 8 > 0 est arbitrairement petit. Pour de tels cubes, on peut trouver une constante c_n, dépendant uniquement de n, telle que

á(n)r(Qi)ⁿ = c_nvolⁿ(Qi)

On déduit que Hⁿ 6 c_nvolⁿ.

Pour chaque Qi on introduit une famille de boules _(Bi,j)j>1 et un ensemble négligeable Ni vérifiant les conclusions du Lemme 2.1.9; en particulier, Hⁿ(Ni) 6 c_n · 0 = 0. On a donc

H^n(A) 6

X8 i=1

H^n(Qi) =

X8 i=1

(E j>1

H^n(Bi,j) + H^n(Ni))

_X8

i=1

_X8

i=1

_X
j>1

Bi_,j) =

_E8

6

i=1

volⁿ(U

j>1

volⁿ(Bi_,j) =

volⁿ(Qi) 6 Lⁿ(A) + 8

111

Lemme 2.1.11 Soit A ? Illⁿ et supposons que 0 6 s < t < +8 et 8 > 0. Alors :

H^sä(A) > 8^s-tH^tä(A). (2.13)

D'EMONSTRATION :

Soit {Ui} un 8-recouvrement de A. Comme diam(Ui)^s = diam(Ui)^s-^t · diam(Ui)^t et diam(Ui)^s-^t > 8^s-^t, alors H^sä(A) > 8^s-^tH^tä(A).

111

Selon le Lemme 2.1.11, on a le théor`eme suivant :

Th'eor`eme 2.1.12

Soit A ? Rⁿ et supposons que 0 6 s < t < +8. Alors :

1. H^s(A) < +8 = H^t(A) = 0.

2. H^t(A) > 0 = H^s(A) = +8.

06 On peut le montrer facilement si nous utilisons (2.13)

D'EMONSTRATION :

1. Soit ä > 0 et supposons que {Ui}i?N satisfait diam(Ui) 6 ä et

á(s)
·

E8 ( ₂ )diam(Ui))s

6 7-1^sä

(A) + 1 6 7-1^s(A) + 1

i=1

On obtient	7-1^tä(A) 6 á(s) ·	X8 ~diam(Ui) ~t 2 i=1
á(t) = · á(s) · á(s)			X8 ~diam(Ui) ^~s ~diam(Ui) ~t-s 2 2 i=1

:((st)) (7-1^s(A) + 1)
· (2ä)t s
·

Pour ä ? 0, on obtient 7-1^t(A) = lim ä?0

7-1^tä(A) = 0.

2. l'assertion 2 est une consequence immediate de 1.

111

Section 2.2

Dimension de Hausdorff

D'apr`es le Theor`eme 2.1.12, la mesure s-dimensionnelle d'un ensemble vaut d'abord l'infini pour s petit, puis zero si s d'epasse un certain seuil, qui est precisemment la dimension de l'ensemble. Alors on a la definition suivante :

D'efinition 2.2.1 La dimension de Hausdorf f² d'un ensemble F est donn'ee par :

dimH(F) := sup{s : 7-1^s(F) = +8} = inf{s : 7-1^s(F) = 0}. (2.14)

On a donc

(

+8 si s < dimH(F)

7-1^s(F) = (2.15)

0 si s > dimH(F)

La dimension de Hausdorff satisfait les proprietes suivantes :

2. Que certains auteurs appellent «dimension de Hausdorff-Besicovitch».

H^s(F)

+8

0

		s

dimH(F)

FIGURE 2.1 --- Graphe de H^s(F) en fonction de s pour un ensemble F Th'eor`eme 2.2.2 (Propri'et'es de la dimension de Hausdorff)

1. A ? B = dimH(A) 6 dimH(B) ³. (Monotonie)

2. dimH (U Ai) = sup dimH(Ai). (Stabilit'e d'enombrable) 8

1. Si A ? 118ⁿ un ensemble d'enombrable, alors dimH(A) = 0.

2. Si A ? 118ⁿ un ensemble ouvert, alors dimH(A) = n.

3. dimH([0, 1]ⁿ) = n.

D'EMONSTRATION :

i=1

1. A ? B implique que H^s(A) 6 H^s(B). Donc on a dimH(A) = sup{s : H^s(A) = +8} 6 sup{s : H^s(B) = +8} = dimH(B).

8

2. Une cons'equence imm'ediate de la monotonie donne dimH ( U Ai I ?-. dimH(Ai), pour

i=1

tout 1 6 i 6 8. Alors

dimH		[ 8 i=1	Ai)> sup 16i68dimH(Ai).
Dans l'autre càot'e, si s > sup 16i68	dimH(Ai), alors H^s(Ai) = 0 pour tout 1 6 i 6 8. Donc

3. si A ? iRⁿ alors dimH(A) 6 n.

~

U Ai) = 0, qui donne i=1

dimH

[ 00 i=1

Ai)6 sup 16i600dimH(Ai).

00

3. Supposons A = {ai}. On a H⁰({ai}) = 1 et de plus H^s({ai}) = 0 pour tout s > 0

i=1

et i > 1. Ca implique que dimH({ai}) = 0 et par la partie 2 du theoreme, on a

dimH(A) = sup 16i600

dimH({ai}) = 0.

4. Comme A ? 118ⁿ, alors dimH(A) 6 n, et comme A contient une boule n-dimensionnelle (car tout ouvert de Illⁿ est un reunion denombrable de boules ouvertes n-dimensionnelles et bornees), alors dimH(A) > n. D'o`u l'egalite.

5. D'apres la partie 4 du Theoreme 2.1.10, on a Hⁿ([0, 1]ⁿ) = Lⁿ([0, 1]ⁿ) = 1 et par la partie 3 du màeme Theoreme, on a H^s([0, 1]ⁿ) = 0, ?s > n. Alors

dimH([0, 1]ⁿ) = inf{s : H^s([0, 1]ⁿ) = 0} = n.

El

Proposition 2.2.3 Soit F ? Illⁿ et soit f : F ? Ill^m une application lipschitzienne de constante c > 0. Alors, pour tout s > 0, on a

dimH(f(F)) 6 dimH(F) (2.16)

D'EMONSTRATION :

Si s > dimH(F), alors par la Proposition 2.1.5, on a H^s(f(F)) 6 c^sH^s(F) = 0 car H^s(F) = 0. Donc si H^s(f(F)) = 0, alors s > dimH(f(F)).

Ainsi, si s > 0 et s > dimH(F), alors s > dimH(f(F)). Donc dimH(f(F)) 6 dimH(F).

El

Corollaire 2.2.4 Soit f : F ? Ill^m une application bi-lipschitzienne, i.e.

? 0 < c1 6 c2, c1|x - y| 6 |f(x) - f(y)| 6 c2|x - y| (2.17)

Alors

dimH(f(F)) = dimH(F). (2.18)

Ce corollaire d'evoile une proprietefondamentale de la dimension de Hausdorff. «C'est l'invariance de la dimension de Hausdorff par des applications bi-lipschitziennes». Ainsi, deux ensembles de dimensions differentes ne peuvent avoir d'applications bi-lipschitziennes entre eux.

En general, la dimension donne certaines proprietes topologiques de l'ensemble. Par exemple, chaque ensemble de dimension plus petite que 1 est totalement discontinu comme le montre la proposition suivante.

Rappellons qu'un espace E est dit totalement discontinu si la composante connexe de chacun de ses points est l'ensemble reduit a ce point.

Proposition 2.2.5 Un ensemble F ? Rⁿ avec dimH(F) < 1 est totalement discontinu.

D'EMONSTRATION :

Soient x et y deux points distincts de F. Definissons une application f : Rⁿ ? [0, 1[ par f(z) = |z - x|. Comme f est contractante car |f(z) - f(w)| < |z - w|, on obtient par la Proposision 2.2.3 que dimH(f(F)) .<, dimH(F) < 1. Ainsi, f(F) est un sous-ensemble de R de mesure H¹ ou longueur nulle et a donc un complement dense. Choisissons r avec r ?/ f(F) et 0 < r < f(y), il s'ensuit que

F = {z ? F :|z - x| < r} ? {z ? F :|z - x| > r}

Donc F est la reunion de deux ouverts disjoints, l'un contenant x et l'autre y, donc x et y appartiennent a` deux composantes connexes differentes de F.

Th'eor`eme 2.2.6 (Dimension des graphes)

Soit f : Rⁿ ? R^m une fonction lipschitzienne et soit A une partie mesurable de Rⁿ. On note G(f, A) = {(x, f(x)) : x ? A} le graphe de f sur A. Alors

dimH(G(f, A)) = n si Lⁿ(A) > 0 (2.19)

Remarque 2.2.7

- De manière generale, la dimension de Hausdorff d'un graphe est superieure ou egale a` la dimension de l'espace de depart ; elle peut être strictement superieure pour des applications qui sont seulement Hàolderiennes (ou encore moins regulières) et pas Lipschitziennes.

Section 2.3

Calculs des dimensions

4. L1(C) = L^1(

T00 k=1

Ck) = lim k-+oo

L1 (Ck) = kli>m00 (23) = 0.

Nous allons a` present calculer les dimensions de Hausdorff de quelques ensembles simples et bien connus. Commençons par l'exemple utilisepar Hausdorff lui-même pour illustrer sa notion de dimension.

Exemple 2.3.1 L'ensemble triadique de Cantor :

L'ensemble triadique de Cantor est d'efinit comme la limite des ensembles ferm'es Ck, o`u C0 = [a, b] (prenant [a, b] = [0, 1]) et Ck est obtenu a` partir de _{Ck_1} en supprimant le tiers (ouvert) central de chacune des composantes connexes de _{Ck_1.} L'ensemble r'esultant est clairement de mesure de Lebesgue nulle ⁴, on peut se demander quelle est sa dimension.

FIGURE 2.2 - Premi`eres etapes de la construction de l'ensemble triadique de Cantor

Th'eor`eme 2.3.2

log 3.

Soit C l'ensemble triadique de Cantor. Alors dimHC ₌log 2 La dimension de Hausdorff est dejàplus difficile a` calculer. Par ailleurs, on peut faire un calcul heuristique simple en tirant parti de la construction auto-similaire de l'ensemble C et la proposition de changement d'echelle 2.1.4.

CALCUL HEURISTIQUE :

L'ensemble de Cantor se divise en sa partie gauche C_g = C n [0, 3 1] et sa partie droite Cd = Cn[²₃,1], toutes deux egales a` l'ensemble de Cantor multiplie par un facteur ₃¹. Comme C est reunion disjointe de ces deux parties, C = C_g ? Cd. On a pour tout s > 0

2

H⁸(C) = H⁸(C_g) + H⁸(Cd) = ₍₃ 1)8 H8 (C) + (31)8 H8 (C) = ₃₈H⁸ (C)

ce qui impose 3^s = 2, i.e. s =

log 2

log 3.

On peut le faire par un calcul rigoureux mais avec moins des conditions.

CALCUL :

Notons Ck la reunion des intervalles de longueur 3-^k, appeles intervalles fondamentaux,

lors de la ^k`eme etape dans la construction de C = _T8 Ck. Soit {Ui} le recouvrement de C

k=0

composede 2^k intervalles de longueur 3-^k. Comme C est compact (voir [4]), on peut toujours supposer que les Ui forment une collection finie de sous-intervalles fermes de [0, 1]. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

H^s(C) = lim k?8

1-k s k (C) = lim á(s) · 2^k · (- 2 ) . ? k8

k

Apr`es rearrangement des termes, H^s(C) = á(s) lim . Or, cette limite tend vers 0

2s k?k8 ( 2 3s

2 8 pour verge 1, et elle 32s

lorsque ₃ 1lle di a l'infini > 1. Autrement dit, elle se situe entre 0

et +8 lorsque 2

= 1, c'est-`a-dire pour s = log 2 Donc, la dimension de Hausdorff de

3s log 3

log 3.

Remarque 2.3.3

- La methode de calcul «heuristique» utilisedans le Theor`eme 2.3.2 donne la vraie reponse pour la dimension de plusieurs ensembles auto-similaire.

l'ensemble triadique de Cantor est log 2

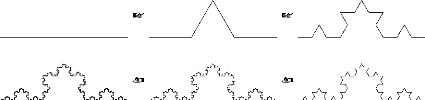
Exemple 2.3.4 La courbe de von Koch :

On obtient la courbe de Koch par it'erations a` partir du segment [0, 1] en remplacant le tiers central par un triangle 'equilat'eral de cot'e le tiers qu'on enl`eve, puis en recommencant cette op'eration a` l'infini sur chaque segment de la figure obtenue.

Th'eor`eme 2.3.5 Soit K la courbe de Koch. Alors dimHK = log 4

log 3.

CALCUL HEURISTIQUE :

La courbe de von Koch se divise en quatre partie egaux a` la courbe de von Koch multiplie₁ par un facteur ₃. On a pour tout s > 0

H^s(K) = 4 · H^s(¹₃K) = 4 Hs(K)

3s

11 Z'

FIGURE 2.3 - Premi`eres etapes de la construction de la courbe de von Koch ce qui impose 3^s = 4, i.e. s = log 4

log 3.

CALCUL :

Soit {UiI le recouvrement de K composede 4^k intervalles de longueur 3-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(K) = lim k?8

7-1^s3-k (K) = lim á(s) · 4k (32k) s = lim á(s) ( 38) 4 koo k--oo 2^8 ?

4 4

Or, cette limite tend vers 0 lorsque < 1, et elle diverge a l'infini pour > 1. Autrement

3s 3s

dit, elle se situe entre 0 et +Do lorsque 4 = 1, c'est-`a-dire pour s = log 4. Donc, la dimension

3s log 3

log 3^.

Exemple 2.3.6 La courbe de Koch quadratique (type 1) :

On obtient La courbe de Koch quadratique (type 1) par it'erations a` partir du segment [0, 1] en remplacant le tiers central par trois cot'es d'un carr'e, puis en recommencant cette op'eration a` l'infini sur chaque segment de la figure obtenue.

de Hausdorff de la courbe de von Koch est log 4

Th'eor`eme 2.3.7

Soit K1 la courbe de Koch quadratique de type 1. Alors dimHK1 = log 5

log 3.

CALCUL HEURISTIQUE :

La courbe de Koch quadratique de type 1 se divise en cinq parties egales a` la courbe de 1

Koch quadratique multipliepar un facteur ₃. On a pour tout s > 0

5

7-1^s(K1) = 5
· 7-1^s(₃K1) = _3s 7-1^s(K1

11 Z'

FIGURE 2.4 - Premi`eres 'etapes de la construction de la courbe de Koch quadratique 1

ce qui impose 3^s = 5, i.e. s =	log 5
	log 3.

CALCUL :

Soit {UiI le recouvrement de K1 compos'e de 5^k intervalles de longueur 3-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(K1) = lim k?8

k 7-1^s-k (K1) = lim á(s) · 5k (32k )s = li k-- 28 m á(s) ( 38) 5 k?8 oo

5 8 pour < 35s

Or, cette limite tend vers 0 lorsque ₃ 1 et elle diverge a l'infini > 1. Autrement

dit, 5

elle se situe entre 0 et +cc lorsque = 1, c'est-`a-dire pour s = log 5 Donc, la dimension

3s log 3

log 3^.

Exemple 2.3.8 La courbe de Koch quadratique (type 2) :

On obtient la courbe de Koch quadratique (type 2) par iterations a` partir du segment [0, 1]
en le partageant sur huit segments de màeme longueur et en joignant les points suivants

de Hausdorff de la courbe de Koch quadratique de type 1 est log 5

consecutivement :

p0=(0,0)	p1=(0.25,0)	p2=(0.25,0.25)
p3=(0.5,0.25)	p4=(0.5,0)	p5=(0.5,-0.25)
p6=(0.75,-0.25)	p7=(0.75,0)	p8=(1,0),

puis en recommencant cette operation a` l'infini sur chaque segment de la figure obtenue.

11 Z'

FiGuRE 2.5 - Premi`eres etapes de la construction de la courbe de Koch quadratique 2 Th'eor`eme 2.3.9

log 4 2

Soit K2 la courbe de Koch de type 2. Alors dimHK2 ₌log 8 3 CALCuL HEuRisTiQuE :

La courbe de Koch quadratique de type 2 se divise en huit partie egales a` la courbe de

1

Koch quadratique multipliepar un facteur ₄. Pour tout s > 0

7-1^s(K2) log 8	= =	8 · 3 2	1 7-1^s(4	=4s^87-1^s(K1)
impose 4^s 8, i.e. ce qui = s = log 4

CALCuL :

Soit {UiI le recouvrement de K1 composede 8^k intervalles de longueur 4-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(K2) = lim 7-1^s4-k(K2) = lim k?8 k?8

8k ( 4-k s ..m á(s) ( 8 )k á(s) · = 11 2 k?8 2^s 4^s)

8 8

4s

Or, cette limite tend vers 0 lorsque 4s < 1 et elle diverge a` l'infini pour > 1. Autrement

8

dit, elle se situe entre 0 et +Do lorsque = 1, c'est-`a-dire pour s = log 8. Donc, la dimension

4s log 4

de Hausdorff de la courbe de Koch quadratique de type 2 est 3.

2

Exemple 2.3.10 Le flocon de von Koch :

Le flocon de Koch s'obtient de la même facon que la courbe de von Koch 2.3.4, en partant d'un triangle equilateral au lieu d'un segment de droite, et en effectuant les modifications en orientant les triangles vers l'exterieur.

FIGURE 2.6 - Premi`eres étapes de la construction d'un flocon de von Koch

Th'eor`eme 2.3.11

Soit FK un flocon de von Koch. Alors dimHF K ₌log 4

log 3.

CALCUL :

Comme le flocon de Koch est une réunion finie des courbes de von Koch FK =

3

U Ki et

i=1

par la propriété2 du Théor`eme 2.2.2 on a :

3

log 4

dimH(FK) = dimH U Ki = sup dimH(Ki) = dimH(K) = log 3

15i53 i=1

Exemple 2.3.12 Le triangle de Sierpinski :

On obtient le triangle de Sierpinski par iterations a` partir d'un triangle equilateral duquel on enl`eve le triangle central, i.e. celui dont les sommets sont les milieux des cotes du triangle de depart, et on recommence cette operation a` l'infini sur chaque triangle restant.

FIGURE 2.7 - Premi`eres étapes de la construction d'un triangle de Sierpinski

Th'eor`eme 2.3.13

log 2.

Soit S le triangle de Sierpinski. Alors dimHS ₌log 3

CALCUL :

On voit que le recouvrement optimal utilise des boules de diam`etre 8 = 2 · ^v3. Notons

2k

que 8 tend vers 0 lorsque k tend vers l'infini. Dans chaque cas, on utilise 3^k boules. Ainsi, en

supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve

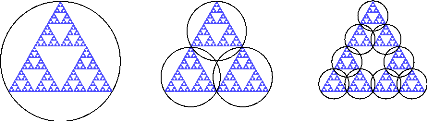
FIGURE 2.8 - Recouvrements d'un triangle de Sierpinski

H^s(S) = lim ä-.0

H^sä(S) = lim k-.00

s v3 á(s) · 3k 2k 3 = V3 · a(s) ( 2s)

Or, cette limite tend vers 0 lorsque 3 3 < 1 et elle diverge a` l'infini pour > 1. Autrement

2s 2s

dit, elle se situe entre 0 et +8 lorsque 3 = 1, c'est-`a-dire pour s = log 3 Donc, la dimension

2s log 2

log 2.

Exemple 2.3.14 Le tapis de Sierpinski :

L'id'ee de l'ensemble de Cantor est de couper un segment en parties 'egales, d'enlever une de ces parties, et de recommencer. C'est cette id'ee qui pr'eside aux tapis de Sierpinski que nous allons examiner.

de Hausdorff du triangle de Sieprinski est log 3

Th'eor`eme 2.3.15

Soit S le tapis de Sierpinski. Alors dimHS = log 8log 3.

FIGURE 2.9 - Premieres étapes de la construction d'un tapis de Sierpinski

Voir l'exemple prochain pour le calcul concernant cet exemple.

Exemple 2.3.16 L'éponge de Menger :

On obtient l'éponge de Menger par itérations a` partir d'un cube qu'on découpe en 27 cubes de cotés le tiers du premier, puis on enlêve le petit cube central et les 6 cubes ayant une face commune avec lui, on recommence cette opération a` l'infini sur chaque cube restant. Avec d'autre maniêre si chaque face de l'éponge de Menger est un tapis de Sierpinski.

Théorème 2.3.17

log 20

Soit M l'éponge de Menger. Alors dimHM =

FIGURE 2.10 - Premieres étapes de la construction de l'éponge de Menger

log 3 .

D'une maniere générale, McMullen, est dans [22], démontre que la dimension de Hausdorff d'une carpette de Sierpinski généraliséR qui définie par

( 00X ! }

\' 00

xk yk

R = nk , : (xk, yk) ? A (2.20)

_mk

k=1 k=1

o`u A c {(a, b) : 0 6 a < n, 0 6 b < m, n m} telle que dimH(R) = logm

m-1 P j=0

) tlogn m o`u j

log r

tj est le nombre de i tels que (i, j) ? A. Si n = m, on a dimH(R) = avec r = |A|.

log n

11 Z'

Pour l'exemple 2.3.14, on a n = m = 3 et r = 8 et pour l'exemple 2.3.16 on prend n = m = 3 et r = 20.

Exemple 2.3.18 La courbe de Peano :

On obtient la courbe de Peano par it'erations a` partir du segment [0,1] en le partageant sur neuf segments de màeme longueur et en joignant les points suivants cons'ecutivement :

p0 = (0,0) p1 = (¹₃,0) p2 = (¹₃,¹₃)

p3 = (²₃,¹₃) p4 = (²₃, 0) p5 _=(13, 0)

p6 = (3¹, 3) p7 ₌(2_{3, 3})

p8 = (²₃, 0)

p9 = (1, 0).

puis en recommencant cette op'eration a` l'infini sur chaque segment de la figure obtenue.

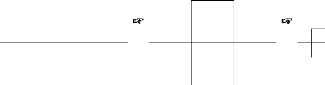
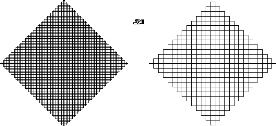
FIGURE 2.11 - Premi`eres étapes de la construction de la courbe de Peano

Th'eor`eme 2.3.19 log 9 Soit P la courbe de Peano. Alors dimHP^=log 3

= 2.

CALCUL :

De même facons, soit {Ui} le recouvrement de P compos'e de 9^k intervalles de longueur 3-^k. Ainsi, en supposant que ce recouvrement est celui pour lequel l'infinimum est atteint, on trouve :

7-1^s(P) = lim ä?0

7-1^sä(P) = lim k?8

^k á(s) . 9k (3 k) = lim á(s) ( 9 ) . 2 k?8 2s 3s

Cette limite se situe entre 0 et +oo lorsque 9 = 1, c'est-h-dire pour s = log 9. Donc, la

3s log 3

dimension de Hausdorff de la courbe de Peano est 2.

CHAPITRE 3

DIMENSION TOPOLOGIQUE

«Dimension nf.(latin dimensio) 'Etendue mesurable d'un corps dans tel ou tel sens»

-Larousse 2003-

Pour définir la dimension topologique, nous avons besoin de rappeler quelques notions sur les espaces topologiques.

Un espace topologique E est dit T0-espace si pour tout x, y E E, x =6 y, il existe un ouvert contenant uniquement un des deux points et pas l'autre.

Il est dit T1-espace si pour tout x, y E E, x =6 y il existe deux ouverts U et V tels que x E U, y E/ U, x E/ V et y E V . Autrement dit, si pour tout x E E, on a {x} est un fermé. Il est clair que tout T1-espace est un T0-espace.

Un espace topologique E est dit T2-espace ou espace de Hausdorff¹ si pour tout couple (x, y) de points distincts, il existe deux ouverts disjoints U et V contenant respectivement x et y. Il est clair que tout T2-espace est un T1-espace.

De plus, E est dit regulier si, pour tout x E E et pour tout ferméF C E tel que x E/ F, il existe deux ouverts U et V tels que x E U, F C V et U n V = 0. S'il est T1- espace et régulier, on dit que E est T3-espace. Il est clair que tout T3-espace est un T2-espace.

Un espace topologique E est dit compl`etement regulier si, pour tout x E E et pour tout ferméF C E tel que x E/ F, il existe une fonction continue f : E -+ [0,1] telle que

1. Que certains auteurs appellent «espace séparé».

1 1

f (x) = 0 et f (y) = 1 pour tout y E F. Comme U = f-1([0, ₂ [) et V = f -¹(] ₂, 1]) sont deux

ouverts de E et x E U, F C V avec UnV = 0, tout espace completement regulier est regulier.

On dit que E est T₃1 ₂-espace ou espace de Tychonoff s'il est T1-espace et completement regulier.

Proposition 3.0.20 Soit E un espace topologique. On a alors :

T₃ 1 2 = T3 = T2 = T1 = T0.

Soit E un espace topologique. On appelle recouvrement ouvert de E une famille (Oi)i?I de parties ouvertes de E telles que E = Ui?IOi. ^Si (Oi)i?I et (O⁰j)j?J sont des recouvrements de E, on dit que (O _j)j?J est un rafinement de _(Oi)i?I si

Vj E J,?i E I, tel que O⁰ _jC Oi (3.1)

Un recouverement _(Oi)i?J de E est dit sous-recouvrement d'un autre recouvrement (Oi)i?I de E si J C I. En particulier, chaque sous-recouvrement est un rafinement.

Un espace topologique E est dit compact si E est un espace de Hausdorff et de tout recouvrement ouvert de E on peut extraire un sous-recouvrement fini.

Un ensemble A d'un espace topologique E est dit fonctionnellement ferm'e si A = f-¹(0) pour une certaine fonction continue f : E [0, 1]. Clairement, tout ensemble fonctionnellement fermeest un ferme.

Le complementaire d'un ensemble fonctionnellement fermede E s'appele fonctionnellement ouvert. Clairement, tout ensemble fonctionnellement ouvert est un ouvert. La reunion denombrable et l'intersection finie d'ensembles fonctionnellement ouverts sont des fonctionnellement ouverts. (voir [7] pour plus de details)

On appelle recouvrement fonctionnellement ouvert (resp. ferm'e) d'un espace topologique E toute famille de fonctionnellement ouverts (resp. fermes) de E qui est un recouvrement de E.

Rappelons qu'une base d'un espace topologique E est une famille d'ouverts B de E tel que pour tout ouvert U de E, il existe une sous famille B' de B tel que U = U B.

B?B⁰

? Tout espace z'ero-dimensionnel est un T_q i -espace

Un espace topologique E est dit zéro-dimensionnel si E est un T_i-espace non vide et admet une base de parties a` la fois ouvertes et fermées (clopen en anglais).

Un espace topologique E est dit fortement zéro-dimensionnel s'il est de Tychonoff non vide et tout recouvrement fini fonctionnellement ouvert {Ui}16i6k de E contient un rafinement ouvert fini tel que vinVj = Ø si i L j. Il est claire que le rafinement m

contient des parties a` la fois ouvertes et fermées. On conclut que tout espce fortement zérodimensionnel est un espace zéro-dimensionnel.

Soit F une famille de parties d'un ensemble E. Un ordre d'une famille F est le plus grand entier n tel que la famille F contient n+1 ensembles avec intersection non vide ou «+8» s'il n'existe pas d'entier. Par covention, une famille est d'ordre -1 si elle est vide. Il est clair qu'elle est d'ordre 0 si elle contient des ensembles deux a` deux dijoints. L'ordre d'une famille F est notépar ordF.

D'efinition 3.0.21 (Dimension topologique) Soit E un espace de Tychonoff et soit n un entier > -1, on dit que :

? dimTE = -1 si E = Ø.

? dimTE = 0 si E est un espace fortement zéro-dimensionnel.

? dimTE 6 n si tout recouvrement fini fonctionnellement ouvert O de E admet un rafinement fini fonctionnellement ouvert O' avec ord O' 6 n.

? dimTE = n si dimTE 6 n et l'inégalitédimTE 6 n - 1 n'est pas vérifié. ? dimTE = +8 si l'inégalitédimTE 6 n n'est pas vérifiépour tout n.

Le nombre dimTE s'appelle dimension topologique de Cech-Lebesgue de l'espace E.

Remarque 3.0.22

- Le nombre dimTE est un entier > -1.

- Si E et F deux espaces homéomorphe, alors dimTE = dimTF.

- Si M un sous-espace de E alors dimTM 6 dimTE.(voir [7] pour plus de détails)

Nous nous restreindrons dans la suite de ce document a` l'étude de la dimension topologique sur les espaces métrisables seulement. On peut alors définir la dimension topologique de la facons suivante :

BELLAL ? LEs FRAcTALs ET LEuR GgoMgTRiE ? BENTERKI

D'efinition 3.0.23 Soit E un espace m'etrisable a` base d'enombrable. On d'efinit la dimension topologique de E par r'ecurrence :

? dimTE = --1 si E = O.

? dimTE = 0 si sa topologie admet une base de parties a` la fois ouvertes et ferm'ees, soit encore une base de parties a` fronti`ere vide (ou de dimension -1). On dit aussi que E est totalement discontinu.

? dimTE .<, n si sa topologie admet une base d'ouverts a` fronti`ere de dimension au plus n -- 1.

? dimTE = n s'il est de dimension au plus n mais n'est pas de dimension au plus n -- 1. ? dimTE = +oo s'il n'existe pas de n tel qu'il soit de dimension au plus n.

Exemple 3.0.24

? Les points sont de dimension topologique 0.

? Les courbes sont de dimensions topologique 1.

? La dimension topologique d'une surface est 2.

? La dimension topologique d'un volume est 3.

Exemple 3.0.25 Poussi`ere de Cantor :

La dimension topologique de poussi`ere de Cantor est 0.

FIGURE 3.1 - Premières étapes de la construction du Poussière de Cantor

CHAPITRE 4

LA G'EOM'ETRIE DES FRACTALS

«The most beautiful thing we can experience is the
mysterious. It is the source of all true art and science.»
-Albert Einstein-

Benoit Mandelbrot (1982) a défini des objets spéciaux qui s'appelent des fractals par «A subset of Illⁿ is a fractal if its topological dimension is less than its fractal dimension ¹». Apr`es cette phrase, nous avons la définition suivante.

D'efinition 4.0.26 Un fractal est un objet dont la dimension de Hausdorff est strictement supérieure a` la dimension topologique.

Exemple 4.0.27 - Comme la dimension topologique du poussi`ere de Cantor de l'exemple

3.0.25 est 0 et sa dimension de Hausdorff est 1 (voir [9, p. 34]), alors la poussi`ere de Cantor est un objet fractal.

- Les objets d'efinis dans la section § 2.3 sont tous des fractals.

Remarque 4.0.28 Un fractal est un objet qui a les deux propriétés suivantes :

air Irrégulier a` toutes les échelles (i.e. si, même en le regardant de plus en plus pr`es (par exemple avec un zoom), il apparaàýt toujours irrégulier (non lisse))

air Auto-similaire (i.e. s'il se décompose en un nombre fini de parties, toutes ces parties sont similaires a` l'objet principale).

1. Elle signifie la dimension de Hausdorff, et malgrél'existence de plusieures dimensions (Minkowski, packing, ...), la dimension de Hausdorff possède les bonnes propriétés mathématiques et exprime le mieux possible la dimension fractale recherchée pour beaucoup de sous-ensembles intéressants.

Exemple 4.0.29

1

1. Le triangle de Sierpenski T contient trois copies similaires a` T avec un facteur ₂.

2. La courbe de von Koch K contient quatre copies similaires a` K avec un facteur 1

3.

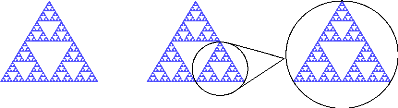
FiGuRE 4.1 - Exemple d'auto-similarit'e
On peut dire alors qu'un fractal est un objet dont chaque 'el'ement est aussi un objet fractal.

Section 4.1

Syst`eme de fonctions it'er'ees

Les systemes de fonctions it'er'ees (IFS) constituent une facon de construire des fractales. Leur principe repose sur le th'eoreme du point fixe dans les espaces m'etriques. Quelques rappels sur les espaces m'etriques sont maintenant donn'es.

D'efinition 4.1.1 Soit (E, d) un espace métrique. Une application S : E --+ E est dite contraction sur E s'il existe un nombre c avec 0 < c < 1, tel que :

d(S(x), S(y)) .<, c
· d(x, y), Vx, y E E (4.1)

Le nombre c est appeléfacteur de contraction de S. Une contraction est donc une application continue.

Si on a l'égalitéd(S(x), S(y)) = c
· d(x, y), Vx, y E E. Alors S transforme les ensembles en des ensembles similaires et est appellée une similarit'e.

Soit _(xn)n?N une suite de points d'un espace metrique (E, d). Elle est dite suite de Cauchy

si

?å > 0, ?N_E E N, ?n, m > N_E : d(x_n, x_m) < å. (4.2)

Dans un espace metrique (E, d) toute suite convergente est une suite de Cauchy, mais la reciproque n'est pas vraie en general. Pour cela on definit un espace complet comme etant un espace metrique (E, d) tel que toute suite de Cauchy dans E est convergente dans E.

On definit maintenant une metrique sur les sous-ensembles de E. On note K(E) l'ensemble de tous les sous-ensembles compacts non vides de E. Pour a E E, et A, B E K(E), on definit la distance entre a et B par

d(a, B) := min{d(a, b) : b E B} (4.3)

et la distance entre A et B par

06 dist(A, B) =6 dist(B, A).

dist(A, B) := max{d(a, B) : a E A} (4.4)

Notons que dist ne definit pas une distance sur K(E). Dans la suite du document, on notera dist par d.

Lemme 4.1.2 Soient (A, B, C) E K³(E) alors

d(A U B,C) = max{d(A, C), d(B, C)} (4.5)

D'EMONSTRATION :

d(A U B, C) = max{d(x, C) : x EAU B}

= max{max{d(x, C) : x E A}, max{d(x, C) : x E B}} = max{d(A, C), d(B,C)}.

On appelle 8-voisinage d'un ensemble A E K(E) l'ensemble des points a` distance inferieure a` 8 > 0 de A, il est ^note

Vä(A) := {x E E : ?a E A, d(x, a) < 8} (4.6)

BELLAL i' LES FRACTALS ET LEUR G'EOM'ETRIE ' BENTERKI

D'efinition 4.1.3 On munit K(E) d'une structure d'espace metrique en definissant la distance de Hausdorff dH(A, B) de deux sous-ensembles A et B de K(E) comme etant le plus petit nombre 8 tel que le 8-voisinage de A contient B et vice-versa :

dH(A, B) := inf{8 > 0,A ? Vä(B) et B ? Vä(A)} (4.7)

On peut aisement verifier que

dH(A, B) := max{d(A, B), d(B, A)} (4.8)

La distance de Hausdorff dH verifie les proprietes suivantes. Pour tous A, B, C ? K(E), on a OO dH(A, B) > 0 avec egalitesi, et seulement si, A = B,

® dH(A, B) = dH(B, A),

(c) dH(A, B) 6 dH(A, C) + dH(C, B)

Lemme 4.1.4 Soient (A, B, C, D) ? K⁴(E) alors

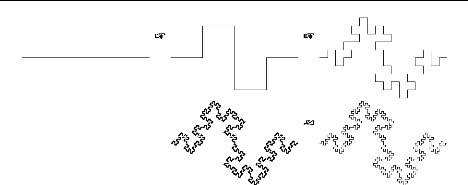
dH(A U B,C U D) 6 max{dH(A,C), dH(B,D)}. (4.9)

D'EMONSTRATION :

dH(A U B,C U D) = max{d(A U B,C U D),d(C U D, A U B)}

= max{max{d(A, C U D), d(B,C U D)}, max{d(C, A U B), d(D, A U B)}} 6 max{max{d(A, C), d(B, D)}, max{d(C, A), d(D, B)}}

= max{dH(A, _C), ^dH(B, D)}.

111

D'efinition 4.1.5 Soit S ? E un sous-ensemble de l'espace metrique (E, d). La partie S est dite precompacte si, pour tout å > 0, il existe un ensemble fini de points {yi}ⁿi=1 ? S tel que, pour tout x ? S, on a d(x, yi) < å, pour un certain yi ? {yi}ni=1.

Th'eor`eme 4.1.6

Soit ? E o`u (E, d) est un espace metrique complet. Alors, a est compact si et seulement si a est fermeet precompact.

Lemme 4.1.7 Soit (E, d) un espace métrique, {An}⁸n=1 une suite de Cauchy de points de K(E), et soit {nj}8 _j=1une suite d'entiers telle que ni < nj, ?i < j. S'il existe une suite de Cauchy {xnj ? Anj} dans (E, d), alors il existe une suite de Cauchy {ex_n ? An}⁸n=1 telle que x_n = xnj, ?j ? N.

D'EMONSTRATION :

Construisons la suite {ex_n ? An}⁸n=1 de la facon suivante :

- Pour chaque n ? {1, ... ,n1}, prenons ex_n ? {x ? A_n : d(x, xn1) = d(x_n1, A_n)}. Ce point existe car A_n est compact.

- De màeme, pour chaque j ? {1, 2, ...} et chaque n ? {nj + 1, ... ,nj+1}, prenons ex_n ? {x ? A_n : d(x, xnj+1) = d(xnj+1, An)}.

Montrons que cette suite a les proprietes souhaitees.

- Par construction, ex_n ? A_n.

- De plus, ^exnj = xnj. En effet, pour n1, on a choisi ^exn1 ? {x ? An1 : d(x,xn1) = d(xn1,An1)}. ^Mais, d(xn1,An1) = 0 car xn1 ? An1 et d(x,x_n1) = 0 ? x = x_n1. D'o`u ^exn1 =xn1 et de màeme ^exnj+1 = xnj+1.

Enfin, {ex_n ? An}⁸n=1 est une suite de Cauchy. En effet,

?å > 0, ?N1 : nj,nk > N1 d(xnk,xnj) < å/3

?å > 0, ?N2 : m, n > N2 dH(A_m, A_n) < å/3

Soit N = max{N1, N2} et m,n > N avec nj < n < nj+1, N < nk < m < nk+1 alors

d(ex_n, ex_m) = d(ex_n, _xnj+1) + d(xnj+1, xnk+1) +d(xnk+1, exm)

= d(xnj+1, A_n) + å/3 + _d(xnk+1, A_m)

= d(Anj+1, A_n) + å/3 + d(Ank+1, Am)

= dH(Anj+1, A_n) + å/3 + dH(Ank+1, Am)

= å 111

Proposition 4.1.8 Si (E, d) est un espace métrique complet, alors (K(E), dH) est aussi un espace métrique complet.

D'EMONSTRATION :

Soit {Xn} une suite de Cauchy dans K(E). Alors il existe une suite ån ? 0 et un entier N ? N tels que ?m, n > N, dH(Xm, Xn) < ån donc ?m, n > N, Xm ? Vån(Xn).

kv Prenant ån = 1/2n

On pose X = {x ? E : ?(x_n) ? X_n et x est valeur d'adh'erence de (x_n)}. Montrons que X ? K(E) i.e. que X est compact et non-vide.

On va commencer par montrer que X est ferm'e. Soient y ? X et (y_n) une suite de X tendant vers y. Pour chaque entier m, y_m est limite d'une suite (x_n) tel que x_n ? X_n. On choisit maintenant pour chaque y_m un point x_nm ? X_nm de la suite (x_n) correspondante pour construire une sous-suite _(xnm) telle que d(x_nm, y_m) ? 0 quand m ? Do. Pour satisfaire a` la d'efinition de X, on d'efinit une suite (xk) a` partir de la sous-suite _(xnm) o`u l'on choisit xk quelconque dans Xk si k n'appartient pas a` l'ensemble des n_m. Alors

dH(xnm, y) C dH(xnm, ym) | ·Nor · } ?0 m?8

+ dH(ym, y) | {z } ?0 m?8

.

Donc y est valeur d'adh'erence de (xk) donc y ? X . Ainsi X ? X donc X est ferm'e. De plus, comme X est ferm'e dans E qui est complet, X est complet.

Montrons que X est pr'ecompact. Soit å > 0. Il existe clairement N tel que X ? V_å(XN). Pour tout y ? X, il existe x_n ? XN tel que d(y, x_n) < å. Pour n > N, comme X_n est compact, on peut le recouvrir par un nombre fini de boules B(zi, å) de centres zi ? X_n et de rayons å. Les boules de centres zi et de rayons 2å recouvrent donc X. On supprime les zi inutiles, ceux pour lesquels B(zi, 2å) n X = Ø.

Il reste les zi pour, i ? {1, . . . , M}. On d'etermine alors, pour tout i ? {1, . . . , M}, un 'el'ement z0 i de X tel que d(zi, z⁰_i) < 2å (car on a supprim'e les zi inutiles). Les boules B(z⁰_i, 4å) forment alors un recouvrement fini de X qui est donc pr'ecompact.

Il convient de montrer que X est non-vide, ce qui sera fait en même temps que de montrer la convergence des X_n vers X au sens de la distance de Hausdorff. Il faut voir que pour tout å > 0 il existe un N tel que pour n > N, on ait X ? V_å(X_n) ce qui a d'ejà'et'e vu, et X_n ? V_å(X). Pour ce faire, on se fixe x ? X_n avec n tel que å_n < å. On considère alors

n0 > n	t.q	ån0 < å/2^1	et	xn0 ? Xn0 : d(x,xn0) < å/2^1
n1 > n0	t.q	ån1 < å/2^2	et	xn1 ? Xn1 : d(x, xn1) < å/2^2
	...
np > np-1	t.q	ånp < å/2p^+1	et	xnp ? Xnp : d(x, xnp) < å/2p^+1

...

La suite des _xnp est de Cauchy dans (E, d) qu'il est complet donc elle converge vers un
certain y ? X car y est (la seule) valeur d'adh'erence de la suite _(xnp) ^o`u xn_p ? X_np ; on

peut a` nouveau completer la suite des x_n pour n_p 6 n 6 n_p+1, il suffit de prendre un point quelconque de X_n.

En sommant les distances, on obtient que d(x, y) < 6 donc x ? V_å(X), par suite on a l'inclusion X_n ? V_å(X). X est non vide, car pour tout 6 > 0, il existe X_n ? V_å(X). La suite de Cauchy {X_n} converge donc vers X ? K(E) au sens de Hausdorff, dH(X_n, X) ? 0 quand n ? 8, donc (K(E), dH) est complet.

111

Lemme 4.1.9 Soit S : E -? E une contraction sur l'espace m'etrique (E, d), alors S renvoie K(E) dans lui-màeme.

D'EMONSTRATION :

Soit F un sous-ensemble compact non-vide de E, alors F ? K(E). 'Evidemment, S(F) = {S(x) : x ? F} est non-vide. Montrons que S(F) est compact. Prenons une suite de points {yn = S(xn)}⁸_n=1 infinie dans S(F). Alors, on a une suite de points {xn}⁸n=1 infinie dans F. Mais F est compact alors il existe une sous-suite {xnk}⁸k=1 convergeant vers un element disons x0 de F. Par continuitede la contraction, la sous-suite {ynk = S(xnk)}⁸k=1 devra converger vers S(x0) ? S(F).

111

Lemme 4.1.10 Soit S : E -? E une contraction de facteur c sur l'espace m'etrique (E, d), alors la transformation S : K(E) ? K(E) d'efinie par

S(B) = {S(x) : x ? B}, ?B ? K(E) (4.10)

est une contraction sur (K(E), dH) de facteur c.

D'EMONSTRATION :

Soit B, C ? K(E) alors,

dH(S(B), S(C)) = max{d(S(B), S(C)), d(S(C), S(B))} 6 max{c · d(B, C), c · d(C, B)}

6 c · max{d(B, C), d(C, B)}

= c · dH(B, C).

El

Lemme 4.1.11 Soit (E, d) un espace m'etrique et soit {S_n : n = 1, 2, ... , N} un ensemble de contractions sur (K(E), _d7i) dont le facteur de contraction est c_n pour chaque n. Si on d'efinit S : K(E) -? K(E) par

N

S(B) = U S_n(B) (4.11)

n=1

alors S est une contraction sur K(E) de facteur c = max{c_n : n = 1, 2, ... , N}.

D'EMONSTRATION :

Demontrons le lemme pour N = 2. Soit B, C ? K(E) alors,

d7i(S(B), S(C)) = d7i(S1(B) ? S2(B), S1(C) ? S2(C))

6 max{d7i(S1(B), S1(C)), d7i(S2(B), S2(C))} 6 max{c1d7i(B, C), c2d7i(B, C)}

= c · d7i(B, C), c = max{c1, c2}

Le cas N > 2 se montre par induction.

III

Th'eor`eme 4.1.12 (Th'eor`eme de point fixe de Banach)

Soit (E, d) un espace m'etrique complet et soit S : E -? E une application contractante. Alors S a un unique point fixe xS ? E, c-`a-d : S(xS) = xS, et de plus, pour tout x ?

E, lim n-+oo

S^n(x) = xS o`u S^n(x) = S(S(· · · S -v.- n fois

(x)), et on a

1

6

1 - c

d(x, S(x))

_cn

d(Sⁿ (x), xS) 6 1 - _cd(S(x), x). (4.12)

D'EMONSTRATION :

Soit S contractante de facteur de contraction c. Soit x ? E. Soient n,m deux entiers. Alors

d(Sⁿ(x), S^m(x)) 6 c · d(S^n-1(x), S^m-1(x)) 6 c^min{n,m}d(x, S|^m-n|(x))

Or, d'apres l'inegalitetriangulaire,

d(x, S^k(x)) 6 d(x, S(x)) + d(S(x), S²(x)) + · · · + d(S^k-1(x), S^k(x)) 6 (1 + c + c² + · · · + c^k-1)d(x, S(x))

Il vient alors

d(Sⁿ(x), S^m(x)) 6 cmin{n,m} 1 1- _cd(x, S(x)) (4.13)

Le membre de droite de cette inegalitepeut àetre rendu aussi petit que l'on veut, a` condition de
choisir n,m suffisamment grands. La suite (Sⁿ(x))_n?N est donc de Cauchy. Comme l'espace

est complet, cette suite converge dans E vers un point xS = lim n?8 contractante, elle est continue, de sorte que		S^n(x). Comme S est
S(xS) = S( lim S^n(x)) = lim n?8 n?8	S^n+1(x) = xS

De plus, xS est unique. En effet, si yS est un autre point fixe, alors d(xS, yS) = d(S(xS), S(yS)) 6 c · d(xS, yS), et donc d(xS, yS) 6 0 donc d(xS, yS) = 0 et par suite xS = yS

cⁿ

- _cd(S (x), x).

pour (4.13) avec m = 0 on trouve d(Sⁿ(x), xS) 6

¹

111

D'efinition 4.1.13 Un systeme de fonctions iterees ou IFS consiste en un espace metrique complet (E, d) et un ensemble fini de contractions S_n : E ? E de facteurs c_n pour n = {1, 2, ... , N}. On note l'IFS par {S_n, n = 1, 2, ... , N} et son facteur de contraction est c = max{c1 , c2, . . . ,cN}.

Th'eor`eme 4.1.14 (Hutchinson)

Soit {S_n, n = 1, 2, ... , N} un IFS dans (E, d) d'un facteur de contraction c = max{c1, c2, . . . , _cid -. La transformation S : K(E) ? K(E) definie par :

N

S(B) = U S_n(B), ?B ? K(E) (4.14)

n=1

est une contraction sur l'espace (K(E), 4.1) de facteur c. Son unique point fixe qui s'appelle l'attracteur A ? K(E) est

N

A = S(A) = U S_n(A) (4.15)

n=1

est donnepar

A = lim k?8

S^k(B), ?B ? K(E) (4.16)

et

cⁿ

dH(Sⁿ(B), A) 6 _{1 c}dH(S(B), B). (4.17)

En particulier, pour n = 0, on obtient

d7i(B, A) .<, 1 1 _cd7i(S(B), B). (4.18)

D'EMONSTRATION :

La preuve de ce théorème est immédiate par le Lemme 4.1.11, et théorème de point fixe 4.1.12 et puisque K(E) est complet.

Exemple 4.1.15 Ensemble classique de Cantor :

Soit l'espace m'etrique (R,| · |). Consid'erons l'IFS {S1, S2} o`u

1 1 2

3

S1(x) = ₃x, S2(x) = ₃x + , ?x ? IR

1

1. V'erifions que c'est un IFS et que son facteur de contraction est c = 3 .

pour cela il faut avoir :

- Un espace m'etrique complet. On a IR est un espace m'etrique complet muni de la distance usuelle.

- Un nombre fini de contractions. Ici ce sont : 1

0 S1(x) = ₃, Soient x, y ? IR, alors,

d(S1(x), S1(y)) = |x 3 - ^Y₃|

=

1 3.

|x - y|

= ¹₃.d(x, y)

1

1

® S2 = 3

2

et S1 est en effet une contraction de facteur c1 = ₃.

x +

₃, soient x, y ? IR alors

d(S2(x), S3(y))	= =			^2
		^23 |^x3 + - 1 3. |x - y|	^Y3 -	3|

= ¹₃.d(x, y)

donc S2 est une contraction de facteur c2 = ₃, alors un facteur de contraction

1

c = max{c1, c2} = max{¹ 3, ¹ ₃} = 1 3

2. Soit C0 = [0, 1]. Calculons Ck = S^k(C0), k = 1, 2, ...

C1 = S(C0) = S1(C0) ? S2(C0)

= S1([0,1]) ? S2([0, 1])

= ¹3[0,1] ? 1 ₃[0,1] + 2 3

= [0,13]? [² ₃,1]

C2 = S(C1) = S1(C1) ? S2(C1)

=	S1([0,	13]	? [2 3,	1])	? S2([0,	13]	?	[2 3,	1])
=	31[0,^13]	?	[23, 1]	?	^31[0, 13] ?	[23,	1]	+	23

= [_0, 19] ? [² 9, 13] ? [23, 79] ? [89, 1]

· · ·

Ck = S(Ck-1) = S1(Ck-1) ? S2(Ck-1)

= 1 3Ck-1? {¹3Ck-1 + ²₃}

Il s'ensuit que lorsque n tend vers l'infini, on retrouve l'ensemble classique de Cantor. L'attracteur (l'ensemble classique de Cantor) de cet IFS est :

A = lim k?8 = lim k?8

S^k(C0) 3Ck-1 ? {1 1 3Ck-1 + 2 3}

= ¹₃A ? {¹₃A + 2 3}

4.1.1 Dimensions des ensembles auto-similaires ²

L'un des avantages d'utilisation de l'IFS est que la dimension de l'attracteur est facilement calculable en termes de contractions. En prenant maintenant des similarites S1, . . . , SN : E ? E avec E un espace metrique complet, on peut utiliser le theoreme suivant dont la demonstration est dans [9, p. 130].

Th'eor`eme 4.1.16

Soient Si des similarites de rapports ci < 1, i = 1, . . . , N. S'il existe un ensemble non-vide ouvert et borneV tel que

V ? _[N Si(V ) (4.19)

i=1

2. Que certains auteurs appellent «Dimension d'homothétie ».

2

et les Si(V ), i = 1, . . . ,N sont deux a` deux disjoints, alors pour l'attracteur F de l'IFS {S1, . . . , SN}v'erifiant

N

F= Si(F) (4.20)

i=1

on a dimH(F) = s o`u le nombre s est solution de l''equation

N

i=1 c^s_i = 1 (4.21)

De plus, pour cette valeur de s, on a 0 < H^s(F) < 8.
Par exemple, pour l'ensemble triadique de Cantor, on prend V =]0, 1[. On a V ?	2 U i=1	Si(V )

x +

avec S1 = 3

1
x et S2 = 1

3

C1)s 1 s log 2

2 3) log 3

₃. On a alors dimHC = s avec s est solution de l''equation

N

Si F = U Si(F) avec l'union «presque disjointe», on a

i=1

H^s(F) =

N i=1

H^s(Si(F)) =

N i=1

c^siH^s(F)

Si nous savons que 0 < H^s(F) < 8 on trouve l''equation (4.21).

Pour r'esoudre l''equation (4.21), on utilise les m'ethodes num'eriques comme par exemple la m'ethode de Newton (voir [6, p. 885]) qui trouve le z'ero de la fonction g o`u

N

g(x) = i=1 c^x_i - 1 (4.22)

de d'eriv'e

g'(x) =

XN i=1

log ci · c^x (4.23) i

Alors, on trouve s tel que

ENi=1 cixk - 1

x0 = 0, xk+1 = xk - N s = limx k.

_Ei

log ci · _cxk k--oo

i

Si on prend par exemple la courbe de Koch quadratique modifi'e K_m (Figure 4.2) qui obtient par it'erations a` partir du segment [0, 1] en le partageant sur cinq segments et en joignant les points suivants cons'ecutivement :

11 Z'

FIGURE 4.2 - Premi`eres etapes de la construction du courbe de Koch quadratique modifie

1 1

Le fractal K_m verifiel'equation (4.20) avec c1 = c3 = c5 = ₃et c2 =c4 = ₅. La methode

de Newton donne la solution de l'equation (4.21), qui est de la forme

1)⁸ 1)⁸

3 (₃ + 2 (₅ = 1, (4.24)

alors on trouve s tel que

s = lim xk.

3 log (s)(3 1,)xk

+ 2log (5 1)
· (51)xk ,

x0 = 0, xk+1 = xk

₃ Girk + 2 (5)xk _ 1

k-+oo

k	0	1	2	3	4	5	6	7
xk	0	0.6140	1.0563	1.2447	1.2714	1.2719	1.2719	1.2719

Donc, la valeur s = dimH(K_m) 1.2719.

Si les transformations Si du Theor`eme 4.1.16 ne sont que des contractions on obtient egalement des variantes.

Proposition 4.1.17 Soient S1, . . . , SN des contractions avec ci < 1 pour chaque i. Suppo-

sons que F soit invariant pour les Si : F =

N U i=1

Si(F). Alors dimH(F) < s o`u

N i=1

c^8i = 1.

p1 p0 = (0, 0) = (¹ 0) p2 = ₍1 1₎

21

3,5

p3 = (₃, ₅) p4 = (₃, 0)

p5 = (1, 0).

puis en recommencant cette operation a` l'infini sur chaque segment de la figure obtenue.

4.1.2 Syst`eme de fonctions it'er'ees affines dans Ill²

Une application f : 1[8² ? 1[8² est dite affine si elle est de la forme

f(x) = Lx + b (4.25)

avec L une application lineaire, donnetoujours par des matrices, et b ? 1[8². Cette application est alors de la forme

l1,1 l1,2 x b1

f x y ) l2,1 l2,2 ) y ) + b2

Une rotation d'un angle è est donnepar la matrice orthogonale

O = cos è - sin è

sinè cosè

(4.26).

Th'eor`eme 4.1.19 (Th'eor`eme de collage)

Soient F ? K(E) et 6 > 0. Soit {S_n,n = 1,2, ... , N} un IFS de facteur de contractant c = max{c_n,n = 1, ... N}, et soit S : K(E) -? K(E) d'efinie dans l''equation (4.11) tel que

d(F, S(F)) < ₆ (4.27)

Alors A l'attracteur de IFS v'erifie :

di-t(F, A) .<, 1 ⁶ c (4.28)

D'EMONSTRATION :

En prenant B = F dans l'equation (4.18), on obtient

1 ¹ c

di-t(F, A) .<, di-t(S(F),F)

6

1 - c

Si L = c · O alors f est une similaritede facteur c.

Th'eor`eme 4.1.18

Si l'application affine f dans (4.25) une contraction alors son point fixe est xf = (I - L)-1b.

BELLAL i' LES FRACTALS ET LEUR G'EOM'ETRIE ' BENTERKI

Le théoreme du collage porte donc bien son nom : pour approcher un objet par l'attracteur d'un IFS, il suffit que l'union des images de l'objet par les applications de l'IFS soit proche de l'objet.

Exemple 4.1.20 Poussi`ere de Cantor :

Considerons l'IFS {S1, S2, S3, S4} o`u

x 1 0 x

4 0

S1 4 ) 2

S2 x y

) 1 ! ! 1 4 0 x = + 4 0 1 y 0 4

!.

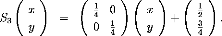
1 0 x 34

S4

(

x

1 ) y) + 4

⁴1)

4

On verifie facilement que {S1, S2, S3, S4} est un IFS de facteur c = 1. Exemple 4.1.21 La courbe de von Koch :

4

U Si avec

i=1

La courbe de von Koch K (Figure 2.3.4) est obtient au moyen de fonction F = les Si sont des similarite de facteur ³¹ donne par

S1

1 0 x 0

! .

; 3 0 3y ) 0) .

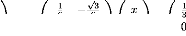
S2 x

!= \6 16 ) 3

y

66

! 1 N/3 1

= 6 _N/3 6) x + 2N/3 .

1

-6 6 y 6

S3 x

y

1 0 x

S4 x = 3 ) H .

y 0 3 ) ¹ Y

3 0

La suite des iterees {Si : 1 .<, i .<, 4} forme un IFS de cette fractale.

x 4

1 0 2

X 1

S3 4 ) y) 34)

1 - N/3 x 1

0

BELLAL LEs FRAcTALs ET LEuR GgoMgTRiE BENTERKI

1

₃,

Si on choisit B l'intervale d'unite sur l'axe des x, alors d(B,S(B)) = _4v dH(B, S(B)) = 1

d(S(B), B) = . Par la relation (4.17) on trouve dH(Sⁿ(B), K)

2v3 3n(1 1 - _1/3)dH(S(B),B) =

1

4 · 3n-1v3.

M'ethodes de construction des attracteurs :

D'apres le Theoeme 4.1.14, il existe un unique attracteur. Mais comment le construire? ALGORITHME 1 :

Soient {S1, . . . , SN} un IFS dans E et A leur attracteur.

O Soit k = 0 et choisissons, arbitrairement, un compact non vide P0 de E.

N ® On calcul Pk+1 = S(Pk) = U i=1

Si(Pk).

(c) Si k au-dessous un seuil donne, retour a` ®, sinon arràet.

Le seuil de l'algorithme dependre par le facteur de contraction c et la distance entre l'ensemble de depart P0 et l'attracteur A. On a

si k > log(å/dH (P0, A))

dH(Pk, A) < c^kdH(P0, A) < å,

.

log c

Cependant, cet algorithme n'est pas tres efficace car il exige beaucoup de calculs. Pour remedier a` ce probleme, on procede un algorithme stochastique comme suivant : ALGORITHME 2 : (s'appele aussi «Chaos game»(voir [27, p. 22]))

Soit {S1, . . . , SN} un IFS et attachons a` chaque Si une probabilitepi de telle sorte que

N i=1

pi = 1.

m Soit k = 1 et choisissons un point y0 de E.

® On choisit au hasard une des fonctions Si (la probabiliteque Si soit choisie est pi).

(c) On calcul yk = Si(yk-1).

CD Si k au-dessous un seuil donne, retour a` ®, sinon arràet.

D'efinition 4.1.22 Un IFS avec probabilites est un IFS {S1, . . . , SN} avec des probabilit'es p1, . . . , pN attach'ees aux fonctions S1, . . . , SN.

Exemple 4.1.23 Le triangle de Sierpinski :

1

L'IFS de ce fractal contient trois similarités affines Si de factaeur ₂ o`u Si(x) = Lix + bi

avec

Attachons les probabilités 0.2, 0.3 et 0.5 a` S1, S2 et S3 respectivement. On obtient un IFS avec probabilités que l'on peut représenter sous forme de tableau.

)

0 b2 0.5 ) 14

0 , 0 b3 = N/3 .

4

L1 = L2 = L=

0 0.50.5 0

i	l1,1	l1,2	l2,1	l2,2	b1	b2	pi
1	0.5	0	0	0.5	0	0	0.2
2	0.5	0	0	0.5	0.5	0	0.3
3	0.5	0	0	0.5	1 4	43	0.5

Avec cette méthode, on arrive a` construire des fractals de la nature.

Exemple 4.1.24 La foug`ere de Barnsley :

L'IFS de cette fractale contient quatre contractions affines Si(1 < i < 4) at Si(x) = Lix +bi avec

,

,
,

L1 = 0 0 ) 0.5

=0 0.160 b1 0

0.849 0.037

0.

L2 =

-0.037 0.849 b2 0.183075

!

L3 = 0.197 -0.226

0.400

, b3 =

0.226 0.197 0.049

.

-0.15 0.283 0.575

0.260 0.237 ) b4 =

-0.084

L4 =

)

Attachons les probabilités 0.01, 0.85, 0.07 et 0.07 a` S1, S2, S3 et S4 respectivement. On obtient un IFS avec probabilités que l'on peut représenter sous forme de tableau.

i	l1,1	l1,2	l2,1	l2,2	b1	b2	pi
1	0	0	0	0.16	0.5	0	0.01
2	0.849	0.037	-0.037	0.849	0.075	0.183	0.85
3	0.197	-0.226	0.226	0.197	0.400	0.049	0.07
4	-0.15	0.283	0.260	0.237	0.575	-0.084	0.07

FiGuRE 4.3 - La fougère de Barnsley

Section 4.2

Syst`eme de fonctions it'er'ees complexes

Soit f : C -? C une fonction polynàomiale de degrén > 2, i.e.

f(z) =

Xn i=0

aiz^i : ai ? C et an =6 0 (4.29)

et soit la suite des itérées _(fk)k>0 avec f^k est k-fois compositions de f, on dit que z est un point fixe de f si f(z) = z et f^k(z) = z, ?k ? N. On dit que z est un point périodique de f s'il existe p > 2 tel que fp(z) = z et fp^k(z) = z avec k ? N. On appelle le nombre p la période de z et l'ensemble {z, f(z), . . . , fp^-1(z)} une orbite d'un point p-périodique. La suite (f^k(z))k_EN peut aussi converger vers un point fixe ou une orbite d'un point p-périodique.

Si f est une fonction analytique, soit w un point p-périodique de f. On pose A = (fp)'(w) et on dit que

- w est un point attractif si 0 6 |A| < 1.

- w est un point répulsif si |A| > 1.

De plus, w est un point neutre si |A| = 1.

4.2.1 Les ensembles de Julia

D'efinition 4.2.1 L'ensemble de Julia de f, noteJ(f) est l'adherence de l'ensemble des points periodiques repulsifs de f. Et on appelle le complement de J(f) noteF(f) = C\J(f) l'ensemble de Fatou.

Exemple 4.2.2 Soit f une fonction definie par f(z) = z², ainsi f^k(z) = z^2k. Les points p^-p eriodique de f verifient :

fp(z) = z ? z^2p = z

? z2p-1 = 1

Alors z est de la forme z = e2ðiè et donc (e2Ðiè)2p-1 = 1. Alors è(2p - 1) ? N et donc

2iÐk

z ? {e^2p-1, 0 = k = 2p - 2}

Ce sont des points repulsifs, car pour un tel z0 p-periodique, on pose zk = f^k(z0) (0 .<.. k < p)

(fp)'(z0) = [f(fp-1)]0(z0) = f0(fp-1(z0))(fp-1),(z0)

f⁰(f^k(z0))

=

p-^1II k=0

f^0(zk)

=

p-¹_II
k=0

=

p-^1II k=0

2zk = 2p

p-^1II k=0

zk

|(fp)0(z0)| = 2p > ¹

L'ensemble de Julia J(f) est donc le cercle unite|z| = 1.

D'efinition 4.2.3 Soit U un ouvert de C et soit gk : U ? C une famille de fonctions analytiques. La famille {gk} est dite normale sur U si, toute suite extraite de {gk} admet une sous-suite qui converge uniformement sur tout compact K ? U, soit vers une fonction analytique bornee, soit vers 8, i.e.

lim k,l?8

sup z?K

|gnk(z) - gnl(z)| = 0 ou lim k?8

inf z?K

|gnk(z)| = 8.

8 8

une famille normale, alors _U gk(U) = C ou il existe un w ? C tel que _U gk(U) = C\{w}.

k=1 k=1

La famille {gk} est normale au point w s'il existe un ouvert V de U contenant w tel que {gk} soit une famille normale sur V .

Th'eor`eme 4.2.4 (Montel)

Soit {gk} une famille de fonctions analytiques complexes sur un ouvert U. Si {gk} n'est pas

D'efinition 4.2.5 Soit f : U ? C une fonction complexe, on d'efinie :

J0(f) = {z ? C : la famille {f^k}k?N n'est pas normale en z}.
F0(f) = {z ? C : la famille {f^k}k?N est normale en z}.

On remarque que F0(f) est un ouvert, et donc J0(f) est fermédans C.

Lemme 4.2.6 Soit f un polynàome et soit r = max{1,

2 +v.n-1 1,, .1 Laj=0 I "'.7 I } Alors, pour tout |z| = |an|

r, on a |f(z)| = 2|z|. De plus, on a _k?8 lim f^k(z) = 8 et donc _(fk)k?N converge uniform'ement dans V = {z ? C :|z| = r} = C\B(0,r).

D'EMONSTRATION : Si |z| = r, on a

|an||z| -		Xn- 1 j=0		|aj||z|^j-n+1 = |an||z| -	Xn- 1 j=0	|aj| = 2.
Donc |f(x)| = |z|^n-^1(|an||z| -	n-1P j=0		|aj||z|j-^n+1) = 2|z|.

De plus, si |f(x)| = 2|z|, on trouve par récurrence que |f^k(x)| = 2^k|z| ? 8 et alors

lim k?8

|f^k(x)| ? 8.

Proposition 4.2.7 Soit f une fonction d'efinie comme (4.29) on a :

1. J0(f) =6 Ø.

2. J0(f) est compact.

3. J0 est invariant par f et f-¹, c`a-d J0 = f(J0) = f-¹(J0). D'EMONSTRATION :

1. Supposons que J0(f) = Ø. Alors, pour chaque r > 0, la famille {f^k} est normale sur la boule ouvert B(0, r). Comme f est un polynàome, on peut choisir r assez grand pour que B(0, r) contienne un point z pour lequel |f^k(z)| ? 8, et également un point fixe w pour f, avec f^k(w) = w, ?k ? N. Une sous-suite de {f^k} ne peut alors converger uniformément ni vers une fonction analytique bornée ni vers 8 sur tout compact de B(0, r) qui contient a` la fois z et w, ce qui contredit la normalitéde {f^k}.

2. Comme le degréde f = 2, on peut trouver r (d'après le Lemme 4.2.6) tel que |f(z)| > 2|z| si |z| > r d'o`u |f^k(z)| > 2^kr si |z| > r.

Ainsi, f^k(z) ? 8 uniformément sur l'ouvert V = {z ? C : |z| > r} = C\B(0, r). Par définition, {f^k} est normale sur V , donc V ? C\J0(f). On obtient alors que J0(f) ? B(r, 0) donc il est borné, et par suite compact.

3. Il est équivalent de montrer que le complément F0(f) est invariant. Soit V un ouvert avec {f^k} normale sur V . Comme f est continue, f^-1(V ) est un ouvert. Soit (f^k%) une sous-suite de {f^k}. Alors (f^k%+1) admet une sous-suite (f^k0%⁺¹) uniformément convergente sur les compacts de V . Si D est un compact de f^-1(V ), alors (f^k0%⁺¹) converge uniformément sur f(D), donc (f^k0%) converge uniformément sur D.

Ainsi, {f^k} est normale sur f^-1(V ), donc F0 ? f^-1(F0) et f(F0) ? F0. Les deux autres inclusions s'obtiennent de la même manière, en utilisant que f est une application ouverte.

Proposition 4.2.8 J0(f^m) = J0(f) ?m ? N.

D'EMONSTRATION :

Il suffit de montre F0(f^m) = F0(f), Si chaque suite extraite de {f^k} admet une sous-suite uniformément convergente sur un ensemble donné, c'est aussi vraie pour {fmk}k>1. Donc F0(f) ? F0(f^m).

Si K est un compact et {gk} une famille convergeant uniformément sur K vers une fonction bornée ou vers 8, il en est de même pour {h ? gk} pour tout polynàome h.

Ainsi, si {f^mk}k>1 est normale sur un ouvert V , la famille

{f^mk+r}k>1 l'est aussi, pour r ? {0, . . . ,p - 1}. Mais toute suite extraite de {f^k}k>1 contient une infinitéde termes de la suite (f^mk+r)k>1 pour un entier r avec 0 = r = p-1, qui admet une sous-suite uniformément convergente sur les compacts de V .

Donc {f^k} est normale, et F0(f) ? F0(f^m).

Lemme 4.2.9 Soit f un polynàome de degrén et soit U un voisinage d'un point w ? J0(f). Alors

oo

W := f^k(U) = C\{z0}

k=1

telle que z0 ? F0(f) et est indépendant de w et de U.

D'EMONSTRATION :

Par definition de J0, la famille {f^k} n'est pas normale en w, la premi`ere partie decoule donc du Theor`eme de Montel 4.2.4, donc existe un point z0 ? C verifie que W = C\{z0}. Soit zi (1 < i < n) les racines de l'equation f(z)-z0 = 0. Si zi ? W pour tout i ? {1, ... ,n}, on a z0 = f(zi) ? f(W) ? W, impossible car z0 ?/ W donc zi ?/ W, Comme C\W est au plus un seul point z0, alors zi = z0 (1 = i = n) et f(z) - z0 = c.(z - z0)ⁿ.

Supposon que |z - z0| = r := (2|c|)-¹/⁽ⁿ-¹⁾.on a

|f(z) - z0| = |c|.|z - z0|n |c|

2|c|.|z - z0| =¹ -

2 z0|,

1 r

et |f^k(z) - z0| = 2k 2k

< . On deduire que f^k(z) est converge uniformement sur le

disque B(z0, r) qui contient z0, alors {f^k}k=1 est normale en z0.

Th'eor`eme 4.2.10 Soit U un ouvert qui v'erifie U n J0 =6 Ø, et soit w ? une infinit'e de valeurs de k. D'EMONSTRATION :

S8 k=1

f^k(U), alors f-^k(w) n U =6 Ø pour

Si W = _S8 f^k(U) =6 C, soit z0 qu'il definie dans Lemme 4.2.9, et k1 = min{k : w ?

k=1

f^k(U)}, alors il existe z1 ? U tel que : f^k1(z1) = w.

Dans le cas W = C\{z0}, on a z1 =6 z0 car f^k1(z0) = z0 =6 w. Donc z1 ? W, par recurrence on
peut construiseune suite _(kj)8j=0 croissant et autre suite (zj)⁸j=0 ? C verifie f-^k(zj)n U =6 Ø.

Th'eor`eme 4.2.11

Pour tout w ? J0(f) alors :

[8 J0(f) = k=1

f-^k(w). (4.30)

D'EMONSTRATION :

Si w ? J0(f), alors f-^k(w) ? J0(f) par la Proposition 4.2.7, donc

[8 k=1

f^-k(w) ? J0

[8 k=1

f-^k(w) ? J0

00

Soit U un ouvert rencontre J0 on a d'après le Lemme 4.2.9 w E U f^-k(U) et donc

k=1

00 00 U f^-k(w) n U =6 0 et J0 c U f^-k(w). k=1 k=1

Proposition 4.2.12 J0 est un ensemble parfait, i.e. ferm'e et sans points isol'es.

D'EMONSTRATION :

Soient w E J0(f) et U un voisinage de w. Il faut montrer que U contient d'autres points de J0(f). On considère trois cas separemment.

(a) w n'est pas un point periodique de f : Par le Theorème 4.2.11 on a U n J0(f) =6 0, k > 1, U n f^-k(w) =6 0, donc U contient un point different de w car w n'est pas un point fixe ou periodique.

(b) f(w) = w point fixe de f : Si f^-1(w) = w, alors comme dans la demonstration du Lemme 4.2.9, w E/ J0(f). Il existe donc un point v =6 w avec f(v) = w et contient dans J0 par invariance de f^-1. Donc par la Proposition 4.2.7 (3), on trouve U n f^-k(v) =6 0 pour un k > 1.

(c) fp(w) = w pour un p > 1 : Par la Proposition 4.2.8, J0(f) = J0(fp), donc en appliquant (b) a` fp, on voit que U contient d'autres points de J0(fp) = J0(f) different de w.

On deduire que J0 sans points isoles et comme il est ferme, il est parfait.

Th'eor`eme 4.2.13

Soit f une fonction polynàomiale de degr'e n > 2, alors J0(f) = J(f).

D'EMONSTRATION :

Soit w un point repulsif de f de periode p, donc w est un point fixe repulsif de g = fp. Supposons que Ig^kl est normale en w ; alors w possède un voisinage ouvert V sur lequel une sous-suite (g^ki) converge uniformement vers une fonction analytique finie g0 (elle ne peut pas converger vers Do car g^k(w) = w Vk).

Comme g est analytique, la derivee converge egalement (g^ki)'(z) -+ g0'(z) si z E V . Or la
formule de derivation d'une composee donne que |(g^ki)'(w)| = |(g'(w))^ki -+ Do car w est un

point fixe repulsif, |g'(w)| > 1. Ceci contredit la finitude de g⁰₀(w), donc {g^k} ne peut àetre normale en w.

Ainsi w ? J0(g) = J0(fp) = J0(f) par la Proposition 4.2.8. De plus, J0(f) est ferme, donc J(f) ? J0(f).

Soit K = {w ? J0(f) tel qu'il existe z =6 w avec f(z) = w et f'(z) =6 0}. Supposons que w ? K. Gràace au Theoreme 4.2.14 ci-dessous Il existe alors un voisinage ouvert V de w sur lequel on peut trouver localement une inverse analytique f-¹ : V ? C\V tel que f(f-¹(z)) = z pour z ? V . Definissons une famille de fonctions analytiques {hk} sur V par

f^k(z) - z

f-¹(z) - z

.

hk(z) =

Soit U un voisinage ouvert de w avec U ? V . Comme w ? J0(f), la famille {f^k} n'est pas normale et donc par definition, la famille {hk} n'est pas normale sur U. Par le Theoreme de Montel 4.2.4, hk(z) doit prendre la valeur 0 ou 1 pour un certain k et z ? U. Dans le premier cas, f^k(z) = z pour un z ? U ; dans le second cas, f^k(z) = f-¹(z) donc f^k+1(z) = z pour un z ? U. Donc U contient un point periodique de f, d'o`u w ? J(f). On a montreque

K ? J(f) et donc K ? J(f) = J(f).

De plus K contient tous les points de J0(f) sauf un nombre fini. Comme J0(f) ne contient pas de point isolepar la Proposition 4.2.12, donc J0(f) = K ? J(f).

Th'eor`eme 4.2.14

Soit f une fonction holomorphe sur un voisinage de point z0 ? C tel que f'(z0) =6 0. Il existe
un voisinage U de z0, et un voisinage V de w0 = f(z0) avec U n V = Ø et une application

holomorphe unique f sur V tel que

^ef(w0) = z0 et

w = f(z) ? z = ^ef(w). ?z ? U

D'efinition 4.2.15 Soit w un point fixe attractive de f (tel que w ? C ou w = 8). On d'efinie l'ensemble

A(f,w) := {z ? C : k?8 lim f^k(z) = w}

le bassin d'attraction de w.

On peut deduire que A(f, w) = f-^k(A(f,w)).

Th'eor`eme 4.2.16

Si w un point fixe attractive de f, alors A(f,w) est un ouvert et A(f,w) ? F0.

Pour la preuve voir [11, p. 115].

Th'eor`eme 4.2.17

Si w est un point fixe attactive de f ou si w = 8 alors ?A(f,w) = J(f), o`u ?A(f, w) la fronti`ere de l'ensemble A(f, w).

D'EMONSTRATION :

(i) J(f) ? ?A(f,w)? : Soit z ? J(f). Par la Proposition 4.2.7 (3) on a f^k(z) ? J(f) pour tout k ? N et ne converge pas vers un point fixe attractif w, donc z ?/ A(f, w) , et on a pour tout U est un voisinage de z, l'ensemble f^k(U) contient des points de A(f, w) pour un certain k par le Lemme 4.2.9, donc U n f^-k(A(f, w)) = U n A(f, w) =6 Ø, on d'eduire donc z ? ?A(f,w).

(ii) ?A(f,w) ? J(f)? : On suppose que z ? ?A(f,w)/J(f), alors il existe un ouvert voisinage U de z et la suite {f^k}k?N admet une sous-suite convergente soit vers une fonction analytique, soit vers w = 8. Cette sous-suite converge vers w sur V nA(f, w), donc elle est converge w dans V qui contient z, alors z ? A(f, w) ce qui contredit z ? ?A(f,w).

4.2.2 L'ensemble de Mandelbrot

On va etudier les ensembles de Julia des polynàomes de la forme

f_c(z) = z² + c

En choisissant bien á et â et en posant h(z) = áz + â avec á =6 0, on peut obtenir n'importe quelle fonction quadratique f en conjuguant f_c avec h tel que

á

á²z² + 2áâz + â² + c - f(z) = h^-1(f_c(h(z))) = â

Comme h est une similitude, l'ensemble de Julia de toute fonction quadratique f presente la màeme structure que celui de f_c pour un certain c ? C.

Si on calcul l'inverse de fonction f_c pour z =6 c, on obtient les valeurs #177;(z - c)¹/² sont appelees les deux branches de f _c -1(z).

On rappel qu'un lacet est une courbe fermee, de classe C¹ et simple (i.e., sans point d'auto-intersection), et le terme huit est pour une courbe ferm'ee de classe C¹ avec un unique point d'auto-intersection.

D'efinition 4.2.18 On définit l'ensemble de Mandelbrot comme l'ensemble des param`etres

c pour lesquels l'ensemble de Julia de f_c est connexe

M = {c ? C, J(f_c) est connexe}.

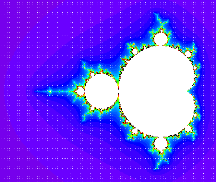
FIGURE 4.4 - Ensemble de Mandelbrot

Cette definition n'est pas pratique, on obtient une autre en utilisant le lemme suivant. Lemme 4.2.19 Soit C un lacet dans le plan complexe.

(i) Si c est a` l'intérieur de C, alors f _c -¹(C) est un lacet, avec l'intérieur de f_c -¹(C) est l'image réciproque de l'intérieur de C.

(ii) Si c est un point de C, alors f_c -¹(C) est un huit, et l'image réciproque de l'intérieur de C est l'intérieur des deux lacets.

D'EMONSTRATION :

On a f-1

c (z) = #177;(z - c)1/2 ^et (f_c -¹)'(z) = #177;21(z - c)-1/2 qui est non-nul si z =6 c. Ainsi, si on choisit une des branches de f-1

c , l'ensemble f_c -¹(C) est localement une courbe de classe

C¹.

(i) Supposons que c soit a` l'interieur de C. Prenons un point initial w sur C et choisissons l'une des deux valeurs f-1

c (w). En faisant varier continàument f-1

c (z) quand z decrit C, le point f_c -¹(z) trace une courbe de classe C¹. Quand z retourne en w, f _c -¹(w) prend sa seconde valeur. Si z traverse C encore une fois, f-1

c (z) continue a` decrire une courbe C¹, qui se referme quand z retourne en w pour la seconde fois.

Comme c ?/ C, on a 0 ?/ f_c -¹(C), donc f'_c(z) =6 0 sur f _c -¹(C). L'application f_c est donc localement une bijection de classe C¹, au voisinage des points de f-¹ _c(C). En particulier, z ? f_c -¹(C) ne peut àetre un point d'auto-intersection de f_c -¹(C), sinon fc(z) serait un point d'auto-intersection de C.

Comme f_c est une application continue qui envoie le lacet f-1

c (C), et aucun autre point, sur le lacet C, le polynàome f_c doit aussi envoyer respectivement l'interieur et l'exterieur de f-1

c (C) sur l'interieur et l'exterieur de C. Les deux branches de f-¹ _csont donc correspondre l'interieur de C avec l'interieur de f-1

c (C).

(ii) On le prouve d'une mani`ere similaire a` (i), en remarquant que si C0 est un arc de courbe de classe C¹ passant par c, alors f-1

c (C0) consiste en deux arc de courbes passant par 0, qui s'intersectent, ce qui donne le point d'auto-intersection et le huit.

Th'eor`eme 4.2.20

L'ensemble de Mandelbrot est un ensemble des param`etres c pour lesquels l'orbite {f^k(0)}⁸_k=1 est born'e, i.e. M = {c ? C, {f^k_{c (0)}k=1} est born'e }.

D'EMONSTRATION :

On montre d'abord que si {f^k_c (0)} est borne, alors J(f_c) est connexe. Soit C un cercle dans C centrea` l'origine, assez grand pour que tous les points {f<sup>k</sup><sub>c</sub> (0)} soient a` l'interieur de C, pour que f_c -¹(C) soit dans l'interieur C , et f^k_c (z) ? 8 pour tout z dans l'exterieur de C. Comme c = f_c(0) est a` l'interieur C, d'apr`es le Lemme 4.2.19 (i) f_c -¹(C) est un lacet contenu dans l'interieur C. De màeme, f_c(c) = f²_c (0) est a` l'interieur C de C et f-<sup>1</sup> <sub>c</sub>envoie l'exterieur de C sur l'exterieur de f<sub>c</sub> -<sup>1</sup>(C), donc c est a` l'interieur de f_c -¹(C). Donc f_c -²(C) est un lacet contenu dans l'interieur de f_c -¹(C). Ainsi de suite {f_c -^k(C)} consiste en une suite de lacets, chacun contenant le suivant dans son interieur.

Soit K l'ensemble fermedes points qui sont a` l'interieur ou sur les lacets f<sub>c</sub> -<sup>k</sup>(C) pour tout k. Si z ? C\K, un certain iteref<sup>k</sup><sub>c</sub> (z) sera a` l'exterieur de C et donc f^k_c (z) ? 8. On a A(f, 8) = {z ? C : lim fk c (z) ? 8} = C\K.

k?8

D'apr`es le Theor`eme 4.2.17, J(f_c) est la fronti`ere de C\K, qui est bien sir aussi la fronti`ere de K. Mais K est l'intersection d'une suite decroissante de fermes simplement connexes, donc K est simplement connexe et sa fronti`ere est donc aussi connexe. Donc J(f_c) est connexe.

On montre que si J(f_c) connexe alors {f^k_c (0)} est borne. Il est equivalent de montrer que J(f_c) n'est pas connexe si {f^k_c (0)} n'est pas borne. Soit C un cercle assez grand pour que f_c -¹(C) soit a` l'interieur de C, que tous les points z a` l'exterieur de C tel que f^k(z) ? cc et tel que pour un certain p, le point fp-1

c (c) = fp_c (0) ? C avec f_c ^k(0) a` l'interieur ou a` l'exterieur de C, selon que k est plus petit ou plus grand que p. Comme dans la premi`ere partie, on construit une suite d'ensembles {f_c -^k(C)}, chacun contenant le suivant dans son interieur.

Toutefois, l'argument ne tient plus quand on arrive au lacet f_c ¹-p(C), car c ? f_c ¹-p(C) et le Lemme 4.2.19 (i) ne s'applique pas, Par le Lemme 4.2.19 (ii), on obtient que H := f_c -p(C) est un huit a` l'interieur du lacet f<sub>c</sub> <sup>1</sup>-p(C), avec f<sub>c</sub> envoyant l'interieur de chaque partie de H dans l'interieur de f<sub>c</sub> <sup>1</sup>-p(C). L'ensemble de Julia J(f<sub>c</sub>) doit àetre a` l'interieur des lacets de H, car les autres points sont iteres vers cc. Comme J(f_c) est invariant par fc ^-1 , des parties de J(f_c) doivent àetre contenues dans chaque lacet de H. Ainsi, le huit H rend J(f_c) non connexe.

Th'eor`eme 4.2.21

Soit |c| > ₄¹(5 + 2v6), alors J(f_c) est totalement discontinu, et est attracteur (au sens de (4.15)) par les contractions donn'ees par les deux branches de f c -1 (_z) = #177;(z - c)¹/² pour z proche de J(f_c). De plus si c grand

2 log 2

dimH(J(f_c)) '-'

log 4|c|^.

Th'eor`eme 4.2.22

Si |c| < ₄¹ alors J(f_c) est une courbe ferm'ee simple.

4 1 1

Il faudrait ensuite etudier les cas oii. < |c| < ₄(5 + 2v6), mais ils sont plus difficiles car f_c

a plusieurs points periodiques et nous ne les traiterons pas.

Les cas les plus d'elicats sont quand c est sur la fronti`ere de l'ensemble de Mandelbrot, on a d'apr`es [23, 24, 25] qui sont assurent que dimH(J_c) = 2 . De plus, signalons cependant qu'il existe un resultat affirmant que la fronti`ere de l'ensemble de Mandelbrot est un fractal avec dimH?M = 2.

Syst`eme de fonctions it'er'ees sur lAction 43'

multifonctions

Dans cette section, on introduit la methode de l'IFS sur l'espace des fonctions a` valeurs ensemblistes ou multifunctions.

Rappellons qu'une multifonction F : X Y est une fonction de X vers P(Y ) ou 2^Y . On appelle graphe de F l'ensemble

graph F := {(x, y) E X × Y : y E F(x)}. (4.31)

Si F(x) est un ferme, compact ou convexe on dit que F est ferme, compact ou convexe respectivement. Notons F : X ? K(Y ) les multifonctions a` valeur compact.

Soit (X, B, _au) un espace mesurefini; une multifonction F : X Y est dite mesurable si

pour tout ouvert O ? Y on a

F^-1(O) := {x E X : F(x) n O =6 Ø} E B. (4.32)

Une fonction f : X ? Y est une selection de F si f(x) E F(x), ?x E X. Dans la suite on suppose que Y est compact et F(x) est compact pour tout x E X. On definit

F(X,Y ) := {F : X ? K(Y )}. (4.33)

On definit deux metriques dans F(X, Y ); la premiere est

d8(F, G) := sup x?X

dH(F (x), G(x)) (4.34)

et la deuxieme avec au une mesure finie et p > 1 par

? f 1/p

d_p(F, G) :=

dH(F (x), G(x))^pdau(x) . (4.35)

X

Proposition 4.3.1 L'espace (F(X,Y ),d₈) est un espace metrique complet.

D'EMONSTRATION :

Il est evidament claire que d₈(F, G) = 0 ssi F = G et d₈(F, G) = d₈(G, F). De plus, pour F, G, H ? F(X, Y ) on a

d8(F, G) = sup x?X		dH(F(x), G(x))
6 sup x?X	(dH(F(x), L(x)) + dH(L(x), G(x)))
6 sup x?X		dH(F(x),L(x)) + sup x?X	d(L(x), G(x))

= d₈(F, L) + d₈(L, G).

Pour montrer qui l'est complet, soit F_n une suite de Cauchy de F(X, Y ) alors pour å > 0 il existe n0(å) tel que pour m,n > n0(å) on a d₈(F_n, F_m) < å. Alors pour tout x ? X on a dH(F_n(x), F_m(x)) 6 å et la suite F_n(x) est de Cauchy dans K(Y ). Comme elle est complet il exist A(x) tel que dH (F_n(x), A(x)) ? 0 quand n ? +8. Alors pour tout x ? X et pour tout n,m > n0(å) on trouve dH(F_n(x), F_m(x)) 6 å, et pour m ? +8 on a dH(F_n(x), A(x)) 6 å et donc d₈(F_n, A) 6 å.

111

Proposition 4.3.2 d_p est un (pseudo-) m'etrique dans F(X,Y ).

DEMONSTRATION :

Elle est clair que d_p(F, G) = 0 si et seulement si dH(F(x), G(x)) = 0 pour u-presque partout, alors si et seulement si F(x) = G(x) pour presque tout x ? X. De plus, que d_p est symetrique. Pour l'inegalite triangulaire, soit F, G, H ? F(X, Y ) on a (`a, l'aide de l'inegalite de Minkowski : 11f + gIlLp 6 11 f 11Lp + 11g11Lp (voir [13]))

? 1/p

?

? d_p(F,G) =

X

?

6 ?

I ? dH(F (x), G(x))^pdu(x)

I [dH(F(x), H(x)) + dH(H(x), G(x))]^pdu(x)

) 1/p

X

?

6 ?

I 1/p

d₇.₁(F (x), H (x))P d_iu(x)) + I dHi(H (x), G(x))^p du(x)

= d_p(F, H) + d_p(H , G).

X

_X) 1/p

On trouve que d_p est un pseudo-metrique pour des fonctions differentes sur un ensemble u-negligeable qui sont de distance nulle.

Proposition 4.3.3 Soit Y un intervale compact de IR et supposons que F(x) soit convexe pour tout x ? X et pour tout F ? F(X,Y ). Supposons que tout F ? F(X, Y ) soit mesurable. Alors (F(X,Y ),d_p) est complet.

D'EMONSTRATION :

Pour montrer qu'il est complet, soit F_n une suite de Cauchy d'elements de F(X, Y ), alors, pour tout E > 0, il existe n0(E) > 0 tel que, pour tout m, n > n0(E), on ait dp(Fn, F_m) < E. Comme F_n(x) est compact et convexe, alors F_n(x) = [min F_n(x), max F_n(x)]. Les fonctions ö^*_n(x) = min F_n(x) et ö^**_n (x) = max F_n(x) sont mesurables et

1ö^*_n(x) ? ö^*_m(x)1L, C d_p(F_n, F_m) 1ö^**_n (x) ? ö^**_m(x)1L, C d_p(F_n, F_m)

et donc ö^*_n et ö^**_n sont de Cauchy dans Lp(X). Alors il existe ö^* et ö^** tel que ö^*_n ? ö^* et ö^**_n ? ö^** avec la metrique usuel dans Lp. Si on construit F(x) = [ö^*(x), ö^**(x)] alors

? Z

d_p(F_n, F ) = ? dH(F_n(x), F(x))^pdu(x)

_?1/p

= (Imax{|ö;1(x) ? ö^*(x)|^p, |ö^**_n(x) ? ö^**(x)|^pu

}d(x)

?

_?1/p

?

_?1/p1/p

1|ö,(x) ? ö,(x)|^pdu(x) 1|ö,7(x) ? ö^**_n(x)|^pdu(x)

X X

?
?

?

Dans la suite, on definit deux types d'operateurs de l'IFS sur F(X, Y ).

L'op'erateur «Union» :

Soient Si : X ? X sont des fonctions de X dans X et öi : K(Y ) ? K(Y ) sont des contractions au sens de la distance de Hausdorff de facteurs ci < 1 avec i ? {1,. . . , N}. On

définit T : F(X,Y ) ? F(X, Y ) par

N

T(F)(x) := öi(F(S1¹(x))). (4.36)

i=1

Proposition 4.3.4 Si c = max{ci : 1 6 i 6 N} < 1. Alors T est une contraction sur l'espace (F(X, Y ), d₈)

D'EMONSTRATION : Soient F, G ? F(X,Y )

6 sup x?X

max 16i6N

dH(öi(F(S^-i

^1(x))), öi(G(Si^1(x))))

6 sup x?X

max 16i6N

ci dH(F(S^-i

^1(x)), G(S^-1 i (x)))

6 c sup z?X

dH(F(z), G(z))

= c d8(F,G).

~

d8(T(F), T(G)) = sup x?X

dH

[ N i=1

öi(F(Si^1

(x))),

N i=1

öi(G(Si^1(x))))

Proposition 4.3.5 Supposons que du(Si(x)) 6 si du(x) avec si > 0. Alors

dp(T(F),T(G)) 6 E 16i6N

!1/p cp i si dp(F,G).

D'EMONSTRATION : Soient F, G ? F(X,Y )

)

d_p(T(F),T(G)) = (.1 U öi(F(ST¹(x))), _U öi(G(ST¹(x))) ) du(x)

16i6N 16i6N

X

Z max d (öi(F(Si¹ (x))),öi(G(Si¹(x))))^p du(x)

X

?

6 ?

_?1/p

?

_?1/p

?

? Z

6 _?1max_N cP dH(F(Si¹(x)), G(Si¹(x)))^p du(x)

X

Soit Mi c Si(X) defini par

Mi = {x E X : dH(F (S^-1

i (x)), G(S^-1

i (x))) dH(F (S^-1

j (x)), G(S^-1 j(x))) Vj}

L'ensemble Mi contient tous les points pour lesquels la ^i`eme image donne la plus grande distance de Hausdorff. Alors

_?1/p

?

? d_p(T(F),T (G)) 6 ^E cYidH (F (x)), G(S1¹(x)))^p du(x)

16i6N Mi

_Z

X cp dH ~F (S^-1

i (x)), G(ST¹(x)))^p du(x)

i

^16i6NSi(X)

_?1/p

??

?

?

6 ?

? 6 ?	ZX cp i si dH(F(z), G(z))^p du(z) 16i6N X		?1/p ?
E= 16i6N		!1/p cp i si dp(F,G).

~

L'op'erateur «Somme» :

Avec les màemes donnees que dans l'operateur «Union». On definit T : T(X,Y ) -+ T(X, Y ) par

T(F)(x) := E

pi(x)öi(F(Si^1 (x))) (4.37)

16i6N

avec la somme dependant de x o`u x E Si(X) et E 16i6N

pi(x) = 1.

Proposition 4.3.6 d₈(T(F),T(G)) 6 sup E pi(x) ci) d₈(F,G).

x?X 1`i`N

D'EMONSTRATION : Soient F, G E T(X, Y )

d8(T(F), T(G)) = sup x?X

EdH 16i6N

X pi(x)öi(F(Si^1 (x))), 16i6N

pi(x)öi(G(Si^1 (x))))

sup > pi(x) cidH(F (S^-1

i (x)), G(S^-1

i (x)))

x?X 16i6N

sup E pi(x) ci) d₈(F, G).

~

^x?X16i6N

Lemme 4.3.7 Soit ai E ,i = 1, . . . , N. Alors

~~~~~

X 16i6N

ai

~~~~~

6C(N)^p E 16i6N

|ai| ,

avec C(N) = N(p-1)/p.

Proposition 4.3.8 Soient pi = sup_x pi(Si(x)) et si > 0 tel que du(Si(x)) 6 sidu(x). Alors

dp(T(F), T(G)) 6 C(N) E i

!1/p cp i sp i pp dp(F, G). i

Pour la preuve voir [16].

Conclusion et perspectives

Les travaux pr'esent'es dans cette thèse concernent les fractals et plus particulièrement la th'eorie qui permet de les g'en'erer par la technique des systèmes de fonctions itérées (IFS).

Après l'avoir appliqu'ee a` (R, R<sup>2</sup> et C), nous avons regard'e son application a` l'espace plus g'en'eral des multifonctions qui a` des applications dans des domaines informatiques et notamment celui de la compression des images (voir [16]).

Plusieurs questions se r'evelent d'ores et d'ejàint'eressantes.

- Quelles sont les conditions sur un espace pour pouvoir y construire des fractals?

- Y-a-t-il une m'ethode g'en'erale d'int'egration de fonctions mesurables sur un ensemble de type fractal?

- Que se passe t-il si les contractions de l'IFS sont des multifonctions?

- Quelles sont les op'erations (somme, produit, sous-espaces, ...) qui pr'eservent la propri'et'es d'être fractal?

Cette thèse nous a permis 'egalement d'acqu'erir des comp'etences en topologie et en th'eorie de la mesure pour pouvoir acc'eder a` des problèmes de s'elections et de cross-s'elections mesurables dans le cadre des multifonctions ou dans celui des groupes topologiques en g'en'eral.

ANNEXE

PROGRAMMES SUR LES FRACTALS

Dans cette annexe, nous avons présentéquelques programmes sous Matlab® servant a` illustrer la construction des différents types de fractals. Nous avons présentéla construction

de fractals selon la technique des systèmes de fonctions itérées (IFS). Nous avons ^appliquécette méthode a` l'aide des approches probabiliste seulement.

Section .1

L'ensemble de Cantor

function Cantor shg

clf reset

set(gcf,'color','white','menubar','none', ... 'numbertitle','off','name','Fractal Cantor')

x = 1/2 ;

h = plot(x,'.'); black = [0 0 0]; set(h,'markersize',1,'color',black,'erasemode','none');

axis([0 1 0 1]) axis off

stop = uicontrol('style','toggle','string','stop', ...

'background','white');

drawnow

p = [ .8 .9];

cnt = 1;

tic

while ^-get(stop,'value')

r = rand;

if r < p(1)

x = 1/3*x ; else

x = 1/3*x + 2/3;

end

set(h,'xdata',x); drawnow

cnt = cnt + 1;

end

t = toc;

s = sprintf('%8.0f points in 7.6.3f seconds',cnt,t); text(0.25,0,s,'fontweight','bold'); set(stop,'style','pushbutton','string','close','callback','close(gcf)')

Section .2

Courbe de von Koch

function Koch_curve

shg

clf reset

set(gcf,'color','white','menubar','none', ... 'numbertitle','off','name','Fractal Koch curve') x = [1; 0];

h = plot(x(1),x(2),'.');

red = [1 0 0];

set(h,'markersize',1,'color',red,'erasemode','none'); axis([0 1 -0.5 1])

axis off

stop = uicontrol('style','toggle','string','stop', ... 'background','white');

drawnow

p = [ 0.15 .35 .5 1];

A1 = [ 1/3 0; 0 1/3];

A2 = [ 1/6 -sqrt(3)/6; sqrt(3)/6 1/6]; b2 = [1/3; 0];

A3 = [ 1/6 sqrt(3)/6; -sqrt(3)/6 1/6]; b3 = [0.5; sqrt(3)/6];

A4 = [ 1/3 0; 0 1/3]; b4 = [2/3; 0];

cnt = 1;

tic

while ~get(stop,'value')

r = rand;

if r < p(1)

x = A1*x ;

elseif r < p(2)

x = A2*x + b2;

elseif r < p(3)

x = A3*x + b3;

else

x = A4*x+b4;

end

set(h,'xdata',x(1),'ydata',x(2)); drawnow

cnt = cnt + 1;

end

t = toc;

s = sprintf ('%8.0f points in %6.3f seconds',cnt,t); text(.25,-.5,s,'fontweight','bold'); set(stop,'style','pushbutton','string','close','callback','close(gcf)')

Section .3

Triangle de Sierpenski

function Sierpinski

shg

clf reset

set(gcf,'color','white','menubar','none', ...

'numbertitle','off','name','Fractal Sierpenski') x = [0; 0];

h = plot(x(1),x(2),'.');

darkblue = [0 0 1]; set(h,'markersize',1,'color',darkblue,'erasemode','none'); axis([0 1 0 1])

axis off

stop = uicontrol('style','toggle','string','stop', ... 'background','white');

drawnow

p =	[ 0.2	0.3	0.5];
A = [	.5	0; 0	.5];
b2 =	[0.5;	0];	b3 = [1/4;	sqrt(3)/4];

cnt = 1;

tic

while ~get(stop,'value')

r = rand;

if r < p(1)

x = A*x ;

elseif r < p(2)

x = A*x + b2; elseif r < p(3)

x = A*x + b3 ;

end

set(h,'xdata',x(1),'ydata',x(2));

drawnow

cnt = cnt + 1;

end

t = toc;

s = sprintf('%8.0f points in %6.3f seconds',cnt,t); text(0.25,-0.01,s,'fontweight','bold'); set(stop,'style','pushbutton','string','close','callback','close(gcf)')

Section .4

Foug`ere de Barnsley

function fern

shg

clf reset

set(gcf,'color','white','menubar','none', ... 'numbertitle','off','name','Fractal Fern') x = [.5; .⁵];

h = plot(x(1),x(2),'.');

darkgreen = [0 2/3 0]; set(h,'markersize',1,'color',darkgreen,'erasemode','none');

axis([0.3 0.8 0 1])

axis off

stop = uicontrol('style','toggle','string','stop', ... 'background','white');

drawnow

p = [ .85 .92 .99 1];

A1 = [ 0 0 ; 0 .16]; b1 = [0.5; 0];

A2 = [ .849 .037; -.037 .849]; b2 = [0.075; 0.183];

A3 = [ .197 -.226; .226 .197]; b3 = [0.4; 0.049];

A4 = [-.15 .283; .260 0.237]; b4 = [0.575; -0.084];

cnt = 1;

tic

while ~get(stop,'value') r = rand;

if r < p(1)

x = A1*x + b1;

elseif r < p(2)

x = A2*x + b2;

elseif r < p(3)

x = A3*x + b3;

else

x = A4*x;

end

set(h,'xdata',x(1),'ydata',x(2));

drawnow

cnt = cnt + 1;

end

t = toc;

s = sprintf('7.8.0f points in 7.6.3f seconds',cnt,t); text(-1.5,-0.5,s,'fontweight','bold'); set(stop,'style','pushbutton','string','close','callback','close(gcf)')

Section .5

Poussi`ere de Cantor

function Cantordust

shg

clf reset

set(gcf,'color','white','menubar','none', ... 'numbertitle','off','name','Fractal Cantordust') x = [.5; .⁵];

h = plot(x(1),x(2),'.');

black = [0 0 0];

set(h,'markersize',1,'color',black,'erasemode','none'); axis([-3 3 0 10])

axis off

stop = uicontrol('style','toggle','string','stop', ... 'background','white');

drawnow

p = A = [ b2 =

[ 0.5 .25 [0.25;

.72 0; 0];

.89 1]; 0 .25]; b1 = [0; b3 = [0.5; 0.75];

0.5]; b4 =

[0.75;

0.25];

cnt = 1;

tic

while ~get(stop,'value')

r = rand;

if r < p(1)

x = A*x + b1; elseif r < p(2)

x = A*x + b2; elseif r < p(3)

x = A*x + b3; else

x = A*x;

end

set(h,'xdata',x(1),'ydata',x(2));

drawnow

cnt = cnt + 1;

end

t = toc;

s = sprintf('7.8.0f points in 7.6.3f seconds',cnt,t); text(.2,-.05,s,'fontweight','bold'); set(stop,'style','pushbutton','string','close','callback','close(gcf)')

Section .6

Tapis de Sierpenski

function tapis_de_Sierpinski

shg

clf reset

set(gcf,'color','white','menubar','none', ... 'numbertitle','off','name','Fractal tapis de Sierpinski') x = [0; 0];

h = plot(x(1),x(2),'.');

blue = [0 0 1];

set(h,'markersize',1,'color',blue,'erasemode','none');

axis([0 1 0 1])

axis off

stop = uicontrol('style','toggle','string','stop', ...

'background','white');

[ .1	.3	.5	.6 .75 .85		.9	1];
[ 1/3	0;	0	1/3];	b2 =	[0;	1/3];
[0; 2/3];		b4 =	[1/3;	0];	b5 =	[1/3;	2/3];
[2/3;	0];	b7 =	[2/3;	1/3]; b8 = [2/3; 2/3];

drawnow p = A = b3 = b6 =

cnt = 1;

tic

while ~get(stop,'value')

r = rand;

if r < p(1)

x = A*x;

elseif r < p(2)

x = A*x + b2; elseif r < p(3)

x = A*x + b3; elseif r< p(4)

x = A*x+b4; elseif r< p(5)

x = A*x + b5; elseif r< p(6)

x= A*x + b6; elseif r<p(7)

x= A*x + b7;

else

x= A*x + b8;

end

set(h,'xdata',x(1),'ydata',x(2));

drawnow

cnt = cnt + 1;

end

t = toc;

s = sprintf('7.8.0f points in 7.6.3f seconds',cnt,t); text(.2,-.05,s,'fontweight','bold'); set(stop,'style','pushbutton','string','close','callback','close(gcf)')

Section .7

L'ensemble de Julia

7.7.L'ensemble Julia avec c=-.745429

col=30;

m=400;

cx=0;

cy=0;

l=1.5;

x=linspace(cx-l,cx+l,m); y=linspace(cy-l,cy+l,m); [X,Y]=meshgrid(x,y);

c= -.745429;

Z=X+i*Y;

for k=1:col;

Z=Z.^2+c;

W=exp(-abs(Z));

end

colormap prism(256)

pcolor(W);

shading flat;

axis('square','equal','off');

Pour voir d'autre ensemble de Julia il suffit modifier le nombre c o`u le polynàome Z. Par exemple prenant c=0.32+0.034i et Z=Z.^3+c.

Section .8

L'ensemble de Mandelbort

col=20;

m=400;

cx=-.6;

cy=0;

l=1.5;

x=linspace(cx-l,cx+l,m); y=linspace(cy-l,cy+l,m); [X,Y]=meshgrid(x,y);

Z=zeros(m);

C=X+i*Y;

for k=1:col;

Z=Z.^2+C;

W=exp(-abs(Z));

end

colormap copper(256); pcolor(W);

shading flat;

axis('square','equal','off');

Pour voir d'autre ensemble de Mandelbort il suffit modifier le polynàome Z. Par exemple prenant Z=Z.^3+c.

R'ef'erences bibliographiques

[1] Alleche B. Quelques résultats sur la consonance, les multi-applications et la séquentialité. Th`ese de Doctorat (PhD) mathématiques, Universitéde Rouen, 1996.

[2] Barnsley M. F. Fractals Everywhere. Academic Press, Boston, 5^ème edition, 1993.

[3] Berger M. A Panoramic View of Riemannian Geometry. Springer, France, 2002.

[4] Bourbaki N. Topologie générale Chapitres 1-4. 'Eléments de mathémtique. SpringerVerlag Berlin, 2007.

[5] Bouziad A. and Calbrix J. Théorie de la mesure et l'intégration. Universitéde Rouen, 1993.

[6] Bronshtein I.N. Semendyayev K.A. Musiol G. et Muehlig H. Handbook of Mathematics. Springer-Verlag Berlin, 5^ème edition, 2007.

[7] Engelking R. General Topology. Heldermann Verlag Berlin, 1989.

[8] Falconer K.J. The Geometry of Fractal Sets. Cambridge University Press, Cambridge, 1985.

[9] Falconer K.J. Fractal Geometry. Mathematical Foundations and Applications. Wiley, New York, 2^ème edition, 1990.

[10] Gerald E. Measure, Topology, and Fractal Geometry. Springer, 2^ème edition, 2008.

[11] Helmberg G. Getting acquainted with fractals. Walter de Gruyter, 2007.

[12] Henrikson J. Completeness and total boundedness of the Hausdorff metric. 1999.

[13] Herbin R. et Gallouët T. Mesure et Integation. Universitéde Provence, 2008.

[14] Hutchinson J. Fractals and self-similarity. Indiana Journal of Mathematics 30, pages 713747, 1981.

[15] Julia G. M'emoire sur l'it'eration des fonctions rationnelles. Journal de math'ematiques pures et appliqu'ees, 8(1) :p. 47-246, 1918.

[16] Mendivil F. et Vrscay E.R. La Torre D. Iterated function systems on multifunctions. 2004.

[17] La Torre D. et Mendivil F. Iterated function systems on multifunctions and inverse problems. 2004.

[18] Lajoie J. La g'eom'etrie fractale. Master's thesis, Universit'e du Qu'ebec a` trois-rivi`eres, 2006.

[19] Mandelbrot B. B. Fractal aspects of the iteration of z -+ Az(1 -- z) for complex A, z. Ann. N. Y. Acad. Sci., 357 :249-259, 1980.

[20] Mandelbrot B. B. The Fractal Geometry of Nature. Freeman, San Francisco, 1982.

[21] Marian G. et Constantin P.N. Chaotic dynamical systems. An introduction. University of Craiova, Universitaria Press, 2002.

[22] McMullen C. The Hausdorff dimension of general Sierpi'nski carpets. Nagoya Math. J., 96,1-9, 1984.

[23] McMullen C. Area and Hausdorff dimension of Julia sets of entire functions. Transaction of the American mathematical society, 300(1), March 1987.

[24] Mitsuhiro S. The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets. April 1991.

[25] Olivier B. et Michel Z. Quelques r'esultats sur la dimension de Hausdorff des ensembles de Julia des polynàomes quadratiques. Fundamenta mathematicae, 151, 1996.

[26] Olivier E. Les dimensions fractales. Master's thesis, 2006.

[27] Peter M. Fractal geometry. From self-similarity to Brownian motion. Universit·at Kaiserslautern, 2000/2001.

[28] Rudin W. Principles of Mathematical Analysis. Dunod, ^3`eme edition, 1976.

[29] Rudin W. Analyse r'eelle et complexe. Cours et exercices. Dunod, ^3`eme edition, 1987.

For
this thesis,
we have used the
LATEX 2_E packages of
the society ma-
thematics of
France.