|
Année Scolaire 2021-2022
|
Université Mohammed il de
Rabat
Faculté des Sciences Juridiques,
Economiques
et Sociales d'Agdal
|
|
MEMOIRE DE FIN D'ETUDE POUR L'OBTENTION
DU DIPLOME DU
MASTER EN SCIENCES DE GESTION
OPTION : FINANCE
MESURE DE L'INTERDEPENDANCE
DU MARCHE BOURSIER MAROCAIN
Présenté et soutenu par :
Mohammed EL MASSAADI
Membres de jury :
M. Mohamed Yassine EL HADDAD FSEJS AGDAL
Encadrant
M. Saâd BENBACHIR FSEJS AGDAL
Suffragant
Mme Jalila AIT SOUDANE FSEJS AGDAL
Suffragant
Remerciements
« Celui qui ne remercie pas les gens ne remercie pas
Le Dieu »
En préambule de ce
mémoire, je remercier mon Dieu qui m'honorer de la patience et du
courage durant ces années d'apprentissage et de formation à ce
jour d'élaboration de mon mémoire d'obtention de Diplôme de
Master en Sciences de Gestion.
J'aimerai bien exprimer toute ma
gratitude à mes grands-parents, ma chère maman, ma chère
femme et amie, et toute ma famille, qui m'ont encouragé et soutenu tout
au long de mon parcours universitaire. Veuillez trouver dans ce mémoire
un modeste témoignage de mon admiration et toute ma gratitude, de mon
affection la plus sincère et de mon amour le plus profond.
Je tiens à remercier
particulièrement mon professeur et encadrant, Monsieur Yassine
EL HADDAD, Professeur à la Faculté des Sciences
Juridiques, Economiques et Sociales -Agdal, pour son encadrement, son suivi,
son aide durant l'élaboration de ce travail de recherche, aussi pour son
encouragement et sa compréhension de notre raccourcissement.
J'adresse mes vifs remerciements
à tous mes Honorables Professeurs, sans exception, qui ont
contribué à la personne que je suis, ils ont tous marqué
mon parcours d'apprentissage et d'éducation, en particulier les
professeurs qui m'ont enseigné durant ces deux ans de MSDG.
Je tiens à remercier mon cher
ami Mohammed BERAICH, pour ses conseils précieux, son encouragement, son
aide et son soutien.
Je tiens à présenter
aussi mes remerciements à toute personne ayant participé de
près ou de loin à la réalisation de ce modeste travail par
leurs inestimables conseils et contributions.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 2 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 3 sur 113
Résumé
Ce mémoire de recherche de fin d'étude contribue
à l'étude, l'analyse de la relation qui existe entre l'indice
principal de la Bourse des valeurs de Casablanca « MASI » et huit
indices sectoriels les plus essentiels de l'économie nationale, à
savoir : Assurances, Banques, Télécommunications, Bâtiments
& Matériaux de construction, Pétroles & Gaz,
Participation & Promotion immobilières, Transport et Loisirs &
Hôtels. Nous utilisons le modèle
d'hétéroscédasticité conditionnelle
autorégressive généralisé d'Engle (2002), afin de
bien analyser et étudier les corrélations dynamiques, durant la
période allant du 1er Janvier 2016 au 31 mai 2022.
Les résultats empiriques obtenus, des rendements et de
la volatilité des indices sectoriels, indiquent qu'il une contagion dans
le secteur boursier marocain. Nous avons constaté qu'il y a une force
corrélation conditionnelle dynamique entre le secteur bancaire et le
« MASI ».
Mots clés : MASI,
Volatilité conditionnelle ; corrélation conditionnelle dynamique
; Contagion ; EGARCH ; DCC-GARCH.
Abstract
The empirical results obtained, of the returns and the
volatility of the sectorial indexes, indicate that there is a contagion in the
Moroccan stock market sector. We found that there is a strong dynamic
conditional correlation between the banking sector and the main index of the
Casablanca Stock Exchange.
This present research contributes to the study, analysis of
the relationship between the main index of the Casablanca Stock Exchange "MASI"
and eight sectorial indices most essential to the national economy, namely:
Insurance, Banks, Telecommunications, Buildings & Construction Materials,
Oil & Gas, Real Estate Participation & Promotion, Transport and Leisure
& Hotels. We use the generalized autoregressive conditional
heteroscedasticity model of Engle (2002), in order to properly analyze and
study the dynamic correlations, during the period from January 1, 2016 to May
31, 2022.
The empirical results obtained, of the returns and the
volatility of the sectorial indexes, indicate that there is a contagion in the
Moroccan stock market sector. We found that there is a strong dynamic
conditional correlation between the banking sector and the MASI.
Keywords : MASI, Conditional
Volatility; Dynamic Conditional Correlation; Contagion; EGARCH; DCC-GARCH
Sommaire
Page
9
11
12
13
14
14
15
16
17
18
19
21
21
63
64
65
66
70
149
92
95
96 102 105 109 111
Introduction générale
Chapitre 1 : Revue de la littérature
Introduction
I. La Volatilité
II. La Transmission de la volatilité
III. La corrélation
IV. Modèle de la corrélation dynamique
(DCC-GARCH)
Conclusion
Chapitre 2 : Faits stylisés du marché boursier
marocain (BVC)
Introduction
I. Complexité de la modélisation des séries
financières
II. Faits stylisés
III. Pré-estimation des séries des rendements du
MASI et Indices Sectoriels
Conclusion
Chapitre 3 : Mesure de l'interdépendance du
marché boursier marocain par les modèles de corrélation
conditionnelle dynamique DCC-GARCH.
Introduction
I. Modèles GARCH univariés
II. Modèles GARCH multivariés
III. Modélisation de la corrélation
dynamique
IV. Prévisions de l'interdépendance
Conclusion
Conclusion générale
Annexe A : Programme Eviews
Annexe B : Programme Matlab
Annexe C : Programme R (DCC-GARCH)
Bibliographie
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 4 sur 113
Liste des abréviations
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 5 sur 113
ADF : Augmented Dickey Fuller.
AR : Autoregressive.
ARCH : Autoregressive Conditional
Heteroskedasticity.
ARMA : Autoregressive Moving Average.
ASSUR : Assurances.
BAT&MC : Bâtiments et
Matériaux de Construction.
BVC : Bourse des values de Casablanca.
BAM : Bank Al-Maghreb
BQ : Banques.
CCC : Constant Conditionnel correlation
General Autoregressive Conditional Heteroskedasticity
DCC-GARCH : Dynamic Conditional Correlation
General Autoregressive Conditional Heteroskedasticity.
EGARCH : Exponential General Autoregressive
Conditional Heteroskedasticity
HOT : Loisirs et Hôtellerie.
LJB : Ljung-Box
LM-ARCH : Lagrange Multiplier Autoregressive
Conditional Heteroskedasticity
MASI : Moroccan All Shares Index.
MA : Moving Average.
PP_IMMO : Participation et Promotion
Immobilières.
PET&GAZ : Pétroles et Gaz
TELECOM : Télécommunications
TRANS: : Transport.

Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 6 sur 113
Liste des Tableaux
Page
Figures du Chapitre 1 Figures du Chapitre 2
:
Tableau 1 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice principal
« MASI ».
Tableau 2 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Assurances ».
Tableau 3 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Banques ».
Tableau 4 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Bâtiment et MC ».
Tableau 5 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Pétroles et Gaz ».
Tableau 6 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« P.P Immobilières.
Tableau 7 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Télécommunications ».
Tableau 8 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Transport ».
Tableau 9 : Histogramme et statistiques
du rendement géométrique (log-return) de l'indice sectoriel
« Loisirs et Hôtellerie ».
Tableau 10 : Statistiques descriptives
de l'indice « MASI » et des indices de huit secteurs
d'activité étudiés.
Tableau 11 : Matrice
variance-covariance des rendements géométriques des huit secteurs
d'activité et l'indice « MASI ».
Tableau 12 : Matrice des
corrélations non conditionnelles des séries des rendements
géométriques des huit indices et le « MASI ».
Tableau 13 : Coefficients de
sensibilité des séries de rendements des
géométriques des huit secteurs d'activité avec le «
MASI ».
Tableau 14 : Classement des huit
indices sectoriels selon l'interdépendance avec l'indice principal
« MASI ».
Tableau 15 : Test de
stationnarité ADF pour la série des valeurs de l'indice «
MASI ».
Tableau 16 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Assurances ».
Tableau 17 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Bancaire ».
Tableau 18 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Télécommunications ».
Tableau 19 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Bâtiments et M. de Construction ».
Tableau 20 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Pétroles et Gaz ».
Tableau 21 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Participation et Promotion Immobilières ».
Tableau 22 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Transport ».
Tableau 23 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Loisirs et Hôtellerie ».
Tableau 24 : Test de
stationnarité ADF pour la série des rendements de l'indice «
MASI ».
Tableau 25 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Assurances ».
Tableau 26 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur bancaire.
Tableau 27 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur des «
Télécommunications ».
Tableau 28 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Bâtiments et MC ».
Tableau 29 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Pétroles et Gaz ».
Tableau 30 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « P.P Immobilières ».
Tableau 31 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Transport ».
Tableau 32 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Loisirs et Hôtellerie
».
Tableau 33 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice « MASI »
Tableau 34 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « Assurances ».
Tableau 35 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel «
Télécommunications »
Tableau 36 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « P.P Immobilières
»
Tableau 37 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « Pétroles &
Gaz »
24
25
26
26
27
27
28
28
29
32
37
37
38
38
39
40
40
41
42
42
43
43
44
45
45
46
46
47
47
48
48
49
50
51
52
53
54

55
56
57
58
60
60
60
61
61
61
61
62
62
74
76
78
80
82
84
86
88
90
93
Tableau 38 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « Bâtiments &
MC » Tableau 39 : Test d'autocorrélation
LJB pour la série des rendements géométriques de l'indice
Bancaire.
Tableau 40 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice « Transport ».
Tableau 41 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice « Loisirs & Hôtellerie
» Tableau 42 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice
MASI
Tableau 43 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
Assurances ».
Tableau 44 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
Télécommunications »
Tableau 45 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
P.P Immobilières » Tableau 46 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
Pétroles & Gaz » Tableau 47 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
Bâtiments & MC » Tableau 48 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice
Bancaire Tableau 49 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
Transport ». Tableau 50 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
Loisirs & Hôtellerie » Figures du Chapitre
3
Tableau 1 : Estimation du modèle
DCC-GARCH pour l'indice principal « MASI » et l'indice sectoriel
« Assurances ». Tableau 2 : Estimation du
modèle DCC-GARCH pour l'indice principal « MASI » et l'indice
Bancaire.
Tableau 3 : Estimation du modèle
DCC-GARCH pour l'indice principal « MASI » et l'indice «
Télécommunications ». Tableau 4 :
Estimation du modèle DCC-GARCH pour l'indice principal « MASI
» et l'indice sectoriel « Bâtiments et MC».
Tableau 5 : Estimation du modèle DCC-GARCH
pour l'indice principal « MASI » et l'indice sectoriel «
Pétroles & Gaz». Tableau 6 :
Estimation du modèle DCC-GARCH pour l'indice principal « MASI
» et l'indice sectoriel « P.P Immobilières».
Tableau 7 : Estimation du modèle DCC-GARCH
pour l'indice principal « MASI » et l'indice sectoriel «
Transport». Tableau 8 : Estimation du
modèle DCC-GARCH pour l'indice principal « MASI » et l'indice
sectoriel « Loisirs & Hôtellerie».
Tableau 9 : Degré de contagion
financière des huit indices sectoriels.
Tableau 10
: Prévision du degré de contagion financière
des banques
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 7 sur 113

Liste des Figures
Page
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 8 sur 113
Figures du Chapitre 1 :
Figures du Chapitre 2 :
Figure 1 : Cours et rentabilité
géométrique (log-return) du principal indice boursier marocain
« MASI ».
Figure 2 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Assurances ».
Figure 3 : Cours et rentabilité
géométrique (log-return) de l'indice
Bancaire.
Figure 4 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Télécommunications ».
Figure 5 : cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Bâtiments et Matériaux de
construction »
Figure 6 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Pétroles et Gaz»
Figure 7 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Participation& Promotion
Immobilière ».
Figure 8 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Transport ».
Figure 9 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Loisirs et Hôtellerie».
Figure 10 : QQ-plot du rendement
géométrique (log-return) du principal indice de la B.V.C.
Figure 11 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Assurances »
Figure 12 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Banques ».
Figure 13 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Télécommunications »
Figure 14 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Bâtiments & Matériaux de construction».
Figure 15 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Pétroles & Gaz ».
Figure 16 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Participation & Promotion
immobilières ».
Figure 17 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Transport ».
Figure 18 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Loisirs & Hôtels ».
Figure 19 : Clusters de
volatilité sur les rendements géométriques du principal
indice « MASI ».
Figure 20 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Assurances ».
Figure 21 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Banques ».
Figure 22 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Bâtiment et M.C
».
Figure 23 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Participation et
Promotion
Immobilière »
Figure 24 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Pétroles et Gaz
».
Figure 25 : Clusters de volatilité sur
les rendements de l'indice sectoriel «
Télécommunications ».
Figure 26 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Transport ».
Figure 27 : Clusters de volatilité sur
les rendements de l'indice sectoriel « Loisirs et
Hôtellerie ».
Figure 28 : Corrélogramme
d'autocorrélation des rendements de le« MASI ».
Figure 29 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Assurances ».
Figure 29 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Télécommunications ».
Figure 31 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Participation & Promotion
Immobilières ».
Figure 32 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Pétroles & Gaz ».
Figure 33 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Bâtiments & Matériaux de
construction ».
Figure 34 : Corrélogramme
d'autocorrélation des rendements de l'indice Bancaire.
Figure 35 : Corrélogramme
d'autocorrélation des rendements de l'indice sectoriel «
Transport ».
Figure 36 : Corrélogramme
d'autocorrélation des rendements de l'indice sectoriel «
Loisirs & Hôtellerie ».
21
22
22
22
22
23
23
23
23
29
30
30
30
31
31
31
31
32
34
34
34
35
35
35
35
36
36
50
51
52
53
54
55
56
57
58

75
77
79
81
83
85
87
89
92
Figures du Chapitre 3
Figure 1 : Corrélation conditionnelle
dynamique entre l'indice « Assurances » et le« MASI
» estimée par
DCC-GARCH(1,1).
Figure 2 : Corrélation conditionnelle
dynamique entre l'indice Bancaire et le« MASI »
estimée par DCC-
GARCH(1,1).
Figure 3 : Corrélation conditionnelle
dynamique entre l'indice « Télécommunications
» et le « MASI »
estimée par DCC-GARCH(1,1).
Figure 4 : Corrélation conditionnelle
dynamique entre l'indice « Bâtiments et MC» et le
« MASI » estimée
par DCC-GARCH(1,1).
Figure 5 : Corrélation conditionnelle
dynamique entre l'indice « Pétroles & Gaz» et le
« MASI » estimée par
le modèle DCC-GARCH(1,1).
Figure 6 : Corrélation
conditionnelle dynamique entre l'indice « Participation et
Promotion Immobilières» et
le« MASI » estimée
DCC-GARCH(1,1).
Figure 7 : Corrélation conditionnelle
dynamique entre l'indice « Transport » et le « MASI
» estimée par le
modèle DCC-GARCH(1,1).
Figure 8 : Corrélation conditionnelle
dynamique entre l'indice « Loisirs & Hôtellerie»
et le« MASI » estimée
par le modèle
DCC-GARCH(1,1).
Figure 9 : Prévision de la
corrélation entre le« MASI » et les huit indices
sectoriels.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 9 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 10 sur 113
Introduction Générale
La majorité des crises financières et
économiques sont dues, généralement d'une sous-estimation
des risques liés à certains actifs, le fameux exemple de cette
mauvaise estimation, celle des subprimes débutée en 2007,
à cause d'une sous-estimation du risque des crédits immobiliers
par les banques américaines, et malgré la
réactivité des pouvoirs publics, l'institution financière
« Lehman Brothers », n'a pas su s'en sortir. La faillite de Lehman
Brothers a déclenché une crise bancaire qui s'est
transformée après en une crise financière en touchant les
indices du marché boursier américain. Cette crise s'est
propagée ensuite aux grandes bourses mondiales par effet de contagion
financière, les économies développées sont ainsi
plongées dans une récession sévère et la crise
financière a touché l'économie réelle qui souffrait
déjà de plusieurs problèmes macroéconomiques en
particulier les taux de chômage et d'inflation élevés.
Dans la crise des subprimes 2007-2009, en plus les principaux
indices des bourses mondiales, les indices sectoriels ont aussi
contribué au déclenchement de cette crise elle s'est
propagée à toute l'économie du monde pour devenir une
crise systémique touchant la sphère réelle de
l'économie.
Depuis cette crise financière, plusieurs financiers et
économistes ont remis en cause la notion de l'interdépendance des
systèmes financiers, et le degré de liaison entre eux, ainsi que
les relations de dépendances de chaque indice boursier principal et tout
le marché des actions afin de bien savoir et connaître à
l'avance le secteur qui peut transmettre une telle contagion des risques.
Il était donc impossible de définir la contagion
à partir de tests d'évolution des liens entre les marchés.
Il est nécessaire de déterminer comment les chocs se transmettent
entre les marchés et que seuls certains mécanismes peuvent
véhiculer des phénomènes de contagion (comme l'imitation
ou le moutonnement). Pour prendre une définition plus
générale de la contagion et la définissons comme tout
canal qui transmet un choc d'un pays à un autre, un choc partagé
à une région ou entres des firmes appartenant au même
système financier.
La littérature économique se focalise sur
l'effet de contagion et montre qu'il s'appuie sur les liens entre banques. En
effet, les banques sont particulièrement impliquées dans les
systèmes de paiement en réseau, tels que les systèmes de
règlement -ou les systèmes de compensation, fonctionnant comme
des réseaux d'échange d'argent. Ces systèmes de paiement
ou d'échange de créances forment un réseau de relations
financières reliant les établissements bancaires Il est possible
donc de parler d'architecture des réseaux interbancaires en faisant
référence à la topologie de ces liens d'affaires unissant
les banques
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 11 sur 113
La multitude de crise, de crash et des
événements de risques qui ont généré des
pertes colossales et des conséquences économiques, sociales et
financières désastreuses ont renforcé le rôle des
autorités financières sur le contrôle bancaire et des
banques centrales en matière de réglementation, de supervision et
de contrôle des institutions financières.
Au Maroc la Bourse des valeurs de Casablanca joue un
rôle primordial dans la mesure de l'économie nationale,
considéré comme un vrai « thermomètre » du
niveau de développement ou récession de notre économie,
par le soutien et le contrôle permanent de la Banque centrale (BAM :
Bank-Al Maghreb), cette action de mesure, faite à travers les
différents secteurs constituant l'ensemble de l'économie
nationale.
Le marché des actions marocain comme tous les
marchés mondiaux, a subi aussi des différentes pertes à
causes de ces multitudes crises financières, une chose qui a
obligé les autorités marocaines, d'adopter des multitudes
réformes, qui ont rendu ce marché plus moderne et adapté
aux besoins économiques et financiers du pays.
L'objectif principal de ce mémoire est l'étude,
l'analyse et la mesure en utilisant le Modèle de corrélation
dynamique (DCC-GARCH), la relation d'interdépendance, entre l'indice
boursier principal du marché marocain des actions (B.V.C) et chacun des
huit indices des secteurs le plus principaux dans l'économie nationale,
afin de bien savoir le secteur le plus lié au marché.
Ce mémoire va répondre à la
problématique suivante : Comment peut-on utiliser la
volatilité comme un indicateur qui permet de mesurer la
corrélation entre un l'indice principal de la Bourse Marocaine et ses
indices sectoriels ainsi que leur dépendance ? Quel est le niveau et le
degré de cette dépendance dans le marché des actions
marocains ? Et quel est le secteur le plus dépend de l'indice principal
?
Pour se faire, ce mémoire a été
structuré en trois (03) chapitres : le premier chapitre est
consacré pour une revue de littérature des différents
concepts et notions intégrés dans cette recherche. Le
deuxième chapitre relate les principaux faits stylisés du
marché des actions. Le troisième chapitre est dédié
à la mesure de l'interdépendance du marché des actions
(Bourse des Valeurs de Casablanca), en utilisant le modèle de
corrélation conditionnelle dynamique DCC-GARCH.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 12 sur 113
1. Chapitre 1 : Revue de littérature
Introduction
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 13 sur 113
L'évolution récente de la volatilité
paraît trouver d'abord ses origines dans le repli durable et
prononcé des cours des actions depuis les sommets atteints en 2000, la
multiplication des chocs sur la sphère financière, l'augmentation
des incertitudes géopolitiques et macroéconomiques, ainsi que la
remise en cause par les investisseurs de la qualité des actifs
financiers dans un contexte marqué par une fragilisation des structures
financières des entreprises
Ce premier chapitre « Revue de littérature
» d'ordre théorique et conceptuel, sera donc
consacré à l'analyse de la revue de littérature relative
à notre sujet de recherche, surtout en ce qui concerne ceux ayant une
relation avec la volatilité des marchés boursiers. Sur ceux on
présentera dans un premier temps la volatilité du marché
boursier en mettant l'accent sur la volatilité en tant que mesure de
risque, sa transmission d'un indice à l'autre ou d'un pays à
l'autre et aussi le principe de corrélation entre les différents
actifs comme mesure de la relation d'évolution. Ensuite dans un second
temps nous mettons en lumière sur les différents modèles
d'estimation, dans ce chapitre on va citer seulement les modèles
univariés.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 14 sur 113
1.1. La volatilité
Le modèle de volatilité, dont le pionnier est le
prix Nobel d'économie Robert Engle (2003), permet aux chercheurs de
suivre quotidiennement l'évolution d'un large éventail de
marchés à l'aide de méthodologies de pointe
développées par des équipes de recherche
universitaires.
Il existe de nombreux modèles de mesure du risque
basés sur la volatilité et la distribution des rendements qui
peuvent être utilisés pour tester ces mesures de risque pour une
variété d'actifs.
La volatilité est un terme utilisé pour
décrire le degré auquel quelque chose peut changer. La
volatilité est définie comme la fréquence à
laquelle la valeur d'un actif quelconque fluctue autour d'une tendance
centrale1. La volatilité est importante dans l'étude
de l'économie et de la finance car elle est au coeur de nombreuses
décisions économiques et financières. Une autre raison de
sa présence dans la recherche et la littérature est qu'elle est
impossible à contrôler. L'impossibilité de la
maîtriser complètement conduit à une compréhension
fondamentale de ses mécanismes de diffusion. Il est crucial de
définir la volatilité avant de commencer. La volatilité du
marché étant une variable non observable, on tente de la mesurer
à l'aide d'une variable observable. Par conséquent, les
variations de prix d'un actif financier sont utilisées pour la mesurer.
Dans sa forme la plus élémentaire, la volatilité est
définie comme la différence entre les types de rendement des
actifs (Ramlall, 2010). Par conséquent, il s'agit d'une échelle
de risque. La volatilité présente quelques
caractéristiques bien connues : elle varie dans le temps dans une
fourchette de 1 à 5, et elle est autonome. En effet, les prix sont
hystériques, et la volatilité des périodes
précédentes a un impact sur la volatilité d'aujourd'hui.
La volatilité a tendance à être asymétrique et
à se regrouper. L'asymétrie de la volatilité est un
phénomène qui a été observé dans plusieurs
études empiriques, et elle augmente davantage après des chocs
négatifs que positifs. Dans les données financières, il
est également possible de voir que les petits chocolats sont suivis de
petits chocolats, et que les gros chocolats sont suivis de gros chocolats. Le
terme "regroupement de la volatilité" est utilisé pour
décrire ce phénomène.
Engle et al. (1990) distinguent deux effets visibles de la
transmission de la volatilité : l'effet des vagues de chaleur et l'effet
de la pluie de météorites. L'hypothèse d'un vent chaud
suggère que la source de la volatilité est le pays ou le
marché étudié. L'hypothèse de la pluie
météoritique, en revanche, suggère que la
volatilité est le résultat d'une transmission entre
différents pays ou marchés.
1 p. 281 .Bensafta et Semedo, (2011).
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 15 sur 113
1.2. La transmission de la volatilité
Depuis la mondialisation financière, le transfert de la
volatilité d'un pays à l'autre a pris de l'importance. Depuis le
milieu des années 1980, la mondialisation financière est devenue
une composante à part entière du paysage financier, favorisant
les mouvements des marchés internationaux entre les pays
développés (Kose, Prasad, Rogoff et Wei, 2009). Ce processus
financier comprend la déréglementation, la
désintermédiation et le démantèlement. Ce dernier
joue un rôle crucial dans la transmission de la volatilité. Le
terme "décloisonnement" fait référence à la
suppression des cloisons ou des barrières. Les frontières qui
existaient auparavant entre les différents marchés et pays se
sont réduites ou ont disparu. Les marchés financiers
internationaux sont devenus plus interdépendants à des
degrés divers. La volatilité des marchés a augmenté
pendant les crises financières, tout comme les corrélations entre
eux. Les marchés financiers sont devenus de plus en plus
interdépendants à l'échelle mondiale, ce qui les rend plus
vulnérables aux catastrophes financières. Par conséquent,
la suppression des frontières facilite la propagation de la
volatilité entre les pays. Par conséquent, les crises se
propagent plus rapidement d'une économie à l'autre. Malgré
les avantages de la mondialisation financière, tels que l'augmentation
du partage international des risques, la compétitivité et
l'efficacité, le risque de propagation des crises financières
au-delà des frontières a également augmenté
(Claessens, Kose et Terrones, 2010).
1.3. La corrélation
La force d'une relation entre deux actifs est mesurée
par la corrélation ; le coefficient linéaire de
corrélation varie entre -1 et 1. S'il est égal à 1, la
relation entre les deux actifs est assez forte, et les marchés
financiers fluctuent dans la même direction. Par conséquent, la
corrélation permet d'évaluer le risque car elle évalue la
contagion entre les actifs (par exemple, si un actif baisse fortement, comment
les autres actifs sont-ils réagir).
Ces dernières années, on dispose de plus
d'informations sur les crises financières, qui surviennent
fréquemment et entraînent des dépressions
économiques. Dans la littérature sur les crises
financières, le terme "contagion financière" est
fréquemment utilisé. En effet, l'étude des crises
économiques et de leurs conséquences permet de déterminer
comment un choc qui commence dans un pays se propage rapidement à de
nombreux marchés dans le monde. Les premiers travaux empiriques sur la
contagion financière étaient basés sur la comparaison des
coefficients de corrélation de Pearson entre les marchés
financiers en période d'accalmie et en période de crise. Pendant
une crise, le phénomène de contagion est détecté
par des augmentations significatives du coefficient de corrélation. Le
coefficient de corrélation entre les rendements boursiers a
été utilisé par King et Wadhwani (1990) et Lee et Kim
(1993) pour examiner l'impact du crash boursier, arrivé aux Etats-Unis
en 1987, sur les marchés des autres pays. Les résultats
empiriques montrent que pendant la crise, les coefficients de
corrélation entre les différents marchés ont
augmenté de manière significative.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 16 sur 113
1.4. Modèle de corrélation dynamique
(DCC-GARCH)
Engle (2002) introduit le modèle à
corrélations conditionnelles dynamiques, le DCC-GARCH, en permettant
à la matrice de corrélations conditionnelles de varier dans le
temps. Ce modèle est une généralisation du modèle
CCC-GARCH de Bollerslev (1990).
Le modèle DCC-GARCH est défini comme :
|
rt = Pt + £t
|
(1)
|
Et = Ht1/2 nt =
at nt
|
(2)
|
Ht = DtRtDt
|
(3)
|
|
Avec :
rt : Vecteur de rendements
de n actifs au temps t de dimension nx1 ;
ut : Vecteur de rendements
espérés conditionnels de n actifs au temps t de dimension
nx1 ;
Et : Vecteur d'erreurs
conditionnelles i.i.d au temps t de dimension nx1 ;
Les résidus conditionnels Et sont
distribués selon une loi normale de moyenne 0 et de
varianceHt. E[et] = 0 et Var[et]
= Ht ;
Ht : Matrice de variance
conditionnelle de Et au temps t de dimension nxn ;
Dt : Matrice diagonale des
écarts-types conditionnels de Et au temps t de
dimension nxn ;
Rt : Matrice de
corrélation conditionnelle de Et au temps t de
dimension nxn ; et le vecteur %est i.i.d c'est un bruit blanc de
moyenne nulle et de variance égale à 1. avec E( nt
) = 0 Et Var( nt ) = 1
La matrice Ht est divisée en deux
matrices Dt et Rt. Les
éléments de la matrice Dt proviennent des
modèles GARCH uni-variés estimés pour chacune des
séries.
La matrice Ht désigne la matrice de
variance-covariance conditionnelle :
_ aMt aitaMtpit
Ht 2 ) (04)
aitaMtpit ait
Où ait et aMt
désignent les écarts types conditionnels et pit la
corrélation conditionnelle.
On suppose que les corrélations conditionnelles
variables dans le temps pit rend pleinement compte de la
dépendance entre les rentabilités des firmes et du marché.
Formellement, cette hypothèse implique que les innovations -itet
£Mt sont distribuées indépendamment au moment t.
Conclusion
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 17 sur 113
Les crises financières ont conduit à
l'apparition d'un nombre important d'indicateur de volatilité, issus
soit du monde académique, soit des institutions en charge des politiques
économiques. L'analyse de l'interdépendance entre les
différents indices boursiers, fait qui fait partie importante des
travaux de recherche au sein du FMI et réunit à la fois les
chercheurs au niveau académique et les responsables de la
réglementation financière.
Dans ce premier chapitre on a fait un aperçu des
écrits sur la volatilité, du fait que notre revue s'est
basée sur deux volets. Dans le premier, nous avons essayé de
vulgariser le concept de la volatilité en rappelant son utilité.
Alors on peut dire que la volatilité est une variable non observable,
ainsi le fait qu'on ne peut pas la contrôler est une autre raison qui
justifie sa présence dans les recherches.
Dans le deuxième volet, nous avons
synthétisé les principaux acquis en matière d'estimation
de la volatilité en distinguons entre les différentes classes de
modèles univariés à volatilité conditionnelle (de
type ARCH), à volatilité stochastique, à volatilité
implicite et historique. Des modèles bien représentatifs de
chaque classe sont caractérisés tant dans leurs hypothèses
et leurs dynamiques que dans leur performance au niveau des tests subis.
Dans ce qui suit nous allons étudiés,
empiriquement, la relation existant entre le MASI, et les principaux indices
sectoriels de la bourse des valeurs de Casablanca, dans le premier chapitre une
analyse approfondie de chaque indice individuel, puis en deuxième
chapitre la relation entre le MAST et chaque secteur d'activité.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 18 sur 113
2. Chapitre 2 : les faits stylisés du
marché boursier
marocain : La Bourse des valeurs de
Casablanca
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 19 sur 113
Introduction
La Bourse des Valeurs de Casablanca, marché officiel de
négociation de différentes actions, représente le «
thermomètre » de l'économie nationale du pays,
contrôlée par Banque Al-Maghreb (BAM), qui est en plus de ses
missions traditionnelles, telles que l'émission des billets, le
contrôle de la politique monétaire du pays, il contribue aussi
bien au Maroc que dans le monde, à l'évolution et
l'épanouissement de l'économie nationale, surtout lorsqu'il
s'agit de l'esprit concurrentiel et compétitif des
sociétés, ainsi que leur ouverture au niveau international. C'est
pour cette raison que les sociétés ayant le même domaine
activité, ont regroupés dans des secteurs d'activité, en
créant des indices sectoriel, pour être soudées et bien
développées, pour pouvoir résister devant les crises
financières et les risques. Suite à l'avènement de
plusieurs crises financières dans le monde, la BVC est aujourd'hui de
plus en plus des entités clés du système financier dans
son ensemble. Nous allons dans ce chapitre présenter les faits
stylisés des principaux secteurs d'activité qui regroupent les
entreprises et sociétés cotées en bourse.
L'étude et la modélisation des séries
financières présentent un débat très
intéressant dans le domaine de la finance. De nombreux travaux de
recherche ont tenté de comprendre le comportement stochastique des
séquences financières. À cet égard, on peut citer
Cont (2000) et Swell (2011). Ces deux articles mettent en lumière les
principales propriétés empiriques observées sur la plupart
des marchés financiers. Les pics fins et
l'hétéroscédasticité sont l'un des points forts de
la série financière.
Au terme de ces études, les auteurs mettent en
évidence des propriétés atypiques par rapport à la
distribution normale des rendements financiers en série. En fait, les
queues de la distribution des récompenses semblent être plus
épaisses que celles de la régularité normale. Ceci est
donné par le coefficient d'aplatissement qui affiche une valeur
supérieure à 3 (la valeur lorsque le coefficient d'aplatissement
est normal). La leptokurticité est l'un des aspects complexes des
marchés financiers. Il est souvent utilisé pour
caractériser la distribution non normale des rendements boursiers.
Concernant l'hétéroscédasticité,
ce phénomène a été introduit pour la
première fois par Engle (1982) et transformé par l'existence de
l'effet autorégressif à volatilité conditionnelle (effet
ARCH) généralisé par Bollerslev (1986) avec le processus
GARCH.
L'objectif principal de ce chapitre est de présenter
ces faits stylisés, propriétés statistiques
communément observées sur le marché officiel des actions
au Maroc (BVC). À cet effet, nous allons mener une étude
empirique sur l'évolution de l'indice principal de la Bourse marocaine
« MASI » et clôturer les valeurs indiciaires des secteurs
d'activité des sociétés cotées en bourse entre le
1er janvier 2016 et le 31 mai 2022, soit 1596
valeurs.
Nous commençons par la mise en évidence des
faits stylisés des séries financières des rendements
géométriques des cours des indices sectoriels et de l'indice
principal « MASI », nous faisons une analyse graphique, descriptive
et économétrique de toutes ces séries, nous effectuons
aussi les tests de non stationnarité, de normalité,
d'autocorrélation et
d'hétéroscédasticité.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 20 sur 113
2.1. Complexité de la modélisation des
séries financières
Il est complexe de modéliser les séries
financières (prix d'action, taux d'intérêt, taux de change
etc...) par des modèles stochastiques linéaires comme les
modèles ARMA. Les séries financières se
présentant sous différentes formes selon la fréquence
d'observation (seconde, minute, heure, jour, etc.) se caractérisent par
l'existence de régularités statistiques connues sous le nom de
faits stylisés. Mandelbrot (1963) a mis en évidence un ensemble
de faits stylisés apparaissant plus ou moins nettement dans les
séries financières en fonction de la fréquence
d'observation ou périodicité de la série et de sa nature.
Les séries de prix d'actif et de rendements présentent
généralement un certain nombre de propriétés
similaires suivant leur périodicité.
Il existe beaucoup de mesures de rendement d'un indice
boursier, celle fréquemment utilisée est le rendement
géométrique ou le log-rendement, qui consiste à calculer
le logarithme du différentiel des valeurs en t et t
- 1 :
On définit donc le rendement de ce titre à
l'instant t par :
|
rt = log
|
(PP_t
t1 I avec t = 1, 2, ... n (1)
|
Avec :
rt : Le rendement géométrique
d'un titre au temps t.
Pt : Le prix d'un titre au temps t.
Nous raisonnons souvent sur les rendements logarithmiques
lorsqu'il s'agit de l'analyse des
séries financières, pour permettre la
comparaison avec d'autres séries financières. En outre, comme
nous allons voir dans la suite de notre étude, la série des
valeurs des actifs financiers n'est pas stationnaire, pour cette raison nous
passons à la différenciation logarithmique du premier ordre pour
rendre la série stationnaire, ce qui permet l'estimation des
paramètres du modèle retenu.
Dans ce qui suit nous présentons un certain nombre de
propriétés observées dans les actifs financiers.
Propriété 1 :
Stationnarité
v La série des prix (Pt) est non
stationnaire d'ordre deux.
v La série des rendements géométriques
(rt) est stationnaire d'ordre deux.
Propriété 2 :
Autocorrélations des carrés des
variations de prix
v La série ( rt2) des
carrés des rendements géométriques présente
généralement de fortes autocorrélations
v La série des rendements géométriques
(rt) est caractérisé par des
autocorrélations très faibles.
Propriété 3 : Queues de
distribution épaisses
Les tests classiques de normalité rejettent nettement
l'hypothèse d'une distribution normale. Les queues des distributions
empiriques des rendements sont généralement plus épaisses
que celles d'une loi gaussienne, on dit que la distribution leptokurtique.
Rappelons que la Kurtosis d'une variable aléatoire X
est le moment centré d'ordre 4 :
Kurtosis de X= 1.1.4 = E[(X -
E(X))4] (2)
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 21 sur 113
La Kurtosis est une mesure de l'épaisseur des queues de
distributions. Si la Kurtosis excède 3 (queues épaisses) la
distribution est dite leptokurtique, si la Kurtosis est inférieure
à 3, la distribution est dite platikurtique. Pour une loi normale, la
Kurtosis est égale à 3, la distribution est dite
mésokurtique
Une autre mesure équivalente est également
utilisée, le degré d'excès de Kurtosis définie par
:
Degré d'excès de
Kurtosis=
|
E[(X-E(X))4]
|
(3)
3
|
|
|
Cette dernière mesure se compare par rapport à
la loi normale qui se caractérise par une distribution à queue
plate avec un degré d'excès de Kurtosis égal à
0.
Propriété 4
: Clusters de Volatilité
On observe empiriquement que de fortes variations des
rendements sont généralement suivies de fortes variations. On
constate un regroupement des extrêmes en cluster ou paquets de
volatilités.
Ce fait stylisé remet en cause l'hypothèse
d'homoscédasticité généralement adopté dans
les modèles linéaires.
Propriété 6 :
Asymétrie
La distribution des cours est généralement
asymétrique, c'est à dire qu'il y a plus de mouvements forts
à la baisse qu'à la hausse
Un test simple de l'hypothèse de symétrie
consiste à tester la nullité du moment centré d'ordre
trois de la distribution, appelé la Skewness défini par :
La Skewness ???? ??= L?? = ??[(?? -
??(??))??] (4)
Une autre mesure d'asymétrie est aussi
utilisée, le coefficient de Skewness défini par :
??[(??-?? (??))?? ] (5)
Coefficient de Skewness =
(??????(??))??
? Un coefficient positif indique une distribution
décalée à gauche de la médiane, et donc une queue
de distribution étalée vers la droite.
? Un coefficient négatif indique une distribution
décalée à droite de la médiane, et donc une queue
de distribution étalée vers la gauche.
2.2. Faits stylisés du marché
financier
Dans ce chapitre, nous allons utiliser les cours journaliers
de l'indice principal du marché boursier marocain « MASI »,
ainsi que les cours journaliers des indices de huit principaux secteurs
d'activité de l'économie nationale, à savoir le secteur
Bancaire, des Assurances, des Télécommunications, Bâtiments
& Matériaux de construction, Loisirs et Hôtels, du Transport,
Pétroles & Gaz et en dernier lieu le secteur « Participation et
Promotion immobilières ». Après une analyse
préliminaire, en essayant d'analyser la sensibilité des
rentabilités de l'indice de chaque secteur d'activité aux
fluctuations du rendement de l'indice principal « MASI », puis on
présenter les différents résultats empiriques qui y
afférents.
L'objectif majeur de cette section est d'exposer les
propriétés statistiques observées fréquemment dans
la plupart des marchés financiers. Pour ce faire, nous allons
procéder à l'étude empirique de l'évolution de
l'indice « MASI », et des huit secteurs d'activité choisi dans
cette étude, durant la période allant du 01/01/2016 au
31/05/2022, soit 1 596 cours.
Les données ont été
téléchargées du site officiel de la Bourse des
valeurs de Casablanca (
www.casablanca-bourse.com).
2.2.1 Analyse graphique :
Les figures présentées ci-dessous
présentent l'évolution des cours et des rendements
géométriques de l'indice principal de la bourse de Casablanca et
huit (08) indices sectoriels, durant la période allant
du 01/01/2016 au 31/05/2022.
La figure 1 affiche les séries des prix et des
rendements géométriques du principal indice « MASI
».
Prix de l'Indice Principal
"MASI"
15,000 14,000 13,000
12,000 11,000 10,000 9,000
8,000
|
|
|
16 17 18 19 20 21 22
Rendement Géométrique de l'Indice
Principal "MASI"
.06 .04 .02 .00
-.02 -.04 -.06 -.08
-.10
|
|
|
16 17 18 19 20 21 22
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 22 sur 113
Figure 1 : Cours et
rentabilité géométrique (log-return) de l'indice principal
du marché boursier « MASI ».
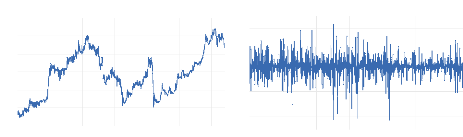
La figure 2 présente les séries des prix et des
rendements géométriques de l'indice sectoriel « Assurances
».
6,000
5,500
5,000
4,500
4,000
3,500
3,000
Prix de l'indice "Assurances"
16 17 18 19 20 21 22
Rendement Géométrique de l'Indice
"Assurances"
16 17 18 19 20 21 22
.08
.06
.04
.02
.00
-.02
-.04
-.06
-.08
-.10
Figure 2 : Cours et
rentabilité géométrique (log-return) de l'indice sectoriel
« Assurances ».
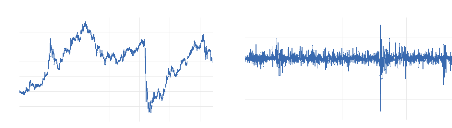
La figure 3 présente les séries des prix et des
rendements géométriques de l'indice du secteur Bancaire.
Prix de l'Indice "BANQUES"
Rendement Géométrique de l'Indice
"BANQUES"
14,000
13,000
12,000
11,000
.08
.04
.00
-.04
-.08
-.12
10,000
9,000
16 17 18 19 20 21 22
16 17 18 19 20 21 22
16,000
15,000
Figure 3 : Cours et
rentabilité géométrique (log-return) de l'indice
Bancaire.
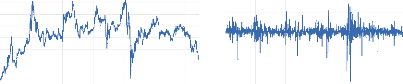
La figure 4 présente les séries des prix et des
rendements géométriques de l'indice sectoriel «
Télécommunications ».
Prix de l'Indice
"Télécommunications"
2,400
2,300
2,200
2,100
2,000
1,900
1,800
1,700
1,600
21 22
Rendement Géométrique de l'Indice
"Télécommunications"
.08
-.12
16 17 18 19 20 21 22
-.04
-.08
.04
.00
Figure 4 : Cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Télécommunications ».
La figure 5 présente les séries des prix et des
rendements géométriques de l'indice sectoriel «
Bâtiments et Matériaux de construction ».
Prix de l'Indice "BÂTIMENTS ET
M.CONSTRUCTION" Rendement Géométrique
de l'Indice"BAT ET M.CONSTRUCTION"
21 22
16 17 18 19 20
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 23 sur 113
24,000 22,000
20,000 18,000 16,000 14,000
12,000 10,000
16
17
18
19
20
21
.08
.04
.00
-.04
-.08
22 -.12
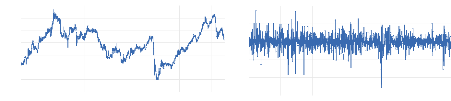
Figure 5 : cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Bâtiments et Matériaux de construction »
La figure 6 présente les séries des prix et des
rendements géométriques de l'indice sectoriel «
Pétroles et Gaz».
Prix de l'Indice
"PETROLES_GAZ" Rendement Géométrique
de l'Indice "PETROLES_GAZ"
21 22
16 17 18 19 20
16 17 18 19 20 21 22
24,000
20,000
16,000
12,000
8,000
4,000
.08
.04
.00
-.04
-.08
-.12
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 24 sur 113
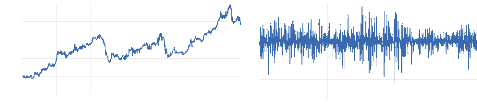
Figure 6 : cours et rentabilité
géométrique (log-return) de l'indice sectoriel «
Pétroles et Gaz»
La figure 7 présente les séries des prix et des
rendements géométriques de l'indice sectoriel «
participation et promotion immobilière ».
Prix de l'Indice "PROMOTION
IMMOB" Rendement Géométrique de
l'Indice "PROMOTION IMMOB"
20,000 16,000
12,000 8,000 4,000
0
|
|
.12 .08
.04 .00 -.04 -.08
|
|
|
-.12
|
|
|
|
Figure 7 : cours et
rentabilité géométrique (log-return) de l'indice sectoriel
« Participation & Promotion Immobilière ».
La figure 8 présente les séries des prix et des
rendements géométriques de l'indice sectoriel « Transport
».
.12
.08
.04
Rendement Géométrique de l'Indice
"TRANSPORT"
Prix de l'Indice "TRANSPORT"
1,600
-.12
16 17 18 19 20 21 22
16 17 18 19 20
21 22
.00
2,400
-.04
2,000
-.08
3,600
3,200
2,800
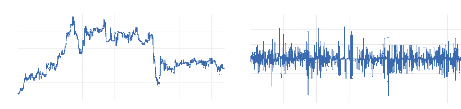
Figure 8 : cours et
rentabilité géométrique (log-return) de l'indice sectoriel
« Transport ».
La figure 9 présente les séries des prix et des
rendements géométriques de l'indice sectoriel « Loisirs et
Hôtellerie».
900 800
700 600 500 400
300
|
Prix de l'Indice "HOTELLERIE"
|
.12 .08
.04 .00 -.04 -.08
-.12
|
Rendement Géométrique de l'Indice
"HOTELLERIE"
|
|
|
|
16 17 18 19 20 21 22
|
|
|
Figure 9 : cours et
rentabilité géométrique (log-return) de l'indice sectoriel
« Loisirs et Hôtellerie».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 25 sur 113
La figure 1 présente les séries des prix et des
rendements géométriques de l'indice boursier « MASI »
sur la période étudiée. On constate que les cours du
« MASI » sont caractérisés par une tendance parfois
haussière et parfois baissière tandis que ses rendements
géométriques ont enregistré une forte volatilité
durant la période étudiée, en atteignant parfois des
niveaux très bas de performance.
Les figures 2, 3, 4, 5, 6, 7, 8 et 9 montrent que les indices
sectoriels individuels ont suivi la même tendance que l'indice principal
dans sa tendance. Dans ce qui suit dans ce chapitre, nous allons faire une
analyse descriptive et économétrique de l'indice principal et
indices sectoriels du marché boursier (Assurances, Banques,
Télécommunications, Bâtiments & Matériaux de
construction, Pétroles & Gaz, Participation & Promotion
immobilières, Transport et Loisirs & Hôtels).
2.2.2 Analyse descriptive
Pour avoir une idée très fiable sur
l'évolution des données au cours du temps, on s'intéresse
aux statistiques descriptives des données (moyenne, écart type,
minimum, maximum, Skewness et Kurtosis). Le test de normalité des
séries temporelles étudiée dans ce sujet, est basé
primordialement aux coefficients « Skewness », « Kurtosis »
et la statistique du test de « Jarque-Bera ».
Le tableau 1 affiche l'histogramme et les statistiques
descriptives des rendements géométriques de l'indice « MASI
».
600 500 400 300 200 100
0
|
|
|
|
|
Series: MASI
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000206
Median 0.000272
Maximum 0.053054
Minimum -0.092317
Std. Dev. 0.007353
Skewness -1.853794
Kurtosis 30.75269
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 52100.56
Probability 0.000000
|
|
|
|
|
|
|
|
Tableau 1 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
« MASI ».
Dans le premier tableau sont représentés les
différents paramètres statistiques de la série des
rendements géométrique de l'indice « MASI », sur la
période étudiée. On constate que la représentation
graphique de la série des rendements géométriques prend
une forme leptokurtique :
? Le coefficient d'aplatissement (Kurtosis k=
30.75269 est plus grand que 3, celui de la distribution normale. ? Le
coefficient d'asymétrie (Skewness s = -1.853794 #
0) dans le cas d'une distribution normale. Le tableau montre un
coefficient de Skewness significativement négatif, ce qui nous permet de
déduire que la distribution est asymétrique et que la
probabilité d'obtenir des rendements inférieurs à la
moyenne étant supérieure à celle d'obtenir des rendements
plus élevés que la moyenne.
La valeur de la Kurtosis de 30.75269 est largement
supérieure à 3 qui correspond à celle de la loi gaussienne
suggère une queue épaisse de la distribution.
La lecture analytique des paramètres de «
Skewness » et de « Kurtosis »
conduit aux évidentes constations concluent dans les différentes
études des cours boursiers. Généralement, ces coefficients
sont différentes de 0 et 3, ce qui indique que la série des
rendements géométriques du « MASI » est n'est pas
normale mais plutôt asymétrique avec des queues épaisses
caractérisant une distribution leptokurtique. Ce qui nous conduit au
rejet de l'hypothèse de normalité.
De davantage, on représente un récapitulatif de
ces différentes propriétés dans l'histogramme de la
série des rendements, et cela en partageant les rendements journaliers
de l'indice principal du marché boursier. On remarque bien que la
distribution des rendements n'est pas normalement aplatie. Elle a en
particulier des queues de distribution trop épaisses (Kurtosis =
30.75269 > 3).
En outre, le test de Jarque Bera qui donne une p-value
égale à 0,000000 (sous l'hypothèse nulle H0, La
p-value est la probabilité d'obtenir une statistique aussi extrême
(pour ne pas dire aussi grande) que la valeur observée sur
l'échantillon. La p-value à un seuil de confiance
préalablement défini (traditionnellement 5 %). Dans notre cas
p-value < 5% et donc on rejette H0 : les données suivent une loi
normale) pratiquement nulle.
La valeur très élevée de la statistique
de Jarque-Bera (JB) de 52100.56 confirme le rejet de l'hypothèse nulle
de la normalité des rendements géométriques pour cet
indice. Ce qui nous conduit à confirmer la non-normalité de la
série des rendements géométriques de l'indice principal
« MASI ».
Les tableaux (2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9) affichent
respectivement les statistiques descriptives des rendements
géométriques du cours des huit indices sectoriels
étudiés dans ce mémoire (Assurances, Banques,
Télécommunications, Bâtiments & MC, Pétroles
& Gaz, P.P immobilières, Transport et Loisirs & Hôtels).
Ces tableaux incluent aussi les histogrammes des rendements
géométriques des cours de ces indices.
600 500 400 300 200 100
0
|
|
|
|
|
|
|
|
Series: ASSURANCES
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000262
Median 0.000193
Maximum 0.067062
Minimum -0.085039
Std. Dev. 0.013541
Skewness -0.602697
Kurtosis 9.394267
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 2813.821
Probability 0.000000
|
|
|
|
|
|
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 26 sur 113
-0.08 -0.06 -0.04 -0.02 0.00 0.02 0.04 0.06
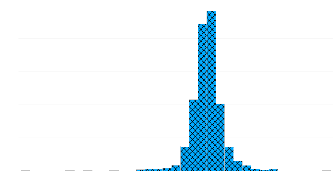
Tableau 2 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Assurances ».
500
400
300
200
100
Le tableau 2 des rendements géométriques de
l'indice sectoriel « Assurances », montre une Skewness
négative de -0.602697 ce qui nous permet de déduire que les
rendements géométriques pour cet indice ont une longue queue
à droite. La valeur de la Kurtosis de 9.394267, est largement
supérieure à 3, (celle de la loi normale), ce qui explique une
queue épaisse de la distribution. La valeur élevée de la
statistique de Jarque-Bera (JB) 8213.821 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MAST
».
Series: BANQUES
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 9.60e-05
Median 0.000204
Maximum 0.065637
Minimum -0.103011
Std. Dev. 0.009099
Skewness -1.379363
Kurtosis 22.21553
Jarque-Bera 25044.63
Probability 0.000000
Tableau 3 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Banques ». Le tableau 3 des rendements
géométriques du cours de l'indice sectoriel « Banques
», montre une Skewness négative de -1.379363 ce qui nous permet de
déduire que les rendements géométriques pour cet indice
ont une longue queue à droite. La valeur de la Kurtosis de 22.21553, est
largement supérieure à 3, ce qui explique une queue
épaisse de la distribution. La valeur élevée de la
statistique de Jarque-Bera (JB) 25 044.63 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MAST
».
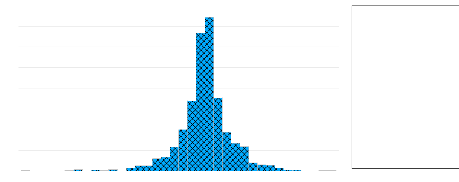
400
350
300
250
200
150
100
50
Series: BAT_MC
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000143
Median 0.000182
Maximum 0.070042
Minimum -0.101991
Std. Dev. 0.014411
Skewness -0.529689
Kurtosis 8.092728
Jarque-Bera 1798.240
Probability 0.000000
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 27 sur 113
Tableau 4 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Bâtiment et MC ».
Le tableau 4 des rendements géométriques du
cours de l'indice sectoriel « Bâtiments et MC », montre une
valeur de Skewness négative de -0.529689 ce qui nous permet de
déduire que les rendements géométriques pour cet indice
ont une longue queue à droite. Le coefficient de la Kurtosis affiche une
valeur de 22.21553, qui est supérieure à 3, celle correspondante
à la loi gaussienne, ce qui explique une queue épaisse de la
distribution. La valeur très élevée du paramètre de
Jarque-Bera (JB) qui est égal à 1798.240 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MASI
».
600 500
400 300 200 100
|
|
|
|
|
|
|
|
Series: PETROLES &
GAZ
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000551
Median 0.000000
Maximum 0.073292
Minimum -0.087289
Std. Dev. 0.015600
Skewness -0.248322
Kurtosis 7.022547
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 1091.747
Probability 0.000000
|
0
|
|
|
|
|
|
|
|
|
|
|
-0.075 -0.050 -0.025 0.000 0.025 0.050
0.075
Tableau 5 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Pétroles et Gaz ».
Le tableau 5 des rendements géométriques du
cours de l'indice sectoriel « Pétroles et Gaz », montre une
Skewness négative de -0.248322 ce qui nous permet de déduire que
les rendements géométriques pour cet indice ont une longue queue
à droite. La valeur de la Kurtosis de 7.022547, est largement
supérieure à 3, celle correspondante à la loi gaussienne,
ce qui explique une queue épaisse de la distribution. La valeur
élevée de la statistique de Jarque-Bera (JB) 1091.747 confirme le
rejet de l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MASI
».
300 250
200 150 100
50
0
|
|
|
|
|
|
|
|
|
|
Series: PROMOTION IMMO
Sample 1/05/2016 5/31/2022
Observations 1595
Mean -0.000634
Median -0.000581
Maximum 0.090888
Minimum -0.104202
Std. Dev. 0.019702
Skewness -0.162483
Kurtosis 5.890305
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 562.2020
Probability 0.000000
|
|
|
|
|
|
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 28 sur 113
-0.100 -0.075 -0.050 -0.025 0.000 0.025 0.050
0.075
Tableau 6 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « P.P Immobilières.
Le tableau 6 des rendements géométriques du
cours de l'indice sectoriel « Bâtiments et MC », montre une
valeur de Skewness négative de -0.162483 ce qui nous permet de
déduire que les rendements géométriques pour cet indice
ont une longue queue à droite. Le coefficient de la Kurtosis affiche une
valeur de 5.890305, qui est supérieure à 3, celle correspondante
à la loi gaussienne, ce qui explique une queue épaisse de la
distribution. La haute valeur de Jarque-Bera (JB) = 562.2020 confirme le rejet
de l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MASI
».
700
600
500
400
300
200
100
0

Series: TELECOM
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 6.70e-05
Median 0.000000
Maximum 0.056536
Minimum -0.100845
Std. Dev. 0.009296
Skewness -1.243981
Kurtosis 21.42858
Jarque-Bera 22981.45
Probability 0.000000
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance
2021-2022 Page 29 sur 113
-0.100 -0.075 -0.050 -0.025 0.000 0.025
0.050
Tableau 7 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Télécom ».
Le tableau 7 des rendements géométriques du
cours de l'indice sectoriel « Télécom », montre un
Skewness négative de -0.529689, ce qui nous permet de déduire que
les rendements géométriques pour cet indice ont une longue queue
à droite. Le coefficient de la Kurtosis affiche une valeur de 21.42858,
qui est supérieure à 3, celle correspondante à la loi
gaussienne, ce qui explique une queue épaisse de la distribution. La
valeur très élevée du paramètre de Jarque-Bera (JB)
qui est égal à 22981.45 confirme le rejet de l'hypothèse
nulle de la normalité des rendements géométriques pour cet
indice aussi bien que l'indice « MASI ».
900 800
700 600 500 400 300
200 100
0
|
|
|
|
|
|
Series: TRANSPORT
Sample 1/05/2016 5/31/2022
Observations 1595
|
|
|
|
|
|
|
|
|
|
Mean 0.000168
Median 0.000000
Maximum 0.087665
Minimum -0.100192
Std. Dev. 0.016234
Skewness -0.010929
Kurtosis 8.827230
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 2256.732
Probability 0.000000
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 8 : Histogramme et
statistiques du rendement géométrique de l'indice sectoriel
« Transport ».
Le tableau 8 des rendements géométriques du
cours de l'indice sectoriel « Transport », montre un Skewness
négative de -0.010929, ce qui nous permet de déduire que les
rendements géométriques pour cet indice ont une longue queue
à droite. Le coefficient de la Kurtosis affiche une valeur de 8.8272.30,
qui est supérieure à 3, celle correspondante à la loi
gaussienne, ce qui explique une queue épaisse de la distribution. La
valeur très élevée du paramètre de Jarque-Bera (JB)
qui est égal à 2256.732 confirme le rejet de l'hypothèse
nulle de la normalité des rendements géométriques pour cet
indice aussi bien que l'indice « MASI ».
.
700 600 500 400
300 200 100
0
|
|
Series: LOISIRS &
HOTELERIE
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 1.55e-05
Median 0.000000
Maximum 0.095277
Minimum -0.105171
Std. Dev. 0.024546
Skewness -0.048587
Kurtosis 5.674482
Jarque-Bera 475.9943
Probability 0.000000
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 30 sur 113
Tableau 9 : Histogramme et statistiques
du rendement géométrique de l'indice sectoriel « Loisirs et
Hôtellerie »
Le tableau 9 des rendements géométriques du
cours de l'indice sectoriel « Loisirs et Hôtellerie », montre
un Skewness négative de -0.048587, ce qui nous permet de déduire
que les rendements géométriques pour cet indice ont une longue
queue à droite. Le coefficient de la Kurtosis affiche une valeur de
5.674482, qui est supérieure à 3, celle correspondante à
la loi gaussienne, ce qui explique une queue épaisse de la distribution.
La valeur très élevée du paramètre de Jarque-Bera
(JB) qui est égal à 475.9943 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que l'indice « MAST
».
Quantile-Quantile QQ-Plot :
Nous utilisons le graphique quantile-quantile QQ-plot pour
vérifier si la série des rendements géométriques du
cours des indices est normalement distribuée.
Le QQ-plot est situé sur une ligne droite à 45
degrés si la distribution empirique est identique à la
distribution théorique (normale).
La figure 10 affiche le QQ-plot de la distribution empirique
des rendements géométriques du principal indice de la B.V.C par
rapport à la distribution normale.
.03 .02 .01
.00
-.01
-.02
-.03
|
|
|
-.10 -.08 -.06 -.04 -.02 .00 .02 .04
.06
Figure 10 : QQ-plot du rendement
géométrique (log-return) du principal indice de la B.V.C.
Quantiles of MAST
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance
2021-2022 Page 31 sur 113
Les figures (11 ; 12 ; 13 ; 14 ; 15 ; 16 ; 17 et 18) affichent
respectivement les QQ-plot de la distribution empirique des rendements
géométriques des huit indices sectoriels étudiés,
par rapport à la distribution normale.
.06 .04 .02
.00 -.02 -.04 -.06
|
|
|
-.10 -.06 -.02 .00 .02 .04 .06
.08
Quartiles of ASSURANCES
Figure 11 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Assurances
»
.04 .03 .02 .01
.00
-.01
-.02
-.03
-.04
|
|
|
-.12 -.08 -.04 .00 .04 .08
Quantiles of BANQUES
Figure 12 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Banques
».
.04 .03 .02
.01 .00
-.01
-.02
-.03
-.04
|
|
|
-.12 -.08 -.04 .00 .04 .08
Quantiles of
Télécommunications
Figure 13 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Télécommunications »
.06 .05 .04
.03 .02 .01 .00
-.01
-.02
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 32 sur 113
-.12 -.08 -.04 .00 .04 .08
Cimantiles of BAT MC
Figure 14 : QQ-plot du rendement
géométrique de l'indice sectoriel « Bâtiments &
MC».
.06 .04 .02 .00
-.02
-.04
-.06
|
|
|
-.12 -.08 -.04 .00 .04 .08
Figure 15 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Pétroles & Gaz ».
.08 .06 .04 .02
.00 -.02 -.04 -.06
-.08
|
|
|
Quantiles of PET_GAZ
-.12 -.08 -.04 .00 .04 .08 .12
Quantiles of P.P IMMO
Figure 16 : QQ-plot du rendement
géométrique de l'indice sectoriel « P.P immobilières
».
.06 .04 .02 .00
-.02
-.04
-.06
|
|
|
-.12 -.08 - .00 .04 .08 .12
Qu
anlitiles of TRANSPORT
Figure 17 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Transport
».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 33 sur 113
.100 .075 .050 .025
.000
-.12 -.08 -.04 .00 .04 .08 .12
Figure 18 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Loisirs
& Hôtels ».
Quantiles of HOTELLERIE
L'analyse des figures présentées ci-dessus
montre que les rendements géométriques des distributions
empiriques de l'indice principal et des indices sectoriels choisis dans notre
recherche indiquent des écarts des queues plus épaisses que
celles de la distribution normale par rapport à la normale.
Le tableau 10 englobe les statistiques descriptives (moyenne,
écart type, minimum, maximum, Skewness et Kurtosis) des rendements
géométriques du « MASI » et des indices sectoriels
choisis dans notre échantillon.
Indices
|
Moyenne
|
Ecart-Type
|
Minimum
|
Maximum
|
Skewness
|
Kurtosis
|
MASI
|
0,000206
|
0,007353
|
-0,092317
|
0,053054
|
-1,853794
|
30,75269
|
ASSURANCES
|
0,000262
|
0,013541
|
-0,085039
|
0,067062
|
-0,602697
|
9,394267
|
BANQUES
|
0,0000960
|
0,009099
|
-0,103011
|
0,065637
|
-1,379363
|
22,21553
|
BAT_MC
|
0,000143
|
0,014411
|
-0,101991
|
0,070042
|
-0,529689
|
8,092728
|
PET_GAZ
|
0,000551
|
0,015600
|
-0,087289
|
0,073292
|
-0,248322
|
7,022547
|
PROMOIMMO
|
-0,000634
|
0,019702
|
-0,104202
|
0,090888
|
-0,162483
|
5,890305
|
TELECOMU
|
0,0000670
|
0,009296
|
-0,100845
|
0,056536
|
-1,243981
|
21,42858
|
TRANSPORT
|
0,000168
|
0,016234
|
-0,100192
|
0,087665
|
-0,010929
|
8,827230
|
HOTELERIE
|
0,0000155
|
0,024546
|
-0,105171
|
0,095277
|
-0,048587
|
5,674482
|
|
Tableau 10 : Statistiques
descriptives de l'indice « MASI » et des indices de huit secteurs
d'activité étudiés.
On constate, d'après une étude analytique du
tableau des statistiques descriptives, que les huit secteurs d'activité
de notre étude ont enregistrés des baisses dans leurs rendements
géométriques très proches l'un de l'autre, environ 10%
à l'exception des indices sectoriels « Assurances » et «
Pétroles & Gaz » qui ont enregistré respectivement un
rendement minimal de 8.5% et 8.7%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance
2021-2022 Page 34 sur 113
Pour la volatilité, les écart-types
montrent que :
v Les valeurs le plus volatiles : Le secteur
« Loisirs et Hôtellerie » avec un écart
type de 0.024546 suivi du secteur « Participation et promotion
immobilière » avec un écart type de 0,019702.
v Les valeurs moyennement volatiles sont : Le
secteur « Transport » avec un écart-type de 0.016234 suivi du
secteur « Pétroles & Gaz » avec un écart-type de
0.015600, puis le secteur des Bâtiments et MC.
v Les valeurs ayant une volatilité plus faible
: Le secteur des Assurances avec un écart type de 0.013541 puis
le secteur « Télécommunications » avec
écart-type de 0.009296 en dernier ressort, le secteur Bancaire avec un
écart type de 0.009099.
Les différentes variables de notre étude se
rassemblent dans un point commun est que leurs coefficients d'aplatissement
affichent des valeurs supérieurs à 3 (Kurtosis >
3), ils ont ainsi une distribution leptokurtique plus tranchante
qu'une distribution normale, avec des valeurs concentrées autour de la
moyenne et les queues sont épaisses. Cela signifie une forte
probabilité pour les valeurs extrêmes. Aussi ces variables ont
tous des coefficients d'asymétrie négatifs (Skewnes
< 0), c'est-à-dire une répartition
asymétrique à gauche, la majorité des cours sont
concentrés à la côté gauche de la moyenne.
Les courbes QQ-plots ne sont pas droites et ont des formes en
S. Ceci permet de confirmer les résultats
précédents des statistiques descriptives par
rapport au rejet de la normalité des rendements
géométriques. Les distributions des actifs sont significativement
différentes de la distribution normale au seuil de 5%. L'application du
test Jarque-Bera aux séries des rendements a confirmé la
non-normalité des séries
étudiées.
Les spécifications GARCH adoptées sont
susceptibles d'expliquer une part significative de la non-normalité de
ces séries.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 35 sur 113
2.2.3 Analyse économétrique
2.2.3.1. Accumulation de la volatilité
(Volatility clustering)
La volatilité de la série du rendement
géométrique change avec le temps, pour démontrer ce
caractère important des séries des rendements, il est
intéressant de présenter les courbes des séries de
rendements géométriques.
Pour visualiser ce phénomène de fluctuation de
la volatilité (cluster de volatilité) on présente les
graphes des séries des rendements géométriques de l'indice
« MASI » ainsi que les huit indices sectoriels.
Les figures 19 ; 20 ; 21 ; 22 ; 23 ; 24 ; 25 ; 26 et 27,
affichent les clusters de volatilité de la série des rendements
géométriques pour l'indice « MASI » et pour les huit
indices sectoriels du marché boursier marocain.
Volatility clusters of "MASI"
|
.06 .04 .02
.00 -.02 -.04 -.06 -.08
-.10
|
|
|
16 17 18 19 20 21 22
|
Figure 19 : Clusters de
volatilité sur les rendements géométriques du principal
indice « MASI ».
Volatility clusters of
"Assurances"
|
.08 .06 .04
.02 .00 -.02
-.04 -.06 -.08 -.10
|
|
16 17 18 19 20 21 22
Figure 20 : Clusters de
volatilité sur les rendements de l'indice sectoriel « Assurances
».
Volatility clusters of "Banques"
|
.08 .04 .00 -.04
-.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 21 : Clusters de
volatilité sur les rendements de l'indice sectoriel « Banques
».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 36 sur 113
Volatility clusters of "Batiments et
MC"
|
.08 .04 .00 -.04
-.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 22 : Clusters de
volatilité sur les rendements de l'indice sectoriel «
Bâtiment et M.C ».
Volatility clusters of "Promotion
Immobilière"
|
.12 .08 .04 .00
-.04 -.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 23 : Clusters de
volatilité sur les rendements de l'indice sectoriel «P.P
Immobilière »
Volatility clusters of "Pétroles et
Gaz"
|
.08 .04 .00 -.04
-.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 24 : Clusters de
volatilité sur les rendements de l'indice sectoriel «
Pétroles et Gaz ».
Volatility clusters of
"Télécommunications"
|
.08 .04 .00 -.04
-.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 25 : Clusters de
volatilité sur les rendements de l'indice sectoriel «
Télécommunications ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 37 sur 113
Volatility clusters of
"Transport"
|
.12 .08 .04
.00 -.04 -.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 26 : Clusters de
volatilité sur les rendements de l'indice sectoriel « Transport
».
Volatility clusters of
"Loisirs & Hôtellerie"
|
.12 .08 .04
.00 -.04 -.08 -.12
|
|
|
16 17 18 19 20 21 22
|
Figure 27 : Clusters de
volatilité sur les rendements de l'indice sectoriel « Loisirs et
Hôtellerie ».
Nous observons empiriquement que de faibles variations des
rendements géométriques sont généralement suivies
de fortes variations et que de fortes variations sont
généralement suivies de faibles variations. Nous constatons
également un regroupement des extrêmes en clusters ou paquets de
volatilités. Ce type de phénomène remet en cause
l'hypothèse d'homoscédasticité (constance de la
volatilité).
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 38 sur 113
2.2.3.2. Analyse de l'interdépendance
Le tableau 11 affiche la Matrice variance-covariance des
séries des rendements géométriques de l'indice « MASI
», ainsi que les huit indices sectoriels choisis.
|
MASI
|
ASSUR
|
BAT_MC
|
BANQUES
|
HOTEL
|
P_IMM
|
PET_GAZ
|
TELECOM
|
TRANS
|
|
MASI
|
0,000054
|
0,0000386
|
0,0000748
|
0,0000584
|
0,0000306
|
0,0000665
|
0,0000388
|
0,0000484
|
0,0000212
|
|
ASSUR
|
0,0000386
|
0,000183
|
0,000045
|
0,0000306
|
0,0000251
|
0,0000425
|
0,0000304
|
0,0000262
|
0,0000152
|
|
BAT_MC
|
0,0000748
|
0,000045
|
0,000208
|
0,0000603
|
0,000044
|
0,0000697
|
0,0000381
|
0,0000474
|
0,0000264
|
|
BANQUES
|
0,0000584
|
0,0000306
|
0,0000603
|
0,0000827
|
0,000028
|
0,0000624
|
0,0000312
|
0,0000448
|
0,0000217
|
|
HOTEL
|
0,0000306
|
0,0000251
|
0,000044
|
0,000028
|
0,000602
|
0,0000658
|
0,0000286
|
0,0000193
|
0,0000303
|
|
P_IMM
|
0,0000665
|
0,0000425
|
0,0000697
|
0,0000624
|
0,0000658
|
0,000388
|
0,0000495
|
0,0000525
|
0,0000431
|
|
PET_GAZ
|
0,0000388
|
0,0000304
|
0,0000381
|
0,0000312
|
0,0000286
|
0,0000495
|
0,000243
|
0,0000203
|
0,0000139
|
|
TELECOM
|
0,0000484
|
0,0000262
|
0,0000474
|
0,0000448
|
0,0000193
|
0,0000525
|
0,0000203
|
0,0000864
|
0,0000175
|
|
TRANS
|
0,0000212
|
0,0000152
|
0,0000264
|
0,0000217
|
0,0000303
|
0,0000431
|
0,0000139
|
0,0000175
|
0,000263
|
Tableau 11 : Matrice
variance-covariance des rendements géométriques des huit indices
sectoriels et l'indice « MASI ».
Le tableau 12 affiche la Matrice des corrélations non
conditionnelles des séries des rendements géométriques des
huit secteurs et de l'indice « MASI ».
|
MASI
|
ASSUR
|
BAT_MC
|
BQ
|
HOTEL
|
P_IMM
|
PET_GAZ
|
TELECOM
|
TRANS
|
|
MASI
|
1
|
0,388277
|
0,705941
|
0,873189
|
0,169472
|
0,459465
|
0,338755
|
0,708683
|
0,177853
|
|
ASSUR
|
0,388277
|
1
|
0,230636
|
0,248359
|
0,075511
|
0,159446
|
0,143925
|
0,207906
|
0,069157
|
|
BAT_MC
|
0,705941
|
0,230636
|
1
|
0,460027
|
0,124395
|
0,245501
|
0,169393
|
0,354227
|
0,11281
|
|
BQ
|
0,873189
|
0,248359
|
0,460027
|
1
|
0,125276
|
0,348386
|
0,219903
|
0,530178
|
0,147254
|
|
HOTEL
|
0,169472
|
0,075511
|
0,124395
|
0,125276
|
1
|
0,13618
|
0,074747
|
0,084457
|
0,076139
|
|
P_IMM
|
0,459465
|
0,159446
|
0,245501
|
0,348386
|
0,13618
|
1
|
0,161204
|
0,287007
|
0,134731
|
|
PET_GAZ
|
0,338755
|
0,143925
|
0,169393
|
0,219903
|
0,074747
|
0,161204
|
1
|
0,139973
|
0,055066
|
|
TELECOM
|
0,708683
|
0,207906
|
0,354227
|
0,530178
|
0,084457
|
0,287007
|
0,139973
|
1
|
0,115886
|
|
TRANS
|
0,177853
|
0,069157
|
0,11281
|
0,147254
|
0,076139
|
0,134731
|
0,055066
|
0,115886
|
1
|
Tableau 12 : Matrice des
corrélations non conditionnelles des séries des rendements
géométriques des 8 indices sectoriels et le « MASI
».
L'analyse de la corrélation non conditionnelle
présentée dans le tableau 12 montre qu'il y a une
corrélation positive entre les rendements géométriques des
huit indices sectoriels et ceux de l'indice « MASI », ce qui confirme
la transmission de la volatilité entre le « MASI » et les huit
indices sectoriels.
En effet, les huit indices sectoriels choisis
varient dans le même sens avec l'indice « MASI » et ils ont une
corrélation positive avec le marché boursier.
De plus, la corrélation la plus
élevée est de 0,873189
entre l'indice « MASI » et le secteur bancaire, alors
que le coefficient de corrélation le plus faible
est celui du secteur « Loisirs et Hôtellerie » et
l'indice « MASI » qui est de
0,169472.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 39 sur 113
Les résultats de l'analyse graphique de
l'évolution des valeurs journalières des différentes
actions sont confirmés par ces résultats empiriques.
Le tableau 13 affiche les coefficients de sensibilité
des séries de rendements des géométriques des huit indices
sectoriels avec l'indice principal du marché boursier.
|
Indices sectoriels
|
Beta (coefficient de sensibilité)
|
|
Assurances
|
0,71
|
|
Banques
|
1,08
|
|
Bâtiments & Matériaux de construction
|
1,39
|
|
Télécommunications
|
0,90
|
|
Pétroles & Gaz
|
0,72
|
|
Participation & Promotion immobilières
|
1,23
|
|
Loisirs & Hôtels
|
0,57
|
|
Transport
|
0,39
|
Tableau 13 : Coefficients de
sensibilité des séries des rendements géométriques
des 8 indices sectoriels et le « MASI ».
Le tableau 14 affiche le classement des huit indices sectoriels
selon l'interdépendance avec le « MASI ». L'objectif est alors
d'identifier le secteur d'activité de premier rang en termes de
contribution au risque du marché boursier.
|
Classement
|
Corrélation avec l'indice sectoriel
|
Coefficient de sensibilité
Béta
|
|
1
|
Banques
|
0,873189
|
Bâtiments & Matériaux de construction
|
1,39
|
|
2
|
Télécommunications
|
0,708683
|
Participation & Promotion immobilières
|
1,23
|
|
3
|
Bâtiments & Matériaux de construction
|
0,705941
|
Banques
|
1,08
|
|
4
|
Participation & Promotion
immobilières
|
0,459465
|
Télécommunications
|
0,90
|
|
5
|
Assurances
|
0,388277
|
Pétroles & Gaz
|
0,72
|
|
6
|
Pétroles & Gaz
|
0,338755
|
Assurances
|
0,71
|
|
7
|
Transport
|
0,177853
|
Loisirs & Hôtels
|
0,57
|
|
8
|
Loisirs & Hôtels
|
0,169472
|
Transport
|
0,39
|
Tableau 14 : Classement des huit
indices sectoriels selon l'interdépendance avec l'indice principal
« MASI ». 2.3. Pré-estimation des séries des
rendements de l'indice « MASI » et des huit indices
sectoriels.
Nous allons décrire dans cette partie, les principaux
faits stylisés en analysant les valeurs de clôture et les
rendements géométriques journaliers des séries en
question. Nous allons commencer tout d'abords par la propriété de
stationnarité des séries des valeurs,
ainsi que celles des rendements géométriques, puis on va
s'intéresser à la propriété
d'autocorrélation des rendements
géométriques, enfin on va tester
l'hétéroscédasticité des
résidus des rendements géométriques des séries
étudiées. Les différents tests de ce chapitre sont
réalisés, en utilisant les logiciels de programmation
économétrique Matlab et Eviews.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 40 sur 113
2.3.1 Test de non stationnarité des
séries des prix journaliers :
En analysant les courbes des cours de clôture
journaliers des différents secteurs, nous remarquons que ces courbes
montrent tantôt une tendance baissière, tantôt une tendance
haussière avec des pics récurrents, ainsi ce type de courbe ne
reflète pas la stationnarité.
On voit clairement sur les graphes des valeurs quotidiennes
présentés dans les figures 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9,
que ces processus sont non stationnaires, et cela provient de l'inclusion de la
tendance qui est une caractéristique des séries des cours.
Pour confirmer statistiquement le non stationnarité des
séries des prix, nous allons appliquer les tests de stationnarité
Augmented-Dickey Fuller ADF (Dickey et Fuller
(1979)).
? L'hypothèse nulle :
la série des valeurs est stationnaire.
? L'hypothèse alternative :
la série des valeurs est non stationnaire.
Nous choisissons les seuils de signification 1%, 5% et 10%.
2.3.1.1. Test de non stationnarité des valeurs
de l'indice « MASI » :
En analysant les courbes des cours de clôture et des
rendements géométriques de l'indice « MASI » (Figure1),
nous remarquons que la courbe des valeurs de cet indice montre tantôt une
tendance baissière, tantôt une tendance haussière avec des
pics récurrents, ainsi ce type de courbe ne reflète pas la
stationnarité.
On voit clairement sur le graphe de la série des
valeurs de l'indice « MASI » présenté dans la figure 1,
que ce processus est non stationnaire.
Le tableau 15 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes de l'indice « MASI
».
|
Null Hypothesis: MASI Index has a unit root Exogenous: Constant,
Linear Trend
Lag Length: 1 (Automatic - based on SIC, maxlag=23)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-2.158396
|
0.5121
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 15 : Test de
stationnarité ADF pour la série des valeurs de l'indice «
MASI ».
Le tableau 15 montre que la valeur statistique ADF est
-2.158396 et que la p-value associée est 0.5121. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de valeurs
journalières de l'indice MASI n'est pas stationnaire.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 41 sur 113
2.3.1.2. Test de non stationnarité des valeurs
du secteur « Assurances ».
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur « Assurances »
(Figure2), nous remarquons que la courbe des valeurs de ce secteur montre
tantôt une tendance baissière, tantôt une tendance
haussière avec des pics récurrents, ainsi ce type de courbe ne
reflète pas la stationnarité. On voit clairement sur le graphe de
la série des valeurs du secteur « Assurances »,
présenté dans la figure 2 que ce processus est non
stationnaire.
Le tableau 16 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes de l'indice sectoriel
« Assurances ».
|
Null Hypothesis: Sector Assurances has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 1 (Automatic - based on SIC, maxlag=23)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-1.921156
|
0.6428
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 16 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Assurances ».
Le tableau 16 montre que la valeur statistique ADF est
-1.921156 et que la p-value associée est 0.6428. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de
valeurs journalières du secteur Assurances n'est pas
stationnaire.
2.3.1.3. Test de non stationnarité des valeurs
du secteur Bancaire.
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur bancaire (Figure3), nous
remarquons que la courbe de la valeur de ce secteur montre tantôt une
tendance baissière, tantôt une tendance haussière avec des
pics récurrents, ainsi ce type de courbe ne reflète pas la
stationnarité.
On voit clairement sur le graphe de la série des
valeurs du secteur bancaire présenté dans la figure 3 que ce
processus est non stationnaire.
Le tableau 17 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du
secteur bancaire.
|
Null Hypothesis: Sector Banks has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -1.959724
|
0.6222
|
|
Test critical values: 1% level -3.963807
5% level -3.412629
10% level -3.128280
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
Tableau 17 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Bancaire ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 42 sur 113
Le tableau 17 montre que la valeur statistique ADF est
-1.959724 et que la p-value associée est 0.6222. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de
valeurs journalières du secteur bancaire n'est pas
stationnaire.
2.3.1.4. Test de non stationnarité des valeurs
du secteur des Télécommunications.
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur des
Télécommunications (Figure4), nous remarquons que la courbe de la
valeur ce secteur montre tantôt une tendance baissière,
tantôt une tendance haussière avec des pics récurrents,
ainsi ce type de courbe ne reflète pas la stationnarité.
On voit clairement sur le graphe de la série des
valeurs du secteur des Télécommunications présenté
dans la figure 4 que ce processus est non stationnaire.
Le tableau 18 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du secteur des
Télécommunications.
|
Null Hypothesis: Sector TELECOM has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 1 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-3.583423
|
0.0315
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 18 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Télécommunications ».
Le tableau 18 montre que la valeur statistique ADF est
-3.583423 et que la p-value associée est 0.0315. Notons que la valeur
statistique est supérieure à la valeur critique au niveau de 1%,
Nous rejetons ainsi l'hypothèse de stationnarité.
Aux seuils de 5% et 10%, on a les valeurs statistiques
(-3.412631 et -3.128281), sont inférieure à la valeur critique de
-3.583423, on accepte ainsi l'hypothèse de stationnarité des
valeurs de la série des Télécommunications aux seuils de
5% et 10%.
Conclusion : la série de valeurs
journalières du secteur des Télécom n'est pas stationnaire
au seuil de 1%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 43 sur 113
2.3.1.5. Test de non stationnarité des valeurs
du secteur « Bâtiments et Mat de construction »
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur « Bâtiments et MC
» (Figure5), nous remarquons que la courbe de la valeur ce secteur montre
tantôt une tendance baissière, tantôt une tendance
haussière avec des pics récurrents, ainsi ce type de courbe ne
reflète pas la stationnarité.
On voit clairement sur le graphe de la série des valeurs
du secteur « Bâtiments et MC » présenté dans la
figure 5 que ce processus est non stationnaire.
Le tableau 19 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du secteur «
Bâtiments et MC ».
|
Null Hypothesis: Sector BAT_MC has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 1 (Automatic - based on SIC, maxlag=23)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-2.358898
|
0.4012
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 19 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Bâtiments et M. de Construction ».
Le tableau 19 montre que la valeur statistique ADF est
-2.358898 et que la p-value associée est 0.4012. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de
valeurs journalières du secteur « Bâtiments MC »
n'est pas stationnaire.
2.3.1.6. Test de non stationnarité des valeurs
du secteur « Pétroles et Gaz ».
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur « Pétroles et Gaz
» (Figure6), nous remarquons que la courbe de la valeur ce secteur montre
tantôt une tendance baissière, tantôt une tendance
haussière avec des pics récurrents, ainsi ce type de courbe ne
reflète pas la stationnarité.
On voit clairement sur le graphe de la série des
valeurs du secteur « Pétroles et Gaz » présenté
dans la figure 6 que ce processus est non stationnaire.
Le tableau 20 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du secteur «
Pétroles et Gaz ».
|
Null Hypothesis: Sector PET_GAZ has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -2.286267
|
0.4407
|
|
Test critical values: 1% level -3.963807
5% level -3.412629
10% level -3.128280
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
Tableau 20 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Pétroles et Gaz ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 44 sur 113
Le tableau 20 montre que la valeur statistique ADF est
-2.286267 et que la p-value associée est 0.4407. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de
valeurs journalières du secteur « Pétroles et Gaz »,
n'est pas stationnaire.
2.3.1.7. Test de non stationnarité des valeurs
du secteur « Participation et Promotion Immobilières »
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur « P.P Immo »
(Figure7), nous remarquons que la courbe de la valeur ce secteur montre
tantôt une tendance baissière, tantôt une tendance
haussière avec des pics récurrents, ainsi ce type de courbe ne
reflète pas la stationnarité.
On voit clairement sur le graphe de la série des
valeurs du secteur « P.P Immo », présenté dans la
figure 7 que ce processus est non stationnaire.
Le tableau 21 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du secteur « P.P
Immo ».
|
Null Hypothesis: Sector PROMO_IMMO has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 1 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -2.303491
|
0.4313
|
|
Test critical values: 1% level -3.963811
5% level -3.412631
10% level -3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
Tableau 21 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Participation et Promotion Immobilières ».
Le tableau 21 montre que la valeur statistique ADF est
-2.303491 et que la p-value associée est 0.4313. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de
valeurs journalières du secteur « P.P Immobilières »
n'est pas stationnaire.
2.3.1.8. Test de non stationnarité des valeurs
du secteur « Transport ».
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur « Transport »
(Figure8), nous remarquons que la courbe de la valeur ce
secteur montre tantôt une tendance baissière, tantôt une
tendance haussière avec des pics récurrents, ainsi ce type de
courbe ne reflète pas la stationnarité.
On voit clairement sur le graphe de la série des
valeurs du secteur « Transport » présenté dans la
figure 8 que ce processus est non stationnaire.
Le tableau 22 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du secteur «
Transport ».
|
Null Hypothesis: Sector TRANSPORT has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -2.562264
|
0.2980
|
|
Test critical values: 1% level -3.963807
5% level -3.412629
10% level -3.128280
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
Tableau 22 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Transport ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 45 sur 113
Le tableau 22 montre que la valeur statistique ADF est
-2.562264 et que la p-value associée est 0.2980. Notons que la valeur
statistique est supérieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Nous rejetons ainsi l'hypothèse de stationnarité.
Conclusion : la série de
valeurs journalières du secteur « Transport »
n'est pas stationnaire.
2.3.1.9. Test de non stationnarité des valeurs
du secteur « Loisirs et Hôtellerie ».
En analysant les courbes des cours de clôture et des
rendements géométriques du secteur « Loisirs et
Hôtellerie » (Figure7), nous remarquons que la courbe de la valeur
ce secteur montre tantôt une tendance baissière, tantôt une
tendance haussière avec des pics récurrents, ainsi ce type de
courbe ne reflète pas la stationnarité. On voit clairement sur le
graphe de la série des valeurs du secteur « Loisirs et
Hôtellerie », présenté dans la figure 7 que ce
processus est non stationnaire.
Le tableau 23 affiche les résultats obtenus du test de
stationnarité ADF pour les valeurs quotidiennes du secteur «
Loisirs et Hôtellerie ».
|
Null Hypothesis: Sector Hôtellerie has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-2.314519
|
0.4252
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963807
-3.412629
-3.128280
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 23 : Test de
stationnarité ADF pour la série des valeurs du secteur «
Loisirs et Hôtellerie ».
Le tableau 23 montre que la valeur statistique ADF est -2.314519
et que la p-value associée est
0.4252. Notons que la valeur statistique est supérieure
aux valeurs critiques aux niveaux de 1%, 5% et 10%. Nous rejetons ainsi
l'hypothèse de stationnarité.
Conclusion : la série de valeurs
journalières du secteur « Loisirs et Hôtellerie »
n'est pas stationnaire.
Les résultats précédents affirment que
toutes les séries des prix des cours sont non stationnaires. Pour rendre
les séries stationnaires, nous procédons au calcul du rendement
logarithmique (log-return) de valeurs quotidiennes des séries.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 46 sur 113
2.3.2 Test de stationnarité des séries
des rendements géométriques (log-return)
En analysant les courbes des séries des rendements
géométriques semblent stationnaires autour d'une moyenne
constante, et des variations qui prennent des valeurs tant positives que
négatives autour de la moyenne, ce qui est une propriété
principale des séries de rendements géométriques.
On voit clairement sur ces graphes des rendements
géométriques (log-return) présentés dans les
figures 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9, que ces processus sont
stationnaires
Pour confirmer statistiquement la stationnarité des
séries des rendements géométriques, nous allons appliquer
les tests de stationnarité Augmented-Dickey Fuller ADF (Dickey et Fuller
(1979)). ? L'hypothèse nulle : la
série des rendements géométriques est
stationnaire.
? L'hypothèse alternative
: la série des rendements géométriques
est non stationnaire. Nous choisissons les seuils de
signification 1%, 5% et 10%.
2.3.2.1. Test de stationnarité des rendements
géométriques (log-return) de l'indice « MASI » :
Le tableau 24 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques de
l'indice « MASI ».
|
Null Hypothesis: MASI Log-return has a unit root Exogenous:
Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -33.99381
|
0.0000
|
|
Test critical values: 1% level -3.963811
5% level -3.412631
10% level -3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
Tableau 24 : Test de
stationnarité ADF pour la série des rendements de l'indice «
MASI ».
Le tableau 24 montre que la valeur statistique ADF est
-33.99381 et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques de l'indice « MASI » est
générée par un processus
stationnaire.
2.3.2.2. Test de stationnarité des rendements
géométriques (log-return) du secteur « Assurances ».
Le tableau 25 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur « Assurances ».
|
Null Hypothesis: Sector Assurances Log-return has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -47.84054
|
0.0000
|
|
Test critical values: 1% level -3.963811
5% level -3.412631
10% level -3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
Tableau 25 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Assurances ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 47 sur 113
Le tableau 25 montre que la valeur statistique ADF est -47.84054
et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur « Assurances » est
générée par un processus
stationnaire.
2.3.2.3. Test de stationnarité des rendements
géométriques (log-return) du secteur « Bancaire ».
Le tableau 26 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur Bancaire.
|
Null Hypothesis: Sector Banques Log-return has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-38.74156
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 26 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur bancaire.
Le tableau 26 montre que la valeur statistique ADF est
-38.74156 et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur bancaire est
générée par un processus
stationnaire.
2.3.2.4. Test de stationnarité des rendements
géométriques (log-return) du secteur «
Télécommunications ».
Le tableau 27 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur des « Télécommunications ».
|
Null Hypothesis: Sector Télécommunications
Log-return has a unit root Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-36.74119
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 27 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur des «
Télécommunications ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 48 sur 113
Le tableau 27 montre que la valeur statistique ADF est -36.74119
et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur des «
Télécommunications » est générée par
un processus stationnaire.
2.3.2.5. Test de stationnarité des rendements
géométriques (log-return) du secteur « Bâtiments et MC
».
Le tableau 28 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur « Bâtiments et MC ».
|
Null Hypothesis : Sector BAT_MC Log-return has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-42.42033
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 28 : test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Bâtiments et MC ».
Le tableau 28 montre que la valeur statistique ADF est -42.42033
et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur « Bâtiments et MC
» est générée par un processus
stationnaire.
2.3.2.6. Test de stationnarité des rendements
géométriques (log-return) du secteur « Pétroles et
Gaz ». Le tableau 29 affiche les résultats obtenus du
test de stationnarité ADF pour les rendements géométriques
du secteur « Pétroles et Gaz ».
|
Null Hypothesis: Sector PET_GAZ Log-return has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-41.71974
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 29 : test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Pétroles et Gaz ».
Le tableau 29 montre que la valeur statistique ADF est
-41.71974 et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 49 sur 113
Conclusion : la série des
rendements géométriques du secteur « Pétroles et Gaz
» est générée par un processus
stationnaire.
2.3.2.7. Test de stationnarité des rendements
géométriques (log-return) du secteur P.P Immobilières
».
Le tableau 30 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur « Participation et Promotion Immobilières ».
|
Null Hypothesis: Sector Part & Promo Immobilières
Log-return has a unit root Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-32.10782
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 30 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « P.P Immobilières ».
Le tableau 30 montre que la valeur statistique ADF est -31.10782
et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur « P.P Immobilières
» est générée par un processus
stationnaire.
2.3.2.8. Test de stationnarité des rendements
géométriques (log-return) du secteur « Transport ».
Le tableau 31 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur « Transport ».
|
Null Hypothesis: Sector Transport Log-return has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-41.66050
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 31 : test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Transport ».
Le tableau 31 montre que la valeur statistique ADF est
-41.66050 et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur « Transport » est
générée par un processus
stationnaire.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 50 sur 113
2.3.2.9. Test de stationnarité des rendements
géométriques (log-return) du secteur « Loisirs et
Hôtellerie ».
Le tableau 32 affiche les résultats obtenus du test de
stationnarité ADF pour les rendements géométriques du
secteur « Loisirs et Hôtellerie ».
|
Null Hypothesis: Sector Loisirs & Hôtellerie Log-return
has a unit root Exogenous: Constant, Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=23)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-41.88031
|
0.0000
|
|
Test critical values: 1% level
5% level 10% level
|
-3.963811
-3.412631
-3.128281
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Tableau 32 : Test de
stationnarité ADF pour la série des rendements
géométriques du secteur « Loisirs et Hôtellerie
».
Le tableau 32 montre que la valeur statistique ADF est
-41.88031 et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et 10%. Donc l'hypothèse nulle de la racine unitaire est
rejetée.
Conclusion : la série des
rendements géométriques du secteur « « Loisirs et
Hôtellerie » est générée par un
processus stationnaire.
2.3.3 Test d'autocorrélation des rendements
géométriques
L'autocorrélation d'une série temporelle ou d'un
processus désigne la corrélation du processus par rapport
à une version décalée dans le temps de lui-même.
Il existe un grand nombre de tests d'autocorrélation,
les plus utilisés sont ceux de Box et Pierce (1970) et Ljung et Box
(1978).
Statistiquement, l'autocorrélation est testée
à l'aide de la statistique Ljung-Box. En effet, la statistique Q(m) de
Ljung-Box (1978) permet de tester l'hypothèse d'indépendance
sérielle d'une série (ou si la série est un bruit blanc).
Plus spécifiquement, cette statistique teste l'hypothèse que les
m coefficients d'autocorrélation sont nuls. Elle est basée sur la
somme des autocorrélations de la série et elle est
distribuée selon une loi Chi-carrée avec m degrés de
liberté.
Pour chaque secteur, nous allons présenter le
corrélogramme d'autocorrélations des rendements
géométriques journaliers. On effectue ensuite le test Ljung et
Box (1978) (LJB) pour tester la significativité de
l'autocorrélation des rendements géométriques.
Les hypothèses testées sont :
? Hypothèse nulle .
· «
Les autocorrélations des rendements géométriques
ne sont pas significatives » ?
Hypothèse alternative .
· « Les
autocorrélations des rendements géométriques
sont significatives » Nous choisissons
les seuils de signification 1%, 5% et 10%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 51 sur 113
2.3.3.1. Test d'absence d'autocorrélation des
rendements géométriques de l'indice « MASI » :
La figure 28 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
« MASI » :
Figure 28 : Corrélogramme
d'autocorrélation des rendements de l'indice principal « MASI
».
Selon le corrélogramme des rendements journaliers de
l'indice principal « MASI », il y a des pics significatifs.
Nous remarquons que les valeurs de coefficients
d'autocorrélation sont très faibles. La série des
rendements géométriques est caractérisé donc par
des autocorrélations très faibles.
Cela veut dire que la corrélation entre la
rentabilité d'aujourd'hui et les rentabilités passées est
très faible. Les résultats du test d'autocorrélation LJB
sont présentés dans le tableau 33 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
86.9747
|
37.5662
|
0.0000
|
|
5%
|
86.9747
|
31.4104
|
0.0000
|
|
10%
|
86.9747
|
28.4120
|
0.0000
|
Tableau 33 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice « MASI »
Le tableau 33 montre que la valeur statistique LJB est 86.9747
et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est largement supérieure aux valeurs critiques aux niveaux
de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée.
Conclusion : il y a une autocorrélation entre
les rendements de l'indice « MASI ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 52 sur 113
2.3.3.2. Test d'absence d'autocorrélation des
rendements géométriques de l'indice sectoriel « Assurances
» La figure 29 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
sectoriel « Assurances » :
Figure 29 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel « Assurances
».
Selon le corrélogramme des rendements journaliers l'indice
sectoriel « Assurances », il y a des pics significatifs.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 34 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
85.2384
|
37.5662
|
0.0000
|
|
5%
|
85.2384
|
31.4104
|
0.0000
|
|
10%
|
85.2384
|
28.4120
|
0.0000
|
Tableau 34 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « Assurances ».
Le tableau 34 montre que la valeur statistique LIB est 85.3454
et que la p-value associée est 0,0000. Notons que la valeur
t-statistique est largement supérieure aux valeurs critiques aux niveaux
de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée.
Conclusion : il y a une
autocorrélation entre les rendements de l'indice sectoriel «
Assurances ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 53 sur 113
2.3.3.3. Test d'absence d'autocorrélation des
rendements géométriques de de l'indice sectoriel «
Télécommunications » :
La figure 30 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
sectoriel « Télécommunications » :
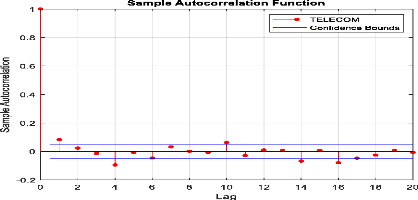
Figure 29 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Télécommunications ».
Selon le corrélogramme des rendements journaliers l'indice
sectoriel « Télécommunications », il y a des pics
significatifs.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 35 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
61.9623
|
37.5662
|
0.00000
|
|
5%
|
61.9623
|
31.4104
|
0.00000
|
|
10%
|
61.9623
|
28.4120
|
0.00000
|
Tableau 35 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel «
Télécommunications ».
Le tableau 35 montre que la valeur statistique LJB est 61.9623
et que la p-value associée est 0,00000. Notons que la valeur
t-statistique est largement supérieure aux valeurs critiques aux niveaux
de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée.
Conclusion : il y a une
autocorrélation entre les rendements de l'indice sectoriel «
Télécommunications ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 54 sur 113
2.3.3.4. Test d'absence d'autocorrélation des
rendements géométriques l'indice sectoriel « Participation
& Promotion Immobilières » :
La figure 31 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
sectoriel « Participation & Promotion Immobilières » :
Figure 31 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel « P.P
Immobilières ».
Selon le corrélogramme des rendements journaliers l'indice
sectoriel « P.P Immobilières », il y a des pics
significatifs.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 36 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
90.9498
|
37.5662
|
0.00000
|
|
5%
|
90.9498
|
31.4104
|
0.00000
|
|
10%
|
90.9498
|
28.4120
|
0.00000
|
Tableau 36 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « P.P Immobilières
».
Le tableau 36 montre que la valeur statistique LJB est 90.9498
et que la p-value associée est 0,00000. Notons que la valeur
t-statistique est largement supérieure aux valeurs critiques aux niveaux
de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée.
Conclusion : il y a une
autocorrélation entre les rendements de l'indice sectoriel « P.P
Immobilières ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 55 sur 113
2.3.3.5. Test d'absence d'autocorrélation des
rendements géométriques de l'indice sectoriel «
Pétroles& Gaz »
La figure 32 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
sectoriel « Pétroles & Gaz » :
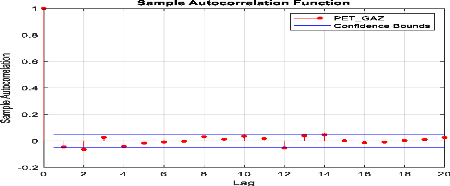
Figure 32 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel «
Pétroles & Gaz ».
Selon le corrélogramme des rendements journaliers
l'indice sectoriel « Pétroles & Gaz », presque tous les
pics sont non significatifs, ce qui confirme la propriété de non
corrélation des rendements.
Nous remarquons que les valeurs de coefficients
d'autocorrélation sont très faibles. La série des
rendements géométriques est caractérisé donc par
des autocorrélations très faibles.
Cela veut dire que la corrélation entre la
rentabilité d'aujourd'hui et les rentabilités passées de
l'indice sectoriel « Bâtiments & Matériaux de
construction » très faible.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 37 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
30.6356
|
37.5662
|
0.0602
|
|
5%
|
30.6356
|
31.4104
|
0.0602
|
|
10%
|
30.6356
|
28.4120
|
0.0602
|
Tableau 37 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « Pétroles &
Gaz ».
Le tableau 37 montre que la valeur statistique LIB est 30.6356
et que la p-value associée est 0,0602. Notons que la valeur
t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5%
et elle n'est pas largement supérieure à la valeur critique au
niveau de 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée au seuil de 10% (seuil significatif).
Conclusion : il y a une faible
autocorrélation entre les rendements de l'indice sectoriel «
Pétroles & Gaz » au seuil de 10%, car le test est n'est pas
significatif aux seuils de 1% et 5%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 56 sur 113
2.3.3.6. Test d'absence d'autocorrélation des
rendements géométriques de l'indice sectoriel «
Bâtiments & Matériaux de Construction » :
La figure 33 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
sectoriel « Bâtiments & Matériaux de construction »
:
Figure 33 : Corrélogramme
d'autocorrélation des rendements l'indice sectoriel
«
Bâtiments & Matériaux de construction ».
Selon le corrélogramme des rendements journaliers
l'indice sectoriel « Bâtiments & MC » presque tous les pics
sont non significatifs, ce qui confirme la propriété de non
corrélation des rendements.
Nous remarquons que les valeurs de coefficients
d'autocorrélation sont très faibles. La série des
rendements géométriques est caractérisé donc par
des autocorrélations très faibles.
Cela veut dire que la corrélation entre la
rentabilité d'aujourd'hui et les rentabilités passées de
l'indice sectoriel « Bâtiments & Matériaux de
construction » très faible.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 38 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
28.6313
|
37.5662
|
0.0953
|
|
5%
|
28.6313
|
31.4104
|
0.0953
|
|
10%
|
28.6313
|
28.4120
|
0.0953
|
Tableau 38 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice
sectoriel « Bâtiments
& Matériaux de construction ».
Le tableau 38 montre que la valeur statistique LIB est 28.6313
que la p-value associée est 0,0953. Notons que la valeur t-statistique
est inférieure aux valeurs critiques aux niveaux de 1%, 5% et presque
égale à la valeur critique au niveau de 10 Donc
l'hypothèse nulle de non corrélation des rendements est
rejetée au seuil de 10% (seuil significatif).
Conclusion : il y a une faible
autocorrélation entre les rendements de l'indice sectoriel «
Bâtiments & MC », au seuil de 10%, car le test est n'est pas
significatif aux seuils de 1% et 5%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 57 sur 113
2.3.3.7. Test d'absence d'autocorrélation des
rendements géométriques de l'indice bancaire :
La figure 34 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
bancaire :
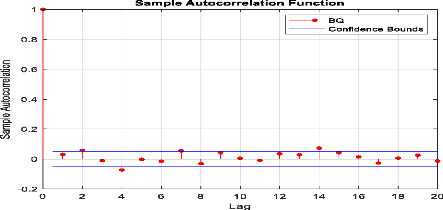
Figure 34 : Corrélogramme
d'autocorrélation des rendements de l'indice Bancaire.
Selon le corrélogramme des rendements journaliers de
l'indice Bancaire presque tous les pics sont non significatifs, ce qui confirme
la propriété de non corrélation des rendements.
Nous remarquons que les valeurs de coefficients
d'autocorrélation sont très faibles. La série des
rendements géométriques est caractérisé donc par
des autocorrélations très faibles.
Cela veut dire que la corrélation entre la
rentabilité d'aujourd'hui et les rentabilités passées de
l'indice Bancaire est très faible.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 39 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
42.6877
|
37.5662
|
0.0022
|
|
5%
|
42.6877
|
31.4104
|
0.0022
|
|
10%
|
42.6877
|
28.4120
|
0.0022
|
Tableau 39 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice Bancaire.
Le tableau 39 montre que la valeur statistique LJB est 42.6877 et
que la p-value associée est 0,0022. Notons que la valeur t-statistique
n'est pas largement supérieure aux valeurs critiques aux niveaux de 1%,
5% et 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée. Conclusion : il y a
une faible autocorrélation entre les rendements de l'indice Bancaire
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 58 sur 113
2.3.3.8. Test d'absence d'autocorrélation des
rendements géométriques de l'indice sectoriel « Transport
» La figure 35 affiche le corrélogramme
d'autocorrélation des rendements géométriques de l'indice
sectoriel « Transport » :
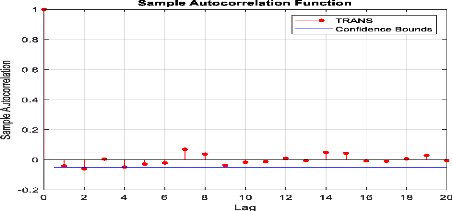
Figure 35 : Corrélogramme
d'autocorrélation des rendements de l'indice sectoriel « Transport
».
Selon le corrélogramme des rendements journaliers de
l'indice sectoriel « Transport » presque tous les pics sont non
significatifs, ce qui confirme la propriété de non
corrélation des rendements.
Nous remarquons que les valeurs de coefficients
d'autocorrélation sont très faibles. La série des
rendements géométriques est caractérisé donc par
des autocorrélations très faibles.
Cela veut dire que la corrélation entre la
rentabilité d'aujourd'hui et les rentabilités passées de
de l'indice sectoriel « Transport » est très faible.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 40 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
35.8831
|
37.5662
|
0.0159
|
|
5%
|
35.8831
|
31.4104
|
0.0159
|
|
10%
|
35.8831
|
28.4120
|
0.0159
|
Tableau 40 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel « Transport ».
Le tableau 40 montre que la valeur statistique LJB est 35.8831
et que la p-value associée est 0,0159. Notons que la valeur
t-statistique et inférieure à la valeur critique au niveau de 1%,
et n'est pas largement supérieure aux valeurs critiques aux niveaux de
5% et 10%. Donc l'hypothèse nulle de non corrélation des
rendements est rejetée.
Conclusion : il y a une faible
autocorrélation entre les rendements de l'indice sectoriel «
Transport », aux niveaux de 5% et 10%..
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 59 sur 113
2.3.3.9. Test d'absence d'autocorrélation des
rendements géométriques de l'indice « Loisirs &
Hôtellerie » : La figure 35 affiche le
corrélogramme d'autocorrélation des rendements
géométriques de l'indice sectoriel « Loisirs &
Hôtellerie » :
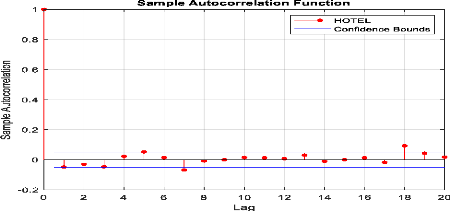
Figure 35 : Corrélogramme
d'autocorrélation des rendements de l'indice sectoriel « Loisirs
& Hôtellerie ».
Selon le corrélogramme des rendements journaliers de
l'indice sectoriel « Loisirs & Hôtellerie » presque tous
les pics sont non significatifs, ce qui confirme la propriété de
non corrélation des rendements.
Nous remarquons que les valeurs de coefficients
d'autocorrélation sont très faibles. La série des
rendements géométriques est caractérisé donc par
des autocorrélations très faibles.
Cela veut dire que la corrélation entre la
rentabilité d'aujourd'hui et les rentabilités passées de
de l'indice sectoriel « Loisirs & Hôtellerie » est
très faible.
Les résultats du test d'autocorrélation LJB sont
présentés dans le tableau 41 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
42.4114
|
37.5662
|
0.0024
|
|
5%
|
42.4114
|
31.4104
|
0.0024
|
|
10%
|
42.4114
|
28.4120
|
0.0024
|
Tableau 41 : Test
d'autocorrélation LJB pour la série des rendements
géométriques de l'indice sectoriel
« Loisirs &
Hôtellerie ».
Le tableau 41 montre que la valeur statistique LJB est 42.4114
et que la p-value associée est 0,00000. Notons que la valeur
t-statistique n'est pas largement supérieure aux valeurs critiques aux
niveaux de 1%, 5% et 10%. Donc l'hypothèse nulle de non
corrélation des rendements est rejetée.
Conclusion : il y a une faible
autocorrélation entre les rendements de l'indice sectoriel «
Loisirs & Hôtellerie ».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 60 sur 113
2.3.4 Test
d'hétéroscédasticité
Une autre hypothèse est empiriquement abordée
est celle de l'hétéroscédasticité qui signifie que
la volatilité variable dans le temps. Or, les fluctuations et les
soubresauts que connait incessamment le paysage financier laissent
présager l'existence d'un effet autorégressif à
volatilité conditionnelle (effet ARCH) présent dans la composante
stochastique des séries financières. Compte tenu des
imperfections enregistrées au niveau des modèles classiques, et
en prenant conscience des restrictions des hypothèses, de nouveaux
modèles mathématiques ont été mis en place en vue
d'assurer une modélisation optimale des actifs financiers à
savoir les modèles autorégressifs à volatilité
conditionnelle hétéroscédastique simples et
généralisés (ARCH et GARCH) développés par
Engle (1982).
Ces modèles ont le principal avantage de prendre en
compte principalement la dynamique temporelle variable de la volatilité
(l'hétéroscédasticité) et également la
leptokurticité des rendements traduisant un excès de Kurtosis
(coefficient mesurant l'aplatissement des distributions). Cet excès de
Kurtosis est l'un des indicateurs de la non-normalité.
L'évolution des modèles ne s'arrête pas
là. De nouvelles classes de modèles seront mises en place
notamment les extensions des modèles GARCH à savoir l'exponentiel
GARCH connu sous le sigle EGARCH et le GARCH fractionnaire
intégré connu sous le sigle de FIGARCH. L'extension a
été établie après avoir constaté
empiriquement que les modèles ARCH et GARCH sont des modèles
symétriques (dans le sens où les bonnes et les mauvaises
nouvelles ont le même impact sur les rendements futurs et donc sur la
volatilité). En effet, le modèle GARCH asymétrique ou
EGARCH a été adopté quand l'économiste Black a
remarqué que les bonnes et les mauvaises nouvelles ont des impacts
différents sur la volatilité contrairement au modèle
GARCH.
Ce phénomène d'asymétrie signifie que les
mauvaises nouvelles tendent à faire augmenter la volatilité avec
une ampleur plus importante que les bonnes nouvelles. Ce qui indique
l'existence d'une sensibilité de la volatilité à
l'égard des chocs.
On parle d'homoscédasticité lorsque la variance
est constante.
L'hétéroscédasticité signifie que
la dispersion des résidus a tendance à augmenter ou à
diminuer en fonction des valeurs ajustées, plus
généralement, elle se manifeste quand la dispersion des
résidus varie en fonction des variables explicatives. Non seulement
L'hétéroscédasticité influence les tests de
significativité mais surtout, elle fausse les intervalles de
prévision. Nous allons présenter, un test permettant de
détecter une hétéroscédasticité
éventuelle. Le test ARCH ou test du multiplicateur de Lagrange qui a
été introduit par Engle (1982).
Avant de modéliser la moyenne conditionnelle et la
volatilité conditionnelle pour les séries des rendements
géométriques, nous testons d'abord
l'hétéroscédasticité de la série des
résidus des rendements géométriques.
Les hypothèses testées sont :
? Hypothèse nulle : la série des
résidus des rendements géométriques est
homoscédastique.
? Hypothèse alternative : la
série des résidus des rendements géométriques est
hétéroscédastique.
Nous choisissons les seuils de signification 1%, 5% et 10%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 61 sur 113
2.3.4.1. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « MASI » : Les
résultats du test sont présentés dans le tableau 42 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
74.8277
|
6.6349
|
0.0000
|
|
5%
|
74.8277
|
3.8415
|
0.0000
|
|
10%
|
74.8277
|
6.6349
|
0.0000
|
Tableau 42 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements géométriques de l'indice «
MASI ».
Les résultats du test montrent que la T-Statistique de
74.8277 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
Le test ARCH-LM fournit une preuve solide pour rejeter
l'hypothèse nulle. Ce rejet est une indication de l'existence d'effets
ARCH dans la série des résidus et, par conséquent, la
variance de la série des rendements géométriques de
l'indice principal « MASI » n'est pas constante pour toutes les
périodes spécifiées.
2.3.4.2. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « Assurances » :
Les résultats du test sont présentés dans le tableau 43
:
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
77.5163
|
6.6349
|
0.0000
|
|
5%
|
77.5163
|
3.8415
|
0.0000
|
|
10%
|
77.5163
|
2.7055
|
0.0000
|
Tableau 43 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice « Assurances ».
Les résultats du test montrent que la T-Statistique de
77.5163 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
2.3.4.3. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « Télécom
» : Les résultats du test sont présentés dans le
tableau 44 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
45.2143
|
6.6349
|
0.00000
|
|
5%
|
45.2143
|
3.8415
|
0.00000
|
|
10%
|
45.2143
|
2.7055
|
0.00000
|
Tableau 44 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice «
Télécommunications ».
Les résultats du test montrent que la T-Statistique de
45.2143 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 62 sur 113
2.3.4.4. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « P .P
Immobilières » : Les résultats du test sont
présentés dans le tableau 45 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
121.0210
|
6.6349
|
0.00000
|
|
5%
|
121.0210
|
3.8415
|
0.00000
|
|
10%
|
121.0210
|
2.7055
|
0.00000
|
Tableau 45 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice « P.P Immobilières
».
Les résultats du test montrent que la T-Statistique de
121.0210 est supérieure aux valeurs critiques aux niveaux de 1%, 5% et
10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
2.3.4.5. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « Pétroles&
Gaz » : Les résultats du test sont présentés dans le
tableau 46 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
22.8644
|
6.6349
|
0.0000
|
|
5%
|
22.8644
|
3.8415
|
0.0000
|
|
10%
|
22.8644
|
2.7055
|
0.0000
|
Tableau 46 : test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice « Pétroles & Gaz
».
Les résultats du test montrent que la T-Statistique de
22.8644 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
2.3.4.6. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice sectoriel «
Bâtiments & Matériaux de Construction » :
Les résultats du test sont présentés dans le
tableau 47 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
55.8012
|
6.6349
|
0.0000
|
|
5%
|
55.8012
|
3.8415
|
0.0000
|
|
10%
|
55.8012
|
2.7055
|
0.0000
|
Tableau 47 : test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice « Assurances ».
Les résultats du test montrent que la T-Statistique de
55.8012 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
2.3.4.7. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice bancaire : Les
résultats du test sont présentés dans le tableau 48 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
69.4288
|
6.6349
|
0.0000
|
|
5%
|
69.4288
|
3.8415
|
0.0000
|
|
10%
|
69.4288
|
2.7055
|
0.0000
|
Tableau 48 : test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice Bancaire.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 63 sur 113
Les résultats du test montrent que la T-Statistique de
69.4288 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
2.3.4.8. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « Transport » :
Les résultats du test sont présentés dans le tableau 49
:
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
21.9477
|
6.6349
|
0.0000
|
|
5%
|
21.9477
|
3.8415
|
0.0000
|
|
10%
|
21.9477
|
2.7055
|
0.0000
|
Tableau 49 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements
géométriques de l'indice
sectoriel « Transport ».
Les résultats du test montrent que la T-Statistique de
21.9477est largement supérieure aux valeurs critiques aux niveaux de 1%,
5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
2.3.4.9. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice sectoriel « Loisirs
& Hôtellerie » :
Les résultats du test sont présentés dans le
tableau 50 :
|
Significance level
|
t-stat
|
Critical value
|
P-value
|
|
1%
|
131.7507
|
6.6349
|
0.0000
|
|
5%
|
131.7507
|
3.8415
|
0.0000
|
|
10%
|
131.7507
|
2.7055
|
0.0000
|
Tableau 50 : Test
d'hétéroscédasticité LM-ARCH pour la série
des résidus des rendements de l'indice « Loisirs &
Hôtellerie ».
Les résultats du test montrent que la T-Statistique de
131.7507 est largement supérieure aux valeurs critiques aux niveaux de
1%, 5% et 10%, donc on rejette l'hypothèse nulle.
Conclusion : on accepte alors
l'hypothèse alternative de
l'hétéroscédasticité des résidus.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 64 sur 113
Conclusion
Empiriquement, nous pensons que les faits stylisés
mettent en évidence des propriétés statistiques communes
à l'ensemble des séries financières. En fait, la
distribution des rendements est avec des queues plus épaisses que la loi
normale. Nous notons également qu'il n'y a pas d'autocorrélation
des rendements géométriques, mais il existe une
autocorrélation des rendements géométriques au
carré, ce qui nous amène à rejeter l'hypothèse de
bruit blanc selon laquelle les rendements sont indépendants et
identiquement distribués.
Dans ce chapitre nous avons mis en évidence des faits
stylisés des séries financières des rendements
géométriques des indices sectoriels individuels et de l'indice
principal de la bourse du pays, nous avons fait une analyse graphique,
descriptive et économétrique de toutes ces séries, nous
avons effectué aussi les tests de non stationnarité, de
normalité, d'autocorrélation et
d'hétéroscédasticité.
Nous allons essayer capter ces faits stylisés dans la
modélisation de la corrélation dynamique et la volatilité
conditionnelles des différents indices que ça soit le principal
indice « MAST » ou des huit indices boursiers des principaux secteurs
d'activité choisis dans notre étude.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 65 sur 113
3. Chapitr3 : Mesure de l'interdépendance
de l'indice « MASI » et les
indices sectoriels
par les modèles DCC-GARCH
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 66 sur 113
Introduction
La modélisation et la prévision de la
volatilité ainsi que la corrélation sont des thématiques
qui présent un intérêt important pour les chercheurs,
praticiens et les universitaires, surtout les derniers décennies, et qui
ont devenu un domaine fertile de recherche. La volatilité et la
corrélation sont deux concepts complexes et primordiales en finance,
ayant une grande importance surtout dans les opérations de mesure de
l'incertitude (pour la volatilité) et d'interdépendance (pour la
corrélation) dans des différentes phénomènes
financières tels que l'optimisation de portefeuille, la gestion des
risques, l'évaluation des instruments financiers. Un nombre assez
important des articles, consacrés à la modélisation de la
volatilité conditionnelle et la corrélation dynamique, ont
été rédigés et publiés par des
académiciens et des chercheurs dans les dernières
années.
Les modèles GARCH univariés traitent la
volatilité de chaque actif, par contre les modèles GARCH
multivariés permettent de modéliser à la fois la
corrélation dynamique et la volatilité.
Dans les domaines de l'étude de la stabilité
financière, la mesure de l'interdépendance permet de
déterminer les secteurs ou institutions ayant une importante influence
dans un système financier donné. La mesure de
l'interdépendance peut classer des secteurs d'activité en
fonction de l'interdépendance de leurs cours avec l'indice principal du
pays.
Le présent chapitre met en évidence les
relations d'interdépendance entre le principal indice de la Bourse
Marocaine « MAST » et les indices des primordiaux secteurs
d'activité de l'économie nationale choisis dans notre
échantillon.
L'objectif principal de ce chapitre est d'analyser
l'interdépendance de l'indice principal et des huit indices sectoriels
de notre étude, en utilisant le modèle DCC-GARCH. On a
utilisé une fréquence quotidienne de données dans notre
échantillon, est qui étalée du 01 janvier 2016
au 31 mai 2022, hors les jours
fériés.
Nous allons décrire les fondements théoriques
des modèles GARCH univariés et multivariés, nous
détaillons en particulier le modèle de Corrélation
Conditionnelle Dynamique « DCC-GARCH » qui nous permettra de
prévoir les relations d'interdépendance sur le court terme entres
les cours.
Dans la dernière section, nous présentons les
résultats obtenus à partir de la mise en oeuvre du modèle
DCC-GARCH. Nous présentons les résultats empiriques des
estimations du modèle DCC-GARCH (1.1) obtenus pour chaque indice
sectoriel et faire une conclusion en fournissant une brève comparaison
des résultats et nous ferons aussi une prévision de
la corrélation future pour chaque indice sur un horizon de
100 jours suivant le 31/05/2022 (la date de la dernière observation de
notre mémoire).
Les résultats empiriques indiquent des degrés
variables d'interdépendance entre les indices sectoriels et le principal
indice de la Bourse marocaine (B.V.C), et que le secteur bancaire
s'avère un secteur de grande importance systémique
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 67 sur 113
3.1. Modèles GARCH univariés
3.1.1 Modèle moyenne mobile ????(??) d'ordre q
Soit (Xt)t?Z un processus stochastique. On dit que (Xt
)t ? Z admet une représentation moyenne
mobile MA(q) d'ordre ?? s'il existe un polynôme retard A(L)
d'ordre q et un bruit blanc (åt)t??? tels que : Xt = ì
+ A(L)åt (1)
Où A(L) = ?q AiLi
i=0 avec A0 = 1 et Aq ? 0
q
åt (2)
On a donc : Xt = ì + ?AiLi
i=0
Xt = ì + åt +
A1åt-1 + A2åt-2 + ? + Aqåt-q (3)
Le processus (Xt)t??? est modélisé donc comme une
combinaison linéaire des valeurs passées
décalées d'ordre q du bruit blanc
åt et d'une constante égale à sa moyenne.
Où
ì : constante (E(Xt) = ì)
Li: opérateur retard d'ordre i de
Xt
Ai: coefficient du retard d'ordre i de
Xt
åt: sont i. i. d de moyenne 0 et de variance
Ó. (åt ? i. i. d(0, Ó))
3.1.2 Modèle autorégressif ????(??)
d'ordre p
Soit (Yt)t??? un processus stochastique. On dit que (Yt)t???
admet une représentation autorégressive AR(p) d'ordre p s'il
existe un polynôme retard Ö(L) d'ordre p et un bruit blanc
(åt)t??? tels que :
Ö(L)Yt = c + åt (4)
|
p
Où Ö(L) = ? ÖiLi
i=0 p
|
avec Ö0 = 1 et Öp ? 0
|
|
On a donc :
|
? ÖiLi
|
Yt = c + åt (5)
|
i=0
Yt + Ö1Yt-1 + Ö2Yt-2 +
? + ÖpYt-p = c + åt (6)
Le processus (Yt)t??? est modélisé donc comme une
combinaison linéaire de ses valeurs passées
décalées d'orde p, d'une constante et d'un bruit
blanc gaussien.
Où
c : constante
Li: opérateur retard d'ordre i de
Yt
Öi: coefficient du retard d'ordre i de
Yt
åt: sont i. i. d de moyenne 0 et de variance
Ó. (åt ? i. i. d(0, Ó))
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 68 sur 113
3.1.3 Modèle autorégressif moyenne mobile
???????? (??, ??)
Soit (Zt)t?Z un processus stochastique. On dit que (Zt)t?Z
admet une représentation autorégressive moyenne mobile ARMA(p, q)
d'ordres ?? et ?? s'il existe un polynôme retard A(L) d'ordre q, un
polynôme retard Ö(L) d'ordre q et un bruit blanc (åt)t?Z tels
que :
Ö(L)Zt = c + A(L)åt (7)
|
p
Où Ö(L) = ? ÖiLi
i=0 q
|
avec Ö0 = 1et Öp ? 0
|
|
et A(L) = ? AiLi
i=0
|
avec A0 = 1 et Aq ? 0
|
p q
|
On a donc :
|
? ÖiLi i=0
|
Zt = c + ?AiLi
i=0
|
åt (8)
|
Zt + Ö1Zt-1 + Ö2Zt-2 +
? + ÖpZt-p = c + åt + A1åt-1 +
A2åt-2 + ? + Aqåt-q (9)
Le processus (Zt)t??? est modélisé donc comme
une combinaison linéaire de ses valeurs passées
décalées d'orde p, d'une constante et des valeurs
passées décalées d'ordre q du bruit blanc
åt.
Où
c : constante
Öi: coefficient du retard d'ordre i de
Zt
Ai: coefficient du retard d'ordre i de
åt
åt: sont i. i. d de moyenne 0 et de variance
Ó. (åt ? i. i. d(0, Ó))
3.1.4 Modèle autorégressif
héteroscedastique ????CH (??, ??)
Les processus ARCH visent également à rendre
compte du fait que la variance conditionnelle n'est pas constante et proposent
une façon de l'estimer basée sur le carré des rendements.
D'après ce qui vient d'être dit, on traitera cette classe de
modèle avec méfiance : il est possible que la volatilité
soit non constante au cours du temps, mais qu'un modèle ARCH ou leur
généralisation GARCH ne captent pas cet effet, voire concluent
dans certains cas à l'absence de dépendance temporelle dans les
rendements.
On présente dans ce qui suit les modèles ARCH et
GARCH ainsi que leurs principales propriétés.
Les modèles furent initialement proposés par
Engle (1982) et Bollerslev (1986), Tim Bollerslev étant le
thésard de Robert Engle. Le premier modèle fut celui d'Engle, et
visait à obtenir une modélisation de la variance conditionnelle
de l'inflation (en glissement mensuel) de la Grande Bretagne. Un modèle
ARCH (1) est de la forme :
{
??t = vht ??t 2 ht = ??0 + ??1??t-1 avec
??t~??(0,1); ht représente la variance
conditionnelle du processus ??t. Les moments
conditionnels sont les suivants :
E[??t |ht] = E[vht??t |ht] =
vht E[??t |ht] = 0
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 69 sur 113
Il s'agit donc encore de processus applicables à des
séries préalablement centrées, comme dans le cas des ARMA.
Notons que les séries des rendements sont théoriquement
naturellement centrées : La variance conditionnelle n'a plus rien
à voir avec celle des ARMA :
V [??t |ht] = V [vht£t |ht]
= ht V [£t |ht] = ht
E[£t2|ht] //
E[£t2|ht] = 1 (Par
hyp????hès??)
= ht
Ainsi, contrairement aux modèles ARMA, la variance
conditionnelle d'un processus ARCH n'est pas constante au cours du temps. C'est
ce qui fait tout l'intérêt de ces processus, notamment pour les
séries financières. Gardons cependant à l'esprit que ces
modèles s'appuient sur une mesure de la variance proche de
??t2. En effet, on a :
E[??t2|ht] =
E[ht£t2|ht]=ht
Ceci tient simplement au fait que ??t soit
naturellement un processus centré. Si ces modèles
semblent d'un abord pratiques, il n'en reste pas moins qu'ils
produisent naturellement des erreurs de
mesure sur la volatilité.
Le calcul des moments non conditionnels permet de
déterminer quelques conditions à remplir
afin de s'assurer de la stationnarité du processus. On
détermine l'espérance à l'aide de la loi des
espérances itérées :
??[??t] = ??[E[??t|ht]]
= E[0]
=0
Pour ce qui de la variance, il est possible de procéder
par récurrence. Utilisons tout d'abord la
loi de la décomposition de la variance :
V [??t] = E[V [??t |ht]] + V
[E[??t |ht]]
= E[ht] + 0
On en déduit alors l'équation suivante :
V[??t] = E[ht]
= E[co0 + co1??t-1
2 ]
= co0 + co1E[??t-1
2 ]
= co0 + co1V[??t-1]
On obtient ainsi une formule de récurrence permettant
de déterminer la variance non conditionnelle du processus. Il suffit,
pour y parvenir, d'itérer la formule n fois, puis comme dans le cas des
ARMA, de passer à la limite. On sait que :
V[??t] = co0 + co1V[??t-1] V [??t-1] = co0
+ co 1V[??t-2] V [??t-2] = co0 + co 1V [??t-3]
D'où :
V [??t] = co0 +
co1(co0 + co1(co 0 + co1V [??t-3]))
= co0(1 + co1 + co12) + co13 V
[??t-3]
D'où la formule générale :
??

V [??t] = co0 (1 + ?
co1?? ) + co1??+1V [??t-(??+1)]
??=1
= co0 1 co1?? 1 +
co1n+1V[xt-(n+1)]
i-0 J
D'où si |co1| < 1, on a , lorsque n - +00
co0
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 70 sur 113
n
V [xt] = 1 -- co1
Cette dernière condition est nécessaire pour
assurer l'existence de la variance, c'est à dire :
V[xt] < 00
Cette condition est nécessaire pour obtenir un processus
stationnaire (variance finie et indépendante
du temps). Il est nécessaire d'imposer une seconde
condition : les variances conditionnelle et non
conditionnelle doivent être naturellement positives (la
variance est le carré de l'écart type). La positivité
de la variance conditionnelle implique naturellement que :
co0 > 0
co1 > 0
Ces deux conditions impliquent naturellement que la variance non
conditionnelle, dotée de la
condition |co1|< 1, soit positive. Remarquons finalement que,
dans le cadre d'un processus ARCH, la
variance conditionnelle ne coïncide pas avec la variance non
conditionnelle, ce qui est précisément ce que
nous recherchions.
Ultime propriété d'un processus ARCH (1), il est
possible de montrer que le carré du processus
admet une représentation AR (1).
Notons vt la différence entre
xt2et ht. On a alors :
ht = co0 + co1xt-1
2
H xt2 -- vt = co0 +
co1V[xt--1]
H xt2 = co0 + co1V[xt_1] +
vt
On retrouve ainsi un processus AR (1) sur les carrés des
résidus. Ceci a plusieurs implications pratiques :
- D'une part, un processus ARCH (1) ne semble pas saisir de
façon adéquate les processus de volatilité
financière : on a vu lors des applications des processus
ARMA que la volatilité de certains actifs semble présenter
une structure plus proche des ARMA (retour à la moyenne en
cas de choc importants) que des AR. Il sera
donc nécessaire de complexifier légèrement
la chose, afin d'accommoder cette caractéristique empirique.
- Seconde implications pratique, l'identification d'un ARCH (1)
ne doit pas poser de
problème, si l'on s'appuie sur ce qui a été
dit plus haut au sujet des AR : il suffit d'étudier les
fonctions d'autocorrélations simple et partielle pour se
faire une idée de l'ordre du processus à
retenir. On étudiera ceci au cours des applications
empiriques proposées plus loin.
Ce qui vient d'être dit au sujet des ARCH (1) peut se
généraliser aisément au cas des processus ARCH(p).
Un processus ARCH(p) est un processus xt qui est de la
forme :
{xt= -/ht et
2
ht = co0 + co1xt-??
avec et--N(0,1) .
Comme précédemment, on fournit les moments
conditionnels :
E[xt|xt-1] = 0
V [xt |xt-1] = ht
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 71 sur 113
Conditionnellement à l'information disponible à
la date t, un processus GARCH est un processus de moyenne (conditionnelle)
nulle et de variance égale à h??. Qu'en est-il des moments
non-conditionnels ? L'espérance ne pose pas de problème, à
la condition d'utiliser la loi des espérances itérées :
E[????] = 0
Pour ce qui est la variance, il est ici nécessaire de
déterminer, comme précédemment, une formule de
récurrence pour parvenir finalement à exprimer la variance en
passant à la limite. On ne refait pas ici les calculs :
on se contente de fournir le résultat. Si |? ??1,?? <
1
?? , alors la variance du processus existe et est de la forme
:
??=1
??[????] = ??0
1-? ??1,??
?? ??=1
3.2. Modèles GARCH multivariés
Les modèles GARCH univariés à
volatilité conditionnelle présentés
précédemment se contentent d'analyser individuellement les
séries financières tout en ignorant l'interdépendance avec
les autres séries. Ainsi, l'analyse de la volatilité, en tant que
proxy de risque, doit se faire dans une optique de risques multiples. Tant que
les modèles GARCH univariés ne tiennent pas compte de la
corrélation entre les actifs, nous allons passer aux modèles
multivariés afin de capter les liens dynamiques entre ces actifs. Ces
modèles nous permettent également d'analyser les
interdépendances éventuelles entre les institutions
financières et de cerner les mécanismes de transmission des
chocs.
Plusieurs travaux de recherche dans la littérature
économétrique ont essayé de décrire et d'analyser
la corrélation variable dans le temps entre les rendements des actifs
financiers, Bollerslev (1988) à Engel (2002) en passant par Wooldridge,
Kroner et Claessens (1991) et Mezrich (1996), ont introduit une analyse
dynamique sur la corrélation el la volatilité des actifs
financiers.
Dans ce chapitre nous allons faire un bref aperçu sur
les modèles hétéroscédastique multivariés et
nous détaillons seulement le modèle DCC-GARCH utilisé dans
la partie pratique dans notre étude.
3.2.1 Modèle CCC-GARCH
Le modèle CCC-GARCH (Constant Conditional Correlation)
proposé par l'économètre Bollerslev (1990) permet
d'estimer la covariance conditionnelle en se basant sur l'hypothèse que
la corrélation entre les variables reste constante alors que la variance
est variable dans le temps.
3.2.2 Modèle DCC-GARCH
Les modèles GARCH multivariés à
corrélations conditionnelles décomposent la matrice de
corrélations en deux composantes, soit celle des écarts-types et
celle des corrélations conditionnelles. Bollerslev (1990) introduit le
premier modèle de corrélations qui est le modèle à
corrélations conditionnelles constantes (CCC-GARCH). Il propose un
modèle où les variances et covariances conditionnelles varient
dans le temps et les corrélations conditionnelles restent constantes.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 72 sur 113
Engle (2002) introduit le modèle à
corrélations conditionnelles dynamiques, le DCC-GARCH, en permettant
à la matrice de corrélations conditionnelles de varier dans le
temps. Ce modèle est une généralisation du modèle
CCC-GARCH de Bollerslev (1990).
Le modèle DCC-GARCH est défini comme :
???? = ???? + ???? (1)
???? = ????1/2 ???? = ???? ???? (2)
???? = ???????????? (3)
Avec :
???? : Vecteur de rendements de n actifs au
temps t de dimension nx1 ;
???? : Vecteur de rendements
espérés conditionnels de n actifs au temps t de dimension ????1
;
???? : Vecteur d'erreurs conditionnelles i.i.d
au temps t de dimension ????1 ;
Les résidus conditionnels ???? sont distribués
selon une loi normale de moyenne 0 et de variance ????. ??[????] = 0 ????
??????[????] = ???? ;
???? : Matrice de variance conditionnelle de
???? au temps t de dimension nxn ;
???? : Matrice diagonale des écarts-types
conditionnels de ???? au temps t de dimension nxn ;
???? : Matrice de corrélation
conditionnelle de ???? au temps t de dimension nxn ;
et le vecteur çtest i.i.d c'est un bruit
blanc de moyenne nulle et de variance égale à 1. avec E( ???? ) =
0 Et ??????( ???? ) = 1
C'est un modèle d'estimation en deux étapes, la
première étape consiste à estimer la variance
conditionnelle avec un modèle GARCH
univarié pour chacune des séries, dans la
deuxième étape, on utilise les résidus standardisés
obtenus dans la première étape pour estimer les paramètres
de la matrice des corrélations dynamiques. Ce modèle comporte des
conditions permettant à la matrice de covariances d'être positive,
définie en tout temps ainsi qu'à la covariance d'être
stationnaire.
Cependant, dans notre travail de recherche nous utiliserons un
?????? - ?????????? (1,1) bivarié pour analyser les relations de
transfert de volatilité entre l'indice principal « MASI » et
les indices des huit secteurs d'activités, c'est la forme la plus simple
du modèle ?????? - ??????????.
|
Le modèle ?????? - ?????????? (1,1) bi-varié est
présenté par :
2 = ???? + ????????-1 2 + ????????-1 2
h??,?? = ????,??
2
h??,?? = ???2?,?? = ???? + ???????2?-1 + ????????-1
' ) + ????????????-1
???? = (1 - ???????? - ????????)?? + ????????(????-1????-1
???? = ????*-1????????*-1
|
(11)
(12)
(13)
(14)
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 73 sur 113
Les paramètres à estimer sont :
???? ???? ???? : Représentant respectivement la
volatilité conditionnelle moyenne des rendements du marché et de
l'institution financière i ;
???? ???? ???? : Appelés paramètres ARCH
mesurant la sensibilité des rendements géométriques aux
chocs du marché ;
???? ???? ???? : Sont les paramètres GARCH qui mesurent la
persistance.
L'estimation du modèle DCC-GARCH se fait par la
méthode du maximum de vraisemblance.
Les avantages du modèle DCC-GARCH sont la
modélisation directe de la covariance ainsi que sa flexibilité.
Nous allons essayer de mettre en pratique ce modèle pour cerner les
mécanismes de transmissions de volatilité entre l'indice du
secteur bancaire et les différentes banques.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 74 sur 113
3.3. Modélisation de la corrélation
conditionnelle:
Ce chapitre de notre recherche sera consacré au
traitement des différents résultats obtenus à partir de la
mise en oeuvre du modèle de corrélation conditionnelle dynamique
« DCC-GARCH ». En premier lieu on va essayer de
présenter les résultats empiriques des estimations du
modèle DCC-GARCH (1.1) obtenus pour chaque secteur d'activité et
faire une conclusion en fournissant une brève comparaison des
résultats.
Nous avons jusqu'à présent, analysé
indépendamment les variations du rendement des indices dans un cadre
univarié, sans tenir compte des interactions avec l'indice principal
« MASI ». D'ailleurs, Nous avons expliqué les raisons de la
volatilité importante des rentabilités des valeurs des
différents secteurs. Cela peut être expliqué par la
durée prolongée de confinement et d'arrêt de
l'activité économique. En fait, la forte interdépendance
entre les marchés via les phénomènes de contagion, est
souvent exacerbée par les crises2.
Notre étude contribue à l'ensemble des
connaissances en introduisant une méthode efficace d'estimation du
risque dans un marché dynamique. Ce modèle offre une nouvelle
façon de modéliser le risque de contagion plutôt que
d'utiliser les méthodes traditionnelles. En outre, il est
suggéré que seuls les modèles dynamiques devraient
être considérés pour l'estimation de
l'interdépendance dans un marché boursier dynamique. De
même, les investisseurs et les experts financiers peuvent augmenter leur
confiance dans le marché en adoptant ce modèle DCC-GARCH pour
l'estimation du risque.
Ainsi, nous allons essayer d'aborder le
phénomène de contagion, en procédant à l'analyse
des mécanismes de transmission de la volatilité de l'indice
« MASI », en tant que marché générateur de
crise, vers les autres indices sectoriels. Nous allons faire appel à un
modèle GARCH multivarié à corrélations
conditionnelles dynamiques (DCC-GARCH).
Les modèles à volatilité conditionnelle
que nous avons exploités précédemment sont des
modèles univariés. Ils se contentent d'analyser une seule
série financière ignorant les interactions avec les autres
séries. Ainsi, l'analyse de la volatilité, en tant que proxy de
risque, doit se faire dans une optique de risques multiples. Tant que les
modèles GARCH univariés ne tiennent pas compte de la
corrélation entre les indices, nous allons passer aux modèles
multivariés afin de capter les liens dynamiques entre ces indices.
Ces modèles nous permettent également d'analyser
les interdépendances éventuelles entre les différents
indices boursiers étudiés et de cerner les mécanismes de
transmission des chocs. C'est dans cette optique que s'inscrit ce chapitre
ayant pour objectif principal d'appréhender la transmission des chocs du
marché des actions à travers l'indice principal « MASI
» en tant qu'indice générateur de crise, vers les autres
indices sectoriels.
Dans notre analyse empirique en se basant sur le coefficient
de corrélation non conditionnel et sur le coefficient de
sensibilité (béta) nous avons prouvé l'existence d'une
forte interdépendance entre le marché des actions et les indices
des différents secteurs d'activité de l'économie
nationale
Nous allons donc utiliser le modèle DCC-GARCH pour
cerner le phénomène de contagion financière.
2 Idier, (2011)
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 75 sur 113
3.3.1 Modélisation de l'interdépendance
de l'indice « MAST » et les huit indices sectoriels: Résultats
empiriques du modèle DCC-GARCH (??, ??) :
Les modèles univariés de la famille GARCH sont
incapables de capturer la volatilité de manière efficace. Le
modèle DCC est un modèle beaucoup plus efficace pour traiter la
volatilité car les paramètres estimés par le modèle
DCC indiquent l'efficacité du modèle dans le marché
boursier marocain. Nous allons commencer tout d'abord par l'analyse de
l'interaction entre le « MASI » et l'indice sectoriel «
Assurances ».
3.3.1.1. Estimation du modèle DCC-GARCH (??, ??)
pour les rendements géométriques de l'indice sectoriel «
Assurances » et l'indice « MAST ».
Le tableau 1 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques du secteur des Assurances.
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
Masi
Tndex
|
Equation de la moyenne
|
|
ø1
|
0.000451
|
0.000136
|
3.3165
|
0.000911
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.8724
|
0.000000
|
|
á1
|
0.203335
|
0.023617
|
8.6097
|
0.000000
|
|
â1
|
0.691917
|
0.030906
|
22.3878
|
0.000000
|
|
Persistance : á1 + â1
|
0.895252
|
|
Secteur
Assurances
|
Equation de la moyenne
|
|
ø1
|
0.000383
|
0.000298
|
1.2861
|
0.198406
|
|
Equation de la variance
|
|
Ù
|
0.000015
|
0.000005
|
3.3209
|
0.000897
|
|
á1
|
0.130940
|
0.029491
|
4.4400
|
0.000009
|
|
â1
|
0.789433
|
0.045058
|
17.5202
|
0.000000
|
|
Persistance : á1 + â1
|
0.920373
|
|
Masi/
Assurances
|
Equation de la corrélation
|
|
á??????
|
0.011579
|
0.008586
|
13.4785
|
0.171505
|
|
â??????
|
0.908928
|
0.028783
|
31.5785
|
0.000000
|
|
Persistance : á?????? + â??????
|
0.0.920507
|
Tableau 1 : Estimation du
modèle DCC-GARCH pour l'indice principal « MASI » et l'indice
sectoriel « Assurances ».
Nous remarquons d'après le tableau 1 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre le « MASI »,
le principal indice de la Bourse marocaine et l'indice sectoriel «
Assurances », que les coefficients du modèle de corrélation
conditionnelle DCC-GARCH sont statistiquement significatifs au seuil de 1%.
Les paramètres conjoints á?????? ????
â?????? sont plus significatifs que les paramètres individuels ??
et ?? qui sont estimés du modèle GARCH univarié. Cela
montre que la volatilité capturée par la méthode GARCH
(1,1) est sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 76 sur 113
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal à
zéro
(aocc 0), le coefficient I3occ est largement supérieur
à zéro (I3occ >>> 0), et la somme de deux
qui est
inférieure à 1 ( aocc + I3occ < 1).
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir aocc + I3occ = 0.011579 + 0.908928 =
0.920507 < 1, ce qui suggère que la matrice de corrélation
estimée Dt est définie positive.
Le coefficient I3occ étant égal à
0.920507 est proche de la valeur de 1, cette valeur du coefficient beta montre
une forte corrélation conditionnelle entre les deux indices. Le
coefficient aocc étant égal à 0.011579
est proche de 0. D'autre part, les deux coefficients sont
statistiquement significatifs( p - value < 5%), cette significativité
des coefficients confirme la sensibilité de l'indice « Assurances
» « MASI ».
La persistance de la corrélation conditionnelle
calculée à travers la somme de aocc et RDcc et est
très importante, elle atteint 0.920507 est proche de 1.
Nos résultats montrent que le rendement l'indice
sectoriel « Assurances », est influencé par la
volatilité de l'indice MASI. Les chocs de volatilité du
marché ont un effet persistant sur le rendement du cours du secteur des
assurances. Au vu de ces résultats concluants, nous pouvons conclure que
les deux indices sont fortement interdépendants.
La figure 1 affiche la corrélation conditionnelle
dynamique entre l'indice principal « MASI » et l'indice sectoriel
« Assurances », estimée par le modèle DCC-GARCH (1,1)
:
MASI-ASS
|
.6 .5 .4 .3
.2 .1
|
|
|
16 17 18 19 20 21 22
|
Figure 1 : Corrélation
conditionnelle dynamique entre l'indice « Assurances » et le «
MASI » estimée par le modèle DCC-GARCH(1,1).
La figure 1 illustre la corrélation conditionnelle
entre l'indice « Assurances » et le « MASI », la
corrélation conditionnelle estimée entre les deux indices reste
en général non stable avec de faibles fluctuations, elle fluctue
dans l'ensemble entre 0.25 et 0.45. On remarque aussi que la corrélation
diminue vers le 1er trimestre de l'année 2017 jusqu'au
0.11.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 77 sur 113
3.3.1.2. Estimation du modèle DCC-GARCH (1, 1)
pour les rendements géométriques de l'indice du secteur bancaire
et l'indice « MASI ».
Le tableau 2 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques de l'indice bancaire.
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
Masi
Index
|
Equation de la moyenne
|
|
Il1
|
0.000451
|
0.000136
|
3.3118
|
0.000927
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.9378
|
0.000000
|
|
á1
|
0.203335
|
0.023544
|
8.6364
|
0.000000
|
|
131
|
0.691917
|
0.030795
|
22.4685
|
0.000000
|
|
Persistance : á1 + 131
|
0.895252
|
|
Secteur
Assurances
|
Equation de la moyenne
|
|
Il1
|
0.000339
|
0.000171
|
1.9770
|
0.048045
|
|
Equation de la variance
|
|
Ù
|
0.000007
|
0000001
|
13.2427
|
0.000000
|
|
á1
|
0.148133
|
0.018106
|
8.1816
|
0.000000
|
|
131
|
0.755418
|
0.024826
|
30.4285
|
0.000000
|
|
Persistance : á1 + 131
|
0.903551
|
|
Masi/
Assurances
|
Equation de la corrélation
|
|
áocc
|
0.053644
|
0.010801
|
4.96668
|
0.000001
|
|
13occ
|
0.917910
|
0.018355
|
50.0077
|
0.000000
|
|
Persistance : áocc + 13occ
|
0.971554
|
Tableau 2 : Estimation du
modèle DCC-GARCH pour l'indice « MASI » et l'indice
Bancaire.
Nous remarquons d'après le tableau 2 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre le « MASI »,
le principal indice de la Bourse marocaine et l'indice du secteur bancaire, que
les coefficients du modèle de corrélation conditionnelle
DCC-GARCH sont statistiquement significatifs au seuil de 1%.
Les paramètres conjoints áocc et
13occ sont plus significatifs que les paramètres individuels a et [3 qui
sont estimés du modèle GARCH univarié. Cela montre que la
volatilité capturée par la méthode GARCH (1,1) est
sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux indices est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal
à zéro (áocc 0), le coefficient 13occ est
largement supérieur à zéro (13occ >>> 0), et la
somme
de deux qui est inférieure à 1 ( áocc
+ 13occ < 1).
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir áocc + 13occ = 0.053644 + 0.917910 =
0.971554 < 1, ce qui suggère que la matrice de corrélation
estimée Dt est définie positive.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 78 sur 113
Le coefficient I3occ étant égal
à 0.917910 est proche de la valeur de 1, cette valeur
du coefficient beta montre une forte corrélation conditionnelle entre
les deux indices. Le coefficient aocc étant égal
à 0.053644 est proche de 0. D'autre part, les deux
coefficients sont statistiquement significatifs( p - value <
5%), cette significativité des coefficients confirme la
sensibilité de l'indice Bancaire à l'indice principal « MASI
». La persistance de la corrélation conditionnelle calculée
à travers la somme de aDcc et IDCc et est
très importante, elle atteint 0.917910 est proche de
1.
Nos résultats montrent que le rendement de l'indice du
secteur Bancaire est influencé par la volatilité de l'indice
« MASI ». Les chocs de volatilité du marché ont un
effet persistant sur le rendement de l'indice du secteur Bancaire. Au vu de ces
résultats concluants, nous pouvons conclure que les deux indices sont
fortement interdépendants.
La figure 2 affiche la corrélation conditionnelle
dynamique entre l'indice Bancaire et l'indice principal « MASI »
estimée par le modèle DCC-GARCH (1,1) :
MASI/BQ
|
.92 .88 .84
.80 .76 .72 .68
|
|
|
16 17 18 19 20 21 22
|
Figure 2 : Corrélation
conditionnelle dynamique entre l'indice Bancaire et le « MASI »
estimée par le modèle DCC-GARCH(1,1).
La figure 2 illustre la corrélation conditionnelle
entre le secteur « Assurances » et l'indice « MASI », la
corrélation conditionnelle estimée entre les deux indices reste
en général non stable avec de faibles fluctuations, elle fluctue
dans l'ensemble entre 0.75 et 0.86. On remarque aussi que la corrélation
diminue vers le début de l'année 2017 jusqu'au 0.7.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 79 sur 113
3.3.1.3. Estimation du modèle DCC-GARCH (??, ??)
pour les rendements géométriques de l'indice sectoriel «
Télécommunications » et l'indice principal « MASI
».
Le tableau 3 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques de l'indice du « Télécom
».
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
MASI
Index
|
Equation de la moyenne
|
|
ø1
|
0.000451
|
0.000136
|
3.3139
|
0.000920
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.8340
|
|
|
0.203335
|
0.000000á1
0.023818
|
8.5370
|
0.000000
|
|
â1
|
0.691917
|
0.031119
|
22.2342
|
0.000000
|
|
Persistance : á1 + â1
|
0.895252
|
|
Secteur
Télécommunications
|
Equation de la moyenne
|
|
ø1
|
0.000317
|
0.000181
|
1.7522
|
0.079746
|
|
Equation de la variance
|
|
Ù
|
0.000003
|
0.000001
|
2.8802
|
0.003974
|
|
á1
|
0.111326
|
0.025743
|
4.3246
|
0.000015
|
|
â1
|
0.856596
|
0.032048
|
26.6982
|
0.000000
|
|
Persistance : á1 + â1
|
0.967922
|
|
MASI/
Télécommunications
|
Equation de la corrélation
|
|
á??????
|
0.075614
|
0.038143
|
1.9824
|
0.047440
|
|
â??????
|
0.764581
|
0.147708
|
5.1763
|
0.000000
|
|
Persistance : á?????? + â??????
|
0.840195
|
Tableau 3 : Estimation du
modèle DCC-GARCH pour le « MASI » et l'indice «
Télécommunications ».
Nous remarquons d'après le tableau 3 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre l'indice « MASI
», le principal indice de la Bourse marocaine et l'indice sectoriel «
Télécommunications », que les coefficients du modèle
de corrélation conditionnelle DCC-GARCH sont statistiquement
significatifs au seuil de 1%.
Les paramètres conjoints á?????? ????
â?????? sont plus significatifs que les paramètres individuels ??
et ?? qui sont estimés du modèle GARCH univarié. Cela
montre que la volatilité capturée par la méthode GARCH
(1,1) est sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal à
zéro (á?????? 0), le coefficient â?????? est largement
supérieur à zéro (â?????? ??? 0), et la somme de
deux qui est inférieure à 1 ( á?????? +
â?????? < 1).
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 80 sur 113
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir aocc + I3occ = 0.075614 + 0.764581
= 0.840195 < 1, ce qui suggère que la matrice de
corrélation estimée Dt est
définie positive.
Le coefficient I3occ étant
égal à 0.841095 est proche de la valeur de 1,
cette valeur du coefficient beta montre une forte corrélation
conditionnelle entre les deux indices. Le coefficient aocc
étant égal à 0.075614 est proche
de 0. D'autre part, les deux coefficients sont statistiquement
significatifs( p - value < 5%), cette
significativité des coefficients confirme la sensibilité de
l'indice « Télécom » au « MASI ».
La persistance de la corrélation conditionnelle
calculée à travers la somme est très importante, elle
atteint 0.840195 est proche de 1.
Nos résultats montrent que le rendement de l'indice
sectoriel « Télécommunications » est influencé
par la volatilité de l'indice principal « MASI ». Les chocs de
volatilité du marché ont un effet persistant sur le rendement de
l'indice sectoriel « Télécommunications ».
Au vu de ces résultats concluants, nous pouvons
conclure que les deux indices sont fortement interdépendants.
La figure 3 affiche la corrélation conditionnelle
dynamique entre l'indice principal « MASI » et l'indice sectoriel
«Télécommunications », estimée par le
modèle DCC-GARCH (1,1) :
MASI-TELECOM
|
.8 .7 .6 .5
.4 .3
|
|
|
16 17 18 19 20 21 22
|
Figure 3 : Corrélation
conditionnelle dynamique entre l'indice « Télécom » et
le « MASI » estimée par le modèle DCC-GARCH(1,1).
La figure 3 illustre la corrélation conditionnelle
entre l'indice sectoriel « Télécommunications » et le
« MASI », la corrélation conditionnelle estimée entre
les deux indices reste en général non stable avec de faibles
fluctuations, elle fluctue dans l'ensemble entre 0.5 et 0.7. On remarque aussi
que la corrélation diminue vers le début de l'année 2018
jusqu'au 0.3.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
3.3.1.4. Estimation du modèle DCC-GARCH (1, 1)
pour les rendements géométriques de l'indice sectoriel «
Bâtiments et MC» et l'indice principal « MASI ».
Le tableau 4 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques de l'indice « Bâtiments et MC».
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
MASI
Index
|
Equation de la moyenne
|
|
Il1
|
0.000451
|
0.000136
|
3.3280
|
0.000875
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.7768
|
|
|
0.203335
|
0.000000á1
0.023785
|
8.5489
|
0.000000
|
|
I31
|
0.691917
|
0.031131
|
22.2261
|
0.000000
|
|
Persistance : á1 + I31
|
0.895252
|
|
Secteur
Bâtiments et MC
|
Equation de la moyenne
|
|
Il1
|
0.000516
|
0.000292
|
1.7679
|
0.077081
|
|
Equation de la variance
|
|
Ù
|
0.000047
|
0.000014
|
3.3352
|
0.000852
|
|
á1
|
0.221462
|
0.055538
|
3.9876
|
0.00067
|
|
I31
|
0.553276
|
0.096736
|
5.7194
|
0.000000
|
|
Persistance : á1 + I31
|
0.774738
|
|
MASI/
Bâtiments et MC
|
Equation de la corrélation
|
|
áDCC
|
0.077747
|
0.017547
|
4.4309
|
0.000009
|
|
I3DCC
|
0.783195
|
0.057778
|
13.5553
|
0.000000
|
|
Persistance : áDCC + I3DCC
|
0.860942
|
Tableau 4 : Estimation du
modèle DCC-GARCH pour le « MASI » et l'indice «
Bâtiments et MC».
Nous remarquons d'après le tableau 4 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre le « MASI »,
et l'indice sectoriel « Bâtiments et MC», que les coefficients
du modèle de corrélation conditionnelle DCC-GARCH sont
statistiquement significatifs au seuil de 1%.
Les paramètres conjoints áDCC et
I3DCC sont plus significatifs que les paramètres individuels a et [3 qui
sont estimés du modèle GARCH univarié. Cela montre que la
volatilité capturée par la méthode GARCH (1,1) est
sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal
à zéro (áDCC 0), le coefficient
I3DCC est largement supérieur à zéro
(I3DCC >>> 0), et la somme de
deux qui est
inférieure à 1 ( áDCC + I3DCC <
1).
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir áDCC + I3DCC = 0.077747 +
0.783195 = 0.860942 < 1, ce qui suggère que la matrice de
corrélation estimée Dt est définie positive.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 81 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 82 sur 113
Le coefficient I3occ étant
égal à 0.860942 est proche de la valeur de 1,
cette valeur du coefficient beta montre une forte corrélation
conditionnelle entre les deux indices. Le coefficient apcc
étant égal à 0.077747 est proche
de 0. D'autre part, les deux coefficients sont statistiquement
significatifs( p - value < 5%), cette
significativité des coefficients confirme la sensibilité de
l'indice sectoriel « Bâtiments et MC» au « MASI ». La
persistance de la corrélation conditionnelle calculée à
travers la somme est très importante, elle atteint 0.860942
est proche de 1.
Nos résultats montrent que le rendement de l'indice
« Bâtiments et MC» est influencé par la
volatilité du « MASI ». Les chocs de volatilité du
marché ont un effet persistant sur le rendement de l'indice sectoriel
« Bâtiments et MC». Au vu de ces résultats concluants,
nous pouvons conclure que les deux indices sont fortement
interdépendants.
La figure 4 affiche la corrélation conditionnelle
dynamique entre le « MASI » et l'indice «Bâtiments et
MC», estimée par le modèle DCC-GARCH (1,1) :
MASI/BAT&MC
|
.80 .75 .70
.65 .60 .55 .50
|
|
|
16 17 18 19 20 21 22
|
Figure 4 : Corrélation
conditionnelle dynamique entre l'indice sectoriel « Bâtiments et
MC»
et l'indice principal « MASI » estimée par le
modèle DCC-GARCH(1,1).
La figure 4 illustre la corrélation conditionnelle
entre l'indice sectoriel « Bâtiments et MC» et l'indice
principal « MASI », la corrélation conditionnelle
estimée entre les deux indices reste en général non stable
avec de faibles fluctuations, elle fluctue dans l'ensemble entre 0.6 et 0.75.
On remarque aussi que la corrélation diminue vers le début de
l'année 2020 jusqu'au 0.55.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
3.3.1.5. Estimation du modèle DCC-GARCH (??, ??)
pour les rendements géométriques de l'indice sectoriel «
Pétroles & Gaz» et l'indice principal « MASI ».
Le tableau 5 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques de l'indice du secteur des
Télécommunications.
|
Variable
|
Paramètre
|
Value
|
Std.
Error
|
t-stat
|
Pr(>|t|)
|
|
MASI
Index
|
Equation de la moyenne
|
|
ø1
|
0.000451
|
0.000136
|
3.31495
|
0.000917
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.85800
|
|
|
0.203335
|
0.000000á1
0.023699
|
8.57972
|
0.000000
|
|
â1
|
0.691917
|
0.030949
|
22.35665
|
0.000000
|
|
Persistance : á1 + â1
|
0.895252
|
|
Secteur
Pétroles & Gaz
|
Equation de la moyenne
|
|
ø1
|
0.000784
|
0.000352
|
2.22904
|
0.025811
|
|
Equation de la variance
|
|
Ù
|
0.000008
|
0.000001
|
5.71643
|
0.000000
|
|
á1
|
0.078802
|
0.013114
|
6.00896
|
0.000000
|
|
â1
|
0.892047
|
0.016152
|
55.22817
|
0.000000
|
|
Persistance : á1 + â1
|
0.970849
|
|
MASI/
Pétroles & Gaz
|
Equation de la corrélation
|
|
á??????
|
0.003711
|
0.008218
|
0.451610
|
0.651552
|
|
â??????
|
0.979108
|
0.081109
|
12.07148
|
0.000000
|
|
Persistance : á?????? + â?? ????
|
0.982819
|
Tableau 5 : Estimation du modèle
DCC-GARCH pour l'indice principal « MASI » et l'indice sectoriel
« Pétroles & Gaz».
Nous remarquons d'après le tableau 5 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre l'indice « MASI
», le principal indice de la Bourse marocaine et l'indice sectoriel «
Pétroles & Gaz», que les coefficients du modèle de
corrélation conditionnelle DCC-GARCH sont statistiquement significatifs
au seuil de 1%.
Les paramètres conjoints á?????? ????
â?????? sont plus significatifs que les paramètres individuels ??
et ?? qui sont estimés du modèle GARCH univarié. Cela
montre que la volatilité capturée par la méthode GARCH
(1,1) est sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal à
zéro (á?????? 0), le coefficient â?????? est largement
supérieur à zéro (â?????? ??? 0), et la somme de
deux qui est inférieure à 1 ( á?????? +
â?????? < 1).
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 83 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 84 sur 113
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir aocc + I3occ = 0.003711 + 0.979108
= 0.982819 < 1, ce qui suggère que la matrice de
corrélation estimée Dt est
définie positive.
Le coefficient I3occ étant
égal à 0.982819 est proche de la valeur de 1,
cette valeur du coefficient beta montre une forte corrélation
conditionnelle entre les deux indices. Le coefficient aocc
étant égal à 0.003711 est proche
de 0. D'autre part, les deux coefficients sont statistiquement
significatifs( p - value < 5%), cette
significativité des coefficients confirme la sensibilité de
l'indice sectoriel « Pétroles & Gaz» à l'indice
principal « MASI ».
La persistance de la corrélation conditionnelle
calculée à travers la somme est très importante, elle
atteint 0.982819 est proche de 1.
Nos résultats montrent que le rendement de l'indice
sectoriel « Pétroles & Gaz» est influencé par la
volatilité de l'indice principal « MASI ». Les chocs de
volatilité du marché ont un effet persistant sur le rendement de
l'indice sectoriel « Pétroles & Gaz».
Au vu de ces résultats concluants, nous pouvons
conclure que les deux indices sont fortement interdépendants.
La figure 5 affiche la corrélation conditionnelle
dynamique entre l'indice principal « MASI » et l'indice sectoriel
«Pétroles & Gaz», estimée par le modèle
DCC-GARCH (1,1) :
MASI-PETRO&GAZ
|
.6 .5 .4 .3
.2 .1
|
|
|
16 17 18 19 20 21 22
|
Figure 5 : Corrélation
conditionnelle dynamique entre l'indice « Pétroles & Gaz»
et le « MASI » estimée par DCC-
GARCH(1,1).
La figure 5 illustre la corrélation conditionnelle
entre l'indice sectoriel « Pétroles & Gaz» et l'indice
principal « MASI », la corrélation conditionnelle
estimée entre les deux indices reste en général non stable
avec de faibles fluctuations, elle fluctue dans l'ensemble entre 0.2 et 0.4. On
remarque aussi que la corrélation diminue vers le 4éme
trimestre de l'année 2019 jusqu'au 0.11.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
3.3.1.6. Estimation du modèle DCC-GARCH (1, 1)
pour les rendements géométriques de l'indice sectoriel «
Participation et Promotion Immobilières» et l'indice principal
« MASI ».
Le tableau 6 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques de l'indice « P.P
Immobilières».
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
MASI
Index
|
Equation de la moyenne
|
|
Y'1
|
0.000451
|
0.000136
|
3.3201
|
0.000900
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.8612
|
|
|
0.203335
|
0.000000á1
0.023785
|
8.6186
|
0.000000
|
|
131
|
0.691917
|
0.030900
|
22.3924
|
0.000000
|
|
Persistance : á1 + 131
|
0.895252
|
|
Secteur
Participation
et Promotion
Immobilières131
|
Equation de la moyenne
|
|
Y'1
|
-0.001400
|
0.000415
|
-3.3723
|
0.000745
|
|
Equation de la variance
|
|
Ù
|
0.000033
|
0.000013
|
2.6263
|
0.008699
|
|
á1
|
0.236700
|
0.051398
|
4.6052
|
0.000004
|
|
0.690442
|
0.074243
|
9.2997
|
0.000000
|
|
Persistance : á1 + 131
|
0.927142
|
|
MASI/ Participation et Promotion
Immobilières
|
Equation de la corrélation
|
|
áocc
|
0.050706
|
0.020260
|
2.5028
|
0.012323
|
|
13occ
|
0.864414
|
0.057187
|
15.1156
|
0.000000
|
|
Persistance : áocc + 13occ
|
0.91512
|
Tableau 6 : Estimation du
modèle DCC-GARCH pour le « MASI » et l'indice « P.P
Immobilières».
Nous remarquons d'après le tableau 6 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre le « MASI »,
le et l'indice « Participation et Promotion Immobilières», que
les coefficients du modèle de corrélation conditionnelle
DCC-GARCH sont statistiquement significatifs au seuil de 1%.
Les paramètres conjoints áocc et
13occ sont plus significatifs que les paramètres individuels a et [3 qui
sont estimés du modèle GARCH univarié. Cela montre que la
volatilité capturée par la méthode GARCH (1,1) est
sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal
à zéro (áocc 0), le coefficient
13occ est largement supérieur à zéro
(13occ >>> 0), et la somme de
deux qui est
inférieure à 1 ( áocc + 13occ < 1).
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir áocc + 13occ = 0.050706 + 0.864414 =
0.91512 < 1, ce qui suggère que la matrice de corrélation
estimée Dt est définie positive.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 85 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 86 sur 113
Le coefficient â?????? étant égal à
0. 91??12 est proche de la valeur de 1, cette valeur du coefficient beta montre
une forte corrélation conditionnelle entre les deux indices. Le
coefficient á?????? étant égal à 0.050706
est proche de 0. D'autre part, les deux coefficients sont
statistiquement significatifs( p - value < 5%), cette significativité
des coefficients confirme la sensibilité de l'indice sectoriel «
Participation et Promotion Immobilières» à l'indice
principal « MASI ».
La persistance de la corrélation conditionnelle
calculée à travers la somme est très importante, elle
atteint 0.91??12 est proche de 1.
Nos résultats montrent que le rendement de l'indice
sectoriel « Participation et Promotion Immobilières» est
influencé par la volatilité de l'indice principal « MASI
». Les chocs de volatilité du marché ont un effet persistant
sur le rendement de l'indice sectoriel « Participation et Promotion
Immobilières».
Au vu de ces résultats concluants, nous pouvons
conclure que les deux indices sont fortement interdépendants.
La figure 6 affiche la corrélation conditionnelle
dynamique entre l'indice principal « MASI » et l'indice sectoriel
«Participation et Promotion Immobilières», estimée par
le modèle DCC-GARCH (1,1) :
MASI/PROMO&IMMO
|
.6 .5 .4 .3 .2 .1
|
|
|
16 17 18 19 20 21 22
|
Figure 6 : Corrélation
conditionnelle dynamique entre l'indice « P.P Immobilières» et
le « MASI » estimée par DCC-GARCH(1,1).
La figure 6 illustre la corrélation conditionnelle
entre l'indice sectoriel « Participation et Promotion
Immobilières» et l'indice principal « MASI », la
corrélation conditionnelle estimée entre les deux indices reste
en général non stable avec de faibles fluctuations, elle fluctue
dans l'ensemble entre 0.25 et 0.47. On remarque aussi que la corrélation
diminue vers la fin du 2éme trimestre de l'année 2019
jusqu'au 0.15.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
3.3.1.7. Estimation du modèle DCC-GARCH (??, ??)
pour les rendements géométriques de l'indice sectoriel «
Transport» et l'indice principal « MASI ».
Le tableau 7 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements
géométriques de l'indice « Transport ».
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
MASI
Index
|
Equation de la moyenne
|
|
ø1
|
0.000451
|
0.000136
|
3.30986
|
0.000933
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.89789
|
0.000000
|
|
á1
|
0.203335
|
0.023785
|
8.62075
|
0.000000
|
|
â1
|
0.691917
|
0.030876
|
22.44095
5
|
0.000000
|
|
Persistance : á1 + â1
|
0.895252
|
|
Secteur
Transport
|
Equation de la moyenne
|
|
ø1
|
0.000026
|
0.000376
|
0.68097
|
0.495893
|
|
Equation de la variance
|
|
Ù
|
0.000026
|
0.000010
|
2.59330
|
0.009506
|
|
á1
|
0.077027
|
0.019475
|
3.95524
|
0.000076
|
|
â1
|
0.824760
|
0.043992
|
18.74779
|
0.000000
|
|
Persistance : á1 + â1
|
0.901787
|
|
MASI/
Transport
|
Equation de la corrélation
|
|
á??????
|
0.011222
|
0.008117
|
1.38258
|
0.166793
|
|
â??????
|
0.970774
|
0.026907
|
36.07836
|
0.000000
|
|
Persistance : á?????? + â??????
|
0.981996
|
Tableau 7 : Estimation du
modèle DCC-GARCH pour le « MASI » et l'indice «
Transport».
Nous remarquons d'après le tableau 7 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre le « MASI »,
et l'indice « Transport», que les coefficients du modèle de
corrélation conditionnelle DCC-GARCH sont statistiquement significatifs
au seuil de 1%.
Les paramètres conjoints á?????? ????
â?????? sont plus significatifs que les paramètres individuels ??
et ?? qui sont estimés du modèle GARCH univarié. Cela
montre que la volatilité capturée par la méthode GARCH
(1,1) est sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision.
Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal à
zéro (á?????? 0), le coefficient â?????? est largement
supérieur à zéro (â?????? ??? 0), et la somme de
deux qui est inférieure à 1 ( á?????? +
â?????? < 1).
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 87 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 88 sur 113
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir aocc + I3occ = 0.011222 + 0.970774
= 0.981996 < 1, ce qui suggère que la matrice de
corrélation estimée Dt est
définie positive.
Le coefficient I3occ étant
égal à 0. 981996est proche de la valeur de 1,
cette valeur du coefficient beta montre une forte corrélation
conditionnelle entre les deux indices. Le coefficient aocc
étant égal à 0.011222 est proche
de 0. D'autre part, les deux coefficients sont statistiquement
significatifs( p - value < 5%), cette
significativité des coefficients confirme la sensibilité de
l'indice sectoriel « Transport» à l'indice principal «
MASI ».
La persistance de la corrélation conditionnelle
calculée à travers la somme est très importante, elle
atteint 0.981996 est proche de 1.
Nos résultats montrent que le rendement de l'indice
sectoriel « Transport» est influencé par la volatilité
de l'indice principal « MASI ». Les chocs de volatilité du
marché ont un effet persistant sur le rendement de l'indice sectoriel
« Transport».
Au vu de ces résultats concluants, nous pouvons
conclure que les deux indices sont fortement interdépendants.
La figure 7 affiche la corrélation conditionnelle
dynamique entre l'indice principal « MASI » et l'indice sectoriel
«Transport», estimée par le modèle DCC-GARCH (1,1) :
MASI/TRANS
|
.5 .4 .3 .2
.1 .0
-.1
-.2
|
|
|
16 17 18 19 20 21 22
|
Figure 7 : Corrélation
conditionnelle dynamique entre l'indice « Transport » et le «
MASI » estimée par DCC-GARCH(1,1).
La figure 7 illustre la corrélation conditionnelle
entre l'indice sectoriel « Transport» et l'indice principal «
MASI », la corrélation conditionnelle estimée entre les deux
indices reste en général non stable avec de faibles fluctuations,
elle fluctue dans l'ensemble entre -0.05 et 0.15. On remarque aussi que la
corrélation diminue vers Le 2éme trimestre de
l'année 2018 jusqu'au -0.15.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
3.3.1.8. Estimation du modèle DCC-GARCH (??, ??)
pour les rendements géométriques de l'indice sectoriel «
Loisirs & Hôtellerie» et l'indice principal « MASI ».
Le tableau 8 affiche l'estimation de l'équation de la
moyenne conditionnelle, l'équation de la variance et l'équation
de la corrélation pour la série des rendements de l'indice
Loisirs & Hôtellerie.
|
Variable
|
Paramètre
|
Value
|
Std. Error
|
t-stat
|
Pr(>|t|)
|
|
MASI
Index
|
Equation de la moyenne
|
|
ø1
|
0.000451
|
0.000136
|
3.31850
|
0.000905
|
|
Equation de la variance
|
|
Ù
|
0.000005
|
0.000001
|
8.86809
|
0.000000
|
|
á1
|
0.203335
|
0.023630
|
8.60476
|
0.000000
|
|
â1
|
0.691917
|
0.030960
|
22.34859
|
0.000000
|
|
Persistance : á1 + â1
|
0.895252
|
|
Secteur
Loisirs
&
Hôtellerie
|
Equation de la moyenne
|
|
ø1
|
-0.000106
|
0.000538
|
-0.19801
|
0.843033
|
|
Equation de la variance
|
|
Ù
|
0.000063
|
0.000024
|
2.66927
|
0.007602
|
|
á1
|
0.123767
|
0.024641
|
5.02280
|
0.000001
|
|
â1
|
0.769598
|
0.053521
|
14.37947
|
0.000000
|
|
Persistance : á1 + â1
|
0.893365
|
|
MASI/
Loisirs &
Hôtellerie
|
Equation de la corrélation
|
|
á??????
|
0.001540
|
0.004573
|
0.33677
|
0.736291
|
|
â??????
|
0.973566
|
0.022900
|
42.94990
|
0.000000
|
|
Persistance : á?????? + â??????
|
0.975106
|
Tableau 8 : Estimation du modèle
DCC-GARCH pour l'indice principal « MASI » et l'indice sectoriel
« Loisirs & Hôtellerie».
Nous remarquons d'après le tableau 8 exhibant les
paramètres du modèle DCC-GARCH (1.1) entre l'indice « MASI
», le principal indice de la Bourse marocaine et l'indice sectoriel «
Loisirs & Hôtellerie», que les coefficients du modèle de
corrélation conditionnelle DCC-GARCH sont statistiquement significatifs
au seuil de 1%.
Les paramètres conjoints á?????? ????
â?????? sont plus significatifs que les paramètres individuels ??
et ?? qui sont estimés du modèle GARCH univarié. Cela
montre que la volatilité capturée par la méthode GARCH
(1,1) est sous-estimée, mais la volatilité capturée par le
modèle DCC-GARCH est plus traitée et estimée avec plus de
précision. Cependant, les paramètres de corrélation
DCC-GARCH pour la période étudiée sont également
différents de zéro, ce qui implique que la corrélation
entre les deux cours est dynamique.
Nos résultats sont cohérents avec ceux de la
théorie. Le coefficient est approximativement égal à
zéro (á?????? 0), le coefficient â?????? est largement
supérieur à zéro (â?????? ??? 0), et la somme de
deux qui est inférieure à 1 ( á?????? +
â?????? < 1).
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 89 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 90 sur 113
De plus, Ces paramètres de corrélation
stimulés montrent une adhésion à la restriction qui leur
est imposée, à savoir aocc + I3occ = 0.001540 + 0.973566
= 0.975106 < 1, ce qui suggère que la matrice de
corrélation estimée Dt est
définie positive.
Le coefficient I3occ étant
égal à 0.975106 est proche de la valeur de 1,
cette valeur du coefficient beta montre une forte corrélation
conditionnelle entre les deux indices. Le coefficient aocc
étant égal à 0.001540 est proche
de 0. D'autre part, les deux coefficients sont statistiquement
significatifs( p - value < 5%), cette
significativité des coefficients confirme la sensibilité de
l'indice « Loisirs & Hôtellerie» au « MASI ». La
persistance de la corrélation conditionnelle calculée à
travers la somme est très importante, elle atteint 0.975106
est proche de 1.
Nos résultats montrent que le rendement de l'indice
sectoriel « Loisirs & Hôtellerie» est influencé par
la volatilité de l'indice principal « MASI ». Les chocs de
volatilité du marché ont un effet persistant sur le rendement de
l'indice sectoriel « Loisirs & Hôtellerie». Au vu de ces
résultats concluants, nous pouvons conclure que les deux indices sont
fortement interdépendants.
La figure 8 affiche la corrélation conditionnelle
dynamique entre l'indice principal « MASI » et l'indice sectoriel
«Loisirs & Hôtellerie», estimée par le modèle
DCC-GARCH (1,1) :
MASI/HOT
|
.35 .30 .25
.20 .15 .10 .05 .00
-.05
|
|
16 17 18 19 20 21 22
Figure 8 : Corrélation
conditionnelle dynamique entre l'indice « Loisirs &
Hôtellerie» et le « MASI » estimée par
DCC-GARCH(1,1).
La figure 8 illustre la corrélation conditionnelle
entre l'indice sectoriel « Loisirs & Hôtellerie» et
l'indice principal « MASI », la corrélation conditionnelle
estimée entre les deux indices reste en général non stable
avec de faibles fluctuations, elle fluctue dans l'ensemble entre 0.01 et 0.20.
On remarque aussi que la corrélation diminue vers le 1er
trimestre de l'année 2020 jusqu'au -0.05.
Il est clair qu'il existe une corrélation dynamique
conditionnelle entre les deux indices qui évolue en fonction du temps
bien le coefficient est parfois grand et parfois petit.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 91 sur 113
3.4. Analyse de l'interdépendance du
marché boursier (MASI et ses principaux secteurs).
Les résultats présentés ci-dessus
montrent que la persistance des chocs à court terme sur les
corrélations dynamiques est plus grande entre le « MASI » et
l'indices bancaire en raison de sa valeur de á élevée.
Les graphes (1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 et 8)
présentés ci-dessus affichent les niveaux des corrélations
conditionnelles dynamiques estimés selon l'approche DCC-GARCH de Engle
(2002). Il semble que l'évolution de ces corrélations dynamiques
affiche des tendances variées. Ainsi, les résultats
précédents prouvent l'existence d'une forte
interdépendance entre l'indice principal « MASI » et les
indices des huit indices étudiés. Nous avons utilisé le
modèle DCC-GARCH (1,1) pour cerner le phénomène de
contagion financière.
Les graphes nous montrent que la corrélation dynamique
du rendement géométrique de chaque indice sectoriel avec l'indice
principal varie d'un secteur à autre, nous allons ainsi calculer les
moyennes et les valeurs minimales et maximales des coefficients de
corrélation pour nous informer sur le niveau de corrélation entre
chaque secteur individuel et l'indice principal de la BVC.
Dans le tableau 9 nous présentons les statistiques
descriptives (moyenne, minimum et maximum) des corrélations dynamiques
entre chaque indice et l'indice du marché pour cerner le
phénomène de contagion financière.
|
Secteurs
|
Moyenne
|
Maximum
|
Minimum
|
|
Banques
|
0.809092
|
0.911272
|
0.701961
|
|
Bâtiments et MC
|
0.667164
|
0.793439
|
0.545538
|
|
Télécommunications
|
0.600051
|
0.762447
|
0.305706
|
|
Pétroles & Gaz
|
0.310235
|
0.591341
|
0.126238
|
|
Assurances
|
0.323488
|
0.575857
|
0.154174
|
|
Parti et Promo Immobilières
|
0.353694
|
0.542060
|
0.147765
|
|
Transport
|
0.082714
|
0.412827
|
-0.152203
|
|
Loisirs & Hôtellerie
|
0.119340
|
0.305948
|
-0.042059
|
Tableau 9 : Degré de contagion
financière des huit indices sectoriels.
Les résultats présentés dans le tableau 9
nous montrent que la contagion financière est assez évidente pour
l'indice bancaire, moyenne pour les indices sectoriels « Bâtiments
et MC » « Télécom », et moins évidente pour
les cinq autres indices sectoriels (Assur, Pétroles & Gaz, P.P Immo,
Transport et Hôtellerie).
Interprétation des résultats de la
modélisation de la contagion financière pour chaque paire
(Indice du secteur - Indice principal).
Indice bancaire-Indice principal «MASI»
:
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice bancaire et l'indice « MASI » est de
0.809092. Il s'agit d'un "effet de liaison" très net.
Ce qui implique que les deux indices ne sont pas indépendants dans le
temps. Les résultats DCC-GARCH mettent en évidence une contagion
du marché à l'indice bancaire. La corrélation
conditionnelle entre le marché et l'indice bancaire fluctue entre
0,70 (Min) et 0,91 (Max) ce qui montre que
cet indice présente une forte corrélation dynamique avec le
marché.
Indice Bâtiments et MC-Indice principal
«MASI» :
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 92 sur 113
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Bâtiments et MC et l'indice « MASI
» est de 0.667164 largement supérieur à 5.
Ce qui implique que les deux indices sont dépendants dans le temps. La
corrélation conditionnelle entre le marché et l'indice bancaire
fluctue entre 0,55 (Min) et 0,79 (Max) ce qui
montre que cet indice présente une forte corrélation dynamique
avec le marché.
Indice Télécommunications-Indice
principal «MASI» :
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Télécommu et le « MASI »
est de 0.600051. Ce qui implique que les deux indices sont
dépendants dans le temps. La corrélation conditionnelle entre le
marché et l'indice Télécommunications fluctue entre
0,31 (Min) et 0,76 (Max) ce qui montre que
cet indice présente une forte corrélation dynamique avec le
marché.
Indice Pétroles & Gaz-Indice principal
«MASI» :
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Pétroles & Gaz et l'indice « MASI
» est de 0.310235. Ce qui implique que les deux indices
sont faiblement dépendants dans le temps, la corrélation
conditionnelle entre le marché et l'indice Pétroles & Gaz
fluctue entre 0,13 (Min) et 0,6 (Max) ce qui
montre que cet indice présente une moyenne corrélation dynamique
avec le marché.
Indice Assurances-Indice principal «MASI»
:
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Assurances et l'indice « MASI » est de
0.323488. Ce qui implique que les deux indices sont faiblement
dépendants dans le temps, la corrélation conditionnelle entre le
marché et l'indice Assurances fluctue entre 0,15 (Min)
et 0,58 (Max) ce qui montre que cet indice présente une
moyenne corrélation dynamique avec le marché.
Indice Participation et Promotion
Immobilières-Indice principal «MASI» :
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Participation et Promotion Immobilières et
l'indice « MASI » est de 0.353694. Ce qui implique
que les deux indices sont faiblement dépendants dans le temps, la
corrélation conditionnelle entre le marché et l'indice
Participation et Promotion Immobilières fluctue entre 0,15
(Min) et 0,54 (Max) ce qui montre que cet indice
présente une moyenne corrélation dynamique avec le
marché.
Indice Transport-Indice principal «MASI»
:
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Transport et l'indice « MASI » est
de 0.082714. Ce qui implique que les deux indices sont
très faiblement dépendants dans le temps, la corrélation
conditionnelle entre le marché et l'indice Transport fluctue entre
-0,15 (Min) et 0,41 (Max) ce qui montre que
cet indice présente une faible corrélation dynamique avec le
marché.
Indice Loisirs & Hôtellerie-Indice
principal «MASI» :
La valeur moyenne du coefficient de corrélation
conditionnelle entre l'indice Loisirs & Hôtellerie et l'indice «
MASI » est de 0.119340 proche de zéro. Ce qui
implique que les deux indices sont faiblement dépendants dans le temps.
La corrélation conditionnelle entre le marché et l'indice Loisirs
& Hôtellerie fluctue entre -0,04 (Min) et
0,31 (Max) ce qui montre que cet indice présente une
faible corrélation dynamique avec le marché.
3.5. Prévisions de l'interdépendance
Le but ultime de la modélisation de la matrice de
corrélation entre les huit indices étudiés des secteurs
d'activité de l'économie nationale et l'indice du marché
des actions (B.V.C) est de pouvoir fournir des estimations de la
corrélation entre chaque paires d'indice (indice sectoriel-MAST)
à chaque instant ?? + h ; [1,. ., ??]
étant la fenêtre temporelle au cours de laquelle la
matrice a été estimée.
La prévision de la matrice de corrélations
????+h = ????+h????+h????+h à l'instant
?? + h s'effectue en deux étapes. ? Dans une
première étape, les variances conditionnelles de chaque indice
sont estimées suivant le processus GARCH (1,1) qui les modélise.
La matrice ????+h est à ce stade
estimée.
? Dans la deuxième étape, les
éléments de la matrice de corrélations sont
estimés. Cependant, il faut noter qu'ils ne sont pas estimés
directement : les éléments de la matrice ????
qui sont estimés, vu les corrélations, ne sont que
le rapport de ces variances covariances. Comme vu précédemment,
la structure de la matrice corrélation conditionnelle dynamique suit un
processus GARCH multivarié non-linéaire.
La figure 9 ci-dessous retrace l'estimation de la
corrélation entre l'indice principal « MAST » et les huit
indices sectoriels, sur les 100 jours suivant le 31/05/2022 (date de la
dernière observation dans notre échantillon de
données).
.9
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 93 sur 113
.0
10 20 30 40 50 60 70 80 90 100
|
ASSURANCES BANQUES
BAT&MC PET&GAZ
HOTELERIE PROMO_IMMO
TELECOMU TRANSPORT
|
Figure 9 : Prévision de la
corrélation entre l'indice principal « MAST » et les huit
indices sectoriels.
Dans le tableau 10 nous présentons les statistiques
descriptives (moyenne, minimum et maximum) des prévisions
estimées des corrélations entre chaque indice sectoriel et
l'indice « MAST », l'indice principal de la
Bourse de Casablanca, pour prévoir le
phénomène de contagion financière avec un horizon de
100 jours.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 94 sur 113
Secteurs
|
Moyenne
|
Minimum
|
Maximum
|
|
Banques
|
0.825697
|
0.813428
|
0.855560
|
|
Bâtiments et MC
|
0.676180
|
0.673654
|
0.708779
|
|
Télécommunications
|
0.614659
|
0.612361
|
0.649096
|
|
Parti et Promo Immobilières
|
0.368814
|
0.317533
|
0.375653
|
|
Assurances
|
0.333111
|
0.330457
|
0.333492
|
|
Pétroles & Gaz
|
0.315220
|
0.310022
|
0.318208
|
|
Loisirs & Hôtellerie
|
0.131600
|
0.129801
|
0.134513
|
|
Transport
|
0.090786
|
0.089743
|
0.092646
|
Tableau 10 : Prévision du
degré de contagion financière des banques
En se basant soit sur l'analyse graphique (figure 9) soit sur
l'analyse descriptive (tableau 10) des résultats des prévisions
de la corrélation sur un horizon de 100 jours, l'indice
sectoriel le plus corrélé avec l'indice principal est celui des
banques avec une moyenne forte et proche de 0.85, suivi par
l'indice « Bâtiments et Matériaux de Construction » une
moyenne de 0,68, indice des Télécommunications avec une moyenne
de 0.37, Participation et Promotion Immobilières, Assurances,
Pétroles & Gaz, Loisirs & Hôtellerie, et finalement
l'indice « Transport » qui semble présentant une
faible corrélation avec le « MASI » , avec une
moyenne égale à 0.091.
Nous constatons aussi que toutes ces corrélations sont
positives. En outre, la corrélation entre l'indice « MASI » et
les indices sectoriels : Assurances, Pétroles & Gaz, Loisirs &
Hôtellerie et Transport, semblent constante avec des faibles moyennes
(0.33, 0.31, 0.13 et 0.09). Tandis que les quatre autres
secteurs (Banques, Bâtiments et MC, Télécommunications et
Participation et Promotion Immobilières), présentent une tendance
baissière dans leurs corrélations avec le marché.
Interprétation des résultats de la
prévision de la contagion financière pour chaque paire (Indice
sectoriel i - Indice principal « MASI ») sur un horizon de 100 jours
futurs.
Indice Bancaire-Indice MASI :
La valeur moyenne du coefficient de corrélation
conditionnelle prévue entre le secteur bancaire et l'indice MASI est de
0.825697. Ce qui implique que les deux indices ne seront pas
indépendants dans les 100 prochains jours suivant le 31/05/2022. Les
résultats DCC-GARCH mettent en évidence une contagion de l'indice
de la B.V.C à l'indice bancaire. La prévision de la
corrélation entre le l'indice de la BVC et l'indice sectoriel fluctue
entre 0,81(Min) et 0,86(Max) ce qui montre que cet indice présente une
forte corrélation dynamique avec le principal indice de la BVC dans le
futur.
Indice Bâtiments & MC-Indice MASI
:
La valeur moyenne du coefficient de corrélation
prévue entre l'indice Bâtiments & Matériaux de
Construction et l'indice MAST est proche de 0.68, fluctue entre 0.673(Min) et
0,708(Max), Ce qui implique que les deux indices sont dépendants dans le
temps avec une corrélation moyenne.
Indice Participation et Promo
Immobilières-Indice MASI :
Indice Télécommunications-Indice MASI
:
La valeur moyenne du coefficient de corrélation
estimée l'indice Télécommunications et l'indice MASI est
de 0.61, fluctue entre 0.612(Min) et 0,649(Max), ce qui implique que les deux
indices sont dépendants dans le temps, la corrélation
estimée entre l'indice MASI et ce secteur est moyenne
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 95 sur 113
La valeur moyenne du coefficient de corrélation
prévu l'indice Participation & Promotion Immobilières et
l'indice MASI est de 0.37, Ce qui implique que les deux indices seront
faiblement dépendants dans le temps aux 100 jours futurs.
Indice Assurances-Indice MASI :
La valeur moyenne du coefficient de corrélation
prévue les 100 prochains jours entre l'indice sectoriel des Assurances
et l'indice MASI est de 0.333, Ce qui implique que les deux indices sont
faiblement dépendants dans le temps, la corrélation
conditionnelle entre l'indice MASI et cet indice sectoriel est stable à
une moyenne de 0.33 ce qui montre que cette action présente une faible
corrélation dynamique avec l'indice MASI.
Indice Pétroles & Gaz-Indice MASI
:
La valeur moyenne du coefficient de corrélation
estimée entre l'indice Pétroles & Gaz et l'indice MASI est de
0.32, Ce qui implique que la corrélation conditionnelle entre CES DEUX
INDICES est faible dans le futur.
Indice Hôtellerie-Indice MASI
:
La valeur moyenne du coefficient de corrélation
prévue les 100 prochains jours entre l'indice Loisirs &
Hôtellerie et l'indice MASI est de 0.13 proche de 0, ce qui implique que
la corrélation conditionnelle entre CES DEUX INDICES est faible dans le
futur.
Indice Transport-Indice MASI :
La valeur moyenne du coefficient de corrélation
prévue entre l'indice du secteur du Transport et l'indice MASI est de
0.090786 très proche de 0, ce qui qui implique que la
corrélation conditionnelle entre les deux indices est faible dans le
futur. Surtout que cette valeur reste stable durant les 100 jours futurs.
Conclusion
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 96 sur 113
Dans ce chapitre empirique, notre essentiel but est de
réaliser une modélisation de la corrélation dynamique des
rendements géométriques de chaque indice sectoriel et le
rendement géométrique du principal indice de la Bourse marocaine
(MAST), pour bien étudier la liaison et l'interdépendance des
indices boursiers de huit principaux secteurs d'activité avec le
marché des actions Marocain (B.V.C).
Pour cette raison, nous avons appliqué le modèle
DCC-GARCH (1,1) sous l'hypothèse de la loi de Gauss. Le prix P??
d'un titre de chaque indice sectoriel au temps t a été
converti en rendement
géométrique r?? , avec r??
= log ( P??
P??-??) avec ?? = ??,??, ... n
Après l'analyse préliminaire effectuée
dans le chapitre précèdent, nous avons appliqué le
modèle DCC-GARCH (1,1) pour faire une modélisation et une
prévision de la corrélation dynamique entre les l'indice
principal de la B.V.C et les indices sectoriels, les résultats
empiriques ont montré des "effets de liaison" évidents entre
l'indice principal et les cours de chaque indice sectoriel d'activité,
le degré de cette liaison varie d'un indice sectoriel à un autre.
En outre, il y a une influence des chocs des rendements
géométriques de l'indice principal sur les rendements
géométriques des indices sectoriels individuels. Nous pouvons
appeler cela une "contagion de volatilité ".
Cela signifie que la volatilité de l'indice « MAST »
renforcera la volatilité de chaque secteur.
Dans ce chapitre, nous avons étudié la relation
de dépendance entre les huit indices sectoriels composant notre
échantillon avec l'indice principal. Ainsi, nous avons établi la
liste des indices des secteurs les plus et les moins corrélés
avec l'indice principal.
Finalement, nous avons fourni des prévisions sur les
100 prochains jours suivant la date du 31/05/2022 (vu que
notre base de données se limite à cette date) et dressé la
liste des indices qui présentent une interdépendance avec
l'indice principal. L'indice bancaire peut être considéré
comme le secteur le plus lié à l'indice « MAST », vu le
degré de corrélation important de cet indice avec le
marché.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 97 sur 113
Conclusion générale
Mesurer l'interdépendance et la contagion
financière dans le marché des actions d'un pays autrement dit sa
bourse des valeurs est une tâche délicate suite au manque de
quelque données dites confidentielles dont l'accès n'est pas
public, la multitude d'indicateurs et d'outils de mesure et de quantification,
et aussi dans notre cas le nombre des sociétés cotées en
bourse et intégré dans l'un des secteurs d'activité
reconnu, d'après le dernier rapport de FMI, la majorité des
chiffres d'affaire réalisé dans le secteur même, informel.
Dans ce mémoire, nous avons essayé d'appliquer les mesures qui se
basent sur les données du marché boursier et sur seulement huit
secteurs les plus principaux.
Ce mémoire propose basée sur les données
du marché publié officiellement sur le site de la Bourse des
Valeurs de Casablanca, pour modéliser l'interdépendance de son
indice principal avec ses indices sectoriels, pour identifier et classer les
secteurs d'activité selon leur importance et son niveau de liaison.
L'interdépendance entre les différents secteurs
d'activités (prenant exemple les banques avec le secteur Bâtiments
et MC), et le phénomène de la contagion financière, sont
deux canaux fondamentaux que peuvent déclencher une crise
économique ou financière3. La mesure et l'explication
de l'interconnexion entre les indices des secteurs d'activité entre eux
et aussi avec le MAST, ainsi la structure du réseau du marché
officiel des actions marocain (B.V.C), représentent des
thématiques de recherche les plus importantes en finance.
Cependant, les secteurs d'activité en
général n'ont pas la même ampleur de transmission de risque
de crise financière ni la même importance dans l'économie
nationale, on peut comparer en aucun cas, comme exemple, le secteur
interbancaire, avec celui des Loisirs & Hôtellerie. En effet, les
modèles de modélisation doivent être capables de les
classer par cet ordre d'importance. Ce classement et l'objectif principal de
notre mémoire de recherche.
En effet, la chute de la valeur de l'actif d'un indice
sectoriel individuel risque de mettre en péril les autres indices
sectoriels du marché boursier, chaque secteur est exposé au
risque de ses propres chocs, aux chocs des valeurs des actions des autres
secteurs ainsi qu'aux chocs du marché. La chute de la valeur de chaque
indice sectoriel risque de se propager à travers le marché
boursier marocain en affectant les autres indices sectoriels du
marché.
3 Voir (Diamond et Dybvig, 1983 ; Chari et
Jagannathan, 1988) pour la ruée bancaire (Allen et Gale, 2000 ; Freixas,
Parigi et Rochet, 2000) pour la contagion bancaire
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 98 sur 113
Le but principal de ce mémoire de recherche est
d'examiner, en utilisant le modèle utilisé est le DCC GARCH
d'Engle (2002), le transfert de la volatilité et la mesure du
degré de la corrélation « la contagion » entre le
marché boursier marocain (MAST) et ses indices sectoriels durant la
période allant du 1er janvier 2016 jusqu'au 31 mai 2021. En
outre, nous avons trouvé dans tous les résultats de ce
mémoire mettent le secteur bancaire dans le premier rang des indices
sectoriels du marché boursier, chose qui est très logique pour
une économie en voie de développement comme le Maroc, qui est
liée aux institutions financières avec un degré
très haut, les résultats pour les autres secteurs peuvent
être considérés faibles et non significatifs.
Suite à la succession de plusieurs crises
financières et la gravité de leurs conséquences sur la
stabilité financière et économique des pays, les
autorités du comité de surveillance de risque systémique
de la banque centrale doivent prévoir le risque pour éviter un
scenario d'effondrement du marché boursier marocain. Elles doivent avoir
une liste qui classe les différentes indices sectoriels par ordre
d'importance systémique pour avoir une politique d'intervention et de
maitrise de propagation de risque pour éviter les conséquences de
la faillite et de la contagion à court et à long terme. La
détermination du secteur clé en termes d'importance dans le
marché boursier permettra donc de concentrer l'intervention des
autorités monétaires de Bank-Al Maghreb sur ce secteur. Les
autorités de la banque systémique doivent aussi intervenir pour
prendre les mesures prudentielles nécessaires.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 99 sur 113
Tableau des matières
REMERCIEMENTS 2
RESUME 3
ABSTRACT 3
SOMMAIRE 4
LISTE DES ABREVIATIONS 5
LISTE DES TABLEAUX 6
LISTE DES FIGURES 8
INTRODUCTION GENERALE 10
1. CHAPITRE 1 : REVUE DE LITTERATURE 12
INTRODUCTION 13
1.1. LA VOLATILITE 14
1.2. LA TRANSMISSION DE LA VOLATILITE 15
1.3. LA CORRELATION 15
1.4. MODELE DE CORRELATION DYNAMIQUE (DCC-GARCH) 16
CONCLUSION 17
2. CHAPITRE 2 : LES FAITS STYLISES DU MARCHE BOURSIER MAROCAIN :
LA BOURSE DES VALEURS
DE CASABLANCA 18
INTRODUCTION 19
2.1. COMPLEXITE DE LA MODELISATION DES SERIES FINANCIERES 20
2.2. FAITS STYLISES DU MARCHE FINANCIER 22
2.2.1 Analyse graphique : 22
2.2.2 Analyse descriptive 25
2.2.3 Analyse économétrique 35
2.2.3.1. Accumulation de la volatilité (Volatility
clustering) 35
2.2.3.2. Analyse de l'interdépendance 38
2.3. PRE-ESTIMATION DES SERIES DES RENDEMENTS DE
L'INDICE « MASI » ET DES HUIT INDICES
SECTORIELS. 39
2.3.1 Test de non stationnarité des séries des
prix journaliers : 40
2.3.1.1. Test de non stationnarité des valeurs de
l'indice « MASI » : 40
2.3.1.2. Test de non stationnarité des valeurs du
secteur « Assurances ». 41
2.3.1.3. Test de non stationnarité des valeurs du
secteur Bancaire. 41
2.3.1.4. Test de non stationnarité des valeurs du
secteur des Télécommunications. 42
2.3.1.5. Test de non stationnarité des valeurs du
secteur « Bâtiments et Mat de construction » 43
2.3.1.6. Test de non stationnarité des valeurs du
secteur « Pétroles et Gaz ». 43
2.3.1.7. Test de non stationnarité des valeurs du
secteur « Participation et Promotion
Immobilières » 44
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 100 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 101 sur 113
2.3.1.8. Test de non stationnarité des valeurs du
secteur « Transport ». 44
2.3.1.9. Test de non stationnarité des valeurs du
secteur « Loisirs et Hôtellerie ». 45
2.3.2 Test de stationnarité des séries des
rendements géométriques (log-return) 46
2.3.2.1. Test de stationnarité des rendements
géométriques (log-return) de l'indice « MASI » : 46
2.3.2.2. Test de stationnarité des rendements géométriques
(log-return) du secteur
« Assurances ». 46
2.3.2.3. Test de
stationnarité des rendements géométriques (log-return) du
secteur « Bancaire ».
47
2.3.2.4. Test de stationnarité des
rendements géométriques (log-return) du secteur
« Télécommunications ».
47
2.3.2.5. Test de stationnarité des rendements
géométriques (log-return) du secteur « Bâtiments
et
MC ». 48
2.3.2.6. Test de stationnarité des
rendements géométriques (log-return) du secteur «
Pétroles et
Gaz ». 48
2.3.2.7. Test de stationnarité
des rendements géométriques (log-return) du secteur P.P
Immobilières ». 49
2.3.2.8. Test de
stationnarité des rendements géométriques (log-return) du
secteur « Transport ».
49
2.3.2.9. Test de stationnarité des
rendements géométriques (log-return) du secteur « Loisirs
et
Hôtellerie ». 50
2.3.3 Test d'autocorrélation des rendements
géométriques 50
2.3.3.1. Test d'absence d'autocorrélation des
rendements géométriques de l'indice « MASI » : 51
2.3.3.2. Test d'absence d'autocorrélation des rendements
géométriques de l'indice sectoriel
« Assurances » 52
2.3.3.3. Test d'absence
d'autocorrélation des rendements géométriques de de
l'indice sectoriel
« Télécommunications » :
53
2.3.3.4. Test d'absence d'autocorrélation des rendements
géométriques l'indice sectoriel
« Participation & Promotion Immobilières
» : 54
2.3.3.5. Test d'absence d'autocorrélation des rendements
géométriques de l'indice sectoriel
« Pétroles& Gaz » 55
2.3.3.6. Test
d'absence d'autocorrélation des rendements géométriques de
l'indice sectoriel
« Bâtiments & Matériaux de
Construction » : 56
2.3.3.7. Test d'absence d'autocorrélation des
rendements géométriques de l'indice bancaire : 57
2.3.3.8. Test d'absence d'autocorrélation des
rendements géométriques de l'indice sectoriel
« Transport » 58
2.3.3.9. Test d'absence
d'autocorrélation des rendements géométriques de l'indice
« Loisirs &
Hôtellerie » : 59
2.3.4 Test
d'hétéroscédasticité 60
2.3.4.1. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice
« MASI » : 61
2.3.4.2. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice
« Assurances » : 61
2.3.4.3. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice
« Télécom » : 61
2.3.4.4. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice « P .P
Immobilières » :
62
2.3.4.5. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice «
Pétroles&
Gaz » : 62
2.3.4.6. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice sectoriel
« Bâtiments & Matériaux de
Construction » : 62
2.3.4.7. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice bancaire :
62
2.3.4.8. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice
« Transport » : 63
2.3.4.9. Test
d'hétéroscédasticité des résidus des
rendements géométriques de l'indice sectoriel
« Loisirs & Hôtellerie » : 63
CONCLUSION 64
3. CHAPITR3 : MESURE DE L'INTERDEPENDANCE DE L'INDICE « MASI
» ET LES INDICES SECTORIELS
PAR LES MODELES DCC-GARCH 65
INTRODUCTION 66
3.1. MODELES GARCH UNIVARIES 67
3.1.1 Modèle moyenne mobile MA(q)
d'ordre q 67
3.1.2 Modèle autorégressif AR(p)
d'ordre p 67
3.1.3 Modèle autorégressif moyenne mobile
ARMA (p, q) 68
3.1.4 Modèle autorégressif
héteroscedastique ARCH (p, q) 68
3.2. MODELES GARCH MULTIVARIES 71
3.2.1 Modèle CCC-GARCH 71
3.2.2 Modèle DCC-GARCH 71
3.3. MODELISATION DE LA CORRELATION CONDITIONNELLE: 74
3.3.1 Modélisation de l'interdépendance de
l'indice « MASI » et les huit indices sectoriels:
Résultats empiriques du modèle DCC-GARCH
(1, 1) : 75
3.3.1.1. Estimation du
modèle DCC-GARCH (1, 1) pour les
rendements géométriques de
l'indice sectoriel « Assurances » et l'indice
« MASI ». 75
3.3.1.2. Estimation du modèle DCC-GARCH
(1, 1) pour les rendements
géométriques de
l'indice du secteur bancaire et l'indice « MASI ».
77
3.3.1.3. Estimation du modèle DCC-GARCH (1,
1) pour les rendements géométriques de
l'indice sectoriel « Télécommunications
» et l'indice principal « MASI ». 79
3.3.1.4.
Estimation du modèle DCC-GARCH (1, 1)
pour les rendements géométriques de
l'indice sectoriel « Bâtiments et MC» et
l'indice principal « MASI ». 81
3.3.1.5. Estimation du
modèle DCC-GARCH (1, 1) pour les
rendements géométriques de
l'indice sectoriel « Pétroles & Gaz» et
l'indice principal « MASI ». 83
3.3.1.6. Estimation du
modèle DCC-GARCH (1, 1) pour les
rendements géométriques de
l'indice sectoriel « Participation et Promotion
Immobilières» et l'indice principal « MASI ».
85
3.3.1.7. Estimation du modèle DCC-GARCH (1,
1) pour les rendements géométriques de
l'indice sectoriel « Transport» et l'indice
principal « MASI ». 87
3.3.1.8. Estimation du
modèle DCC-GARCH (1, 1) pour les
rendements géométriques de
l'indice sectoriel « Loisirs &
Hôtellerie» et l'indice principal « MASI ».
89
3.4. ANALYSE DE L'INTERDEPENDANCE DU MARCHE BOURSIER (MASI ET SES
PRINCIPAUX
SECTEURS). 91
3.5. PREVISIONS DE L'INTERDEPENDANCE 93
CONCLUSION 96
CONCLUSION GENERALE 97
TABLEAU DES MATIERES 99
ANNEXE A : PROGRAMME EVIEWS 103
ANNEXE B : PROGRAMME MATLAB 106
ANNEXE C : PROGRAMME R 109
BIBLIOGRAPHIE 112
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 102 sur 113
Annexe A : Programme Eviews
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 103 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 104 sur 113

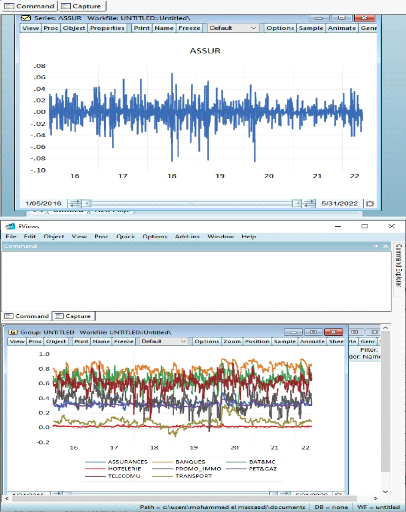
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 105 sur 113
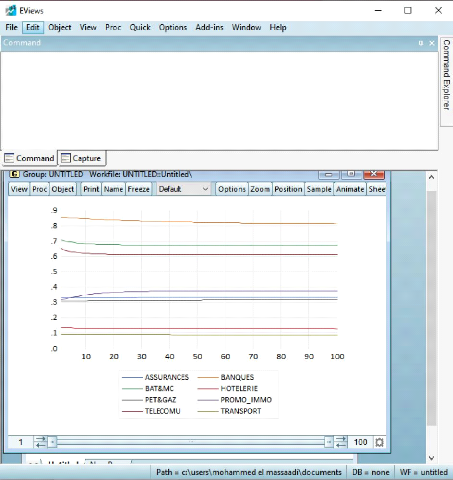
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 106 sur 113
Annexe B : Programme Matlab
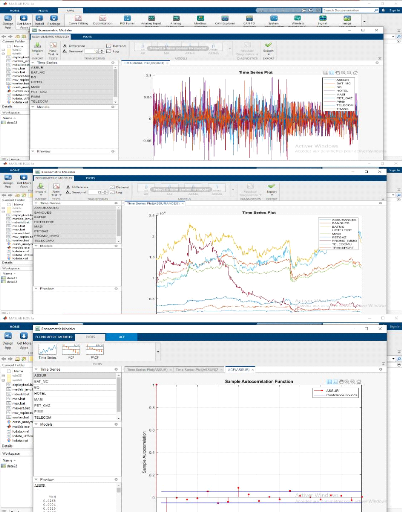
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 107 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 108 sur 113
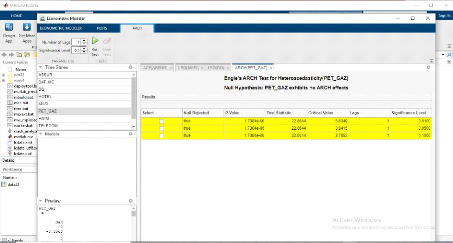
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 109 sur 113
Annexe C : Programme R
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 110 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 111 sur 113
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 112 sur 113
Bibliographie
+ Acemoglu, D., Ozdaglar, A., and Tahbaz-Salehi, A. (2014).
Systemic Risk and Stability in Financial Networks. Working Paper.
+ Acharya, V. V. and Steffen, S. (2012). Analyzing Systemic Risk
of the European Banking Sector. In: Handbook on Systemic Risk, J.-P. Fouque and
J. Langsam (Editors), Cambridge University Press.
+ Acharya, V. V. and Yorulmazer, T. (2007). Too Many to Fail - An
Analysis of Time-Inconsistency in Bank Closure Policies. Journal of Financial
Intermediation, 16, 1-31.
+ Acharya, V. V. and Yorulmazer, T. (2008). Cash-in-the-Market
Pricing and Optimal Resolution of Bank Failures. Review of Financial Studies,
21, 2705-2742.
+ Acharya, V. V., Engle, R., and Richardson, M. (2012). Capital
Shortfall: A New Approach to Ranking and Regulating Systemic Risks. The
American Economic Review, 102 (3), 59-64.
+ Acharya, V. V., Engle, R., Figlewski, S., Lynch, A., and
Subrahmanyam M. (2009). Centralized
Clearing for Credit Derivatives. Financial Markets, Institutions
and Instruments,18 (2), 168-170.
+ Acharya, V. V., Pedersen, L. H., Philippon, T., and Richardson,
M. P. (2010). Measuring Systemic Risk. Working Paper, NYU.
+ Adams, Z., Füss, R., and Gropp, R. (2010). Modeling
Spillover Effects Among Financial
Institutions: A State-Dependent Sensitivity Value-at-Risk
(SDSVaR). Approach Working Paper, European Business School.
+ Adrian, T. and Brunnermeier, M. K. (2011). CoVaR. Working
Paper, Princeton University and Federal Reserve Bank of New York.
+ Adrian, T. and Shin, H. S. (2014). Procyclical Leverage and
Value-at-Risk. Review of Financial Studies, 27, 373-403.
+ Agarwal, V., Jiang, W., Tang, Y., and Yang, B. (2013).
Uncovering Hedge Fund Skill from the Portfolio Holdings they Hide. The Journal
of Finance, 68, 739-783.
+ Ahmad, Z., and H. Ibrahim. (2002), A study of Performance of
The KLSE Syariah Index, Malaysian Management Journal 6 (1 & 2): 25-34.
+ Brasseul, J.(2004), Histoire des faits économiques,
Armand Colin,Markets Economic Letters, Vol. 22, pp. 375-380.
+ Calvet (L.) et Fisher (A.) (2007), Multi-frequency news and
stock returns, Journal of Financial Economics, vol. 86, p. 178-212.
+ Chakrabarty,K (2014), Cadre pour la conduite de la politique
macro-prudentielle en Inde : expériences et perspectives, Banque de
France
· Revue de la stabilité financière, N°
18.
+ Charles, A and Darné, O and Pop, A (2010) ,Are Islamic
Indexes More Volatile Than Conventional Indexes? Evidence from Dow Jones
Indexes, working paper, LEMNA.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 113 sur 113
+ Chiadmi, MS,. Ghaiti, F. (2012), Modeling Volatility Stock
Market using the ARCH and GARCH Models: Comparative Study between an Islamic
and a Conventional Index (SP Shariah VS SP 500), International Research Journal
of Finance and Economics ISSN 1450- 2887 Issue 91.
+ Cihak, M. et H. Hesse. (2008), ,Islamic Banks and Financial
Stability : An Empirical Analysis,, IMF Working Paper.
+ Jacquier, E., N. G. Polson, P. E. Rossi (2004), «Bayesian
analysis of stochastic volatility models with fat-tails and correlated errors,
Journal of Econometrics, 122, (1), 185-212.
+ Kendall W., Liang F., Wang J., (2005). «Markov Chain Monte
Carlo, Innovations and Applications». World Scientific Publishing Co. Pte.
Ltd.
+ Paolella, M. S., (1997). «Using Flexible GARCH Models with
Asymmetric Distributions». Inst. für Statistik und Ökonometrie,
1997 - 70 pages.
+ Pesaran, B., & Pesaran, M. H. (2007). Modelling
Volatilities and Conditional Correlations in Futures Markets with a
Multivariate t Distribution (No. 2906). Institute of Labor Economics (IZA).
+ Pontines, V., & Siregar, R. Y. (2012). Exchange rate
asymmetry and flexible exchange rates under inflation targeting regimes:
Evidence from four East and Southeast Asian countries. Review of International
Economics, 20(5), 893-908.
+ Poon, S.H. (2005). «A Practical Guide to Forecasting
Financial Market Volatility», John Wiley & Sons Ltd.
+ Rachev T., Hsu S., Bagasheva S., Fabozzi J., (2008).
«Bayesian methods in finance». John Wiley & Sons, Inc.
+ Sandman, G., Koopman, S.J., (1998). «Estimation of
Stochastic Volatility Models via Monte Carlo Maximum Likelihood». Journal
of Econometrics, 87, 271-301.
+ Shephard N., (2005). «Stochastic Volatility: Selected
Readings (Advanced Texts in Econometrics)». Oxford University Press.
+ Tsay, R. S., (2010). «Analysis of Financial Time
Series». Wiley series in probability and statistics, by John Wiley &
Sons Ltd.
| 


