Memoire Online - Mesure de l'interdépendance du marché boursier marocain par le modèle DCC-GARCH

2.3.3.2. Test d'absence d'autocorrélation des rendements géométriques de l'indice sectoriel « Assurances » La figure 29 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Assurances » :

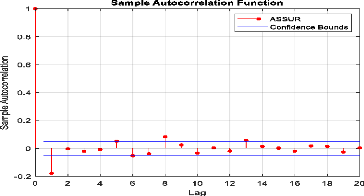
Figure 29 : Corrélogramme d'autocorrélation des rendements l'indice sectoriel « Assurances ».

Selon le corrélogramme des rendements journaliers l'indice sectoriel « Assurances », il y a des pics significatifs.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 34 :

Significance level	t-stat	Critical value	P-value
1%	85.2384	37.5662	0.0000
5%	85.2384	31.4104	0.0000
10%	85.2384	28.4120	0.0000

Tableau 34 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice sectoriel « Assurances ».

Le tableau 34 montre que la valeur statistique LIB est 85.3454 et que la p-value associée est 0,0000. Notons que la valeur t-statistique est largement supérieure aux valeurs critiques aux niveaux de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée.

Conclusion : il y a une autocorrélation entre les rendements de l'indice sectoriel « Assurances ».

2.3.3.3. Test d'absence d'autocorrélation des rendements géométriques de de l'indice sectoriel « Télécommunications » :

La figure 30 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Télécommunications » :

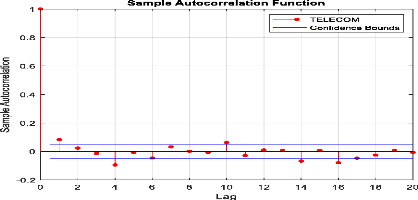
Figure 29 : Corrélogramme d'autocorrélation des rendements l'indice sectoriel « Télécommunications ».

Selon le corrélogramme des rendements journaliers l'indice sectoriel « Télécommunications », il y a des pics significatifs.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 35 :

Significance level	t-stat	Critical value	P-value
1%	61.9623	37.5662	0.00000
5%	61.9623	31.4104	0.00000
10%	61.9623	28.4120	0.00000

Tableau 35 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice sectoriel « Télécommunications ».

Le tableau 35 montre que la valeur statistique LJB est 61.9623 et que la p-value associée est 0,00000. Notons que la valeur t-statistique est largement supérieure aux valeurs critiques aux niveaux de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée.

Conclusion : il y a une autocorrélation entre les rendements de l'indice sectoriel « Télécommunications ».

2.3.3.4. Test d'absence d'autocorrélation des rendements géométriques l'indice sectoriel « Participation & Promotion Immobilières » :

La figure 31 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Participation & Promotion Immobilières » :

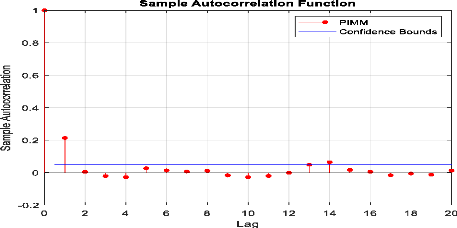
Figure 31 : Corrélogramme d'autocorrélation des rendements l'indice sectoriel « P.P Immobilières ».

Selon le corrélogramme des rendements journaliers l'indice sectoriel « P.P Immobilières », il y a des pics significatifs.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 36 :

Significance level	t-stat	Critical value	P-value
1%	90.9498	37.5662	0.00000
5%	90.9498	31.4104	0.00000
10%	90.9498	28.4120	0.00000

Tableau 36 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice sectoriel « P.P Immobilières ».

Le tableau 36 montre que la valeur statistique LJB est 90.9498 et que la p-value associée est 0,00000. Notons que la valeur t-statistique est largement supérieure aux valeurs critiques aux niveaux de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée.

Conclusion : il y a une autocorrélation entre les rendements de l'indice sectoriel « P.P Immobilières ».

2.3.3.5. Test d'absence d'autocorrélation des rendements géométriques de l'indice sectoriel « Pétroles& Gaz »

La figure 32 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Pétroles & Gaz » :

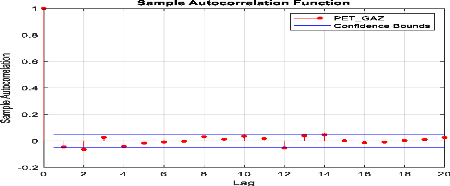
Figure 32 : Corrélogramme d'autocorrélation des rendements l'indice sectoriel « Pétroles & Gaz ».

Selon le corrélogramme des rendements journaliers l'indice sectoriel « Pétroles & Gaz », presque tous les pics sont non significatifs, ce qui confirme la propriété de non corrélation des rendements.

Nous remarquons que les valeurs de coefficients d'autocorrélation sont très faibles. La série des rendements géométriques est caractérisé donc par des autocorrélations très faibles.

Cela veut dire que la corrélation entre la rentabilité d'aujourd'hui et les rentabilités passées de l'indice sectoriel « Bâtiments & Matériaux de construction » très faible.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 37 :

Significance level	t-stat	Critical value	P-value
1%	30.6356	37.5662	0.0602
5%	30.6356	31.4104	0.0602
10%	30.6356	28.4120	0.0602

Tableau 37 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice sectoriel « Pétroles & Gaz ».

Le tableau 37 montre que la valeur statistique LIB est 30.6356 et que la p-value associée est 0,0602. Notons que la valeur t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5% et elle n'est pas largement supérieure à la valeur critique au niveau de 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée au seuil de 10% (seuil significatif).

Conclusion : il y a une faible autocorrélation entre les rendements de l'indice sectoriel « Pétroles & Gaz » au seuil de 10%, car le test est n'est pas significatif aux seuils de 1% et 5%.

2.3.3.6. Test d'absence d'autocorrélation des rendements géométriques de l'indice sectoriel « Bâtiments & Matériaux de Construction » :

La figure 33 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Bâtiments & Matériaux de construction » :

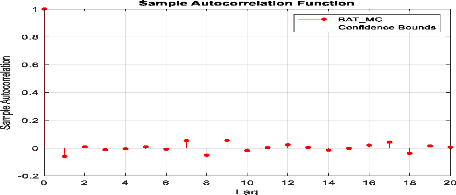
Figure 33 : Corrélogramme d'autocorrélation des rendements l'indice sectoriel
« Bâtiments & Matériaux de construction ».

Selon le corrélogramme des rendements journaliers l'indice sectoriel « Bâtiments & MC » presque tous les pics sont non significatifs, ce qui confirme la propriété de non corrélation des rendements.

Nous remarquons que les valeurs de coefficients d'autocorrélation sont très faibles. La série des rendements géométriques est caractérisé donc par des autocorrélations très faibles.

Cela veut dire que la corrélation entre la rentabilité d'aujourd'hui et les rentabilités passées de l'indice sectoriel « Bâtiments & Matériaux de construction » très faible.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 38 :

Significance level	t-stat	Critical value	P-value
1%	28.6313	37.5662	0.0953
5%	28.6313	31.4104	0.0953
10%	28.6313	28.4120	0.0953

Tableau 38 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice
sectoriel « Bâtiments & Matériaux de construction ».

Le tableau 38 montre que la valeur statistique LIB est 28.6313 que la p-value associée est 0,0953. Notons que la valeur t-statistique est inférieure aux valeurs critiques aux niveaux de 1%, 5% et presque égale à la valeur critique au niveau de 10 Donc l'hypothèse nulle de non corrélation des rendements est rejetée au seuil de 10% (seuil significatif).

Conclusion : il y a une faible autocorrélation entre les rendements de l'indice sectoriel « Bâtiments & MC », au seuil de 10%, car le test est n'est pas significatif aux seuils de 1% et 5%.

2.3.3.7. Test d'absence d'autocorrélation des rendements géométriques de l'indice bancaire :

La figure 34 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice bancaire :

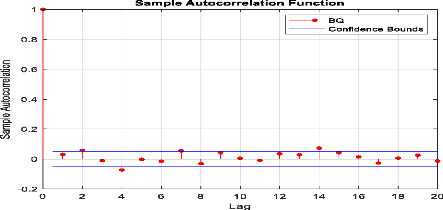
Figure 34 : Corrélogramme d'autocorrélation des rendements de l'indice Bancaire.

Selon le corrélogramme des rendements journaliers de l'indice Bancaire presque tous les pics sont non significatifs, ce qui confirme la propriété de non corrélation des rendements.

Nous remarquons que les valeurs de coefficients d'autocorrélation sont très faibles. La série des rendements géométriques est caractérisé donc par des autocorrélations très faibles.

Cela veut dire que la corrélation entre la rentabilité d'aujourd'hui et les rentabilités passées de l'indice Bancaire est très faible.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 39 :

Significance level	t-stat	Critical value	P-value
1%	42.6877	37.5662	0.0022
5%	42.6877	31.4104	0.0022
10%	42.6877	28.4120	0.0022

Tableau 39 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice Bancaire.

Le tableau 39 montre que la valeur statistique LJB est 42.6877 et que la p-value associée est 0,0022. Notons que la valeur t-statistique n'est pas largement supérieure aux valeurs critiques aux niveaux de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée. Conclusion : il y a une faible autocorrélation entre les rendements de l'indice Bancaire

2.3.3.8. Test d'absence d'autocorrélation des rendements géométriques de l'indice sectoriel « Transport » La figure 35 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Transport » :

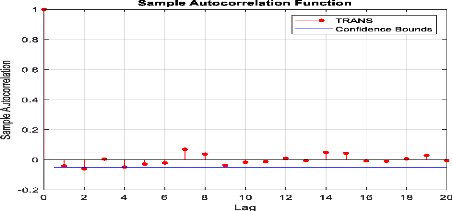
Figure 35 : Corrélogramme d'autocorrélation des rendements de l'indice sectoriel « Transport ».

Selon le corrélogramme des rendements journaliers de l'indice sectoriel « Transport » presque tous les pics sont non significatifs, ce qui confirme la propriété de non corrélation des rendements.

Nous remarquons que les valeurs de coefficients d'autocorrélation sont très faibles. La série des rendements géométriques est caractérisé donc par des autocorrélations très faibles.

Cela veut dire que la corrélation entre la rentabilité d'aujourd'hui et les rentabilités passées de de l'indice sectoriel « Transport » est très faible.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 40 :

Significance level	t-stat	Critical value	P-value
1%	35.8831	37.5662	0.0159
5%	35.8831	31.4104	0.0159
10%	35.8831	28.4120	0.0159

Tableau 40 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice sectoriel « Transport ».

Le tableau 40 montre que la valeur statistique LJB est 35.8831 et que la p-value associée est 0,0159. Notons que la valeur t-statistique et inférieure à la valeur critique au niveau de 1%, et n'est pas largement supérieure aux valeurs critiques aux niveaux de 5% et 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée.

Conclusion : il y a une faible autocorrélation entre les rendements de l'indice sectoriel « Transport », aux niveaux de 5% et 10%..

2.3.3.9. Test d'absence d'autocorrélation des rendements géométriques de l'indice « Loisirs & Hôtellerie » : La figure 35 affiche le corrélogramme d'autocorrélation des rendements géométriques de l'indice sectoriel « Loisirs & Hôtellerie » :

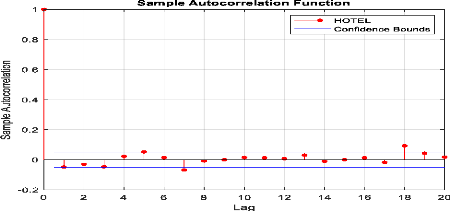
Figure 35 : Corrélogramme d'autocorrélation des rendements de l'indice sectoriel « Loisirs & Hôtellerie ».

Selon le corrélogramme des rendements journaliers de l'indice sectoriel « Loisirs & Hôtellerie » presque tous les pics sont non significatifs, ce qui confirme la propriété de non corrélation des rendements.

Nous remarquons que les valeurs de coefficients d'autocorrélation sont très faibles. La série des rendements géométriques est caractérisé donc par des autocorrélations très faibles.

Cela veut dire que la corrélation entre la rentabilité d'aujourd'hui et les rentabilités passées de de l'indice sectoriel « Loisirs & Hôtellerie » est très faible.

Les résultats du test d'autocorrélation LJB sont présentés dans le tableau 41 :

Significance level	t-stat	Critical value	P-value
1%	42.4114	37.5662	0.0024
5%	42.4114	31.4104	0.0024
10%	42.4114	28.4120	0.0024

Tableau 41 : Test d'autocorrélation LJB pour la série des rendements géométriques de l'indice sectoriel
« Loisirs & Hôtellerie ».

Le tableau 41 montre que la valeur statistique LJB est 42.4114 et que la p-value associée est 0,00000. Notons que la valeur t-statistique n'est pas largement supérieure aux valeurs critiques aux niveaux de 1%, 5% et 10%. Donc l'hypothèse nulle de non corrélation des rendements est rejetée.

Conclusion : il y a une faible autocorrélation entre les rendements de l'indice sectoriel « Loisirs & Hôtellerie ».

2.3.4 Test d'hétéroscédasticité

Une autre hypothèse est empiriquement abordée est celle de l'hétéroscédasticité qui signifie que la volatilité variable dans le temps. Or, les fluctuations et les soubresauts que connait incessamment le paysage financier laissent présager l'existence d'un effet autorégressif à volatilité conditionnelle (effet ARCH) présent dans la composante stochastique des séries financières. Compte tenu des imperfections enregistrées au niveau des modèles classiques, et en prenant conscience des restrictions des hypothèses, de nouveaux modèles mathématiques ont été mis en place en vue d'assurer une modélisation optimale des actifs financiers à savoir les modèles autorégressifs à volatilité conditionnelle hétéroscédastique simples et généralisés (ARCH et GARCH) développés par Engle (1982).

Ces modèles ont le principal avantage de prendre en compte principalement la dynamique temporelle variable de la volatilité (l'hétéroscédasticité) et également la leptokurticité des rendements traduisant un excès de Kurtosis (coefficient mesurant l'aplatissement des distributions). Cet excès de Kurtosis est l'un des indicateurs de la non-normalité.

L'évolution des modèles ne s'arrête pas là. De nouvelles classes de modèles seront mises en place notamment les extensions des modèles GARCH à savoir l'exponentiel GARCH connu sous le sigle EGARCH et le GARCH fractionnaire intégré connu sous le sigle de FIGARCH. L'extension a été établie après avoir constaté empiriquement que les modèles ARCH et GARCH sont des modèles symétriques (dans le sens où les bonnes et les mauvaises nouvelles ont le même impact sur les rendements futurs et donc sur la volatilité). En effet, le modèle GARCH asymétrique ou EGARCH a été adopté quand l'économiste Black a remarqué que les bonnes et les mauvaises nouvelles ont des impacts différents sur la volatilité contrairement au modèle GARCH.

Ce phénomène d'asymétrie signifie que les mauvaises nouvelles tendent à faire augmenter la volatilité avec une ampleur plus importante que les bonnes nouvelles. Ce qui indique l'existence d'une sensibilité de la volatilité à l'égard des chocs.

L'hétéroscédasticité signifie que la dispersion des résidus a tendance à augmenter ou à diminuer en fonction des valeurs ajustées, plus généralement, elle se manifeste quand la dispersion des résidus varie en fonction des variables explicatives. Non seulement L'hétéroscédasticité influence les tests de significativité mais surtout, elle fausse les intervalles de prévision. Nous allons présenter, un test permettant de détecter une hétéroscédasticité éventuelle. Le test ARCH ou test du multiplicateur de Lagrange qui a été introduit par Engle (1982).

Avant de modéliser la moyenne conditionnelle et la volatilité conditionnelle pour les séries des rendements géométriques, nous testons d'abord l'hétéroscédasticité de la série des résidus des rendements géométriques.

? Hypothèse nulle : la série des résidus des rendements géométriques est homoscédastique.

? Hypothèse alternative : la série des résidus des rendements géométriques est hétéroscédastique.

Mesure de l'interdépendance du marché boursier marocain par le modèle DCC-GARCH

Conclusion : il y a une autocorrélation entre les rendements de l'indice « MASI ».

2.3.4 Test d'hétéroscédasticité