1.3 Notions et définitions
La représentation mentale d'un graphe est
généralement aisée et la notion de noeud et liaison est le
plus souvent comprise de manière intuitive. Cependant, l'utilisation
d'une terminologie précise se révèle nécessaire
dès qu'il s'agit d'approfondir l'étude de ces ensembles.
Voici listées les notions utilisées dans notre
contexte de travail ; à noter que certaines définitions
données peuvent tenir compte de notre point de vue. Pour une information
plus complète il est possible de consulter plusieurs ouvrages de
référence tels que [Berge-1958] [Berge-1970]
[Bollobas-1998].
Arc
Un arc est le nom donné à une liaison ou à
une arête dans un graphe dirigé.
Arête
Élément reliant deux points d'un graphe.
Généralement représenté par un segment de droite.
Dans la matrice d'adjacence du graphe la présence de l'arête est
représentée par un 1 et son absence par un 0.
Arête orientée
Une arête orientée est une arête
présentant un sens. Un des pairs est un émetteur l'autre un
récepteur. On parle aussi d'arc. Les arêtes orientées sont
des éléments des graphes orientés.
Arête
pondérée
Une arête pondérée est une arête
présentant un poids. Ce poids est une valeur numérique permettant
de comparer la validité des arêtes. Les arêtes
pondérées sont des éléments des graphes
pondérés.
Centralité
La centralité d'une arête e, notée
cB(e), est définie comme le nombre de plus court(s) chemin(s)
entre toutes paires de noeuds contenant e : ainsi, si la centralité
d'une arête est grande, on peut s'attendre à ce qu'elle se trouve
à l'interface entre deux communautés du graphe
considéré. Cette notion peut facilement être étendue
aux noeuds en considérant le nombre de plus court(s) chemin(s) passant
par un noeud donné. Une arête à forte centralité est
considérée comme un séparateur possible de
communautés.
2
5 4
1
3
6
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
B
D Z
A
C
cB(e)=32
X
W
Y
Liste des plus courts chemins passant par l'arête
[C-X/X-C] en considérant le graphe comme dirigé
|
A-W
|
A-X
|
A-Y
|
A-Z
|
W-A
|
X-A
|
Y-A
|
Z-A
|
|
B-W
|
B-X
|
B-Y
|
B-Z
|
W-B
|
X-B
|
Y-B
|
Z-B
|
|
C-W
|
C-X
|
C-Y
|
C-Z
|
W-C
|
W-C
|
Y-C
|
Z-C
|
|
D-W
|
D-X
|
D-Y
|
D-Z
|
W-D
|
W-D
|
Y-D
|
Z-D
|
Figure 1.3 : Exemple d'arête ayant une
centralité élevée et étant susceptible de
séparer deux communautés.
Chemin
Un chemin d'un noeud A à un noeud Z est une suite de
noeuds reliés par des arêtes tel qu'il est possible de se
déplacer du noeud A au noeud Z en parcourant les noeuds du chemin.
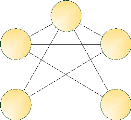
Clique
Une clique peut être définie comme une figure
connectée de trois noeuds minimum d'un graphe non dirigé dans
laquelle on ne peut rajouter ni lien ni noeud. En effet, chacun des noeuds doit
être connecté à tous les autres noeuds et il ne doit pas
exister de noeud connecté à tous ces noeuds qui ne seraient pris
en compte. La clique est aussi définie comme un sous-graphe complet.
1.3. Notions et définitions 31
Figure 1.4 : Exemple de clique de 5 sommets. Figure 1.5 :
En noir, un exemple de clique formée par
les noeuds 1,2 et 3 dans un graphe.
1.3. Notions et définitions 32
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
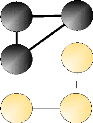
Composante connexe
Une composante connexe est une partie du graphe où il
existe au moins un chemin pour rejoindre tous les noeuds de la composante
connexe. Si un graphe est seulement et totalement composante connexe, on
utilise le terme de graphe connexe.
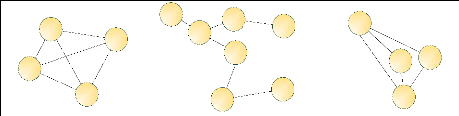
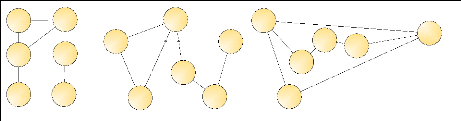
Figure 1.6 : Graphe à 3 composantes
connexes.
Degré
Dans un graphe dans lequel un noeud ne peut pas recevoir de
liaison avec lui-même, le degré d'un noeud est simplement le
nombre de noeuds avec lequel il existe une liaison. On parle aussi du nombre de
noeuds voisins.
Si le graphe est défini comme acceptant des liaisons
autoportées, ses liaisons autoportées ont par convention un poids
double.
|
Degré des noeuds du graphe
|
|
Graphe
|
|
|
Noeud
|
Degré
|
|
|
|
|
|
A
|
3
|
|
B
|
3
|
|
|
|
|
|
|
C
|
4
|
|
|
D
|
3
|
|
|
E
|
3
|
|
|
|
A
B
E
C
D
Figure 1.7 : Exemple de valeur de degré pour les
noeuds d'un graphe incluant une liaison autoportée.
Densité d'un graphe
La densité est le rapport entre le nombre
d'arêtes présentes dans le graphe étudié sur le
nombre maximal d'arêtes possible sur un graphe contenant le même
nombre de noeuds. Dans le cas où le nombre de liaisons par noeud n'est
pas limité, ce nombre maximal est, pour un graphe de n
éléments, le nombre de paires possibles que l'on peut noter
(combinaison de n
éléments d'ordre 2) soit cn 2= 2 ( n
n-2) ! ! .
Diade
Une diade est une paire de noeuds connectés.
1.3. Notions et définitions 33
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
Diamètre d'un graphe
Le diamètre d'un graphe est la distance la plus
élevée entre deux noeuds en utilisant le chemin le plus direct.
Une géodésique est l'un des plus courts chemins entre deux
sommets donnés. Le diamètre d'un graphe peut être
défini comme le plus long chemin géodésique du graphe.
Diamètre
effectif
Le diamètre d'un graphe est défini comme une
distance maximale et peut donc être une valeur non représentative
car trop marginale. Pour éviter cette dérive, plusieurs auteurs
proposent de mesurer le diamètre effectif ou petit diamètre
[Leskovec&al-2005]. Le diamètre effectif ou petit
diamètre est le nombre minimum de sauts ou liaisons dans lequel une
fraction (ou quantile q, par exemple q = 90%) de toutes les paires de noeuds
connectés sont présentes.
Graphe (et
représentation)
Un graphe est, dans sa représentation dessinée,
un ensemble de points dont certaines paires sont reliées par un lien. Le
positionnement des points et la longueur des liaisons ne sont pas
significatives. Ainsi, le graphe de la figure 1.8 est le même quelles
qu'en soient les représentations.
2
5
1
4
3 2
3
6
1
5
4
6
2
1
5
4
6
3
Figure 1.8- Plusieurs représentations
dessinées d'un même graphe.
Il est aussi possible de représenter un graphe par une
représentation matricielle. Plusieurs types de matrices
[matrix] existent. La plus connue et usuelle est la matrice
d'adjacence MA. Les noeuds sont présents en abscisses
et ordonnées, la jonction de deux noeuds étant alors par
convention représentée par un 1 si une liaison existe et un 0 si
ce n'est pas le cas.
La matrice des degrés est aussi couramment
utilisée. Elle donne, en plus de la matrice des liaisons, des
informations sur la valeur des degrés des noeuds. La matrice Laplacienne
non normalisée L est la matrice résultante de
MD- MA.
1.3. Notions et définitions 34
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
On utilise aussi la matrice Laplacienne normalisée.
Dans ce cas-là, la fonction de normalisation N(x,y) est
égale à 0 si x et y ne partagent pas de
liaison, égale à 1 si x= y et
degré (x ) > 0, et égale à v ( )
( ) sinon.
|
MA-Matrice d'adjacence
|
MD-Matrice des degrés
du graphe ou
matrice
diagonale.
|
ML-Matrice Laplacienne
non
normalisée
|
|
Matrice Laplacienne
normalisée
|
|
|
|
|
|
|
|
|
|
|
|
v
|
v
|
|
]
|
[ ]
|
|
v
|
|
|
v
|
|
|
[
|
|
|
[ ]
|
v
|
|
|
v
|
|
|
|
|
|
|
|
|
|
]
|
|
v
|
|
|
|
|
|
|
[
|
|
v
|
|
|
Tableau 1.1 : Représentations matricielles du
graphe de la figure 1.8.
Graphe de terrain
Ensemble d'objets naturels ou existants physiquement dans le
monde réel dont les interactions sont exprimables par des arêtes
entre paires d'objets. Les graphes de terrains sont ainsi constitués
d'éléments aussi divers que des personnes humaines
échangeant des mails, des ordinateurs échangeant des trames IP,
des mots présents dans la même définition, etc.
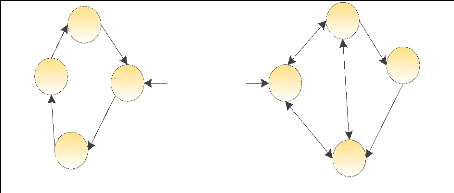
Graphe dirigé
Un graphe dirigé est un graphe dont les liaisons
appelées arcs ont un sens. Un des noeuds est un émetteur et
l'autre un récepteur. Un exemple bien connu de graphe dirigé est
l'arbre généalogique inversé. Se lisant du haut vers le
bas, le sens de l'arc du haut vers le bas signifie « Parent de ».
Parent de
Parent de

Grand-père
paternel
Grand-mère
paternelle
Parent de Parent de


Grand-père
maternel
Grand-mère
maternelle
Parent de Parent de

Mère
Père

Enfant
Figure 1.9 : Exemple de graphe
dirigé.
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
Graphe pondéré
Un graphe pondéré est un graphe dans lequel les
noeuds et les liaisons peuvent recevoir une valeur numérique. Ces
valeurs peuvent être soit calculées par des informations sur le
graphe lui-même soit être des informations complémentaires.
Par exemple dans un réseau social d'échange par Emails, les
acteurs peuvent être pondérés par la somme de tous les
Emails reçus et chaque liaison par le nombre d'Emails
échangés.
2 201 578
391
656
588
Lyon
480 778
360 272
323
Marseille
847 084
Toulouse
444 392
Paris
Figure 1.10 : Graphe de villes de France. Les villes
sont pondérées par le nombre d'habitants et les liaisons par la
distance à vol d'oiseau.
Graphe pondéré et
dirigé
Un graphe pondéré et dirigé va cumuler
des arcs et des pondérations. Le graphe d'un site web est naturellement
un graphe dirigé et pondéré. Les pages du site
représentent ici les noeuds et les arcs représentent les liens.
La pondération des noeuds peut être donnée par le nombre de
liens sortant de chaque page du site, les arêtes seront dirigées
comme le sont les liens entre les pages et pondérées par le
nombre de liens.
1

Paiement
2
Accueil
3
1

Chariot
5
1
3
1
1

Recherche
1
1
Catalogue
1
Produits
5544
5544
Fiche détail
Produit
1

1
Support
1
2
1
Contact
2
1.3. Notions et définitions 35
Figure 1.11 : Exemple de graphe dirigé et
pondéré d'un site web d'E-commerce.
1.3. Notions et définitions 36
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
Graphe bi-connexe
Un graphe est dit bi-connexe s'il existe entre chaque noeud au
moins deux chemins complètement distincts. Une autre définition
possible est que la suppression de n'importe quel lien permet au graphe de
rester une composante connexe.
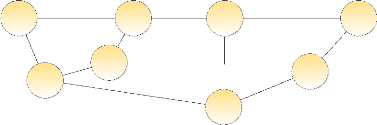
Figure 1.12 : Exemple de graphe bi-connexe.
K-clique
Une K-clique est une clique de K sommets. Chaque sommet
possédant un degré de valeur k-1, le nombre de liaisons
est donc de k * (k-1)/2.
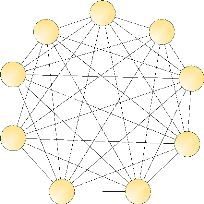
Figure 1.13 : Exemple de K-clique avec K= 9. Le graphe
est constitué de 9 noeuds et 36 liaisons.
Liaison
Autre nom donné à une arête.
Méga-graphe
Afin d'indiquer rapidement un ordre de grandeur du nombre de
noeuds inclus dans un (grand) graphe, on peut parler de Méga-graphe pour
les graphes contenant plus d'un million d'objets.
1.3. Notions et définitions 37
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
Modularité et module
La notion de modularité a été
développée par Newman [Newman-2004-2]. Son but
est de comparer la proportion relative de liaisons d'un sous-graphe avec le
nombre de liens d'un sous-graphe de même taille construit
aléatoirement en respectant la valeur statistique de présence de
liaisons de l'ensemble du graphe.
La valeur de modularité d'un sous-graphe est comprise
entre [-1,1]. La valeur est supérieure à 0 si le nombre de liens
intra sous-groupe est supérieur au nombre de liens du sous-graphe
aléatoire créé en respectant la proportionnalité de
liaisons présente dans le graphe complet.
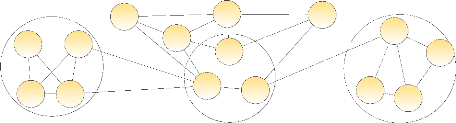
S 1
S2
S3
Figure 1.14 : Exemple de calcul de
modularité.
Pour un sous-graphe S, le nombre de liens internes à S
est noté LS, le nombre de liens dans le graphe est noté LG. La
somme des degrés des noeuds présents dans le sous-graphe S est
notée DS. La modularité du sous-graphe S sera
considérée comme valide si la modularité de S est
supérieure à 0 soit : MS = (LS / LG) - (DS /
(2LG))2 > 0
Dans l'exemple de la figure 1.14, nous sélectionnons
arbitrairement 3 sous-graphes. Sachant que LG=26,
Pour S1, LS1=
6, DS1 =14 on a donc MS1= 6/26 -
(14/52)2 = + 0.158 Pour S2, LS2=
1, DS2 = 12 on a donc MS2= 1/26 -
(12/52)2 = - 0.014 Pour S3, LS3=
5, DS3 =12 on a donc MS3= 5/26 -
(12/52)2 = + 0.139
Comme on peut le constater, les sous-graphes S1 et S3 sont
bien des modules. S2 n'en est pas un, son score de modularité
étant négatif. Ce critère de modularité est
aujourd'hui très utilisé.
Partition
Une partition est un élément constitutif d'un
graphe, structuré de telle sorte que chaque partition contient un nombre
proche de noeuds et que l'ensemble des partitions contient tous les noeuds.
1.3. Notions et définitions 38
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
Taux de clustering ou
d'agrégation
Le taux de clustering ou d'agrégation d'un graphe est
la moyenne du rapport pour chaque noeud du nombre réel de liaisons
existantes entre ses voisins et le nombre maximum théorique possible de
ces liaisons.
Par exemple, pour un noeud X, il existe K
noeuds avec lesquels il est connecté. Si le nombre de liaisons
n'est pas limité pour chacun des noeuds, le nombre de liaisons maximales
entre ces noeuds est K(K-1) /2. Le coefficient de clustering pour le
noeud X dans un graphe non pondéré où le nombre
de liaisons entre les noeuds voisins de X est égal à
LK sera alors de :
LK /( K(K-1) /2
Le coefficient de clustering du graphe sera la moyenne de ces
valeurs pour l'ensemble des noeuds n du graphe.
? ( ( ) )
Ce coefficient peut être vu comme une mesure statistique
de la transitivité. Plus ce coefficient est élevé, plus la
probabilité que les noeuds soient liés entre eux est forte.
Autrement dit, pour rester dans un exemple des réseaux sociaux plus le
taux de clustering est élevé plus il y de chance « que les
amis de X soient amis entre eux ».
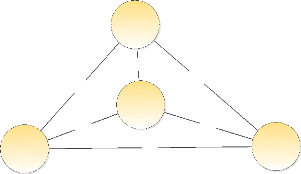
Triade
La triade, est une figure connectée de trois
éléments comprenant trois sommets et trois liaisons. Les triades
ont une importance particulière dans les réseaux sociaux,
notamment car elles sont garantes de phénomènes impossibles aux
diades, tels que la médiation et, de plus, sont porteuses de
transitivité [Faust-2010].
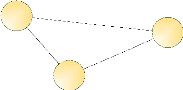
Figure 1.15 : Exemple de triade.
Voisins (noeuds et sommets voisins)
Les noeuds connectés au noeud X sont dits voisins de X.
1.4. Grands graphes de terrain 39
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
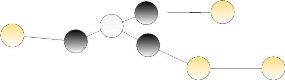
X
Figure 1.16 : En noir, les voisins du noeud
X.
| 


