1.2 Historique
Les premières études sur la théorie des
graphes sont celles effectuées par Leonhard Eulervdans avec sa recherche
d'une solution au problème des ponts de Königsberg (Euler 1736). La
ville de Königsberg située en Prusse est alors constituée de
deux iles reliées par sept ponts (cf. figure 1.1). La ville se nomme
aujourd'hui Kaliningrad.
1.2.1 Le problème
Le problème posé est de trouver un chemin
permettant de passer sur chaque pont en n'empruntant chaque pont qu'une seule
fois.
|
Plan de la ville
|
Plan simplifié
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
île
|
|
|
|
|
île
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Terre
|
|
|
|
|
|
|
Figure 1.1 : Les sept ponts de
Königsberg.
rive A
rive A
C
B
île B
rive D
Rivière
ferme
Pont
Leonhard Euler va dessiner un schéma où rives et
îles seront représentées par des
points et chaque pont comme des « fils » entre ces
points, créant ainsi un graphe (cf. Figure
1.2).
île C
rive D
1.2.2 La réponse par le graphe
Les points de terre ferme sont les noeuds ou sommets du
graphe. Les noeuds et sommets représentent toujours les objets
connectés du graphe. Habituellement un noeud (ou un sommet)
représente un objet actif du graphe. Dans un réseau social, les
noeuds représentent des personnes et par transposition, les connections
leurs relations sociales, par exemple.
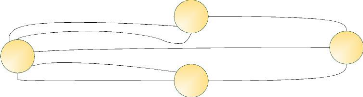
Nb de ponts=3
A
B
Nb de ponts=3
C
Nb de ponts=5
D
Nb de ponts=3
Figure 1.2 : Les sept ponts de Königsberg dans une
représentation graphique.
1.2. Historique 29
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
Une fois la représentation graphique
créée, la question : « Peut-on faire un parcours passant par
les sept ponts en n'utilisant qu'une seule fois chaque pont ? » se
résume à : « Existe-t-il un chemin pour revenir d'un point
ferme à un autre, différent de celui pris pour aller ? ». Si
nous notons à coté de chaque noeud (point de terre ferme) le
nombre de ponts (cf. figure 1.2), il devient évident que ce nombre
étant toujours impair, il ne sera pas possible depuis un point de terre
ferme visité en « milieu » de promenade de revenir directement
au point précédent sans réemprunter un pont
déjà utilisé.
Cette caractéristique n'est pas nécessaire pour
tous les noeuds. Elle l'est cependant pour au moins deux : celui de
départ et celui de fin. Aucun point de terre ferme n'étant
accessible par un nombre pair de pont, la réponse est finalement qu'il
n'est pas possible d'effectuer la promenade demandée.
La représentation graphique nous permet donc d'affirmer
qu'il n'existe pas de solution à ce problème.
Il est par ailleurs intéressant de noter certains
enseignements fournis par ce travail fondateur :
? C'est la pondération des éléments de terre
ferme par le nombre de ponts qui permet de trouver la réponse au
problème.
? Une fois le graphe créé, il n'est plus
nécessaire de le parcourir pour connaître les informations nous
permettant de répondre à la question posée. La
localisation des ponts et des points de terre ferme n'a plus d'importance. Et
on pourrait tout à fait répondre à la question sans
représenter les fils entre les points de terre ferme.
Comme on peut le voir, une représentation d'un
réseau par un graphe permet de répondre à une question
donnée. La représentation et les informations à
représenter sont à choisir en fonction de la nature du graphe et
de la question à résoudre. Dans notre travail nous aurons donc
à rechercher une représentation graphique la plus efficace
possible, pour répondre à nos questions de regroupement.
Nous nous devons aussi de souligner que cette étude
porte sur un réseau d'usage (nos promeneurs utilisent les ponts) et de
« terrain » au sens premier du mot.
1.3. Notions et définitions 30
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
| 


