1.12 Lethality
Lethality is the percentage of the death toll among confirmed
virus cases. The first fatality assessment was released on 14 February by the
Chinese Center for Disease Control and Prevention (Chinese CDC), among the
first 44, 672 confirmed cases it was then estimated at (2.3%) .
Lethality varies according to the conditions in which patients
are treated and their access to hospital services. It is different from one
country to another. Globally the WHO has estimated it to be around 3.4 % (the 3
March 2020).
With the increase in cases of the disease worldwide, WHO
estimates the percentage of death rate from COVID- 19 to 2.2% as of 17 December
2020.
If it seemed spared for a long time or almost, the African
continent is now affected like the rest of the world, even if the number of
cases remains limited. The first case of COVID- 19 in Africa appeared in
February 2020 in Egypt. A sudden increase in the number of cases is observed in
July
1.13. CONCLUSION 15
Master's thesis II * Molecular Atomic Physics and
Biophysics Laboratory-UYI * YAMENI STEINLEN DONAT D
(c)2021
and August, then the contaminations slowed down again. The
following table presents the results of the pandemic in some African countries
during the period of August 31, 2021 [14, 15].
.
|
Countries
|
N.Cas
|
healing Cas
|
N.death
|
Lethality%
|
|
Soudan
|
37699
|
3163
|
2831
|
6.2
|
|
Egypte
|
288162
|
238580
|
16727
|
5.5
|
|
Liberia
|
5459
|
2715
|
148
|
4.4
|
|
Cameroon
|
82064
|
80433
|
1354
|
1.7
|
Table 1.1: Lethality.
1.13 Conclusion
In this chapter, we were talking about generalities about the
Coronavirus disease. COVID-19 is a newly identified highly infectious disease
originating in Wuhan, China, December 2019, which quickly spread like wildfire
causing death and devastation around the world. In order to limit the spread of
the pandemic, the States will organize the response. The need therefore arises
in the next chapter to build a compartmental model to predict the possible
scenarios of transmission and spread of the disease.
CHAPTER II
MATHEMATICAL MODEL AND
METHODS OF INVESTIGATIONS
2.1 INTRODUCTION
Infectious disease models are increasingly used to predict a
range of future possibilities to aid and support knowledge development and
decision making at the scientific, medical and health levels.
In this chapter, we present the actual calculation of the
reproduction rate with control measures Rc, which is an
important quantity to characterize epidemic diseases, through the stability
analysis.
2.2 Formulation of the model
The fundamental tool in the study of COVID-19 dynamics is the
mathematical model in that it allows for a better understanding of the impacts
of various non-pharmaceutical control measures (governmental and personal) on
the population dynamics of the new COVID-19 disease.
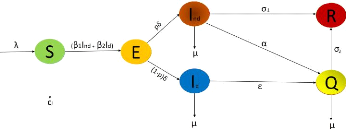
16
Figure 2.1: Compartmental structure of the
model.
2.2. FORMULATION OF THE MODEL 17
Master's thesis II * Molecular Atomic Physics and Biophysics
Laboratory-UYI * YAMENI STEINLEN DONAT D
(c)2021
|
À
|
Recruitment of sensitive individuals
|
|
/31
|
Transmission rate of undetected infected
|
|
/32
|
Transmission rate of detected infected
|
|
cf
|
Containment rate of sensitive individuals
|
|
ä
|
Incubation rate
|
|
p
|
Fraction of exposures that become infected undetected
|
|
u
|
Disease-induced mortality rate
|
|
€
|
Quarantine rate of detected infectious
|
|
a
|
Quarantine rate of undetected infectious
|
|
a1
|
Recovery rate of undetected infectious
|
|
a2
|
Recovery rate of quarantined individuals
|
|
O
|
Represents the fraction of the total population that uses a face
mask
|
|
ø
|
proportion of the population that maintains the minimum distance
required to prevent infection
|
Table 2.1: Representation of model
parameters.
A model is a tool that allows to give a simple representation of
a phenomenon.
The total human population at time (t), denoted Nh(t)
is divided into a mutually exclusive subgroup of susceptible individuals
S(t), exposed individuals E(t), undetected infectious individuals
Ind(t), detected infectious individuals Id(t),
quarantined individuals Q(t), recovered individuals R(t).
Nh(t) is given by
Nh(t) = S(t) + E(t) + Ind(t) + Id(t) + Q(t) +
R(t).
The model of the transmission dynamics of COVID-19 in a
population is given by the following
2.2. FORMULATION OF THE MODEL 18
Master's thesis II * Molecular Atomic Physics and Biophysics
Laboratory-UYI * YAMENI STEINLEN DONAT D (c)2021
system of deterministic nonlinear differential equations in (2-1)
built by Nkamba et al [5],
???????????????? ?
?
????????????????? Sÿ= ë -
(â1Ind + â2Id)S -
CfS,
Eÿ = (â1Ind +
â2Id)S - äE, ÿInd
= päE - (ó1 + á +
u)Ind, ÿId = (1 -
p)äE - (å + u)Id, Qÿ = åId
+ áInd - (ó2 + u)Q,
Rÿ = ó1Ind + ó2Q.
(2.1)
with the table describing the state associated variables and
parameters in the model(2-1) while figure (2-1) gives the schematic diagram of
the model(2-1).
Mathematical models without demographic parameters (i.e. birth
and natural death) in equations (2-1) have been widely used to study the
dynamics of epidemics [16, 17, 19]. Demographic parameters, including natural
births and deaths, can be excluded when dynamically exchanging an epidemic that
occurs within weeks or months [18, 19, 20, 21, 22]. If we introduce parameters
used by Okuonghae and Omame [23], that
represent social distancing and use of face masks of infection from the basic
model (2-1), in which a new parameter ø represents the proportion of the
population that maintains the minimum distance required to prevent infection
(at least 1 meter apart), and another parameter è represents the
fraction of the population that use face masks (where it is assumed that face
masks are effectively high whenever they are in public, so that 0 <
è < 1), the basic model (2-1) now becomes.
|
?
???????????????? ?
?????????????????
|
Sÿ= ë - (1 - è)(1
- ø)(â1Ind +
â2Id)S - CfS, Eÿ= (1
- è)(1 - ø)(â1Ind +
â2Id)S - äE,
ÿInd = päE -
(ó1 + á + u)Ind,
(2.2)
ÿId = (1 - p)äE -
(å + u)Id,
Qÿ = åId + áInd -
(ó2 + u)Q, Rÿ= ó1Ind
+ ó2Q.
|
It is imperative to specify that in the framework envisaged in
this work, the strict adoption of the use of face masks has been encouraged
well into the current outbreaks in Cameroon, particularly
2.3. BASIC PROPERTIES OF THE MODEL 19
in the city of Yaounde and Douala.
| 


