Dynamics of covid-19 pandemic in cameroon : impacts of social distanciation and face mask wearing

2.3 Basic properties of the model

Let be:

S(0), E(0), I_nd(0), Id(0), Q(0), R(0),

the initial data.

The solutions (S, E, _Ind, Id, Q, R) of the model (2.2), when they exist, are positive for all t > 0. à t = 0, N(0) = N0 and

dS dt

= ë - (1 - ø)(1 - è)(â1Ind + â2Id)S - cfS, d _dt[S(t)ñ(t)] = ëñ(t).

From where

t

ñ(t) = exp( f [(1 - ø)(1 - è)(â1I_nd(s) + â2Id(s)) + cf]ds) > 0

0

is the integration factor. Hence, integrating this last relation with respect to t, we have

t

S(t)ñ(t) - S(0) = f ëñ(s)ds,

0

So that the division of both side by ñ(t) yield. The solution is given by:

t

S(t) = [S(0) + f ëñ(s)ds]ñ^-1(t) > 0. (2.3)

0

A similar procedure is used to prove that

E(t) > 0 and I_nd(t), Id(t), Q(t), R(t) > 0 for all t > 0.

N(t) = S(t) + E(t) + I_nd(t) + Id(t) + Q(t) + R(t),

dN(t) dt

=

dS(t) + dt

dE(t) + dt

dInd(t) + dt

dId(t) + dt

dJ(t) + dt

dR(t) dt

. (2.4)

Master's thesis II * Molecular Atomic Physics and Biophysics Laboratory-UYI * YAMENI STEINLEN DONAT D (c)2021

Replacing each derivative with its value in the right-hand member gives :

dN(t) dt

= ë - cfS - uInd - uId - uQ

Master's thesis II ? Molecular Atomic Physics and Biophysics Laboratory-UYI ? YAMENI STEINLEN DONAT D (c)2021

2.4. LOCAL ASYMPTOTIC STABILITY OF DISEASE-FREE EQUILIBRIUM (DFE) OF THE MODEL (2-2) 20

dN(t) = À - d0N, dt

where

d0 = min(cf, ii).

That implies that

lim t--+-oo

À supN(t) = . (2.5) do

2.4 Local asymptotic stability of disease-free equilibrium (DFE) of the model (2-2)

The COVID-19 model (2-2) has a DFE, obtained by setting the rights of the equations in model (2-2) to zero, given by

N(t) = 8(t) + E(t) + Ind(t) + Id(t) + Q(t) + R(t).

For t = 0, we have

N(0) = 8(0) + E(0) + Ind(0) + Id(0) + Q(0) + R(0)

î0 = (8*,E*,I* _{nd,I* d},Q^*,R^*) = (8(0),0,0,0,0,0) (2.6)

Where 8(0) = cf ë

2.4.1 Basic reproduction number

fi is the rate of new infections in the compartment, F is the matrix of new infections. We will then restrict this system to the infected populations (E, Ind, Id, Q). When we evaluate the partial derivatives of (E, Ind, Id, Q) we obtain the matrix [F] next:

2.4. LOCAL ASYMPTOTIC STABILITY OF DISEASE-FREE EQUILIBRIUM (DFE) OF THE MODEL (2-2) 21

?

? ? ? ? ? ? ?

f_i =

,

?

? ? ? ? ? ? ?

(1 - è)(1 - ø)(â1Ind + â2Id)S

0

0

0

?

? ? ? ? ? ? ?

F=

afi(c0) aE

afj(c0) aE

afk(c0) aE

af_m(c0) aE

afi(c0) aInd

afj(c0) aInd

afk(c0) aInd

af_m(c0) aInd

afi(c0) aId

afj(c0) aId

afk(c0) aId

af_m(c0) aId

₁ ,

afi(c0) aQ

afj(c0) aQ

afk(c0) aQ

af_m(c0) aQ

₁ .

Master's thesis II * Molecular Atomic Physics and Biophysics Laboratory-UYI * YAMENI STEINLEN DONAT D (c)2021

?

0 (1 - è)(1 - ø)(â1)S(0) (1 - è)(1 - ø)â2S(0) 0

? ? _?0 0 0 0
F = ? ? ?

0

?0 0 0

0 0 0 0
Now let's look for the matrix of individuals between compartments. V - is the rate of transfer of individuals out of the compartment V + is the rate of transfer of individuals into the compartment by all other means

Vi = V - - V +,

where

V - =

? ? ? ? ? ? ? ?

äE (ó1 + á + u)Ind (å + u)Id (ó2 + u)Q

1

, V + =

?0 ? ? ?päE ? ? ? ?(1 - p)äE åId + áInd

1

, Vi=

? ? ? ? ? ? ? ?

äE (ó1 + á + u)Ind - PäE (å + u)Id - (1 - p)äE (ó2 + u)Q - åId - áInd

1

.

Master's thesis II ? Molecular Atomic Physics and Biophysics Laboratory-UYI ? YAMENI STEINLEN DONAT D (c)2021

2.4. LOCAL ASYMPTOTIC STABILITY OF DISEASE-FREE EQUILIBRIUM (DFE) OF THE MODEL (2-2) 22

V =

? ? ? ? ? ? ? ?

?Vi ?E ?Vj ?E ?Vk ?E ?Vm ?E

?Vi ?Ind ?Vj ?Ind ?Vk ?Ind ?Vm ?Ind

?Vi ?Id ?Vj ?Id ?Vk ?Id ?Vm ?Id

?Vi ?Q ?Vj ?Q ?Vk ?Q ?Vm ?Q

? ? ? ? ? ? ? ?

,V =

? ? ? ? ? ? ? ?

ä 0 0 0 -pä ó1 + á + u 0 0 -(1 - p)ä 0 ? + u 0 0 -á -? ó2 + u

? ? ? ? ? ? ? ?

The matrix FV ^-1 called next generation matrix is given by

FV -1 =

? ? ? ? ? ? ? ?

ëâ1(1-è)(1-ø)p + ëâ2(1-è)(1-ø)(1-p) ëâ1(1-è)(1-ø) ëâ2(1-è)(1-ø) 0 cf (ó1+á+u) cf (?+u) cf (?+á+u) cf (?+u) 0 0 0 0 0 0 0 0 0 0 0 0

1

.

Let's find the eigenvalues of the matrix FV ^-1, we calculate the determinant det(ëI4 - F V ^-1),

det(ëI4 - FV ^-1) =

? ? ? ? ? ? ? ?

ë- X1 X2 X3 0 0 ë 0 0 0 0 ë 0 0 0 0 ë

1

.

where

{

X1 = ëâ1(1-è)(1-ø)p cf (ó1+á+u) + ëâ2(1-è)(1-ø)(1-p) , cf (?+u) X2 = ëâ1(1-è)(1-ø) cf (?+á+u) , X3 = ëâ2(1-è)(1-ø) cf (?+u) .

(2.7)

The eigenvalues are obtained by calculating det(ëI4 - FV -1) = 0. We obtain the following characteristic equation:

ë(ë²(ë - X1)) = 0.

The maximum eigenvalue of this matrix is R_c. Thus, it follows from [24] that the basic reproduction number of the model(2-2), noted R_c is given by

Master's thesis II * Molecular Atomic Physics and Biophysics Laboratory-UYI * YAMENI STEINLEN DONAT D (c)2021

2.4. LOCAL ASYMPTOTIC STABILITY OF DISEASE-FREE EQUILIBRIUM (DFE) OF THE MODEL (2-2) 23

R_e = (1 - è)(1 - ø)ë[ pâ1₊ (1 - p)â2]. (2.8)

cf (ó1 + u + á) (? + u)

2.4.2 Local stability of balance without disease (DFE)

Theorem 2.4. The DFE (Disease-Free Equilibrium) is locally asymptotically stable when R_e < 1 and unstable when R_e > 1.

Proof. The local stability of the model is analyzed by the Jacobian matrix of the system at the equilibrium point î0 = (_ef^ë , 0, 0, 0, 0, 0).

It is recalled that this number of reproductions is defined in the presence of control measures (social distancing and wearing a face mask).

J(î0) =

? ? -(cf) 0 -â1(1 - è)(1 - ø)S(0) -â2(1 - è)(1 - ø)S(0) 0 0 ? ? ? ? ?0 -ä â1(1 - è)(1 - ø)S(0) â2(1 - è)(1 - ø)S(0) 0 0 ? ? ? ? ? ?0 pä -(ó1 + á + u) 0 0 0 ? ? ? ? ? ?0 (1 - p)ä 0 -(? + u) 0 0 ? ? ? ? ? ?0 0 á ? -(ó2 + u) 0 ? ? ? è 0 ó1 0 ó2 0

The characteristic equation of this matrix is obtained by computing det(ëI6 - J(î0)) = 0

det =

? ? ë + cf 0 -â1(1 - è)(1 - ø)S(0) -â2(1 - è)(1 - ø)S(0) 0 0 ? ? ? ? ?0 ë + ä â1(1 - è)(1 - ø)S(0) â2(1 - è)(1 - ø)S(0) 0 0 ? ? ? ? ? ?0 pä ë + (ó1 + á + u) 0 0 0 ? ? ? ? ? ?0 (1 - p)ä 0 ë + (? + u) 0 0 ? ? ? ? ? ?0 0 á ? ë + (ó2 + u) 0 ? ? ? è 0 ó1 0 ó2 ë

det(ëI6 - J(î0)) = 0 This means

ë(ë + U)(ë + X)[ë³ + ?1ë² + ?2ë + ?3]. (2.9)

Master's thesis II ? Molecular Atomic Physics and Biophysics Laboratory-UYI ? YAMENI STEINLEN DONAT D (c)2021

2.4. LOCAL ASYMPTOTIC STABILITY OF DISEASE-FREE EQUILIBRIUM (DFE) OF THE MODEL (2-2) 24

We asked, in order to simplify the calculations:

{	U = cf, V = ó1 + á + u, W = ? + u. Y = ó2 + u.

The first three eigenvalues are:

ë1 = 0, ë2 = -cf, ë3 = -(ó2 + u). (2.10)

The three other eigenvalues are obtained by solving

ë3 + ?1ë² + ?2ë + ?3 = 0, (2.11)

where

{

?1 = V + W + ä, ?2 = (V + W)ä + ä(1 - è)(pâ1 + (1 - p)â2), ?3 = V Wä(1 - è)Rc.

(2.12)

According to the ROUTH-HURWITZ, the solutions of (2.9) have positive real parts when :

?1 > 0, ?2 > 0, ?3 > 0, et ?1?2 > 0. More clearly,

?1, ?2, ?3 > 0 when R_c < 1, This means that ?1?2 > ?3

All calculations done, we see clearly that ?1?2 > ?3.

?1?2 > ?3 when R0 < 1

So î0 is locally asymptotically stable.

2.5. GLOBAL ASYMPTOTIC STABILITY OF THE DISEASE-FREE EQUILIBRIUM OF MODEL (2.2) 25

2.5 Global asymptotic stability of the disease-free equilibrium of model (2.2)

Theorem 2.4. The endemic equilibrium î^* = (S^*, E*, _I*nd, Id^*,Q^*,R^*) of the model exists and is globally asymptotically stable when R0 > 1 .

Proof. To demonstrate the global stability of the endemic equilibrium, we construct a Lyapunov function [25, 26],

æ = X1E + X2Ind + X3Id + X4Q. (2.13)

æ = ₍ëâ1(1 - è)(1 -ø)p₊ cf(ó1 + á + u)

Where

ëâ2(1 - è)(1 - ø)(1 - p) ëâ1 ëâ2

)E + cf(ó1 + u + á)Ind + Id, (2.14)

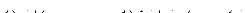
cf(? + u) cf + ?

æÿ = ₍ëâ1(1 - è)(1 - ø)p cf(ó1 + á + u) +

ëâ2(1 - è)(1 - ø)(1 - p) ëâ1

) E^ÿ+ ÿInd+ ëâ2 ^ÿId. (2.15)

cf(? + u) cf(ó1 + u + á) cf(? + u)

ëâ2(1 - p)

let's replace the derivatives of ^ÿE, _ÿInd, ^ÿId in the expression(2.12), we obtain:

(2.16)

æÿ =[ëâ1p

cf(ó1 + á + u) +

cf(? + u) ](1 - è)(1 - ø)(â1Ind + â2Id)(1 - è)(1 - ø)

(1 - è)(1 - ø)ëâ1 cf

Ind - (1 - è)(1 - ø)ëâ2 cf

Id.

Master's thesis II ? Molecular Atomic Physics and Biophysics Laboratory-UYI ? YAMENI STEINLEN DONAT D (c)2021

æÿ = [Rc](â1Ind + â2Id) - (1 - è)(1 - ø)ëâ1 cf

Ind - (1 - è)(1 - ø)ëâ2 cf

Id. (2.17)

from where

æÿ = [Rc](1 - è)(1 - ø)(â1Ind + â2Id) - (1 - è)(1 - ø)ëâ1 cf

Ind - (1 - è)(1 - ø)ëâ2 cf

Id. (2.18)

Thus æ < 0 if and only if R_c < 1, and if æ = 0 and if E = Ind = Id = 0 therefore æ is a lyapunov function for the system (2-2). Thus it follows by the La Salle invariance principle [27] that the DFE of model (2-2) is globally asymptomatically stable when R_c < 1.

2.6. CONCLUSION 26