Analyse des séries chronologiques. les modèles ARCH et GARCH

1.4.2 Modèle non linéaire

Par conséquent, l'hypothèse de processus ARMA stationnaire ne per-met pas de prendre en compte d'une part les mécanisme d'asymétrie et d'autre part les rupture de forte amplitude. D'oñ la nécessite d'aller vers des modélisations non linéaires. L'espérance conditionnelle E (Xt/Zt_1) est la meilleurs approximation au sens de l'erreur quadratique moyenne de t par une fonction des valeurs passés. Il existe une infinité de processus non linéaire susceptible de représenter les propriétés des séries financières. Compbell, Lo et Mackinlay [1997] ont proposé le cadre suivant pour décrire un processus non linéaire :

Xt = g ( t-1, t-2,...) + h ( t-1, t-2,...)

on la fonction g(.) correspondant a la moyenne conditionnelle du processus X et on la fonction h(.) correspondant a un coefficient de proportionnalité entre X et le choc _t cela permet de classifier les processus non linéaire en deux parties :

1) Processus non linéaire en moyenne pour lesquelles g(.) est non linéaire.

2) Processus non linéaire en variance pour lesquelles h(.)est non linéaire.

Cette classification permet de regrouper la plupart de modèles non linéaire. Dans ce domaine le papier de Engle [1982] << Autoregressive Conditional Heteroskedasticity with Estimates of the variance of UK inflation -Economica->> a ouvert la voie a la modélisation ARCH et a ses nombreux développements. C'est précisément sur cette voie que mon document portera par l'essentiel. Mais avant cela, on va présenter un modèle non linéaire portant proche des modèles ARCH.

Modèle BL <<Granger et Anderson [1978]>>

Les modèles bilinéaires présente la particularité d'être a la fois linéaire en X et mais de ne pas d'être a ces deux variables prise conjointement. Un modèle BL d'ordre, noté par le signe BL (p, q, P, Q), s'écrit ainsi sous la forme :

Xt = , + X p cbiXt_ + X q j t-j + _XP X Q ~ijXt~i tj (1.1)

i=1 j=0 i=1 j=1

'y (h) =

~ 2 + A2E (X2 ) .2 si h = 0 t_2 0 si h ~

1

avec 0 = 1, (c_p, q, APi, AiQ ) E ^*4, V (i, i) et on €t désigne un bruit blanc éventuellement gaussien, c'est a dire un bruit blanc fort, cette l'hypothése assure l'existance de la variance. Certain des processus bilinéaires ont des proprietés proches de celles des modèles ARCH que nous étudions dans ce document.

Exemple 1.4.1 Comsidéroms um cas particulier de processus BL (0, 0, 2, 1) de type:

Xt = €t + A Xt_2 €t_ (1.2)

on A E et €t est identiquement indépendante distribué (0, cr²). Ce

processus est centré, puisque le bruit est indépendant du passé (donc coy (€t_1,Xt_2) = 0),

E (Xt) = E (€t) + A E (Xt_2 €t-1)

= E (€t) + A E _{(Xt_2)} E (€t-1) = 0.

Sa fonction de d'autocovariance est donné par:

'y (h) = E (Xt Xt_h)

= E [(€t + AXt_2 €t-1) (€t--h + AXt_2_h €t_1_h)] = E (€t €t--h) + A²E (Xt_2 €t--i Xt_2_h €t_1_h) +AE (Xt_2 €t-1€t--h) + AE (Xt_2_h €t-1--h €t)

pour h > 1, il n'apparait aucun terme en €2 t_h et puisque l'opérateur espérance est linéaire, la fonction 'y (h) est par conséquant nulle. En revanche, pour h = 0, on a :

'y (0) = E (€2 ) + A2E (X2 )

) E (€2

t t_2 t_1

= a² + A2E (X2 ) a2

t2

Ainsi la fonction générale d'autocovariance s'écrit :

La variance marginale de ce processus est V (Xi) = 2

1_A2a2. Tl existe

une solution stationnaire du seconde ordre de l'équation (1.2) a condition A²cr² < 1. Paralelement, la variance conditionnelle du processus X se dérive directement a partir de l'équation (1.2) :

]

V (Xt/Xt_2) = 2 [1 + A2X2 t_2

La variance conditionnel le du processus X dépend des valeurs passées de ce processus. On retrouve un effet de type ARCH. Ceci illustre le fait que plusieurs modélisations non linéaires peuvent être envisagées si l'on souhaite modéliser la dynamique dans la volatilité conditionnelle.

Exemple 1.4.2 On vérifie sur le graphique (1.1) que le modêle BL BL(0, 0, 2, 1) avec A = 0.2 est capable de générer des cluster de volatilité comme ceux observés sur données financiêres.

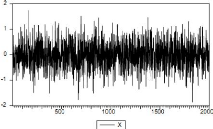
Figure 1.1 : Simulation d'un processus
BL(O,O,2,1).

Modèles TAR

Les modèles autorégressifs a seuil ou TAR ont été proposés par Tong [1978]. Tlles a introduits comme des approximations discrètes des modèles non linéaires. Tls permettent de reproduire des phénomènes tels qu'un cycle limite.

Supposons que le processus Yt vérifie au temps t une équation parmi plusieurs équations différente selon la valeur d'une variable (autre que Yt).

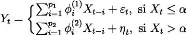
Chaque equation correspond a un regime. Dans le cas d'un seuil unique et d'une variable Xt,

Exemple 1.4.3 Considérons le cas de modeles AR (1) avec un seuil unique

{0⁽¹⁾Xt-i + Et, si Xt_i < a

Xt =

Tong a considers l'existance de plusieurs seuils. La variable Xt, est une variable exogene, soit une variable (Yt) retardée (Yt_d). Dans ce dernier cas, on parlera eventuellement de modele SETAR. Il est a noter que les bruits Et et n_t sont independants et peuvent etre de variance differente.

0⁽²⁾Xt-1 + Et, si Xt_1 > a

avec le même bruit. Une condition nécessaire et suc/cante d'existence d'une solution stationnaire et 0⁽¹⁾ < 1, 0⁽²⁾ < 1 et 0(1)0(2) < 1.

La série ci-dessous correspond a une simulation de la série

--0.2 Xt_1 + Et, si Xt_i < 1

Xt =

0.9 Xt_1 + Et, si Xt_i > 1

avec un bruit blanc gaussien, centré réduit,

Figure 1.2 : Simulation de processus TAR.

Ce type de processus, la aussi, permet d'avoir des queues de distribution plus épaisses (en l'occurence ici pour les fortes valeurs de Yt - queue a droite).

Er 1 01) Xt__z + Et, si Xt < a

{ Xt

Yt =

r 4

²⁾Xt

_

i +

n

_t, si > a

Une écriture équivalente du modèle a seuil a deux régimes, avec un seul reatard, ou une seule variable exogène ( Xt ou Yt_i), est la suivante

Y=

+

0

⁽²⁾Xt

_

i + si Xt >

a,

{

6 ^.₁ #177; 0¹⁾ Xt_i #177; E_t, Si X_t <

cela équivalent a

Yt = (81 + 0⁽¹⁾Xt-i 1 lix_t<_a + (82 + 0⁽²⁾Xt-i 1 lix_t>_a + ut,

on (ut) est une séquence de bruits indépendants, dont la variance est de la forme

V (ut) = cr,²1Ex_t<_a + o-²,₇1Ex_t>_a.

Les modeles SETAR

Toutefois, dans cette classe de modèles, les travaux ont dans leur trés grande majorité portè sur la sous-classe des processus TAR et tout particulièrement celle des SETAR certainement en raison de moindres dificultés d'estimation. Ainsi, un SETAR a un seul changement de régime aura pour écriture :

61 + Er 1 0(¹⁾ Xt--i €it, si Xt_d < ~

Xt = 2

+ (2)

i Xt~i + E2t, si Xt_d > ~

et plus généralement, un SETAR (K, p1,..., pk, d) s'écrira :

Xt =

XK k=1

+

Pk i=i

)^,0^1°) iXt--i + Ekt x E (Xt-d E Rt)

on

{1 si Xt_d < ~

lit =

0 si Xt_d > a

Exemple 1.4.4 La Figure représente le graphique des données simulées provenant du modèle AR (1) et du modèle SETAR. Il s'agit de modèles simulés avec 200 observations et avec les paramètres suivants :

- pour le modèle AR (1) : Xt = 0:5 Xt_i + Et

- pour le modèle SETAR : Xt = -- 0.3Xt_1 (1 -- + Et

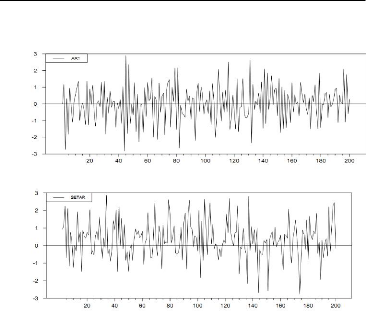
Figure 1.3 : Comparaison entre le processus AR et SETAR.

Exemple 1.4.5 Si on fait une analyse visuelle des deux graphiques, on constate que le pattern de ces deux modéles est différent. Une première différence est l'échelle des valeurs simulées qui est plus grande pour le modéle AR (1). Une deuxiéme différence vise la moyenne et la variance de la variable dépendante des modéles. L'analyse descriptive présentée au Tableau suivant permet de constater que la moyenne du modéle AR (1) est trés proche de zéro et plus petite que celle le modéle SETAR, mais sa variance est plus grande que celle du modéle SETAR. Les valeurs de skewness et d'excés de kurtosis permettent de rejeter l'hypothése de normalité pour les deux modéles.

	AR(1)	SETAR
Moyenne	0.0483*	0.4069*
Variance	1.8619*	1.0854*
Skewness	-0.1607*	0.3703*
Kurtosis(Exc.)	-0.2268*	-0.0043*

Table 4.1 : Analyse descriptive pour les modéle AR (1) et SETAR.

Note : *indique que les tests sont significatifs a un niveau de con/lance de 95%.