Analyse des séries chronologiques. les modèles ARCH et GARCH

Chapitre 2

Modèles ARCH et GARCH

2.1 Modèle ARCH

Dans le but de palier aux insuffi sance des représentations ARMA(p, q) pour les problèmes monétaires et financiers, Engle propose une nouvelle classe de modèles autorégressifs conditionnellement hétéroscédastiques (ARCH) apte à capter le comportement de la volatilité dans le temps. Le modèle

est formé de deux équations. La première met en relation le rendement et certaines variables qui l'expliquent et la seconde modélise la variance conditionnelle des résidus. Le principe proposé par Engle consiste à introduire une dynamique dans la détermination de la volatilité en supposant que la variance est conditionnelle aux informations dont nous disposons. Il avance une spécification ARCH(p) on le carré des innovations, c'est-à-dire la variance du terme d'erreur au temps t, dépend de l'importance des termes d'erreur au carré des p périodes passées. Le modèle ARCH(p) permet de générer des épisodes de volatilité importante suivis d'épisodes de volatilité plus faibles.

2.1.1 Definition et representation

Soit (Xi) un processus AR(1), tel que X = 8+a Xt_1 +"t, avec a < 1 et "t ~ Al (0, cr²) est un bruit blanc gaussien.

Alors, La moyenne et la variance inconditionnelles de X s'écrivent :

8

E (Xi) = 1 - a

₈2

et

V (Xt) = 1 - a2

Aussi :

( )

E Xt/Xt_1= Et_1 [Xi] = 8 + a Xt_1

La moyenne conditionnelle de Xt dépend de l'information disponible au temps t - 1 et n'est pas nécessairement constante. Par contre, la variance conditionnelle est fixe et ne dépend de l'information disponible au temps t - 1 en raison de l'hypothèse de constance de la volatilité :

( ) ( )

V Xt/Xt_1 = E (Xi - E (Xt))² /Xt_i

( )

= E €2 t /Xt_i = 2

En fait, l'hypothèse que les résidus soient des bruits blancs forts nous amène a ce résultat. Un bruit blanc fort implique que les residus ont une moyenne nulle et ils sont non correlés dans le temps. De plus, tout comme la variance inconditionnelle, la variance conditionnelle est constante. Cette dernière condition est peu réaliste parce que la variabilité dans le temps des variances est un fait stylisé bien établi en finance.

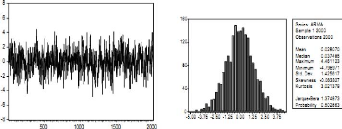
Exemple 2.1.1 La figure suivante présente une simulation d'un processus AR(1) :

Figure 2.1 : Simulation d'un processus AR (1).

En effet, le processus AR(1) est un processus gaussien : les queues de distribution sont moins épaisse que les queues observées sur la variance de l'indice CAC40 et on n'observe pas de période de haute volatilité. Les modêles ARCH (simulé ci-dessous) permettent, eux, de mieux prendre en compte ce genre de comportement :

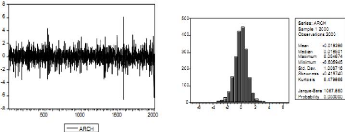
Figure 2.2 : Simulation d'un processus ARCH (1).

Les queues de distribution peuvent être plus épaisse que celle des lois normales (kurtosis de 6,47 avec les paramétres choisis), et on observe, comme sur les données empiriques, des zones de forte variabilité (volatilité).

Commançant par présenter le modèle ARCH(1).

Modèle ARCH(1)

Supposons que la variable Yt peut être expliqué dans un modèle dynamique linéaire avec les variables prédéterminée X et le vecteur de paramétres /,

Yt = X⁰ _t + "t (2.1)

on X est le vecteur des variables exogènes et correspond aux variables expliquant les rendements, inclus les valeurs décalé de variable dépendante et _t est un vecteur d'espérance nulle et de variance cr². On suppose que "2 _t suit un processus autorégressif AR(p)

"2 t = o + çb1€2 _t1 + ~ ~ ~ + p"2 _tp + Vt (2.2)

avec vt est un bruit blanc. L'ensemble d'information _It1 contient tout les informations qui est disponible a savoir les donnees de rendements à l'instant t -- 1, ainsi It1 = {Y_1, Yt-2, _;Xt_1, Xt_2, --}. Si le vecteur des parametres est connu, cet ensemble d'information contient egalement tous les residus a l'instant t -- 1, puisque

st-i = Yt-t -- Yt_t_r3, i = 1, 2, ...

La variance conditionnelle de 4, _{t ;}peut etre ecrit comme suit :

ht = V = E [E? (2.3)

donc Et/It_1 s Al (0, hi) :

L'idee d'Engle, mettait la variance conditionnelle de la serie des carrees des erreurs comme une fonction des erreurs retarde, de temps, de parametre et variables previsible :

{01 = 0^-2 (Et-1, Et-2, ... , t, 13) Et = nt ht, nt est i.i.d

avec E (rat) = 0 et V (rat) = 1. Il choisit une forme de fonction pour 14 tel que 4 = c+Eⁱ:_₁ cbiE?_i, avec c > 0 et cbi > 0 pour i = 1, 2, ... ,p et c, {ci}P₁ sont des constantes. Cette condition est necessaire pour 4 soit non negative. On obtient le modele ARCH(p) , suivant :

Et nt ht = nt

u uc v +

X p i=i

i"2 ti

on nt est bruit blanc faible, tel que E (ra_t) = 0 et V (rat) = ² ~: Definition 2.1.1 Un processus Et satisfait une representation ARCH(1) si

Et =lit ht (2.4)

avec

ht = c + 1"² (2.5)

t1

et oit _lit est bruit blanc faible, tel que E (ra_t) = 0 et V (rat) = ² ~:

Dans ce systeme, le processus Et est caracterise par des autocorrelations nulle E (EtE₈) = 0 pour t =6 s ce qui signifie que les termes d'erreurs Et sont non correles dans le temps. En effet, Et reste un bruit blanc mais dit faible. Un bruit blanc faible implique que les residus ont une moyenne nulle et ils

sont non corrélés dans le temps. Ainsi, la variance conditionnelle varie dans le temps, mais Et est non conditionnellement homoscédastique, c'est-à-dire qu'il y a l'existence d'une variance inconditionnelle finie.

On peut établir des résultats intéressants, nous pouvons écrire le modele ARCH sous deux autres formes. Prenons un modele ARCH (1) pour les illustrer.

1. Forme d'équilibre :

4 = .² + 01 (4_1 - a²)

Sachant que a² = 1-01, c nous retrouvons la forme habituelle du modele ARCH (1) ainsi :

14 = 1 + 01 (Et-1 C C 01 1 -- 01 )

C

2

= + 01Et-1 ~

1 -- 01 1 1C -- 01

= C + 014_1.

2. Autorégressive dans les erreurs au carré

"2 t = h2 t + Vt

oil vt = 4 - N.

Et en ayant les informations disponibles jusqu'au temps t-1 : E [vt/It_i] = E [Et/1^-t_1] -- E [ht/1-t_1] = ht2 -- ht2 = 0 est processus d'innovation pour

E?. Ainsi cette écriture précédente correspondant çà celle d'un processus AR (1) sur le carré E?

Et² = C + 01E²t--1 + Vt- (2.6)

On sait que ce processus Et est stationnaire au seconde ordre si et seulement si 1011 < 1, c'est à dire que la variance marginale est constante. Exemple 2.1.2 Les graphiques montrent l'évolution des processus Et dans

le cas d'un modèle ARMA a gauche, d'un modèle ARCH (1) au centre, et du rendement de l'indice CAC40 a droite.

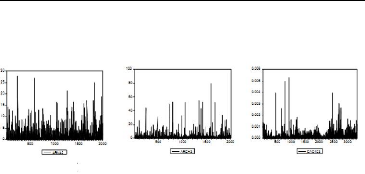
Figure 2.3 : L'^~evolutions de processus E2 t .

Exemple 2.1.3 Les graphiques ci-dessous permettent de comparer un processus AR (1) et un processus ARCH (1)

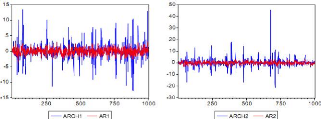
Figure 2.4 : Comparaison entre les processus AR (1) et ARCH
(1).

On peut déduire de ces différentes écritures, un certain nombre de propriétés qui pourront être étendues au cas des processus ARCH (p).