IV.2. Un exemple de régression PLS sur variables
explicatives orthogonales
La relation entre Y et les trois variables explicatives
importe peu. Mais en revanche, nous avons choisi trois variables explicatives
complètement orthogonales les unes par rapport aux autres.


Partie 2 : Utilisation de la régression PLS sur des
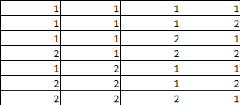
cas limites Voici les statistiques des différentes séries
:

Et la matrice des corrélations :
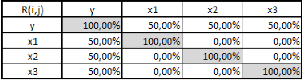
On observe donc que la variable Y est corrélée
à 50% à chacune des trois variables explicatives, qui elles ne
sont pas du tout corrélées entre elles.
Si on effectue une régression PLS à une
étape, on obtient le modèle suivant : y = 0.5*x1 + 0.5*x2 +
0.5*x3 -- 0.75
Le coefficient de détermination de la régression
est de 75%.
On constate que le modèle reste inchangé et que
le résultat ne s'améliore pas selon que l'on passe à une
régression PLS(2), PLS(3), ou qu'on pratique une régression
linéaire multiple.
On constate également que le coefficient de la
régression (75%) est égale à la somme des coefficients de
corrélation des différentes variables explicatives avec la
variable expliquée, élevés au carré :
(0.5)2 + (0.5)2 + (0.5)2 = 0.75. Cela ne peut
être le cas que lorsque les variables explicatives sont orthogonales, ou
du moins quand chaque variable explicative explique sa propre part de la
variance de Y, sans empiéter sur l'explication livrée par les
autres. Chaque variable explique donc 25% distincts de la variance de
Y.
IV.3. Conclusions
Si les variables explicatives étaient liées les une
aux autres, il y a de fortes chances que plusieurs de ces variables
expliqueraient des fractions identiques de la variance de Y.
Prenons un cas extrême qu'il n'est pas besoin
d'illustrer pour comprendre : Soit Y une variable expliquée,
corrélée à 100% à ses deux variables explicatives,
elles-mêmes alors forcément corrélées entre elles
à 100%. Le coefficient de régression ne saurait dépasser
100% et être égal à 200%. Les deux variables expliquent
parfaitement Y individuellement. L'ajout de l'autre variable n'apporte donc
rien en qualité de la
régression, puisqu'elle explique exactement la même
fraction (ici, 100%) de la variance de Y.
Si on reprend notre analyse «
Poids/Taille/Activité/Calories », on s'aperçoit que si on
fait la somme des corrélations au carré variable
expliquée/variable explicatives, on obtient : 89.84%2 +
4.68%2 + 71.77%2 = 132.44%. Il est donc évident
que les variables explicatives sont corrélées entre elles, et
qu'il y a des « recoupements » au niveau de leur pouvoir explicatif
respectif de la variance de la variable Poids, puisque, dans le meilleur des
cas (régression linéaire multiple), on obtient un coefficient de
détermination de la régression de 98.08%.
On voit donc que le coefficient de la régression peut
être supérieur ou inférieur à la somme des
coefficients de détermination variable expliquée/variables
explicatives :
- Supérieure lorsqu'il y a une compensation d'effets de
plusieurs variables explicatives.
- Inférieure quand les variables explicatives expliquent
des fractions identiques de la variance de la variable expliquée.
Bien entendu, les deux phénomènes peuvent se
produire conjointement et il est alors très difficile de s'y
retrouver.
Toujours est-il que la régression PLS, à
l'étape 1, passe complètement outre la
multicolinéarité des variables. A l'étape 2, c'est plus
délicat, car on commence à s'intéresser aux relations
entre les résidus, délaissés par la «
régression brutale » de la première étape. On
n'explique pas encore toute la relation (sauf s'il n'y a que deux étapes
possibles), puisqu'on ne s'intéresse qu'aux covariances des
résidus des variables explicatives par rapport à la variable
expliquée (on ne s'intéresse pas aux relations des résidus
des différentes variables explicatives entre eux). On procède
étape par étape. Lorsqu'il y autant d'étapes que de
variables explicatives, il n'est pas possible de trouver des relations
supplémentaires entre les résidus.
Pourquoi cette convergence entre régression PLS(p) et
régression linéaire multiple ? Parce qu'il est impossible de
former plus de « p » composantes indépendantes à partir
d'un sous-espace comprenant « p » variables. Lorsqu'on en arrive
à « p » composantes, on a forcément pris en compte
toute l'inertie des variables explicatives. Comme, à la «
pième » étape, toute l'inertie a été prise en
compte, et qu'aucun pouvoir explicatif supplémentaire n'a
été créé (chaque composante étant
formée à partir des « p » variables, elle ne peut
apporter aucun pouvoir explicatif n'existant pas dans ces « p »
variables), on ne peut obtenir résultat qui soit meilleur ou moins bon
que celui obtenu par la méthode des MCO, puisque finalement, on utilise
la méthode des MCO pour régresser Y par rapport aux composantes
t1, F, tp.

53
Le résultat sera forcément égal. La
régression PLS(p) est l'équivalent strict d'une régression
linéaire multiple au sens des MCO. Les étapes
précédentes peuvent donc être vues comme des
régressions linéaires multiples partielles, puisqu'on prend
progressivement en compte l'inertie des variables explicatives. En fait, on la
prend « partiellement » en compte, avant de faire une
régression par la méthode des moindres carrés ordinaires.
D'où la signification des initiales de la régression PLS :
Partial Least Squares, c'est-à-dire les « moindres carrés
partiels ».
La régression PLS est donc une forme de
généralisation de la méthode des MCO.
| 

