1.C.3. Rapport d'acceptation
De tous ce que nous avons jusqu'ici mentionné comme
élément important pour l'obtention rapide et efficace d'un
système à l'état d'équilibre, nous avons pu
généré un processus de Markov et avec ce dernier, nous
avons pu retrouver de nouveaux états avec une probabilité. Mais
cependant, il est difficile pour nous de prévoir le processus de Markov
approprié si nous nous trouvons dans un état donnée,
à sa bonne probabilité, et recherchons l'état suivant.
Bien qu'il soit encore possible d'utiliser les conditions suscitées,
nous pourrions ainsi suggérer plusieurs processus mais jusque là
sans pouvoir avoir la bonne probabilité de déclenchement, c'est
à dire celle nous permettant de transiter vers un état suivant
tout en respectant les équations (1.34) et
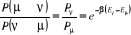 (1.42). (1.42).
La bonne nouvelle cependant est que nous n'aurions pas
à faire cela ! En réalité, il y'a dégât
lorsque nous nous laissons le choix de n'importe quel algorithme pour
générer de nouveaux états et de ce fait il est
nécessaire d'avoir une probabilité de transition souhaitée
par introduction d'une condition d'acceptation du taux de transition.
L'idée cachée derrière cette acceptabilité est la
suivante :
Nous mentionnions précédemment que nous
prévoyons introduire une probabilité de transition de base 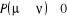 si nous le voulions. En posant í = u dans l'équation
(1.42), nous obtenons une tautologie (1 = 1). Ceci voudrait souligner que la
condition de balance détaillée est toujours
vérifiée pour si nous le voulions. En posant í = u dans l'équation
(1.42), nous obtenons une tautologie (1 = 1). Ceci voudrait souligner que la
condition de balance détaillée est toujours
vérifiée pour 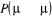 quelque soit la valeur de cette probabilité. Nous avons encore
une certaine flexibilité sur comment nous choisirons les autres valeurs
de quelque soit la valeur de cette probabilité. Nous avons encore
une certaine flexibilité sur comment nous choisirons les autres valeurs
de 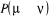 pour pour . Nous pouvons donc ajuster la valeur de n'importe quelle . Nous pouvons donc ajuster la valeur de n'importe quelle 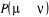 telle que la règle de fermeture (1.34) soit
vérifiée par simplement compensation de cet ajustement avec un
autre ajustement équivalent mais opposé telle que la règle de fermeture (1.34) soit
vérifiée par simplement compensation de cet ajustement avec un
autre ajustement équivalent mais opposé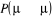 . La seule dont nous avons à observer est que . La seule dont nous avons à observer est que 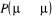 ne passe jamais hors de ses limites (soit ne passe jamais hors de ses limites (soit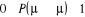 ). Si nous faisons cet ajustement, nous pourrions ainsi nous arranger
pour que l'équation (1.42) soit satisfaite en faisant un changement
simultané aussi sur ). Si nous faisons cet ajustement, nous pourrions ainsi nous arranger
pour que l'équation (1.42) soit satisfaite en faisant un changement
simultané aussi sur 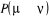 et alors l'on aura conservé leurs rapports. et alors l'on aura conservé leurs rapports.
Autrement dit, ces conditions nous donnent assez de
liberté sur les possibilités d'opérer des transitions sur
chaque site aux probabilités que nous souhaitons. Pour voir cela,
décomposons le rapport de transition en deux parties, soit 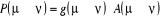 où où 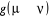 est la probabilité sélective (ou la probabilité
d'un état initial u de donner en fin d'étape un autre état
í) et est la probabilité sélective (ou la probabilité
d'un état initial u de donner en fin d'étape un autre état
í) et 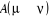 étant le rapport d'acceptation. étant le rapport d'acceptation. 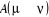 (Tel que (Tel que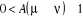 ), nous indique si nous devons commencer sur un état donné
u. Le choix de sa valeur nous est aussi libre. Choisir ), nous indique si nous devons commencer sur un état donné
u. Le choix de sa valeur nous est aussi libre. Choisir 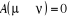 est équivalent à dire la certitude est équivalent à dire la certitude 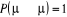 qui n'est cependant pas un cas que nous rechercherons. Il est donc
à proscrire ! De ce qui précède, nous avons aussi une
totale liberté sur le choix de qui n'est cependant pas un cas que nous rechercherons. Il est donc
à proscrire ! De ce qui précède, nous avons aussi une
totale liberté sur le choix de 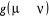 depuis la contrainte (1.42) qui fixe le ratio depuis la contrainte (1.42) qui fixe le ratio
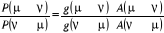 (1.43). (1.43).
Remarquons que 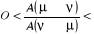 ? ? et et peuvent prendre n'importe qu'elle valeur souhaitée. peuvent prendre n'importe qu'elle valeur souhaitée.
Notre contrainte supplémentaire donnée par la
relation de fermeture (1.34) sera aussi satisfaite étant donnée
que la somme limitera à l'état de la chaîne de Markov
où nous avons commencé la sommation. Le cycle peut donc
être déterminé à n'importe quelle niveau !
Ainsi, dans le but de créer notre algorithme de Monte
Carlo, nous créerons un algorithme qui générera les
états successifs simplement avec les données de 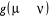 et nous sélectionnerons ensuite les états qui nous sont
utiles par la condition d'acceptation et nous sélectionnerons ensuite les états qui nous sont
utiles par la condition d'acceptation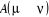 que nous choisirons telle qu'elle satisfera à l'équation
(1.43). Ceci devra satisfaire toutes les requêtes des probabilités
de transition tel que lorsque l'algorithme atteindra l'équilibre, l'on
tirera la vraie probabilité de Boltzmann. que nous choisirons telle qu'elle satisfera à l'équation
(1.43). Ceci devra satisfaire toutes les requêtes des probabilités
de transition tel que lorsque l'algorithme atteindra l'équilibre, l'on
tirera la vraie probabilité de Boltzmann.
Tout ceci paraît plaisant, mais il faudra tenir compte
de ce que si le taux d'acceptation est faible, notre algorithme paraîtra
immobile, ce qui bloquera naturellement l'évolution du système.
Il faut donc trouver un algorithme qui évoluera entres les états
pour un large échantillonnage. Il est impératif à veiller
à raccourcir le temps de traitement de notre matrice. Rechercher donc un
algorithme qui respectera un temps convenable par rapport à
l'échantillonnage qu'on dispose. Il suffit pour cela de remarquer que
l'équation (1.43) ne fixe que le taux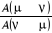 d'acceptation entre deux états distinct dans n'importe quelle
direction avec la contrainte que ce taux est compris entre 0 et 1 bien qu'on
puisse mathématiquement le multiplier proportionnellement par un
coefficient réel. d'acceptation entre deux états distinct dans n'importe quelle
direction avec la contrainte que ce taux est compris entre 0 et 1 bien qu'on
puisse mathématiquement le multiplier proportionnellement par un
coefficient réel.
La meilleure chose que nous puissions faire toutefois est de
le garder, mais de tenir compte des caractéristiques des
différents états en présence dans la probabilité de
sélection  et d'introduire aussi faiblement que nous pouvons le rapport
d'acceptation idéal (c'est à dire celui qui génère
de nouveaux états avec la vraie probabilité de transition). et d'introduire aussi faiblement que nous pouvons le rapport
d'acceptation idéal (c'est à dire celui qui génère
de nouveaux états avec la vraie probabilité de transition).
Le bon algorithme est celui qui conserve le rapport
d'acceptation (c'est à dire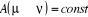 ) ! ) !
| 


