Efficience des marchés et Méthodes de Monte Carlo : Peut-on réaliser des profits anormaux au moyen de l'Analyse Technique ?

B. Les tests d'efficience

Comme nous l'avons souligné précédemment, le cadre théorique de l'hypothèse d'efficience des marchés énoncée par Fama (1965) est longtemps resté trop générique, et par conséquent difficile à tester empiriquement. Ce qui l'a amené à distinguer trois types d'efficience informationnelle des marchés. Nous allons succinctement présenter deux des trois types d'efficience informationnelle, en ayant soin de présenter plus en détail l'efficience faible, qui siège au coeur de notre étude par la suite.

1. L'Efficience forte et semi forte

L'efficience forte stipule que les prix des marchés reflètent à chaque instant l'historique des
prix, l'information publique, ainsi que l'information privée. Les tests mettent en évidence des

rendements anormaux après des décisions importantes concernant le titre considéré, mais non rendues publiques (avant l'annonce d'une OPA mais après sa décision, par exemple).

L'efficience semi-forte stipule elle, que les prix des marchés reflètent à chaque instant, toute l'information contenue dans l'historique des cours boursiers, et toute l'information publique. Les tests tentent de détecter la présence d'éventuels rendements anormalement élevés sur les périodes suivant une bonne nouvelle, ou anormalement faibles sur les périodes suivant une mauvaise nouvelle. Si tel est le cas, l'anomalie d'efficience informationnelle est incompatible avec l'efficience semi-forte.

« Une attitude raisonnable penche en faveur de l'efficience semi-forte des marchés. Selon certaines études, il n'est pas possible de systématiquement tirer profit d'une information connue de tous, pour réaliser des profits anormaux, si l'on tient compte des coûts de transactions, et cela compte tenu de la rémunération du risque encouru ». (Pontrait et Poncet, 2008, p. 35)

2. L'Efficience faible

L'efficience au sens faible postule que l'ensemble des informations disponibles comprend uniquement l'historique des prix, et par conséquent des rentabilités.

Les tests d'efficience faible cherchent à détecter une éventuelle auto-corrélation dans le temps des rendements successifs des titres. S'il y a bien auto-corrélation, c'est-à-dire, si l'on peut prévoir les rentabilités futures à partir des rentabilités passées, alors sous certaines conditions, l'efficience se trouve invalidée. Deux types de tests sont utilisés pour aboutir :

a. Les tests directs

Des tests directs visant à déterminer l'efficience ont été réalisés par Fama & Blume (1966). Leur test de « méthode des filtres » consistait essentiellement à comparer le marché avec un portefeuille naïf. Leurs résultats aboutirent à la validation totale de l'efficience

De même, Hakkio & Rush (1989) ont testé les relations inter-marchés pour déterminer si l'interdépendance des cours permettait d'obtenir des profits anormaux. Ces tests réalisés au moyen de méthodes de co-intégration, ont abouti à l'invalidation de l'Efficience.

D'autres tests directs ont permis de mettre en évidence des « anomalies » d'efficience informationnelle des marchés, comme l'« effet taille » de Banz (1981), l'« effet janvier » de Reinganum (1983), ou encore l'« effet vendredi 13 » de Kolb & Rodriguez (1987)

b. Les tests indirects

Les tests indirects sont en grande partie des tests de marche aléatoires ou de processus stochastiques (cf glossaire) visant à vérifier si les rentabilités futures peuvent être déterminées à partir des rentabilités passées.

Mais parmi l'abondante littérature visant à tester l'efficience faible des marchés, de plus en plus d'études portent sur l'analyse technique, qui par essence n'a d'objet que la réalisation de profits anormaux dans un environnement incertain, au moyen des informations uniquement contenues dans les cours.

? De l'Analyse Technique et de ses critiques...

Depuis son apparition, dont la plus ancienne technique est attribuée à Charles Dow dans les années 1800, l'analyse technique ne fait pas l'unanimité au sein de la communauté académique. Notamment à cause de son manque de rigueur et de cadre théorique. Mais aujourd'hui, ce formalisme prend corps dans un courant de recherche alternatif à la finance néoclassique ou moderne, au sein de la finance comportementale (Orléan, 2008).

Pour proposer une définition de l'analyse technique, citons Benoît Mandelbrot (1997), qui dit de l'ambition de ses praticiens, dans son ouvrage Fractal, hasard et finance p.137 :

« [l]es praticiens de l' « analyse technique » ont l'ambition de prévoir l'avenir sur la base des évolutions du passé. » Ce qui au passage, montre bien que l'analyse est un test d'efficience faible. Puis, il poursuit la phrase suivante en clarifiant :

« Leurs méthodes sont subtiles, mais rarement décrites assez précisément pour permettre une
vérification. Dans les cas exceptionnels où l'on a pu les vérifier, leurs affirmations se sont

révélées sans fondements. Nous le verrons dans le cas des « filtres » proposés par S.S Alexander. »

Dans l'article de Jensen & Benington (1970), ledit Alexander (1961, 1964) est également cité aux côtés de Fama & Blume (1966) pour mentionner qu'effectivement les stratégies de trading basées sur l'analyse technique ne surperforment pas la stratégie Buy & Hold, et est cité aux côtés de James (1968) et Van Horne & Parker (1967) pour mentionner les mêmes résultats, avec des méthodes de moyennes mobiles en particulier.

Mais dans le même article, Jensen & Benington (1970) citent ensuite, Robert A. Levy (1967a, b) qui par une méthode d'analyse technique ainsi nommée des « forces relatives » ou « portfolio upgrading », obtient des résultats significativement supérieurs à ceux de la stratégie Buy & Hold.

Quelle attitude alors avoir face à l'analyse technique? Est-elle une méthode indirecte fiable pour tester l'efficience faible des marchés?

Brock, Lakonishok & LeBaron (1992), ont fait remarquer que l'attitude de l'académie envers la discipline est bien résumée par Malkiel (1981) qui écrivait :

« Obviously, I am biased against the chartist. [...] Technical analysis is anathema to the academic world. Our bullying tactics are prompted by two considerations : (1) the method is patently false ; and (2) it 's easy to pick on. ».

Mais ils concluront en fournissant des résultats sans équivoque sur les performances d'outils simples d'analyse techniques, comme les moyennes mobiles ou les bandes de support et résistances.

Comme une réponse à cette dernière critique de Malkiel (1981), Lo, Maymaysky & Wang (2000), dans « Foundation of Technical Analysis : Computational Algorithms, Statistical Inference, and Empirical Implementation » ont réalisé une approche mathématique très formelle et rigoureuse, de ce qu'il convient encore parfois de nommer dans certains milieux et selon eux, la « voodoo finance ». Ils ne manquent d'ailleurs pas non plus de citer Malkiel (1996), comme ayant largement contribué à cette décrédibilisation de l'analyse technique dans son livre A Random Walk down Wall Street, concluant en ces termes :

« [u]nder scientific scrutinity, chart-reading must share a pedestral with alchemy ».

, avec o. l'écart-type de l'échantillon, et n la taille de l'échantillon.

x -- u0

o.

t=

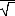
Cependant, Lo et al. (2000) rappellent dans l'article sus-cité, que nombre de contributions ont été faites depuis, en faveur de l'analyse technique. Comme les études de Tabell & Tabell (1964), Trynor & Ferguson (1985), Brown & Jennings (1989), Jegadeesh & Titman (1993), Blume, Easley, & O'Hara (1994), Chan, Jegadeesh, & Lakonishok (1996), Lo & MacKinlay (1997), Grundy & Martin (1998), et enfin Rouwenhorst (1998).

Et faisant référence aux contributions les plus directes dans cette discipline, Lo et al. citent Pruitt & White 1988), Neftci (1991), Neely, Weller & Dittmar (1997), Neely & Weller (1998), Chang & Osler (1994), Osler & Chang (1995), Allen & Karjalainen (1999), et enfin Brock, Lakonishok, and LeBaron (1992), notamment grâce à des méthodes simples de moyennes mobiles pour ces derniers. A cette liste, j'ajoute également Osler (2003).

Brock et al. guideront structurellement l'étude empirique de ce mémoire.

s Méthodes de calcul des significativités des rentabilités

Diverses méthodes de significativités statistiques sont utilisables, afin d'éviter notamment le data-snooping (cf glossaire). Citons à ce titre John D. Lyon, Brad M. Barber, & Chih-Ling Tsai (1999) pour des méthodes de tests sur les anomalies d'efficience à long terme, Robert J. Shiller (1981) sur les mesures de volatilité, et enfin Ryan Sullivan, Allan Timermann, & Halber White (1999), pour des méthodes de bootstraping sur des performances de stratégies type analyse technique.

Globalement, ces articles évoquent les mêmes outils, et dans chaque cas, des p-values, où des probabilités critiques sont obtenues, permettant de valider ou d'invalider l'hypothèse nulle.

i) La t-statistic ou test t de Student : testant l'hypothèse nulle selon laquelle la moyenne x de l'échantillon considéré s'approche d'une valeur théorique ì0, avec une probabilité déterminée par l'intervalle de confiance de la variable x - ì0. L'intervalle de

confiance choisi est souvent de 95% (ou 99%) ce qui autorise une marge d'erreur de 5% (ou 1%)

Le t de Student est alors donné par la formule générale ci-dessous :

ii) Le Bootstraping : Méthode de rééchantillonage de données à partir d'un échantillon initial sans aucune nouvelle donnée, d'où son nom de bootstrap. Ces rééchantillonages se font par simulations probabilistes (dites de Monte-Carlo), ici suivant des modèles de formation des cours boursiers.

Les bootstraps peuvent donc se faire à partir de simples simulations de marches aléatoires, jusqu'à des simulations stochastiques bien plus élaborées, telles que les modèles ARCH ou GARCH. Citons à cet effet Brock et al. (1992). Ces derniers les utilisent tous, sauf le mouvement brownien géométrique.

iii) Le ratio de Sharpe : utilisé pour comparer les performances à celle de la stratégie Buy & Hold, parfois complété par des simulations de type Monte-Carlo. Ryan Sullivan et al. (1999), ont utilisé ce type de méthode pour asseoir la significativité de leurs tests.

S ? R ? r o.

, avec R le taux de rendement de l'indice considéré, r le référentiel de comparaison

choisi, et o. l'écart-type du taux de rendement de l'indice considéré. Dans le cadre des tests d'efficiences faible, il s'agit souvent du rendement de la stratégie Buy & Hold.

iv) Les méthodes de Monte-Carlo :

Elles servent dans les méthodes de rééchantillonage pour un test t de Student, un bootstrap ou un ratio de Sharpe. La littérature est abondante sur le sujet, mais le meilleur exemple d'utilisation de cette méthode dans les tests d'efficience faible est l'étude faite par Brock et al. (1992).

A l'ensemble de ces méthodes, auxquelles s'ajoutent l'ensemble des outils classiques de statistique descriptive, notamment dans le cas d'échantillons gaussien ou supposés comme tels, nous avons trouvé intéressant d'ajouter un test de Bartlett, sur le modèle de Brock et al. (1992).