CHAPITRE 2 : MATERIELS ET METHODES
La démarche de cette méthodologie peut se
décomposer en trois étapes :
1) choix d'une méthode d'expérimentation
2) l'analyse des résultats
3) l'acquisition progressive des connaissances
Choix d'une méthode
d'expérimentation
Le choix d'une méthode d'expérimentation est
tributaire d'une bonne définition de la
problématique à traiter. Tous les facteurs
pouvant avoir une influence sur la réponse doivent être pris en
compte dans l'établissement du plan d'expériences.
Description de problème
D'une manière générale, la description
d'un problème, quel qu'il soit, consiste à répondre
à
un certain nombre de questions que résument la
méthode de SADO connue sous le nom de méthode de
?QQCQQP?( G.Sad et al.,1991).
Ces questions sont les suivantes :
> Q : En quoi consiste le problème ?
> Q : Qui est gêné par le problème ? Qui
est le demandeur de l'étude ?
> C : Combien de cas ? Combien ça coûte ?
> Q : Où cela se passe-t-il ?
> Q : Quand cela arrive-t-il ?
> P : Pourquoi est un problème ?
L'établissement du plan d'expériences
(J.Goupy,2017) afin d'optimiser la réponse consiste en
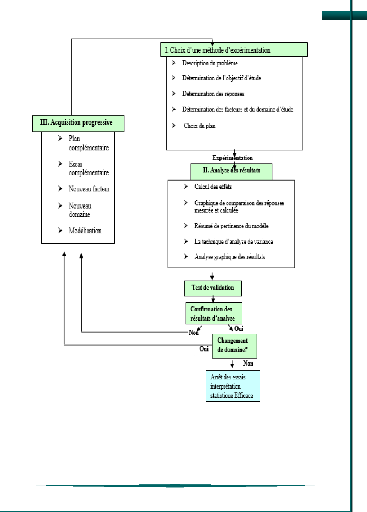
la démarche suivante (figure 8):
27
CHAPITRE 2 : MATERIELS ET METHODES
Figure 8 : L'établissement du plan
d'expériences (J.Goupy,2017).
28
CHAPITRE 2 : MATERIELS ET METHODES 2.3.1.3. Choix du plan
d'expérience
Le choix du plan sera guidé par l'analyse de tous les
points précédents. On distingue plusieurs types de plans :
Les plans factoriels complets à deux
niveaux
Pour ces plans le nombre de niveaux de chaque facteur est
restreint à deux et le nombre des
essais réalisés est égal à
2n (n représente le nombre de facteurs). Le modèle
mathématique postulé relatif à ce plan est le suivant :
y=b0+?bixik+??bijxikxjk+4k
Où,
y : réponse xi, xj : niveau attribuer au facteur i, j
b0 : valeur de réponse au centre du domaine d'étude
bi : l'effet du facteur i
bij : l'interaction entre i et j
åk : résidu (écart)
b- les plans de surface de réponse
Ces plans permettent d'établir des modèles
mathématiques de second degré (modèle quadratique
complet).
y=b0+?bixik+??bijxikxjk+?bikxik2+ 4k
Parmi les plans de seconds degrés les plus employés
citons
> les plans composites centrés
> Les plans de Box-Behnken
> les plans hybrides
29
CHAPITRE 2 : MATERIELS ET METHODES
2.3.1.4. Analyse des résultats de
calcul
De nombreux logiciels commerciaux sont spécialement
conçus pour les plans d'expérience (JMP, Minitab, Statisca,
etc...). Ces logiciels permettent dans un premier temps, de définir la
matrice d'expérience et dans un deuxième temps le traitement des
données expérimentales obtenues. Pour l'analyse des
résultats de nombreuses rubriques existent dans les logiciels traitant
des plans d'expériences (sommaire d'ajustement, analyse de variance,
etc...) qui donnent les informations nécessaires avec une bonne
appréciation des résultats (modèles obtenus).
Graphique de comparaison des réponses
mesurées et réponses estimées
Plus les points du graphique sont proche de la première
bissectrice, plus le modèle rend assez
bien compte des réponses, et vice-versa (figure
9).

s
Réponse (mesurée)
s
s
s
s
s
s
s
ss
s
s
s
Réponse (estimée)
Figure 9 : Graphique de comparaison de
réponse mesurée et estimée
b. Résumée de la pertinence du
modèle (qualité descriptif)
La pertinence de modèle est généralement
vérifiée par le coefficient de détermination
(R2). Ce coefficient varie entre 0 et 1, plus il
est proche de 1 plus les réponses calculées seront fortement
corrélées avec les réponses expérimentales
(J.Goupy, 2017).
2.3.1.5. La technique d'analyse de variance
L'analyse de variance (ANOVA) permet de comparer les variances
des valeurs calculées
par le modèle et les résidus. Cette analyse
constitue un test statistique (test de Fisher-Snedecor) et elle fournit les
réponses aux questions suivantes (K.Sandrine, 2004):
30
| 


