3.4. La géométrie sphérique
Dans la géométrie elliptique, on part de
l'hypothèse que la somme des angles d'un triangle est supérieure
à deux angles droits. Et par un point, il ne passe aucune droite
parallèle à une droite donnée.
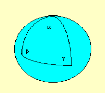
Fig. 3.2. La somme des angles d'un triangle est
supérieure à 180°.
Définition 3.8.
La géométrie elliptique, communément
appelée géométrie de Riemann ou encore
géométrie sphérique est un espace
sphérique à trois dimensions, espace fini et cependant sans
bornes, à courbure régulière, alternative au postulat
euclidien des parallèles.
1 La Grande Encyclopédie Larousse,
p.5386.
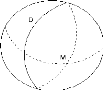
Fig.3.3. Il n'existe aucune droite passant par le point M
et parallèle à la droite D.
Remarque 3.8.
- La géométrie sphérique est bien
représentée par la surface d'une sphère. - Les points sont
les paires de points antipodes d'une sphère.
- Les droites sont les grands cercles (c'est-à-dire dire
les cercles ayant le même centre que la sphère).
3.5. La géométrie hyperbolique et le
logiciel NonEuclid 3.5.1. La géométrie
hyperbolique
Définition 3.9.
La géométrie hyperbolique, communément
appelée Géométrie de Lobatchevski est un espace courbe
où on peut tracer une infinité de parallèles à une
droite donnée et passant par un même point. Dans cette
géométrie, la somme des angles d'un triangle est
inférieure à deux angles droits.
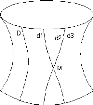
Fig. 3.4. Il existe une infinité de droites qui comme
d1, d2 et d3 passent par le point M et sont parallèles à
la
droite D.
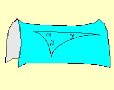
Fig.3.5. La somme des angles d'un triangle est
inférieure à 180°.
Hormis le cinquième postulat, la
géométrie hyperbolique respecte toutes les autres
définitions d'Euclide. Une droite est toujours définie comme la
ligne de plus court chemin joignant deux points sur une surface. Il existe
plusieurs modèles de géométrie hyperbolique à deux
dimensions : le disque de Poincaré, le demi-plan de Poincaré,
...
3.5.2. Le logiciel NonEuclid
Avant de présenter le logiciel NonEuclid,
définissons d'abord ce que c'est une pseudosphère.
Definition 3.10.
Comme la sphère, la pseudosphère peut
être pensée comme une surface de dimension 2. La sphère est
plus petite que le plan: elle est finie, alors que le plan est infini. Une
pseudosphère, elle, est plus grande que le plan. Les deux sont
infinis, cependant la pseudosphère offre plus de place. C'est pourquoi,
on dit que la pseudosphère est d'une infinité plus dense que le
plan.
Puisque la pseudosphère est plus grande que le plan, il
est très difficile de la représenter dans nos dessins
régis par la géométrie euclidienne. Mais il y a une
méthode pour faire entrer une pseudosphère à
l'intérieur d'une région circulaire. Cette méthode est
appelée, Le modèle de Poincaré pour la
géométrie hyperbolique, et c'est le modèle utilisé
par NonEuclid.
Definition 3.11.
NonEuclid est un logiciel qui permet de
représenter l'espace courbe de la géométrie
hyperbolique. C'est donc un modèle de la géométrie
hyperbolique.
Pour construire les segments et droites dans ce modèle,
nous utilisons des cercles orthogonaux au cercle frontière. Ainsi, sur
la première figure ci-dessous les segments sont des arcs de cercles
orthogonaux au cercle blanc. Pour la deuxième figure, A étant le
centre du cercle frontière, les centres des cercles orthogonaux sont
à l'infini, ce sont des droites ....
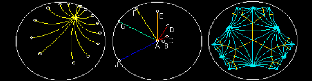
Fig.3.6.1: Segments égaux de même
extrémité.
Fig. 3.6.2: Segments de longueur 0.25, 0.5, 1.0,
2.0, 4.0, 8.0 et 16.0 Unités.
Fig. 3.6.3: Pavage de triangles
égaux.
Quand un point approche du cercle frontière, sa
distance au centre devient infinie. La figure 3.6.1. montre un ensemble de
segments tous de longueur 3.00 unités. Notons que plus le segment est
proche du cercle frontière, plus il apparaît court. Cet ensemble
de segments représente les rayons d'un cercle (ils sont égaux et
ont une même origine). L'ensemble des segments de la figure 3.6.2., ont
un point de départ commun au centre du cercle frontière. AB a une
longueur 0.25 unités. AC une longueur de 0.5 unités. En tournant,
chaque segment est deux fois plus long que le précédent. Les deux
derniers (AG et AJ) semblent avoir la même longueur, pourtant AJ (un demi
pixel de plus) a deux fois la longueur de AG.
Quand on utilise NonEuclid pour marquer des points,
on constate que le curseur ne peut dépasser une distance de 10
unités du centre sans sortir du modèle. Sur un écran, nous
sommes limités à la résolution d'un pixel1.
Cependant, la distance entre le dernier point accessible à
l'écran et la frontière est infinie.
| 


