A nos parents, NGUESHE LUPANZA et NZEBA TSHIALU, nous
dédions ce travail.
REMERCIEMENTS
Au terme de nos études de premier cycle à
l'université de Kinshasa, faculté des Lettres et Sciences
Humaines, Département de Philosophie, nous nous trouvons dans
l'obligation de nous acquitter d'un agréable devoir, celui de remercier
tous ceux qui, de façon directe ou indirecte, ont contribué
à notre formation.
Ainsi, nous témoignons notre reconnaissance
à l'endroit des autorités académiques, des professeurs,
des chefs de travaux et assistants de l'Université de Kinshasa, en
général, et de ceux de la Faculté des Lettres et Sciences
Humaines, en particulier, pour leurs encadrements et enseignements de
qualité.
Nous remercions particulièrement et infiniment
monsieur le professeur MUTUNDA MWEMBO qui, en dépit de ses multiples
occupations, nous a appris la logique et a accepté de guider nos pas
dans l'élaboration du présent travail.
Dans le même ordre d'idée, nous
témoignons notre gratitude envers le professeur PANGADJANGA qui nous a
enseigné la logique ancienne ainsi que le chef de travaux Henri Jacob
NDOBO qui, depuis le premier graduat jusqu'à ces jours, ne cesse de nous
encourager, de nous conseiller et de nous encadrer dans la voie que nous avions
choisie : la logique.
Par la même occasion, nous remercions nos oncles et
tantes ; nos cousins et cousines ; de façon
singulière, nous remercions notre cousin Pascal TSHIALU pour ses
encouragements et ses conseils.
Que tous nos amis : Alain Tshimanga, Ami Daniel
Kamonika, le Pasteur Willy Ngogo, Jimmy Kabamba, Arlette Yoka, Marianne N'yoka,
Belinda Kitoko, Olga Kemi, Marie Ngudia, Papy Matona, Marcel Imboyo, Pembi
Kwete, Hugo Atangongbe, Jonathan Kankonde, Jean Louis Nsimba, Mputu Muyembi,
Misi Mungala, Consolat Mutshipayi, Cimanga Mabika, Felix Kinzini, Thomas
Ndjekambudi, Patrick Bashizi, Rachel Ikongo, Ana Lufuka, Dominique Iyiya,
Nelson Mayele, Willy Bakatuelkeja, Charles Mbadu, Nevil Lubaki, Yvette Liaki,
Tonton Mundabi, Gasky, Mbambi, Dieudonné Ebondo ; se sentent
honorés à travers cette réalisation !
« La logique est la science (semblable)
à la balance (...) or toute science qui n'est pas évaluée
par la balance n'est pas certaines et, en vérité, n'est pas
science. Par conséquent, on ne peut se dispenser d'acquérir la
science de la logique »
Avicenne, le Livre de
science
«Grâce à l'emploi de cet art (la
logique combinatoire), il ne devrait plus y avoir matière à
discussion entre philosophes qu'il n'y en a entre comptables. Il leur suffirait
de prendre en main leur crayon, de s'asseoir devant un tableau et de se dire
mutuellement : " Et bien ! Calculons !" »
Leibniz, l'art
combinatoire
«Les mathématiques que nous avons à
construire sont les mathématiques de l'esprit
humain »
George Boole, les lois de la
pensée
INTRODUCTION
GÉNÉRALE
Au terme de notre premier cycle, où nous sommes
convié à choisir un auteur ou une thématique sur qui ou
sur quoi exercer l'intellect et dont le fruit (de l'exercice)
témoignerait du background accumulé tout au long de notre
parcours universitaire ainsi que d'une certaine maîtrise du domaine qui
est nôtre (la philosophie), il nous est paru propice de cogiter sur la
logique formelle, sur son évolution et sur sa révolution
paradigmatique. Celle-ci, nous l'attribuons, non sans raison, à George
Boole.
D'entrée de jeu, nous pouvons nous demander quel
intérêt peut revêtir un tel thème. En effet, le choix
de ce sujet se justifie pleinement en ce que :
- Ce travail nous présente une certaine
manière, mieux une autre manière d'appréhender la logique
et son histoire.
- Ce travail nous dit de quelle façon George Boole
a rompu avec la tradition aristotélicienne, notamment en identifiant les
structures de la nouvelle logique à celle de
l'algèbre ;
- Boole est, à plus d'un égard, le
père de la logique moderne et son algèbre a des applications
dans plus d'un domaine.
L'objectif que nous poursuivons est très modeste,
à savoir : dégager les principaux cycles de
l'évolution historique de la science logique depuis l'antiquité
jusqu'au dix-neuvième siècle, plus précisément
jusqu'à l'avènement de Boole.
D'emblée, certaines questions surgissent-elles
dans notre entendement. En voici quelques unes :
- Quels sont les grands moments de la logique formelle
depuis ses origines jusqu'au dix-neuvième siècle ?
- Quels sont les apports des uns et des autres dans la
construction de l'édifice de la logique ?
- La syllogistique traditionnelle et la logistique moderne
fonctionnement-elles sur base d'un même paradigme ?
C'est à cette triple interrogation que le lecteur
peut espérer trouver certaines réponses dans les lignes qui vont
suivre
L'hypothèse qui sous-entend cette investigation
est la suivante : la logique moderne opère sur base d'un paradigme
mathématique alors que la syllogistique traditionnelle fonctionne sur
des moules empruntés, sinon similaires à ceux des sciences de la
nature.
Vu la proportion de temps qui nous a est impartie ainsi
que les imperfections inhérentes à notre nature humaine, il nous
a semblé intéressant de circonscrire notre champ de recherche.
Aussi, comme il est indiqué dans le titre de notre travail, nous
aborderons la question de la logique depuis les présocratiques
jusqu'à George Boole.
Ainsi, pour mener à bien cette quête, nous
nous proposons de procéder de manière à la fois
historique, réflexive et critique.
Aussi, nous répartissons cette dissertation en
quatre chapitres. Le premier nous précise les sens des mots que nous
rencontrerons fréquemment dans cette étude ; le
deuxième nous présente la science normale de la logique ou la
syllogistique traditionnelle ; le troisième nous dresse les
portraits de ceux qui ont constitué la science extraordinaire de la
logique ; et le dernier dévoile la révolution proprement
dite de la logique formelle. Bien entendu, nous terminerons par une conclusion
générale.
CHAPITRE PREMIER :
PRECISIONS TERMINOLOGIQUES
Il nous semble impérieux, avant d'entrer dans le
vif de notre sujet, de clarifier rapidement quelques concepts fondamentaux qui
constituent l'objet de notre investigation. Ainsi, ce chapitre comprend-il deux
points essentiels. Le premier se rapporte à l'analyse du contenu du mot
logique et le second nous relève le sens de la révolution
opérée par Boole, à la lumière de la conception de
l'histoire des sciences de Thomas Samuel KUHN.
1.1.
Logique
Pour mieux saisir le sens du terme logique, nous avons
subdivisé ce point en trois moments dont le premier est une approche
étymologique ; le deuxième, une approche
définitionnelle; et le troisième est une approche
mathématique.
1.1.1. Approche étymologique
Etymologiquement, le terme logique dérive du
grec : à la fois du verbe Légein, du substantif
logos et du qualificatif logikê.
Le verbe légein1(*) signifie à la fois dire, exprimer,
réfléchir. Le verbe légein désigne ainsi
une certaine catégorie d'activités qui distingue l'homme des
autres animaux et qui a pour ressort, vraisemblablement, la raison.
Le substantif logos2(*) est également polysémique. Il
désigne ce que nous pouvons traduire par : parole, discours,
argument, recherche, théorie.
Héraclite d'Ephèse ainsi que les
stoïciens donnent à ce mot un sens bien singulier. Selon eux,
Logos, désigne l'Esprit Universel qui gouverne et ordonne le
monde. Mieux, logos désigne l'ordre du monde. Aussi, est-il
qualifié de Loi-mère.(3(*))
Enfin, le qualificatif logikê4(*) signifie simplement ce qui
est relatif au bon sens, ce qui se rapporte à la raison, à
l'ordre du monde.
1.1.2. Approche définitionnelle
proprement dite
Le raisonnement est une propriété
essentielle de l'homme. Aussi, Aristote définit-il l'homme comme
«un animal raisonnable ». Soit le raisonnement
suivant :
Les apôtres étaient
douze.
Or, Pierre était
apôtre.
Donc, Pierre était
douze
Il n'est nullement besoin de disposer de tout un arsenal
des règles syllogistiques pour se rendre compte que ce raisonnement
n'est pas valide. Même celui qui n'a jamais appris la logique
aristotélicienne refusera la conclusion selon laquelle Pierre
était douze. Ce petit exemple nous prouve à suffisance qu'il
existe une sorte de logique naturelle, spontanée, laquelle est conforme
au bon sens naturel. Cette logique spontanée est l'apanage de tout homme
en tant qu'il est homme, c'est-à-dire en tant qu'un être capable
de justifier ses actes, d'une manière ou d'une autre.
Cependant, pour éviter les fallacies et pour de
raison de rigueur, il faudrait recourir à la science logique, laquelle
nous est définie par Joseph DOPP comment : « une
science qui détermine quelles sont les formes correctes (ou valides) de
raisonnement »(5(*)). Une autre définition nous vient de Robert
BLANCHE. Pour ce dernier, la logique est « une théorie du
raisonnement correct et de ses conditions »(6(*)). Signalons aussi la
définition que LALANDE donne à ce terme. Selon lui, la logique
est une : «science ayant pour objet de déterminer, parmi
toutes les opérations intellectuelles tendant à la connaissance
du vrai, lesquelles sont valides et lesquelles ne les sont
pas »(7(*)). En
définitive, la science logique étudie les conditions de
possibilité d'un raisonnement correct.
Précisons que le terme logique est apparu pour la
première fois dans le titre de l'ouvrage de Démocrite (8(*)) (460-371 ACN) : Des
questions de logique, autrement dit des canons, dont ne subsistent que
des fragments. Mais que signifiait le terme logique pour
Démocrite ? Difficile de le savoir. Aristote lui-même n'a
jamais employé ce mot. Il désignait sa science tantôt par
l'adverbe logiquement, tantôt par le terme dialectique.
Kotarbinski nous apprend ce qui suit : « Aristote note que
le créateur de la dialectique avait été Zénon
d'Elée (490-430), et il appelle dialectique l'art de la
spéculation verbale pratiqué par les éléates. Ce
sont les stoïciens qui employaient le terme dialectique pour
désigner l'objet qui nous intéresse »(9(*)).
Au premier siècle avant notre ère, les
élèves d'Aristote publièrent ses écrites relatifs
à ses recherches logiques sous le titre général d'organon.
Mais la question relative à l'appellation de cette science sera
complètement résolue au XVIIIème siècle.
En effet, «c'est KANT (1724-1804) qui forge le terme logique formelle. Il
appelle ainsi le système de la logique existant avant lui, dont
l'essentiel consistait en la syllogistique. Il estime que c'est là un
système achevé, parfait, qui n'a aucune chance de se
développer à l'avenir et lui oppose la logique transcendantale,
qui n'est autre chose que la façon particulière dont il a
développé le système des
catégories »(10(*)).
1.1.3. Approche mathématique
La logique dans un contexte mathématique ne
saurait se comprendre sans la notion d'algorithme. Ce dernier se définit
comme «un semble de règles opératoires dont l'application
permet de résoudre un problème énoncé au moyen d'un
nombre fini d'opérations »11(*) André LALANDE renchérit en ce
sens : «ensemble de symboles et de procédés de
calcul »(12(*)).
Pour information, l'algorithme est une algèbre
inventée par un mathématicien arabe du IXème
siècle (PCN) répondant au nom de AL Kharezmi
(13(*)). Le terme
algorithme serait la déformation du nom de AL Kharezmi.
La logique moderne ou la logistique est donc une sorte
d'algèbre ou de structure algébrique qui s'applique aux
catégories (au sens aristotélicien) de la quantité et de
la qualité. George Boole note à propos que l'algèbre de la
logique est « une méthode qui repose sur l'emploi des
symboles dont on connaît les lois générales de combinaisons
et dont les résultats admettent une interprétation
cohérente »(14(*)).
Depuis le début du 20ème
siècle, la logique se développe sous deux aspects : l'un
est dit syntaxique et l'autre sémantique.
Le point de vue syntaxique considère les symboles
utilisés comme dépourvus de toute signification. Ainsi p ne
sera rien d'autre que la seizième lettre minuscule de l'alphabet
français et ce sera en tant que lettre minuscule qu'elle sera
combinée de telle ou telle façon avec d'autres lettres ou
d'autres signes. Le point de vue syntaxique apparaît ainsi comme un
calcul.
Pour le point de vu sémantique, p désignera
une proposition vraie ou fausse et c'est en tant que proposition vraie ou
fausse qu'elle sera reliée à d'autres propositions. Ce second
point de vue s'offre plutôt comme une langue artificielle, car les
symboles sont considérés comme pourvus de signification.
Voilà ce que nous pouvions dire de l'approche
mathématique de la logique.
I.2. Révolution
paradigmatique
Le contenu du terme révolution et la notion de
paradigme nous viennent de la conception de l'histoire des sciences de Thomas
Samuel Kuhn.
En effet, Kuhn estime qu'à certains moments,
toute science subit une révolution et que cette révolution
comprend essentiellement trois étapes. A savoir : la science
normale, la science extraordinaire et la révolution proprement dite ou
le changement de paradigme opératoire.
«La science normale est la forme la plus courante de
l'activité scientifique »(15(*)). Elle est caractérisée par le fait
qu'elle exploite un paradigme autour duquel se rassemble, à un moment
déterminé, une communauté scientifique également
bien déterminée. Sur ce, Kuhn dit que la science normale
«est une activité de recherche essentiellement régie par des
paradigme collectivement établis ; elle reflète la nature
du paradigme qui la régente et la conditionne »(16(*)).
Quant au paradigme, il peut être compris comme un
modèle (explicite ou implicite) qu'une communauté scientifique
exploite en vue de régler ses activités de recherche. Notons
qu'en science normale, le paradigme est érigé en une tradition
solidement partagée par les membres de ladite communauté. De
cette façon, nous pouvons affirmer que la science normale progresse de
manière cumulative, parce que opérant sur base d'un
modèle unique.
La science extraordinaire est pratiquée dans
l'état de crise qui prélude à une révolution
scientifique. Lorsque le paradigme en cours est constamment confronté
à des anomalies, à des résultats qui ne correspondent pas
aux prédictions attendues de son exploitation, il arrive que ces
anomalies deviennent actives et se développent d'une manière
irréversible et irrésistible. Le paradigme entre alors en crise.
Selon Kuhn, la crise signifie « qu'on se trouve devant l'obligation
de renouveler les outils »(17(*)). C'est alors que prendra place un type de recherche
nouveau, celui de la science extraordinaire. Ce nouveau type de
recherche est caractérisé par le fait que les principes et les
méthodes qui fondent la science en question sont soumis à une
discussion critique de type philosophique, de nouveaux modèles sont
proposés jusqu'à ce que l'un deux finisse par emporter
l'adhésion d'une partie au moins de la communauté qui subit la
crise.
Ainsi, y aura-t-il révolution proprement dite
lorsque la transition de la science extraordinaire aura pris fin,
c'est-à-dire lorsque ladite communauté scientifique abandonnera
l'ancien paradigme pour finalement adhérer à un nouveau qui
déterminera alors la révolution de cette science. Un
véritable bouleversement ! Une rupture !
Nous estimons que la thèse de Kuhn se justifie et
se vérifie à travers l'histoire. Dans les lignes qui suivent,
nous tâcherons d'illustrer cette thèse et de la
démontrer.
CHAPITRE DEUX : LA
SCIENCE NORMALE DE LA LOGIQUE
Nous pouvons beau dire que la science normale de la
logique ou la syllogistique traditionnelle, par rapport à la logique
moderne, est qualitative, non symbolique et qu'elle repose essentiellement sur
le principe du tiers exclu. Cela est certes vrai, mais n'explique en rien le
paradigme qui la rend si différente de la logistique.
Notre thèse est que la syllogistique
traditionnelle utilise un paradigme emprunté, sinon similaire à
celui des sciences de la nature.
En effet, la science logique est
considérée comme l'invention d'Aristote Bien entendu quelques
présocratiques et socratiques ont abordé cette question bien
avant le stagirite. Cependant, il a le mérite d'avoir su
systématiser et ordonner cette science.
Ainsi, pour justifier notre thèse, nous allons
d'abord étudier les présocratiques, ensuite les socratiques, puis
les post-socratiques et, enfin, nous terminerons par les auteurs du
moyen-âge.
II.1. Antiquité
II.1.1. Les
présocratiques
Les présocratiques étaient des
physiologues. Par définition, la physiologie
est « l'étude du fonctionnement normale d'un organisme
vivant ou de ses parties » (18(*)). Là, c'est le sens actuel de ce terme. En
réalité, nos physiologues présocratiques étudiaient
plutôt le « physis » (le monde) pour en
connaître le principe explicatif. Pour les uns, ce principe était
le feu ; pour d'autres, l'être ; pour d'autres encore,
l'atome... même l'un des plus grands mathématiciens de
l'antiquité, Pythagore, s'est adonné à l'étude des
nombres justement pour comprendre l'univers.
Ceci étant, nous allons survoler quelques uns de
ces physiologues par rapport à leur contribution à
l'élaboration de la science logique.
· HERACLITE D'EPHESE (567-480 ACN)
Héraclite part de l'idée selon laquelle le
principe explicatif de l'univers est le feu. Comme toute chose, pense-t-il, est
intrinsèquement constituée de feu et que le feu a la
propriété de tout consumer, il en déduit qu'aucun
être ne peut garder deux fois le même état dans deux moments
différents. Voici sa célèbre
formule : « tout est en flux, tout meut à la
manière d'un fleuve, tout change toujours, rien ne demeure
jamais » (19(*))
c'est pourquoi, dans cette optique, le changement de l'être demeure aussi
longtemps que survit l'être lui-même. Ainsi, la véritable
harmonie naît précisément de la coexistence et de la lutte
des contraires. Quant au logos, c'est-à-dire la loi suprême de
l'univers, loi qui n'a pas créé le feu, mais qui le manipule et
le régit comme un enfant, il se maintient en qualité de loi-
mère.
En logique, la contribution d'Héraclite est
appelée principe de contradiction. Il signifie qu'il est possible de
concevoir à la fois, sous un même angle et dans le même
contexte, « p » et « non p ». En
termes clairs, il est possible qu'une chose soit et ne soit pas à la
fois.
Il nous semble évident qu'Héraclite ait
exploité le paradigme physiologique (au sens présocratique) pour
aboutir à son principe logique,
· Parménide et Zénon d'Elée
Parménide (VIème siècle
ACN) affirme tout le contraire d'Héraclite. Pour
lui, « l'être est et le non - être n'est
pas » ce qui revient à la formulation implicite du principe
d'identité. Ce principe signifie, logiquement qu'un même terme
doit toujours, au cours d'un même raisonnement, représenter un
même concept. Autrement dit, les concepts logiques doivent être
fixes, immuables, car le vrai et le faux sont intemporels, c'est-à-dire
invariables aussi bien dans le temps que dans l'espace.
Quant à Zénon d'Elée
(Vème siècle ACN), disciple de Parménide, nous
disons qu'il nous a offert le premier recours au raisonnement par l'absurde (la
reductio ad absurdum) (20(*)) et nous a fait noter l'impossibilité de
traduire en toute rigueur, une réalité continue par un langage
discontinu ; et une réalité mouvante par un langage
statique. Sur ce, nous pouvons nous référer au
célèbre argument de la dichotomie d'Achille et de la
tortue : Achille qui court vite ne saura jamais rattraper la tortue, car
il est obligé, à chaque fois, de faire la moitié de la
motié de la distance qui le sépare de la tortue.
· Démocrite d'Abdère (Vème
siècle ACN)
Pour Démocrite, le principe explicatif de
l'univers n'est ni l'eau, ni l'air, ni le feu (etc.), mais plutôt
l'atome. C'est par l'atome que s'explique la naissance et la mort de
l'être. Pour lui, l'atome demeure foncièrement homogène,
indestructible qualitativement et quantitativement ; les atomes sont en
nombre infini et tout le réel se réduit à la
réalité des atomes qui, en se mouvant, en se regroupant et en se
dissociant dans le vide par pression et par choque, forment les multiples et
divers êtres de l'univers en même temps qu'ils occasionnent leur
mort par leur dissociation.
Notons que Démocrite est l'auteur de Des
questions logiques, autrement dit des canons, quoique l'on arrive point
à savoir le sens qu'il donnait au terme logique.
De lui, l'on retient cependant le principe logique de
coexistence des contradictions.
II.1.2. les socratiques
La période socratique est
caractérisée par le fait que les recherches tournent autour de
l'homme et non plus sur le physis.
· Protagoras d'Abdère et Gorgias de
Léontini
Protagoras d'Abdère (Vème
siècle ACN) et Gorgias de Léontini (485-380) s'inspirent du
principe empiriste de Démocrite. Le premier affirme que
« l'homme est la mesure de toute chose ». Pour le
second, « la vérité n'existe pas ; ce qui
existe, c'est plutôt une bonne argumentation ».
En résumé, l'école de Protagoras et
de Gorgias « soutient que la vérité est une
construction relative au contexte et que le critère d'une argumentation
vraie est sa force de persuasion » (21(*)).
· Socrate (470-399ACN)
Socrate a mené une lutte acharnée contre
les sophistes. Selon lui, la vérité ne peut qu'être
absolue. Il était ainsi préoccupé de vérité
pour la bonne conduite de la société. Il disait à ce
propos : « si l'homme connaît le bien à faire,
il le fera nécessairement ; car s'il fait le mal, c'est simplement
parce qu'il ignore le bien à faire ». Aussi, va-t-il s'atteler
à l'étude des notions, des concepts grâce à la
maïeutique (art d'accoucher de la vérité) et de l'ironie
(art de détruire les connaissances apparemment vraies).
Signalons que Socrate n'accordait pas beaucoup
d'importance aux mathématiques. A ces propos, il « disait
qu'il fallait apprendre la géométrie jusqu'à ce qu'on fut
capable de mesurer une terre que l'on veut acheter, vendre, diviser ou la
bourrer... mais qu'on passât l'étude de la géométrie
jusqu'aux problèmes les plus difficiles, c'est ce qu'il
désapprouvait ; il disait qu'il n'en voyait pas l'utilité.
Ce n'est pas qu'il les ignora lui-même, mais il prétendait que la
recherche de ces problèmes est faite pour consumer la vie de l'homme et
le détourner d'autres études utiles » (22(*))
· Platon (428/427-348/347 ACN)
Disciple de Socrate et fondateur de l'académie,
Platon alla au delà de la maïeutique et de l'ironie pour nous
proposer la dialectique. Pour lui, la vérité se trouve dans les
jugements et que la dialectique nous permet justement d'atteindre cette
vérité. René taton nous apprend
que « Platon s'intéressait aux mathématique et
aucun des problèmes qui préoccupaient les mathématiciens
de son époque ne lui était étranger » (23(*)). D'ailleurs,
n'était-il pas affiché au fronton de l'Académie
que « nul n'entre ici s'il n'est
géomètre » ?
Signalons que, pour Platon, les objets
mathématiques occupent un plan intermédiaire entre le monde
idéel ou la theoria et la doxa ou les objets sensibles.
De ce qui précède, il transparaît
clairement que, pour Platon, les mathématiques n'occupent pas le premier
rang dans son échelle épistémologique et que le sensible
lui sert de tremplin, mieux de passage obligé pour accéder au
monde des idées.
II.1.3. Les post-
socratiques
· Aristote (384 - 322 ACN)
Par son effort de systématisation, Aristote peut
être considère comme l'inventeur de la science logique. Disciple
de Platon et membre de l'Académie, il deviendra par la suite penseur
autonome, puis fondera le Lycée. Il était également un
grand naturaliste.
Les écrits d'Aristote se rapportant à la
logique, on le sait, ont été réunis par ses disciples sous
le nom d'organon (instrument) et comportaient cinq livres, à
savoir :
1° les catégories
2° De
l'interprétation
3° les analytiques
4° les topiques
5° les réfutations
sophistiques
Nous supposons que cette logique d'Aristote est connue
de tous. Aussi, allons-nous nous contenter de porter quelques petites critiques
sur elle.
En gros, la logique aristotélicienne, qui a subi,
sinon bénéficié de l'apport de ses disciples proches et
lointains, s'inspirait, à notre avis, de deux modèles : la
zoologie et la géométrie. Force nous est de constater que le
zoologique l'emportait sur le géométrique qui se faisait sentir
à peine. Nous nous justifions en évoquant quelques anomalies du
système aristotélicien du point de vue formel, lesquelles sont
tributaires de ce penchant zoologique.
Aristote, en effet, classe les prédicats en dix
catégories ou classes d'êtres ou encore genre suprêmes.
Notons qu'une catégorie peut être prédicat de divers
sujets, mais ne peut être sujet d'aucun énoncé, car on ne
peut rien en dire. Cette classification ne nous renvoie-elle pas ou ne nous
suggère-t-elle pas la zoologie ?
De plus, la théorie de la définition des
concepts d'Aristote, laquelle exige un genre proche et une différence
spécifique pour définir un concept, ne nous renvoie-elle pas non
plus à la zoologie ?
Aussi, ce penchant zoologique pose -t-il problème,
de fois, au niveau formel. A titre exemplatif, nous évoquerons le cas de
la première règle du syllogisme catégorique, laquelle
stipule que « le syllogisme ne comporte que trois propositions
comprenant trois termes univoques ». En réalité, cette
règle suppose et implique l'analyse préalable des contenus des
termes du syllogisme. Or une science qui se veut formelle doit justement faire
abstraction des contenus des termes pour ne retenir que leurs formes.
Conséquence : la logique aristotélicienne n'est pas
totalement formelle.
Outre, la démonstration de bamalip, mode
concluant de la quatrième figure qu'aurait inventée Galien
(129-199 PCN), en barbara pose aussi problème, car la conversion dite
par accident, que permet la lettre P de bamalip, ne s'applique qu'aux
propositions universelles E et A. Aussi, on est en droit de se demander au nom
de quelle inférence transforme-t-on le « I » de
bamalip en « A ».
· Les Mégaro - stoiciens
L'école de Mégare et celle de la stoa sont
intimement liées. L'une a pour fondateur Euclide de Mégare et
l'autre Zénon de Cittium.
Euclide de Mégare (450 - 380 ACN), disciple de
Socrate, puis fondateur de l'école mégarique ( à ne pas
confondre avec Euclide d'Alexandrie, l'auteur présumé des
Eléments) a lui même subi l'influence des
éléates, surtout celle de Zénon d'Elée avec sa
dialectique. Euclide s'est orienté à la recherche de
difficultés, de subtilités, de procédés paradoxaux
et eut des disciples célèbres comme Eubulide de Millet, Diodore
de Cronos, Stilton et Philon de Mégare. Cette école a
exercé une certaine influence sur Zénon de Cittium
(333/332-261/260 ACN), fondateur de l'école stoïcienne.
Quant à l'école de la Stoa, MUTUNDA MWEMBO
nous apprend que « dans cette école, les maîtres et
les disciples font graviter la science autour d'une triade constituée
par la physique, la logique et la morale » (24(*)).
Notons que leur science est essentiellement empirico-
panthéiste. En effet, les stoïciens sont convaincus
que « le monde est Dieu et que Dieu est aussi cette
matière » (25(*)). Du coup, étudier le monde, c'est chercher
à découvrir Dieu. Sur le plan logique, les conséquences
sont telles qu'il n'y a pas de place pour un syllogisme
catégorique.
Aussi, les stoïciens favorisaient-ils le syllogisme
hypothétique, car l'homme doit poursuivre le cours naturel des
événements, la loi du monde.
Brachard accuse l'adaptation de la logique d'Aristote et
celle de Mégaro-stoïciens par les médiévaux, car les
deux logiques relèvent de deux philosophies bien
différentes : celle de la substance (Aristote) et celle de
l'événement (les Mégaro-stoïciens). A ce propos, il
dit ce qui suit : « la substance s'exprime naturellement
par un nom et l'événement par une proposition, la marque
distinctive de la logique stoïcienne par rapport à la logique
péripatéticienne était d'être une logique des
propositions, et non plus une logique des noms » (26(*)).
L'une des figures les plus importantes de la Stoa est
Chrysippe, celui-ci a toujours été reconnu, dans
l'antiquité, même par ses adversaires, comme un très grand
logicien, mis au même rang qu'Aristote et même quelque fois avant
lui. Diogène Laerce disait : « si les dieux ont une
logique, c'est celle de Chrysippe » (27(*)) et non celle d'Aristote, sous entendu.
En effet, « Chrysippe (281 - 208 ACN)
achèvera d'intégrer à la doctrine stoïcienne les
éléments de la dialectique mégarique, scellant ainsi entre
les deux écoles une parenté solide. De cette alliance,
résultera une tradition de recherche féconde qui laissera des
découvertes significatives dans le domaine de la logique. Ces
découvertes, on le sait, non seulement touchent aux principes
fondamentaux de la logique, mais aussi comportent des lois logiques et des
rudiments de formalisation » (28(*))
De plus, la logique mégaro-stoïcienne
était axiomatisée à sa manière. Elle admettait cinq
indémontrables ou axiomes que voici :
1° si le premier alors le second, or le premier, donc
le second ;
2° si le premier alors le second, or pas le
second ; donc pas le premier ;
3° pas à la fois le premier et le second, or
le premier ; donc pas le second ;
4° ou le premier ou le second, or le premier ;
donc pas le second ;
5° le premier ou le second, or pas le second ;
donc le premier.
II.2. Moyen âge
II.2.1. La Scolastique
La logique est devenue scolastique à partir du
moment où elle a été enseignée dans des
écoles, ou sens des universités. « C'est surtout
dans les traductions et les commentaires de Boèce que l'on
commença à prendre contact avec les oeuvres logiques
d'Aristote » (29(*))
La logique scolastique comprend trois grands moments,
à savoir : l'ars vetus, l'ars nova, logico modernorum
(30(*))
L'ars vetus est centré sur le contenu de
l'Isagoge de Porphyre, des catégories et des
interprétations traduits par Boèce. Cette période est
dominée par la personnalité de pierre Abélard (1079 -
1142). Ce dernier a écrit dialectica.
L'ars nova est fondée sur la
totalité de l'organon. La diffusion de l'ars nova a été
assurée par des savants comme Albert le grand et Thomas d'Aquin
quoiqu'ils étaient plus philosophes que logiciens, car ils voyaient dans
la logique un simple instrument au service de la théologie et de la
philosophie.
C'est avec Guillaume d'Occam, inventeur de la fameuse
science des conséquences, Jean Bouridan et Albert de Saxe que
la logique médiévale prendra sa forme propre. C'est justement ce
que l'on a appelé logico modernorum.
II.2.2. Le monde Arabe
Les traductions d'Aristote par les arabes manifestaient
l'intérêt que ceux-ci avaient pris à son oeuvre ; ils
voyaient en lui le premier philosophe, le deuxième étant
AL-Fabari qui, au début du 10ème siècle, avait
fait de l'étude de la logique un élément indispensable de
la culture islamique. Si nous en croyons Blanché, c'est lui qui a
introduit le terme technique de « prémisses »
(31(*))
Le troisième philosophe, Avicenne, avait
lui-même écrit un important traité de logique, lequel
constitue la première partie de le livre de science. En effet,
ce grand esprit affirmait que « la logique est la science
(semblable à) la balance (...) or toute science qui n'est pas
évaluée par la balance n'est pas certaine et, en
vérité, n'est pas science. Par conséquent, on ne peut se
dispenser d'acquérir la science de la logique » (32(*))
Dans le chapitre consacré à l'étude
des syllogismes de connexion (syllogismes hypothétiques), force est de
constater l'effort de mathématisation qu'il déploie sur les
figures de ces syllogismes, lesquelles sont plutôt des variantes du
syllogisme hypothétique développées de façon
originale.
De plus, ce qu'il appelle démonstration par
supposition est une belle illustration de la règle de substitution.
A titre exemplatif, pour une proposition du genre « quelques A
ne sont pas B », étant donné que ce
« quelques A » est nécessairement quelque chose,
soit D ; alors nous dirons « nul D n'est B ».
L'influence arabe sur les scolastiques occidentaux est
surtout celle d'Averroès, dont les commentaires sur l'oeuvre d'Aristote
sont, peu de temps après sa mort en Espagne, en 1198, introduits
à Paris et à Oxford. Et d'ailleurs, les scolastiques avaient
coutume à le nommer simplement « le
commentateur ».
II.2.3. Les maîtres
hindous
Deux maîtres hindous du 6ème et
7ème siècle (PCN) passent pour les théoriciens
de la dialectique, mieux de la logique indienne. Ces deux maîtres sont
DIGNAGA (33(*)), auteur
d'un ouvrage intitulé Pramana-Samuccaya et de son grand commentateur,
maître Dharmakviti, auteur d'importants traités de logique
comme :
- Pramana Vartika : principal ouvrage comprenant
quatre chapitres traitant de l'inférence, de la validité, de
la connaissance, de la perception et du syllogisme.
- Pramana Vaniscaya et Nyaya-bindu, des
abrégés du Pramana vartika, etc.
De façon globale, la doctrine hindouiste
distingue six points de vue (Nyaya, Vaisheshika, Shankya, Yoga, Mimansha et
Vedanta) (34(*)), lesquels
sont conçus comme autant de vision de la vérité
perçue sous des angles différents, donc
complémentaires.
Force est de constater que le Nyaya (la logique)
constitue un couple avec le vaisheshika (système philosophique indien
ayant trait aux spécificités de la réalité du
monde. Ce système recense et spécifie les constituants de
l'univers). Nous voyons clairement que même les indiens savaient
intuitivement, mieux établissaient nettement un certain rapprochement
entre la logique et les sciences de la nature.
Le Nyaya ou la logique hindouiste distingue quatre formes
d'arguments que voici :
1° la constatation directe ou l'observation. C'est la
perception directe par les sens. Cette perception représente ainsi une
forme d'argument.
2° le deuxième argument est assez
spécial et on le nomme comme suit : «l'inférence de ce
que l'on voit fait ce que l'on ne voit pas ». A notre humble avis, ce
raisonnement est fort similaire à l'induction et au raisonnement par
analogie.
3° le couple classique à cinq membres que
voici :
a) La proposition ;
b) La raison ;
c) La déclaration à l'appui ;
d) L'application ;
e) Et la conclusion.
Cette forme de raisonnement est une sorte
d'épichérème qui se développe de façon
naturelle. Voici un exemple de cette inférence, un exemple tiré
de la culture hindoue :
a) La proposition : la montagne a du feu (le
volcan).
b) La raison : en raison de la
fumée ;
c) La déclaration à l'appui : tout ce
qui a de la fumée a du feu ;
d) L'application : il en est de même de la
cuisine et non du lac ;
e) La conclusion : par conséquent, il en est
ainsi ;
4° Le témoignage verbal ou écrit d'une
autorité (l'argument d'autorité).
CHAPITRE TROIS: LA SCIENCE
EXTRAORDINAIRE DE LA LOGIQUE
Ce troisième chapitre nous décrit la
science extraordinaire de la logique et nous l'avons réparti en deux
grands moments : le premier nous présente diverses tentatives
entreprises pour sortir de la crise de la logique ancienne et le second nous
présente les précurseurs de Boole.
III.1. Propositions de
nouveaux modèles
· Raymond Lulle (1235-1315)
Par sa date de naissance, Lulle est certes un
médiéval, mais par ses idées, (lesquelles étaient
trop en avance sur son siècle), il peut être
considéré comme un précurseur de la logique
combinatoire.
Après avoir mené une vie de troubadours,
après s'être mariée et avoir eu deux enfants, il se senti
mystérieusement appelé à changer sa vie. Ainsi, quitte
-t-il sa femme et ses enfants et s'impose un triple projet, à
savoir : écrire des livres dénonçant les erreurs des
infidèles, fonder des collèges pour l'enseignement des langues
en vue de la prédication et évangéliser les
musulmans.
Après une très abondante production
littéraire, il expose sa méthode dans son ouvrage fondamental
Ars Magna et Ultima, ainsi que dans l'Ars brevis,
qui en est un abrégé. Le but de sa méthode était
de prouver les vérités de la foi. Cette méthode ressortait
de la logique formelle et s'apparente aux mathématiques les plus
modernes. Notons aussi que Raymond Lulle nourrissait l'idée d'une langue
universelle.
Selon lui, chaque branche du savoir se ramène
à un petit nombre de catégories de base. La combinaison de
celles-ci fournissent l'indéfinie diversité des connaissances
accessibles à l'esprit humain.
« Lulle prend pour point de départ un
certain nombre de termes fondamentaux, parmi lesquels on trouve les noms des
qualités, des relations, les particules caractéristiques de
diverses espèces de question et bien d'autres. Il soumet cet alphabet
de son art à divers arrangements permettant de passer en revue tous les
ensembles possibles faits de ces éléments. Il bâti enfin
une machinerie composée de cercles concentriques et doués de
mouvements indépendants »(35(*))
En effet, Lulle voyait dans son Grand Art une
sorte de Super-Science, une métascience. Son ambition peut se
résumer comme suit : découvrir des combinaisons logiques
à l'aide d'un dispositif mécanisé, donc sans erreur.
Cependant, sa tentative devait tourner court car les aides mécaniques
dont il disposait restaient trop sommaires et rudimentaires.
Néanmoins, il a été
apprécié par nombre d'intellectuels et de philosophes
postérieurs comme Nicolas de Cues, Pic de la Mirandole, Girdano Bruno
et surtout par Leibniz.
· Francis Bacon (1561-1626)
Adversaire de la scolastique, Bacon était
habité, voire hanté par l'idée de restaurer les sciences
et de substituer aux hypothèses et aux subtiles argumentations, qui
étaient alors en usage dans des écoles, l'observation et les
expériences. A ce titre, il peut être considéré
comme le père de l'empirisme et de la méthode
expérimentale.
En 1620, il publia le novum organum où il
expose une logique nouvelle qu'il oppose à l'antique méthode
d'Aristote. Dans l'étude des faux raisonnements, sa meilleure
contribution a été la doctrine des idoles. En effet, les idoles
ou obstacles à l'appréhension des choses sont des modes
d'enfermement de l'esprit en lui-même et des causes d'immobilisme. Il y a
au total quatre idoles (36(*)) que voici :
1° Idola tribus ou idoles de la tribu : elles
sont inhérentes au genre humain et à l'entendement en
général. Exemple : généraliser trop vite
à partir d'un petit nombre de cas sans se soucier des
contre-exemples.
2° Idola specus ou idoles de la caverne :
celles-ci sont des préjugés propres à chaque individu et
dont il est le prisonnier. Il s'agit de sa constitution, de son
tempérament, de son caractère, de ses goûts, de son
éducation ; bref, ce sont des aberrations
particulières.
3° Idola fori ou idoles de la place publique ou
encore idoles du forum : elles sont constituées des
préjugés provenant des relations sociales et du langage, car les
mots créent un rapport fallacieux aux choses.
4° Idola theatri ou idoles du
théâtre : celle-ci sont liées au mode de
présentation et de transmission du savoir. En d'autres termes, elles
proviennent des théories et des systèmes philosophiques, car tous
ces systèmes sont autant de pièces de théâtre que
les philosophes ont mis au jour, comme autant de mondes imaginaires.
Outre, Bacon considérait qu'il y a trois sortes
d'inductions, à savoir :
1° l'induction spontanée de l'esprit, laquelle
est la plus souvent erronée ;
2° l'induction traditionnelle, laquelle
procède par énumération des cas positifs, cette induction
s'expose à la ruine par le premier cas contradictoire ;
3° l'indiction du novum organum. Celle-ci
découvre les lois de la nature et les causes des
phénomènes en se fondant sur le plus grand nombre possible de
comparaison et d'exclusion, donc sur les cas positifs et négatifs au
même moment.
· René Descartes (1596- 1650)
De prime abord, nous disons que Descartes n'a pas
écrit un livre traitant expressément de la logique. Mais, nous
trouvons des précieux renseignements concernant la mathesis
universalis ou la méthode universelle aussi bien dans Les
règles pour la direction de l'esprit (1628) que dans Le
discours de la méthode pour bien conduire sa raison et rechercher la
vérité dans les sciences (1637), mieux connu sous le titre
abrégé de Discours de la méthode. Voici comment
il formule cette méthode universelle en quatre
règles :
1° ne recevoir jamais aucune chose pour vraie que je
la connusse évidemment être telle (règle de
l'évidence) ;
2° diviser chacune des difficultés que
j'examinerais en autant de parcelles qu'il se pourrait et qu'il serait requis
pour les mieux résoudre (règle de l'analyse) ;
3° conduire par ordre mes pensées en
commençant par les objets les plus simples et les plus aises à
connaitre pour monter peu à peu, comme par degré, jusqu'à
la connaissance des plus composés et supposant même de l'ordre
entre ceux qui ne se précèdent point naturellement les uns les
autres (règle de l'analyse) ;
4° faire partout des démembrements si entiers
et des revues si générales que je fusse assuré de ne rien
omettre (règle du dénombrement) (37(*)).
Ces précieux conseils du Discours de la
méthode ont influencé largement les logiciens de
Port-Royal : Antoine Arnould (1612-1694) et Pierre Nicole
(1625-1695).
Outre, l'idée de l'invention d'une
caractéristique universelle, on la retrouve seulement dans ses
correspondances avec Mersenne (38(*)).
Descartes avait aussi étudié la logique,
qu'il dénonçait l'inefficacité et l'insuffisance, et l'art
de Lulle, qu'il y avait décelé le danger d'une
mécanisation de la pensée. A ce propos, il
disait : « j'avais un peu étudié,
étant jeune, entre les parties de la philosophie, à la logique
(...) mais en les examinant, je pris garde que, pour la logique, ses
syllogismes et la plupart de ses autres instructions servent plutôt
à expliquer à autrui les choses qu'on sait ou même, comme
l'art de Lulle, à parler sans jugement de celles qu'on ignore,
qu'à les apprendre » (39(*))
III.2. Les
précurseurs de BOOLE
· Gottfried Wilhelm LEIBNIZ (1646-1716)
« L'un des motifs directeurs de
l'activité intellectuelle de Leibniz était l'idée qui le
poursuivait depuis sa prime jeunesse de fonder une langue artificielle,
à l'aide de laquelle il serait possible de raisonner, d'une
manière calquée sur la façon si stricte et certaine dont
on effectue les opérations de calcul ». (40(*)) Lulle a rêvé de
quelque chose de pareil, mais il ne disposait pas de ressources
nécessaires pour réaliser ce rêve. De plus, Raymond Lulle
mêlait à ses schémas la théologie et la
mystique.
Leibniz, par contre, avait l'esprit rivé sur
l'arithmétique et l'algèbre. Il estimait aussi que le contenu de
tout terme est un caractère soit simple, soit composé de
caractères simples. En termes clairs, toute proposition n'est que la
combinaison de concept sujet et de concept prédicat ; et que tout
concept complexe est analysable en concepts simples dont les relations sont
codifiables en formules combinatoires symboliques.
Notre auteur voyait dans son art combinatoire une sorte
d'algèbre universelle utilisable pour évaluer logiquement
n'importe quelle proposition, même en morale et métaphysique. Il
disait : « grâce à l'emploi de cet art, il ne
devrait plus y avoir matière à discussion entre philosophes qu'il
n'y en a entre comptables. Il leur suffirait de prendre en main leur crayon, de
s'asseoir devant un tableau et de se dire mutuellement : Et
bien ! Calculons » (41(*)).
Leibniz s'attendait à obtenir deux objets
simultanés : construire un système de nomenclature
universelle, qu'il appelait characteristica universalis, et
établir les principes d'une sorte de calcul qui remplacerait le
raisonnement, et qu'il appelait calculus ratiocinator. Cette
caractéristique universelle est appelée idéographie par
Kotarbinski, car les signes graphiques désignent la compréhension
ou l'objet des idées de façon directe et non par
l'intermédiaire d'une reproduction des mots correspondants du langage
phonétique.
Leibniz propose ainsi un modèle
arithmétique de la combinatoire (42(*)) dont il espère tirer une logique de
l'invention. Les concepts sont représentés par des nombres. On
peut ainsi définir tous les prédicats possibles d'un sujet
donné en utilisant la règle de calcul des combinaisons
ci-dessous :
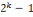
K représente le nombre de termes simples entrant
dans la définition du terme complexe. Le problème inverse de
trouver tous les sujets possibles pour un prédicat donné revient
à déterminer toutes les combinaisons où peut entrer la
combinaison correspondant à ce terme prédicat. A supposer que
n soit le nombre total des termes simples et que k représente
le nombre de la combinaison du prédicat, la formule à appliquer
s'énoncera comme suit :
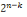
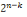 - 1
- 1
En éliminant la possibilité
d'identité entre le prédicat et le sujet, la formule de calcul
devient :
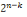
Voyons maintenant le problème du nombre de
syllogismes requis pour démontrer une proposition, en excluant le cas
où le sujet et le prédicat appartiennent à la même
classe d'ordre (cas de l'identité). Soit k le nombre de facteurs
(termes) simples de p (prédicat) et n le nombre de facteurs simples de s
(sujet) ; en raison de l'exclusion de s lui- même, la formule donne
ce qui suit :
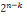
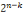 - 2
- 2
Leibniz propose d'utiliser de telles ressources
combinatoires pour résoudre des problèmes en droit, en physique,
en théologie, etc.
Ainsi, sans y parvenir, Leibniz s'efforça toute sa
vie de construire une machine capable d'épuiser automatiquement toutes
les combinaisons de principe. Malheureusement, ce mode de raisonnement porte en
lui-même un germe empoisonné : le risque de tomber dans la
mécanisation de la pensé tel que Descartes l'avait
signalé...
De plus, Kotarbinski nous renseigne ce qui
suit : « Ni Raymond Lulle, ni Leibniz, ni personne n'est
encore entièrement parvenu à ce jour à construire une
idéographie universelle suffisamment pratique, ni à
édifier au moyen de cette idéographie un nombre suffisant de
formes de raisonnement qui permettent de calculer en quelque sorte toutes les
formes d'un raisonnement correct » (43(*)).
Toutefois, Leibniz a élaboré un certain
nombre de formules logiques, entre autres celle de calcul propositionnel,
connues des stoïciens et des spécialistes
médiévaux.
· Bernard BOLZANO (1781-1848)
Bernard BOLZANO est un mathématicien
précoce, théologien catholique et philosophe original. Il a
consacré le reste de sa vie aux mathématiques, à la
logique et à la philosophie. Son oeuvre fut longtemps méconnue.
Pourtant, il a introduit dans la logique les variables, défini
correctement la limite et, avant Cantor, s'est servi du concept d'ensemble. Ses
travaux ont également porté sur les fonctions et la
théorie des nombres.
Il est aussi connu pour le théorème qui
porte son nom : théorème de BOLZANO, lequel s'énonce
comme suit : « entre deux valeurs qui donnent des
résultats de signe opposé, il y a au moins une solution
réelle de l'équation » (44(*)). Un demi-siècle plus
tard, ce même théorème sera développé
conjointement avec Karl Weierstrass et portera alors le nom de
théorème de Bolzano-Weierstrass. Ainsi, il s'énoncera
comme suit « une fonction réelle continue entre a et b,
positive pour a et négative pour b, s'annule au moins une fois entre a
et b ». (45(*))
Pour ce, il définit le concept de continuité et celui de nombre
réel.
· WILLIAM HAMILTON (1788-1856)
Son souci majeur semble celui de vouloir exprimer et
formuler explicitement ce qui n'est pensé que sous une forme implicite.
Ceci va l'amener à élaborer une doctrine de la quantification du
prédicat permettant de distinguer dans une proposition telle
que « tous les hommes sont des animaux » les deux
propositions suivantes :
1° tous les hommes sont tous les
animaux ;
2° tous les hommes sont quelques animaux.
Cette pratique mène Hamilton à concevoir la
proposition comme une équation à réduire les trois types
communément reconnus de conversion à la seule conversion simple
et à esquisser une nouvelle notation logique.
Les disciples de Leibniz, on le sait, ont essayé
de développer la logique formelle en s'y intéressant
essentiellement sous l'angle des relations entre les compréhensions des
termes. Au lieu d'évoluer dans la compréhension des termes,
Hamilton va plutôt vers l'extension. Son souci étant qu'il
faille « exprimer explicite ce qui est pensé
implicite » (46(*)).
Aussi, son nom est lié à la tentative
d'enrichir la syllogistique de ce que l'on appelle « la
quantification du prédicat ». Ceci consiste à faire
précéder le prédicat d'un quantificateur, ce qu'on ne fait
pas lorsqu'on énonce les propositions du carré logique. Ainsi, au
lieu de ces quatre propositions (A, E, I, O,), nous obtenons les huit
suivantes :
U : tous les S sont tous les P ;
I : quelques S sont quelques P ;
A : tous les S sont quelques P ;
Y : quelques S sont tous les P ;
E : aucun S n'est aucun P ;
W : quelques S ne sont pas quelques
P ;
: aucun S ne sont quelques P ;
O : quelques S ne sont aucun P.
· Auguste de Morgan (1806-1878)
Mathématicien londonien, Auguste De Morgon formule
deux lois de la logique qui portent son nom et notées comme
suit :
· (a+b)' = a'.b' ou 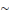
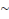 (pvq)
(pvq) 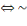
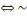 p
p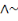
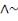 q
q
· (a .b)' = a'+b' ou 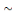
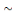 (p
(p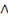
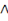 q)
q) 
 p
p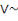
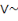 q
q
Ces deux lois logiques sont appelées
théorèmes de De Morgan, pourtant nous les rencontrons
déjà au moyen-âge chez Guillaume d'Occam.
De Morgan représente, en quelque sorte, le trait-
d'union entre la syllogistique traditionnelle et la logique algébrique
moderne. En effet, il a orienté ses efforts vers un enrichissement, une
généralisation et une systématisation de la syllogistique.
Cependant, sa culture de mathématicien familiarisé avec
l'algèbre a influé sur sa méthode. A ce propos,
Kotarbinski dit « l'enrichissement et en même temps
l'homogénéisation de la syllogistique traditionnelle consiste ici
avant tout dans la quantification non seulement des sujets, mais
également des attributs (ce qui constitue un trait qui est commun avec
Hamilton), et, en outre, dans le fait qu'il introduit de façon aussi
étendue que possible des termes négatifs et non seulement des
termes positifs (ce qui, dans l'exposé de la logique traditionnelle
n'apparaît que pour les obversions et les forment en dépendant,
dans le cas de transfert de la négation de la copule à
l'attribut » (47(*))
Voici l'économie de la logique de De
Morgan :
Les termes positifs (comme homme, mortel) sont
désignés par des majuscule : X, Y, Z, alors que les termes
négatifs (comme non-homme, immortel ou non-mortel) leur correspondant
par des minuscules : x, y, z.
Un terme quantifié universellement (comme tout
homme, aucun mortel) est accompagné d'un croissant dont la
convexité est tournée vers l'extérieur.
Exemple :
X 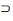
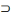 ou
ou 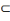
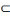 X.
X.
Un terme à quantification partielle (certains
hommes, certains mortels) est accompagné d'un croissant en sens
contraire. Exemple : X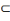
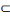 ou
ou 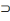
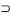 X.
X.
Deux termes avec croissants juxtaposé sans signe
intermédiaire ou reliées à l'aide de deux points
disposés horizontalement forment une proposition affirmative. Exemple
X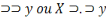
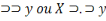
Deux termes avec croissants reliées par un point
forment une proposition négative. Exemple : X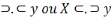
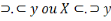
Ainsi, fort des informations ci-hautes, nous pouvons, par
exemple, formaliser les propositions d'Hamilton selon le modèle de De
Morgan. P
|
Les propositions d'Hamilton
|
Leurs équivalents chez De Morgan
|
|
U : Tous les S sont tous les P
I : Certains S sont certains P
A : Tous les S sont certains P
Y : Certains S sont tous les P
E : Aucun S n'est aucun P
W : Certains S ne sont pas certains
P
: Aucuns S ne sont certain P
O : Certains S ne son aucuns P
|
X 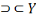 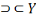
X 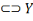 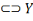
X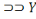 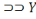
X 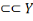 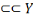
X 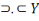 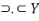
X 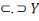 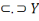
X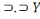 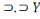
X 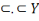 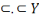
|
Dans ce même ordre d'idée, l'obversion de X
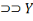
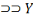 nous donnera X
nous donnera X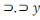
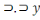 .
.
Comme l'on peut s'en rendre compte, De Morgan n'avait
pas prévu des foncteurs pour connecter les propositions entre elles.
Aussi, va-t-il élaborer la théorie de la relation pour
que, dans les schémas de la syllogistique
généralisée, les membres représentés par les
termes soient reliés par des relations arbitraires et pas
nécessairement par les relations d'inclusion ou de non inclusion.
Exemple : soit le raisonnement suivant :
X..LY
Y..MZ
X..LMZ
Si nous posons L pour la fraternité, M pour la
paternité alors ce raisonnement se lira comme suit : X est le
frère de Y, et Y le Père de Z, alors X est le frère du
père de Z (en clair, l'oncle de Z).
CHAPITRE QUATRE: LA
RÉVOLUTION DE LA LOGIQUE FORMELLE
Ce dernier chapitre comprend trois points. Le premier
est relatif à George Boole : il nous décrit la situation
socio-culturelle ainsi que scientifique qui permit à Boole de forger sa
pensée et présente en même temps l'essentiel de la logique
des classes. Le deuxième point dresse les portraits des continuateurs de
Boole et leurs contributions à l'algèbre de la logique. Quant au
troisième point, c'est une étude comparative de la logique des
classes et celle des propositions inanalysées.
IV.1. George Boole ou le
père de la logique moderne (48(*))
IV.1.1. Eléments
bio-bibliographiques
George Boole est né le 2 novembre 1815 à
Lincoln (Royaume Uni) et mort le 8 décembre 1864 à Ballintemple
(Irlande).
Issu d'une famille pauvre, George n'avait pas les moyens
financiers nécessaires d'aller à l'université. Cependant,
ses capacités intellectuelles étaient très remarquables.
Presque seul, il a appris le latin, l'allemand, le français et
l'italien. Obligé de travailler pour soutenir sa famille, il devient
enseignant à 16 ans.
Quatre ans plus tard, Boole fonde et dirige sa propre
école. C'est à ce moment là que le jeune autodidacte se
plonge dans l'étude des mathématiques auxquelles son père
l'avait initié dès l'enfance. Bénéficiant des
moyens de l'institut de Mécanique de sa ville, il se confronte aux
oeuvres d'Isaac Newton, de Pierre Simon Laplace et de Joseph Louis Lagrange.
Mais très vite, il commence ses propres recherches.
Ainsi, en 1839, il publie sa première
étude dans le Cambridge mathématical journal. Cette
publication et l'appui qu'il obtient du cercle des algébristes de
Cambridge (Babbage, Herschel, Peacoke, Gregory) lui permettent de s'imposer
petit à petit comme une personnalité importante du monde des
mathématiques.
Notons que déjà le 11 septembre 1835, il
épousa Mary Eversest, nièce du Sir George Eversest, le
responsable de la mission cartographique qui bâptisa le mont Everest.
C'est donc avec Mary qu'il aura cinq filles : Mary, Margaret, Alicia, Lucy et
Ethel Lilian.
En 1844, après la publication d'un mémoire
d'analyse dans les philosophical transactions, la Royal
society lui décerne une médaille.
Notons aussi que l'oeuvre de Boole s'est d'abord
formée au contact des algébristes de Cambridge à qui il a
emprunté l'idée d'un symbolisme algébrique fondé
sur les opérations fondamentales (+, X, -) et détaché des
quantités (nombre et grandeur), puis au contact du renouveau de la
logique en Grande Bretagne sous l'influence de W Hamilton et de De Morgan, dont
la théorie de la quantification du prédicat permettait
d'envisager les propositions sous la forme d'équations entre deux
notions définies en extension.
En 1847, il publie Mathematical Analysis of
logic dans lequel il définit la logique comme à la fois un
calcul de signes arbitraires et comme expression des lois de la pensée.
Puis an investigation into the laws of thought, on which are founded the
mathematical theories of logic and probabilities en 1854. Là, Boole
généralise son analyse algébrique de la logique
traditionnelle en exprimant toutes lois comme valables pour une algèbre
des seuls nombres 0 et 1, représentant respectivement la classe nulle
et l'univers de discours des objets concevables. Il définit ensuite la
notion générale de fonction logique. Ainsi, peut -il
considérer la syllogistique comme un cas particulier d'une
méthode algébrique plus générale.
Les travaux de Boole, plus tard, trouveront des
applications dans des domaines aussi divers que les systèmes
informatiques, la théorie des probabilités, les circuits
électriques et téléphoniques, etc.
En 1849, Boole se voit proposer une chaire de professeur
des mathématiques au Queen's College de Cork, en Irlande. En
1857, il est nommé membre de la Royal Society.
Par la suite, Boole s'est intéressé aux
équations différentielles à travers deux traités
qui auront une influence certaine : tratise on diffirential
Equations (1859) et treatise on the calculus of finite differences
(1860).
George Boole mourra d'une pneumonie le 8 décembre
1864. Il avait pris froid après s'être rendu au collège.
Croyant au principe d'analogie, Mary l'avait alité et aspergé
d'eau pour le guérir. Hélas, sans succès!
Tout compte fait, la contribution fondamentale de Boole
à la Logique est double : d'une part, cette discipline se trouve avec
lui intimement associée aux mathématiques dans la lignée
de l'idéal Leibnizien d'une caractéristique universelle et,
d'autre part, elle se trouve associée aux structures algébriques
avec le courant de l'algèbre de Boole et du calcul des classes
qui allait se développer dans la seconde moitié du XIXème
siècle avec Venn, Jevons, L. Caroll, Peirce et Schröder. A bien
des égards, ce courant, qui repose sur la notion de
vérité, de validité et d'interprétation d'une
proposition dans un univers possible, représente une approche
sémantique de la logique distincte de
l'approche syntaxique et
axiomatique qui allait être celle de Frege et
de Russell, et qui reposait sur une conception différente de la
quantification et non pas sur le calcul des classes. "Cette approche
sémantique, qui fut celle de Löwenhein et de Skolem, n'a rejoint
l'approche axiomatique que dans les années 1930, et a fait preuve de sa
fécondité quand un mouvement d'abstraction supplémentaire
a conduit à la formation de la notion de structure et à la
théorie plus générale des algèbres de Boole
(Huntington: 1933), ouvrant la voie à d'autre rapprochement entre
logique et algèbre au sein de la théorie des
modèles"(49(*)).
IV.1.2. Eléments de la
logique des classes
A. Les classes, les symboles
littéraux et les opérateurs de base
· Les classes
Il y a principalement deux classes chez Boole : la
classe universelle ou l'univers de discours des
objets concevables symbolisé par 1 et la classe nulle
représentée par O. Ces deux classes sont des constantes. A ce
propos, Lalande définit une classe logique de la manière suivante
: " ensemble d'objets définis par le fait que ces objets
possèdent tous et possèdent seuls un ou plusieurs
caractères communs" (50(*)). La classe nulle ou vide ne possède qu'un
seul caractère, celui d'être nulle ou vide.
· Les symboles littéraux
Les symboles littéraux tels que x, y, z (...),
qui représentent les choses visées par les concepts et qui
correspondent aux substantifs et aux adjectifs, sont eux-mêmes des
classes quelconques, mieux des sous -classes de la classe universelle, à
la seule différence que les symboles littéraux sont des
variables, c'est-à-dire qu'ils n'ont pas des contenus fixes, ils n'ont
des contenus que ceux qu'on leur attribue.
Soit la proposition suivante : tout mariage
est heureux.
Intentionnellement (c'est-à-dire en
compréhension), le prédicat heureux désigne la
classe de toute chose heureuse alors qu'extentionnellement il désigne au
moins un individu de la classe des choses heureuses: le mariage.
Quant à la classe complémentaire, elle est
obtenue par la soustraction de la classe universelle par une classe quelconque
et sa formule donne : (1-x) ou (1-y) ou encore (1-z).
· Les opérateurs de base
Boole utilisait quatre opérateurs de base (+, .,
-, =) qui représentent respectivement la réunion ou la somme de
deux classes, l'intersection de deux classes ou le produit logique, l'exception
de certains éléments dans une classe donnée et
l'identité extentionnelle, laquelle identité correspond à
la copule Est de la forme de la proposition classique
S est P.
Un cinquième opérateur "v" est le
sélectionneur de la classe des éléments communs à x
et y, c'est-à-dire que c'est le quantificateur particulier. Par
conséquent, une variable précédée de "v"
est particulier alors que celle qui n'en est pas précédée
est universelle.
B. Les lois fondamentales de la logique
des classes
La logique des classes comporte un certain nombre des
lois, lesquelles sont des axiomes facilitant le maniement aisé des
opérateurs de base.
a. La commutativité
|
Formulation de la loi
|
Son interprétation en langage ordinaire
|
|
x.y= y.x
|
Moutons blancs équivaut à blancs
moutons
|
|
x+y= y+x
|
Moutons et boeufs équivaut à boeuf et
moutons
|
b. L'associativité
|
Formulation de la loi
|
Son interprétation en langage ordinaire
|
|
x.(y.z) = (x. y).z
|
L'intersection de x et y inter z équivaut à
l'intersection de x inter y et z
|
|
X + (y+z) = (x + y)+z
|
La réunion de x et y union z équivaut
à la réunion de x union y et z
|
c. La distributivité
|
Formulation de la loi
|
Son interprétation en langage ordinaire
|
|
x.(y+z) = (x. y)+ (z.x)
|
Les africains (hommes et femmes) équivaut à
les hommes africains et les femmes africaines
|
|
x. (y-z) = (x .y) - (x.z)
|
Les africains (les hommes mais pas les femmes)
équivaut à les hommes africains mais pas les femmes
africaines
|
d. La loi des indices ou l'idempotence
|
Formulation de loi
|
Son interprétation en langage ordinaire
|
|
x.x. = x2 =x
|
La reproduction des congolais par des congolais donne des
congolais
|
Cette loi signifie qu'une itération donne
toujours la même classe. En termes clairs, cet axiome signifie que la
reproduction d'une classe par elle-même donne cette même
classe.
Notons qu'en algèbre, xn=x si et
seulement si x =0 ou n =1.
e. La loi de la
complémentarité
|
Formulation de la loi
|
Son interprétation en langage ordinaire
|
|
1-x
|
Le complément de X= 1 - x si nous posons : x =
hommes, alors la classe complémentaire de homme est non homme,
c'est-à-dire tout ce qui n'est pas homme.
|
Il semble clair que lorsque des lois semblables sont
données, il devient possible de travailler à l'aide d'un calcul
abstrait. On peut ainsi opérer des transformations d'équation
sans se soucier de ce que représentent x, y ou z.
C. Interprétation de la logique
des classes
La logique des classes peut être
interprétée de différentes manières. C'est
justement ces différences dans l'interprétation qui ont
été à la base du courant de l'algèbre
de Boole, mieux des algèbres de
Boole, car ces algèbres Booléennes sont
différentes les unes des autres par le fait qu'elles
n'interprètent pas toutes de la même manière les
opérateurs de base (+, ., -, =). Il sied de préciser que le
courant des algèbres de Boole n'est pas l'oeuvre exclusive de Boole
seul, quantité de chercheurs y ont apporté leur
contribution.
Toutefois, Boole distinguait deux types de propositions,
à savoir : les propositions primaires et les propositions
secondaires(51(*)).
Les propositions primaires sont dépourvues de
valeurs de vérité, c'est-à-dire qu'elles ne sont ni
vraies ni fausses ni disponibles à l'être. Bref, ces propositions
ne reçoivent aucune valeur de vérité.
Nous nous proposons d'illustrer quelques exemples des
propositions primaires.
Soit la proposition suivante : tout y est
x.
En algèbre classique, nous pouvons la
représenter comme suit : y.x = y. On pourra la lire de la manière
suivante : l'intersection de y et x équivaut à y pour signifier
que tout y est x.
En logique des classes, conformément aux
informations fournies ci-haut, nous pouvons formaliser la même
proposition comme suit : y = x et on lira tout y est
x, car le signe de l'identité correspond à la
copule est.
Comme nous le savons déjà, Boole a
été influencé par la théorie de la quantification
de W. Hamilton, laquelle a été reprise et améliorée
par De Morgan. Aussi, notre propositions s'écrira de la manière
suivante : y = v x et se lira tous les y sont quelques x, car
v est l'opérateur de sélection de la classe des
éléments communs à y et x. Autrement, c'est le
quantificateur particulier.
Maintenant nous pouvons formaliser les propositions de
W. Hamilton à l'aide de la logique des classes.
|
Termes mnénotechiques
|
Propositions classiques
|
Logiques de classes
|
|
U
|
Tous les y sont tous x
|
y = x
|
|
I
|
Quelques y sont quelques x
|
vy = vx
|
|
A
|
Tous les y sont quelques x
|
y = vx
|
|
Y
|
Quelques y sont tous les x
|
vy= x
|
|
E
|
Aucune y n'est aucun
|
y= (1-x)
|
|
W
|
Quelques y ne sont pas quelques x
|
vy = v(1-x)
|
|
Aucuns y ne sont quelques x
|
y =v(1-x)
|
|
O
|
Quelques y ne sont aucun x
|
vy = (1-x)
|
Jusque là, tout semble simple. Cependant, lorsque
l'on veut donner la forme d'une équation du premier degré
à ces propositions, les difficultés interviennent.
-x
En algèbre classique, l'équation y = x
équivaut à y -x = 0, car il y a un principe mathématique
qui stipule que : " si vous ajoutez une même quantité aux deux
membres de l'équation, l'égalité ne change pas ". Ainsi,
comme c'est x que nous voulons déplacer, on ajoutera aux deux membres
de l'équation la quantité , ce qui nous donnera : y -x =
x-x; et par la simplification, nous obtiendrons : y - x = 0.
En logique des classes, cette permutation n'est pas
valide, car elle entrainerait l'interprétation suivante : le
complément de x, c'est-à-dire y, est nulle.
Toutefois, avec le cinq axiomes que nous avions
évoqués, il y a lieu de faire plusieurs permutations
valides.
Quant aux propositions secondaires, nous disons qu'elles
portent sur des classes de moments du temps où elles sont vraies. En
termes clairs, les propositions secondaires sont pourvues de valeurs de
vérité temporaires. Cela signifie que les propositions
secondaires peuvent être vraies à un moment et fausses à
un autre. Néanmoins, c'est par elle (les propositions secondaires) que
Boole exprime la plupart des opérations propres à la
syllogistique traditionnelle (conversions, syllogismes, etc.) et définit
la notion générale de fonction logique. Il peut ainsi
considérer la syllogistique comme un cas particulier d'une
méthode algébrique plus générale.
Voici un exemple d'une proposition secondaire :
Soit la proposition suivante : "les richesses se
composent de substances quantitativement limitées, échangeables,
donnant du plaisir ou protégeant contre la souffrance".
En posant :
W : les richesses;
S : substances quantitativement
limitées;
T: échangeables;
P : donnant du plaisir;
r: protégeant cotre la
souffrance.
Nous obtiendrons l'Ebf (expression bien formée)
suivante:
W= st[p+r (1-p)]
IV.2. Les continuateurs de
Boole
· William Stanley Jevons (52(*))
William Stanley Jevons est né à Liverpool
le 1er septembre 1835. Il fut économiste et logicien
anglais. Il est aussi considéré comme co-fondateur de
l'école néo-classique et de la révolution
marginaliste.
Son père était commerçant dans le
secteur de la métallurgie. A quinze ans, il est envoyé à
la junior school de l'university
college de Londres où il s'intéressait
particulièrement à la botanique et à la chimie. Les
ennuis financiers de sa famille liée à la faillite de la
société de son père en 1847 le pousse à accepter un
poste en Australie où un nouvel institut de frappe monétaire a
été établie suite à la découverte de mines
d'or.
Durant son séjour, il s'intéresse à
l'économie en lisant la richesse des nations
d'Adm Smith, les principes d'économie
politique de John Stuart Mill et les introductory
lectures of political economy de Richard Whately, etc.
En octobre 1859, il retourne en Angleterre et reprend
ses études à l'university college où il obtient
son master of arts. En 1863, il entre dans le corps enseignant d'Owens
college. En 1865, son livre the coal question établir sa
réputation comme économiste traitant des faits.
En 1866, il devient professeur de Logique et de
Philosophie Morale, puis professeur d'économie politique.
En 1867, il se marie avec Henrietta, la fille du
propriétaire du Manchester Guardian et est
élu en 1872 à la Royal Society.
En 1876, Malade, il démissionne d'Owens
college pour accepter un enseignement plus léger à
l'university college. En 1880, il quitte cet établissement pour
consacrer son énergie déclinante à la recherche. Il meurt
en 1882.
Jevons a travaillé sur la logique en
parallèle avec ses recherches en économie. En 1863, il publie un
petit volume intitulé pure logic or the logic of quality
apart from quantity, basé sur la logique de Boole
à laquelle il a enlevé ce qu'il considérait comme un faux
habillage mathématique.
Dans les années qui suivirent, il s'attacha
à la construction d'une machine logique appelée logic
piano qu'il présenta à la Royal society en 1870.
Cette machine permettait d'arriver mécaniquement aux conclusions
induites par un jeu de prémisses. Cette machine découle de ce
qu'il considérait comme " le grand et universel principe de tout
raisonnement" (53(*))
qu'il exposa en 1869 sous le titre the substitution of
similars. L'idée est que, comme dans les équations
d'algèbre, il est possible, dans les problèmes logiques, de
substituer à un énoncé un élément
doté des mêmes propriétés.
Dans les années qui suivirent, il fit
paraître ses élémentary lessons on
logic, lequel devint " la logique symbolique" standard des
manuels de la fin du XIX siècles en raison de sa
simplicité.
Dans un texte plus ambitieux paru en 1874 sous le titre
The principle of science, il énonce et développe
l'idée selon laquelle l'induction est simplement l'inverse de la
déduction. Toutefois, comme il est difficile de tenir compte de toutes
les causes possibles, Jevons en déduit que les lois
générales sont, au mieux, seulement probables. Pour lui, les
probabilités servent à mesurer des espérances
rationnelles.
Outre l'une de ses idées majeures, celle de
processus mécaniques a été à la base de la
technique des tables de vérité, technique
développée par Charles Sanders Peirce (54(*)).
En fin, Jevons, se range aux côté de Whewel
pour défendre l'explication hypothético-déductive des
théories scientifiques contre l'inductivisme de Bacon et de
Mill.
· Schröder friedrich Wilhemln Karl Ernst (55(*))
Ernst Schröder est né le 25 novembre 1841
à Mannheim et mort le 16 juin 1902 à Karlsruhe. C'est un
mathématicien et logicien allemand. Toute sa vie fut consacrée
à l'étude et à l'enseignement des mathématiques et
de la logique. Il ne fut jamais marié. Son travail a porté sur la
logique et l'algèbre de Boole. C'est un personnage majeur de l'histoire
de la logique symbolique, car il fait une belle synthèse des oeuvres de
De Morgan, George Boole, Hugh Maccol et particulièrement charles
Sanders Peirce.
En 1860, il entre à l'université de
Heidelberg où il obtient deux ans plus tard son doctorat. Une bourse
lui est alors accordée pour l'Université de Königsberge. Il
y suivra durant deux ans des cours et séminaires en
mathématiques et en physique. En 1865, il est nommé maître
de conférence (chef de travaux) en mathématiques à
l'école polytechnique fédérale de Zurich.
En 1876 il obtient une chaire de Mathématiques au
Polytecnische Schule de Karlsruhe où il passa le reste de sa vie.
Bref, il a appris les Mathématiques à Heidelberg, à
Konigsberg et à Zurich auprès de Hesse, Kirchhoff et Franz
Ernst Neumann.
Les premiers travaux de Schröder portant sur
l'algèbre et la logique ont été menés sans qu'il
connaisse les logiciens anglais De Morgan et George Boole. Il s'appuyait sur
les travaux d'Ohm, Hankel, Hermann et Robert Grassmann, issu de
l'école traditionnelle Allemand en algèbre combinatoire et
analyse algébrique. En 1873, Schröder découvrit les travaux
de Boole et de De Morgan sur la logique. Il y intégrera les
idées importantes dues à Charles Sanders Peirce, Notamment les
notions de subsomption (l'équivalent de l'inclusion pour les
prédicats) et de quantification.
Schröder a également apporté des
contributions originales à l'algèbre, à la
théorie des ensembles ordonnées comme les treillis ou les nombres
ordinaux. Avec Georg Cantor, il découvrit le théorème de
Cantor-Bernstein-schröder. Bien que sa démonstration de 1898 fut
imparfaite, Félix Bernstein (1878-1956) la corrigea dans sa
thèse.
L'oeuvre monumentale de Schröder est les
vorlesungen über die algebra der logik
(leçons sur l'algèbre de la logique). Cette oeuvre constituait
une somme complète sur l'état de la logique symbolique à
la fin du XIXème siècle, car elle eut une influence
considérable sur l'émergence de la logique mathématique au
XXème siècle.
Les différences entre Schröder et Boole sont
essentiellement les suivantes :
Chez Boole, la négation, qui
était définie à partir de la soustraction, est
considérée maintenant comme une opération
primitive;
La somme logique n'est plus
interprétée dans un sens exclusif, mais plutôt dans un
sens non exclusif;
L'identité n'est plus la seule
relation, il s'y ajoute l'implication et l'identité comme
l'équivalence;
a = (a=1)
De plus, la logique de Boole n'était pas une
véritable logique propositionnelle. Boole n'excluait pas qu'une
même proposition puisse avoir des valeurs de vérité
distinctes à des moments distincts du temps (cas des propositions
secondaires). Pour faire face à cette situation, Schröder ajoutera
aux lois fondamentales de la logique propositionnelle l'axiome suivant:
Cet axiome énonce que pour toute proposition a,
tel que a est l'équivalent de la proposition a est
équivalent à 1 (où 1 symbolise n'importe
quelle proposition vraie, mieux qui serait vraie à tous les moments du
temps). Cet axiome, en fait, signifie qu'une proposition est vraie si et
seulement si elle est toujours vraie.
En outre, il a introduit la notion des coefficients de
relation.
Tout compte fait, bien qu'elle soit axée surtout
sur la logique des classes et qu'elle se situe dans la ligne de Boole et non
de Frege ou de Russell, l'oeuvre de Schröder a exercé une influence
non négligeable sur le développement de la logique
mathématique dans la première moitié du
XXème siècle, comme en témoignent les travaux
de Löwenheim et de Thoralf Skolem. Pour citer un autre exemple, "Zermelo a
présenté ses axiomes pour la théorie des ensembles dans la
notation Peirce-Schöder et pas, comme on aurait pu s'y attendre, dans
celle de Russell-Whitehead"(56(*)).
IV.3. Etude comparative
entre la logique des classes et celle des propositions inanalysées
"L'expression proposition
désigne un énoncé du langage ordinaire mais
considérée du point de vue formel qui est celui de la logique.
En clair, cela signifie que l'on traite seulement d'un certain type
d'énoncés et que l'on néglige dans ce type
d'énoncés une série de paramètres qui seront sans
incidence logique "(57(*)).
Les propositions envisagées ici sont ce qu'on
appelle des fonctions de vérité. Ce
sont des énoncés descriptifs d'un état de fait et
susceptibles d'être vrais ou faux. S'il y a adéquation entre la
proposition et le fait décrit, la proposition est vraie ; dans le cas
contraire, elle est fausse.
En effet, la notion de fonction de vérité a
été introduite en logique par Frege (1848-1925). Elle signifie
que "une proposition logique n'est à priori ni vraie ni fausse; elle est
disponible, capable de revêtir l'une de ces deux valeurs de
vérité; le problème en logique n'est pas de savoir si
telle proposition est vraie ou fausse, mais de savoir ce qui advient lorsqu'on
la considère soit comme vraie, soit comme fausse"(58(*)).
Toutefois, une proposition logique est soit simple, soit
complexe. Elle est simple dans l'exemple suivant : tout homme est
mortel. C'est-à-dire qu'il n'est pas possible de
l'analyser en des propositions plus simple que ça. Par contre, la
proposition s'il peut alors il fait beau est
complexe, car elle est composée de deux proposition simples, à
savoir il peut et il fait
beau.
La première étape du calcul propositionnel
est la formalisation des énoncés du langage ordinaire.
Pour réaliser ce travail, le calcul propositionnel
fournit trois outils : les variables propositionnelles, les opérateurs
ou foncteurs logiques et les signes de ponctuations.
1. Les variables propositionnelles (p, q, r, ...)
symbolisent des propositions simples quelconques. Si la même variable
apparait plusieurs fois dans une expression donnée, elle symbolise
chaque fois la même proposition;
2. Les cinq opérateurs ou foncteurs logiques: ~,
Ë, í, et ;
3. Les signes de ponctuation se réduisent aux
parenthèses, crochets et accolades ouverts et fermés : ( ), [
], { }.
Maintenant, nous pouvons comparer la logique des classes
avec la logique des propositions inanalysées au moyen du tableau
suivant:
|
Logique des classes
|
Logique des propositions inanalysées
|
|
N°
|
Noms
|
Descriptions
|
Symboles
|
Noms
|
Descriptions
|
symboles
|
|
01
|
Le Complément des classes
|
L'exception des certains éléments dans une
classe donnée
|
-
|
La négation
|
C'est un opérateur unaire ou monadique. Il ne porte
que sur une proposition, ex ~p
|
~
|
|
02
|
Le produit logique
|
L'intersection de deux classes
|
.
|
La conjonction
|
C'est un opérateur binaire elle met en relation
deux propositions ou deux expressions. Elle est vraie lorsque ces deux
arguments sont vrais ex p Ë q
|
^
|
|
03
|
La somme logique
|
La réunion de deux classes
|
+
|
La disjonction
|
Elle est un opérateur binaire. Elle est vraie
lorsque au moins l'un de ces membres est vrai.
Ex : p í q
|
v
|
|
04
|
L'identité
|
La copules est
|
=
|
L'équivalence ou la bi- implication
|
Elle est aussi binaire. L'équivalence entre deux
propositions est vraie si celles -ci ont la même valeur de
vérité, elle exprime une forme d'identité. Ex : p
q
|
|
|
05
|
L'inclusion
|
L'inclusion d'une classe dans une autres
|
|
L' implication
|
Elle est également binaire. Elle est fausse si
l'antécédent est vrai et le conséquent faux, vraie dans
les autres cas. Ex : p? q
|
?
|
|
06
|
Les symboles littéraux
|
Les classes quelconques ce sont des variables
|
X, y, z...
|
Les variables propositionnelles
|
Elle désignent les énoncés du langage
ordinaire
|
p,q,r,...
|
|
07
|
La classe universelle
|
Univers du discours
|
1
|
La tautologie
|
Loi logique ou expression valide
|
pv ~p
1101
0110
|
|
08
|
La classe vide
|
Classe nulle
|
0
|
Contradiction logique
|
Expression fausse sur toutes les lignes.
|
p ^~p
1001
0010
|
CONCLUSION
GÉNÉRALE
A la lumière de tout ce qui précède,
il sied de préciser que notre étude a porté sur
l'évolution et la révolution paradigmatique de la science
logique depuis les présocratiques jusqu'à Boole. Pour ce, nous
l'avions répartie (cette étude) en quatre chapitres.
Le premier chapitre a clarifié les concepts
opératoires, à savoir : logique et révolution
paradigmatique. Pour définir le terme logique, nous avions
utilisé trois approches différentes, mais complémentaires.
Pour l'approche étymologique, le mot logique dérive du grec,
à la fois du substantif logos, du qualificatif
logikê et du verbe legéin. L'approche
définitionnelle proprement dite a présenté la logique
comme l'étude des conditions de possibilités d'un raisonnement
correct. A l'approche mathématique, nous avions distingué la
tendance syntaxique de la tendance sémantique. Quant à la
révolution paradigmatique, nous l'avions scrutée avec Thomas
Samuel Kuhn et avions dégagé ses principaux moments qui sont :
la science normale, la science extraordinaire et la révolution
proprement dite.
Le deuxième chapitre a traité de la
science normale de la logique, celle-ci fonctionnait sur base d'un paradigme
emprunté aux sciences de la nature. Nous l'avions montré avec les
présocratiques (paradigme physiologique); avec Aristote qui utilisait un
modèle à la fois Zoologique et géométrique,
où le zoologique l'emportait sur le géométrique; nous
avions également montré que la logique
mégaro-stoïcienne était intimement liée, mieux
inséparable avec leur physique et leur morale, car les trois
constituaient la triade sur laquelle leur science se fondait, laquelle science
était essentiellement empirico-théiste. Les scolastiques et les
arabes médiévaux ont enrichi et perfectionné la
syllogistique traditionnelle. Nous avions aussi mis en exergue l'apport des
maîtres hindous en logique.
Le troisième chapitre du présent travail
avait pour tâche d'étudier la science extraordinaire de la
logique. Celle-ci, de Raymond Lulle à De Morgan, est
caractérisée par diverses propositions des nouvelles idées
et des nouvelles méthodes (quoique certaines restèrent non
abouties).
Le dernier chapitre a porté sur la
révolution proprement dite de la science logique en montrant et
démontrant l'innovation de l'oeuvre de Boole. Celle-ci sera
simplifiée et perfectionnée par Jevons, Peirce et Schröder.
Ceux-ci enrichissent l'oeuvre de Boole et lui donne la forme symbolique que
nous connaissons sous le nom d'Algèbre de la logique.
Tout compte fait, nous avons démontré que
la syllogistique traditionnelle fonctionne sur base d'un paradigme
emprunté, sinon similaire à celui des sciences de la nature et
que la logique symbolique moderne opère sur base d'un modèle
mathématique.
BIBLIOGRAPHIE
I. Ouvrages
1. Aristote, Organon, I catégories, II De
l'interprétation, Paris, Librairie philosophique J. Vrin, 1969,
153p.
· Organon, III. Les premiers
analytiques, Paris, Librairie philosophique J. Vrin, 1971,
334p
· Organon, IV. Les seconds
analytiques, Paris, Librairie philosophique J. Vrin, 1938,
251p
· Organon, V. les topiques, Paris,
Librairie philosophique J. Vrin, 1974, 368p
· Organon, VI. Les réfutations
sophistiques, Paris, Librairie philosophique J. Vrin, 1939,
155p
2. Avicenne, Le livre de science I (logique,
métaphysique), Paris, Les belles lettres, 1955, 241p.
3. Blanché, R., La logique et son histoire.
D'Aristote à Russell, Paris Armand colin, 1970, 366p.
4. Bochenski, I.M., Précis de logique
mathématique, Bussum (PAYS Bas) F.G Kroonder, 1948, 90p.
5. Boll M., et Reinhart, Histoire de la logique,
Paris, PUF, 1961, 128p.
6. Boole G., The mathématical analysis of
logic, Oxford, Basil Black well, 1847, 82p.
7. Chauvineaux, J., La logique moderne, Paris,
PUF, 1957, 128p.
8. Colerus, E, Les grandes époques des
mathématiques et leurs maîtres. De Pythagore à
Hilbert, Paris, Flammarion, 1937, 317p.
9. Cori, R et Lascar, D., Logique
mathématique, 1. Calcul
propositionnel, algèbre de Boole, Calcul
des prédicats, Paris,
Dunod, 2003, 385p.
10. Cori, R et Lascar, D., Logique
mathématique, 2. Fonctions
récursives, Théorème de
Gödel, Théorie des ensembles, Théorie des
modèles, Paris, Dunod, 2003, 347p.
11. Descartes, R, Discours de la méthode,
Paris, Hatier, 1924,
12. Dirven, E., Introduction aux logiques,
(3ème éd.), Kinshasa, Ed. Loyala, 1990, p205p.
13. Dopp, J., Notion De logique formelle,
Louvain, Nauwelaerts, 1972 ; 304p.
14. Flegg, H., La logique de Boole et son
utilisation, Paris, Dunod, 1967, 245p.
15. Husserl, E, Logique formelle et
transcendantale, Paris, PUF, 1957, 447p.
16. Imbert, C., Pour une histoire de la logique, Un
héritaghe platonicien, Paris, PUF, 1999, 302p.
17. Kotarbinski, T, Leçon sur l'histoire de la
logique, Paris, PUF, 1964, 388 p.
18. Kuhn, T.S, Structure des révolutions
scientifiques, Paris, Flammarion, 1972.
19. Lewis, C., Logique sans peine, Paris,
Hermann, 1966, 288p.
20. MAYOLA MAVUNZA LWANGA, Logique,
parémiologie et argumentation, Kinshasa, science et
discursivité, 2004, 144p.
21. MUTUNDA MWEMBO, Eléments de logique,
Kinshasa, MédiaSpaul, 2006, 112p.
22. Piaget (DIR), Logique et connaissance
scientifique, Paris, Gallimard, 1967, 1345p.
23. Scholz, H, Esquisse d'une histoire de la
logique, Paris, Ed. Montaigne, 1968, 156p.
24. TATON, R, La science antique et
médiévale. Des origines à 1450, Tome I, Paris, PUF,
1957.
II. Articles
1. « Algèbre de Boole (
logique) » in http :www.wikipédia.org/logique
2. Bachimont, B, « Logique : histoire et
formalismes. De liebniz à Boole » , in
http://wwwuniversité
de technologie de compiègne, org/ligique.
3. Feys R., « Boole as a logician», in
varia n° 4/22
4.
http://www.wikipédia.org/bernard Bolzano
5.
http://www.wikipédia.org/George Boole
6.
http://www.wikipédia.org/Leibniz
7.
http://www.wikipédia.org/Ernest schröder
8. Mutombo, M, « un petit aperçu sur la
logique classique » in revue philosophique de Kinshasa, vol XIV,
n° 25-26, 2000, pp.145-169.
III. Notes de cours
1. MBOLOKALA IMBULI, Syllabus d'histoire de la
phisophie antique, 2004.
2. NDOBO KOTI, Abstract d'Eléments de logique
de Mutunda, cours de logique destiné aux étudiants de
premier graduat en sciences économiques, 2004-2005.
3. TSHIAMALENGA NTUMBA, Notes de cours de philosophie
orientale.
IV. Dictionnaires et encyclopédie
1. Bailly, M.A., Dictionnaire
Grec-Français, Paris, Hachette, 1929.
2. BOISACQ, E, Dictionnaire étymologique de la
langue grecque, Paris, librairie C, Klincsieck 1923,
3. Dictionnaire le Petit Larousse, grand format,
Paris, Larousse, 2002.
4. Huisman D., (Dir)- Dictionnaire des
philosophes,
A-J, Volume 1, Paris, PUF, 1984.
- Dictionnaire des philosophes
K-Z, Volume 2, Paris, PUF, 1984.
5. LALANDE, A, Vocabulaire technique et critique de la
philosophie, Paris, PUF, 1991
6. MATTEI J.F., - Encyclopédie philosophique
universelle, III. Les oeuvres philosophiques, Dictionnaire, Tome1, Paris,
PUF, 1992.
- Encyclopédie philosophique
universelle, III. Les oeuvres philosophiques, Dictionnaire, Tome
2, Paris, PUF, 1992.
TABLE DES
MATIÈRES
REMERCIEMENTS
II
INTRODUCTION
GÉNÉRALE
1
CHAPITRE PREMIER : PRECISIONS
TERMINOLOGIQUES
3
1.1. LOGIQUE
3
1.1.1. Approche
étymologique
3
1.1.2. Approche
définitionnelle proprement dite
4
1.1.3. Approche
mathématique
6
I.2. RÉVOLUTION
PARADIGMATIQUE
7
CHAPITRE DEUX : LA SCIENCE NORMALE
DE LA LOGIQUE
9
II.1. ANTIQUITÉ
9
II.1.1. Les
présocratiques
9
· HERACLITE D'EPHESE
(567-480 ACN)
10
· Parménide et
Zénon d'Elée
11
· Démocrite
d'Abdère (Vème siècle ACN)
11
II.1.2. les socratiques
12
· Protagoras
d'Abdère et Gorgias de Léontini
12
· Socrate (470-399ACN)
12
· Platon (428/427-348/347
ACN)
13
II.1.3. Les post- socratiques
14
· Aristote (384 - 322
ACN)
14
· Les Mégaro -
stoiciens
15
II.2. MOYEN ÂGE
17
II.2.1. La Scolastique
17
II.2.2. Le monde Arabe
18
II.2.3. Les maîtres
hindous
19
CHAPITRE TROIS: LA SCIENCE
EXTRAORDINAIRE DE LA LOGIQUE
22
III.1. PROPOSITIONS DE NOUVEAUX
MODÈLES
22
· Raymond Lulle
(1235-1315)
22
· Francis Bacon
(1561-1626)
23
· René Descartes
(1596- 1650)
25
III.2. LES PRÉCURSEURS DE
BOOLE
26
· Gottfried Wilhelm LEIBNIZ
(1646-1716)
26
· Bernard BOLZANO
(1781-1848)
29
· WILLIAM HAMILTON
(1788-1856)
29
· Auguste de Morgan
(1806-1878)
30
CHAPITRE QUATRE: LA RÉVOLUTION
DE LA LOGIQUE FORMELLE
34
IV.1. GEORGE BOOLE OU LE PÈRE DE LA
LOGIQUE MODERNE ()
34
IV.1.1. Eléments
bio-bibliographiques
34
IV.1.2. Eléments de la logique des
classes
37
A. Les classes, les symboles
littéraux et les opérateurs de base
37
· Les classes
37
· Les symboles
littéraux
37
· Les opérateurs de
base
38
B. Les lois fondamentales de la
logique des classes
38
a. La commutativité
39
b. L'associativité
39
c. La distributivité
39
d. La loi des indices ou
l'idempotence
40
e. La loi de la
complémentarité
40
C. Interprétation de la
logique des classes
41
IV.2. LES CONTINUATEURS DE BOLLE
43
· William
Stanley Jevons ()
43
·
Schröder friedrich Wilhemln Karl Ernst ()
46
IV.3. ETUDE COMPARATIVE ENTRE LA LOGIQUE DES
CLASSES ET CELLE DES PROPOSITIONS INANALYSÉES
48
CONCLUSION
GÉNÉRALE
51
BIBLIOGRAPHIE
53
TABLE DES MATIÈRES
56
* 1 Cfr BOISACQ, E,
Dictionnaire étymologique de la langue grecque, Paris,
librairie C, Klincsieck 1923, p585. Et Bailly, A, Dictionnaire Grec
Français, Paris, Librairie Hachette, 1929, p1200.
* 2 Idem
* 3 Cfr Notes de cours
d'histoire de la philosophie Antique dispensé par le professeur
Mbolokala Imbui, 1ère graduat.
* 4 BOISACQ, op.cit,
p.585 et Bailly, op.cit, p.1200
* 5 Cité par MUTUNDA
MWEMBO, Eléments de logique, Kinshasa Médias, Paul,
2006, p.8.
* 6 Idem
* 7 LALANDE, A,
Vocabulaire technique et critique de la philosophie,
13ème édition, Paris, PUF, 1980, p.572.
* 8 Cfr Kotarbinski, T,
Leçon sur l'histoire de la logique, Paris, PUF, 1964, p.5.
* 9 Idem
* 10 Ibidem
* 11 Dictionnaire le
Petit Larousse, Grand Format, Paris, Larousse, 2002, p.53
* 12 LALANDE, A,
Op.cit, p.35
* 13 Idem
* 14 George Boole, An
investigation of the Laws of thought (1854), cité par Jean-Blaise
Grise in logique et connaissance scientifique, Paris, Gallimard, 1967,
p.139.
* 15 Denis Huisman,
Dictionnaire des philosophes, Paris, PUF, 1984, p.1463.
* 16 Kuhn, T.S,
Structure des révolutions scientifiques, Paris, Flammarion,
1972, p.240.
* 17 Idem, p.98.
* 18 Dictionnaire le
Petit Larousse, grand format, op.cit, p.778
* 19 Platon, Cratyle
402, cité par MBOLOKALA IMBULI, op.cit.
* 20 Cfr MUTUNDA MWEMBO,
op.cit. p.16
* 21 NDOBO KOTI,
Abstract d'éléments de logique de MUTUNDA, cours de
logique destiné aux étudiants de premier graduat en sciences
économiques, 2004-2005, p.2
* 22 Xenophon
(mém, IV, 7) cité par René TATON, la science
antique et médiévale. Des origines à 1450.
TOME I, paris, PUF, 1957, p.210
* 23 René TATON,
idem, p.249.
* 24 MUTUNDA MWEMBO,
Eléments de logique, op.cit, p21
* 25 MBOLOKALA IMBULI,
op.cit
* 26 Cité par Robert
Blanché, La logique et son histoire. D'Aristote à
Russell, Paris, Armand Colin, 1970, p.92.
* 27 Cité par MUTUNDA
MWENMBO, op.cit p.22
* 28 Idem, p.21.
* 29 Blanché,
op.cit, p. 140
* 30 Idem.
* 31 Ibidem p.147
* 32 Avicenne, Le livre
de science I (logique, métaphysique), Paris, Les belles lettres,
1955, p.241.
* 33 Cfr MUTUNDA MWEMBO,
Op.cit, p.39.
* 34 Ce paragraphe ainsi que
ceux qui suivent s'inspirent de TSHIAMALENGA NTUMBA, Notes de cours de
philosophie orientale.
* 35 KOTARBINSKI,
op.cit, p.99.
* 36 Cfrt JEAN FRANCOIS
MATTEI, Encyclopédie philosophique universelle, III. Les
oeuvres philosophiques, dictionnaire, TOME1, Paris, p943
* 37 Cfr. René
Descartes, Discours de la méthode, Paris, Hatier, 1924,
p.p.35-36.
* 38 Cfr. JAEN- FRANCOIS
MATTEI, op.cit, p. 1085
* 39 Descartes,
op.cit, p.35
* 40 Kotarbinski,
op.cit, p. 131
* 41 Leibniz, l'art
combinatoire, cité par «
http : //fr.wikipedia.Org/leibniz »
* 42 Cfr. JEAN- FRANCOIS
MATTEI, op.cit, p. 1274
* 43 Kotarbinski,
op.cit, p.p 132-133
* 44 Cfr.
« http:// fr.wikipedia.Org/ Bernard Bolzano »
et JEAN-FRANCOIS MATTEI, op.cit p.p 1625-1626
* 45 Idem
* 46 Kotarbinski,
op.cit, p.145
* 47 idem
* 48 Ce point s'inspire de
«
http://fr.wikipédia.org/george
Boole » et Jean-françois Mattei, op.cit,
pp.1630-1631.
* 49 Jean François
Mattei, Op.cit, p.1630.
* 50 Lalande,
Op.cit, p.
* 51 Cfr Jean
François Mattei, op.cit, p.1630
* 52 Cet exemple nous
l'empruntons à J. Sleszynski, le calcul logique de Boole, p.21,
cité par Kortarbinski,, op.cit, , p.166.
* 53 Cfr, «http: //
fr.wikipédia.org/wiki/william stanley Jevons"
* 54 Cfr Jean -
François Mattei, op.cit, p.1868.
* 55 Idem, pp.2826-2827 et
http://fr.wikipédia.org/ernstschröder
* 56
"http://fr.wikipédia.org/Ernst Schröder"
* 57
"http://www.centredelogiquie.org/lalogique pour les nuls"
* 58 MUTUNDA MWEMBO,
op.cit, pp.50-51.



