CHAPITRE IV : IMPACT DE L'UTILISATION D'UN MODELE
INTERNE
SUR LA VALORISATION DU BILAN EN ASSURANCE NON-VIE ?
Dans ce chapitre, nous nous proposons de valider notre
hypothèse de travail à l'aide de quelques données que nous
allons simuler en nous basant également sur les données issues
des derniers résultats comptables des entreprises d'assurance en France.
Afin de rendre nos comparaisons claires et sans ambiguïté, nous
considérons deux entreprises fictives, Ariskov-vie et Ariskov-non-vie,
spécialisées chacune respectivement dans les secteurs vie et
non-vie. Nous commençons donc ce chapitre par notre démarche
méthodologique, ensuite, nous présentons très
brièvement les méthodes utilisées pour réaliser nos
calculs et faire nos comparaisons, et, nous finissons par une synthèse
des résultats et une confrontation de ces derniers avec ceux
trouvés par d'autres auteurs notamment Serrant (2006) et les
éventuelles extensions du sujet.
SECTION I : Approche méthodologique et
données utilisées
Nous présentons donc ici la démarche que nous
adoptons pour réaliser nos calculs et comparaisons.
PARAGRAPHE 1 : Démarche méthodologique
adoptée
Il est question dans ce chapitre de valorisation de bilan,
commençons par présenter les éléments d'un
bilan28 en assurance.
Le bilan d'une société décrit la situation
de l'entreprise à la date d'inventaire ou de clôture des comptes.
Il est constitué pour un assureur de trois principaux
éléments à savoir :
- au passif, les dettes et engagements, constitués
essentiellement des provisions techniques ; - à l'actif, les biens et
créances, essentiellement des placements financiers ;
- la différence de ces deux éléments
constitue les capitaux ou fonds propres ou encore situation nette comptable
(SCN) qu'on retrouve également au passif.
Nous réalisons nos comparaisons à l'aide des
ratios de couvertures. Le ratio de couverture se calcule comme le rapport entre
la marge constituée au bilan et l'exigence de marge. Bien qu'il existe
plusieurs ratios de couvertures -couverture des engagements, couverture
bilancielle de la
28 Ce que nous avons largement présenté
dans les chapitres précédents ; voir par exemple schéma
n°1.2.3
- 42 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
marge et couverture de la marge brute de solvabilité-
nous utilisons la dernière, couverture de la marge de solvabilité
qui inclut les autres. Il se calcule comme le rapport entre la marge de
solvabilité constituée au bilan (MSC) que nous
détaillerons plus loin et l'exigence de marge de solvabilité (EMS
selon Solvency I et SCR selon Solvency II). Ce calcul est fait, dans ce
mémoire, selon le secteur d'activité (vie ou non-vie), la
méthode utilisée (formule standard ou modèle interne) et
la réglementation adoptée (Solvency I ou Solvency II).
En France, la marge de solvabilité constituée
(MSC) est la somme de la situation nette comptable, de la plus value latente
des placements (PVL-excédent de la valeur de réalisation sur la
valeur comptable) et enfin des possibilités de rappel de cotisations
(pour certaines sociétés mutuelles à cotisations
variables) soit donc :
MSC = SNC + PVL + Rappels de cotisations des
mutuelles.
Une fois la marge de solvabilité constituée
calculée, il faudra déterminer maintenant les exigences
réglementaires ou exigences de marges de solvabilité que nous
avions appelés EMS dans le référentiel Solvency I et que
nous appelons SCR dans le référentiel Solvency II. Rappelons
toutefois que :
Dans le référentiel Solvency I,
- En non-vie,
EMS = max {0,18*prime (<50 M) + 0,16*prime (>50M)}
; {0,26*prime (<35 M) + 0,23*prime (>35M)} )
(
- En vie,
EMS = (0,04*PM) + (0,02*Capitaux sous risques) )
(
Nous avons choisit un pourcentage de 2% des capitaux sous risques
comme une moyenne du pourcentage réglementaire (entre 1 et 3%).
Le SCR en vie ou en non vie est quant à lui calculé
comme nous en avons discuté au chapitre29 2. Nous explicitons
plus loin certaines conditions de calculs.
29 Modèle interne versus formule standard
- 43 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
A partir des exigences de marges constitué (MSC) et
réglementaires (EMS ou SCR selon le référentiel
considéré, la méthode de calcul utilisée et le
secteur d'assurance) nous allons déterminer les ratios de couvertures
correspondants Ri à travers la formule :
Ri = MSC/EMS(ou SCR).
Ce qui est évoqué dans le tableau n° 4.1.1;
dans ce tableau, Bv représente le ratio de couverture de
marge en assurance vie selon le référentiel Solvency II et
calculé à l'aide de la formule standard. Il faut remarquer que
dans le référentiel Solvency I, on n'adoptait pas encore la
formule standard ; le ratio de couverture est unique (Av ou
Anv) et ne dépendait donc pas d'un choix de méthode de
calcul donnée.
Ensuite à partir de ses ratios calculés dans ce
tableau, on calcule l'écart relatif entre la valeur du ratio dans le
référentiel Solvency I et sa valeur dans le
référentiel Solvency II et cela pour chacune des deux
méthodes. Le tableau n°4.1.2 expose ce mode de calcul. Par exemple,
r1,nv représente cet écart (l'évolution) pour le secteur
non-vie et calculé en utilisant la formule standard.
Tableau n°4.1.1 : Calcul des ratios de
couvertures selon la méthode, le secteur d'assurance et
le
référentiel réglementaire.
|
Méthodes
|
Assurance vie
|
Assurance non-vie
|
|
Formule
|
|
Ratio calculé
|
|
Ratio calculé
|
|
standard
|
|
sur la base de
|
|
sur la base de
|
|
Ratio calculé
|
Solvency II
|
Ratio calculé
|
Solvency II
|
|
sur la base de
|
(Bv)
|
sur la base de
|
(Bnv)
|
|
Modèle interne
|
Solvency I
|
Ratio calculé
|
Solvency I
|
Ratio calculé
|
|
(Av)
|
sur la base de
|
(Anv)
|
sur la base de
|
|
|
Solvency II
|
|
Solvency II
|
|
|
(Cv)
|
|
(Cnv)
|
Tableau n°4.1.2 : Evolution des ratios de
couvertures selon la méthode, le secteur d'assurance
et le
référentiel réglementaire.
|
Méthodes
|
|
Assurance vie
|
|
Assurance non-vie
|
|
Formule standard
|
r
|
-
B A
v v
|
r =
1, nv
|
-
B A
nv nv
|
|
1, v =
A
v
|
A
nv
|
|
Modèle interne
|
r
|
-C
C A
v v
|
r =
2, nv
|
- A nv nv
|
|
2, v =
A v
|
A nv
|
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Les hypothèses sur les résultats attendus sont
présentées dans le tableau n°4.1.3 ; par exemple, on
s'attend à ce que l'évolution relative30 du ratio de
couverture de marge en assurance vie en utilisant un modèle interne soit
inférieure qu'en utilisant la formule standard tandis que le
résultat est inversé ou insensible en assurance non-vie. En
d'autres termes que l'utilisation d'un modèle interne est plus
pertinente en vie qu'en non-vie.
Tableau n°4.1.3 : Hypothèses de travail.
|
Secteur
|
Hypothèses
|
|
Assurance vie
|
r 1, v > r 2, v
|
|
Assurance non-vie
|
r 1, nv<r 2, nv
|
Afin de déterminer les exigences de marges
(réglementaires et constituée), il nous faut modéliser les
provisions techniques d'une part et la valeur des actifs ou des placements en
fonction des différents risques. Les précédentes
études d'impacts (QIS) ont montré que le risque
opérationnel représentait entre 2 et 4 % et le risque de
crédit n'était pas aussi important ; nous traiterons donc
seulement les risques de marché (spécialement les risques ALM
pour la vie) et les risques de souscriptions (très importants en
non-vie).
Nous modélisons donc le risque de marché pour
les actifs ; pour les provisions techniques31, nous
modélisons le risque de souscription en vie et en non vie.
Concernant le risque de marché, il s'agit des risques
d'allocation Actif-Passif ou risques systémiques ; il s'agit du risque
liés aux instruments financiers et dont les cours sont susceptibles de
varier. Nous supposons qu'il n'existe pas de supplément de
volatilité dans les portefeuilles d'actifs concentrés (actions et
obligations) ; nous ne modélisons donc pas le risque de concentration.
Nous ne modélisons pas aussi les risques de spread dans
l'hypothèse qu'il n'existe pas de variation des spreads de crédit
au-delà de la courbe des taux sans risque. Bien que l'on ait connu des
crises subprimes dans le secteur de l'immobilier aux Etats-Unis et la hausse
continue du prix du pétrole - deux facteurs qui ont eu beaucoup
d'impacts sur les cours des devises internationales (notamment le dollar et
l'euro)- nous restons dans un cadre restreint de modélisation de risque
de taux d'intérêt et de risque d'actions.
30 Comparaison d'évolution relative simple sans
faire de test statistiques d'égalité de rapport.
31 Constitué de quatre
- 45 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Pour les risques de souscription, il s'agit des risques
liés à une tarification insuffisamment prudente lors de la
souscription ou d'une modification des conditions de souscriptions ou rachats
de contrats. En vie, on a le risque de table (inadéquation de la table
de mortalité au portefeuille), et le risque intrinsèque
(lié au nombre de contrat souscrit) : on modélise donc les
Provisions mathématiques-PM, estimées individu par individu.
Elles représentent la valeur actuelle probable des prestations que
l'assureur doit verser au cours des exercices futurs, au titre des
évènements survenus lors des exercices antérieurs. En
non-vie, ces risques sont constitués par la volatilité du
résultat ou de la sinistralité sur les engagements aussi bien
passés que futurs. Nous ne modélisons ici que les Provisions pour
Sinistres A Payer - PSAP, estimées à partir des modèles de
cadences ou de développements. Comme leurs noms l'indiquent, les PSAP
constituent la valeur estimative des dossiers non encore payés à
la clôture de l'exercice, mais dont les sinistres sont survenus avant la
date d'inventaire, qu'ils soient connus ou non à cette date.
Rappelons donc une fois encore que la modélisation des
risques permet d'avoir la distribution des éléments du bilan
(notamment celle des provisions techniques et des placements). Il existe deux
familles de méthodes pour déterminer les provisions techniques-
PT sans marge de risque: les méthodes déterministes et les
méthodes stochastiques.
La modélisation déterministe des provisions
techniques permet d'estimer en moyenne l'évolution des engagements. Les
paramètres de calcul souvent prudents restent constants ou varient de
façon prédéterminée (exemple de la table de
mortalité). La modélisation dans cette famille de méthodes
pour les PSAP se réalise à l'aide des modèles de cadences
; parmi ces derniers, celui de référence est la méthode de
Chain Ladder. Quant aux Provisions Mathématiques, l'approche contrat par
contrat est préconisée ; qu'il s'agisse des rentes de conjoint ou
d'éducation, des rentes liées à l'arrêt de travail
ou autres rentes.
Les modèles stochastiques de passifs permettent
d'obtenir une fonction de distribution des provisions. Ils sont donc utiles et
se développent de plus en plus depuis quelques années. Ils en
existent trois sous-familles : les modèles paramétriques
basées sur une loi appartenant à une famille connue de loi dont
il faut déterminer les paramètres, les modèles
semi-paramétriques qui ne font pas d'hypothèses a priori
sur la distribution des provisions mais estiment cette distribution et, enfin
les modèles non paramétriques qui simulent des intervalles de
confiance pour les provisions sans aucune hypothèses sur la distribution
de ces provisions mais qui
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
s'appuient sur certaines données de bases (les triangles
de règlements par exemple). Ils nécessitent tous la
définition d'une mesure de risque.
L'objet même de ce chapitre étant de mesurer
l'impact sur le bilan, donc sur les ratios de couvertures, nous ne rentrerons
pas trop dans les détails sur certaines méthodes
utilisées. Nous présentons quelques méthodes ou
détails usuels sur les méthodes utilisées dans la partie
annexes des méthodes. Nous rappelons juste l'idée ou l'intuition
de ces méthodes et leur intérêt pour nos calculs et
éventuellement un petit exemple.
Les modèles stochastiques de passifs sont donc utiles
et se développent de plus en plus depuis quelques années. Ces
modèles utilisent des techniques de simulations. Comme le
précisait Elie et Lapeyre (2001), ces techniques permettent, en
général, d'étudier et d'expérimenter un
système donné dont on connaît les interactions complexes,
de mesurer les effets de certains changements dans les interactions sur le
comportement du système, d'expérimenter de nouvelles situations.
Nous utilisons dans ce mémoire les simulations de Monte Carlo. Les
paramètres à faire varier dépendent du risque à
intégrer et l'élément du bilan à
modéliser.
1) Techniques de simulations
L'approche stochastique de détermination des
éléments du bilan, qu'il s'agisse des provisions ou des
placements, basée sur les méthodes de Monte Carlo a pour but
d'étudier un grand nombre de scénarii ou allures possibles, afin
de déduire une loi de distribution du montant de provisions ou de
placements. Ces méthodes approchent le résultat théorique
recherché en effectuant des tirages selon la loi du
phénomène observé. L'existence d'un
générateur de nombres aléatoires leur sert de base.
Un générateur de nombre aléatoire est un
algorithme fournissant une suite de nombres compris entre 0 et 1. Il existe des
générateurs pseudo aléatoires implémentés
par défaut dans certains langages, notamment C++, Pascal,... qui
produisent des valeurs déterministes et parfaitement prévisibles,
mais qui sont statistiquement satisfaisantes.
Avec les progrès informatiques actuels, les
méthodes de simulations Monte Carlo les plus utilisées sont la
technique de l'inversion de la fonction de répartition qui n'est
réalisable que si l'on connaît une forme explicite et relativement
simple de la fonction de répartition. Une définition sert de base
à cette technique :
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Définition :
Considérons une variable aléatoire réelle X de fonction de
répartition F. On appelle alors inverse généralisée
de F, la fonction notée F-1 définie pour tout
réel y compris entre 0 et 1 par :
F ( y ) = inf x ? R | F ( x )
= y
-1 { }
L'idée de base de cette technique consiste à
simuler des réalisations d'autres variables aléatoires (qu'on ne
connaît pas) à partir de réalisations de variables qui
suivent une loi définie (connue). Le lemme suivant est utilisé
à cet effet :
Lemme : Si U est une variable
aléatoire de loi uniforme U sur [0,1], alors F-1(U) a
même loi que X. Et si de plus, F est continue surR , alors F(X) suit une
loi uniforme U [0,1].
Il arrive parfois que l'on ne dispose pas de formule explicite
pour l'inverse de la fonction de répartition, F-1, c'est le
cas particulier de la loi normale ou lognormale que nous avons largement
utilisé dans ce mémoire ; dans ce cas, on utilise les algorithmes
d'approximation de cette fonction ou des algorithmes spécifiques
à la loi que l'on souhaite travailler. Cependant il existe d'autres
algorithmes de simulation de la loi normale comme par exemple la méthode
de Box Muller ou la méthode du rejet polaire ; des méthodes que
nous n'avons pas utilisées donc que nous ne présentons pas dans
ce mémoire.
2) Mesure du risque
Le montant de la provision avec marge de risque est
calibré à travers l'utilisation des mesures de risque, pour un
ensemble de provisions simulées stochastiquement. La différence
entre la provision avec marge de risque et celle calculée en « Best
Estimate » constitue la marge.
Denuit et Delwarde (2006) définissait une mesure de
risque comme une fonction ñ qui à un risque X associe un nombre
positif noté ñ[X], éventuellement infini ; cette
fonctionnelle est telle que, pour ñ[0] = 0, ñ[X] désigne
le montant minimum qui, additionné à la perte X en début
de période rend la couverture de X "acceptable". C'est donc le capital
dont doit disposer la compagnie pour faire face à une perte
financière de montant X. Parce qu'il est question d'agréger
plusieurs risques ici en tenant compte de leurs dépendances
éventuelles, deux principales propriétés des mesures de
risques nous intéressent ici : le chargement de sécurité
et la propriété de sous-additivité.
Le chargement de sécurité stipule que :
ñ[X] = Å[X] pour tout risque X.
Quant à la propriété de
sous-additivité, elle implique :
ñ[X+ Y]=
ñ[X]+ñ[Y] quels que soient
les risques X et Y.
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
La propriété de sous-additivité est sujette
à débat pour le moment : pour Dhaene et al. (2003), le signe de
l'effet de diversification ñ [X] + ñ
[Y] - ñ [X + Y] devrait
dépendre de la structure de
dépendance existant entre les risques X et Y
considérés.
Il existe un ensemble de mesure de risque, notamment la
Value-at-Risk (Var), la Tail-VaR ou VaR moyenne, la Conditionnal Tail
Expectation (CTE) ou VaR conditionnelle, la mesure de risque de Wang et
beaucoup d'autres.
Dans le cadre des consultations pour l'élaboration des
normes Solvency II, deux mesures de risques sont privilégiées :
la VaR préconisée par le CEIOPS notamment pour l'estimation du
niveau de provisions technique avec marge de risque et la Tail-VaR
préférée par les parties prenantes pour l'estimation du
besoin en capital.
· La Value-at-Risk ou valeur à
risque
Il existe plusieurs définitions de la Valeur à
Risque. Selon Esch, Kieffer et Lopez (1997) ainsi que Jorion (2000), la VaR
d'un portefeuille ou d'un actif, pour une durée T et un niveau de
probabilité á, se définit comme le montant de perte
attendu de façon que ce montant, pendant la période [0,T], ne
devrait pas être plus important que la VaR et ceci avec une
probabilité de (1 - á). Le graphique n° 4.1.1 montre un
exemple de calcul de VaR aux seuils respectifs 75% et 99,5%.
Graphique n°4.1.1 : Exemple de VaR pour
une série de provisions suivant une loi normale.
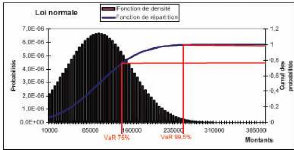
Deux éléments principaux ressortent de cette
définition et il est important de les choisir judicieusement : l'horizon
et le niveau de confiance.
L'horizon qui se doit d'être adapté aux
données et d'être suffisamment court afin d'être
estimable.
Le niveau de confiance doit quant à lui refléter le
degré d'aversion des gestionnaires face au risque de réalisation
d'événements extrêmes sans être trop
élevé. C'est une mesure probabiliste.
- 49 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Ainsi pour une série X donnée,
Pr[X<
VaR(X,á)]=á
On voit bien que la VaR dépend des
propriétés de la série X. Elle fournit une
information sur la charge de sinistres au-delà de laquelle il y a perte
avec la probabilité á et se calcule aisément une fois la
répartition de X connue. Par ailleurs, elle ne vérifie
pas certaines propriétés des mesures de risques notamment les
deux que nous avions cités précédemment. En effet, d'une
part, elle ne fournit pas d'information sur la queue de la distribution de la
série et donc ne possède pas de chargement de
sécurité - on observe des cas de violation de
l'inégalité VaR(X,á) =
Å[X] pour
á = 0.5 du fait de l'asymétrie
liée aux queux de distribution qu'on observe généralement
en assurance-; d'autre part, elle n'est pas sous additive, ce qui signifie
qu'en réalisant la somme des VaR - ce qui sera le cas pour nos
agrégations- de plusieurs branches, on n'a pas une garantie de prudence.
Pour palier à cette insuffisance, nous utilisons d'autres mesures de
risque de la même famille que les VaR mais qui vérifient ces
propriétés : la Tail-VaR et la CTE comme cités ci-
dessus.
~ La Tail Value-at-Risk
La Tail Value at Risk au seuil á d'une distribution X,
noté TVaR (X, á) est définit par :
1
1
î
TVaR X VaR X d
( ; ) ( ; )
á î
=
1 - áá
Ou de façon équivalente pour les lois continues
:
|
T Va R
|
1
( ; ) ( , ) ( , )
X á V aR X á X V aR X
= + á Å ( )
- +
á
1 -
|
Cette mesure est en quelque sorte la moyenne des VaR de
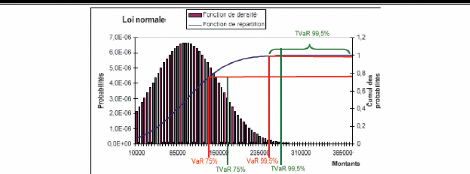
seuil supérieur á. Le graphique n° 4.1.2 montre un exemple
de calcul de VaR et TVaR aux seuils respectifs 75% et 99,5%.
On peut également approcher la TVaR par la
CTE c'est-à-dire la valeur moyenne des pertes au- delà
de la VaR, définie par :
C T E ( X ; á ) [ X /
X V aR ( X , ) ]
= Å > á
Si la fonction de répartition de X est continue, les deux
notions convergent.
Graphique n°4.1.2 : Exemple de VaR et
TVaR pour une série de provisions suivant une loi
normale.
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Comme on le précisait un peu plus haut, la
TVaR vérifie la propriété de
sous-additivité, ce qui explique l'intérêt qui lui est
porté dans les modèles de consolidation impliquant
l'agrégation des risques. Dans le même temps, elle permet de
prendre en compte le comportement de la queue de distribution ; bien que
nécessitant un nombre un peu plus important de simulations.
La VaR et la TVaR constituent les deux outils
de mesures de risque que nous avons utilisé dans ce mémoire en ce
qui concerne les méthodes stochastiques.
3) Synthèse sur les méthodes
utilisées
Les méthodes présentées ci-dessous
concernent les deux secteurs d'activités en fonction de leurs
branches.
Les branches considérées en vie sont: Contrats
liés aux garantis décès et contrats liés aux rentes
(conjoint, éducation). Pour le CEIOPS, il s'agit des branches contrats
avec profits et sans profits, des contrats en unités de compte.
Les branches considérées en non-vie sont:
Responsabilité Civile-RC Matérielle et Dommages Automobile, RC
Corporelle Automobile, Incendie et Dommages aux biens, RC
générale.
Il est évident que dans le cadre de la
détermination des exigences de marges, il faut modéliser d'une
part le passif et d'autre part l'actif et éventuellement de
l'adéquation actif-passif. Nous présentons très
brièvement les modèles utilisés dans ce cadre. Pour
l'actif, et particulièrement le risque de marché, nous ne
distinguons pas les familles de modèles mais pour le passif, cette
présentation est réalisée selon la famille de
méthodes.
+ Le besoin en capital relatif au risque de marché
(actif)
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Pour l'actif, nous présentons très
brièvement le modèle de risque action et de risque obligation.
Notre démarche pour ces types de risque s'inspire complètement du
développement de Le Moine et Kaltwasser (2006). En effet, leur
étude propose une approche des risques de marché (action et
obligation). En marché complet, ils trouvent des résultats qui
permettent de déterminer les besoins en capital pour couvrir ces
risques. Dans un premier temps, ces auteurs montrent que le besoin en capital
est fonction du rendement de l'actif sans risque et de la volatilité du
portefeuille pour le risque action. Dans un second temps, ce besoin en capital
est estimé à partir d'une approche par quantile. Cette
dernière nous intéresse particulièrement pour rester dans
la logique de Solvency II.
Ils se basent sur un modèle Black &
Scholes32, pour le risque action et avec l'introduction du
modèle de taux de Heath, Jarrow & Morton (1987) mais toujours dans
une logique Black & Scholes pour le risque obligataire.
· La marge de solvabilité liée au
risque action.
Considérons un contexte avec un contrat d'assurance vie
en euro, à prime unique P, d'une durée de n ans, et de
taux technique rg et où il n'y a pas de rachat
possible avant le terme. Ainsi, l'engagement de l'assureur est de verser P.
(1+rg)n dans n ans. Il va donc devoir mettre en
provision mathématique la somme PM0= P. (1+
rg)n/(1+ ra)n, où
ra est le taux d'actualisation, c'est à dire le
rendement moyen des actifs sur cette période. Par prudence, ce taux doit
être inférieur au taux technique, la réglementation le
limite d'ailleurs au minimum entre 60% du Taux Moyen des Emprunts d'Etat-TME et
3,5%. Enfin, les actifs ne sont pas vendus avant les n années, les plus
values ne sont donc pas réalisées avant la sortie du contrat
« et il n'y a pas de participation aux bénéfices venant
augmenter les provisions mathématiques avant la sortie. Si on
prévoit une revalorisation à la sortie, celle-ci n'intervient
qu'en cas de rendement élevé des actifs au terme, et cela
n'affecte en rien l'exigence initiale en marge de solvabilité. »
L'assureur va donc placer cette provision mathématique
dans un actif S, qu'on suppose33 suivre un modèle
Black & Scholes :
dS t
St
ì ó
( , ) ( , )
t T dt t T dW
+ t
S PM
0 0
=
32 L'intuition fondamentale de Black et Scholes fut de
mettre en rapport le prix implicite de l'option et les variations de prix de
l'actif sous-jacent. Pour eux, le prix de l'option d'achat est indiqué
implicitement si le sous-jacent est échangé sur les
marchés
33C'est le standard, bien que certaines
améliorations soient apportées en prenant en compte d'autres
paramètres comme les dividendes (BlackScholes-Merton), ou les
options de taux de devises étrangères (modèle de
Garman-Kohlhagen) ou même dans la théorie moderne des taux
d'intérêt de Vasicek.
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
où p est le rendement de l'actif,
ó sa volatilité, est Wt est un mouvement
brownien standard.
Or, placé dans cet actif risqué (et en pratique,
l'actif de l'assureur comporte toujours un risque), une provision
mathématique-PM calculée de manière prudente ne permet pas
toujours à l'assureur de tenir ses engagements. Les assureurs
procèdent généralement par réplication de
portefeuille en identifiant une marge qui servira à couvrir la part
insuffisante de soldes de placement par rapport aux engagements pris.
Le Moine et Kaltwasser (2006) montrent que la marge de
solvabilité-MS peut être déterminée suivant la
formule:
MS = PM * (a -b.r + c.ó)
avec PM la provision mathématique, r le taux sans
risque et la volatilité de l'actif ó sous l'hypothèse de
rendements normaux ; et a et b des constantes réelles qui
dépendent du taux technique et du taux d'actualisation des engagements.
On constate que dans cette expression, la solvabilité n'est pas
seulement fonction des engagements, mais aussi de la qualité des actifs,
ainsi que du degré de prudence dans l'actualisation des engagements.
Ces auteurs montrent que pour rg=
rg =3,2 % ; r=5% et ó=10%, on a :
Marge= Provision mathématique* (0,002836-0,339253
.r+0,654483. ó)
Dans leur approche par quantile, ce qui nous intéresse
le plus, ils montrent que pour le même contrat (vie en euro, à
prime unique P, d'une durée de n ans, de taux technique
rg et sans possibilité de rachat avant le terme),
cette marge peut s'exprimer sous la forme :
MS s PM r e N d s t N d
( ) .(1 ) . . ( 2 ) . ( 1 )
= + - - -
n n t
- - ñ
( )
t a
s s
t t
=
+ ó u t
( ) . , [1, ].
u PM e t n
= ? ?
t
ó 2
ì - t
2
ó 2
s
ln ( ).
t + -
n t ñ +
.(1 ) 2
avec d1
n
PM r
+ a

ó
n t
-

d d n t
2 1
= - -
ó
où (0, 1) et N désignant la densité d'une
loi normale centrée réduite; N(-d ) et N(-d ) les
ut ~ N 1 2
valeurs de cette densité évaluée aux termes
d et d . PM= P.( 1 + r ) /( 1 + r ) la provision
n n
1 2 g a
mathématique à la maturité et
ñ le taux d'intéret sans risque.
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
L'intérêt de cette approche réside dans le
fait qu'à travers cette expression, on peut déterminé le
quantile (1-á)% de la marge de solvabilité ; puisqu'on
connaît la loi suivi par ut. En effet, la marge MS (st) est fonction du
prix st de l'actif à la date t et puisque ce dernier est fonction de ut
alors on peut déduire la loi suivi par MS à la date t par
transformation de la densité d'une fonction composée. Le quantile
est ainsi obtenu par des simulations Monte Carlo.
on a ( ) . , [1, ];
s t s t u t PM e t n
= = ? ?
ì - t
ó 2
2 +óut
dg s
( ) dg s
( )
donc ( ) or ( ) ( ( )). , on a donc la densité de la loi
de l'actif: ( ( )). .
u g s f u f g s ds
= = f g s
ds ds
Le véritable problème dans tous ces
modèles réside dans le choix de la volatilité des actifs.
Ho et Lee (1986) d'une part propose une volatilité, ce que nous avons
d'ailleurs retenue, de la forme :
ó(t,T)=ñ.(T -
t), d'une part et Hull et White propose (): ( )
( , ) 1 T t
t T ñ e ë
= - , ñ
- -
( )
ó ë
étant le rendement de l'actif.
· La marge de solvabilité liée au
risque obligataire.
Dans le cas précédent, on n'a
considéré qu'un portefeuille action qui est simple à
étudier. Mais ce cas ne correspond qu'à une partie de la
réalité, car 75 à 80% de l'actif d'une compagnie
d'assurance, surtout l'assurance vie est en effet, généralement
constitué d'obligations. De plus, pour rester dans la même logique
que Fédor (2006), la nouvelle proposition de directive s'oriente vers
une pérennisation de cette répartition dans les portefeuilles
d'actifs. En effet, considérons pour simplifier qu'il existe sur le
marché des obligations d'échéance n ans, fournissant un
taux fixe rb = rg. Pour simplifier les calculs,
nous supposons que cette obligation ne verse aucun flux avant le terme et verse
à l'échéance le nominal capitalisé au taux
rb.
En investissant les provisions mathématiques dans cet
actif, l'assureur ne prend donc aucun risque financier en l'absence de rachat.
En ce sens, son investissement lui assure de pouvoir fournir le montant garanti
dans les n ans. Le problème se pose lorsqu'il y a une sortie de contrat
: l'assureur doit alors vendre une partie de son actif. S'il y a eu entre temps
une hausse des taux d'intérêt, la valeur de l'obligation aura
baissé, et l'assureur ne pourra tenir son engagement avec la seule vente
de son investissement. Cela suppose que l'assureur trouve sur le marché
les obligations correspondant aux échéances de paiements
(T= n ans), ce qui n'est pas toujours le cas. Si
l'échéance est supérieure aux n années, même
en l'absence de rachats, on se retrouve face dans le même cas de figure,
où une hausse des taux fragilise l'assureur. Dans le cas où la
maturité de l'obligation est inférieure à n ans, une
baisse des taux pose un problème de refinancement, l'assureur ne pouvant
trouver sur le marché des produits permettant d'obtenir un rendement
- 54 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
égalant celui qu'il recevait avec l'obligation
arrivée à terme. La détermination de l'exigence de marge
nécessite l'introduction d'un modèle de taux
d'intérêt : pour rester dans l'esprit Black & Scholes, Le
Moine et Kaltwasser (2006) considère un modèle de taux de Heath
Jarrow Morton. Dans ce modèle, le zéro coupon
d'échéance T est un actif qui verse 1€ à la
date T, son prix à la date t est noté B(t,
T), et sa dynamique donnée par :
dB t T
B ( ( , )( , ) ( , )
t T
, ) = +
ì ó
t T dt t T dW t
B T T
( , ) 1 en l'absence d'opportunité d'arbitrage
=
p(t, T) est l'espérance du taux de rendement
mais à la différence du cas des actions, c'est l'espérance
instantané de B(t,T), et ó(t,T) sa
volatilité. Wt est un mouvement brownien standard. L'absence
d'opportunité d'arbitrage suppose qu'il n'existe aucune stratégie
financière permettant, pour un coût initial nul, d'acquérir
une richesse certaine dans une date future. Dans ce cas, ces auteurs montrent
qu'en l'absence de rachats, qu'il n'y a pas de risque financier à
condition que le taux d'actualisation soit inférieur au taux
d'intérêt des obligations à l'échéance ; ce
qui est assuré par les réglementations. L'introduction de rachats
de contrats avant échéance nécessite la vente d'une partie
des obligations pour couvrir les engagements. Ce que nous n'avons pas
traité ici.
+ Le besoin en capital relatif au risque de
passif
Pour le passif, nous présentons les modèles
selon leur famille. Comme préciser plus haut, nous distinguons deux
familles de méthodes: Les méthodes déterministes et celles
stochastiques.
· Les méthodes
déterministes
L'approche déterministe n'est pas complètement
mise de côté dans le projet de directive Solvency II. En effet,
l'évaluation des provisions en assurance non-vie dépend de la loi
de survenance des sinistres. Et plusieurs modèles permettent cette
évaluation (Chain Ladder, Bornhuetter Ferguson,...). Parmi ces
modèles, il y en a un qui est central : il s'agit de la méthode
Chain Ladder. Le CEIOPS suggère son utilisation dans la
détermination de la meilleure estimation (Best Estimate) des provisions
pour sinistres. Nous faisons usage de cette méthode dans plusieurs
parties de ce mémoire. En assurance vie, nous présentons les
méthodes de détermination des provisions mathématiques.
> La méthode Chain Ladder
La méthode de Chain Ladder est un modèle de
développement par cadences, basé sur le
- 55 -
triangle de liquidation ou des montants cumulés. Ce
triangle est la partie supérieure d'une matrice dont les lignes
représentent les années de survenance (ou origine) des sinistres
et les Réalisé par : Aristide K. VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
colonnes désignent les années de
règlement (ou développements). Ainsi un élément
Xi,j désigne la charge de sinistres survenus à
l'année i+j et payée jusqu'à l'année j. L'intuition
de cette méthode, c'est d'estimer les valeurs futures des prestations
sur la base des prestations passées en fonction du comportement de ces
derniers. Ce comportement est identifié à travers les facteurs de
développement de sinistres. Ces facteurs sont obtenus à partir
des techniques statistiques (moyenne arithmétique,
pondérée ou géométrique). Nous adoptons ici la
moyenne arithmétique. Ainsi donc, pour n année de
développement, le facteur de développement Cj associé
à l'année j est estimé par la formule :
n j n j
- -
X X C
i j i j i j
, 1 , ,
*
1 1
j n j n j
= =
i i
- -
X X
i j i j
, ,
i i
= =
1 1
à
C
, j [1;n-1]
? ?
Les estimateurs ainsi obtenus sont sans biais et non
corrélés.
|
Développement (j)
|
|
Origine (i)
|
1
|
2
|
...
|
n-1
|
n
|
|
1
|
X1,1
|
X1,2
|
...
|
X1,n-1
|
X1,n
|
|
2
|
X2,1
|
X2,2
|
...
|
X2,n-1
|
|
|
...
|
...
|
...
|
...
|
|
|
|
n-1
|
Xn-1,1
|
Xn-1,2
|
|
|
|
|
n
|
Xn,1
|
|
|
|
|
|
|
Coefficient de
développement
|
C1
|
C2
|
...
|
Cn-1
|
|
L'utilisation de cette méthode suppose que, d'une part,
les règlements de sinistres sont stables et, d'autre part, que les
facteurs de développement sont indépendants de l'année
d'origine des sinistres, des hypothèses que nous avons faites aussi. A
partir de ces facteurs de développements estimés, on peut estimer
les valeurs de la partie inférieure de la matrice de
développement, c'està-dire les prestations futures et qu'on
appelle les « ultimes » pour celles de la dernière colonne
:
X à i j = C à j
+ * C à j + * C à n + -
i * X i n + - i pour i 2, , n et j= n
2 i , ,2.
...
, 1 2 1 , 1
? = ... + -
A partir de ces valeurs estimées, notamment les valeurs
de la dernière colonne. Pour chaque ligne i (année de
survenance), la différence Ri, entre la valeur estimée pour cette
colonne et la dernière valeur connue constitue la réserve ou la
provision pour à payer le sinistre survenu à l'année i. La
provision totale pour sinistre à payer R pour les n années de
développement est obtenue par l'expression :
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
n n
R R
==
i
i i
= =
1 1
( , , 1 )
X X - +
à
i n i n i
-
Bien que simple à appliquer, très
utilisée et comme toute méthode, elle a ses limites. Dans un
premier temps, cette méthode est sur paramétrée d'autant
puisqu'il s'agit de réaliser pour un triangle de dimension n,
l'estimation des (n-1) paramètres en disposant de n(n-1)/2 valeurs
connues. Un test de validation du triangle d'entrée est
recommandé. Dans un deuxième temps, les incréments
correspondant aux périodes de développement élevées
comportent peu d'observations. Par exemple le dernier facteur de
développement est déterminé à partir de seulement
deux valeurs et est appliqué à toute la colonne. Pour encadrer ce
phénomène, il est conseillé d'adopter des techniques
d'extrapolation par adéquation à des courbes de
référence. Dans un troisième temps, les « effets
diagonale » dans le triangle dus à des modifications de cadences de
règlements, bien présentes dans certaines branches à
déroulement long , ne sont pas prévus par la méthode-la
progression des paiements cumulés est supposée identique pour
toutes les années de souscriptions. Enfin dans un quatrième, par
principe même de Solvency II qui veut mieux prendre en compte le risque,
cette méthode ne permet pas de mettre en avant la volatilité de
la sinistralité. Heureusement, elle présente l'avantage pratique
et capital d'être facilement corrigeable du fait de son
interprétation aisée.
> Les provisions mathématiques
La Provision Mathématique-PM- est la moyenne
actualisée des flux futurs. Nous considérons le secteur vie avec
des garanties décès et les rentes liées à
l'arrêt de travail. Les risques considérés ici sont
liés à la déformation de table (hausse ou baisse du taux
de mortalité) et l'arrêt de travail dû à une
incapacité ou à une invalidité.
Les garanties décès et le risque de
table
Elles permettent au bénéficiaire (conjoint
survivant ou aux enfants) du contrat de toucher une rente au
décès de l'individu assuré. Le risque pour l'assureur est
donc par exemple d'observer une déformation de la table de
mortalité. Les tables de mortalités décrivent l'extinction
progressive d'une population au cours du temps. Il en existe de deux sortes :
les tables homologuées par l'autorité compétente-produites
par l'Institut National de la Statistique et des Etudes Economiques (INSEE)- et
celles dites « d'expérience » produites, elles, par chaque
assureur et certifiées par un actuaire indépendant de cette
entreprise et agréé. Afin de réaliser des calculs de PM
plus pertinent et adapté aux spécificités du portefeuille
de l'entreprise et du fait de la liberté de choix de tables qui est
donnée aux assureurs, il est préférable d'utiliser les
tables d'expérience. Mais nous réalisons certains graphiques sur
la base de données de l'INSEE. Les formules situées en annexes de
méthodes liées à ce type de risque sont les standards
en
- 57 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
assurance vie. Qu'il s'agisse d'une rente viagère,
d'une rente temporaire ou d'une rente éducation34, la formule
de la PM est globalement la même et à la seule différence
des bornes supérieures de sommation. Pour une rente à prime
unique d'un montant de 1€ annuel, à échoir sans
revalorisation et versées en une fois, la PM est la somme
actualisée du rapport nombre d'individus d'âge x+k sur nombre
d'individus d'âge x.
Les garanties arrêt de travail et les risques
incapacité ou invalidité.
Elles permettent de couvrir les personnes en arrêt de
travail pour le temps qu'elles sont susceptibles de passer dans cet
état. Cet état peut être temporaire ou définitif
pour les individus d'une tranche d'âge donnée. Le risque pour
l'assureur est donc par exemple d'observer une déformation de la table
des cas d'invalidité ou d'incapacité. Les formules situées
en annexes de méthodes liées à ces types de risques sont
les standards en assurance vie. Qu'il s'agisse d'une incapacité ou d'une
invalidité (en attente ou en cours), le principe de calcul de la PM
reste globalement identique au cas évoqué pour les rentes.
Somme toute, l'approche déterministe fournit une unique
estimation à partir d'hypothèses fixes (table de
mortalité, taux d'actualisation), elle décrit un unique
scénario ou réalisation et ne laisse pas place à
l'incertitude. Le risque n'est donc pas appréhendé de
manière optimale par cette famille de méthode. Et selon l'esprit
du projet de directive Solvency II, on devrait s'orienter de plus en plus vers
les approches stochastiques pour déterminer les composantes du bilan,
notamment les provisions. Cependant, les valeurs obtenues par les approches
déterministes constituent une référence quantitative pour
la projection aléatoire des montants de provisions.
· Les méthodes stochastiques
Comme précisé plus haut, nous présentons
dans un premier temps deux méthodes relatives aux PSAP-où nous
modélisons le risque de volatilité-: une méthode de type
paramétrique et une autre de type non paramétrique. Ces deux se
basent sur la méthode Chain Ladder. Dans un second temps, nous
évoquons le risque d'erreur de spécification de table et
d'aggravation du risque (risque intrinsèque) en ce qui concerne les
PM.
> Détermination des PSAP
Méthodes paramétriques
Ce sont des méthodes qui se basent sur une loi appartenant
à une famille connue de lois, dont il suffira d'estimer les
paramètres. Deux lois sont utilisées dans le cadre de notre
étude : la
34 Ici une petite correction liée au nombre
d'individus d'âge k dans la loi de poursuite d'études au niveau de
chaque âge k : le rapport sx+k /sk.
- 58 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
loi normale et la loi log-normale35. Nous retenons
donc comme moyenne de ces lois, la provision calculée par la
méthode déterministe (Chain Ladder). Ensuite, à partir des
données disponibles de chacune des branches considérées,
nous estimons l'écart type. A cet effet, nous adoptons la méthode
de Mack (1993). Cette méthode permet d'estimer la volatilité de
l'estimateur des provisions techniques sur base de la méthode Chain
Ladder. Trois hypothèses soutiennent cette méthode. La
première suppose une indépendance d'exercice ;
c'est-à-dire que les années de survenance sont
indépendantes entres elles. La deuxième hypothèse indique
que, conditionnellement aux montants cumulés des prestations
passées et quelle que soit l'année de survenance du sinistre, le
facteur de développement est en moyenne le même. Enfin, la
troisième porte sur la variabilité au sein du triangle de
liquidation ; elle suppose que la volatilité au cours d'une
période de développement est la même quelle que soit
l'année de survenance du sinistre.
Il conclut que sous ces hypothèses, l'erreur standard de
la provision à constituer (R) peut s'écrire sous la forme :
2 ók
à 2
2
à
fk
n k
-
Cnk
1
j
n n n - 1
mse R mse R C C
à ( à ) à ( à ) à . à
.
= ( )
i in ij
+
i=2 j i k n i
= + = + -
1 1
avec
mse R X
2
i in
=
à ( à ) à . à à
C X
2
+ n k
-
k n i k ik
= + -
1
n-12
ó à1 1
k
Xjk
j 1
et X X
i n i
à à
, 1 , 1 , 1
= ; les sont les valeurs estimées de la partie
inférieure du triangle
- + - + - +
i n i i n i
X
de liquidation.
Une fois les deux paramètres (la moyenne et
l'écart type) estimés et connaissant la loi de distribution de la
provision technique, on peut calculer aisément les VaR et TVaR pour les
niveaux de risque souhaités. Peu aisée à
interpréter, la robustesse de cette méthode est mise en cause
dans certains cas : les triangles « imparfaits » dus aux
données manquantes ou aux sinistres exceptionnels ou même aux
erreurs comptables. Les méthodes non paramétriques facilitent
cette tâche de robustesse et d'interprétation.
Méthode non paramétrique
On a précisé plus haut certaines limites de la
méthode Chain Ladder ; on a évoqué par exemple son
sur-paramétrage et sa sensibilité à une forte variation.
On a dû faire une hypothèse sur la loi de distribution des
provisions techniques : ce qui n'exclut pas des erreurs de
35 Petits rappels sur ces lois en annexes.
- 59 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
spécification de loi. Il convient d'adopter des
méthodes permettant de contourner ces contraintes : le Bootstrap ou
encore la méthode de « rééchantillonnage » offre
cette opportunité. L'intuition de cette méthode, c'est d'obtenir
à partir d'un échantillon initial de taille T donné, de
nouvelles informations statistiques en stimulant plusieurs (N) nouveaux
échantillons de même taille. Autrement dit, on apprend à
partir d'une expérience par répétition. Et comme on dit
souvent qu'avec le temps les choses finissent par devenir normales ; on obtient
ainsi, des estimateurs plus robustes et moins contraints. Cependant, cette
méthode repose sur deux hypothèses qui constituent un peu ses
limites : l'indépendance et une distribution identique
des lois de chacun des éléments composant l'échantillon de
base. Deux hypothèses qui ne sont pas respectées, dans le cadre
des triangles de développement auxquels nous voulons appliquer cette
méthode ; car, les règlements incrémentés ne sont
pas indépendants et leurs distributions ne sont pas identiques -des
paiements de recours ou des développements longs de certaines branches
par exemple, rendent les distributions non identiques. Afin de contourner ce
problème, on utilise le « Residuals Bootstrap » basé,
non pas sur les observations directes du triangle mais les écarts
normés (centrés et réduits) de ces observations à
l'aide des résidus de Pearson. Ainsi donc, pour un triangle de
règlement de taille n, on a pour la cellule (i,j):
R y - ì à
= =
ij ij ij
Rp
i j
, V V
( à ) ( à )
ì ì
ij ij
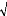
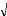
y représente la value observée et celle
prévue par le modèle et ( à ) à la variance dans
ì à V ì ì
=
ij ij ij ij
un modèle de Poisson.
Certaines notations sont nécessaires pour appliquer cette
méthode aux triangles de règlements sur la base de Chain Ladder.
Ainsi, pour la cellule (i, k):
à
- , , , ,
C i k , D i k , D i k et m
à i k désignent les valeurs des triangles
respectivement brutes non cumulées, brutes cumulées,
prédites cumulées et prédites non cumulées ;
- i , k
r représente la valeur dans le triangle des
résidus de Pearson ;
p
( ) *
p
- ,
r représente la valeur dans le nouveau triangle
des résidus, après ré échantillonnage
i k
avec remise du triangle des résidus de Pearson ;
- ,
C * *
et D i k désignent les valeurs des nouveaux
triangles respectivement non cumulées, et
,
i k
cumulées.
Dans un premier temps, on détermine les facteurs de
développement à l'aide de la méthode Chain Ladder
appliquée au triangle de développement des montants
cumulés (Di,k). Dans un deuxième temps, on crée
un nouveau triangle à partir des dernières valeurs observables
(valeurs
|
Réalisé par : Aristide K.
VIGNIKIN
|
- 60 -
|
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
de la diagonale) du triangle de départ et des facteurs
de développement ; les valeurs de la
diagonale sont divisées
par les coefficients de Chain Ladder : on obtient un triangle nommé
Triangle Prédit contenant les valeurs ( mà
i , k ) .
( )
p
Dans un troisième temps, on détermine les valeurs
du triangle des résidus de Pearson ,
rà
i k
( ) *
p
partir de celles du triangle des montants non cumulés ,
ret celles du Triangle Prédit :
i k
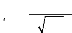
ri
C m
- à
ik i k
,
=
à
( )
p
, k
m i k
,
Dans un quatrième et dernier temps, on réalise
maintenant le Bootstrap. Ce dernier consiste à générer de
nouveaux triangles de montants cumulés par ré
échantillonnage aléatoire des résidus calculés ;
les valeurs de ces montants sont obtenues par la formule :
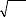
C ik = m i k + r i k × m i
k
* ( )*
à , , p à ,
On finit donc par sommer ces montants et à l'aide la
méthode de Chain Ladder, on obtient ainsi les nouveaux montants
cumulés. On refait l'expérience de cette quatrième phase
plusieurs fois (N) : on obtient ainsi N valeurs différentes des
provisions et on peut ainsi en déduire la loi de distribution.
Toute cette procédure est résumée dans le
schéma n°4.1.1.
A titre complémentaire et en restant dans l'optique de
la nouvelle proposition de directive, nous actualisons ces provisions. En
effet, cette actualisation permet de ramener les valeurs futures
évaluées par la méthode du Bootstrap à la date
courante. Elle est réalisée à partir des taux financiers :
courbe des taux selon la zone ; nous adoptons celui suggéré par
le CEIOPS. Rappelons toute fois cette formule :
C*
ik
C * = pour i+j>n avec tx le taux financier.
simulé actualisé ( )
1 ( /100) i j n
+ -
+ tx i j n
+ -
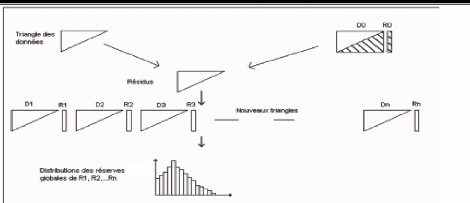
Schéma n°4.1.1 : Synthèse de la
procédure du Bootstrap sur base des triangles
de
liquidation.
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
Source : Dugas (2003).
> Détermination des Provisions
Mathématiques-PM
Il s'agit ici de présenter très brièvement
les méthodes d'identification de la volatilité de la provision
mathématique déterministe plus haut.
Le risque de table
Le risque de table correspond à une déformation
(hausse ou baisse des valeurs) des tables. Cette déformation
dépend du type de contrat modélisé. Pour les rentes, le
risque pour l'assureur est lié à une survie plus longue de
l'assuré. Quant aux contrats en cas de décès, ce risque
est lié à une augmentation des décès. En utilisant
les tables réglementaires TV 88-90 et TD 88-90 associé
respectivement aux contrats vie et décès, on peut observer le
phénomène d'aggravation sur le graphique n° 4.1.1.
Graphique n° 4.1.1 : Risque de table lié
à une aggravation

Il faut noter que la déformation des tables est
croissante depuis quelques années en fonction de
l'âge et n'est
pas homogène. Une observation du graphique n° 4.1.2 qui
représente l'évolution
des taux de mortalité en
fonction de l'âge (sur données de l'INSEE) montre bien ce fait et
révèle
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
dans le même temps, la difficulté de
modélisation. Cependant, Brass (1971) suggère un modèle
qui permet d'appréhender cette déformation. Son modèle est
de la forme :
log ( ) 1 2 log ( )
it q = è + è it q x
ref
x
logit(q) ln ; ] ; [
q Z Z
x
= = ? - 8 +8
avec 1
- q x
x x x
q [0;1], les quotients annuels de décès
observés à l'age x.
x ?
A partir de ce modèle, on peut réaliser une
déformation de la table. En effet, ce modèle
établit
une relation linéaire entre le Logit des quotients de
mortalité étudiés qx et ceux d'une
population
|
q x
de référence qref . Intégrer un
risque de table consiste à simuler une variable ln
Z x =
1 - q
|
x
|
selon une loi N(logit(q x
);ó) où ó est un coefficient
d'abattement36 global des quotients annuels
qx des tables de mortalité et calibré
à 0,88. Ainsi le qx* simulé est
centré autour de sa valeur déterministe issue du logit
appliqué à la table d'entrée. Une fois la première
simulation réalisée, par inversion de la fonction Logit, on
obtient :
|
x
e Z
q e
x Z
= + x
1
|
, ce qui permet de produire une nouvelle table de qx
sur]0 ; 1 [et ainsi d'avoir un
|
modèle de déformation de table. On peut obtenir
donc une distribution des PM. En ce sens, pour une simulation i donnée,
la PMi est donnée par l'utilisation de la
ième table simulée (table des qÇ).
Graphique n° 4.12 : Risque de table lié à une
aggravation
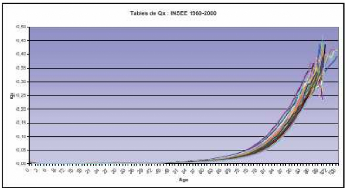
Source : INSEE (2002)
Le risque intrinsèque
36 Il correspond à une faible marge de risque
que l'on estime à 60% de la table d'origine en VaR et appliqué
sur le marché (la plupart du temps par des réassureurs).
- 63 -
Réalisé par : Aristide K.
VIGNIKIN
Solvabilité II : Impact de l'utilisation
d'un modèle interne sur la valorisation du bilan
en
assurance.
En simulant le décès ou la survie de chaque
individu pour l'ensemble des années de projection, on modélise ce
type de risque. Ainsi, pour chaque année de projection, on dispose des
qx simulés notés qx' ; la
probabilité que la rente soit versée est égale à 1-
qx' (survie ou maintient de l'assuré en vie). On effectue
donc un tirage de Bernoulli de paramètre (1- qx') pour
déterminer si la rente est versée (1 si oui et 0 sinon). Les flux
sont ensuite actualisés avec un taux règlement constant pour
toutes les années dont nous avons fait référence plus
haut. Par exemple pour un portefeuille de p individus, d'âge xj à
la souscription, souscrivant à une garantie pour rente de conjoint
temporaire d'un montant de M et un taux d'actualisation constant égal
à r, la provision mathématique associée est donnée
par l'expression :
|
PM
|
i =
|
p
|
X x
- j
|
M
|
|
avec X à l'age limite.
|
|
j =
|
1 0
k j =
|
(1 )
+ r
|
k j
|
On répète ainsi N fois cette simulation pour
obtenir N valeurs de PM et ainsi calculée la VaR associée.
Il est ensuite possible de modéliser conjointement ces
deux risques en tenant compte de leurs structures de dépendance. Nous
nous contentons d'une copule de Gumbel dont nous rappelons les
propriétés à l'annexe des méthodes.
| 


