Chapitre 1 : MODELE CINEMATIQUE
Ce modèle aura pour entrées, les angles de
rotation theta1 et theta3 ( è1 et
è3 ) des roues, et
? ? ?
pour sorties, la position rG , la vitesse vG ,
l'accélération aG et l'orientation alpha du
robot.
1. Terminologie
Symboles
|
Désignation
|
|
|
l13
|
distance entre roues
|
R
|
rayon des roues
|
G1
|
centre de roue 1
|
G2
|
centre de masse du châssis
|
G3
|
centre de roue 3
|
A
|
point médian entre roues, appartenant au
châssis
|
G
|
centre de masse du robot
|
I1
|
point de contact de la roue1 avec le sol
|
I3
|
point de contact de la roue3 avec le sol
|
? ? ? ?
= 1 . 1 + 1 . 1 + 1 . 1
rG rG x x rG y y rG z z
1
|
Vecteur position de la roue 1
|
? ? ? ?
rG rG x x rG y y rG z z
2 = 2 . 1 + 2 . 1 + 2 . 1
|
Vecteur position du châssis
|
? ? ? ?
rG rG x x rG y y rG z z
3 = 3 . 1 + 3 . 1 + 3 . 1
|
Vecteur position de la roue 3
|
? ? ? ?
= 1 . 1 + 1 . 1 + 1 . 1
vG vG x x vG y y vG z z
1
|
Vecteur vitesse de G1
|
? ? ? ?
= 2 . 1 + 2 . 1 + 2 . 1
vG vG x x vG y y vG z z
2
|
Vecteur vitesse de G2
|
? ? ? ?
= 3 . 1 + 3 . 1 + 3 . 1
vG vG x x vG y y vG z z
3
|
Vecteur vitesse de G3
|
? ? ?
ù1 , ù2
et ù3
|
Vitesses angulaires respectivement de la roue 1,
du
châssis et de la roue 3 dans la base d'étude.
|
? ? ? ?
= 1 . 1 + 1 . 1 + 1 . 1
aG a G x x aG y y aG z z
1
|
Vecteur accélération de G1
|
|
? ? ? ?
= 2 . 1 + 2 . 1 + 2 . 1
aG aG x x aG y y aG z z
2
|
Vecteur accélération de G2
|
? ? ? ?
= 3 . 1 + 3 . 1 + 3 . 1
aG aG x x aG y y aG z z
3
|
Vecteur accélération de G3
|
|
Tableau 1 : Terminologie du modèle
cinématique
2. Description des différents mouvements
? ? ?
La base d'étude est la base (x, y, z) ayant
1x , 1y et 1z comme vecteurs de
base. Cette base est liée au sol. Nous la
considérerons donc comme galiléen à condition
de
substituer à la force de gravitation la notion de poids et
d'exclure les mouvements très précis (la
? ?
déviation vers l'est) ou très rapides. [2.4]. Au
robot est lié la base (x1, y1 et z1) ayant 1x1 ,
1y1 et
?
1 z1 comme vecteurs de base. La relation entre les deux
bases est définie par les expressions :
? ? ?
1 x 1 = cosá .1
x+siná.1 y (1)
? ? ?
1 y 1 = - siná .1
x+cosá.1 y (2)
? ?
1 z 1 = 1z (3)
Les différents mouvements sont :
· Roue 1 par rapport au châssis : rotation d'angle
theta1 autour de l'axe y1 (figure 1).
· Roue 3 par rapport au châssis : rotation d'angle
theta3 autour de l'axe y1.
· Châssis par rapport au référentiel
d'étude : mouvement quelconque dans le plan xoy c.à.d. rotation
d'angle alpha autour de l'axe z et translation suivant les axes x et y.
3. Etablissement du modèle
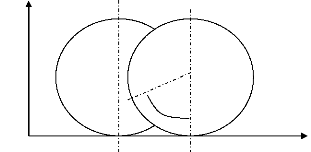
cinématique Pour un roulement sans glissement, on a :
(figure 2)
? ?
vG 1 = R.è& 1
. 1 x 1 (4)
x
z
G1
è
dè
G1'
Figure 2 : Déplacement infinitésimal
d'une roue
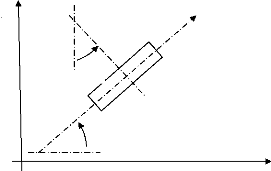
Dans la base fixe, la vitesse de G1 sera donnée par :
(figure 3)
? ? ?
vG = R è&
1 . 1 .(cos . 1 sin . 1 )
á x + á y (5)
De même, pour la roue 3 :
? ? ?
vG = R è&
3 . 3 .(cos . 1 sin . 1 )
y
á
G1
á
x
?
vG1
á x + á y (6)
Figure 3 : Roue1 suivant une orientation
á
?
Vu la non-linéarité du problème
(á est variable avec le temps), la position rG du
robot sera trouvée par intégration numérique.
? ?
rG ? vG dt
1 = 1 (7)
Et :
? ?
rG ? vG dt
3 = 3 (8)
Pour un solide indéformable, la connaissance du
mouvement d'un point quelconque suffit pour décrire complètement
le comportement cinématique de tout le solide. [2.3]. Donc le mouvement
du point médian A est identique à celui du centre de masse G2 du
châssis et à celui du centre de masse G de tout le robot.
De (7) et (8), on a :
? ?
? rG rG
1 + 3
rG = (9)
2
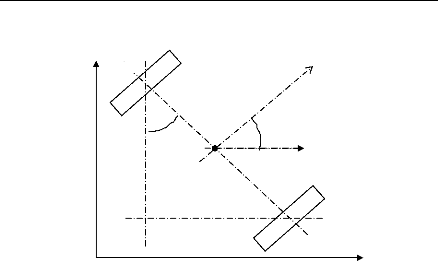
L'orientation du robot sera donnée par : (figure 4)

(10)
rG x
1
- rG x
3
y
rG y rG
-
3 1
DG1
=

DG3
? rG x rG x
- ?
1 3
á arctan
= ? ? (11)
? rG y rG y
-
3 1 ?
Modélisation et simulation d'un robot mobile
sur roues avec le logiciel - 9 -
MATLAB/SIMULINK
G3
x1
y
á
á
A
G1
D
x
Figure 4 : Robot suivant une orientation
á
La vitesse et l'accélération du robot seront :
? R ? ?
vG = ( è & è
&
+ ).(cos . 1 sin . 1 )
á x + á y (12)
2 1 3
?
dvG
dt
(13)
?
aG
| 


