Modélisation et simulation d'un robot mobile sur roues avec le logiciel Matlab/Simulink

3. Méthode des théorèmes généraux

Il est intéressant d'appliquer ces théorèmes à la fois dans le référentiel fixe (absolu) et dans le référentiel mobile lié au châssis pour comparer les résultats. Mais, par soucis de simplification, nous ne travaillerons que dans le référentiel mobile. Les résultats du référentiel fixe seront repris dans les annexes (Annexes 2).

R15

z1

y1

x1

R6

è2

R16

R11

R8

R13

R9

è1

R4

R10

R7

R5

R7

R12

R12

R3

R4

R10

R13

R8

R9

R1

R11

R14

R6

R5

R2

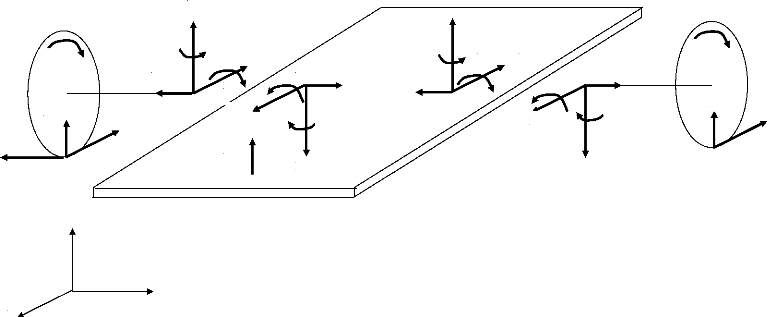
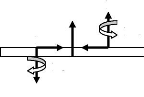
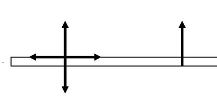
3.1. Diagrammes des corps rendus libres

Roue 1

z1

x1

R4

y1

y1

R2

r

R6

R8

R5

R3

z1

R6

x1

R4

R3

R1

R1

R2

R7

R5

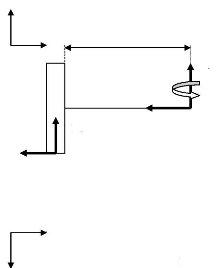
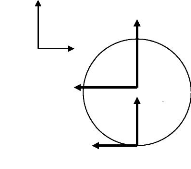
Figure 6 : Projections orthogonales de la roue 1 rendue libre

R14

R11

R5

R10

R8

R6

R13

R14

R11

R9

b

R4

R6

f

R9

R12

R5

R7

e

R10

R4

O2

d

l

c

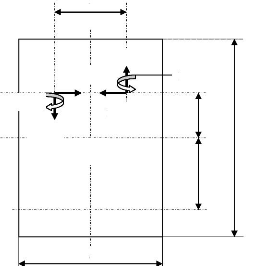
Châssis

R12

R10

R9

X3

R15

Roue 3

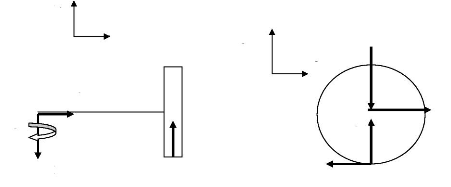
z3

y3

Z3

R11

X3

R16

R15

R11

R13

R10

R9

R15

Y3

MR

& & & &

(39)

2

(è ₁ +è₃) =

R R

-

4 9

3.2. Théorème de la résultante cinétique

3.2.1 Roue 1

Ce théorème, appliqué à la roue 1, donne :

? ? ? ?

d?

m . vG mg z R R x R R y R R z

= - . 1 (

- + - + + +

1 1 1 4 ) . 1 (

1 2 5 ) . 1 (

1 3 6 ) . 1 (33)

1

dt

De l'expression (4):

d ? ? d ? ? ?

è & & + . . 1

è & x R x R

dt

è & & + . . . 1

& & y (34)

è á

vG R x R

= . . 1

= . . 1

1 1 1 1 1 1 1 1 1

dt

Comme nous dérivons dans un référentiel mobile, nous pouvons aussi faire usage du vecteur de DARBOUX pour arriver au même résultat (Voir plus loin).

Soit, en le projetant sur différents axes:

mR è& & 1 = - ( R₁+R₄) (35)

mR .è & 1 .á & = - (R₂ +R₅) (36)

R ₃ + R₆ = m.g (37)

3.2.2 Châssis

Appliqué au châssis, il donne :

? ? ? ? ?

d

m . vG Mg z R R x R R y R R R z

= - . 1 (

+ - + - + + -

2 1 4 9 ) . 1 (

1 5 10 ) . 1 (

1 11 14 6 ) . 1 (38)

1

dt

Soit, en le projetant sur les axes :

MR
2

.

d dt

? MCG

1

=

d dt

? MCG1 rel

? ? + ù 1 ? MC Darb 1 (48) G

(è^&₁ + è & á & = - (40)

3 ). R R

5 10

R ₁₄ + R 11 - R 6 = M . g (41)

3.2.3 Roue 3

Appliqué à la roue 3, il donne :

? ? ? ?

d?

m . vG mg z R R x R y R R z

= - . 1 (

+ - + + -

3 1 9 15 ) . 1 1 10 . 1 (

1 16 11 ) . 1 (42)

1

dt

Soit, en le projetant sur différents axes:

mR è& & 3 = R 9 - R 15 (43)

mR . è & 3. & á= R 10 (44)

R 16 - R 11 = m . g (45)

3.3 Théorème du moment cinétique

3.3.1 Roue 1

Le moment cinétique de la roue 1 en son centre de masse est donné par :

? ?

MCG 1 = I₁ .ù 1 (46)

Soit :

? mR

2

? ?

MC_G = (2 . 1

è & y + z

á & . 1 ) (47)

1 1 1 1

4

La dérivée, dans la base mobile, de l'expression (47) sera :

?

ùDarb 1 est le vecteur de Darboux et vaut :

? ?

ù Darb 1 = á & . 1 z 1 (49)

d

? mR

2

? ? ?

. MC = ( 2 . . 1 2 . 1

- & áè & x á & & . 1 ) (50)

1 1 1 + y

è & & 1 1 + z

dt

G 1

4

Le moment des forces extérieures dans la base (x1, y1, z1) est :

? ? ? ? ? ? ? ? ? ? ? ?

Mext R z R x R y R z r y R x R y R z R x C y R z

= - 1 ( 1 - 1 1 ) 1 ( 1 1 1 ) 1 1 1 )

1 1 × - 1 1 2 ₁ + +

3 1 1 × - 4 1 - 5 ₁ + -

6 1 7 1 + (51)

1 ₁ + 8 1

Soit :

? ? ? ?

Mext R r R R R x R R C y R r R z

= ( . - - + + + + (52)

1 6 2 . ) . 1 ( . ) . 1 ( . ) . 1

7 1 1 1 1 4 8 1

Partant des expressions (50) et (52), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

mR 2

2

è & á & =

1 . R r R R R

- (53)

6 . - 2 . 7

mR 2

2

mR 2

è& & = R R C

+ (54)

1 1 . 1

á& & = +

R R r

. (55)

8 4

4

3.3.2. Chassis

Le moment cinétique du châssis en son centre de masse est donné par :

? ?

MCG 2 = I₂ .ù₂ (56)

Avec :

? ?

ù 2 = á&. 1 z 1 (57)

Soit :

2 2

? M c d

( + ) ?

MC_G = á& (58)

. 1 z

2 1

12

La dérivée, dans la base mobile, de l'expression (58) sera :

.

d dt

? MC G

2

=

d dt

? MCG2 rel

? ? + ù 2 ? MC Darb 2 (59) G

?

ùDarb 2 est le vecteur de Darboux relatif au châssis et vaut :

? ?

2 2

d ? +

M c d

( ) ?

ùDarb 2 = á&. 1 z₁ (60)

. MC

= á&& (61)

. 1 z

dt

G 2 1

12

Le moment des forces extérieures dans la base (X1, y1, z1) est :

? Mext

? ? ? - e ? ? ? f = ? - ? 2 ? 2 ? ? ? b ? ? ? 2 ?

(

x1 , y 1 , z1 )

(

?

?

?

? [ ?

R₄ l 0

? R₅ + 0 A 0 + A - RH

R6

^? ?( x1 , y 1 , z 1 )-b R 14
?(x1 , y 1 , z 1 )f2b e

(

2

?

x1 , y 1 , z1 )

R 11

R₉

? ?

? R R

-

7 12 ?

(62)

+ 0

? ?

? ? R R

- ?

1 , y1 , z1 )

x y z

1 , 1 , 1 ) 13 8 (

? x

Ou bien :

(

2

?

x1 , y 1 , z1 )

( +R₁₁).

₆

b

(R 10 - R5). 2 + R₇ -

f₊ 2

R12 ?

R

2 = I (R 4 - R₉ ).

b +(R 11 , R₆ ).

e-R14

²

.l (63)

Mext

( )e + (R ₄ +R9).

R 13 - R₈

x1 , y 1 , z1 )

f₊ 2

(

R ₁₀ R5

Partant des expressions (61) et (63), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

(R ₆ + R₁₁ )+b (_R10 - R ₅ ) + R 7 - R₁₂ = 0 (64)

2 2

b (R₄ - R₉ ) + e.( R 11 - R₆ )- l. R 14 = 0 (65)

²

(66)

2 _d2 \

M ( c + ⁾á&& = 2

f

12 (R ₄ + R ₉) + e. (R 10 - R ₅) + R 13 - R₈

3.3.3. Roue 3

Comme pour la roue 1, on aura :

? ?

MCG 3 = I ₃ .ù 3 (67)

Soit :

? mR

2

? ?

MC_G = (2 . 1

è & y + z

á & . 1 ) (68)

3 3 1 1

4

La dérivée, dans la base mobile, de l'expression (68) sera :

a

? mR

2

?

? ?

. MC = ( 2 . . 1 2 . 1

- á & è & x á & & . 1 ) (69)

3 3 1 + y

è & & 3 1 + z

at

G 1

4

Le moment des forces extérieures dans la base (x1, y1, z1) est :

? ? ? ? ? ? ? ? ? ? ?

1 ( 1

1 ) 1 ( 1

1 ) 1 1

Mext = - R z R x R z r y R x R y R z R x C y R z

1 11 1

1

× - + - × + - - + -

3 1 15 1 16 1

1 9 1 10 1

12 1 3 1 13 1

(70)

Soit :

? ? ? ?

Mext R r R x R R C y R r R z

= ( . ) . 1 ( . ) . 1 ( . ) . 1

+ + + + - (71)

3 11 12 1 15 3 1 9 13 1

Partant des expressions (69) et (71), le théorème du moment cinétique, projeté sur différents axes, s'écrit :

2

mR

2

2

mR

2

2

mR

è & á & = R r R

+ (72)

3 . 11 . 12

è& & = R R C

+ (73)

3 15 . 3

á& & = R r R

4

- (74)

9 . 13

3.4. Système d'équations à résoudre

Les équations (35), (36), (37), (39), (40), (41), (43), (44), (45), (53), (54), (55), (64), (65), (66), (72), (73) et (74) constituent le système de 18 équations différentielles à 18 inconnues à résoudre avec MATLAB.

Les simplifications et substitutions conduisent au système suivant : De l'équation (54), on trouve :

2 . 2

R R + C

1 1

è& & = 1 (75)

.

m R ²

De (73), on a :

.

i₌2 /65 +2C3 (76) m R 2

(76) dans (35), on tire :

R1 = R4. R +2 C1 (77)

3R

De (36), on tire :

R2 = 2m+M (-R10 -m.R . di. et) (78)

M

De (37), on a :

R ₃ = m. g - R₆ (79)

De (65), on tire :

R =

4 [ ( 6

2 e R R l R R

- +

11 ) . 14 ] 9

+ (80)

b

(44) et (36) dans (40), avec (78), on a :

M

R 5 = R10-

2 m+MR2 (81)

(75), (76) et (80) dans (39) donne :

R6= b .m (R1 +R15) - l R14-R11 (82)

e

(2 m+M).e

(53), avec (36), donne :

R 7 = r . R₆ + mR2 _uA1 xi R. R₂ = 2r.R ₆ 3R.R₂ R.R5 (83)

2 2

2

mR

R = á&& - (84)

r R
.

8 4

4

De (66), on a:

M c d

2 2

2 (

? + ) ?

R = á&& + e R R R R

.( - + -

9 5 10 ) R (85)

8 13 4

?? -

f ?? 12

De (64), on a :

2 ? -

b ?

R = ( 5

R R R R R

10 ) 12

+ - - (86)

11 7 6

f ?? 2 ??

De (72), avec (44), on tire :

(87)

mR ² R R

. + 2 .

r R

10 11

R = - è & á & -

. r R

. = -

12 3 11

2 2

(74) devient :

2

mR

R = r R -

. á&& (88)

13 ⁹ 4

(65) devient :

R14 = R6-R11+Mg (89)

(76) dans (73), on tire :

R R C

. ₉ 2 3

-

3

(90)

R15

R

(45) devient :

R16 = m. g +R₁₁ (91)