Estimation de l'erreur de troncature de l' espace d'états du système d'attente m/m/1: méthode de stabilité forte

2.2.2 La file d'attente M/M/m

On considère un système identique a` la file M/M/1 exceptéqu'il comporte m serveurs identiques et indépendants les uns des autres.

On conserve les hypothèses : processus d'arrivées des clients poissonnien de taux u et temps de service exponentiel de taux ë (pour chacun des serveurs). Ce système est connu sous le nom de file M/M/m. L'espace d'états S est, comme pour la M/M/1 infini, S = {0, 1, 2, ...}. On a un processus de naissance et de mort de taux :

ë_n = ë.

un =

0, si n = 0;

nu, si 0 < n < m; (2.2)

mu, si n = m.

La condition de stabilitéici est ë < mu, et exprime le fait que le nombre moyen de clients qui arrivent a` la file par unitéde temps doit être inférieur au nombre moyen de clients que les serveurs de la file sont capables de traiter par unitéde temps.

On peut donner ð_n comme suit [15] :

ðk = ñkmm

{ (mñ)k

m! , k = m, m + 1, ...

k! , k = 0, 1..., m -- 1; (2.3)

avec,

m-1_X
k=1

mñ)^k k! ].

mñ)^m

ð0 = [1 + m!(1 - ñ) +

Le graphe représentatif du processus de naissance et mort est :

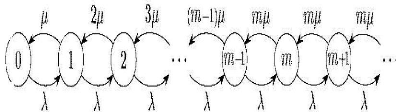
FIGURE 2.3 - Graphe de la file d'attente M/M/m

Caractéristiques de la file M/M/m

La file M/M/m, est plus simple (au niveau des calculs). On calcule d'abord le temps moyen de séjour et on déduit le nombre moyen de clients.

- Temps moyen de séjour W :

Le temps moyen de séjour d'un client se décompose en un temps moyen dans la file d'attente, plus un temps moyen de service. Il suffit alors d'appliquer la formule de Little a` la seule file

1 W = Wq + u

Lq = ë +

1 u

,

Il reste alors a` calculer le nombre moyen de clients en attente dans la file, L_q :

L_q = _X8 ð_n,

n=m+1

L_q = ñ (ë/u)ⁿ

(1 - ñ²) m!mn-m ð0.

o`u, ñ = ë/mu.

On en déduit l'expression du temps moyen de séjour

W = ñ (1 - ñ^2)

(ë/u)^n ð0 + m!m^n-m

1 u

,

- Nombre moyen de clients L :

Le nombre moyen de clients s'obtient alors par application de la formule de Little:

L = WA = A( p (A/u)

⁽¹

n 1

ð0 + ).

- p²) m!m^n-m u

2.2.3 La file d'attente M/M/1/N

On considère un système a` serveur unique identique a` la file M/M/1 exceptéque la capacitéde la file d'attente est finie. On a donc toujours les hypothèses suivantes :

Le processus d'arrivées des clients dans la file est un processus de Poisson de taux A et le temps de service d'un client est une variable aléatoire exponentielle de taux u.

Soit N la capacitéde la file d'attente, c'est le nombre maximal de clients qui peuvent être présents dans le système, soit en attente, soit en service.

Quand un client arrive alors qu'il y a déjàN clients présents dans le système, il est perdu.

Ce système est connu sous le nom de file M/M/1/N, l'espace d'états S est maintenant fini
S = {0, 1, 2, ..., N}, le nombre de clients dans la file ne peut donc jamais »partir» a` l'infini.

De plus, dès qu'un client est autoriséa` entrer, il sortira avec un temps de séjour dans la file fini, puisqu'il correspond au temps de service de tous les clients devant lui et que ce nombre est limitéa` N. Sur un temps très long, le débit de sortie sera donc bien égal au débit d'entrée, ce qui correspond bien a` la stabilitéinconditionnelle du système.

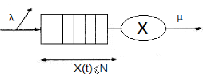
FIGURE 2.4 - Graphe de la file M/M/1/N

On décrit un tel système par le processus {X(t), t = 0} représentant le nombre de clients dans le système a` l'instant »t».

Le processus de naissance et de mort modélisant ce type de file d'attente est alors défini de la façon suivante :

{ A, n < k;

A_n = (2.4)
0, n = k.

{ u, n =6 0;

u_n = (2.5)
0, n = 0.

Régime transitoire

Le graphe représentatif de la file M/M/1/N est donné:

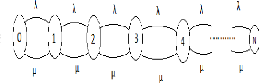
FIGURE 2.5 - Graphe de la file M/M/1/N

D'après ce graphe, on extrait les équations différentielles de Kolmogorov correspondantes au processus X(t) du système M/M/1/N qui sont identiques a` celles du système M/M/1 sauf pour n = N :

P0 0(t) = --ëP0(t) + uP1(t); P ^0 n(t) = --(ë + u)Pn(t) + ëPn-1(t) + uPn+1(t), n = 1, N; (2.6) P ^0 N(t) = --uPn(t) + ëPN-1(t).

Régime stationnaire

On note ð_n = P_n(t) la probabilitéstationnaire d'être dans l'état n (probabilitéque le système contient n clients). Ces probabilités peuvent être calculées en écrivant les équations

d'équilibre, o`u lim n?8

P ^0 n(t) = 0 :

ë

ð_n = u

ðn-1; n = 0...N,

o`u ñ = ë/u.

En appliquant n fois cette relation:

ð_n = ð0ñⁿ n = N,

ð0 :	1					1 - ñ
ð0 =
			N E n=0	ñn			1 - ñN+1 ,
Ou obtient finalement :		ðn = ( 1 - ñ 1 - ñN+1 )ñn.

N

En se servant de la condition de normalisation E ð_n = 1, on peut deduire la probabilite

n=0

Caract'eristiques du syst`eme M/M/l/N

-Nombre moyen de clients dans le syst`eme (L) :

L = ñ 1 - ñ	(N + 1)ñ^N+1
	1 - ñN+1 ,

A nouveau, lorsque N tend vers l'infini et ñ < 1, on retrouve les resultats de la file M/M/1 :

_L = ñ

1 - ñ.

Pour le syst`eme dont la capaciteest limit'ee a` N, le calcul de ë_e se fait comme suit :

ë_e = ë(1 - ð_n),

o`u, (1 - ð<sub>n</sub>) represente la probabilitede »non refus d'un client dans le syst`eme».

ñ L= (1 - ñ)	(N + 1)ñ^N+1
	1 - ñN+1 ,

A l'aide des formules de Little , on obtient

(N + 1)ñ^N+1 1 - ñN

-Nombre moyen de clients dans la file (L_q) :

L_q = L - ñ(1 - ðN) = (1 ^ñ ñ) - 1 - ñN+1 - ñ( 1 - ñN+1),

ñ Nñ^N+1 + ñ

L=

q (1 - ñ) 1 - ñ^N+¹ .

-

textbfTemps moyen de s'ejour el d'attente d'un client dans le syst`eme (W et W_q) : W = L/ë_e , on obtient [14] :

W = (1 + Nñ^N+1 - (N + 1)ñ^N u(1 - ñ)(1 - ñN) ,

W_q

-Nñ^N + (N - 1)ñ^N+1 + ñ

u(1 - ñ)(1 - ñ^N) .