Effets des dispositifs d'amortissement sur les déplacements, vitesses et accélérations des structures

Chapitre IV : Application numérique sur

un oscillateur simple

Application numérique sur un oscillateur simple

IV.1. Introduction

Ce chapitre est consacré à une application portant sur un oscillateur simple. Nous nous intéressons plus exactement à la variation du déplacement en fonction de la variation de l'amortissement en considérant comme source d'excitation le signal sismique d'El Centro.

Nous présentons d'abord l'aspect théorique, suivi d'un organigramme qui résume les étapes de calcul des déplacements.

L'exploitation de cet organigramme nous a permis d'élaborer un programme en FORTRAN dont les résultats de simulation sont représentés graphiquement.

IV.2. Formulation mathématique du problème

On considère un oscillateur simple lié au sol et caractérisé par sa pulsation ù et son coefficient d'amortissement î. Il est soumis aux effets d'un séisme, c'est à dire que son point d'appui se déplace avec une accélération du sol donnée par un accélérogramme, comme par exemple celui d'El Centro du 18 mai 1940.

Figure IV.1 Oscillateur simple

chapitre IV Application numérique sur un oscillateur simple

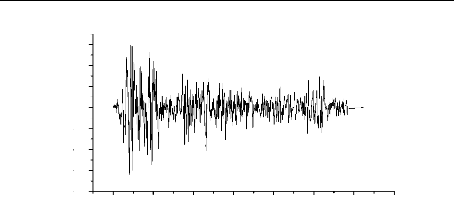
0 5 10 15 20 25 30 35

acceleration m/s2

-0,1

-0,2

-0,3

-0,4

0,3

0,2

0,1

0,0

tem ps s

Graphe IV.1 : Signal séismique d' El- centro

On calcule les déplacements dus au signal sismique avec différentes valeurs

d'amortissement à l'aide de l'intégral du Duhamel :

1

u(t) = ? - (t - )

p îù ô

( ) e

ô sin ( )

ù t d

- ô ô

D

mù_D

t

0

(IV-1)

Cette équation est appelée intégrale de Duhamel, qui est basée sur le principe de superposition. Elle n'est applicable qu'à des systèmes linéaires.

Pour calculer numériquement cette réponse, on a :

sin (ùDt- ùDô)=sinùDt cosùDô - cosùDt sinùDô

Donc :

t t

sin t

(IV-2)

ù c os ù _D t - (t - )

u(t) = D ? - (t- )

îù ô

ô ( ) e îù ô

ù ô ô

( ) e

p cos( ) d - ? p ô sin( )

ù ô d ô

D D

m ù m ù

D 0 D 0

t îùô

1 e

(IV-3)

Posons : A(t)= p ( )

ô ù ô d ô

îù D

? _t cos( )

m ù e

D 0

et

t îùô

1 e

(IV-4)

B(t)= p ( )

ô ù ô d ô

îù D

? _t sin( )

m ù e

D 0

L'équation IV-2 prend la forme suivante:

u(t)= A(t) sinùDt - B(t) cosùDt (IV-5)

En résolvant ces intégrales, on détermine la réponse u(t). Le chargement dynamique p(t)

..

est dû à une accélération ( )

a t d'un signal sismique (El-centro 18 mai 1940 composante SO-

OE par exemple),

Notons que la force effective due à cette accélération est donnée par :

..

P_eff(ô)=-m ( )

a ô

Donc :

t

1 .. - (t- )

u(t) = - ? a îù ô

( ) e

ô sin ù_D ( t d

- ô ô

ù_D

0

(IV-6)

1 t..eùô A(t)= - ? a ( ) ô cos( ) ù ô ô D d îù t ù e D 0 1 t..eùô B(t)= - ?a (ô ) sin( ) ù ô ô D d îù t ùe D 0

(IV-7) (IV-8)

On ne peut pas résoudre ces intégrales par les méthodes classiques. On utilise alors un procédé de sommation :

Ät 1 A

Donc :

A(t)= -

××Ó (t)

ù _D ò

(IV-9)

Ät 1 A B(t)= - × ×Ù (t) ùD ò

(IV-10)

Parmi les méthodes de résolution, il existe trois qui sont les plus souvent utilisées : méthode par simple sommation, méthode de trapèze et méthode de Simpson.

1. Simple sommation (q=1) :

A A ..

? ?(îù t )

Ó = Ó - Ä + - Ä ×

( ) ( ) ( ) cos ( )

t t t a t t ù t t e - Ä

- Ä × (IV-11)

D

?? ?? 1 1

A A ..

? ? ( - Ä

îù t )

( ) ( ) ( (IV-12)

Ù = Ù - Ä +

t t t a t t ) sin (

- Ä × ù t t

- Ä ) × e

D

?? ??

1 1

2. Méthode des trapèzes (ò=2)

A ? A ? ..

..

( ) ( ) ( ) cos ù ( ) îù ( ) cos ù

? Ä t

t = ? t t a t t D t t e ( )

Ó Ó ? Ä + ? Ä × ? Ä ? × + ×

a t D t (IV-13)

? ?

2 ? 2 ?

A A ....

? ? ? Ä

îù t

Ù ( )

t = ( t t a t t

) ( ) sin ù ( t t ) e ( ) a t

( ) sin ù t (IV-14)

D D

Ù ? Ä + ? Ä × ? Ä × + ×

?? ??

2 2

3. Méthode de Simpson (G=³)

A

Ó

(t)

3

A ..

? Ó ( 2 ) ( 2 ) cos

t ? Ä + ? Ä ×

t a t t

?? 3

? îù t t

t t e a t t t t e ( ? Ä

îù

ù ù

D ( 2 ) + ? ? Ä ×

..

( 2 )

)

? Ä 4 ( ) cos ( ) ?

? Ä ? Ä

× ×

D

?? ?? ??

.. + a(t) × cos ùDt

(IV-15)

..

-

2) sin

Ä ×

t

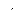
(t-2Ä t) + a(t

A? A

Ù Ù

( )

t = ?

?

3 ? 3

? ? ..?

)

t t e ( 2 )

- Ä

îù t îù t

ù _D ( 2 ) 4 ( ) sin ( )

a t t ù _D t t e (

- Ä - Ä

? × + ? - Ä × - Ä ? ×

? ? ? ? ? ?

.. + a(t) × sin ùDt

(IV-16)

La précision attendue ici de la solution dépend évidemment de la durée de l'intervalle At. En général, cet intervalle doit être choisi suffisamment court à la fois pour que la fonction de

T

chargement et les fonctions trigonométriques soient bien définies : Ät₁₀ .C'est la règle

pratique qui est largement utilisée et qui donne de bons résultats.

La précision et le volume des calculs nécessaires augmentent avec l'ordre du procédé de sommation. En règle générale, la précision accrue que procure la méthode de Simpson justifie son utilisation en dépit d'une plus grande complexité numérique.

Les résultats obtenus sont représentés dans les graphes suivants avec différentes valeurs de coefficients d'amortissements et pulsations :

L'organigramme suivant résume les différentes étapes de résolution de ce problème

Organigramme de résolution

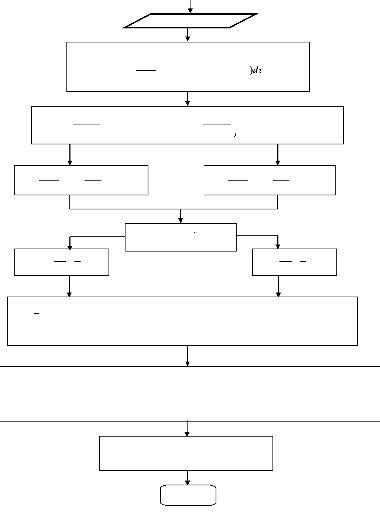
m

ù_D

Lecture des données

t t

u(t) = sinù_D t) e -îù (t- ô) cos( ù_D ô)dô- cosùDt ?

?

ù_D

0

- (t- )

p ( ) e îù ô

ô sin( )

ù ô d ô

D

Intégral DUHAMEL

u(t) = 1 ? p (ô ) _e- 4o(t- ô) sin ù_D ( t -

mù_D

t

0

t₁

_e4oô

A(t)= p ( )

ô ù ô d ô

îù D

? _t cos( )

mùe

D 0

t₁

e^4°ô

B(t)= ? t

p ( )

ô sin( )

ù ô d ô

îù D

m ù e

D 0

Ät 1 A A(t)= - × × Ó (t)

ùò_ò

D

P_eff(ô)=-m ( )

a ô

Ät 1 A B(t)= - × ×Ù (t)

ù_D ò

A

Ó

(t)

cos

3

..

? A

Ó ( 2 ) ( 2 )

t ? Ä + ? Ä ×

t a t t

??

3

? îù t ( - î

ù t t e a t t ù t t e

D ( 2 ) + ? - Ä ×

..

( 2 )

- Ä 4 ( ) cos ( ) ?

- Ä - Ä

× ×

D

?? ?? ??

..

+ a(t ) ×

cos

ù_D t

u(t)= )= A(t) sinùDt - B(t) cosùDt

A? A

Ù Ù

( )

t = ?

?

3 ? 3

? ? .. ?

t t e ( 2 )

- Ä

îù t îù t

ù _D ( 2 ) 4 ( ) sin ( )

a t t ù _D t t e (

- Ä - Ä

? × + ? - Ä × - Ä ? ×

? ? ? ? ? ?

)

..

+ a(t) × sin ùDt

(

sin

..

t - 2Ä t ) + a(t -Ä t) ×

2

FIN

Début