Existence globale des solutions du système couplé maxwell-boltzmann-euler sur un espace temps de Bianchi I.

CHAPITRE TROIS

EXISTENCE GLOBALE DES

SOLUTIONS

^?p,

f,

_u)

3.1 La méthode

Notons par [0, T[ le domaine maximal d'existence de la solution notée (E, donnée par le théorème 2.2 du système (S) avec pour donnée initiale

X0 = (E0, p₀, f0, u0) ? R³ × R³ × L¹(R³) × R³ = E.

Nous voulons prouver que T = +8.

· Si nous avons déjà T = +8, le problème d'existence globale est résolu.

· Nous allons montrer que si nous supposons T < +8, la solution (E,

^?p,

T?u) = X peut

Mémoire de MASTER 33

MOUTNGUI SEE c?UYI 2010-2011.

être prolongée au delà de T, ce qui contredit la maximalité de T.

· La stratégie est comme suit :

Supposons 0 < T < +8, soit t0 ? [0, T[. Nous montrerons qu'il existe ä > 0 indépendant de t0 tel que le système (S) ait une unique solution X = (E, p, f, u) sur [t0, t0 + ä] avec la condition initiale

^?X(t0) = (^?E(t0), ^?p(t0), h0), u(t0)).

Alors, en prenant t0 suffisamment proche de T tel que 0 < T - t0 < ^ä₂, il s'ensuit que T < t0 + ^ä₂, nous pouvons ainsi prolonger la solution X = (^?E,^?p, ^?f,^?u) sur [0, t0 + ^ä₂] qui contient strictement [0, T[ et ceci contredit la maximalité de T. Dans le but de simplifier les notations se sera suffisant si nous pouvons chercher ä tel que 0 < ä < 1.

· Dans ce qui suit nous fixons un nombre r > 0 et nous prenons f0 tel que ?f0? = r, par (2.20) nous avons :

?^?f(t0)? = ?f0? (3.1)

Mémoire de MASTER 34 MOUTNGUI SEE c?UYI 2010-2011.

3.1 La méthode

Nous déduisons de (2.18) et (3.1) que toute solution f de l'équation de Boltzmann sur [t0, t0 + ä] telle que f(t0) = ^?f(t0) satisfait :

I If(t)I I < r , Vt E [t0, t0 + ä] (3.2)

Notons que (3.2) montre que toute solution X = (E, p, f, u) du système (S) sur [t0, t0 +ä] telle que :

satisfait :

(E, p, f, u)(t0) = (

^?E(t0),

p(t0), h0),

^-u^-(t0))

X = (E, p, f, u) E C([t0, t0+ä];1[8³)xC([t0, t0+ä];1[8³)xC([t0, t0+ä]; X_r)xC([t0, t0+ä];1[8³)

où X_r est défini par (1.59), C([t0, t0 + ä]; X_r) par (1.60), avec I = [t0, t0 + ä]. Dans ce qui suit, [0, T[ désigne le domaine maximal d'existence de la solution

X = (E, p, ?f, u) de (S) telle que :

( ^?E(0),^?p(0), ^?f(0), u(0)) = (E0, p₀, f0,u0) E S, I If0I I < r.

Nous prouvons le résultat suivant qui sera utile dans la suite.

Lemme 3.1. Les applications t E(t) ; t p(t) ; t ' u(t) sont uniformement

bornées sur [0, T[ et on a :

| Éⁱ(t)| < (|Eⁱ ₀|+Cⁱ ₈T)e^3CT, V t E [0, T[ , i = 1, 2, 3 (3.3)

|P(t)| < (|pⁱ₀|+Cⁱ₁₁T)e^2CT, Vt E [0, T[ , i = 1, 2, 3 (3.4)

|i(t)| < (|uⁱ₀|+Cⁱ₁₂T)e^(2C+Ci13)T, Vt E [0,T[ , i = 1, 2, 3 (3.5)

où

{	C^i8 = C^i8(a0, b0, r, T) (3.3 bis) Ci11 = Ch (a0, b0, r, T, |Ei0|, ~i,j |öij|) (3.4 bis) Ci12 = 02 (ñ0, a0, b0, r, T, Ei,j |öij|) (3.5 bis) Ci13 = C^i (ñ0, a0, b0, r, T, |E^i 0|, ?i,j |öij|) (3.5 bis) 13

Preuve. 1) Considérons (1.55) dans lequel on pose E = E, f = f et u = u i.e, l'égalité :

Ei = - +2 b Ei+ab2 J gni fdq- ^ui ab2 ^J f dq , sur [0, T[. (1)

C _a b) R3 u^°(u)

q R3

Mémoire de MASTER 35 MOUTNGUI SEE c?UYI 2010-2011.

3.1 La méthode

????

+ 2

aÿ a

bÿ b

????

de (1.3), on a :

= 3C (2)

1

|?u³|

|?u²|

1_, b

,

a

1 b

=

^?u)

?u) =

=

)

u⁰(

u⁰(

Nous avons de (1.4) et (2.6) : |?u1|

?

?

?

et

u⁰(^?u

( ₁ )

z(t) = a0 + b0 1 + a0 + b0 e^CT, ?t ? [0, T[ , où :

z=a, b, 1a, 1b

En utilisant (2.20) (|||

^?f||| = ?f0? = r), on obtient : ^ab2 Jqo fdq- ô Z ab2 ^J f dq???= Cs (3) R3 q u (u) R3

où :

Cⁱ₈ = Cⁱ₈(a0, b0, r, T).

(1), (2) et (3) donnent alors :

|^ÿ?Ei| = 3C|^?Eⁱ|+Cⁱ₈ , i = 1,2,3 (4)

Intégrons (4) sur [0, t] (t ? [0, T[), on obtient :

| ^?E^i(t)| = (|

? t ^?E^i(0)| + C^i 8T) + 3C | ^?E^i(s)|ds 0

où ^?Eⁱ(0) = Eⁱ₀ , i = 1,2,3

donc :

? t

| ^?Eⁱ(t)| = (|Eⁱ ₀|+Cⁱ ₈T)+3C | ^?Eⁱ(s)|ds (5)

0

d'après le lemme de Gronwall on a :

| ^?Eⁱ(t)| = (|Eⁱ₀| + Cⁱ₈T)e^3CT, ? t ? [0, T[ , i = 1,2,3 (3.3)

^?E, p = ^?p, f =

f? et u = ?u i.e, l'égalité :

D'où t ?-? ^?E(t) est uniformement bornée.

2) Considérons (1.56) dans lequel on pose E =

^ÿ?p^i = -2?^i0i?p^i

ûi 2 ? ~c1? 0 (T) f3 fdq-^ab^2giip0(?p)^öik u0(?u) f 3 fdq (6)

3.1 La méthode

?101 =

aÿ a

, ?^202 = ?^303 =

bÿ b

de (1.3) on a :

|2?ⁱ_0i?pⁱ| = 2C|?pⁱ| (7)

d'après (3.3) et en procédant comme ci-dessus, on a avec ¹

u0(?u) = 1 :

????

où :

?Eiab2 ?fdq??

u⁰(

u) I3? = Cs (8)

Cⁱ₉ = Cⁱ (a0, b0, r, T, |Eⁱ ₀|). 9

ab²g³³ = a |?p1| < 1 |P| < 1

b2

ab2g22

De même avec ab²g¹¹ =

a g = g , p0(?p) -- a, p0(?p) -- b

pO(P) = b et 1
u0(?u) = 1, on a :

????

ab^2g^ii

?p^k ? p^0(p)^öik

1? f fdq^????= Ci0 (9) u^0(u)3

où :

Ci10 = Cⁱ (a0, b0, r, T, ? 10

i,k

|öik|).

On déduit de (6), (7), (8), (9) et (3.3) que :

|^ÿ?pi|= 2C|?pⁱ|+Cⁱ (10)

11

où :

?

Ci 11 = Cⁱ (a0,b0,r,T, |Eⁱ ₀|, 11

i,k

|öik|).

Mémoire de MASTER 36 MOUTNGUI SEE c?UYI 2010-2011.

En intégrant (10) on obtient ?t ? [0, T[ :

? t

|?pⁱ(t)| = (|?pⁱ(0)| + Cⁱ₁₁T) + 2C |?pⁱ(s)|ds , ?t ? [0, T[ , i = 1, 2, 3

0

En appliquant le lemme de Gronwall nous avons avec ?pⁱ(0) = pⁱ₀, i = 1,2,3 :

|?pⁱ(t)| = (|pⁱ₀| + Cⁱ₁₁T)e^2CT, ?t ? [0, T[ , i = 1, 2, 3 (3.4)

3.1 La méthode

3) Considérons (1.58) dans lequel nous posons E = l'égalité :

E, f =

f, u =

?u et u^0= u^0(^?u) i.e,

ab²gⁱⁱqj ab2giiöij ~
· ab2gjP0 JR3

jEui qjui = -2ri0iû -ñ0u _R 0 öijf3 q0 fdq + P0(u0)2 u' f fdq + q0?fR3

ab^2gjjû^iûj^?Ej	L2 ui?uj qk 3 fdq - ab çjk ñ0u^0JR3 q0^?fdq (11)
ñ0u^0

De la même façon que ci-dessus on déduit les inégalités suivantes, pour les 2^e et 3^e termes de (11) :

{

|rⁱ_0i| = C

?? (12)

-

ii

j

ii

iñ0

0

0

_ñ0

₀

ab2g

fr q

f ab2g

r

u

JR3 q

" dq +

(u

)2 u JR3 fdq C12

où :

Ci 12 = Cⁱ (ñ0, a0, b0, r, T, ? 12

i,j

|öij|).

Mémoire de MASTER 37

Intégrons (14) sur [0, t] (t ? [0, T[), ce qui donne :

MOUTNGUI SEE c?UYI 2010-2011.

Pour les 4e, 5^e et 6^e termes de (11), on a :

ab2gjj?Ej / q ô fdq-ab2gjj Ejlj f fdq-ab2öjk ~ 0 f q0 fdq û^? ??= Cⁱ₁₃|?u | (13)

C Po JR3 q ñ0u R3ñ^il-ri

R3 q

où :

Ci113 = C13 (ñ0, a0, b0, r, T, |E^i0LE I E i,j

|öij|).

de (11), (12) et (13) on obtient :

| ^ÿûⁱ| = 2C|?uⁱ| + Cⁱ₁₃|u| + Ci12

i.e.

| ^ÿûⁱ| = (2C+Cⁱ₁₃)|i|+Cⁱ₁₂ , i = 1, 2, 3 (14)

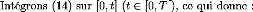
t

û(t)

|

|=(|?uⁱ(0)| + Cⁱ₁₂T) + (2C + Cⁱ₁₃)/ |û(s)|ds , i = 1, 2,3

0

Le lemme de Gronwall donne avec ûⁱ(0) = uⁱ₀, i = 1, 2, 3 :

|iiⁱ(t)| = (|uⁱ₀| + Cⁱ₁₂T)e^(2C+Ci13)T, ?t ? [0, T[, i = 1,2,3 (3.5)
De (3.3), (3.4) et (3.5) on obtient le lemme.

Le lemme 3.1 nous permet de déduire la proposition suivante :

Mémoire de MASTER 38 MOUTNGUI SEE c?UYI 2010-2011.

3.1 La méthode

Proposition 3.1. Il existe 3 constantes R1 > 0, R2 > 0, R3 > 0 telles que :

||| ^?E||| = R1, |||^?p||| = R2, |||^?u||| = R3.

où

R1 = R1(a0, b0, r, T, E0)

R2 = R2(a0, b0, r, T, _öij, E0, p₀)
R3 = R3(ñ0, a0, b0, r, T, _öij, E0, u0).

Preuve. On pose

Ri 1 = Ci 8 + (|E^i 0| + Ci e3C(T+1), i = 1, 2, 3. [ 8T)e3CT] En prenant : 3 R1 = Ri ? 1 i=1 On déduit de (3.3) que : |||^?E||| = R1 On pose : R^i2 = [C1 + (|p^i0| + Ci11T)e2CT1 ^e2C(T+1), i = 1, 2, 3 3 R2 = Ri ? 2 i=1 Et on déduit de (3.4) que : |||^?p||| = R2 En posant : R3 = [Ci12 + (|u^i0| + Ci12T)e(2C+Ci131 ^e(2C+C13)(T+1), i = 1, 3 R3 = Ri ? 3

2,

3.

(3.6) (3.7) (3.8) (3.9) (3.10) (3.11)

i=1

On déduit de (3.5) que :

||| ^?u||| = R3

d'où la proposition.

Comme nous le verrons les nombres R1, R2, R3 sont pris suffisamment grands, pour borner non seulement X mais aussi, toute solution X du problème de Cauchy sur [t0, t0+ä] avec la donnée initiale en t0 ? [0, T[.

Mémoire de MASTER 39 MOUTNGUI SEE c?UYI 2010-2011.