Existence globale de solutions à symétrie sphérique du système d'Einstein-Klein-Gordon.

3.2 Théorème d'existence et d'unicité (théorème principal)

Le théorème suivant donne l'existence et l'unicité de solution pour l'équation intégro-différentielle non linéaire du premier ordre

Théorème 3.2.1 : Soit j E {3, 4}. Supposons que la donnée initiale h0 E C¹([0, +8[), où h0(r) = h(0,r) telle que h(0,r) = O(r-(j-¹)) et ^?_?rh(0,r) = O(r-j). Notons

d = Yh(0,.)YX₀

Mémoire de MASTER

30

3.2. Théorème d'existence et d'unicité (théorème principal)

.Alors il existe ä > 0 tel que si d < ä, alors il existe une unique solution globale h E C¹([0, +8[×[0, +8[) de l'équation intégro-différentielle non linéaire (2.14) pour p E [j, 8[ avec h0 la donnée initiale.Cette solution vérifie

1h(u, r)1 = M(1 + r + ^u)-(j-1) , I?h ?r (u, r)V= M(1 + r + u)^-j. (3.1)

De plus,nous avons e^í , e^ë --> 1 et l'espace-temps devient plat quand u --> +8

Remarque 3.2.1 : Nous déduisons du Théorème 3.2.1 que si h E C¹([0, 8[×[0, 8[) alors h(u,.) est localement C¹ sur [0, 8[ pour u = 0 fixé. Considérons la formule

r

ö(u, r) = 1 f h(u, s)ds

, la fonction qui à s H h(u, s) étant continue sur [0,r], par la formule de la moyenne, il existe c_r E [0,r] tel que h(u, c_r) = r1 f0 r h(u, s)ds en faisant r --> 0, on a c_r --> 0; on déduit donc que ö(u, 0) = h(u, 0) pour tout u = 0.Donc

1 r r

ö(u, r) - ö(u, 0) = r S ₀ h(u, s)ds - S 0 h(u, 0)ds)

1 r

r S 0 (h(u, s) - h(u, 0))ds

1 r

I Is

r Jo Jo ?ódóds

Nous avons donc

1ö(u, r) - ö(u, 0)1 = r supI

2 0<s<rI?h(u, s)

et

sup

0<r<ä

?s

V

?ö(u, r) I = 1 _sup I?h(u, r) I M(ä, u) < 8 ?r 2 0<r<ä ?r

pour tout u = 0. Ceci combiné avec (2.4), nous déduisons que í + ë est localement lipschitzienne sur 1[8₊ pour u = 0 fixé. Des relations (2.10) et (2.13) les fonctions g et g sont aussi localement lipschitziennes.

3.2.1 Éléments de preuve du théorème d'existence de d'unicité

Pour démontrer le théorème 3.2.1, nous allons insister le plus sur le cas j = 3, et donc p E [3, 8[ . Les principaux changements d'estimations pour le cas j = 4 doivent être soulignés. Nous considérons l'application h H .7^-(h), qui est définie comme une solution de l'équation différentielle non linéaire du premier ordre

D.7- = (.7- - h) [^g-_2r^g - 4ðr9 (h)^p+1] - ¹₂rg (h)^p (3.2)

p +

3.2. Théorème d'existence et d'unicité (théorème principal)

avec la condition initiale

F(h)(0,r) = h(0,r) (3.3)

Notons B(O,x) = {f E X : fYX = x}. Alors il est clair que B(O,x) c X c Y . On a les deux lemmes suivants :

Lemme 3.1 : Soit x > 0 tel que d < x. Alors,

F : B(O, x) ? B(O, x)

.

Lemme 3.2 : Il existe = î(x) E]0, 1[ tel que

YF(h1) - F(h2)YY = îYh1 - h2YY

pour tout h1 , h2 E Y . C'est-à- dire que F est contractante dans Y . Alors le théorème du point fixe de Banach, fournit l'existence d'un unique point fixe h E Y tel que F(h) = h.

Prouvons ces deux lemmes qui vont jouer un rôle capital pour la démonstration du théorème principal le Théorème 3.2.1.

3.2.2 Preuve du lemme 3.1

Fixons YhYX = x.

Soit r(u) = X(u; r0) la solution de l'équation différentielle ordinaire. Nous pouvons avoir grâce au Théorème 1.2.1 (théorème de Cauchy-Lipschitz)

dr = - du

1 2

g(u,r), r(0) = r0 (3.4)

Mémoire de MASTER

31

Notons r1(u1) = X(u1, r0), alors (3.4) donne après une intégration sur [0, u1]

1 u1

r1 = r0 - 2 S 0 g(u, X(u; r0))du. (3.5)

En utilisant cette caractéristique, nous pouvons représenter F au moyen d'une intégrale comme suit

^u1 2r - 4ðrg

F(u1, r1) = h(0, r0)exp oeS 0 ~g - g p + 1 %ohé^p+1~ du^'

X

+ Su1 ^u12r - 47rrg 0 exp (S u ~g - g p + 1 (h)^p+^1] du^' [f]X du. X

(3.6)

Mémoire de MASTER

32

3.2. Théorème d'existence et d'unicité (théorème principal)

où

f=-

[1 4ðgr p+1 1 p-1
2r(g ^g) p+ 1 %ohé ₂rg %ohé ] h. (3.7)

En effet :

Posons A(u) = h(u, r(u))expoef ^u1

_u g - g

2r - 4ðrg

p + 1 %ohé^p+1~ du^'. Alors X

dA(u) du

^u12r - 4ðrg = Dh exp oeS u g - g p + 1 %ohé^p+1~ du^' X - h g - g 2r - 4ðrg p + 1 %ohé^p+1~exp oeS u g - g ^u12r - 4ðrg p + 1 %ohé^p+1~ du^' X r g-- g4ðrg p+1 1 pl ~1 g- g4ðrg p+1 ' = j (h - h) [ 2r + 1 %ohé ]-2 rg %ohé } expoef[ 2r + 1 %ohé]dull P 1 P X

h g - g - 4ðrg (hé^p+ⁱ] expoef u1 g - g - 4ðrg %ohé^p+1 du^'

[ 2r p + 1 [ 2r p + 1 ]X

= -h[g - g 4ðrg _%ohép+1 ¹ rg(h)^p-1 - g - 4ðrg %ohé^p+1 du^'

2r p+1 2 ] expoef~1 [⁹2r p + 1 ]X

Par une intégration sur [0, u1], on a :

A(u1) = A(0) ₊4 f ^u1oe-h [^g-_2r^g-⁴+^r9 %ohé^p+1 + 2rg(h)^p-1] expoef u1 [g2rg p+r9 %ohé^p+1~ du^' du

X

^u1 2r - 4ðrg

= h(0, r(0))exp oeS 0 g - g p + 1 %ohé^p+1~ du^'

X

+ f0

^u1 oe-h g - g

2r - 4ðrg p+1%ohép+1 + ¹₂rg(h)^p-1] exp oef g - g

^u1 2r - 4ðrg

p + 1 %ohé^p+1~ du^' du

X

d'où le résultat.

?.7"

.

?r

Pour j = 3, on a :

Dans ce qui va suivre, nous chercherons une majoration de .7" et de

= V¹_r

f^rh(u,s)ds

V

1
· ~

ü Jo (1 + s + s)2(1 + s + u)²Sh(u,s)Sds

r

1 r YhYX ds = x (3.8)

ü
· for

(1 + s + u)² (1 + u)(1 + r + u)

et

s

Sh(u,r) - h(u, r^')S = f ,r V _?s (u, s)I ds = x _Jr'r (1 + s+ u)³

x 1 1

2 (1 + r^' + u)^{2 -}(1 + r + u)2 (3.9)

3.2. Théorème d'existence et d'unicité (théorème principal)

De là, nous avons

]dr^'

1 r

S(h - h)(u, r)S = r S 0 Sh(u, r) - h(u, r^')Sdr^'

=

S0

x rr 1 1

2r Jo L1 + r^' + u)^2-(1 + r + u)²

xr

2(1 + r + u)²(1 + u)

(3.10)

Donc

00 (h -_r h)2 2 002 _x2

24

_Jo

dr =(3.11)

4(1 + u)² (1+ s + u)4ds = 24(1 + u)2 =

Ceci combiné avec (2.12) donne

ð4x² g(u, 0) = exp[- (3.12)

24(1 + u)4] = exp ~-^ðx2

6 ~

En utilisant (2.12)(en dérivant g par rapport à r) et en utilisant l'inégalité (3.10) on a

fr?g rr (h - h)² ðx2 rr s
(u,$)~ds = 4ðds J ds
(~Js Jr'r' s (1 + u)² r' (1+s+u)⁴
ðx² r 1

3(1 + u)2 ~ r'

(1 + r^' + u)3 - (1 + r + u)3 ~ + ðx2

6(1 + u)2 ~ 1 (1 + r^' + u)^{2 -}(1 + r + u)2 ~

(3.13)

Et on obtient

(g - g)(u,r)S¹ = rJo r Sg(u,r)- g(u,r')Sdr'= 1 f r f'r S4g (u,s)Sds
·dr'

ð x2 r r ' r

3r(1 + u)2 _Jo L1 + r^' + u)³ (1 + r + u)³

6r(1 + u)2 Jo (1 + r^' + u)² (1 + r + u)² ð

=

+

]dr^' ]dr^'

x2 r

1 1

Mémoire de MASTER

33

ðx²(r³ - r² - ur²)

6r(1 + u)^3(1 + r + u)3 +	ðx^2r^2
	6r(1 + u)^3(1 + r + u)^2

ðx²(r³ - r² - ur² + r² + ur² + r³)

=

6r(1 + u)³(1 + r + u)³ ðx²r²

(3.14)

3(1 + u)³(1 + r + u)³

3.2. Théorème d'existence et d'unicité (théorème principal)

S0

ds

Nous avons aussi grâce à l'inégalité (3.8) et du fait que g = 1

r _xp+1r

2

s

p

=

2(h)

(1 + u)p⁺¹ (1 + s + u)p⁺¹

+1gds L

_xp+1 r _s2

= (1 + u)p+1 ^S (1 + s + u)^4ds 0

_xp+1 1+r+u 1

(1 + u)p⁺¹ ji+u t4 [(1 + u)² + t² - 2t(1 + u)] dt

= xp+1 _r r3 - 3r(1 + u)

(1 + u)p⁺¹ 3(1 + u)(1 + r +u)³]

_xp+1_r3

= (3.15)

3(1 + u)p⁺²(1 + r + u)³

Donc de (2.13) puis de (3.14) et (3.15) on a

8ð r

Sg - gS = Sg - gS + r(p + 1) S 0 s2ShSp+1gds

8ðxp⁺¹r²

3(p + 1)(1 + u)p⁺²(1 + r + u)³

ðx²r²

= + 3(1 + u)³(1 + r + u )3

M(x² + xp⁺¹)r²

= Car p = 3 (3.16)
(1 + u)³(1 + r + u)³

où M est une constante indépendante de x, u et r. (3.16) avec (3.8) donne

L r Jo u1 [g2rg ^p+ 1 %ohé^p+1du = M(x^2+ xp^+1) Jo u1 2(1 + u)^3(1 + r + u)^3 x

du

r

1

]_X^du

+

4ð up + 1 Jo

8 1 8 1

= M(x² + xp+1)S 2(1 + u)5du + ð S (1 + u)7du (car p = 3)

0 0

ð +

6

M(x² + xp⁺¹)

= 8

= M(x² + xp⁺¹) (3.17)

En utilisant (2.13), (3.12) et (3.15), on a

8ð /,r

J

g = g(u, 0) r(p + 1) o

s²(h)p⁺¹gds

ðx² 8ðxp⁺¹r²

= exp[

6 ] ^-3(p + 1)(1 + u)p⁺²(1 + r + u)³

Mémoire de MASTER

34

exp[

ðx^28ðxp^+1 6 ] - (3.18) 3(p + 1)

Soit x1 une racine de l'équation

exp[-^ðx2] - 8ðxp+1 (3.19)

6 3(p + 1) = 0

Mémoire de MASTER

35

3.2. Théorème d'existence et d'unicité (théorème principal)

Alors la fonction

k = k(x) = exp[-^ðx2 ] - 8ðxP+1 (3.20)

6 3(p + 1)

vérifie 0 < k = 1 pour tout x E [0, x1[ ; en effet k est décroissante sur [0, x1[, on a

0 = x < x1 = k(0) = k(x) > k(x1)

Et comme k(0) = 1 et k(x1) = 0, on a le résultat. De (3.16), on a

1 4ðrg

SfS = 2rS(g - g)SShS + p + 1 ShS^P+2 + ₂rgShS^P

1

= A1 + A2 + A3. (3.21)
De (3.8) et (3.16) nous avons

M(x³ + xP+2) (puisque r < 1 + r + u) (3.22)

2(1 + u)⁴(1 + r + u)³

M(x³ + xP⁺²)r

A1 =< 2(1 + u)⁴(1 + r + u)⁴

Toujours de (3.8) et du fait que de (2.12), g = 1, on a

4ðrxP⁺²

A2 = (p+1)(1+u)P+2(1+r+u)P+2

4ðxP⁺²

= 4(1 + u)P⁺²(1 + r + u)P+1 car p = 3
4ðxP⁺²

= (3.23)

4(1 + u)³(1 + r + u)²

et

rxP A3 = = 2(1 + u)P(1 + r + u)P	4ðxP
	4(1 + u)P(1 + r + u)P-^1

4ðxP =(3.24)

4(1 + u)³(1 + r + u)²

Nous notons que si j = 4, une estimation de A2 et A3 est :

4ðxP⁺²

A2 = (3.25)

4(1 + u)³(1 + r + u)³

4ðxP ( )

A3 = (3.26)
4(1 + u)³(1 + r + u)³

En combinant (3.21) , (3.22), (3.23) et (3.24), on obtient

SfS = 2(1 + u)⁴(1 + r + u)3 + 4(1 + u)³(1 + r + u)3 + 4(1 + u)³(1 + r + u)²

M(x³ + xP⁺²) 4ðxP⁺² 4ðxP

= 3.27
M(x³ + xP + xP⁺²)

(1 + u)³(1 + r + u)2 ( )

Mémoire de MASTER

36

3.2. Théorème d'existence et d'unicité (théorème principal)

Dans le cas où j = 4, de (3.24) on a

M(x³ + xP + xP⁺²)

SfS = (3.28)

(1 + u)³(1 + r + u)³

Grâce au Théorème 1.2.1, on peut poser r(u) = X (u; r1) et des relations (3.18) et (3.20), nous avons

1ru' 1

r(u) = r1 + 2 J §oû, X (u^'; r0))du^' = r1 + ₂(u1 - u)k (3.29)

et puisque k ?]0,1] pour x ? [0, x1[,

u k u1

1 + r(u) + u = 1 + ₂ + r1 + ₂(u1 - u) = k(1 + ₂ + r1)

k

= ₂(1 + r1 + u1) (3.30)

Donc

S0 u1u1 M(x³ + xP + xP⁺²)

[f]_X Sdu =fdu L1 + u)³(1 + r + u)²]_X

M(x³ + xP + xP+2) 8 du

= k²(1 + r1 + u1)2 Jo (1 + u)³

M(x³ + xP + xP+2) (3.31)

2k²(1 + r1 + u1)²

En utilisant (3.29), on obtient

k

r0 = r(0) = r1 + ₂u1 (3.32)

et puisque k ?]0,1] pour x ? [0, x1[, nous avons de (3.1)

d d d

Sh(0,r0)S = (1 + r0)2 =(3.33) (1 + r1 + k 2u1)2 = k²(1 + r1 + u1)²

En combinant (3.6), (3.17), (3.31) et (3.33), nous obtenons

W

SF(u1, r1)S = Sh(0, r0)Sexpoef ^u1 WL 2rg - 4+r9 ] du^'

p X

u1 ^u1 2r - 4ðrg

+ S 0 exp oeS _u W~g - g p + 1 ~ W du^'S [f]_X Sdu

X

M(d + x³ + xP + xP⁺²)exp[M(x² + xP⁺¹)] =3.34

2k²(1 + r1 + u1)2 ( )

Posons maintenant

G(u, r) = F

ar (u, r)

avec

?h

G(0, r0)

= ?r (0, r0)

3.2. Théorème d'existence et d'unicité (théorème principal)

En différenciant (3.2) par rapport à r,on a :

? 1 ?g ?.~ ₌OE?F ?h _f 1 4ðr 1

Dg(u1, r1) = ?r(D.r) ⁺2?r?r ?r ?r [_2r(g-g)-_{p +}9(h)^P+1J
g_h p -r?g h P_- p ?h h p-1 ₊1?g?.~

2 %o ) 2?r %o ) 2rg?r %o ) 2?r?r

1_r ? g - g ?h ₎P 4ðg p+1 4ðr ?g ₎P+1
+ - hé 2 ?r(g - g) - 2r2 - 4ðrg _?r ^%oh) p + 1 ^%ohé-p + 1 ?r %oh)

= 1 4ðrg p+1 1 ?g
[2r(g-g)- p + 1 ^%ohé +2?r]g

1 ? g - g 4ðg p+1 ?h P 4~rr âg ^p+1 %o.r hé

+ (g - g) - - %ohé - 4ðrg %ohé - (h)
2r ?r

2r² p + 1

?

1?

r p +

r

+ ~4ðrg

p + 1 %ohé^p+1 - 1 ?g

2r(g - g) - p ₂rg %ohép-1~ ?h

?r - g 2 %ohé^p - r ?r %ohé^p (3.35)

2

Comme précédemment, nous résolvons l'équation linéaire (3.35) en g, utilisant la caractéristique introduite dans (3.29) pour obtenir :

?h u1 4ðrg p+1 1 ?g 'g(u1,r1)=?r(0,r0)expoeJo [¹2r⁽g-g)-p+1 ^%ohé +2?r]Xdu

u1 u1 ?g
+ S 0 exp oeS u ~ 1 2r(g - g)- 4ðrg

p + 1 %ohé^p+1 + 1 du^' _[f1]X du (3.36)
2 ?r X

où

f1 1 ? (9 9) g - g -- 47rg (h)^p+1 -- 47rrg^Oh (h)^P -- 4irr âg

= (h)^P+i (1 - hé

[2r?r 2r² p + 1 ?r p + 1 ?r

+ ~4ðrg

p + 1 %ohé^p+1 - 1 ?g
2r(g - g) - p ₂rg %ohép-1~ ?h

?r - g 2 %ohé^p - r ?r %ohé^p (3.37)

2

En effet :

Mémoire de MASTER

37

?g

Donc en utilisant la formule

, on a de la relation (3.14), (3.15), (3.8) et du fait

g - g r

?r

3.2. Théorème d'existence et d'unicité (théorème principal)

Posons B(u) = G(u,r(u))exp oe? ^u1

_u [21( p +rg %ohé^p+1 + ^12. _?9]_Xdu^'. Alors,

d _duB(u) = DGexp oef_u^u1

1 4ðrg p+1 1 ?g '

é _[2r(g ^g) p + 1 %oh + 2 ?r]X du

- 1 4ðrg p+1 1 ?g _u1 4ðrg p+1 1 ?g,~[ _2r(g g)p + 1 %ohé + 2 ?r ] expYI _2r(g g) p + 1 %ohé + 2 ?r ]_X du

'l

4ðrg p+1 1 ?g

=G[12r(g-g)- _p+1 %ohé +_2?r]exp{...} - ^g₂ %ohé^p + r?g

?r %ohé^p
· exp {...}

2

1 ? g - g P 4ðg

+ %oF - hé 2r ?r(g ^g) 2r2 - 4ðrg^âh %ohé - %ohép+1 4ðr ?g - %ohé^p+1]exp{...}
?

1?

r p + 1 p +

r

+ ~4ðrg

p+1 %ohé^p+1 - 1 2r(g - g)- ^p ₂rg %ohép-1~ ?h

?r exp{...}

-G[

1 4ðrg p+1 1 ?g
2r(g-g)- p + 1 %oh) +_2?r]exp{...} = ~ 1 ?r(g - g) - g - g

? 2r2 - 4ðg

p + 1 %ohé^p+1 - 4ðrg ?h

?r %ohé^p - 4ðr ?g ?r %ohé^p+1~ %oF - hé exp {...}

2r p + 1

+ [

4ðrg p+1 1 p p-1 ?h g p r ?gp
p + 1 %ohé - _2r(g - g) ₂rg %ohé ] ?r 2 ^%ohé 2 ?r %ohé exp {...}

et intégrant membre à membre sur [0, u1] la dernière égalité, nous avons, puisque B(u1) =

G(u1, r1) = 0,

?F

B(0) = G(0, r0) = ?r (0, r0)

, nous avons le résultat.

Or, nous déduisons de (3.37), puisque 0 < g = 1

Sf1S = oeS 1 ?2r?r(g - g)S 2r2

+ Sg - gS + p + 4ð ShSp⁺¹ + 4ðr ^?h ShSp + p+ 4ðr ShSp⁺¹ V^?g_rV (SFS + ShS)

1 ?r 1 ?

+[

(3.38)

Sg - gS + pgrShS^p-1 + ^4ðr _ShSp+1] ^?h + ¹ShS^p+^rS^?gSShS^p 2r 2 p + 1 ?r ^W 2 2 ?r
= (B1 + B2 + B3 + B4 + B5)(SFS + ShS) + (B6 + B7 + B8) W?h

?r W+ B9 + B10

En dérivant (2.13) par rapport à r on a

?g ?g + ?r ?r

(p f^rs²ShSp⁺¹gds - 9(3.39)81)r2 +

Mémoire de MASTER

38

3.2. Théorème d'existence et d'unicité (théorème principal)

que g < 1

~^gS < Sg - ^gSr⁺(p81)r2 _Jo^rs²ShSp⁺¹ds + p₊1ShSp⁺¹

ðx^2r < 3(1 + u)^3(1 + r + u)3 + 8ðxp^+1r	8ðxp^+1r
	3(p + 1)(1 + u)p^+2(1 + r + u)^3

+ (p + 1)(1 + u)p⁺¹(1 + r + u)p⁺¹

M(x² + x⁴ + xp⁺¹)r

< (3.40)
(1 + u)³(1 + r + u)³

En différenciant g définit par la relation (2.12) puis en utilisant (3.10), nous avons

< 4ðSh - hS2 < ðx2r

?r r (1+u)²(1+ r+u⁴V^?gV (3.41)

En combinant (3.40) et (3.41), on déduit que

1 ? M(x² + x⁴ + xp⁺¹⁾ ðx²

B1 := V2r?r(g ^g)V 2(1 + u)³(1 + r + u)^{3 +}2(1 + u)²(1 + r + u)⁴

< M(x² + x⁴ + xp+1) (3.42)
- (1 + u)²(1 + r + u)³

M(x² + xp⁺¹)

De (3.16), on a

B2 := Sg - gS

2r2 < 2(1 + u)³(1 + r + u)³

< (3.43)
M(x² + x⁴ + xp⁺¹)

(1 + u)²(1 + r + u)³

De (3.8) on a

4ð 4ð xp+1

B3 :=

ShS^p+1 <

p + 1 p + 1 (1 + u)p⁺¹(1 + r + u)p⁺¹

Mémoire de MASTER

39

ðxp⁺¹

< (1 + u)³(1 + r + u)³

< M(x² + x⁴ + xp+1) (3.44)

- (1 + u)²(1 + r + u)³

?h h - h

Puisque = , (3.8) et (3.10) donnent :
?r r

B4 := 4ðr W8_h^hShS^p <_r_4ðr^Sh_r^hSShS^p

x < 4ðr 2(1 + u)(1 + r + u)^2 4ðxp^+1	xp
	(1 + u)p(1 + r + u)p

<

<

2(1 + u)p⁺¹(1 + r + u)p⁺² 2ðxp⁺¹

(1 + u)³(1 + r + u)³
M(x² + x⁴ + xp⁺¹)

< (3.45)

(1 + u)²(1 + r + u)³

3.2. Théorème d'existence et d'unicité (théorème principal)

De (3.8) et (3.41), on a

B _ 4ðr _ShSP+ âg < 47rr xP⁺¹ ðx²r

=

5 p+1 V?rV p + 1 (1 +

¹ u)P⁺¹(1 + r + u)P⁺¹ (1 + u)²(1 + r + u)⁴
4ð²xP⁺³r²

(p + 1)(1 + u)P⁺³(1 + r + u)P⁺⁵

4ðxP⁺³

= (1 + u)P⁺³(1 + r + u)P+3 (car p + 1 > ð et r² = (1 + r + u)²)

=

4ðxP⁺³

(1 + u)³(1 + r + u)³

M(x² + x⁴ + xP⁺³) =(3.46)

(1 + u)²(1 + r + u)³

Comme précédemment, les relations (3.8) et (3.16) impliquent

B6 + B7 := Sg - gS

2r

p + grShS^P-1 = M(x² + xP⁺¹⁾r. pxP-¹r

2 2(1 + u)³(1 + rll ++ u)³ 2(1 + u)P-¹(1 + r + u)P-¹

M(x² + xP-¹ + xP⁺¹)r

= (3.47)

(1 + u)²(1 + r + u)²

De (3.8), on a

4ðrS _IP+1 4ðr xP+1

B8 := p + 1 h p + 1 (1 + u)P⁺¹(1 + r + u)P⁺¹

ðxP⁺¹r

= (1 + u)²(1 + r + u)2 car p + 1 = 4

M(x² + xP-¹ + xP⁺¹)r

=

(3.48)

(1 + u)²(1 + r + u)²

Des relations (3.8) et (3.41), on a :

2

B9 + B10 :=

?

S

S

V?

1 r

r x r xP

₂

g xP 7r

h

P + 2

rV ShSP = 2(1 + u)P(1 + r + u)P + 2 (1+ u)²(1 + r + u)⁴ (1 + u)P(1 + r + u)P

_xP

= 2(1+u)P(1+r+u)P+ _xP

= 2(1 + u)³(1 + r + u)4 +

ðxP⁺²r²

2(1+u)P⁺²(1+r+u)P⁺⁴ ðxP⁺²

2(1 + u)³(1 + r + u)⁴

Mémoire de MASTER

40

M(x³ + xP + xP⁺²)

= 3.49

(1 + u)³(1 + r + u)4 ( )
En utilisant inégalités (3.42) - (3.42), (3.8) et (3.10), nous obtenons

5M(x² + x⁴ + xP⁺¹ + xP⁺³) 2M(x² + xP-¹ + xP⁺¹)Sh - hS M(x³ + xP + xP⁺²)

(1 + u)²(1 + r + u)³ (1 + u)²(1 + r + u)2 + (1 + u)³(1 + r + u)⁴

SS

S

f1

h

) +

5M(x² + x⁴ + xP⁺¹ + xP⁺³) 6M(x³ + x⁵ + xP + xP⁺² + xP+4) + M(x³ + xP + xP⁺²⁾ r

(1 + u)²(1 + r + u)³ (1 + u)³(1 + r + u)4 ¹ (1 + u)³(1 + r + u^l)⁴

(3.50)

+

SFS

3.2. Théorème d'existence et d'unicité (théorème principal)

Maintenant, en utilisant l'inégalité le long de la caractéristique comme dans les relations (3.29) et (3.30), nous savons que

k

1 + r(u) + u = ₂(1 + r1 + u1) (3.51)

et nous obtenons donc en général pour tous entiers naturels q , s et t, il existe m ? Z tels que :

u1

u1 1 du

Jo _x [(1+u)t(l+r+u)q-s _X

=

Lrs

(1+u)t(1+r+u)q du

~

=

=

Mémoire de MASTER

41

2q-s 8 du

2m

00

du

kq-^s(1 + r1 + u1)q-s Jo (1 + u)^t

k^m(1 + r1 + u1)m fo (1 + u)q-s+t-m avec m = q - s

2m

= (3.52)

k^m(q - s + t - m)(1 + r1 + u1)^m

S0

pour q - s + t - m > 1. En appliquant (3.52) sur chaque terme de la majoration de f1 (pour le premier terme on prend t = 2, q = 3, m = 1, ets = 0, pour le deuxième t = m = 3, q = 4, et s = 0 pour le troisième t = m = 3, q = 4, et s = 1) obtenue en (3.50), nous avons :

1

u

1

L1 + u)²(1 + r + u)3]X du

u1

du

_o

S _[f1]X Sdu = SF(u1, r1)S5M(x² + x⁴ + x^p+1 + xp+3)

+ 6M(x³ + x⁵ + x^p + x^p+2 + xp+4) JoL1 + u)³(1 + r + u)⁴

1

X

1

u

( 3 P ^P+2)_o L₁

r

+ M x +x +x + u)³(1 + r + u)4 du

X

10M(x² + x⁴ + xp⁺¹ + xp⁺³)

=

4k(1 + r1 + u1)³

sup TM(1 + r1 + u1)²SF(u1,r1)Sú 0=u1,r1<8

48M(x^3 + x^5 + xp + xp^+2 + xp^+4) + + 4k^3(1 + r1 + u1)^3

M(x^3 + xp + xp^+2) 3k^3(1 + r1 + u1)^3

5M²(d + x³ + xp + xp⁺²)(x² + x⁴ + xp⁺¹ + xp⁺³)exp[M(x² + xp⁺¹)]

= de (3.34) 4k³(1 + r1 + u1)³

13M(x³ + x⁵ + xp + xp⁺² + xp⁺⁴)

+ (3.53) k³(1 + r1 + u1)³

Dans le cas où j = 4, nous avons

S0

u1 10M²(d + x³ + xp + xp⁺²)(x² + x⁴ + xp⁺¹ + xp⁺³)exp[M(x² + xp⁺¹)]

S _[f1]X Sdu = 3k⁴(1 + r1 + u1)⁴
40M(x³ + x⁵ + xp + xp⁺² + xp⁺⁴)

+

(3.54)

k⁴(1 + r1 + u1)⁴

3.2. Théorème d'existence et d'unicité (théorème principal)

De (3.8), on a :

V

4ðrg %ohé^p+1V < 4ðrxp+1
p + 1 (p + 1)(1 + u)p⁺¹(1 + r + u)p⁺¹
4ðxp⁺¹

< (p + 1)(1 + u)p⁺¹(1 + r + u)p

M(x² + x⁴ + xp⁺¹) <(3.55)

(1 + u)4 ,

de (3.16), on a

V

^g-gV < M(x² + xp⁺¹) 2r (1 + u)⁵
M(x²

(1 + u)4+1) (3.56)

et de (3.40), on a

V

I M(x² + x⁴ + xp⁺¹)r _?r' < (1 + u)³(1 + r + u)³ M(x² + x⁴ + xp⁺¹) <car r < 1 + r + u

(1 + u)³(1 + r + u)²

( )

M(x² + x⁴ + xp⁺¹)

< (3.57)
(1 + u)⁴

En combinant (3.55), (3.56) et (3.57), nous obtenons

Wf_o [ 2r

1

u

1du

4ðrg%oh < M(x² + x⁴ + xp⁺¹)f⁸

1 ⁽1 + u)⁴

+ M(x² xp+1) °° du fo (1 + u)⁴

8 du

+ M(x² + x⁴ + x^p+1)

S

0 (1 + u)⁴

< M(x² + x⁴ + x^p+1) (3.58)

De (3.1) et de (3.32) on a pour tout x E [0,x1[

V?h

?r (0, r0)V₍₁ < ~ihoYX03 < 3 1+8d+ul 3 (3.59)

( 0)k( )

. Dans le cas où j = 4, on a

V^?h(0_'r0)V

Ilh0YX0 k4 1 + ^6d u 4 (3.60)

Or ( _o)4 <( 1 ₁)

Donc des relations (3.54), (3.58), (3.59) et du fait que

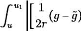
W4ðrg p+1 1?-, , u1 1 4ðrg p+1 1 ?g du'

p + 1 ^%ohé _+2?r]X du'

u = o Wr

2r(9-g)- p + 1 ^%ohé +2Or]X

1 4ðrg p+1 1 ?g '

_fu

[2r(9 g) _

p+1`

+ 1 ~hé + 2 ?r ]_X du

< fu¹1 47rrg p+1 1 ?g '
[2r(g--g)- p + 1 ^%ohé _+2?r]X du

Mémoire de MASTER

fuu1W[21r(g -g)

42

3.2. Théorème d'existence et d'unicité (théorème principal)

on a de (3.53)

SÇ

nn⁽⁽ V_a^h_r (0,r0)S +f:
' (u1,r1)S < S _[f1]X Sdu
·exp[M(x² + x⁴ + x^p+1)]
8d

= k³(1 + r1 + u1)3 exp[M(x² + x⁴ + x^p+1)] 13M(x³ + x⁵ + xp + xp⁺² + xp⁺⁴)

+ exp[M(x² + x⁴ + x^1+p)] k³(1 + r1 + u1)³

5M²(d + x³ + xp + xp⁺²)(x² + x⁴ + xp⁺¹ + xp⁺³)exp[M(x² + xp⁺¹)]

+ exp[M(x² + x⁴ + x^1+p)] 4k³(1 + r1 + u1)³

(3.61)

et par une simplification, nous obtenons

Sy(

1, 1)I_ 16M²(d + x³ + x⁵ + xp + xp⁺²)(1 + x² + x⁴ + xp⁺¹ + xp+3) _P[ ( 2 4 1+p)]
u r < k³(1 + r1 + u1)3 ex 2M(x +x +x

(3.62)

En combinant (3.34) et (3.62), nous avons donc

Y.7-(h)YX = sup u1=0

sup r1=0

{(1 + r1 + u1)^2S.7-(u1,r1)S + (1 + r1 + u1)^3Sy(u1,r1)S}

=

Mémoire de MASTER

43

2k2(d + x³ + xp + xp⁺²)exp[M(x² + x¹⁺p)] M

16M²

+ _k3 (d + x³ + x⁵ + xp + xp⁺²)(1 + x² + x⁴ + x¹⁺p + xp⁺³)exp[2M(x² + x⁴ + xp⁺¹)]

(3.63)

Puisque pour tout x ?]0, x1], 0 < k = 1 alors, k³ = k² et comme on peut toujours trouver M1 et M2 deux réels strictement positifs fonctions de M(par exemple M1 = 17M² et M2 = 2M) tels que

M1

Y.7-(h)YX = k3 (d+x³+x⁵+x^p+x^p+2)(1+x²+x⁴+x^1+p+x^p+3)exp[M2(x²+x⁴+x^p+1)] (3.64)

Des relations (3.54) et (3.60) nous déduisons pour le cas j = 4 qu'il existe N1 , N2 des réels strictement positifs tels que

N1

Y.7-(h)YX = k4 (d+x³+x⁵+x^p+x^p+2)(1+x²+x⁴+x^1+p+x^p+3)exp[N2(x²+x⁴+x^p+1)] (3.65) Soit L la fonction définie par

xk³exp[-M2(x² + x⁴ + xp⁺¹)]

L(x) = M1(1 + x² + x⁴ + xp⁺¹ + xp+3) - (x³ + x⁵ + xp + xp⁺²) (3.66)

Alors on a L(0) = 0, L(x1) < 0, L^'(0) > 0, et L^' est continue sur [0,x1]. Donc il existe x0 ?]0, x1[, tel que L^'(x) > 0 pour tout x ? [0, x0] c'est-à-dire que L est croissante sur

3.2. Théorème d'existence et d'unicité (théorème principal)

[0,x0]. Pour tout x ?]0, x0[,

M1

Y.7-(h)YX = k3 (d + x³ + x⁵ + x^p + x^p+2)(1 + x² + x⁴ + x^1+p + x^p+3)exp[M2(x² + x⁴ + x^p+1)]

= dM1

k3 (1 + x² + x⁴ + x^1+p + x^p+3)exp[M2(x² + x⁴ + x^p+1)]

M1

+ _k3 (x³ + x⁵ + x^p + x^p+2)(1 + x² + x⁴ + x^1+p + x^p+3)exp[M2(x² + x⁴ + x^p+1)]

= x

d + x³ + x⁵ + xp + xp+2

L(x) + x³ + x⁵ + xp + xp+2 grâce à (3.66)

nous déduisons que II.7-(h)IIX = x si d < L(x). Donc pour d < L(x), .7-(h) ? B(O, x).

3.2.3 Preuve du lemme 3.2

Nous allons à présent montrer que l'application h H .7^-(h) est contractante dans Y . Soient h1 et h2 deux solutions de (3.2) avec h1(0, r) = h2(0, r). Supposons que

max{IIh1IIX,IIh2IIX} = x < x1

Posons È = .7-(h1) - .7-(h2) ; h1, h2 ? X et notons pour l = 1, 2 gl := g(hl) et .7-l := .7^-(hl).

Alors, nous obtenons d'une part