Croissance economique et protection de l'environnement : le cas du CO2 au Sénégal

Section 2 : Test sur la relation croissance-environnement au Sénégal

La relation entre croissance et environnement n'a pas la même forme selon le pays et selon les types de polluant. Par conséquence, les politiques environnementales n'ont pas un caractère général, mais spécifique à chaque Etat, compte tenu de la forme de sa CKE.

Dans cette section, spécifierons la relation croissance-environnement et l'estimer pour le cas de la pollution par le CO2 et pour l'exemple du Sénégal. Pour cela, nous disposons des séries : taux de croissance de l'émission de CO2, taux de croissance du PIB et du taux de croissance de la population sur la période 1980-2006 (cf. tableau 3). La période 1980 à 2000 sera la période d'étude et celle de 2001 à 2006 servira de validation du modèle (prévision). En outre, nous utiliserons le logiciel E-views, version 3.1. En effet, ce logiciel s'avère très performant pour les modélisations économétriques. Il permet l'exécution de plusieurs tests et des prévisions.

Les hypothèses :

ü Nous supposons que la relation croissance-environnement est linéaire.

ü La croissance n'est pas pour autant responsable de la pollution de CO2 au Sénégal ;

ü On peut protéger l'environnement tout en poursuivant la croissance économique ;

ü Par une dynamique de dématérialisation on peut aboutir poursuivre les deux objectifs

ü La croissance démographique contribue à accentuer les émissions de CO2.

Croissance économique et protection de l'Environnement
Tableau 3 : Les données d'estimation

Années	Emission of CO2 (tons)	taux de croissance de l'émission de CO2	Population totale	taux de croissance de la population	PIB a prix constant (1999)		taux de croissance du PIB à prix constant (1999)	1980
2 794,170	0	5 538 000	0	1868,6	0		1981
2 812,490	0,65	5 696 370	2,859	1963,3	5,1		1982
2 361,450	-16,03	5 858 630	2,848	2117,3	7,8		1983
2 552,710	8,1	6 025 350	2,846	2004,6	-5,3		1984
2 998,250	17,45	6 197 350	2,855	2079,6	3,7		1985
2 438,030	-18,68	6 375 000	2,866	2147,9	3,3		1986
2 395,890	-1,7	6 556 810	2,852	2214,8	3,1		1987
2 174,950	-9,2	6 742 860	2,837	2349,8	6,1		1988
2 506,910	15,26	6 933 190	2,823	2335,9	-0,6		1989
2 996,050	19,5	7 127 880	2,81	2428,8	4		1990
2 901,520	-3,1	7 327 000	2,793	2412,4	-0,7		1991
3 005,950	3,6	7 476 060	2,034	2474	2,6		1992
3 425,840	13,97	7 656 790	2,417	2504,8	1,2		1993
3 543,090	3,42	7 860 090	2,655	2537,3	1,3		1994
3 847,200	8,58	8 076 860	2,758	2536,9	0		1995
3 466,140	-9,905	8 298 000	2,738	2673	5,4		1996
3 704,300	6,87	8 529 580	2,791	2726,7	2		1997
3 744,610	1,09	8 778 000	2,912	2811,9	3,1		1998
3 821,550	2,05	9 034 000	2,196	2977,8	5,9		1999
4 048,720	5,94	9 287 000	2,8	3166,8	6,3		2000
4 176,960	3,17	9 530 000	2,616	3268,1	3,2		2001
		9 768 000	2,497	3417,8	4,6		2002
		10 007 000	2,447	3440,2	0,7		2003
		10 239 800	2,326	3669,7	6,7		2004
		10 564 303	3,169	3885,6	5,9		2005
		10 817 844	2,33	4104	5,6		2006
		11 077 484	2,4	4198	2,3

Source : African World Bank data 2003; ANSD: Annuaire des statistiques 2006

I/ Spécification du modèle

A/ Spécification du modèle

Les tests empiriques de la CKE se basent sur le l'équation général suivante :

Pit = ai + ?z^T.1 iezi ^(ln Yit )z + Ai Xit + Eit

Avec Pit un indicateur de la dégradation environnementale d'un pays Y à la date t ( en
logarithme), yit le revenu par habitant , Xit un vecteur de co-variables explicatives et Eit le

terme d'erreur.

Cependant beaucoup de controverses se sont soulevées notamment dans le choix du degré de l'équation et dans le choix des variables co-explicatives. Mais pour ce qui nous concerne, dans cette étude, nous utilisons le degré d'ordre un. Ce choix est guidé par le fait que le niveau de revenu du Sénégal n'est pas aussi élevé - si l'on prend en compte le niveau généralement admis comme seuil critique - pour permettre une de telle spécification et de plus les données disponibles ne le permettent pas ; la période d'étude n'est pas très longue.

Toutefois, l'activité économique ne peut s'effectuer sans pollution. L'augmentation de la production se traduit impérativement par l'augmentation des intrants de production, soit de façon moins que proportionnelle soit de façon plus que proportionnelle. Donc la modélisation utilisant les grandeurs en valeur n'aura aucune explication économique puisque le coefficient attendu serait positif. Par contre si on prend les variables en terme de variation, l'interprétation sera plus pertinente et plus économiquement significatif. Les coefficients dans ce cas représentent des élasticités c'est-à-dire la sensibilité par rapport à la variable de référence.

Nous retenons cependant la spécification suivante :

TXEMCO2_t= ao + aiTXPIB_t + a2TXPOP_t + E_t

L'estimation des paramètres nous donnerait des élasticités puisqu'on utilise des taux.

Croissance économique et protection de l'Environnement
B/ Présentation des variables (endogènes et exogènes)

ü TXEMCO2 : est le taux de croissance du PIB. Nous avons choisi le taux de croissance car il mesure la variation et peut avoir la même interprétation que le logarithme. Par ailleurs, le niveau de pollution de CO2 peut être calculé par la méthode proposée par KAYA : la fameuse équation de KAYA qui se résume comme suit :

TEP

PIB

GES =

POP

GES

TEP

PIB

POP

Emissions de CO2

=

Contenu en CO2 de l'énergie

*

Intensité énergétique de l'économie

*

Production par salarié

Population * active

GES : gaz à effet de serre ; TEP : tonne équivalent pétrole ; POP : population active et PIB Pour le contenue en CO2 de tous les types d'énergie, voir annexe 3

ü TXPIB, représente le taux de croissance du PIB en franc constant de 1999. Ceci pour tenter d'éliminer l'effet de l'inflation qui peut biaiser les estimations ;

ü TXPOP, est le taux de croissance démographique ;

ü Et est le terme d'erreur, qui récupère les pertes d'informations. Les erreurs doivent être nulles en moyenne et avoir une variance constante égale à a².

ü ao est la constante et les ai (i = 1,2) sont les coefficients des variables exogenes. Ils

représentent les élasticités par rapport au taux d'émission de CO2.

C/ Evolution des données et test de normalité

Pour qu'il soit possible de faire des inférences statistiques il faut que les erreurs suivent un
processus bruit-blanc c'est-à-dire nulle en moyenne et de variance égale à celle de la variable

expliquée [X (O. a²)]. Ainsi, en effectuant le test de normalité de Jarque Bera on voit que tout

les probabilités sont en moyenne toutes supérieures à 5%, ce nous renseigne que non variables suivent en moyenne un processus bruit blanc.

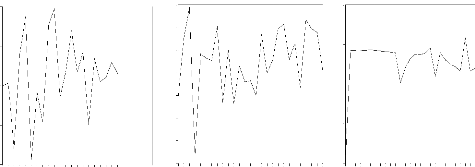
Graphique 4 : Evolution des séries durant la période 1980-2006

Evolution de la série TXEMCO2 Evolution de la série TXPIB Evolution de la série TXPOP

évolution du TXPOP

évolution du TXEMCO2

6

4

2

0

-2

-4

Evolution du PIB

-6

8

4

3

2

1

0

20

10

0

-10

-20

80 82 84 86 88 90 92 94 96 98 00 02 04 06

TXEMCO2

80 82 84 86 88 90 92 94 96 98 00 02 04 06

TXPIB

80 82 84 86 88 90 92 94 96 98 00 02 04 06

TXPOP

D/ Test de stationnarité

Test de Dickey Fuller et test de Phyllips-Perron

Le test de Phillips-Perron prend en compte les erreurs hétéroscédastiques. Partant, il peut être plus intéressant que le test de Dickey Fuller). Les hypothèses sont :

H0 : présence de racine unitaire (non stationnaire)

H1 : absence de racine unitaire (stationnaire)

Augmented Dickey-Fuller Unit Root test on TXEMCO2

ADF Test Statistic	-4.021564	1% Critical Value*	-4.5348
		5% Critical Value	-3.6746
		10% Critical Value	-3.2762

Ici la valeur de l'ADF est supérieure à Critical Value à 5% (-4.021564 < -3.6746). Donc on accepte l'hypothèse H1 : TXEMCO2 est stationnaire.

Phillips-Perron Unit Root test on TXEMCO2

PP Test Statistic	-5.269337	1% Critical Value*	-4.5000
		5% Critical Value	-3.6591
		10% Critical Value	-3.2677

-5.269337 < -3.6591, la variable TXEMCO2 est, aussi, stationnaire avec le test PP

Croissance économique et protection de l'Environnement
Augmented Dickey-Fuller Unit Root test on TXPIB

ADF Test Statistic	-4.192672	1% Critical Value	-4.3738
		5% Critical Value	-3.6027
		10% Critical Value	-3.2367

- 4.192672 < -3.6027 donc, au seuil de 5%, la variable TXPIB est stationnaire.

Phllips-Perron Unit Root test on TXPIB

PP Test Statistic	-6.573341	1% Critical Value*	-4.3552
		5% Critical Value	-3.5943
		10% Critical Value	-3.2321

-6.573341 < -3.5943 donc TXPIB est stationnaire. Même résultat qu'antérieurement.

Augmented Dickey-Fuller Unit Root test on TXPOP

ADF Test Statistic	-4.740035	1% Critical Value*	-4.3738
		5% Critical Value	-3.6027
		10% Critical Value	-3.2367

Au seuil de 5% on accepte la stationnarité avec le test ADF (-4.740035< -3.6027).
Phllips-Perron Unit Root test on TXPOP

PP Test Statistic	-13.73637	1% Critical Value*	-4.3552
		5% Critical Value	-3.5943
		10% Critical Value	-3.2321

-13.73637< -3.5943 donc le série TXPOP est stationnaire au seuil de 5%.

Au terme de cette analyse de stationnarité, nous retenons que nos variables, TXPIB, TXPOP, et TXEMCO2, sont toutes stationnaires avec les deux tests.

Cependant on peut passer à l'estimation des paramètres

II/ Estimation des paramètres

Toutes nos variables étant stationnaires nous pouvons faire l'estimation. Nous utilisons la méthode des Moindres Carrés Ordinaires (MCO) pour estimer les paramètres.

Voici cependant les résultats que nous obtenons :

Tableau 4 : estimation des paramètres par la méthode des MCO

Dependent Variable: TXEMCO2 Method: Least Squares Date: 07/11/08 Time: 10:43 Sample(adjusted): 1980 2000 Included observations: 21 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	3.088455	9.192834	0.335963	0.7408
TXPIB	-1.342563	0.736418	-1.823098	0.0849
TXPOP	1.166994	3.508317	0.332636	0.7433
R-squared	0.155873	Mean dependent var		2.430238
Adjusted R-squared	0.062082	S.D. dependent var		10.12949
S.E. of regression	9.810025	Akaike info criterion		7.536250
Sum squared resid	1732.259	Schwarz criterion		7.685468
Log likelihood	-76.13063	F-statistic		1.661909
Durbin-Watson stat	2.439946	Prob(F-statistic)		0.217605

III/ Les Tests économétriques

A/ Test de significativité et interprétation des coefficients

1. LM test : Fcalculé =1.66 < Fl_u(2, 18) = 3.55. donc le modèle n'est pas globalement significatif.

2. Test de student : Au seuil de 5% les coefficients sont tous non significatifs. Mais au seuil de 10% seul le coefficient du TXPIB est significatif (1.823 > 1.734).

3. Interprétation des coefficients : les coefficients sont interprétés comme des élasticités.

? TXEMCO2	= - 1.3425
?TXP11

Ainsi, si le taux de croissance du PIB augmente de 1 point, alors le taux de croissance de
l'émission de CO2 diminue de -1.3425. En d'autres termes si le PIB croît de a % alors
l'émission de CO2 décroît de -1.3425*a %. De la même manière si la population augmente

de 1%, le taux d'émission de CO2 croît de 1.167%.

Croissance économique et protection de l'Environnement
B/ Test d'Hétéroscédasticité de WHITE

Les erreurs sont très souvent différentes en variance et cela fausse les estimations. C'est pourquoi il est important de faire le test d'hétéroscédasticité. Certes, il y'a plusieurs méthodes pour tester l'homoscédaticité. Mais nous utilisons dans cette étude le test de White sans cross term. On teste, au seuil 5%, la significativité des coefficients de l'équation auxiliaire suivante:

.₁.2

å2 = ao + aitxpib + a2 txpop + a3txpib² + a4txpop² + Vt

Les hypothèses sont :

H0 : ai = a2 = a3 = a4= 0 .(=> le modèle est homoscédastique

H1 : les coefficients sont non tous nuls .(=> le modèle est hétéroscédastique Voici les resultat que nous obtenons avec E-views :

Tableau 5 : Test d hétéroscédasticité de White sans cross term

White Heteroskedasticity Test :
F-statistic Obs*R-squared	0.657255 2.963623	Probability Probability		0.630399 0.563931
Test Equation: Dependent Variable: RESID^2 Method: Least Squares
Date: 07/11/08 Time: 11:21
Sample : 1980 2000
Included observations : 21
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	11.14298	123.2283	0.090425	0.9291
TXPIB	10.58247	11.91884	0.887877	0.3878
TXPIB^2	-1.100599	2.181463	-0.504523	0.6208
TXPOP	-144.0313	180.1326	-0.799585	0.4357
TXPOP^2	61.18570	57.69479	1.060506	0.3047
R-squared	0.141125	Mean dependent var		82.48850
Adjusted R-squared	-0.073594	S.D. dependent var		119.0031
S.E. of regression	123.3043	Akaike info criterion		12.67144
Sum squared resid	243263.2	Schwarz criterion		12.92014
Log likelihood	-128.0502	F-statistic		0.657255
Durbin-Watson stat	1.661663	Prob (F-statistic)		0.630399

Dans ce tableau on voit qu'au seuil de 5% la valeur F-statistic (0.657255) est inférieure à la valeur lue dans la table de Fisher : F (4,16) =3.01. Donc on accepte l'hypothèse nulle (H0). De plus aucun coefficient n'est à l'extérieur de l'intervalle de Student (pour 16 = 20-5 observations). Partant les erreurs ont la même variance. Les estimateurs des MCO sont optimaux

C/ Test d'autocorrélation des erreurs de Durbin Watson

La condition d'utilisation du test de Durbin Watson est satisfaite (nous avons plus de 15 observations et il n'y a pas de variable endogène décalée).

Hypothèses :

H0 : p = 0 les erreurs sont non corrélées (Indépendance des erreurs) H1 : p 0 les erreurs sont liées

Pour n = 21 et k = 2 on a (dans la table de Durbin Watson) : d1=1.13 et d2= 1.54.

p > 0 ? p = 0 ? p < 0

0 1.13 1.54 2 2.46 2.87 4

La valeur donnée par le tableau 4 d'estimation est 2.4399. Donc on se trouve dans la zone d'indépendance, mais à quelques centimes de la zone d'incertitude. Ce résultat est plus visible sur le graphique 5, qui montre une évolution très proche de l'évolution cyclique. On peut, toutefois, accepter l'hypothèse d'indépendance des erreurs.

Graphique 5 : Test d'autocorrélation des erreurs de Durbin Watson

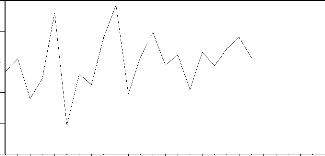
évolution des erreurs

80 82 84 86 88 90 92 94 96 98 00 02 04 06

RESID

20 10 0

- 10

- 20

- 30

L'examen du graphique de l'évolution des erreurs semble présager une auto corrélation des erreurs. En effet, l'évolution des erreurs est très proche de l'évolution cyclique.

D/ Test Reset de RAMSEY

RAMSEY considère que la plupart des mauvaises spécifications résulte du fait que les erreurs ne sont pas souvent nulles en moyenne. D'où l'importance de ce test de spécification L'équation auxiliaire est

Y = aX + bZ + E

H0 : le modèle est bien spécifié

H1 : le modèle est mal spécifié

En effectuant le test dans E-views on voit que la probabilité est de 0.51 > 5%. En prenant les valeurs de Fisher on voit : F-statistic = 0692 > F _critique (1, 16)= 4.49. Donc on conclut que le modèle est très bien spécifié.

E/ Test de stabilité 1. Test de CHOW (Breakpoint 1994)

Chow Breakpoint Test: 1994
F-statistic Log likelihood ratio	0.078984 0.329141	Probability Probability	0.970416 0.954458

La probabilité est largement supérieure à 5% donc on accepte l'hypothèse de stabilité des coefficients. Le modèle est stable.

Le même test effectué sur les périodes 1992 et 1997, correspondant respectivement à la convention de RIO et l'entrée en vigueur du protocole de Kyoto (que le Sénégal a ratifié), conclut à une stabilité des coefficients.

Test de CUSUM

15 10 5 0 -5 - 10 - 15

84 86 88 90 92 94 96 98 00

CUSUM 5% Sig nificance

La courbe ne coupe en aucun point le corridor ; elle reste dans toute la période à l'intérieur du corridor alors le modèle est stable (même résultat)

IV/ Prévision à un horizon de six années

Graphique 6 : Prévision pou l'horizon 2000-2006

40 20 0 - 20 - 40

80 82 84 86 88 90 92 94 96 98 00 02 04 06

TXEMCO2F #177; 2 S.E.

Forec as t: TXEMCO2F

Ac tu a l: TXEMCO2

Forecast sample: 1980 2006 Included observations: 21

Root Mean Squared Error 9.082318

Mean Abs olute Error 7.058438

Mea n Abs. Perc e nt Error 100.6680

Theil Inequality Coefficient 0.614611

Bias Proportion 0.000000

Variance Proportion 0.433889

Covariance Proportion 0.566111

Critère U de THEIL = 0.614611 donc compris entre 0 et 1. Alors la méthode de prévision étudiée est meilleure que la méthode naïve. Nous pouvons, néanmoins, utilisé ce modèle à des fins de prévisions mais il y'a quelques inconvénients car le MAPE est très élevé et le U de THEIL est un peu éloigné de zéro.

V/ Confirmation des prévisions et explication des résultats

Les résultats de l'estimation aboutissent à la conclusion que le taux de croissance des émissions de CO2 n'est pas très expliqué par le taux de croissance du PIB. Le Sénégal semble se trouver dans la deuxième phase de la CKE où l'on observe une relation inverse entre pollution et croissance comme Grossman et Krueger l'on soutenu. Ceci est paradoxal puisque le niveau de revenu permettant un renversement de tendance n'est pas encore atteint. Plusieurs explications peuvent jaillir. Le Sénégal fait il l'exception ou bien qu'est ce qui explique cette tendance à la baisse de la pollution ?

Nous apporterons une réponse précise à cette question en examinant les graphiques de contribution dans les performances économiques et ceux des d'évolution des secteurs.

Croissance économique et protection de l'Environnement Graphique 7 : Evolution du PIB par branche d'activité

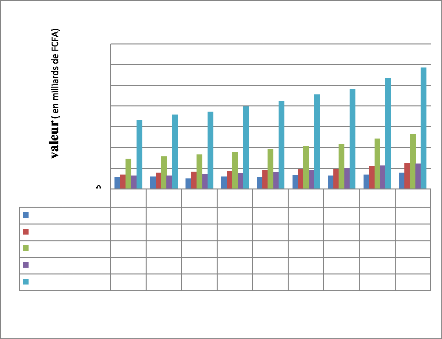
Evolution du PIB par branche d'activité

0	2000	2001	2002	2003	2004	2005	2006	2007	2008
secteur primaire	561,8	584,4	506,3	602,4	578,3	663,6	648,4	697,4	773,2
secteur secondaire	681,8	774,1	830,4	854,6	921,6	938	954	1101,5	1232,2
secteur tertiaire	1458,8	1565,1	1670,1	1781,3	1921,5	2051	2180,1	2425,4	2639,1
adm publique	629,4	651,8	710,8	748	812,5	910,6	1019,7	1115,7	1213,2
totale	3331,8	3575,5	3717,6	3986,4	4233,9	4563,3	4802,2	5340	5857,8

7000

6000

5000

4000

3000

2000

1000

Source : les données nous ont été fournies par l' ANSD

Nous voyons plus clair cela en analysant la dynamique de l'évolution des secteurs de l'économie. Voici quelques graphiques illustrateurs.

Le secteur tertiaire est de loin le secteur le plus dominant dans le PIB du Sénégal (presque la moitié). En effet, le secteur tertiaire tire fort à soi la croissance du PIB. Il a en général la plus grande part de contribution dans la croissance du PIB. Or le secteur tertiaire n'est pas pollueur - hormis le transport, qui n'occupe ici qu'une faible part.

Ainsi, Les propositions de Joseph Schumpeter (voir la théorie de la Destruction-Création) ou la thèse de dématérialisation semblent jouer pleinement leur rôle au Sénégal.

Cependant examinons l'évolution du secteur tertiaire. Le graphique ci-dessous nous en renseigne.

Croissance économique et protection de l'Environnement Graphique 8 : Evolution du secteur tertiaire et du secteur secondaire

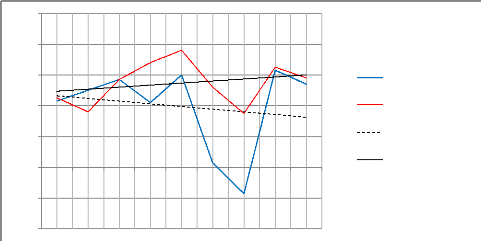
y = 0,131x + 4,808

y = -0,173x + 4,811

secteur secondaire

secteur tertiaire

Linéaire (secteur secondaire)

Linéaire (secteur tertiaire)

10

8

6

4

2

0

-2

2000

2001

2002

2003

2004

2005

2006

2007

2008

-4

Source : les données sont fournies par l'ANSD

Les courbes de tendance révèlent une tendance à la baisse du secteur secondaire et une tendance à la hausse du secteur tertiaire (cela est plus clair avec l'équation des courbes de tendance). Donc une tertiarisation progressive de l'économie Sénégalaise. Cela est très satisfaisant pour une politique de lutte contre la dégradation de l'environnement et donc le développement durable.

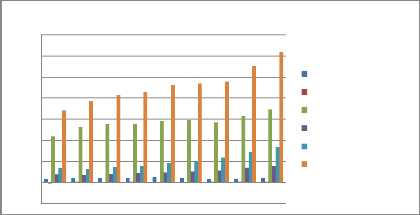
Graphique 9: Composition du secteur industriel

1400

1200

1000

-200

800

400

600

200

0

2000 2001 2002 2003 2004 2005 2006 2007 2008

composition du secteur secondaire

activité extractive fabrication de corps gras autres industires electricité, gaz et eau construction

totale

Source : Base de données ANSD

La composition du secteur industriel Sénégalais est dominée par le secteur des autres industries. En effet pour l'émission de CO2 c'est le secteur de la production d'électricité et le secteur de l'urbanisation qui sont véritablement les plus indexés. Alors que, sur ce graphe, on voit qu'au Sénégal ces secteurs évoluent certes mais pas très menaçantes pour la pollution et aussi ils ne dominent pas l'évolution, ce qui fait que la pollution a tendance à se réduire comme les résultats économétriques l'ont prouvés (voir estimation). Nous avons une dynamique de tertiarisation très rapide pour le Sénégal.

Conclusion et recommandations spécifiques pour le Sénégal

Les résultats de cette modélisation montrent que le produit intérieur brut (PIB) n'est la cause directe de la pollution atmosphérique pour le cas du CO2 au Sénégal. La relation est plutôt inverse. La croissance induit une réduction du taux de croissance de la pollution. Contrairement à certaines analyses qui indexaient au premier chef le PIB comme responsable de la pollution, nous voyons que pour le cas du Sénégal la relation n'est pas très étroite (le coefficient n'est pas significatif au seuil de 5%) et même si à un certain seuil on accepte la relation, le PIB évoluerait en sens contraire au taux de pollution de CO2. Une augmentation du taux de PIB se traduit par une baisse du taux d'émission de CO2. L'explication est clairement fournie par la composition de l'économie Sénégalaise (voir graphiques 7, 8, 9 précédents).

Ainsi, la lutte contre la pollution atmosphérique au Sénégal et pour le cas concernant le CO2, doit être accès sur une politique rigoureuse de croissance économique forte et une incitation à innover des secteurs polluants tels que la production d'électricité et l'urbanisation. Cependant, beaucoup d'études faites sur les pays à revenu très élevé montrent en premier que les hypothèses de Grossman et Krueger se vérifient, mais à partir d'un niveau élève de revenu, le parallélisme revient : une croissance qui détériore l'environnement. Ceci conduit ,donc ,à bien se prévenir des éventualités du futur en essayant progressivement et de façon très modérée - au risque de rendre moins compétitives les entreprises nationales - d'introduire des politiques prenant en compte l'environnement.

A présent, si nous avions disposé des données sur une période très longue avant 1980, on aurait pu tester une relation quadratique. Puisque les résultats montrent que nous sommes sur la deuxième phase de la CKE. Donc, ce courbe de Kuznets environnementale semble s'appliquer bien pour le cas du Sénégal. Mais nous observons une certaines réserve puisque la relation peut avoir une forme cubique. En effet, la pollution peut bel et bien continuer à partir d'un niveau élevé de revenu.