4.1.3 Résultats
Répartition spatiale des arbres selon le
diamètre
L'étude de la répartition spatiale des arbres
selon leur diamètre à 1, 30 m de hauteur a donc été
effectuée sur l'échantillon réduit composé de 131
arbres. Les arbres sont regroupés en 6 classes diamétriques. Ces
classes de diamètre sont définies au Tableau 4.1). La Figure 4.2
représente la distribution spatiale
|
Diamètre à 1, 30 m de hauteur
|
0
|
]0,10[
|
[10,20[
|
[20,30[
|
[30,65[
|
=65
|
|
Classe de diamètre
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
TAB. 4.1 - Classes de diamètre des arbres
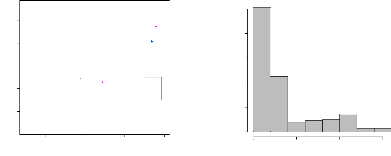
des arbres selon leur classe de diamètre. Comme les
coordonnées spatiales des arbres juvéniles (il s'agit des 91
arbres des classes C1 et C2 ne sont disponibles), ces arbres ne sont donc pas
représentés sur cette figure. Nous pouvons noter que les arbres
de plus faible diamètre (les arbres de la classe C3) ont une
distribution plutôt concentrée sur un seul coté de la
parcelle alors que les individus appartenant aux classes C4, C5 et C6 ont une
distribution assez régulière. L'histogramme du diamètre du
tronc à 1, 30 m est donné par la Figure 4.3. La distribution des
arbres est asymétrique négative. En effet, 146 arbres (soit plus
de 75% de l'effectif total) ont un diamètre inférieur à 40
cm et 154 arbres (soit près de 80% des arbres) ont un diamètre
inférieur à 60 cm. Ainsi, il s'agit plutôt d'une population
d'arbres essentiellement juvéniles. La distribution des arbres par
classe de diamètre présente deux modes; le premier mode (0--20
cm) correspond plutôt aux arbres en régénération
depuis que la parcelle est mise en jachère et le second mode (100--120
cm) représente la distribution des arbres adultes qui se trouvaient
déjà sur la parcelle lorsque celle-ci était encore en
culture (Kelly, 2004; Kelly et al., 2004b).
Locus Allèles Fréquences
157 0.219
B5 161 0.781
E4
114 0.006
116 0.063
119 0.060
120 0.099
121 0.741
123 0.026
125 0.003
127 0.003
201 0.626
F5 205 0.045
209 0.330
224 0.676
E11 228 0.301
230 0.023
E6a
120 0.023
122 0.249
124 0.590
126 0.139
E6b
101 0.033
103 0.280
106 0.293
108 0.105
114 0.155
116 0.135
151 0.027
B3 155 0.973
H4
214 0.186
216 0.745
218 0.065
222 0.003
D10
218 0.030
220 0.248
222 0.252
224 0.321
226 0.076
228 0.073
G7
136 0.013
140 0.029
142 0.006
144 0.400
148 0.510
150 0.042
D6
116 0.071
117 0.081
118 0.155
119 0.612
120 0.071
124 0.009
F1
302 0.003
304 0.474
306 0.513
314 0.010
EffectIf
0 20 40 60 80 100
0
50 100 150
Diamètre à 1,30 m
0 20 40 60 80 100 120 140
X
V
-100 -80 -60 -40 -20 0
?
?
?
?
?
? ? ? ??
? ? ?
? ?
? ?
? ?
?
?
?
?
?
?
?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
? ?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
??
? ?
? ? ?
?
?
? ? ?
?
?
? ??
?
?
?
?
?
?
?
?
?
? ???
?
? ? ? ?
?
?
C 3
C 4
C 5
C 6
?
? ?
?
FIG. 4.2 - Distribution spatiale des arbres par classe de
diamètre
FIG. 4.3 - Histogramme du diamètre des arbres
Mesure de la diversité génétique
L'étude de la diversité génétique
a été réalisée sur le sous échantillon
constitué des 193 individus génotypés. Le Tableau 4.2
donne les fréquences alléliques observées aux 12 locus.
Tous les locus sont polymorphes et le nombre total d'allèles varie de 2
pour le locus B5 à 8 pour le locus E4 (Figure 4.4). La proportion des
locus polymorphes pour lesquels la fréquence allélique la plus
élevée ne dépasse pas 95% est de 85.7% (Tableau 4.4);
ainsi près de 86% des locus présentent des variations
alléliques importantes. Les paramètres mesurant le polymorphisme
des différents locus et les FIS associés à
chaque locus sont présentés au Tableau 4.3. L'indice de fixation
varie de --0.287 (pour le locus F1) à 0.555 (pour le locus G7) (Tableau
4.3). Le taux, Ho, d'hétérozygotes observé
varie de 0.258 (pour le locus G7) à 0.660 (pour le locus F1) et le taux
moyen d'hétérozygotie pour l'ensemble des locus est 0.421
(Tableau 4.3 et Tableau 4.4). Nous notons pour certains locus (les locus E4,
E6b, D10, G7 et D6) une déviation significative par rapport à
l'hypothèse d'équilibre de Hardy-Weinberg au seuil nominal de a =
5%, ce qui correspond à un seuil ajusté de a/12 = 0.00417
(Tableau 4.3). Lorsque nous considérons, non plus individuellement mais
globalement, l'ensemble des locus, l'indice de fixation FIS est
significativement différent de 0.
Analyse en composantes principales
L'ACP a été donc réalisé sur le sous
jeu de données réduit à 193 individus. La Figure 4.5
représente l'éboulis des valeurs propres. Le premier axe
TAB. 4.3 - Caractéristiques des différents locus
|
Locus
|
N
|
na
|
Ho
|
Ha
|
FIS
|
P-value
|
|
B5
|
178
|
2
|
0.337
|
0.342
|
0.018n8
|
0.4500
|
|
E4
|
176
|
8
|
0.318
|
0.432
|
0.266n8
|
0.0042
|
|
F5
|
179
|
3
|
0.430
|
0.498
|
0.139n8
|
0.0250
|
|
E11
|
176
|
3
|
0.466
|
0.452
|
_0.029n8
|
0.6167
|
|
E6a
|
173
|
4
|
0.561
|
0.571
|
0.021n8
|
0.4333
|
|
E6b
|
152
|
6
|
0.500
|
0.782
|
0.363n8
|
0.0042
|
|
B3
|
185
|
2
|
0.373
|
0.406
|
_0.0025n8
|
1.0000
|
|
H4
|
161
|
4
|
0.373
|
0.406
|
0.084n8
|
0.1125
|
|
D10
|
165
|
6
|
0.612
|
0.760
|
0.197n8
|
0.0042
|
|
G7
|
155
|
6
|
0.258
|
0.577
|
0.555n8
|
0.0042
|
|
D6
|
161
|
6
|
0.485
|
0.585
|
0.175n8
|
0.0042
|
|
F1
|
156
|
4
|
0.660
|
0.512
|
_0.287n8
|
1.0000
|
|
Total
|
|
|
|
|
0.1568
|
0.0042
|
N nombre d'individus, na nombre d'allèles au
locus, Ho hétérozygotie observée ;
Ha : hétérozygotie attendue sous
l'hypothèse d'Hardy-Weinberg ;
ns indique que le test d'équilibre d'Hardy-Weinberg est
non significatif au seuil nominal ajusté de 0.0042
TAB. 4.4 - Hétérozygotie moyenne sur les locus
|
Ha
|
H8b
|
Ho
|
P(0.95)
|
P(0.99)
|
Nma
|
|
Population
|
0.497
|
0.499
|
0.421
|
0.917
|
1.000
|
4.500
|
|
Ecart-type
|
0.192
|
0.193
|
0.167
|
|
|
|
Ha : hétérozygotie attendue sous
l'hypothèse d'Hardy-Weinberg ; Ho hétérozygotie
observée ; Hsb hétérozygotie calculée sans biais ;
Nma nombre moyen d'allèles par locus;
P(0.95) et P(0.99) polymorphisme au seuil 95% et 99%
respectivement.
0 2 4 6 8
Nombre d'allele,s
B5 E4 F5 E11 E6a E6b B3 H4 D10 G7 D6 F1
Locus
FIG. 4.4 - Nombre d'allèles observés par locus
principal explique près de 12% de l'inertie et les deux
premiers axes n'expliquent qu'un peu plus de 20% de l'inertie totale. La
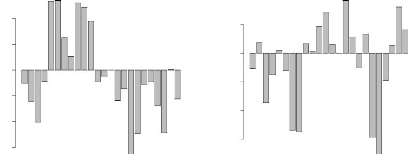
première composante principale oppose d'une part, les locus F5 et E6, et
d'autre part, les locus D10 et D6 (Figure 4.6). La seconde composante oppose,
dans une moindre mesure, les locus H4 et F1 d'une part, aux locus E11 et G7
d'autre part (Figure 4.7). L'observation du cercle des corrélations
permet aussi de confirmer cette opposition entre ces 2 groupes de variables
(Figure 4.8). La projection des individus sur le plan principal est
donnée par la Figure 4.9. Nous pouvons ainsi distinguer le groupe des
individus plutôt semblables du point de vue de leurs génotypes aux
locus F5 et E6 des individus qui sont plutôt semblables aux locus D10 et
D6.
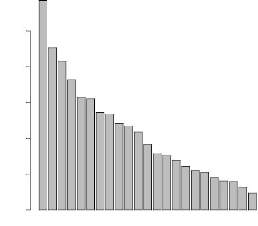
11.7 8.29 6.31 5.44 4.83 4.35 3.14 2.77 2.2 1.8 1.57 0.95
% d'inertie
0 2 4 6 8 10
FIG. 4.5 Eboulis des valeurs propres
Structure génétique spatiale
Test de Mantel Le test de Mantel a été
effectué sur le sous-échantillon
constitué des 58
individus dont les coordonnées spatiales et les
génotypes
à tous les locus sont disponibles. Le test de Mantel
n'est pas significatif
50 CHAPITRE 4. APPLICATIONS
0.4
0.2
0.0
- 0.2
- 0.4
- 0.6
0.2
0.0
- 0.2
- 0.4
- 0.6
B58 B5b E4a E4b F5a F5b El la Ellb Eeaa Rah Elba Bibb B3a B3b
H4a H4b DlOa DlOb G7a G7b Dia Deb Fla Fib
B5a B5b E4a E4b F5a F5b El la Ellb Eeaa Rah Elba Bibb B3a B3b
H4a H4b DlOa DlOb G7a G7b Dia Deb Fla Fib
FIG. 4.6 - Contribution à l'axe 1 FIG. 4.7 ---
Contribution à l'axe 2
|
|
|
|
E6aa
F5a E6ab E6ba
|
|
H4a E6bb F1a
F1b
D10b H4b
D6b B5b B3a
|
|
|
D10a
|
D6a
E4a
|
B5a E4b
G7a G7b
|
B3b
E11bE11a
|
F5b
|
-1.0 -0.5 0.0 0.5 1.0
Axe 1
FIG. 4.8 - Cercle des corrélations
|
26
31
17
|
215
220
221
74
25
175 15 145 144 72 11
164 218
10
58
80 219 151
11416
8990 169 47
83 212
|
154
200
205
132 163
162 196 170
165
131
152 8 166 197
208 194 174
105
34
129
188
142 126 125
104
146 156 103
|
|
91
|
111
214
82
22
|
217 107108
23 112 109 168 182
187
124
213 81 157
2 97
77
87
158
117 41 192 48
70
|
18
120 106
75 128
51 84 119
113
186 11
153 210
147
101
12
33 130
118159
160
|
-6 -4 -2 0 2 4 6
Axe 1
FIG. 4.9 - Représentation des individus sur les axes
principaux
|
Axe 2
|
-1.0 -0.5 0.0 0.5 1.0
|
|
Axe 2
-2 4
2
0
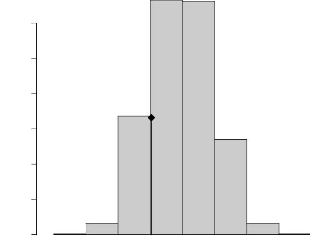
(Figure 4.10). En effet, la statistique de Mantel
observée est ñm = --0.048 et la probabilité
d'observer une valeur supérieure ou égale à cette
dernière valeur sous l'hypothèse nulle, c'est à dire que
les distances génétiques ne sont pas linéairement
corrélées aux distances géographiques, vaut 0.805 (Figure
4.10 et Tableau 4.5).
Test de Mantel
Frequence
0 50 100 150 200 250 300
-0.2 -0.1 0.0 0.1 0.2
Valeur simuléé
FIG. 4.10 - Distribution de la statistique de Mantel; le trait
vertical (en gras) représente la valeur observée de la
statistique de Mantel
Statistique de Mantel observée -0.048 p-value
simulée 0.805
1000 répétitions
TAB. 4.5 - Test de Mantel
Indice de Moran La relation entre la distance
génétique et la distance spatiale est donnée par le
corrélogramme de Moran (Figure 4.11) : il y a une structure
génétique spatiale significative au seuil de 5%. La classe de
distance inférieure à 15.3 m a une structure
génétique significativement différente de celle d'une
distribution spatiale aléatoire des génotypes. Les arbres qui
sont distants de moins de 15 m environ ont donc une structure spatiale
positive, c'est à dire qu'ils ont tendance à être
génétiquement similaires que ne le sont
.


.
.
.
.
.
* ns
-0.15 -0.10 -0.05 0.00 0.05
Incline de Moran
20 40 60 80 100 120 140
distance
FIG. 4.11 - Corrélogramme représentant l'indice de
Moran en fonction de la classe de distance spatiale (* : p - vallue < 5%; ns
: non significatif)
des individus tirés au hasard spatialement. La
structuration spatiale est aussi significative au delà de 140 in. La
population de karité ainsi étudiée présente une
structure spatiale agrégée (indice d'agrégation R = 0.86,p
- value < 0.01). Cette distribution agrégée jusqu'à une
distance d'environ 15 m serait expliquée, d'après Kelly (2004),
par le mode de distribution des semences de karité. En effet, comme le
karité est une espèce barochore, la plupart de ses fruits tombent
sous le houppier de l'arbre. Les résultats d'une étude portant
sur la distance de dispersion des graines de karité dans un parc
agroforestier à MPeresso montrent, en effet, que 95% des graines d'un
arbre donné se retrouvent à moins de 25 m de son houppier (Sanou
et al., 2005). Kelly et al. (2004a) montrent que la distribution spatiale du
karité sur le site de MPeresso devient de plus en plus
agrégée en passant du champ à la jachère et
à la forêt. Les activités agricoles menées au champ
(récolte des fruits, labour, élagage des arbres) expliquent que
la distribution des arbres est moins agrégée et que la structure
spatiale a plutôt tendance à devenir régulière
(Kelly et al., 2004a).
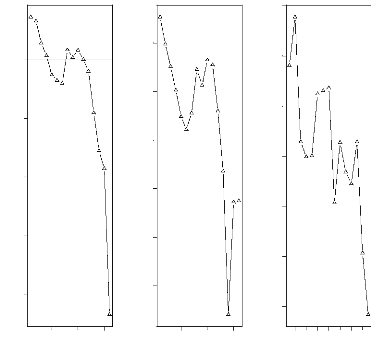
Apparentement en fonction de la distance La Figure 4.12
présente l'estimation de l'apparentement génétique moyen
en fonction de la distance spatiale entre les individus dans la parcelle en
jachère selon deux méthodes d'estimation de l'apparentement par
les moments (Wang (2002); Lynch et Ritland (1999)) et selon la méthode
par maximum de vraisemblance de Milligan (2003). Nous notons de manière
globale que le coefficient d'apparente-
Lynch-Ritland Wang Milligan
- 0.4 -0.3 -0.2 -0.1 0.0
coeffident dapparentement
coeffident dapparentement
- 0.30 -0.25 -0.20 -0.15 -0.10 -0.05
coeffident dapparentement
0.02 0.04 0.06 0.08 0.10 0.12 0.14
20 60 100 140
50 100 150
50 100 150
distance distance distance
(a) (b) (c)
FIG. 4.12 - Estimation du coefficient d'apparentement moyen en
fonction de la distance entre les individus selon 3 méthodes
différentes (Lynch-Ritland, Wang et Milligan
régression linéaire de l'apparentement en
fonction du logarithme de la distance est, dans les deux cas, significativement
négative (pente= --0.030 et la p-value associée vaut p=0.019 pour
la méthode de Wang; pente= --0.038 et la p-value associée est
inférieure à 10-4 pour la méthode de Lynch et
Ritland). Ces résultats sont cohérents avec ceux obtenus avec le
corrélogramme de Moran qui montrent qu'il y a une structure
génétique significative à faible et grande distances. Nous
n'avons, par contre, pas pu effectuer le test de signification du
paramètre de la régression linéaire du coefficient
d'apparentement estimé selon la méthode de (Milligan, 2003) en
fonction de la distance. Nous notons cependant des différences dans
l'allure générale des courbes présentées sur la
Figure 4.12. Tout d'abord certaines valeurs estimées de l'apparentement
par la méthode des moments sont négatives alors que celles
données par la méthode de Milligan sont toutes positives; alors
qu'avec la méthode de Lynch et Ritland, l'apparentement
décroît de manière graduelle de 0 à 100 m puis de
manière abrupte à partir de 120 m, l'estimateur de
l'apparentement de Wang décroît avec la distance jusqu'à
140 m mais a une tendance à croître au delà de cette
distance. Cependant un défaut majeur de ces deux dernières
méthodes est qu'elles fournissent des valeurs estimées
négatives. Ainsi respectivement près de 59% et 61% des valeurs
estimées du coefficient d'apparentement d'un couple d'individus par les
méthodes respectivement de Lynch et Ritland (1999) et Wang (2002) sont
négatives; ce qui n'a pas vraiment de sens du point de vue de
l'interprétation biologique (Milligan, 2003). Le coefficient
d'apparentement moyen estimé selon la méthode de Milligan (2003)
varie de 0.135 pour des individus distants de 10 à 20 m jusqu'à
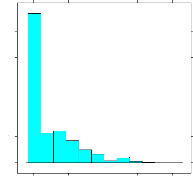
0.017 pour des individus distants de plus de 150 m. La distribution des valeurs
estimées du coefficient d'apparentement de Milligan est
présentée aux Figures 4.13 et 4.14; la distribution est
asymétrique et l'apparentement moyen est faible (0.09). Aussi, il faut
souligner que contrairement aux méthodes d'estimation par les moments,
l'estimation de l'apparentement par maximum de vraisemblance de Milligan (2003)
est toujours comprise dans l'intervalle de définition du
paramètre. Cette contrainte induit par contre un biais pour les valeurs
du paramètre proches de 0; ceci est illustré par les Figures 4.13
et 4.14. Nous notons, en effet, qu'il y a un excès de valeurs
estimées de l'apparentement qui sont proches de 0.
4.2. APPLICATION DU MODÈLE SPATIAL POUR
L'APPARENTEMENT55
0.0 0.2 0.4 0.6 0.8
0.0 0.2 0.4 0.6 0.8
Frequence
40
20
50
30
10
0
?
?
?
?
?
?
? ? ? ?
? ? ? ?

coefficient d'apparentement
FIG. 4.13 - Distribution des valeurs estimées du
coefficient d'apparentement de Milligan
FIG. 4.14 - Boxplot des valeurs estimées du coefficient
d'apparentement de Milligan
| 


