4.3.2 Croisement
Le croisement est une procédure importante dans un
algorithme génétique ou dans un algorithme
mémétique. Cet opérateur permet de construire de nouvelles
solutions à partir de solutions existantes et joue un rôle
important pour la diversification des solutions.
Le croisement (appelé aussi la reproduction) est
l'équivalent de la rencontre de deux parents, produisant deux enfants.
Ces enfants portent une ressemblance à chacun de leurs parents. De
nombreux opérateurs de croisement ont été proposés
: croisement de préservation maximale (maximal preservative
crossover ou MPX) proposé par Mühlenbein et al.
(1988), croisement ordonné de rotation modifié (modified
rotational ordered crossover ou mrOX) proposé par Silberholz et
Golden (2007). Une comparaison de différents opérateurs de
croisements utilisés pour le problème du Voyageur de Commerce a
été présentée par Tsai et al. (2004).
La procédure de croisement que nous proposons ici est
une application de la procédure dropstar,
présentée dans le chapitre 2. On peut aussi noter que cet
opérateur a été inspiré d'un algorithme
proposé par Prins (2004), appliqué à un problème de
Tournées de Véhicules.
Soient Wi 1, .. . , Wi
m et vi1, . . . , vim
respectivement le tour des groupes et le tour des villes d'un individu,
appelé le père. Soient Wj 1, . . . ,
Wj m et vj1, . . . ,
vjm respectivement le tour des groupes et le tour des
villes d'un autre individu de la population, appelé la mère. Un
nouvel individu - un enfant - est construit de la manière décrite
ci-dessous. On peut noter qu'une fois qu'un individu fils a été
construit, le rôle des deux parents est inversé et qu'un
deuxième enfant est obtenu en utilisant le même
procédé.
Chaque ville de la mère est insérée
itérativement dans la séquence de villes du père. L'ordre
dans lequel les villes sont insérées est l'ordre
déterminé par le tour des villes de la mère,
c'est-à-dire que la première ville insérée est la
première ville dans le tour des villes de la mère. Nous
déterminons la position d'insertion d'une ville vjk
de la façon suivante : nous considérons chaque position
d'insertion de vjk entre les villes vil
et vil+1 du père de telle sorte que Wi l =6
Wj k et Wi l+1 =6
Wj k (évitant ainsi que deux groupes identiques ne
se suivent); parmi ces possibilités, on choisit celle minimisant le
coût d'insertion ciljk + cjkil+1 -
cilil+1.
Une fois que chaque ville de la mère est
insérée, nous en déduisons un tour des groupes dans lequel
chaque groupe apparaît deux fois. Nous appelons cette séquence la
séquence maître. Dans (Dauzère-Pérès et
Sevaux, 2004), une séquence maître d'un problème
d'ordonnancement est définie comme une séquence contenant au
moins une séquence optimale. Nous cherchons alors la
sous-séquence optimale réalisable, c'est-àdire pour
laquelle chaque groupe est visité une et une seule fois.
Cette recherche est effectuée par le biais d'un
algorithme de programmation dynamique récursif (voir le chapitre 2 pour
plus de détails), appliqué à un graphe obtenu à
partir du tour contenant chaque groupe en double. Ce graphe est construit selon
la procédure suivante. Un sommet est créé pour chaque
ville de chaque groupe, pour chaque apparition du groupe. Un arc est
ajouté pour chaque paire de noeuds issus de groupe de différentes
positions dans la séquence, dans la direction de la séquence (cf.
Fig. 4.1 pour une vision agrégée du graphe et Fig. 4.2 pour un
extrait du graphe complet). Nous définissons par la suite plusieurs
réductions de graphe (voir section 4.3.3). L'objectif est de trouver le
plus court chemin dans le graphe entre les groupes situés aux deux
extrémités, avec la contrainte que tous les groupes doivent
être visités exactement une fois et que la solution doit
être un cycle.
Avant d'expliquer plus en détails l'algorithme de
programmation dynamique, illustrons le comportement de cet opérateur de
croisement sur un exemple simple. Considérons un ensemble de groupe
W = {W1, . . . , W5}. Les tours de groupes du
père et de la mère sont :
père : W4 W3 W1 W5
W2 W4
mère : W4 W1 W3
W5 W2 W4
La procédure d'insertion définit une
séquence maître de groupes de la forme:
enfant: W4 W1 W3 W1
W5 W2 W3 W2 W5 W4
dans laquelle les groupes issus du père sont
soulignés et les positions d'insertion sont définies en utilisant
les tours des villes des individus.
Le graphe représenté par les figures 4.1 et 4.2
est alors défini implicitement. À partir de ce graphe,
l'algorithme de programmation dynamique détermine un tour des villes
optimal, à partir duquel on déduit une séquence de
groupes, définissant ainsi un nouvel individu. L'implémentation
de cet algorithme est détaillé dans la section 4.3.3.
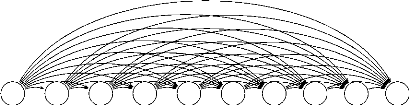
W4 W1 W3 W1 W5 W2 W3 W2 W5 W4
FIGURE 4.1 - Exemple d'un
croisement et du graphe résultant utilisé par la procédure
dropstar : vue avec agrégation des sommets en groupes
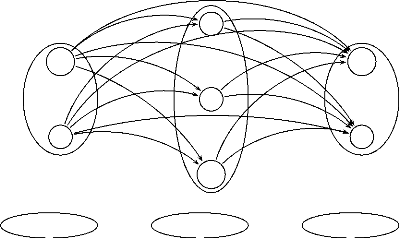
groupe W1
V12
V5
groupe W3
V11
V8
V9
groupe W1
V12
V5
FIGURE 4.2 - Exemple d'un
croisement et du graphe résultant utilisé par la procédure
dropstar : vue détaillée
Le principal avantage de cet opérateur est de
s'étendre sur un très grand espace de solutions. En effet, le
nombre de sous-séquences de groupes de la séquence maître
est égal à 2m oü m est le
nombre de groupes. De plus, pour une sous-séquence donnée, le
nombre de tours de villes est en
O((n/m)m) (on peut facilement se
rendre compte que l'espace le plus large est obtenu lorsque chaque groupe a la
même taille (le même nombre de villes) n/m).
Ainsi, la solution définie par cet opérateur de croisement est la
meilleure parmi O(2m *
(n/m)m). Selon nous, cela permet une
diversification importante et des populations de bonne qualité.
Cependant, le prix à payer est un important coût de
complexité comparé aux opérateurs de croisement
classiques. L'objectif de ce travail est d'évaluer si ce prix est digne
d'intérêt.
Devant la complexité de la procédure de
croisement, un important travail a été effectué afin
d'accélérer cette procédure pour la rendre applicable dans
le cas d'instances de taille importante.
| 


