4.3.3 Implémentation détaillée de
l'opérateur de croisement
Algorithme de programmation dynamique
L'algorithme de programmation dynamique utilisé pour
trouver le plus court chemin dans le graphe est celui présenté
dans le chapitre 2. L'algorithme commence avec des chemins partiels initiaux
associés à chaque noeud du premier groupe. Les chemins partiels
sont ensuite étendus itérativement avec la contrainte que chaque
groupe doit être visité exactement une fois. Cette contrainte est
traitée comme la contrainte d'élémentarité du
chemin, présentée par Feillet et al. (2004). Le graphe
étant acyclique, l'extension des chemins partiels dans l'ordre
topologique des noeuds fournit le chemin optimal.
Dans ce qui suit, nous notons L = (C,
ä1, .. . , äm) un label correspondant
à un chemin partiel, pour lequel C représente le
coût de transport du chemin partiel et äi E {0, 1} indique
si le groupe Wi est présent dans le chemin ou non. L'extension
d'un label à travers un arc est réalisable quand äi
= 0 pour le groupe Wi de la ville de destination, excepté
lorsque ce groupe est le dernier groupe de la séquence. Dans ce cas, les
conditions de réalisabilité sont que la ville de destination est
la première ville du label et que äi = 1 pour 1 i
m.
Un label L1 domine un label
L2, ce qui est noté L1 <
L2, lorsque ces deux labels mènent au même
noeud et que l'on peut être sûr que n'importe quelle extension de
L1 est de coût moindre que l'extension identique pour
L2. Ici, L1 < L2
quand C1 C2,
ä1 i ä2 i pour 1 i m
et que les premières et dernières villes de deux labels
sont
identiques. Dans ce cas, L2 peut être
supprimé.
Bornes inférieures
À chaque fois qu'un label L = (C,
51, . . . , 5m) est étendu vers une ville,
on calcule une borne inférieure sur le coût de n'importe quel
chemin pouvant être obtenu à partir de ce label. Cette borne
inférieure est comparée avec une borne supérieure
initialement définie par le coût de l'individu père. Cette
borne supérieure est valide, puisque le tour des villes du père
existe dans le graphe. La borne supérieure est mise à jour
à chaque fois qu'une nouvelle meilleure solution est trouvée par
l'algorithme. Lorsque la borne inférieure n'est pas inférieure
à la borne supérieure, le label L est
supprimé.
La borne inférieure LB(L) est
donnée par la formule suivante :
LB(L)=C+ ? Clj
{1=j=m,5j=0}
pour laquelle l est la position dans la séquence
maître du groupe vers lequel L vient d'être étendu
et Clj est le coût minimal induit pour la visite
future du groupe Wj.
Clj est calculé comme le coût minimum de
l'arc parmi les arcs dont :
1. la destination est une des villes de la dernière
occurrence du groupe Wj dans la séquence maître,
2. l'origine est une des villes situés entre le groupe en
position l (incluse) et la dernière occurrence du groupe Wj
dans la séquence maître.
Les valeurs Clj sont calculées dans
une phase de prétraitement, dès que la séquence
maître est fixée, pour chaque position l de la
séquence et pour chaque groupe Wj. La complexité de ce
calcul est en O(nm).
On peut noter qu'il peut arriver que la dernière
occurrence de Wj précède la position l. Dans ce
cas, Clj est fixé à une grande valeur et le
label est automatiquement supprimé si 5j = 0, puisque le groupe
Wj est inaccessible.
Réduction du graphe
Le graphe construit à partir de la séquence
maître peut être réduit. Puisque chaque groupe doit
être visité, aucun arc n'est autorisé à passer
au-dessus de toutes les occurrences d'un groupe. De plus, deux occurrences d'un
même groupe n'ont pas à être connectées. Enfin, un
groupe situé à la position j dans la séquence
maître ne doit être connecté qu'avec la première
occurrence de chaque groupe, dans le cas où les deux occurrences
seraient situées après la position j. En effet, dans ce
cas, toute extension possible à partir de la deuxième occurrence
du groupe est aussi possible à partir de la première occurrence
du groupe. La figure 4.3 présente le graphe obtenu à partir de
l'exemple présenté par la figure 4.1 une fois ces règles
appliquées.
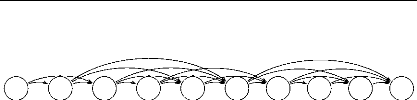
W4 W1 W3 W1 W5 W2 W3 W2 W5 W4
FIGURE 4.3 - Exemple d'un
croisement et du graphe résultant réduit utilisé par la
procédure dropstar : vue avec agrégation des sommets en
groupes
Accélérations heuristiques
La procédure de croisement peut être une
procédure très coûteuse en temps. Dans le but
d'accélérer sa résolution, nous proposons deux
accélérations heuristiques.
Limitation de la taille des listes de chemins partiels
Pendant la déroulement de l'algorithme de programmation
dynamique, une liste de chemins partiels est associée à chaque
ville. Malgré les règles de dominances, ces listes peuvent
être de taille relativement importante. Le but ici est de limiter leur
taille. Une limite unique est fixée (100 dans nos
expérimentations). Un règle d'évaluation est
définie afin de déterminer quels chemins partiels doivent
être supprimés lorsque la taille de la liste dépasse la
limite. L'évaluation eval(L) d'un label L =
(C, ö1, . . . , öm) est :
?{1=j=m} C1j ?
Clj
{1=j=m,öj=0}
pour laquelle UB0 est le coût de l'individu
père et l est la position du chemin partiel dans la
séquence maître. Cette formule cherche à équilibrer
le coût actuel d'un chemin partiel et une évaluation du coût
d'extension (tel que proposée dans la section 4.3.3). Les deux termes
sont normalisés afin que l'évaluation d'un chemin partiel initial
et du chemin partiel correspondant au tour des villes de l'individu père
aient une valeur identique UB0.
UB0
eval(L) = C +
Réduction des groupes Le but ici est
de limiter la taille du graphe, en supprimant des villes de différents
groupes. Une mesure est définie afin d'évaluer l'attrait d'une
ville. Les villes les moins attractives sont supprimées de chaque groupe
de la séquence maître. La mesure quantifiant
l'intérêt de la ville vk du groupe à la position
l de la séquence est :
|
eval(k, l) = ?
vi?-(l) ?
vj?+(l)
|
cik + ckj - cij
|
où -(l) (respectivement,
+(l)) est l'ensemble des villes appartenant aux deux
groupes précédent (respectivement suivant) la position l
dans la séquence maître. Cette mesure indique une tendance du
coût d'insertion de la ville vk dans une solution. En se basant
sur cette mesure, la taille maximale d'un groupe Wi est fixée )
[|Wi|p1, où p est
un paramètre (0.8 dans nos expérimentations). On
peut noter qu'avec cette formule, le pourcentage de villes supprimées
d'un groupe augmente avec la taille du groupe.
Complexité de la procédure de
croisement
Il est intéressant de noter que l'algorithme n'atteint
pas une complexité en temps polynomiale. L'objectif de cette section est
d'apporter plus de précisions quant à la complexité. Dans
cette analyse, nous ne prenons pas en compte les deux
accélérations heuristiques décrites ci-dessus.
Un état est défini pour chaque noeud du graphe
et pour chaque valeur des ressources {ä1, . . . ,
äm}. Le graphe contient 2n villes. Les
ressources äi sont binaires. Ainsi, le nombre d'état est
O(n2m). Le label associé à
un état est étendu vers un maximum de n autres
états. Chaque nouveau label est inséré dans une liste de
labels de taille maxi-male 2m. L'insertion consiste en une
comparaison avec chaque autre label de la liste. Chaque comparaison a une
complexité en O(m). Le coût de l'insertion d'un
nouveau label dans une liste est donc
O(m2m) et le coût d'extension d'un
label O(nm2m).
On peut donc en déduire que la complexité dans
le pire cas de notre algorithme est
O(n2m22m).
Évidemment, on peut espérer que le nombre d'opérations
soit réduit de manière significative en pratique. On peut aussi
noter qu'en limitant la taille des listes des labels, la complexité
devient O(n2m).
| 


