5.6.2 Initialisation de Ù pour la
génération de colonnes
Pour initialiser Ù, on construit une route non
réalisable complète qui passe par l'ensemble des sommets. On
associe à cette route un coût très élevé.
Cette méthode est appelée BigM. Cette route ne sera
ainsi plus sélectionnée dans la suite de la résolution,
dès qu'une solution utilisant uniquement des routes réalisables
existe.
5.6.3 Remontées de colonnes
Le but du problème esclave est de trouver des routes
ayant des coûts réduits négatifs. S'il en existe plusieurs,
ce qui est généralement le cas dans les premières
itérations de la résolution, on peut décider du nombre de
routes et donc du nombre de colonnes à insérer dans l'ensemble
Ù. Pour cela, on peut limiter la taille du nombre de chemins partiels
associés au puits v0 (qui est une copie du sommet
dépôt v0). Une fois que la limite fixée sur le
nombre de chemins partiels est atteinte, la résolution du
sous-problème est arrêtée et les colonnes correspondant aux
chemins partiels associés au puits (qui sont des routes
complètes) sont ajoutées à l'ensemble Ù.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
5.6.4 Problème esclave : ESPPRC
Nous présentons dans cette section les
spécificités du problème esclave pour la résolution
heuristique du problème du 2|RO|L-VRP. Le problème esclave est
résolu par la résolution d'un problème de Plus Court
Chemin Élémentaire avec Contraintes Additionnelles. Les
contraintes additionnelles peuvent être vues pour certaines comme des
contraintes de ressources. La résolution de ce problème se base
donc sur la résolution de l'ESPPRC, telle que présentée
dans la section 5.5.2. Nous définissons dans les sections suivantes les
règles d'extensions de chemins partiels, puis les règles de
dominance entre deux chemins partiels.
Extension d'un chemin partiel
Lors de la résolution du problème de plus court
chemin avec contraintes de ressources, les chemins partiels sont étendus
vers de nouveaux sommets. Les ressources prises en considération ici
sont : la capacité, une borne inférieure sur l'aire
occupée (définie comme la somme des aires des objets
transportés) et le coût (défini comme la somme des
coûts des arcs composant le chemin partiel, les coûts étant
égaux à cij - )ti pour tout arc
(vi, vj)). Lorsque le chemin partiel L dont
l'extrémité terminale est vi, est étendu vers le
sommet vj, le poids est augmenté de dj (où
dj est le poids total des objets du sommet vj). Le coût
est augmenté de cij - )ti. L'aire
occupée est augmentée de
mj
aj = ? wjl × hjl,
définie comme l'aire totale des objets du client j. Une
extension vers le
l=1
sommet vj est donc considérée
uniquement dans le cas où, une fois le sommet vj ajouté,
le poids associé au chemin partiel ne dépasse pas la
capacité totale du véhicule et la borne inférieure sur
l'aire occupée n'est pas strictement supérieure à la
surface de chargement. Dans le cas où ces contraintes sont
vérifiées, le chemin partiel est étendu vers le sommet
vj et le sommet vj est ajouté à la liste des
sommets non atteignables pour ce chemin partiel, afin de s'assurer de
l'élémentarité du chemin.
À l'état initial, le chemin partiel associé
au dépôt est caractérisé par un poids nul, une liste
de sommets non atteignables vide et une aire occupée nulle.
Dominance de deux chemins partiels
Afin de dominer le chemin partiel L2, le
chemin partiel L1 doit être contenu dans au moins un
chemin complet (de dépôt à dépôt) dominant
tous ceux contenant L2. Ceci peut se contrôler en
s'assurant de la réalisabilité d'extensions dominantes pour
L1 à chaque extension réalisable de
L2. Nous comparons donc des chemins qui ont la même
extrémité terminale. Les règles de dominances sont
importantes afin d'éliminer un grand nombre de chemins partiels.
Néanmoins, la vérification de la dominance ou de la non-dominance
peut rapidement s'avérer coûteuse en temps de calcul. Il faut donc
trouver un compromis entre l'efficacité et la complexité. Une
première règle est de s'assurer que toute extension de
L2 est réalisable à partir de
L1. Il suffit alors que L1 soit
5.6. Notre approche : un schéma de Branch & Price
de moindre coût pour être dominant. Une telle
règle est contraignante mais présente l'avantage d'être
robuste car toujours valide. Dans le cas du 2|RO|L-VRP, il faut donc s'assurer
que le coût et la capacité associés au chemin partiel
L1 soient inférieurs à ceux associés
au chemin partiel L2. La gestion de la ressource
correspondante à l'aire occupée est un cas particulier, qui est
précisée dans les sections 5.7.1 et 5.7.2. Afin d'avoir une
dominance sur l'aire occupée valide, la condition suivante doit
être ajoutée : quels que soient les objets futurs à
insérer dans un chargement, s'il existe un chargement réalisable
pour L2, alors il doit exister un chargement possible pour
L1. Du fait de la complexité d'une telle condition,
nous utilisons une règle de dominance heuristique.
Les règles de dominance peuvent néanmoins
être affinées. On peut dire qu'il y a dominance de
L1 sur L2, lorsque l'ensemble des
objets pris séparément de L1 peuvent
être contenus dans les objets de L2. La figure 5.5
illustre une telle dominance. Le label L1 est représenté
par le chargement contenant les objets hachurés. Le label L2
est représenté à droite du label L1. La
troisième figure montre que l'ensemble des objets de L1 peut
être contenu dans les objets de L2, ce qui permet de conclure
que L1 domine L2.
~
~~
~ ~~~
~ ~~~
~ ~~~ ~
~ ~~~
~ ~~ ~ ~~~ ~~
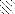

~
~~
~ ~~~
~ ~~~
~ ~~~ ~
~ ~~~
~ ~~ ~ ~~~ ~~
FIGURE 5.5 - Règle de
dominance affinée
Recherche à limitation d'écarts
(LDS)
Lorsqu'on étend un chemin partiel vers tous les
successeurs, le nombre de chemins partiels peut rapidement exploser,
malgré les règles de dominance. Afin de pallier ce
problème, nous utilisons une méthode qui permet de limiter le
nombre de successeurs vers lesquels l'extension des chemins est
réalisée. Cette méthode, appelée recherche à
limitation d'écarts (Limited Discrepancy Search ou LDS), a
été proposée par Harvey et Ginsberg (1995). Le principe de
cette méthode est le suivant. Lorsqu'une heuristique de recherche ne
permet pas de trouver une solution, on peut supposer que le nombre de retours
en arrière correspondant à de « mauvais » choix est
assez faible. Ce procédé a déjà été
utilisé pour un problème de Tournées de Véhicules
par Rousseau et al. (2004), pour le VRPTW.
Dans le cas du 2|RO|L-VRP, cela revient à penser qu'une
bonne tournée est composée de clients proches les uns des autres.
Nous définissons donc un critère permettant de
sélectionner des successeurs prometteurs pour chaque client. Le
critère retenu est
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
le plus proche voisin. Ainsi, un successeur est
considéré comme bon s'il est le plus proche voisin du client
depuis lequel il est étendu. Nous définissons aussi le nombre
maximal de mauvaises liaisons que peut contenir une tournée (une
mauvaise liaison étant définie comme un arc dont le client
correspondant à l'extrémité terminale ne fait pas partie
des successeurs prometteurs du client correspondant à
l'extrémité initiale de l'arc). L'extension d'un chemin partiel
se fait alors vers tous les bons successeurs et vers tous les autres si le
nombre maximum de mauvais successeurs n'est pas atteint par ce chemin
partiel.
Le fait de limiter le nombre de mauvais successeurs peut
soulever certains problèmes. Lorsqu'on cherche une route de coût
négatif, si le problème esclave n'est pas capable de trouver une
telle route, on conclut que le problème maître
relâché est optimal à l'itération courante. Or, sans
limitation sur le nombre de mauvais successeurs, une telle route peut exister.
Ainsi, si à la fin de l'algorithme, aucune colonne de coût
négatif n'est trouvée, l'algorithme est relancé avec un
nombre maximum d'écarts possible augmenté. La recherche à
limitation d'écarts fournit ainsi une méthode exacte combinant
à chaque itération les effets d'une réduction du graphe
avec ceux d'une limitation du nombre de chemins partiels
étudiés.
Première itération : limite d'écarts
à 2
Chemins limités : (y) ; (z) ; (x,z) ;
(y,x)
Chemins : (x,y,z) ; (z,x,y)
Deuxième itération : limite d'écarts
à 3
x
2 2
Chemins limités : (y,z) ; (z,y) y
Chemins : (x,z,y) ; (y,x,z) ; (y,z,x) ;
(z,y,x)
depot
depot
0
1
1
x
y
z
x
y
z
0
2
2
2
1
1
1
y 1
1
z
x 1
z 2
x
y
y
z
x
z
2
0
2
2
2
2
3
2
3
1
z
x
y
y
z
y
z
y
z
x
y
y
x
z
z
x
z
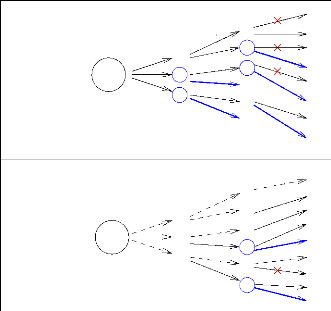
FIGURE 5.6 - Recherche de chemins
élémentaires par un LDS paramétré à 1
bon voisin
L'application de LDS à la recherche de chemins
élémentaires de longueur 3 est illustrée par la figure 5.6
qui retrace les deux premières itérations de l'algorithme. Le
bon
voisin de x est le sommet y, le bon voisin
de y est le sommet x et le bon voisin de z est le
sommet x. Au dessus de chaque arc, est indiqué le nombre
d'écarts du chemin partiel. Lors de la première itération,
cinq extensions (dont l'avant dernier sommet est entouré et dont l'arc
terminal est en gras) sont ignorées car elles atteignent la limite
d'écarts de 2. Ces extensions sont effectuées lors de
l'itération suivante, et ce sont les extensions atteignant la limite
d'écart de 3 qui sont alors ignorées. Dans cet exemple,
lorsqu'une extension vers un bon voisin est impossible, à cause de la
contrainte d'élémentarité par exemple, on considère
toujours la destination de cette extension comme un bon voisin. Les arcs
marqués d'une croix représentent des extensions violant la
contrainte d'élémentarité.
| 


