5.6.5 Problème de chargement séquentiel
à deux dimensions
Le problème de chargement à deux dimensions est
un problème que l'on retrouve fréquemment dans la
littérature. Les méthodes que nous décrivons par la suite
sont des méthodes classiques et qui ont montré leur
efficacité.
Méthodes de calcul de bornes
inférieures
Nous avons appliqué deux calculs de bornes
inférieures sur la hauteur totale d'un chargement à deux
dimensions. Ces bornes ont été définies dans un contexte
dans lequel l'aspect séquentiel n'était pas présent. Elles
restent cependant valides, bien que de qualité inférieures.
À notre connaissance, il n'existe pas de borne inférieure prenant
en compte les contraintes séquentielles.
La première borne est dérivée d'une borne
proposée par Martello et Toth (1990) pour le Two-Dimensional Bin
Packing. Cette borne inférieure se base sur un partitionnement des
objets. Étant donnée une valeur entière q telle
que 1 = q = 1 2W où W est la
largeur de la surface de chargement des véhicules et étant
donné J l'ensemble des objets du chargement, on pose:
K1 = {j ? J : wj > W
- q} (5.35)
1
K2 = {j ? J : W - q
= wj > 2W} (5.36)
1
K3 = {j ? J : 2W
= wj = q} (5.37)
On remarque que deux objets appartenant à K1 ou
K2 ne peuvent être chargés côte à côte
sur la surface de chargement.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
On définit pour tout entier q tel que 1 =
q = 12W la borne suivante :
B(q) = ? hj + max (0, [{ ? wjhj
- ? (W - wj)hj )}\W1) (5.38)
j?K1?K2 j?K3
j?K2
On obtient donc une borne inférieure définie par
:
LS 1= 1=q max=
{B(q)} (5.39)
/2
La complexité de cette borne est en O(n
log n). En effet, Martello et Toth (1990) ont montré qu'on
pouvait limiter les valeurs de q aux différentes valeurs prises
par wj telles
1
que 1 =wj= 2W.
Une autre borne a été proposée par
Martello et al. (2000) pour le problème du Strip
Packing. En considérant que les objets sont rangés par ordre
décroissant de hauteurs,
|
on définit k = max{i :
|
i
?
j=1
|
wj = W} et soit i(l) la
valeur minimale d'index telle que
|
|
wl +
|
i(l)
?
j=1
|
wj > W quel que soit l >
k vérifiant wl +
|
k
?
j=1
|
wj > W. Une borne inférieure est
|
donnée par :
|
LS2= max{hl +
hi(l) : l > k et wl + ?
j=1
|
wj > W} (5.40)
|
La complexité de cette borne est en O(n
log n). Il a été montré qu'il n'existe pas de
relation de dominance entre LS1 et
LS2.
Remplissage heuristique
Nous décrivons maintenant les différents
algorithmes heuristiques que nous avons utilisés pour déterminer
si un chargement est réalisable ou non. Tous ces algorithmes prennent en
entrée une liste d'objets à insérer. Les différents
tris possibles sur cette liste ont des conséquences sur les
résultats des algorithmes. En règle générale, on
considère que la liste est triée selon l'ordre de visite des
clients (pour satisfaire les contraintes de séquentialité des
chargements), puis par ordre décroissant soit sur la largeur des objets,
soit sur la hauteur des objets.
Une première famille d'algorithmes heuristiques sont
les algorithmes par niveau ou par étage. Le chargement est obtenu en
plaçant les objets de gauche à droite, sur des lignes formant
ainsi des niveaux ou des étages. Le premier niveau est le fond de la
surface de chargement (la largeur de la surface). Les niveaux suivants sont
formés
par une ligne horizontale coïncidant avec le haut du plus
grand objet placé au niveau inférieur. On retrouve dans la
littérature trois stratégies classiques pour le chargement
à deux dimensions. Ces stratégies ont été
adaptées à partir d'algorithmes prévus pour le cas
à une dimension. Dans chaque cas, les objets sont triés par ordre
de passage des clients à qui ils appartiennent, puis par ordre
décroissant de hauteur. Soit j l'objet courant et s le
dernier niveau créé :
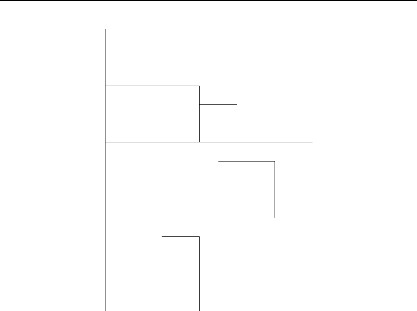
Next-Fit Decreasing Height (NFDH) : L'objet
j est inséré le plus à gauche possible sur le
niveau s, s'il rentre. Si ce n'est pas le cas, on crée un
nouveau niveau (s := s + 1), et j y est
inséré le plus à gauche possible (voir la figure 5.7).
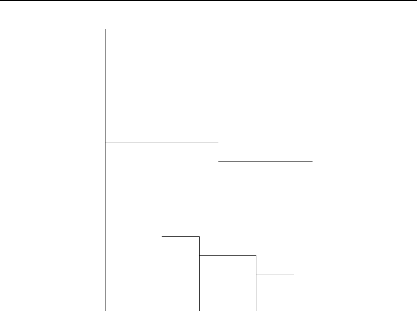
First-Fit Decreasing Height (FFDH) : L'objet
j est inséré le plus à gauche possible sur le
premier niveau dans lequel il rentre. Si aucun niveau ne peut contenir
j, un nouveau niveau est créé de manière
similaire à l'heuristique NFDH (voir la figure 5.8). Pour satisfaire la
contrainte de séquentialité du chargement, on fixe le premier
niveau dans lequel on peut insérer un objet, égal au dernier
niveau créé pour le client précédent. Cet
algorithme présente un intérêt lorsque les clients
proposent un nombre important d'objets. Dans le cas contraire, le chargement
est très proche de celui renvoyé par l'algorithme NFDH.
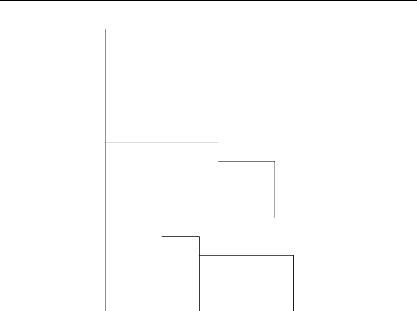
Best-Fit Decreasing Height (BFDH) : L'objet
j est inséré le plus à gauche possible sur le
niveau, parmi ceux sur lesquels il rentre, pour lequel l'espace horizontal
perdu est le plus faible. Si aucun niveau ne convient, un nouveau niveau est
créé tel que décrit précédemment (voir la
figure 5.9). Pour satisfaire la contrainte de séquentialité du
chargement, on fixe le premier niveau dans lequel on peut insérer un
objet, égal au dernier niveau créé pour le client
précédent. Cet algorithme présente un intérêt
lorsque les clients proposent un nombre important d'objets. Dans le cas
contraire, le chargement est très proche de celui renvoyé par
l'algorithme NFDH.
Coffman et al. (1980) ont analysé les
algorithmes heuristiques NFDH et FFDH pour la résolution du
problème de Strip Packing à deux dimensions, pour lequel tous les
objets sont insérés dans une boîte unique dont on cherche
à minimiser la hauteur. Étant donné un problème de
minimisation P et un algorithme heuristique A, on note
A(I) et Opt(I) la valeur renvoyée
par l'algorithme A et la valeur de la solution optimale, pour une
instance I du problème P. Coffman et al. ont
prouvé que, si les hauteurs des objets sont normalisées de telle
sorte que maxj{hj} = 1, alors :
NFDH(I) = 2 x Opt(I) + 1
(5.41)
FFDH(I) = 17
10 x Opt(I) + 1 (5.42)
Les deux bornes sont les plus restrictives, c'est-à-dire
que les facteurs multiplicatifs sont les plus petits possibles.
Nous présentons maintenant plusieurs heuristiques de
chargement dont la plupart dérivent de l'heuristique Bottom Left
proposée initialement par Baker et al. (1980).
Ces algorithmes suivent tous le même principe. Étant
donnée une liste d'objets à insérer, les objets sont
sélectionnés successivement pour être insérés
dans la surface de
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
1
5
3
2
6
4
FIGURE 5.7 - Next Fit Decreasing
Height
chargement. Tout au long de la résolution des
algorithmes, on garde en mémoire une liste ordonnée de positions
de chargements disponibles pour de nouveaux objets. À l'initialisation,
il n'y a qu'une position, la position en bas à gauche (d'où le
nom de Bottom Left). Chaque fois qu'un objet est inséré,
la position à laquelle il est inséré est modifiée
et on ajoute au plus une nouvelle position. Ainsi, la taille de la liste de
positions de chargements disponibles est bornée par le nombre d'objets
insérés, augmenté d' une unité. Les figures 5.10 et
5.11 représentent la gestion de la liste de positions avant et
après insertion d'un objet.
La position pour le placement d'un objet est
sélectionnée à partir d'une liste de positions
disponibles. Ce placement ne doit pas violer les contraintes de chargement
(l'objet ne doit pas dépasser des limites de la surface de chargement,
il ne doit pas chevaucher un autre objet, et enfin, son placement ne doit pas
empêcher le déchargement d'objets situés sur la suite du
parcours). La position choisie va dépendre de l'algorithme de
chargement. Si tous les objets sont placés dans la surface de
chargement, la route est considérée comme réalisable. Dans
le cas contraire, la liste des positions disponibles est ramenée
à la position initiale, et un autre algorithme de chargement est
appelé afin de proposer un chargement de l'ensemble des objets.
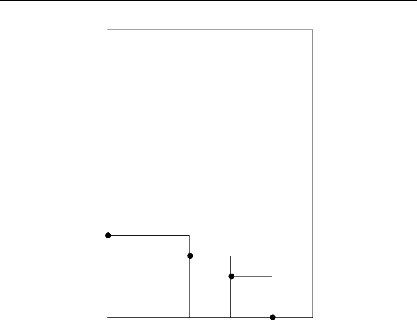
La gestion de la liste des positions est
représentée par les figures 5.10 et 5.11. Pour chaque position,
on ne conserve que deux informations : la hauteur de la position et la longueur
du segment jusqu'à la prochaine position (qui correspond à un
changement
5.6. Notre approche : un schéma de Branch & Price
1
3
2
4
5
6
FIGURE 5.8 - First Fit Decreasing
Height
de hauteur). Pour la position la plus à droite, la
deuxième information est la distance jusqu'au côté droit de
la surface de chargement. On peut remarquer sur la même figure qu'on ne
garde pas en mémoire les positions correspondant à des «
trous ». Étant données les contraintes de
séquentialité, le cas d'un objet pouvant se placer sous un autre
ne peut arriver que pour deux objets du même client. En partant du
principe qu'en cas de chargement non-réalisable, plusieurs ordres de
tris sur les objets seront appliqués, les configurations de trous ont
peu de chance d'empêcher un chargement.
La figure 5.10 représente un chargement pour lequel la
liste de positions disponibles est :
(4,4); (3,2); (2,2); (0,2)
Après insertion d'un objet de largeur 5 et de hauteur 2
telle que présentée dans la figure 5.11, la liste des positions
disponibles devient :
(7,5); (3,1); (2,2); (2,0)
Les figures 5.12 et 5.13 présentent à partir
d'un autre exemple de configuration de chargement les différentes mises
à jour possibles sur la liste des positions possibles après
l'insertion d'un objet.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
1
3
2
4
5
6
FIGURE 5.9 - Best Fit Decreasing
Height
Les heuristiques que nous avons utiisées sont les
suivantes :
Bottom-Left: Proposé par Chazelle
(1983), la position choisie pour chaque objet à in-
sérer est
la position la plus en bas, puis la plus à gauche (voir la figure
5.14).
Improved Bottom-Left: Liu et Teng (1999) ont
développé un algorithme amélioré du Bottom-Left, en
donnant la priorité aux mouvements vers le bas de telle sorte que
l'objet soit déplacé vers la gauche uniquement si aucun mouvement
vers le bas n'est possible (voir la figure 5.15).
Max Touching Perimeter: Cet algorithme a
été proposé par Lodi et al. (1999). Pour chaque
position, on calcule le périmètre des zones de contact entre
l'objet à insérer et les objets déjà
insérés. On choisit alors la position qui maximise ce
périmètre (voir la figure 5.16, appliquée sur le
même exemple que celui présenté par la figure 5.11). Une
variante a été proposée (Max Touching Perimeter No
Wall) qui ne prend pas en considération dans le calcul du
périmètre la zone de contact entre l'objet et les parois de la
surface de chargement.
Ces algorithmes heuristiques offrent un panel de solutions de
chargement. La complexité de ces algorithmes est de l'ordre de
O(n2) (pour chaque objet, on vérifie les
n positions possibles).
(4,4)
4
4
(3,2)
2
3
(2,2)
2
2
(0,2)
FIGURE 5.10 - Représentation
des coordonnées des objets
| 


