3-6 Résolution en analyse statique
3-6-1 Systèmes d'équations
linéaires
L'analyse statique consiste à calculer la
réponse statique linéaire d'une structure soumise à des
charges ponctuelles ou réparties. Dans le cas statique l'énergie
potentielle s'écrit [7]:
Ð=1UtK U
-Ut F (3-40)
2
Les extremums de cette énergie sont :
??/ ?U = KU - F
= 0 (3-41)
D'où:
KU = F (3-42)
La résolution de ce système linéaire
permet de déterminer le vecteur U des déplacements inconnus. On
calculera par la suite, les réactions, les efforts et les contraintes
dans les éléments de la structure
3-6-2 Prise en compte des conditions de déplacement
imposé
Dans l'expression l'équation (3-42), la matrice
de rigidité K de la structure est singulière. Cela implique qu'il
existe des déplacements qui doivent être éliminés en
introduisant les conditions aux limites cinématiques. Avant de
résoudre ce système d'équations pour déterminer le
vecteur U des déplacements inconnus, il faut donc prendre en compte les
conditions aux limites. Pour appliquer cette condition, on élimine les
lignes et les colonnes correspondants dans les matrices K
et M ainsi que du vecteur
F.
3-6-3 Résolution du système
linéaire
La résolution du système permet de
déterminer le vecteur Ui des déplacements inconnus. En pratique,
la matrice K à laquelle on aboutit est de grande taille. Le coût
de la résolution numérique de ces systèmes
d'équations est une partie significative du coût global de
l'analyse. Il existe des méthodes de résolution
appropriées qui tirent profit du caractère symétrique de
la topologie de la matrice de rigidité. La matrice présente
quelques propriétés intéressantes qui peuvent être
exploités pour résoudre efficacement le système
[3]:
- Symétrique,
- Définie positive (toutes les valeurs propres
sont positives), - Disposée en bande autour de la
diagonale,
- A diagonale dominante,
- La matrice K est très bien conditionnée
(conditionnement =1).
Pour que la matrice remplisse les conditions
ci-dessus, il est important de bien numéroter les noeuds. Pour les
structures à deux dimensions, la matrice de rigidité a
généralement la forme de la bande matrice si les points nodaux
sont bien numérotés, tel que la largeur de la bande de la matrice
de rigidité soit plus étroite. Et donc les problèmes de
stockage peuvent être réduites et les équations sont
résolues en utilisant la méthode d'élimination directe au
lieu des itérations, la largeur de la bande pour une structure
assemblée d'éléments finis est trouvée par
l'équation générale suivante [9]:
L = 2[mn
+ ( n -1)]+1 (3-43)
m : La différence maximale entre deux
noeuds d'un même élément fini.
n : Nombre de degrés de liberté
pour chaque noeud.
Exemple de numérotations:
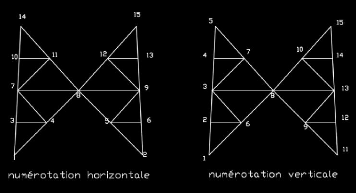
Numérotation horizontale :
Dans cet exemple tel que la numérotation des
points nodaux est horizontale, la largeur de la bande de la matrice pour une
structure à deux dimensions vaut : L=19
Numérotation verticale
Dans cet exemple tel que la numérotation des
points nodaux est verticale, la largeur de la bande de la matrice pour une
structure à deux dimensions vaut: L =
23
Donc la largeur de la bande est minimale dans le premier
système de numérotation c'est à dire la
numérotation horizontale, elle sera donc adoptée dans la suite de
ce travail.
La méthode la plus pratique pour résoudre
ce genre de problème est celle de CHOLESKY (voir. chapitre 3, §
8).
| 


