3-Description de l'etat du centre de gravite de
l'athlete lors de la phase du depart
L'évaluation des actions mécaniques externes
qui s'exercent sur l'athlète lors de la phase du départ de course
vitesse permet à partir de l'application des lois de la mécanique
classique de décrire l'état de son centre de gravité
à tout instant. Toutefois, avant d'énoncer ces lois il importe de
définir la nature des actions mécaniques qui s'exercent sur
l'athlète.
Elles peuvent être classées en deux
catégories :
§ la première comprend les actions de contacts qui
s'exercent sur l'athlète au niveau des
points de contact de son corps avec le milieu extérieur
c'est-à-dire au niveau des mains
et des pieds droits et gauches, noté respectivement
FMd
|
, FMg
|
, FPd
|
et FPg
|
.
|
|
§ la deuxième comprend une action à distance
représentée par la gravitation terrestre
~~
( g
9,81 ms -2
) dont la ligne d'action passe par le centre de gravité de
l'athlète et
dont la direction est donnée par la verticale
descendante. L'intensité de cette force
~~ ~~
définie le poids noté : 9=
mg .
Par la suite, la considération d'un
référentiel galiléen admet l'application des lois de la
mécanique newtonienne à l'athlète. Ces lois permettent de
déduire que :
§ le centre de gravité de l'athlète
possède un mouvement rectiligne uniforme s'il n'est soumis à
aucune force (principe de l'inertie).
§ lorsqu'il est soumis à des forces ( F i
), le centre de gravité de l'athlète possède une
~ ~~
accélération ( a G )
proportionnelle à la résultante de cette force ( R ), et
ayant les mêmes directions et sens que cette dernière (principe
fondamental de la dynamique) tel que
~~ ~~ ~
R= F i = ma G Éq.III.9
§ s'il y a interactions entre un segment S1 de
l'athlète et un solide S2 de son milieu extérieur, les
actions de contacts de S1 sur S2 ( F 1 2 ) et de
S2 sur S1 ( F2 1 ) sont égales

et opposées (sur la ligne d'action S1S2) : F
1 2 = - F2 1 (principe de réciprocité
également dénommé principe d'action-réaction).
Lors de la phase Pret
Au cours de cette phase, le point matériel (athlète
réduit à son centre de gravité) est
considéré en équilibre (état de repos). Cela
signifie que sa position est fixe par rapport à
~~~~
( OG = cte ). Étant initialement
immobile dans 0, la somme des forces externes qui lui sont
appliquées est nulle :
~~ ~~ ~~ ~~ ~~ ~
F Md Ro +F Mg Ro +F Pd Ro +F
Pg Ro + 9G Ro=0
Éq.III.10
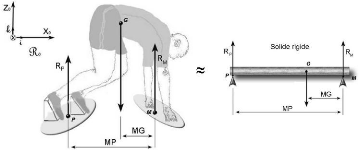
La mesure dynamométrique de ces actions mécaniques
permet de déterminer la
position du centre de gravité (figure 27) du coureur par
rapport à M et P respectivement points
~~
d'applications des résultantes des forces
exercées au niveau des deux mains ( RM) et des deux
~~
pieds ( RP ). Il est possible de représenter par
des vecteurs les actions mécaniques qui s'exercent sur l'athlète
assimilé à un solide rigide (S) de masse (m)
(figure 27).
Dans un souci de simplification de la représentation
figurant ci-dessous, les directions
~~ ~~
des vecteurs RP et RM sont choisies identiques
au poids.
Deuxième partie Chapitre III
9
9
Figure 27 Évaluation de la position du centre de
gravité (G) de l'athlète au repos suite à
son
assimilation à un solide rigide.
L'application du principe fondamental de la statique au solide
(S) permet d'écrire :
5G/ 90 =
0
RG/910
~~~
d'où
/910
~
~~
( )
G,R
~~
~
0
MP.
La connaissance de la distance
représentant l'écart antéropostérieur
entre M et
P (figure 27) ainsi que l'application de la seconde
condition d'équilibre permet de déterminer la position
horizontale du centre de gravité de S suivant l'axe
antéropostérieur OX0 comme suit :
~~~ ~~~ ~~~ ~
DIE( MjiM )
/91,, + OTC( MiP )
/91., + DIE(
AOG )/91,, = 0
~ ~~~~ ~~ ~~~~~ ~~ ~
0 + MP ? R P + MG ? =
Sachant que MPy = 0 , MPz
= 0 et Ry = 0 il devient :
0 1 0 1 0
- ·
R MP + - ·
mg MG = 0
Pz x z x
0 J 0 J 0
-
R · MP
d'oùMGx=
Éq III.11
mg
et PGx = MPx -
MGx Éq.III.12
La position horizontale du centre de gravité
Gx correspond à la position du point d'application
de la résultante des forces qui s'exercent sur l'athlète. C'est
le barycentre des actions mécaniques de contact de l'athlète avec
le milieu extérieur.
Lors de l'impulsion
Lors de l'impulsion, la variation de la quantité de
mouvement du centre de gravité de l'athlète est d'autant plus
grande que les actions mécaniques mesurées sont importantes.
Cette phase débute à l'instant (ta) et prend
fin à l'instant d'éjection (te).
L'application du principe fondamental de la dynamique permet d'exprimer la
variation élémentaire de la quantité de
~~
mouvement du centre de gravité ( mdVG )
suivant un axe donné en fonction de la composante de l'impulsion
élémentaire des forces extérieures suivant le même
axe. Cette relation est exprimée par l'équation suivante :
mg z F F F
Éq.III.13
m · [dV
Gy = 0 + [F M d x + [F A IMgy gx }+ F Pdx + [P g
x
F
Mdy Pdx
d V Gz Pgy
Mdz Mgz Pdz Pgz
· dt
d V Gx 0 F F
F
Pour évaluer la vitesse du centre de gravité de
l'athlète, il faut calculer les variations
|
instantanées d V G
~~
|
tout au long du geste du départ pour ensuite les
cumuler. La variation totale
|
ÄVG
~~
entre l'instant initiale ti et un instant quelconque
t est égale à la somme discrète des d V
G élémentaires suivant la relation suivante :

ti
Ä V G =V Gt
Gt 1
= f R Gdt
V
m
Éq III.14
En posant ti comme étant un instant de la
phase Prêt, il devient possible de déterminer directement
la vitesse du centre de gravité de l'athlète à n'importe
quel instant t. Cela est due au fait que la vitesse du centre de
gravité au cours de cette phase est considérée nulle
~~ ~
( VGti = 0 ) ; ce qui permet d'écrire :
Fx ( t )
VGxt 1
V Gyt = · Nt) · dt


Gz t
Éq.III.15
t
( + F z( t ))
ti
D'après l'équation III.15, l'intensité de la
vitesse du centre de gravité de l'athlète à l'instant
t est proportionnelle à la grandeur de la somme des forces qui
s'exercent sur l'athlète
suivant le même axe. Toutefois, l'athlète est
contraint de générer la plus grande force dans la plus courte
durée (dt).
Possédant la variation de la résultante des
forces qui s'exercent sur l'athlète au cours de la phase d'action, le
calcul de la vitesse instantanée de son centre de gravité est
réalisé par un procédé d'intégration
numérique pas à pas suivant une méthode
d'intégration approchée, dite méthode des trapèzes.
Cette méthode consiste à remplacer un arc de la courbe par un
segment. Il s'agit donc d'une interpolation linéaire.
Les mesures des actions mécaniques sont
échantillonnées à une fréquence de 1000 Hz, ainsi
les intervalles de temps sont relativement petits. Cela assure une exploitation
plus précise des données numériques de forces. L'aire
totale sous la courbe est ainsi divisée sur des intervalles
réguliers représentés par des trapèzes. Ainsi, la
somme des aires représente une approximation de l'intégrale de la
force en question.
Cette méthode est également utilisée pour
estimer la variation de la position du centre
|
~~~~
de gravité de l'athlète ÄOG
|
comme suit :
|
|
|
~~~~ ~~~~ ~~~~ ~~
t
Ä OG= OG t - OG t i = IV G· dt
ti
|
Éq.III.16
|
Lors de la phase aerienne
Le début de la phase aérienne est
déterminé par l'instant d'éjection
(te) qui correspond au décollage du pied avant de
l'athlète. Dès cet instant, toutes les actions de contacts
s'annulent jusqu'à la réception du pied arrière au sol.
Seule l'action de la gravitation terrestre appliquée au centre de
gravité de l'athlète suivant la verticale descendante
(OZ0) continue à être exercée tout au long de
cette phase.
D'après la première loi de Newton, au cours de
cette phase, le mouvement du centre de gravité de l'athlète dans
g0 suivant l'horizontale OX0 et OY0, est un
mouvement rectiligne uniforme (la résistance de l'air est
négligée). L'application des lois du mouvement rectiligne
uniforme permet d'écrire :
x( t ) = xi +
Vxt Vx ( t ) = V =
Vi ax ( t ) = 0
avec x( t) chemin parcouru,
xi position initiale (à t = Prêt),
Vx ( t ) vitesse uniforme, (t) temps
écoulé, vi vitesse initiale et
ax accélération.
Suivant la verticale (OZ0), le centre de gravité
possède un mouvement accéléré d'intensité
2
gz 9 , 81 ms -
= - . L'application des lois du mouvement rectiligne
uniformément
accéléré évalue le
déplacement, la vitesse et l'accélération du centre de
gravité du coureur comme suit :
( ) 2
1
z t = at
+V t+ z V z ( t ) = at+V i
az ( t ) = g
i i
2
La connaissance de l'intensité des composantes de la
vitesse du centre de gravité à te
|
notée V éject
|
,permetdecalculerl'angled'éjection(èéject)ducentredegravité.Cetangleest
|
défini comme étant le degré
d'élévation de la norme de la vitesse d'éjection
) par rapport au plan horizontal. La non prise en compte de

(
V éject
Vé
ject+ V éject + V
éject
2 2 2
x y z
=
la faible vitesse médio latérale (
Vy ) dans le calcul de l'angle d'éjection, et
l'utilisation de la



fonction cosinus fournit un résultat de 8° au lieu
de 6° (soit une erreur relative de 20%) pour
Vx =
3,28 m s , Vy = - 0,27 m s et Vz = 0,37
m s . L'utilisation de la fonction sinus garantie
un résultat fiable indépendamment du nombre de
composante mesurée. L'estimation de l'angle d'éjection sera
obtenue à partir de cette seconde méthode.
| 


