4-Caracterisation de la performance lors d'un depart
de course vitesse
Les variables cinématiques et dynamiques
déterminées suite à la distinction des actions
mécaniques exercées à l'athlète lors d'un
départ de sprint, offrent une quantité d'informations complexes
ne pouvant être assimilées en tant que telles par l'observateur.
Pontier et al. (1990) précise que suite aux progrès de
l'instrumentation ... l'observateur a fini par être
submergé par la masse grandissante des informations ... la
seule réflexion ne suffit plus à opérer la transformation
des données d'observation en éléments de connaissance
... [Pont 90]. En effet, contraint par les limites de ses sens,
l'observateur est dans l'incapacité d'effectuer une observation globale
du geste. Il se voit donc obligé de concentrer son attention sur une
quantité finie d'informations.
Partant de ce constat, depuis une vingtaine d'années,
différents instruments méthodologiques ont été
développés. Ces méthodes de modélisation et
d'analyse de données sont dites multidimensionnelles en opposition aux
méthodes de la statistique descriptive qui ne traitent qu'une ou deux
variables à la fois. Elles permettent la modélisation d'une
grande
quantité d'informations en un petit nombre de
variables synthétiques. Plus exactement, elles tendent à
représenter une grande quantité de variables dans un espace de
dimension moindre sans toutefois perdre de l'information par rapport aux
données de base. L'une des méthodes qui permet cette
modélisation est l'Analyse en Composantes Principales (ACP).
Appliquée à un ensemble de variables tel que celui de la
présente étude, cette méthode factorielle permet de
comprendre et de visualiser comment les effets de phénomènes
a priori isolés se combinent.
L'ACP est donc appliquée27 à un
tableau (m x n) à deux dimensions associant m
individus et n variables. Les individus en nombre de m =
92 représentent les lignes du tableau et comportent l'ensemble des
essais de départ. Les variables en nombre de n = 91 sont les
colonnes et comportent les durées de contact, les instants de mise en
action et de décollage, les forces, les vitesses, les
déplacements et les angles de projections du centre de gravité
à différents instants de la phase du départ de sprint
(Annexe 1-tableau 1). Appliquée à un tel tableau, l'objectif de
l'ACP est une étude exploratoire. Les deux voies principales [Esco 98]
de cette exploration sont :
la transformation en distances euclidiennes des
proximités statistiques entre éléments afin
d'établir un bilan de ressemblances entre les essais de départ et
un bilan des liaisons entre variables. Deux essais se ressemblent d'autant plus
qu'ils possèdent des valeurs proches pour l'ensemble des variables. La
liaison entre deux variables est mesurée par le coefficient de
corrélation linéaire R.
la constitution de nouvelles variables en nombre q
inférieur à n (q le plus réduit
possible) tout en limitant le plus possible la perte d'information. Cette
« réduction de données » permet de créer de
nouvelles variables appelés Composantes Principales (CP). Les
CP engendrées sont des combinaisons linéaires des variables
initiales et doivent permettre la reconstitution, la plus fidèle
possible, des variables initiales.
L'étude des résultats de l'ACP se fait
grâce à l'analyse des différentes représentations
géométriques (plan factoriel) des corrélations entre les
variables ainsi que du nuage des individus [Pont 90].
27 L'ACP est réalisée en utilisant
le logiciel R (Licence GPL Version 2, June 1991 -
http://www.R-project.org) ainsi
que le package ade4 développé par le
Laboratoire de Biométrie et Biologie Évolutive de
l'Université de Lyon (
http://pbil.univ-lyon1.fr/ADE-4/)
4.1-Analyse en composantes principales
Afin de faciliter la lecture du tableau (92 x 91), les 91
variables initiales sont regroupées selon leurs natures. Cinq groupes de
variables sont ainsi créés:
§ Variables temps : regroupent le temps de latence,
la durée d'impulsion, les instants
de mise en action, de force maximale, et de décollage.
La définition de ces instants offre des points de contrôle
uniformes à tous les essais. Cela permet d'effectuer une estimation
relative et objective des autres variables.
§ Variables force : regroupent les composantes et
résultantes de forces exercées au
niveau d'un ou plusieurs appuis à des instants
prédéfinis.
~~
§ Variables vitesse du centre de gravité (
VG ) : regroupent les composantes et la norme de la VG aux
instants prédéfinis.
~~~~
§ Variables déplacement du centre de
gravité (OG
|
) : regroupent les composantes et
|
|
la norme de cette grandeur aux instants
prédéfinis.
§ Variables angle : regroupent les
évaluations de l'angle de projection du centre de gravité aux
instants prédéfinis.
L'analyse du tableau de données comportant les 92
essais et les 91 variables déterminées suite aux mesures
dynamométriques de départ du sprint conduit tout d'abord à
calculer les paramètres descriptifs élémentaires
exprimés dans le tableau 2 en Annexe 1.
Une confrontation simultanée des variables est
effectuée afin d'étudier les degrés de liaisons entre les
variables. Cela conduit à la définition de la matrice des
corrélations. C'est une matrice carrée d'ordre n = 91
regroupant tous les coefficients de corrélation linéaire entre
toutes les variables prises deux à deux. Elle est symétrique par
rapport à sa diagonale principale dont tous les éléments
sont égaux à un.
Dans le souci de faciliter la lecture de cette importante
matrice (Annexe 1-tableau 3) du point de vue dimensions (92 x 91), les
coefficients de corrélations linéaires sont
représentés par un code couleur (figure 44).
Cette matrice de couleur (figure 44) exprime dans son triangle
supérieur les coefficients de corrélations R? [ - 1 1] .
Dans le triangle inférieur (figure 44) sont
représentés les seuls coefficients de corrélations
significatifs28 (p < 0,05). Ce sont les éléments de
la matrice dont la valeur appartient à l'intervalle [ - 0,7 -1] si la
fonction affine est décroissante, et à l'intervalle
[ 0,7 1] dans le cas d'une fonction affine croissante.
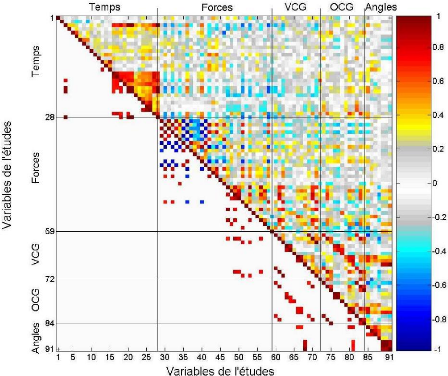
Figure 44 Représentation de la matrice des
corrélations dans le triangle supérieur et de ses
éléments
significatifs (p < 0,05) dans le triangle
inférieur. Les 91 variables sont groupées en cinq groupes
de
variables (temps, force, vitesse du CG (VCG), déplacement du CG
(OCG) et angle de projection du CG).
Les valeurs numériques de cette
représentation sont présentées en annexe 1-tableau
3
La lecture de cette représentation (figure 44) fournit
des éléments de description des associations entre variables.
Cela permet d'avoir une première idée sur le réseau
d'interrelations existant entre les variables. L'analyse en composantes
principales conduit ensuite à une synthèse de ces liaisons.
28 Un coefficient de corrélation R
> 0,7 associé à 92 mesures indique une
corrélation linéaire significative, la probabilité p que
les variables x et y soient décorrélées
est inférieure à 5%.
Il ressort de cette représentation (figure 44) que les
variables temps sont indépendantes de toutes les autres variables de
l'étude. Cette première constatation est en contradiction avec
les études antérieures (§-II) qui soulignent l'existence
d'une relation étroite entre la vitesse du centre de gravité
à l'éjection et le temps de latence ou la durée de
l'impulsion. Cette discordance peut être due à la
différence du niveau d'expertise des populations
étudiées.
Les variables force ne présentent des liaisons qu'avec
quelques variables vitesses telles que la vitesse du centre de gravité
suivant l'axe antéropostérieur et sa norme aux instants de
décollage du pied arrière puis du pied avant. Outre les relations
avec les variables force, les variables vitesses présentent de fortes
liaisons avec les variables déplacement et angle.
Cette première étape exploratrice
détermine un faible degré de dépendance entre les
variables. En effet, parmi les liaisons possibles, seulement 4% sont
effectives. Ce faible pourcentage de liaison entre les variables de
l'étude présente un « diagnostic » pessimiste quant aux
résultats de l'analyse factorielle.
Vue la nature des variables de cette étude, il importe
d'effectuer une standardisation (centrage et réduction) afin de
s'affranchir de l'arbitraire des unités de mesures (Annexe 1.2).
L'analyse des composantes principales devient donc normée (ACPN). Cette
normalisation augmente le poids de la variabilité des variables quelle
que soit leur intensité relative29.
| 


