Contribution à la caractérisation mécanique des critères de qualités du départ de la course vitesse sur 100 m

4.3-Analyse des relations intervariables

Étant le plus souvent inexploitées lors du geste du départ de sprint, les forces maximales exercées au niveau des mains suivant l'axe horizontal et vertical semblent dépendre du pourcentage du poids exercé au niveau de ces mêmes appuis lors de la position Prêt (figure 47).

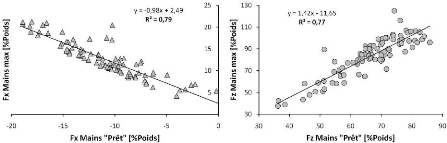
Figure 47 Relations entre la force exercée au niveau des mains lors de la position statique Prêt
et à l'instant où elle est maximale en fonction du poids du corps. Suivant les axes horizontal et vertical

Contrairement, l'étude des forces exercées au niveau du pied arrière lors de la position Prêt et lors de son maximum ne permet pas de déduire une quelconque relation de cause à effet, que ce soit suivant l'axe antéropostérieur ou vertical (figure 48).

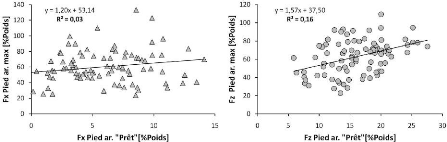
Figure 48 Relations entre la force exercée au niveau du pied arrière lors de la position statique Prêt
et à l'instant où elle est maximale en fonction du poids du corps. Suivant les axes horizontal et vertical

De même, l'intensité de la force exercée au niveau du pied avant, lors de la position Prêt et lors de son maximum (figure 49), ne présente pas de relation de cause à effet significative.

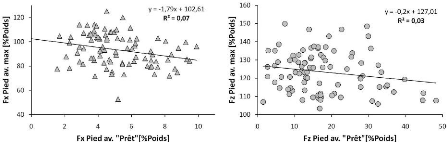
Figure 49 Relations entre la force exercée au niveau du pied avant lors de la position statique Prêt
et à l'instant où elle est maximale en fonction du poids du corps. Suivant les axes horizontal et vertical

Les résultats exposés dans les figures 48 et 49 viennent appuyés ceux de Davila et al. (2006), qui, en effectuant une critique envers les praticiens et entraîneurs, démontrent que l'augmentation de l'intensité des forces horizontales exercées au niveau des pieds, lors de la position Prêt, n'entraîne pas une amélioration significative de la « performance » [Davi 06].

Concernant l'écart antéropostérieur, entre la position du centre de gravité et le point d'application de la résultante des forces exercée au niveau des pieds (GP_x) (§-III.4), les études antérieures [Bren 86 ; Kraa 01] démontrent que l'ordre de cet écart est proportionnel à l'intensité de la force réactive engendrée lors de l'impulsion. Notant aussi que l'exploitation de la seconde loi de Newton (Éq.III.9) montre que, pour une même durée de temps, la variation de la position du centre de gravité de l'athlète est proportionnelle à la résultante des forces

externes qui lui sont appliquées. Il est donc possible d'estimer l'amplitude de la variation de la position antéropostérieure du centre de gravité à partir de la connaissance de sa position initiale par rapport à la résultante des forces exercée au niveau des pieds (GP_x) et/ou des mains (GM_x). L'étude de régression linéaire entre GP_x (exprimée en pourcentage de la distance entre les points d'application des résultants pieds et mains) et sa variation antéropostérieure (61OCG_x) démontre que la corrélation est faible (figure 50a).

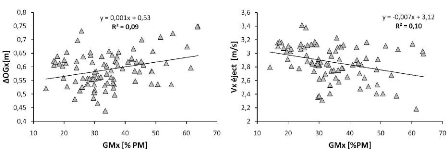
(a) (b)

Figure 50 (a) Relations entre GM_x et AOCG_x, (b) relation entre GM_x et V_x éject
GM_x exprimées en pourcentage de la distance pieds-mains (%PM)

L'absence d'une relation de causalité entre GM_x et AOCG_x (figure 50a), permet de déduire l'absence d'une relation entre GM_x et la vitesse antéropostérieure du centre de gravité à l'éjection, c'est ce que montre la figure ci-dessus (figure 50b).

Vue la très faible intensité de la vitesse verticale à l'éjection, l'étude de régression linéaire entre la vitesse antéropostérieure et sa norme à l'éjection présente une forte corrélation (figure 51). Cela permet de déduire l'une en connaissance de l'autre avec une précision de 99 %.

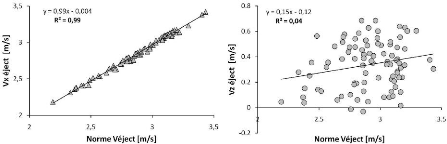
Figure 51 Relation entre la norme de la vitesse d'éjection (Norme Véject), la vitesse horizontale (V_x éject)
et la vitesse verticale (V_z éject) au même instant

L'estimation de la seule vitesse antéropostérieure ne suffit pas pour déterminer l'angle d'éjection. Pour connaître cet angle, il faut bien entendu évaluer les deux composantes de la vitesse, antéropostérieure et verticale.

La présence d'une forte corrélation entre la norme à l'éjection et sa composante horizontale (figure 51) pourrait être interpréter comme suit : plus l'angle d'éjection est faible,

V cos°

plus la vitesse antéropostérieure à cet instant sera importante ( V4ect =

). De même

plus la vitesse antéropostérieure est grande, plus la variation de position du centre de gravité est importante (pour un même intervalle de temps). Or, l'étude de régression de la norme de la vitesse à l'éjection avec l'angle (figure 52a) puis avec la variation de la position antéropostérieure du centre de gravité (figure 52b) montre de faibles corrélations.

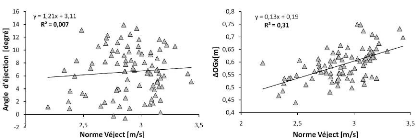
(a) (b)

Figure 52 Relation entre la norme de la vitesse d'éjection, l'angle d'éjection et la variation
antéropostérieure de la position du centre de gravité

La vitesse du centre de gravité à l'éjection est indépendante de la force maximale exercée sur les blocs suivant les deux axes : horizontal (figure 53a) et vertical (figure 53b).

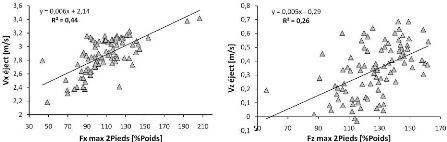
(a) (b)

Figure 53 Représentation graphique de la relation entre la force maximale exercée
au niveau des pieds et la vitesse d'éjection suivant les axes horizontal et vertical

Il est postulé que la vitesse acquise par un point matériel à masse conservative dans un référentiel galiléen est proportionnelle à la résultante des forces qu'il subit en fonction du

temps. L'absence d'une relation directe entre la force et la vitesse dans le cas de cette étude démontre tout l'intérêt d'intégrer le facteur temps (durée d'application de la force). Toutefois, l'étude de la vitesse d'éjection du centre de gravité en fonction du produit de la durée d'impulsion par le maximum de la somme des forces exercées au niveau des pieds ( f (max( F2 pieds)· dt impulsion _)Véjectne permet pas de déduire une quelconque relation

de dépendance entre les deux grandeurs (figure 54).

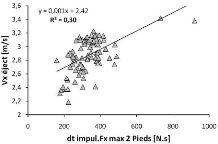
Figure 54 Relation entre la vitesse d'éjection antéropostérieure (V_x éject) et le produit de la durée
d'impulsion (dt impul) par le maximum de la somme des forces antéropostérieures
exercées au niveau des deux pieds (Fx2pieds)

Cette faible corrélation entre le produit de la force maximale (des forces exercées au niveau des deux pieds) par la durée d'impulsion et la vitesse d'éjection démontre que même la prise en compte des forces maximales et du temps d'impulsion ne conduit pas une caractérisation juste de la vitesse d'éjection.

Afin de vérifier ce constat, la relation entre la somme des forces exercées au niveau

~~

des quatre appuis en contact avec le sol ( Fext ) et la vitesse d'éjection est étudiée. La

~~ ~~ relation f(max( F ext ))=V éject

présente un coefficient de détermination linéaire (R^2 = 0,53) ~~ ~~

plus élevé que la relation f(max( F 2 pieds ))=V éject précédente (R² = 0,46).

Toutefois, la relation f(max(EF^-- ext )× dt impulsion)= V éject présentant un coefficient

de détermination R² = 0,40 supérieur à R² = 0,30 mais toujours de faible amplitude, on ne peut donc pas déduire une éventuelle liaison entre ces deux grandeurs.

Nous avons souhaités par ces résultats souligner l'erreur commise par une telle interprétation. Toutefois, la formulation du théorème de la quantité de mouvement (Éq.IV.6) suffit pour démontrer l'erreur conceptuelle faite en se limitant à la force maximale exercée au niveau des pieds pour évaluer la vitesse d'éjection.