Contribution à la caractérisation mécanique des critères de qualités du départ de la course vitesse sur 100 m

4-Effet de la methode de solidification globale sur la definition des angles articulaires

4.1-Definition des angles articulaires

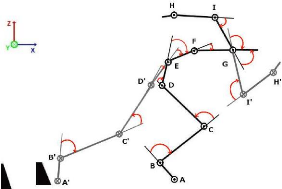
Les angles relatifs appelés aussi angles articulaires sont les angles qui permettent de définir l'orientation d'un repère gt.i+1 par rapport à un repère gt._i . La figure 83 ci-dessous illustre les angles relatifs segmentaires du notre modèle projeté sur le plan sagittal.

gt.0

0

0

0

Figure 83 Configuration de la chaîne cinématique plane, arborescente du départ du sprint.
Illustration des angles relatifs du modèle étudié

Effectuant l'analyse dans un espace 3D, l'orientation globale d'un repère gt.i+1 par

rapport à un repère gt._i se définie par trois rotations (séquences) élémentaires. L'ordre de séquences choisi influe l'amplitude des angles relatifs calculés.

Afin de normaliser les procédures de calcul et éviter l'indétermination des amplitudes articulaires, l'ISB [Wu 02] recommande l'adoption de la séquence de rotation (rot) suivante proposée initialement par Grood (1983) pour l'articulation du genou (§-VII.2) :

rot₁ ( Z _i ø, ) - Flexion/Extension autour de l'axe Zi d'un angle ø

rot₂ ( X _i,è ) 4 Abduction/Adduction autour de l'axe Xi d'un angle è

rot₃ ( Y_i,? ) - Rotation Interne/Externe autour de l'axe Yi d'un angle ö

La matrice de rotation i+1

R_i qui permet le passage de gL_i à gi+1 est définie en

utilisant les matrices de transformation simple (§-III.3.4) pour décrire les trois rotations élémentaires :

C C S S S S C C S S S C

- +

ø ö ø è ö ø è ø ö ø è ö

i i i i i i i i i i i i

[

Ri+1 = rot₁ · rot₂ · rot₃ = S _ø C _öi + C _cfri S e S _so C _cfri C o S S _ö- C _i SèC öi Éq.VII. 13

i

- CS ö i S C è i Cö _i

avec C désigne la fonction cosinus et S la fonction sinus.

Traduisant le passage de g_i à _i+1 , la matrice ⁱ⁺¹

R_i se définit comme étant la matrice dont les colonnes sont les composantes des vecteurs unitaires de R_i+1 exprimées dans g_i . De ce fait, la matrice ⁱ⁺¹

R_i peut aussi s'écrire comme suit :

X X Y X Z X i+1 i i+1 i i+1 i R i+1 = X Y Y Y Z Y i i+1 i i+1 i i+1 i XZ i Y i+1 Z Z i+1 Z i

Éq.VII. 14

dont X_i+1 , Y _i+1 , Z_i+1 et X_i , Y_i , Z_i sont respectivement les vecteurs unitaires de g_i+1 et g_i .

La définition des angles relatifs se fait donc par correspondance entre les termes de la première (Éq.VII.13) et de la deuxième forme (Éq.VII.14) de la matrice ⁱ⁺¹

R_i .

La détermination des amplitudes articulaires se fait donc comme suit :

pour la flexion/extension : S ø iCè i = Y _i+1Xi et Cø _i Cè i = Y _i+1Yi d'où

Y _i+1 X _i Y _i+1 Yi

ø = atan2

i

Éq.VII. 135

,

Cè i Cèi

pour l'abduction/adduction : Sèi = Y _i+1Zi d'où

è_i = asin ( _Yi+1Zi)ou è_i = ð - asin ( Yi+1Zi) Éq.VII. 14

pour la rotation interne/externe : -C _èi S ö _i= X _i+1 Z_i et = Z Z

C è i C ö i i+1 i d'où

atan2 X Z Z Z

i+1 i i+1 ,ⁱ -CèCèi i

Éq.VII. 15

Vu le paramétrage de la chaîne cinématique (§-VII.2), il importe de souligner que, pour un segment donné, l'interprétation des angles diffère selon qu'ils soient du côté droit ou gauche de l'athlète. En effet, en prenant l'exemple de la cuisse droite, une rotation positive autour de l'axe segmentaire Z traduit une flexion alors qu'elle traduit une extension dans le cas de la cuisse gauche. Cette opposition concerne aussi les mouvements d'abduction/adduction. Seule la rotation interne/externe peut être interprétée de la même manière pour les deux côtés du corps.