Chapitre 2
PROBLÈME DE RIEMANN
Dans ce chapitre, nous étudierons en détail le
système de lois de conservation (2.1)
ut+f(u) = 0 dans (0,8) x R
avec la condition initiale
(2.2) u (0, x) = u0 (x) = {
u si x < 0
u+ si x>0
Les quantitées u+ et u sont
respectivement l'état initial à droite et à
gauche du saut à l'origine.
D'une manière générale, la
condition initiale doit être constante par morceaux .
2.1 Ondes Simples
Ici, nous cherchons la solution de (2.1) sous la forme d'ondes
simples de la forme : (2.3) u (t, x) := v (w
(t, x)) (t > 0, x E R)
oùv:R?Rnetw:[0,8)xR?R
sontdesinconnues. En substituant (2.3) dans (2.1), on trouve :
(2.4) wtvÿ (w) + Df (v
(w)) v ÿ(w) w = 0.
Au vu de (1.14) du chapitre 1 avec A = Df,
(2.4) n'aurait de sens que si pour tout 1 <k < n, w
est solution de l'E.D.P
(2.5)
wt+ëk(v(w))w =0,
et v est solution de l'équation
différentielle
(2.6) vÿ(s)
=dk(v(s)).
Si (2.6) et (2.5) sont résolues, avec les conditions
initiales respectives v (0) = u0; u =
v (w ) et u+ = v
(w+), u est appelée une
k-onde simple.
Le point important ici est qu'on puisse
regarder (2.6) comme une équation
différentielle de la fonction vectorielle v et
interpréter (2.5) comme une loi de conservation scalaire
dew.
Question: Dans quelles circonstances pouvons-nous
utiliser les étappes (2.3)-(2.6) pour construire une solution continue
de (2.1)? Examinons en premier l'équation (2.6).
Définition 2.1. Soit u0 fixé
dansRn, on appelle ke- courbe de
raréfaction notée Rk (u0), la courbe
intégrale du champs de vecteur dk qui
passe par u0.
Soit donné la solution v de (2.6), retournant
à (2.5), réécrivant (2.5) sous la forme
wt + fk (w)x =
0
où
Z s
fk (s) = ëk (v
(t)) dt, (s E R)
0
ÿfk (s )
=ëk(v(s))
(2.7) ·fk (s) = Dëk
(v (s))vÿ (s) = Dëk
(v (s))dk (v
(s)).
D'après (2.7), la fonction fk sera strictement :
convexe si Dëk (v (u)) dk (v
(u)) > 0, (u E
Rn)
et concave si Dëk (v (u)) dk
(v (u)) < 0, (u E
Rn);
fk est linéaire si Dëk (v
(u)) dk (v (u)) = 0, (u E
Rn).
Définition 2.2. Le couple (ëk (u)
, dk(u)) est vraiment non-linéaire si : (2.8)
Dëk(v(u))dk(v(u))=60,
(uERn)
Définition 2.3. Le couple (ëk (u)
, dk (u)) est linéairement
dégénéré si : (2.9)
Dëk(v(u))dk(v(u))=0,
(uERn)
Notations
Si le couple (ëk (u0) , dk
(u0)) est vraiment non-linéaire, écrivant :
R+ k (u0) =
{uERk(u0) / ëk(u) >
ëk(u0)} et R- k (u0) =
{uERk(u0)
/ëk(u)<ëk(u0)}
Alors
Rk (u0) = R- k (u0) U
{u0} U R+ k (u0)
2.2 Ondes de raréfaction
Théorème 2.1. (Existence de la
ke-onde de raréfaction).On suppose pour un certain
k E {1....n} que :
(i) le couple (Àk (u) ,
dk(u)) soit vraiment non-linéaire.
(ii) u+ E R+ k (u
).
Alors il existe une solution faible continue u du
problème de Riemann (2.1)-(2.2) appelée k-onde simple, constante
le long du chemin traversant l'origine.
Preuve. 1- Supposant fk strictement convexe, la carte
s i-? Àk (v (s)) est strictement croissante .
Choisir w , w+ E R tels que u
= v (w ), u+ = v
(w+)
Supposons w <w+, considérant alors
le problème de Riemann
wt+fk(w)x = 0
½ w si x < 0
w(0,x) = w+ si x>0
La fonction
|
(2.10)
|
?
?
?
|
w si x <tÀk (u )
æ où Àk (v
((æ))) = x tsi tÀk
(u ) <x < tÀk (u+)
u+ si tÀk (u+)
<x
|
est solution faible continue appelée onde de
raréfaction joignant les états w et
w+.
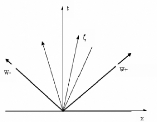
En effet, l'équation (2.5) est trivialement
satisfaite dans les secteurs x < tÀk (w ) ou x
> tÀk (u+) dès que wt
= wx = 0.
Par la suite, on voudrait relier les deux valeurs de w
entre x < tÀk (u ) et x > tÀk
(u+)
par la fonction la plus simple possible. On
aurait donc w (t, x) = ç
(x ) qui dans (2.5)
t
entraine
x
-
t2
x ) ( ( x )))
(x )
çÿ + 1 t Àk v ç
çÿ =0;
t t t
et en posant æ = x t E]Àk
(u ) , Àk (u+) [, on a
bien
(Àk(v(ç
(æ))) ? æ)
çÿ (æ) =0.
En supposant
öÿ =6 0, alors
(w+) [, Àk (y (ö
(æ))) = æ.
Væ E]Àk (w )
, Àk
Ainsi u (t, x) = y (w (t,
x)) où y est la solution de l'équation
différentielle (2.6) qui passe par u est une
solution faible continue par morceaux de (2.1)-(2.2).
Le cas w > w+ est traité
similairement pour fk concave .
| 


