CHAPITRE V :
Application en finance
0. Introduction:
Une option est un produit financier qui donne le droit
à son acheteur d'effectuer une opération portant sur un
sous-jacent (qui peut être une action, une obligation, une cargaison de
pétrole) avant la date d'échéance.
1. Modèle du prix de l'actif:
La théorie des modèles de Black et scholes pour un
actif est un processus stochastique (EDS):
dS = jiS~dt + aS~dW~

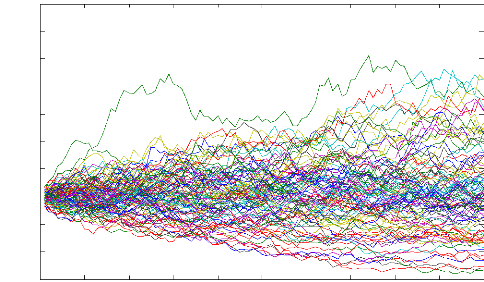
La figure (Fig1) illustre ces échantillons d'un actif,
avec it = 0.1 et 0- = 0.3.
A la date d'échéance t = T, le prix de l'actif est
une variable aléatoire donné par la
densité :
exp (--(~o9(x /S0 ) -- (1 -- 0-2/
2 )T)2)
20-2T
f (x) = ' , pour x > 0
x0-V 2n-T
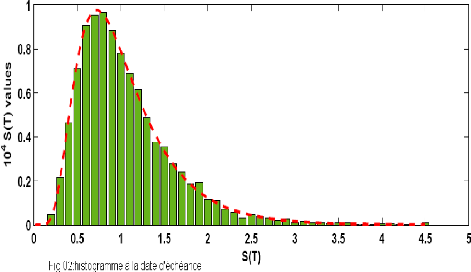
avec f(x) = 0 pour x 0, pour confirmer on donne la figure
(Fig.02), qui illustre l'histogramme où on prend la
valeur finale de l'actif S(T) pour 104 échantillons, et
la courbe présente la densité f(x).
at)
2.4
2.2
0.8
0.6
0.4
1.8
1.6
1.4
1.2
2
1
0 10 20 30 40 50 60 70 80 90 t 100
Fig.01:100 trajectoire d'un actif

0. Formule de Black et Scholes :
La formule de Black-Scholes permet de calculer la valeur
théorique d'une option à partir des cinq données suivantes
:
· St: la valeur actuelle de l'action sous-jacente.
· t : le temps qui reste à l'option avant son
échéance T.
· K: le prix d'exercice fixé par l'option.
· r : le taux d'intérêt sans risque.
· a : la volatilité du prix de l'action.
Le prix théorique d'une option d'achat (call),
qui donne le droit mais pas l'obligation d'acheter l'actif S à la valeur
K à la date T, est caractérisé par son payoff
:
(ST -- K)+ = max(ST -- K; 0)
Le prix de l'option est donné par l'espérance sous
probabilité risque neutre du payoff terminal
actualisé :
C = E( payo f f X e-rT)
De plus, pour employer le modèle du prix de l'actif,
Black et scholes imposent un nombre de supposition de
simplification aux options de marché, alors ils utilisent la
formule suivante pour les valeurs de l'option européenne au
temps t et le prix d'actif S :
C(S, t) = S.Ar(di) -- Ke-r(T-~).Ar(d2)
où
1
log(S/K)+ (r + 2 o-2)(T -- t)
di =
et .Ar(.) est une fonction de la distribution de loi normale
.Ar(0.1) :
|
.Ar(x) =
|
1 r s2
e- 2 ds
112n-
|
Le paramètre r dans la formule est le taux
d'intérêt. Si le prix d'actif aujourd'hui (temps
zéro) est So la valeur de black et scholes call option est C(So, 0).
Le programme (PROG2) fourni une fonction qui donne la valeur
de l'option à la date t et le prix de l'actif S.
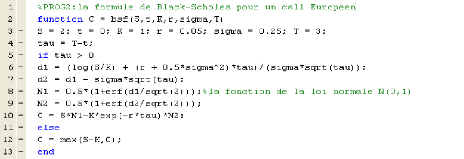
Il donne la valeur de call C = 1.1447 pour t = 0, quand on change
les valeurs de t on obtient autres valeurs de call par exemple :
t = 1 --> C = 1.0972 ; t = 1.5 --> C = 1.0731 .....
a. La méthode de Monte Carlo :
Une propriété plus utilisée pour obtenir
la valeur de l'option de Black et Scholes est d'estimer la moyenne de payoff,
sous la condition de risque it = r, autrement dit, nous pouvons reproduire la
valeur de l'option par fixer it = r dans le modèle de l'actif et
computer la moyenne de payoff de tous les trajectoires de l'actif, dans la
pratique, ceci peut être faire par la simulation de Monte Carlo (moyenner
le payoff sur un grand nombre des trajectoires de l'actif). Pour le call
européen on a seulement besoin de connaitre le prix de l'actif à
l'échéance, ainsi on peut prendre At = T à chaque
échantillon, et on donne le programme (PROG3) :

Ici, Pi est le payoff du ieme trajectoire de
l'actif. La moyenne totale Pmoy est l'estimation de Monte Carlo de
la valeur de l'option. La variance P~ar est utilisée pour donner
l'intervalle de confiance à 95% suivant :
[Pmoy -- 1.96 X Pvar/M ; Pmoy +
1.96 X Pvar/M] Après l'exécution on trouve :
Pmoy = 1.1453 avec l'intervalle de confiance
égal [1.1435 ; 1.1471]
On rappelle qu'on a trouvé avec ces paramètres
dans la première méthode que C = 1.1447 est approché
à la valeur trouvée dans la deuxième méthode. La
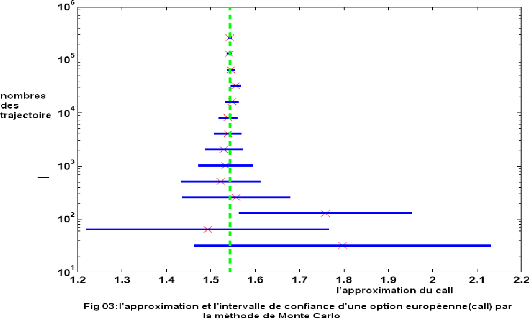
figure (Fig03) montre comment l'approximation de la méthode de Monte
Carlo varie avec le nombre d'échantillon M, ici on prend S = 10, K = 9,r
= 0.06, a = 0.1 et T = 1, les croix dans la figure représentent
l'approximation de Monte Carlo et les lignes horizontales représentent
l'intervalle de confiance de cette approximation, la valeur de Black et Scholes
est représenté par la ligne verticale discontinu.
b. La méthode Binomiale :
On commence par simplifier le modèle du prix de
l'actif, on discrétise l'intervalle de temps de façon
équidistante 0 = to < ti <
·
·
· <
tM = T avec ti. = iAt. Donnons le prix de l'actif au temps
zéro to, on pose que le prix de l'actif au temps ti
fait un mouvement vers le bas avec dS0 ou un mouvement vers le
haut avec uSo, où d < 1 et u > 1, alors au temps t2 les
mêmes mouvements bas/haut sont faits avec les trois possibilités
d2S0, duS0 ou u2S0, et on continue cette restriction, au
temps ti = iLt on obtient i + 1 possibilités donné par :
Sni = di-nunSo, 0 < n < M.
A la date d'échéance ti = tm = T, il y a M + 1
possibilités du prix de l'actif
fSnm}nm _o. Soit f
Cninm_ 0 correspond aux payoffs à la
date d'échéance pour une option d'un call européen, nous
savons que:
Cnm = max(Snm -- K,
0) , 0 < n < M
La méthode binomiale procède par une marche
arrière sur l'intervalle de temps. La valeur de l'option Ct, correspond
au prix de l'actif Sn à la date ti est déterminée comme la
moyenne de deux prix d'actif Sni+1 et SI+i au temps
ti+1. La formule est :
Cni =
e-rAt(p.q++11 + (1 --
p)Sni+1 ) , 0 < n < i , 0 < i < M -- 1
Le paramètre p est considéré comme la
probabilité d'un mouvement vers le haut du prix de l'actif, cette
formule permet de marcher en arrière vers le temps zéro et
déterminer la valeur de l'option C8. Il faut choisit les
paramètres de la méthode telle que le modèle binomial de
l'actif s'accorde avec la version de Black et Scholes quand At --> 0. Une
fois At soit fixé, on aboutit à deux équation pour les
trois paramètres restants, et par conséquence plusieurs
possibilités des solutions, le choix par exemple est :
erAt --d
d = A -- 11A2 -- 1 , u = A + 11242 -- 1 , p
= u --d ,
où A = 2 1 ( e-rAt -- e(r+0-2)At). k
Le programme (PROG4) donne la valeur de l'option par la
méthode binomiale, avec les mêmes paramètres
utilisés dans les méthodes précédentes, la valeur
approximative de l'option W = 1.1448 s'accorde avec la valeur de Black et
Scholes C = 1.1447 .

c. EDP de Black et Scholes :
La formule de Black et Scholes pour la valeur d'une option
européenne (call) intervient comme la solution d'une équation aux
dérivées partielles (EDP). L'EDP est d'une forme parabolique avec
les conditions de Dirichlet, soit x = T -- t la marche temps vers la date
d'échéance, alors l'EDP prend la forme suivante:
2aC 1 a C as a-2S2 rrS + C = 0
(5.1)

ax 2 aS2 as
avec condition initiale :
C(S, 0) = max(S(0) -- K, 0)
et conditions aux limites :
C(0,x) = 0 , C(S, x ) r-r, S -- Ke' , pour S
grand
dans l'intervalle S > 0 et 0 < x < T.
On suit la même procédure du chapitre IV, pour
résoudre cette EDP par les deux méthodes (différences
finies et probabiliste) :

i. Différences finies pour l'EDP de Black et
Scholes :
On subdivise l'intervalle de S , 0 S L, et on utilise le maillage
de différences
finies {jh, ik} avec les pas h = L/NS et k =
T7Nt, la méthode explicite nous permet d'écrire
l'équation (5.1) par :
|
V.i+1 -- Vi J J
k
|
1 (Vi 1 --2VJi + V )
Vi -- Vi a2(jh)2 J+ -1-- r(jh) J+1
J1 + rVi = 0
2
h2 h J
|
Avec VJi r-r, C(jh,ik)
où par la formule matricielle :
yi+1 = Fyi + pi, pour 0 i Nt -- 1,
où F E IR(Ns-1)x(Ns-1) est tridiagonale et pi E
1(Ns-1) est déterminé par les conditions aux
limites.
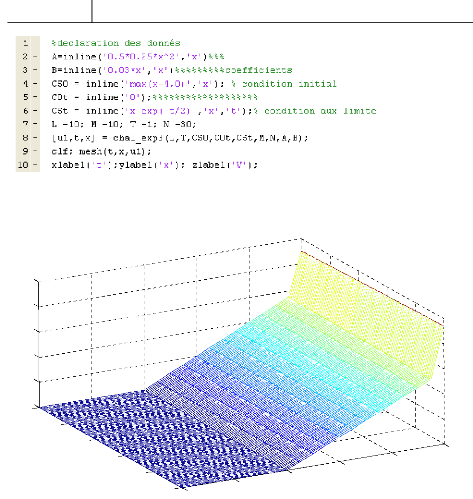
Le programme (PROG5) donne les valeurs de call V à la date
t et au prix S, avec les paramètres T = 1, L = 10, K = 4,r = 0.03, a =
0.5.


Application en finance
Chapitre V
10
0.6
6
0.8
4
0.4
t
8
S
La figure (Fig.4) illustre le résultat de ce programme
:
10
8
6
4
2
0
0
0.2
XS t)
1 2
0
Fig.04:valeurs d'une option européenne(call) par
la méthode des différences finies
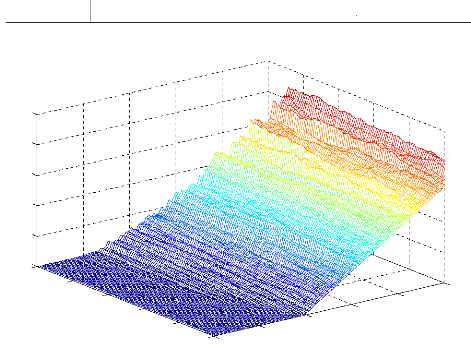
ii. Méthode probabiliste l'EDP de Black et Scholes
:
L'interprétation probabiliste de l'EDP de Black et
Scholes peut donner la valeur de l'option avec les mêmes
paramètres précédents, le programme (PROG6) fait cette
interprétation. On donne premièrement le processus sous-jacent
:
t t
S(t) = So + f rS(s)ds + f o-S(s)dWs
o o
et la solution sera :

C(S, t) = E((S(t) -- K, 0)+exp (r(7' -- t))) Les
valeurs sont données dans la figure (Fig.05):
Application en finance
Chapitre V
0
0
10
8
6
4
2
0
1
C(S,t)
0.8
10
0.6
t
S
8
0.4
6
0.2
4
2
Fig.05:valeurs d'une option européenne (call) par
la méthode probabiliste
conclusion
| 


