Ouverture, capital humain et croissance économique dans la zone MENA (Middle East and North Africa)

1.3. Le modèle de Solow avec capital humain

Dans les contributions de Mankiw, Romer et Weil [1992] et l'annexe mathématique de Barro et Sala-i-Martin [1995], l'étude est faite sur le «modèle de Solow amélioré ⁵» et ses implications pour le taux de croissance à long terme ainsi l'hypothèse de convergence.

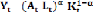
Soit la fonction de production, qui était représenté par le modèle néoclassique de Solow, = où la technologie croit au taux (x) et la population au taux (n),

le stock se déprécie au taux constant (ä). Le taux d'épargne, (s), est aussi.

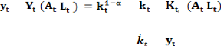
Si on définie toutes les « unités d'efficience du travail» ⁶

On obtient, donc, = / et = / (I -6)

La contrainte budgétaire de l'économie est : =s -(g+ n + ä) dont g est le taux

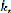
de croissance de progrès technique. A d'état régulier (stationnaire), =0 implique

= ( Et (

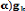
Le taux de croissance de la production par tète est proportionnel à celui du stock de capital par tète,

g_y = (1- (I-7)

Ainsi, l'expression de taux de croissance de la production par tète s'écrie :

4 Jean-Pierre Cling (2006) « Commerce, croissance, pauvreté et inégalité dans les PED : une revue de littérature » p.p(5-12)

⁵ P.Aghion et P.Howtt (1998) « théorie de la croissance endogène »p .p.(47-49)

6- P.Aghion et P.Howtt (1998) « théorie de la croissance endogène »p .p. (554 - 556)

/ = (1 - )(g +n+ ( -1) (I-8)

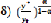
Pour déterminer la vitesse de convergence vers l'état, en tenant compte de l'augmentation de taux de croissance d'une économie en considération, on calcule, au début, le log- linéaire de taux de croissance, puis on applique le développement limité d'ordre 1, on

obtient alors L'équation suivante ; = (g+n+ ) (log - ) (I-9)

La vitesse de convergence, avec la quelle le revenu tend vers la stationnarité, donnée par = (g+n+ ). Le coefficient de convergence est égale à la modification

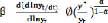
(1-10)

proportionnelle du taux de croissance sous le changement du niveau de revenu, d'où le coefficient = =

L'équation différentielle (I-9) implique

log =(1- )log + log (I-11)

La convergence apparait conditionnelle puisque elle dépend de l'état stationnaire de l'économie considéré, ce n'est que si les paramètre qui déterminent l'état régulier sont identiques que l'équation (1-9) implique que les pays pauvres ont une croissance plus fort que les pays riches .

On définie toutes les unités d'efficiences de nouveau tel que la production est exprimée en fonction de capital humain qui s'écrit sous la forme suivante :

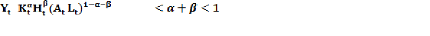
= où 0

(I-12)

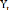
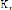
Avec : l'output réel, : le capital physique, : le stock de capital humain et :le

travail brut . Ainsi, la fonction de production par tète est :

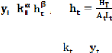
(I-13)

= où

Les équations et gouvernant l'accumulation de capital physique et capital humain

sont respectivement :

(I-14)

= - (g+n+ ) et - (g+n+ )

L'équation (I-14) présente l'état d'équilibre décrivant la démarche de l'équation fondamentale de Solow pour le capital physique, analogiquement pour le capital humain.

Si on divise par k la première équation et par h la seconde , on déduit alors que les valeurs d'état régulier du capital humain et physique dont l'apparition de la croissance à taux constant qui implique la croissance par unité d'efficience du travail nulle ,et donc la décroissance des rendements cumulés des deux facteurs h et k ;

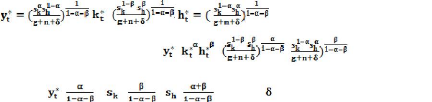
Alors, Ln = ln + ln + ln (n+ g+ ) (I-15)

En linéarisant par le log on aura : = =

,

=

,

(

La modification de notions de facteurs de production, toute en mettant en lumière le rôle de progrès technique, et l'interdépendance internationale économique expliquent l'amélioration de croissance mondiale.

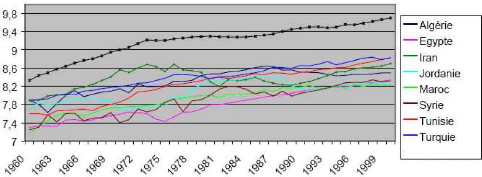
Graphique 1 : Evolution de PIB par tète⁷

Au totale et d'une manière simplificatrice, La croissance mondiale sur très longue période passe par quatre grandes périodes :

· Pendant la deuxième décennie de 20^ème siècle (1914) : PIB / tête mondial est de1000 $ / tète.

· Durant 2000: cet inducteur passe à 6500 $ / tète.

7Dr Mme GUETAT Iméne (2005) « la convergence des revenus des pays M.E.N.A vers sud européenne » p.p.7-14

· Au 20^ème siècle, des périodes de forte croissance interrompues par les guerres et des d'autres catastrophes.

· Entre 1960 et 1985, le taux de croissance moyen de la région M.E.N.A s'est situé à 3.7% par an ⁸Ce taux est inférieur à celui obtenu par l'Asie (4.3%), mais supérieur à celui de l'Amérique latine (1.6%).