Chapitre1 : Equations générales
1.1 Définition du problème:
On considère un écoulement
instationnaire et bidimensionnel d'un fluide visqueux et incompressible dans
une cavité carrée. L'écoulement est engendré sous
l'influence de la viscosité par le mouvement de la paroi
supérieure qui est animée d'une vitesse de translation uniforme,
les autres parois étant immobiles. On a pris comme vitesse de
référence la vitesse de translation de la paroi en mouvement et
comme longueur de référence celle d'un coté.
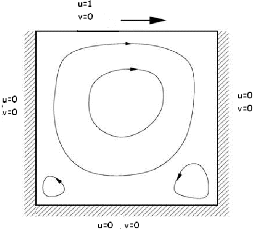
Fig. (1.1) : cavité carrée
entrainée
Un fluide emplit un carré. En chaque point du
carré, la vitesse du fluide est V = (u, v). Le fluide est mis en
mouvement par le déplacement vers la droite de la paroi
supérieure. Les trois autres parois (gauche, droite et
inférieure) sont fixes. Le fluide adhère aux parois. Un
tourbillon central prend naissance puis se stabilise ou oscille en fonction de
la viscosité.
Pour étudier cet écoulement, on se base sur
les équations complètes de Navier-stokes.
1.2 Les équations de base:
1.2.1 Les équations de Navier-stokes
Les équations de Navier-Stokes s'obtiennent en
appliquant le principe fondamental de la dynamique, le principe de conservation
de la masse au mouvement du fluide. Elles se présentent sous la forme
d'un système d'équations aux dérivées partielles
non-linéaire.[1]
001
dV
P .~ ~ 2
3 456.
000000001
P 7 V-T (1.1)
Dans l'hypothèse d'un fluide newtonien,
hypothèse correspondant au comportement de la plupart des liquides et
gaz usuels nous avons les éléments du tenseur des contraintes qui
sont donnés par:
iii = XEkk6ii 7 4E4 (1.2)
Avec:
iii: Éléments du tenseur de
contrainte
Eii: Éléments du tenseur de
déformation
t et A: Coefficients de Poisson caractérisant les
propriétés visqueuses des fluides. Ils représentent
respectivement la viscosité de cisaillement et la viscosité de
dilatation.
Les éléments du tenseur de
déformation sont donnés par :
|
:)* ~
|
(1.3)
; >?~)
= 7 ?~* @
?~* ?~)
|
En reportant ces expressions dans l'équation
(1.1), on obtient:
P .~ ~ 2
3 456.
~ 7 ~~/ 7 9 7 ~456.000000001
divV (1.4)
it et A Vérifient l'équation suivante
:
3A 7 21.1. = 0 (1.5)
En l'absence de forces extérieures, lorsque le
fluide est incompressible l'équation (1.4) devient :
dV
(1.6)
P dt ~ 3456.
000000001 7
~/01
En explicitant la dérivée particulaire
à gauche, c'est-à-dire :
dV
=
dt
aVi_,
at
+ (V. v). V (1.7)
On obtient alors l'équation de Navier-stokes pour
un fluide incompressible:
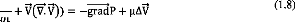
p(OV
a
t
Avec :
p: La masse volumique
u : la viscosité dynamique du fluide
V_1(u, v): Le champ de vitesse du fluide P: la pression
local
1.2.2 L'équation de continuité:
La masse m d'un domaine fluide quelconque D, que l'on
suit au cours du temps reste constante :
dm
dt
= 0 (1.9)
En explicitant la dérivée particulaire de
m, on obtient l'équation globale de conservation de la masse
:
|
dm
dt
|
= Ill p dV = Ill(
|
|
at + div(pV)) dV = 0 (1.10)
|
Cette équation devant être
vérifiée pour tout domaine D, le théorème de
l'intégrale nulle permet d'obtenir l'équation locale de
conservation de la masse dite équation de continuité
:
Op
+ div(pV_1) = 0
(1.11)
at
Si le fluide est incompressible : p = pa
div(V_1) = 0 (1.12)
p à
= 0
Si l'écoulement est stationnaire :
at
div(pV) = pdiv(V) + grad(pV) = 0 (1.13)
+ V(0 V)) = --gradP + u0V(1.8)
La conservation de la masse d'un fluide en mouvement, de
masse volumique p et de champ de vitesse V(M ,t) est traduite par
l'équation locale.
0 p (1.14)
at
7 div(pV) = 0
Les deux équations (1.8) et (1.12)
définissent le système à résoudre (1.15 et 1.16)
suivant :
7 u 7 v =3 V2u
{au au au 1 OP t
at Ox Oy p Ox p
Ov Ov Ov 1 OP [t 2
ay =
at
7 u
Ox
7 v
P
(1.15)
ay7 V v P
Nous avons donc trois équations et trois inconnues
u ,v ,p considérées comme fonctions de x, y ,t . Cette forme des
équations est dite forme dimensionnelle.
La détermination physique du problème
c'est-à-dire l'intégration des équations pour la
détermination des inconnues u, v et p nécessite en outre la
connaissance des conditions initiales et des conditions aux
limites.
| 


