Université de Tunis
Institut Supérieur de l'Education et de la
Formation Continue
Mémoire de mastère en didactique des
mathématiques :
Les émergents spontanés d'une analyse
praxéologique :
Activités du chapitre
« Initiations aux graphes » du manuel scolaire de
mathématiques de troisième année économie et
gestion (EG) comme modèle.
Présenté par : Abderrazak CHAOUACHI
Sous la direction de : Hanène ABROUGUI
HATTAB
Soutenu le 11- 03- 2009 devant le jury composé
de :
Hikma SMIDA : Présidente.
Imed BEN KILANI : Membre.
Hanène ABROUGUI HATTAB: Membre.
Remerciements
Ce travail ne serait pas réalisé
s'il ne tient qu'à mes propres mérites. Je le dois, certainement,
aux personnes qui ont plus de mérite que moi.
Je tiens à
remercier :
· Madame Hanène ABROUGUI HATTAB qui
m'a formé lorsque j'étais élève-inspecteur et puis
en tant qu'étudiant en mastère. Elle a eu la gentillesse de
m'encadrer sur un sujet délicat et très
exigeant.
· La professeure Hikma SMIDA et pour m'avoir
aidé à structurer et approfondir mes connaissances dans le
domaine de la théorie des graphes.
· Monsieur Faouzi BEN CHARRAD, enseignant au
département informatique à la faculté des sciences de
Tunis, pour avoir généreusement consacré plusieurs
journées à m'expliquer certains concepts et algorithmes de la
théorie des graphes.
· Tous les enseignants de l'ISEFC sans
exception.
J'adresse mes remerciements au jury pour avoir
accepté la lourde charge de poser un regard critique sur son
contenu.
Mes remerciements s'adressent
à :
· Hikma SMIDA pour avoir accepté de
présider le jury.
· Monsieur Imed BEN KILANI pour avoir
accepté d'être membre du jury.
Je ne peux passer sous silence le soutien de ma
famille et de mes amis.
Je les remercie de tout mon
coeur.
Sommaire
Chapitre I : Introduction et
problématique
5
I-1. Pourquoi la théorie des
graphes ?
6
I-2. Motivations de la recherche
7
I-3. Problématique et questions de
recherche
9
I-4. Hypothèses de recherche
10
I-5. Outil de recherche
10
I-6. Présentation du mémoire de
recherche
10
Chapitre II : Cadre théorique
14
II-1. Aperçu historique
14
II-2. Présentation de la théorie des
graphes
16
II-3. Cadre théorique didactique
40
II-3.1. Transposition didactique
40
II-3.2. Notions fondamentales
43
Objet, Rapports personnels
43
Personne et individu
43
Institution, rapports institutionnels,
assujettissements
44
II-3.3. Organisation praxéologique
45
Parti pris
épistémologique
45
La notion de praxéologie
ponctuelle
45
Tâche routinière, tâche
problématique, routinisation et naturalisation
46
Praxéologie locale, praxéologie
régionale
47
Ostensifs, non ostensifs
48
II-4. Méthodologie de recherche
53
Chapitre III : Partie analytique
57
III-1. Analyse transpositive
57
III-2. Itinéraire curriculaire et profil
d'un élève de troisième année EG
63
III-3. Organisation du manuel scolaire officiel et
description du chapitre
65
III-3.1.Organisation du manuel
scolaire
65
III-3.2.Description du chapitre
« Initiations aux graphes »
67
III-4. Analyse praxéologique des
activités du chapitre « Initiation aux graphes »
72
III-4.1.Analyse des activités par le
modèle des quatre T
75
III-4.2.Synthèse des commentaires sur
les praxéologies présentées
125
Synthèse des blocs pratico-
techniques
125
Synthèse des blocs
technologico- théoriques
130
Chapitre IV : Conclusions
135
Bibliographie :
139
Annexes
141
Chapitre I :
Introduction et problématique
Chapitre I : Introduction et
problématique
I-1. Pourquoi la théorie des graphes ?
Au moins cinq raisons nous ont amené à choisir
comme objet de recherche la partie des curricula scolaires du cycle secondaire
consacrée à la théorie des graphes :
a) La théorie des graphes est un objet
d'enseignement très récent
La théorie des graphes a été introduite
pour la première fois dans le curriculum scolaire tunisien au
début de l'année scolaire 2006-2007. Il s'agit, en fait, d'une
initiation à cette théorie destinée aux
élèves de troisième année de la section
« économie et gestion (EG) » et qui va se poursuivre
en quatrième année (classe de terminale). Cette théorie
n'est introduite pour la section « techniques
informatiques » qu'en classe terminale et ne fait pas partie des
curricula des autres sections.
b) La théorie des graphes illustre la nouvelle
approche de l'enseignement
Cette théorie illustre l'esprit innovateur de la
réforme 2003 et constitue, par excellence, un choix en phase avec
l'esprit du nouveau curriculum scolaire. En effet, dans la loi d'orientation de
l'éducation et de l'enseignement secondaire de 2003, l'article 51 (titre
I, page 23) stipule que « Les mathématiques et les
sciences sont enseignés dans le but de permettre aux
élèves de maîtriser les différentes formes de
pensée scientifique, de les exercer à l'usage des modes de
raisonnement et d'argumentation, de les doter des compétences de
résolution des problèmes et l'interprétation des
phénomènes naturels et les faits humains ». En
outre, cette unité d'apprentissage permet :
- de résoudre efficacement des problèmes
pratiques ou récréatifs en les modélisant par des
schémas qui se dessinent à l'aide de points et de liaisons entre
ces points.
- de sortir l'élève des activités
mathématiques classiques relevant de la géométrie, des
calculs algébriques, des études de fonctions et de
l'arithmétique.
En plus, elle ouvre un champ d'action pour la
modélisation de situations se rapportant à des domaines
très divers tels que :
- La gestion des ressources humaines : formation des
groupes de travail, gestion des conflits et organisation des séquences
de production.
- Les flots de transport : optimisation des flux de
transports routiers, minimisation des distances d'itinéraires.
- Les sciences informatiques, notamment en ce qui concerne la
conception d'algorithmes de calculs et de procédures.
- Etc.
c) La théorie des graphes n'est pas
enseignée dans les institutions universitaires tunisiennes qui forment
les enseignants de mathématique
La théorie des graphes ne
fait pas partie du cursus universitaire de ceux qui sont qui sont
destinés à enseigner les mathématiques dans les
lycées et les collèges tunisiens. En
plus, rares sont les universitaires de la communauté des
mathématiciens en Tunisie qui ont investi une partie de leurs recherches
dans le domaine de la théorie des graphes considéré par
certains comme « des mathématiques non pures » et
par d'autres comme un sous produit du domaine des recherches
opérationnelles.
d) La théorie des graphes n'a pas fait l'objet
d'une présentation exploitable dans le programme officiel de
mathématique de troisième année économie et
gestion
Le programme officiel de mathématique de
troisième année économie et gestion place le chapitre
« Initiation aux graphes » dans le domaine de
l'algèbre et ne lui consacre qu'un peu plus d'une ligne. En plus, on ne
trouve pas un document d'accompagnement qui permet de pallier à ce
manque d'explicitation.
e) L'enseignant ne dispose que du manuel scolaire pour
échafauder ses leçons
En l'absence de données explicites sur le chapitre
« Initiation aux graphes » et du document d'accompagnement,
l'enseignant est mis dans l'obligation de tirer toutes les informations
concernant les intentions non écrites du programme officiel du seul
document disponible à savoir : le manuel scolaire. Il s'agit, donc,
d'une situation assez inhabituelle pour être considérée
comme très rare et qui peut ne plus se présenter à
l'avenir. Nous considérons cette situation est une chance
inespérée pour pouvoir mener une recherche sur des
activités en ne nous rapportant qu'aux tâches inscrites, à
la nature de chaque question et surtout aux concepts
institutionnalisés.
I-2. Motivations de la recherche
Le système scolaire tunisien s'appuie, en ce qui
concerne les références de l'enseignement des matières,
sur un manuel scolaire unique censé être utilisé par
l'enseignant et par l'élève au cours de l'année scolaire.
En général, au cours d'une leçon, l'enseignant demande
aux élèves de travailler sur une activité, sur un exercice
ou sur un problème qui figure dans le manuel. Les occasions sont assez
rares où l'on observe, dans une classe, se dérouler une
activité qui n'est pas consignée dans le manuel officiel. Il est,
donc, clair que le manuel scolaire est une pièce maîtresse dans
l'acte d'enseignement -apprentissage dans tous les établissements
scolaires tunisiens et conditionne, alors, la qualité de cet
enseignement.
Le manuel scolaire de mathématique de troisième
année économie et gestion est l'oeuvre d'un groupe formé
d'un inspecteur principal, de deux inspecteurs et de deux enseignants. Il a
été évalué par deux inspecteurs principaux. Ce
groupe est devenu, forcément, vu les statuts de ceux qui le composent,
l'institution transpositive et le manuel scolaire produit par cette institution
est forcément la seule source officielle. Car, il n'y a aucune autre
source officielle concernant le chapitre « Initiation aux
graphes », à laquelle il faut se référer et qui
trace les contours du savoir à enseigner de manière explicite. Il
est donc de la plus haute importance d'analyser le contenu du chapitre
« Initiation aux graphes », surtout que l'institution
transpositive n'a pas pris la peine d'indiquer, au début de chaque
chapitre, les objectifs visés ; comme cela se faisait dans les
manuels d'avant la dernière réforme. En plus, il n'y a aucun
document officiel (programme officiel, document d'accompagnement) permettant
une lecture exploitable par l'enseignant ou par le chercheur des intentions
réelles du programme concernant la théorie des graphes.
Ce n'est pas uniquement cet aspect qui est notre principale
motivation.
L'analyse praxéologique en Théorie
Anthropologique du Didactique permet de mettre en relief les structures des
tâches, notamment les techniques mises en oeuvre, les technologies qui
les justifient et les théories auxquelles elles se
réfèrent. Nous nous sommes donc intéressés à
ce qui pourrait émerger d'une analyse praxéologique des
activités du chapitre « Initiation aux graphes »
réalisée en s'appuyant uniquement sur les outils de la
Théorie Anthropologique du Didactique, à savoir : la
transposition didactique, les notions fondamentales, l'organisation
mathématique et surtout la dichotomie fondamentale. L'espoir est que
l'on dispose de suffisamment d'émergents pour pouvoir établir un
rapport personnel de l'individu x dans la position p=
« chercheur » à l'objet o= « chapitre
initiation aux graphes » conforme au rapport institutionnel
Rp(x,I) dans l'institution I= « Programme officiel de
mathématique de troisième année économie et
gestion, chapitre : Initiation aux graphes ». D'un autre
côté, le chapitre « Initiation aux graphes »
est conçu par ses auteurs selon les nouvelles orientations de curricula
scolaires qui mettent l'élève au centre de tout acte
pédagogique. Dans cette perspective, les activités d'approche
doivent être présentées pour mettre l'élève
dans des situations où il doit accomplir des tâches pour
lesquelles il ne dispose d'aucune technique et ainsi lui fournir l'occasion de
se comporter comme un mathématicien en quête d'une
découverte importante. Le plus important dans tout cela est que nous
nous intéressons à un chapitre qui, suite à un survol de
toutes ses activités, nous semble assez fourni en tâches sans
technique connues des élèves.
Ce double constat nous a amené à la
problématique suivante.
I-3. Problématique et questions de recherche
Dans le contexte présenté ci-dessus, un certain
nombre de questions émergent à propos de l'analyse
praxéologique du chapitre « Initiation aux
graphes » du manuel scolaire de troisième année
économie et gestion :
· Quel est le lien organique entre le savoir
savant et le savoir à enseigner présenté dans le chapitre
« Initiation aux graphes » du manuel scolaire ? Quelle
est la typologie des activités de ce chapitre ? Quelle place est
réservée aux activités pour lesquelles il n'y a pas de
technique connue à l'avance par l'élève dans
l'ensemble des activités du chapitre?
· Quelles sont les techniques à
institutionnaliser dans ce chapitre ? A quels ostensifs le chapitre fait
appel pour le bloc pratico technique ? et à quels non ostensifs ces
ostensifs se rapportent ? A quelles technologies les activités du
chapitre « Initiation aux graphes » font appel ? A
quelles théories ce chapitre fait référence?
En somme, le motif principal de notre recherche est :
· L'analyse praxéologique en
Théorie Anthropologique du Didactique (TAD) permet-elle de
répondre spontanément à toutes ces
questions dans le cas de manque d'informations sur les prétentions
du programme officiel?
Rappelons que nous sommes dans une configuration assez
inhabituelle où l'on dispose ni de programme officiel exploitable ni
d'un document d'accompagnement pouvant nous éclairer sur les
praxéologies ciblées. On est amené, donc, à faire
notre analyse praxéologique « à l'aveugle »,
c'est-à-dire sans aucune possibilité de nous rapporter aux deux
documents précédents. Cela est contraire à l'usage qui
veut que l'on se réfère systématiquement au programme
officiel à chaque fois où l'on est dans une situation de choix
des techniques à utiliser. Nous sommes, donc, dans un cas où il
n'y a aucun autre document qui pourrait orienter les choix des techniques
à l'exception de la nature de chaque tâche et de chaque
activité du manuel scolaire officiel unique.
En d'autres termes, la question principale à laquelle
notre travail de recherche essaiera de répondre est :
· Quels sont les émergents
spontanés d'une analyse praxéologique des
activités du chapitre « Initiation aux
graphes » ?
I-4. Hypothèses de
recherche
Ce questionnement nous amène à situer notre
travail de recherche par rapport à l'hypothèse suivante :
H0 : L'analyse praxéologique
des activités du chapitre « Initiations aux graphes» du
manuel scolaire unique de troisième année économie et
gestion permet au sujet x dans la position p= « Celui qui fait
l'analyse praxéologique à l'aveugle» d'avoir, avec
l'objet o= « Chapitre : Initiation aux graphes »
dans l'institution I= « Programme officiel de mathématique de
troisième année économie et gestion. », un
rapport personnel, concernant les émergents de l'analyse (la
typologie des activités, les techniques mobilisées, les
différents ostensifs et non ostensifs), pouvant être
utilisé comme support pour remonter au programme officiel.
I-5. Outil de recherche
L'outil de notre recherche est l'ensemble des activités
du chapitre « Initiation aux graphes » du manuel scolaire
de mathématique de troisième année économie et
gestion (EG).
I-6. Présentation du mémoire de recherche
Nous avons organisé notre mémoire de recherche
en trois chapitres :
v Chapitre II : Cadre
théorique
Ce chapitre est composé de quatre parties :
Aperçu historique, présentation de la théorie des graphes,
le cadre théorique didactique et la méthodologie de recherche.
· Aperçu historique : Dans
cette partie nous exposons, en première partie et assez
brièvement, le chemin suivi par la théorie des graphes depuis
EULER en 1736 et son célèbre problème des sept ponts de
Königsberg jusqu'au traité de Claude
BERGE « Théorie des graphes et ses
applications » publié en 1958. On notera que la théorie
des graphes a atteint un tel développement qu'elle est
considérée, depuis les années 1960, comme un domaine
à part entière des mathématiques.
· Présentation de la théorie des
graphes : Cette partie est consacrée à la
présentation des éléments de la théorie des graphes
en rapport direct avec les connaissances du chapitre « Initiation aux
graphes » du manuel scolaire de mathématique de
troisième année économie et gestion.
· Cadre théorique didactique :
Le travail de recherche que nous avons mené s'inscrit dans le
cadre de la Théorie Anthropologique du Didactique d'Yves Chevallard.
Nous avons présenté, dans cette partie, les principaux concepts
et outils proposés par cette théorie et que nous avons
utilisés dans notre travail de recherche, notamment : la
transposition didactique, rapport personnel et rapport institutionnel,
organisation mathématique, praxéologie locale et
praxéologie régionale, tâche routinière, tâche
problématique, naturalisation, pénurie praxéologique,
ostensifs, non ostensifs, épaisseur ostensive et registres ostensifs.
· Méthodologie de la recherche :
Cette partie est consacrée à la démarche suivie
dans notre recherche. Il s'agit, d'abord, de préparer le terrain pour
une bonne appréhension du travail de recherche sur les organisations
mathématiques des tâches sollicitées dans les
différentes activités du chapitre « Initiation aux
graphes ». Cette préparation concerne : le profil de
l'élève de troisième année économie et
gestion, la transposition didactique externe et l'organisation du chapitre dans
le livre scolaire. Par la suite, nous procéderons à l'analyse
praxéologique, objet de notre travail de recherche.
v Chapitre III : Partie analytique.
Dans cette partie, qui représente le coeur de notre
travail de recherche, nous avons décrit les principaux
résultats :
· Analyse transpositive : Cette
partie est consacrée à l'étude de la transposition
didactique externe selon notre lecture des activités
présentées et les titres des paragraphes du chapitre
« Initiation aux graphes ».
· Itinéraire curriculaire de
l'élève de troisième année EG : Cette
partie est consacrée à l'étude de l'itinéraire
curriculaire et le profil d'un élève de troisième
année économie et gestion.
· Organisation du manuel scolaire et description
du chapitre : Cette partie est consacrée à
l'organisation du manuel scolaire de troisième année
économie et gestion et du chapitre « Initiation aux
graphes ».
· Analyse praxéologique: Cette
partie est consacrée à l'analyse praxéologique des
activités du chapitre « Initiation aux graphes ».
v Chapitre IV : Conclusions.
Au terme de notre travail de recherche, nous tirons les
principaux émergents spontanés de l'analyse praxéologique
à partir des synthèses. Ces émergents concernent:
· les effets de la transposition didactique,
· le profil de l'élève de troisième
année économie et gestion,
· les blocs pratico- techniques,
· les blocs technologico- théoriques
Chapitre II :
Cadre théorique
Chapitre II : Cadre
théorique
II-1. Aperçu
historique
La théorie des graphes est née en 1736 avec la
communication d'Euler dans laquelle il proposait une solution au
célèbre problème des ponts de Königsberg.
Euler proposa le problème suivant : deux
îles (A et B sur la figure ci-dessous) sur la rivière Pregel
à Königsberg étaient reliées entre elles ainsi qu'aux
rivages à l'aide de sept ponts. La question est : lors d'une
promenade, est-il possible de passer sur tous les ponts de la ville une et une
seule fois?
C
B
A
D
Euler introduisit deux nouveautés : d'abord il
remarqua que ce problème peut être remplacé par celui
consistant à tracer une figure géométrique sans lever le
crayon et sans repasser plus d'une fois sur un même trait.
D
B
C
A
En plus, cette façon de présenter ce qui
semblait, à cette époque, comme un casse-tête, et qui
l'aida à expliquer la preuve que ce problème n'a pas de solution
inaugure, en fait, une nouvelle technique de modélisation de situation.
Depuis cette date et jusqu'à la première
moitié du dix neuvième siècle, on ne trouve pratiquement
aucune trace de travaux faits par des mathématiciens sur ce type de
sujet. En 1847, Kirchhoff (1824-1887) et un peu plus tard Cayley (1821-1895)
développeront chacun de son côté la théorie des
arbres. Möbius (1790-1868) présenta, dans l'un de ses cours en
1840, la conjecture des quatre couleurs qui affirme que quatre couleurs
suffisent pour colorier n'importe quelle carte plane. Ce problème resta
à l'état de conjecture jusqu'en 1976, année durant
laquelle Appel et Haken présentèrent une preuve de ce
théorème.
C'est surtout au vingtième siècle que l'on peut
observer une sorte d'engouement des mathématiciens envers la
théorie des graphes, engouement dû en grande partie aux
problèmes, de plus en plus complexes posés par l'économie,
le commerce, l'industrie et surtout par les problèmes d'organisation et
de logistique. C'est à König(1936) que revient l'honneur
d'écrire le premier ouvrage consacré entièrement à
la théorie des graphes.
Claude BERGE (BERGE, 1967), dans son ouvrage
« Théorie des graphes et ses applications »
publié en 1958, donna à cette théorie une structure
unifiée et abstraite rassemblant l'état des résultats
épars des recherches jusqu'à cette date. Ce livre est encore, de
nos jours, considéré comme une référence
incontournable en matière de théorie des graphes. En 1959,
l'informaticien néerlandais Edgser DIJKSTRA a proposé un
algorithme qui permet de déterminer un plus court chemin entre deux
sommets d'un graphe orienté et qui sert, entre autres, aux
systèmes de navigation.
Depuis, la théorie des graphes est devenue un domaine
à part entière des mathématiques au même titre que
l'algèbre, la géométrie et l'analyse.
Nous nous proposons, dans la suite de présenter la
théorie des graphes telle que présentée dans nos jours
dans les publications destinées à la formation des enseignants du
cycle secondaire.
II-2. Présentation de
la théorie des graphes
Présenter le savoir savant
dans un travail de recherche de mastère en didactique des
mathématiques est quelque chose d'inhabituel. Car, le rapport institutionnel à l'objet
« méthodologie de recherche sur la transposition
didactique » nous assujettit à prendre le savoir savant comme
« donné consensuel connu de tous» dans la
communauté des mathématiciens et celle des enseignants de la
discipline. Or, à l'exception du cours
polycopié de Mr Faouzi BEN CHARRADA, enseignant au département
Informatique de la Faculté des Sciences de Tunis, nous n'avons
trouvé aucun autre cours complet ou manuscrit tunisien à qui on
peut faire référence. Ce sont ces
raisons qui nous ont motivées à échafauder une
présentation du savoir savant curriculaire et qui doit, à notre
sens, faire l'objet d'une unité de valeur dans les facultés des
sciences et dans l'école normale en Tunisie. Nous avons, pour cela, tiré les
définitions, propositions de différentes ressources (BERGE,
1967 ; SIGWARD, 2007). Le document (SIGWARD,
2007) mis en ligne nous a été d'un grand secours surtout en ce
qui concerne les démonstrations, les exemples et les applications des
propositions. Nous avons aussi tiré profit
de certains cours mis en ligne sur la Toile, pour la finalisation de certaines
démonstrations ainsi que tout ce qui concerne les formulations et la
mise en application des deux algorithmes présentés. Les connaissances que nous allons présenter ne
forment pas la somme des connaissances sur la théorie des
graphes ; car cela aurait nécessité des centaines de pages.
Il s'agit, plutôt, des connaissances ayant un lien direct avec les
savoirs curriculaires, c'est à dire les savoirs du chapitre
« Initiation aux graphes » de troisième année
section économie et gestion. Ainsi, nous
allons nous limiter aux objets du savoir suivants :
· Définitions d'un
graphe et d'un graphe non orienté. Représentation d'un graphe.
Modélisation d'une situation par un graphe.
· Quelques types de graphes : graphe planaire, multi
graphe, graphe complet, graphe stable et graphe biparti.
· Degré d'un sommet, degré d'un graphe. Lemme des poignées de mains et ses
conséquences.
· Graphe partiel et sous
graphe. Liste et matrice d'adjacence.
· Chaîne, chaîne
simple, chaîne élémentaire et cycle. Graphe connexe. Graphe
eulérien et théorème d'Euler.
· Coloration des sommets d'un
graphe. Nombre chromatique. Encadrement du nombre chromatique. Algorithme de
Walsh et Powell. Arbres et forêts. Graphe
pondéré. Algorithme de Moore-Djikstra.
a) Définitions
Définition d'un graphe
Un graphe orienté fini est un couple G = (V, E)
défini par :
- l'ensemble fini V = {v1, v2, ...,
vn} dont les éléments sont appelés
sommets.
- l'ensemble fini E = {e1, e2, ...,
em} est un sous ensemble du produit cartésien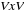 . Les
éléments de E sont appelés arcs.
. Les
éléments de E sont appelés arcs.
Un arc e de l'ensemble E est, donc, défini par un
couple de sommets (vi,vj) appelés les
extrémités de e. vi s'appelle extrémité
initiale qu' on note I(e) et vj est l'extrémité
finale de e, notée T(e) . On dit aussi que ces sommets sont
adjacents,
ou
incidents
avec l'arc e, ou encore que l'arc e est
incident
avec les sommets vi et vj. Un sommet qui n'est adjacent
à aucun autre est dit isolé. L'arc (v,v) est appelé
boucle. On appelle
ordre
d'un graphe le nombre de sommets de ce graphe.
Représentation graphique d'un
graphe
Les graphes, objets de cette théorie, tiennent leur
nom du fait qu'on peut les représenter par des dessins
(étymologiquement : un graphique est un ensemble de lignes). A
chaque
sommet
de G, on fait correspondre un point distinct du plan et on relie par une courbe
simple orientée du sommet initial au sommet final les points
correspondant aux extrémités de chaque arc.
Dans ce graphe, on a :
-L'ensemble V des sommets est :
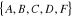
-L'ensemble E des arêtes est :
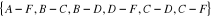
Dans la représentation ci-contre, on pouvait remplacer
chaque flèche par une courbe orientée de
l'extrémité initiale vers l'extrémité finale.
Exemple :
A
B
C
F
D
Définition de graphe non orienté
Graphe non orienté
Si le graphe G= (V,E) vérifie la
propriété suivante :
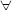 (x,y)
(x,y)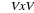 ;
(x,y)
;
(x,y) E
E
 (y,x)
(y,x) E
E
alors le graphe est dit non orienté.
Dans ce cas, le lien entre les sommets x et y est
représenté par une courbe non orientée (afin de ne pas
encombrer le graphe par deux flèches) et on l'appelle arête.
Ainsi, les arcs (x,y) et (y,x) donnent l'arête
x-y.
Dans la suite, nous allons focaliser le travail sur les
graphes non orientés qui sont les objets du programme de la
troisième année économie et gestion. Ces graphes non
orientés sont dits aussi simples car entre deux sommets il n'existe au
maximum une arête. On présentera au paragraphe suivant des graphes
non simples (dits multiples).
b) Utilisation des
graphes
On utilise un graphe pour modéliser une situation dans
laquelle on se propose d'étudier une relation entre des objets
d'intérêt. Les deux questions à lesquelles on doit
répondre sont : Que doit-on considérer comme sommets ?
Quelles sont les arêtes ?
Exemple de situation : Un examen
comporte, outre les matières communes, six matières optionnelles
: Français, Anglais, Espagnol, Mécanique, Dessin industriel et
Informatique. Se présentent à cet examen un groupe de candidats
ayant choisi les options F, A et M; un deuxième groupe, les options D et
E; un troisième groupe, les options M, I et E; enfin, un dernier groupe,
les options A et I. Chaque épreuve occupe une demie- journée et
on ne peut pas programmer dans une même demie- journée, des
épreuves communes à un même candidat. Quelle est la
durée minimale pour organiser les examens de ces options ?
Modélisation :
Il est naturel de prendre comme sommets les matières
optionnelles. Les arêtes, quant à elles, relient uniquement les
matières choisies par un même groupe. Nous verrons au paragraphe
1-10 comment se résout ce problème. L'idéal est de
disposer d'une stratégie sûre pour déterminer dans chaque
problème quels sont les sommets et quelles sont les arêtes. Il
est, cependant, certain, que le point de départ doit être
l'analyse sémantique de la consigne qui devrait déboucher sur un
verbe ou autre locution faisant le lien entre des objets. On pourrait, en
première lecture penser que ce verbe (ou cette locution) indique les
arêtes et que les objets en question sont les sommets. La
fonctionnalité du choix des éléments constitutifs du
graphe est l'élément déterminant quant à sa
pertinence. Dans le tableau suivant on a consigné quelques exemples de
situations modélisables par des graphes.
|
Objet d'intérêt
|
Lien
|
|
existant
|
complémentaire
|
|
Personnes
|
Amitié
|
Pas d'amitié
|
|
Personnes
|
Se saluent
|
Ne se saluent pas
|
|
Personnes
|
Passent le même examen
|
Ne passent pas le même examen
|
|
Régions
|
Ont une frontière terrestre commune
|
N'ont pas une frontière terrestre commune
|
|
Pays
|
Sont en guerre
|
Ne sont pas en guerre
|
On appelle graphe complémentaire le graphe ayant les
mêmes sommets et qui correspond à la relation
complémentaire (ou la négation de la relation).
c) Quelques types de
graphes
1- Dans ce graphe, on a :
-L'ensemble V des sommets est :
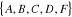
-L'ensemble E des arêtes est :
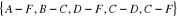
Ce graphe est planaire car deux arêtes quelconques ne se
rencontrent pas.
Graphes planaires : si on arrive à dessiner
le graphe sans qu'aucune arête n'en coupe une autre (les arêtes ne
sont pas forcément rectilignes), on dit que le graphe est
planaire.
A
B
C
F
D
Les graphes planaires sont utiles, entre autres, pour
l'ingénierie des circuits imprimés.
2- Dans ce graphe, on a :
-L'ensemble V des sommets est :
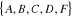
-On a deux arêtes qui relient les sommets A et F.
C'est un multi graphe.
On parle d'ordre de multiplicité d'une arête.
L'ordre de multiplicité de l'arête e= A-F est 2, on
écrit : m(e)=2.
Dans un graphe simple, toutes les arêtes sont d'ordre de
multiplicité au plus égal à 1.
Multi graphes : on peut imaginer des graphes avec
une arête qui relie un sommet à lui-même (une boucle), ou
plusieurs arêtes reliant les deux mêmes sommets. Dans ce cas, on
parle de multi graphe.
B
A
C
F
D
3- Graphe
complet :
c'est un graphe dont chaque sommet est relié directement à tous
les autres sommets.
Dans ce graphe, on a :
-L'ensemble V des sommets est :
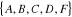
-Chaque arête est reliée directement à toutes
les autres.
B
A
C
F
D
4- Graphe stable : C'est un graphe dont tous les
sommets sont isolés. Autrement dit l'ensemble des arêtes est
vide.
4- Graphe
biparti :
C'est un graphe dont les sommets peuvent être divisés en deux
ensembles X et Y, de sorte que toutes les arêtes du graphe relient un
sommet dans X à un sommet dans Y.
Dans ce graphe biparti, on a :
-L'ensemble X est :
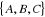
- L'ensemble Y est :
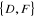
-L'ensemble E des arêtes est :
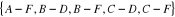
B
A
C
F
D
Les problèmes d'affectation
des personnels aux postes de travail ou aux machines de production sont des
exemples de situations modélisables par des graphes bipartis.
d) Degré d'un
sommet, degré d'un graphe
Degré d'un sommet : Pour un
graphe
ou un multi graphe, on appelle
degré
du sommet v, et on note d(v), le nombre d'
arêtes
incidentes
avec ce sommet. Une
boucle
sur un sommet est comptée deux fois. Dans un graphe
simple,
on peut aussi définir le degré d'un sommet comme étant le
nombre de ses voisins (la taille de son
voisinage).
Degré d'un
graphe : Le degré d'un graphe est le degré maximum
de tous ses sommets. Dans l'exemple ci-dessus, le degré du graphe est 3.
Dans ce graphe on a :
|
Sommet
|
Sommets adjacents
|
Degré
|
|
A
|
B,C,F
|
3
|
|
B
|
A,D
|
2
|
|
C
|
A,D
|
2
|
|
D
|
C,B
|
2
|
|
F
|
A
|
1
|
|
H
|
|
0
|
B
A
C
D
H
F
Un graphe dont tous les
sommets
ont le même
degré
est dit
régulier.
Si le degré commun est k, alors on dit que le graphe est k-
régulier.
Propositions
Proposition :
Si l'ordre d'un graphe est supérieur ou égal
à 2 alors il existe au moins deux sommets différents ayant le
même degré.
Preuve : Supposons que
tous les sommets sont de degrés différents et posons n l'ordre du
graphe. On a, moyennant ré indexation des sommets:
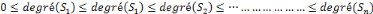
Donc: le degré du sommet S1 est 0 alors que
celui de Sn est n-1. En d'autres termes : le sommet
S1 est isolé et le sommet Sn est relié
à tous les autres sommets. Ce qui est absurde. Ainsi, il y a au
moins :
- deux personnes qui ont le même nombre d'amis.
- deux personnes qui échangent les politesses avec le
même nombre de personnes.
- deux pays qui ont le même nombre de pays
limitrophes.
Lemme des poignées de mains :
La somme des degrés des sommets d'un graphe est
égale à deux fois le nombre d'arêtes.
Conséquences :
- Si le graphe G =(V,E) est r- régulier alors : r
card(V)=2 card(E).
Graphe 3-régulier.
Graphe 2-régulier.
Graphe 1-régulier.
- En conséquence, si un graphe G=(V,E) est 2-
régulier alors card(V)= card(E). La réciproque est fausse, car si
card(V) = card(E) on ne peut pas conclure que le graphe est 2-régulier.
Il peut être non régulier, tout simplement.
- Dans un graphe simple, le nombre de sommets de degrés
impairs est pair.
e) Graphe partiel et
sous- graphe
Définitions
G=(V,E)
G'=(V,E')
Soit G = (V, E) un graphe. Le graphe G' = (V, E') est un
graphe partiel de G, si E' est inclus dans E. Autrement dit, on obtient
G' en enlevant une ou plusieurs
arêtes
au graphe G.
Pour un sous-ensemble de sommets A inclus dans V, le
sous-
graphe de G induit par A est le graphe G' = (A, E(A)) dont l'ensemble des
sommets est A et l'ensemble des arêtes E(A) est formé de toutes
les arêtes de G ayant leurs deux extrémités dans A.
Autrement dit, on obtient G' en enlevant un ou plusieurs
sommets
au graphe G, ainsi que toutes les
arêtes
incidentes
à ces sommets. On dit aussi que G' est engendré par A.
G=(V,E)
Sous- graphe de G
Un graphe partiel d'un sous- graphe
est un sous- graphe partiel de G.
On appelle
clique
un sous- graphe
complet
de G.
Si S est une partie de V. On dit que
S est stable si le sous graphe engendré par S ne contient aucune
arête.
Un stable S est dit maximal si :
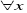 S,
SU
S,
SU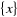 n'est
pas stable. Un stable maximal de cardinalité maximum est dit stable
maximum.
n'est
pas stable. Un stable maximal de cardinalité maximum est dit stable
maximum.
f) Listes et matrice
d'adjacences
Définitions
On peut représenter un graphe en donnant pour chacun de
ses sommets la liste des sommets auxquels il est adjacent. On les appelle
listes d'adjacences. Exemple :
|
Sommet
|
Listes d'adjacences
|
|
1
|
3,4,5
|
|
2
|
3
|
|
3
|
1,2,4
|
|
4
|
1,3,5
|
|
5
|
1,4
|
3
2
1
5
4
En plus, on peut représenter un graphe par une
matrice
M=(mij) où mij 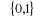 appelée matrice d'adjacences. Dans cette matrice, les lignes et les
colonnes représentent les sommets du graphe. Un 1 à
ième ligne et jème colonne (mij
=1) signifie que le sommet i est adjacent au sommet j. Voici la matrice
d'adjacences d'un autre graphe:
appelée matrice d'adjacences. Dans cette matrice, les lignes et les
colonnes représentent les sommets du graphe. Un 1 à
ième ligne et jème colonne (mij
=1) signifie que le sommet i est adjacent au sommet j. Voici la matrice
d'adjacences d'un autre graphe:
Graphe :
S1
S2
S3
S4
La matrice d'adjacence est :
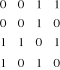
Elle est symétrique
g) Chaîne,
chaîne simple, chaîne élémentaire,
cycle
Soit G= (V, E) un graphe.
On appelle chaîne toute suite
finie de sommets S0, S1, ......,Sk tels que
les arêtes S0-S1, S1-S2,
......, Sk-1-Sk soient des arêtes de G. Cette
chaîne est notée c=
[S0S1.........Sk].
o La longueur de cette
chaîne est le nombre de ses arêtes. Cette longueur est notée
l(c).
o Les sommets S0
et Sk sont appelés extrémité initiale et
finale de la chaîne c. On dit que les sommets S0 et
Sk sont reliés par la chaîne c.
o Une chaîne est dite
simple si toutes ses arêtes sont distinctes.
o Une chaîne est dite
élémentaire si tous ses sommets sont distincts.
o Une chaîne est dite
fermée si ses deux extrémités sont confondues.
o Un cycle est une
chaîne simple fermée.
2
1
3
6
5
4
o La chaîne 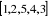 est
élémentaire, donc simple. Elle est de longueur 4.
est
élémentaire, donc simple. Elle est de longueur 4.
o La chaîne 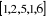 est simple
et non élémentaire.
est simple
et non élémentaire.
o La chaîne 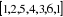 est un
cycle.
est un
cycle.
h) Graphe
connexe
Définition
Un graphe est dit connexe si toute
paire de sommets est reliée par une chaîne.
La plus petite longueur des chaînes reliant deux sommets
est appelée distance de ces deux sommets.
Le diamètre d'un graphe G,
noté  , est la plus grande distance entre deux sommets quelconque de ce
graphe.
, est la plus grande distance entre deux sommets quelconque de ce
graphe.
Exemple
B
Graphe G connexe, d(A,C)=3, 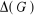 =3.
=3.
A
C
D
E
On peut montrer facilement que la
relation R dans l'ensemble V des sommets :
(S1 R
S2) signifie (S1 et S2 sont relies par
une chaîne)
est une relation symétrique
et transitive. L'ensemble des sommets reliés entre eux engendre un sous
graphe qui s'appelle composante connexe. Ainsi, un
graphe connexe est un graphe qui a une seule composante connexe.
Un point d'articulation est un
sommet dont la suppression augmente le nombre de composantes connexes. Un isthme est une arête dont la suppression
augmente le nombre de composantes connexes. Dans le
graphe connexe G ci-dessus, Le point B est une articulation et l'arête
B-D est un isthme.
i) Graphe
eulérien
Définitions
On dit qu'un graphe est
eulérien
s'il est possible de trouver un
cycle
passant une et une seule fois par toutes les
arêtes.
Ce cycle est dit eulérien.
On dit qu'un graphe est semi- eulérien s'il est
possible de trouver une
chaîne
passant une et une seule fois par toutes les
arêtes.
Cette chaîne est dite eulérienne.
Plus simplement, on peut dire qu'un graphe est eulérien
(ou semi- eulérien) s'il est possible de dessiner le graphe sans lever
le crayon (et sans passer deux fois sur le même trait).
Théorème d'Euler:
Un graphe connexe est eulérien si et seulement si tous
ses sommets sont de degrés pairs.
Un graphe est semi-
eulérien si et seulement si tous ses sommets sont de degrés pairs
ou bien il a uniquement deux de ses sommets de degrés impairs.
Preuve de la première partie :
La condition est nécessaire : en effet, si c est
un cycle eulérien de G et S un sommet de E, à chaque fois qu'on
arrive à S par une arête on en repart par une arête
distincte de la première puisque c est un cycle. Donc S est paire.
La condition est suffisante : en effet, Si S0
est un sommet de V, comme son degré est pair, on peut choisir une
autre arête incidente à S0 et de deuxième
extrémité S1 lequel est adjacent à un autre
sommet S2 (puisque les sommets sont de degrés pairs) et ainsi
de suite jusqu'à revenir au sommet S0. On obtient, ainsi, un
cycle c=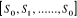 .
.
Si ce cycle contient toutes les arêtes du graphe alors
le graphe est eulérien. Sinon, il existe une arête n'appartenant
pas au cycle précédent d'extrémité un des sommets
Sk de ce cycle. On continue le procédé
précédent jusqu'à revenir au sommet Sk pour
obtenir un cycle c' ne contenant aucune des arêtes du cycle c. La
concaténation des deux cycles c et c' donne un cycle c''. Si c''
contient toutes les arêtes du graphe, on a terminé, sinon on
continue le processus jusqu'à épuisement de toutes les
arêtes puisque le graphe est fini.
S1
S0
Cycle c'
Cycle c
Sk
A titre d'exemple, le graphe G (à gauche ci-dessous)
est eulérien puisque tous les sommets sont de degrés pairs. Par
contre, le graphe G' (à droite ci-dessous) n'est pas eulérien car
on a au moins un sommet de degré impair.
Graphe G' :
Graphe G :
La démonstration
précédente est une technique pour déterminer un cycle
eulérien s'il existe.
De la même manière,
on peut prouver la seconde partie du théorème.
Le graphe G' ci-dessus est semi-
eulérien car il a deux sommets de degrés impairs et il n'est pas
difficile de déterminer dans ce graphe une chaîne
eulérienne dont les extrémités sont ces deux sommets de
degrés impairs.
j) Coloration des
sommets
Définition de la coloration
Soit G = (V, E) un
graphe.
Une coloration de ce graphe est une mise en couleur de tous ses sommets de
sorte que deux sommets adjacents n'ont pas la même couleur.
Comme le montre le graphe ci-dessous, un même graphe
peut avoir plusieurs colorations.
B
V :vert , B :bleu , R :rouge
V :vert , B :bleu
B
V
R
V
V
V
V
B
B
On peut accorder à chaque sommet une couleur distincte
des autres, ce qui montre que la coloration d'un graphe est toujours possible.
Il serait intéressant de pouvoir le faire avec le minimum de couleurs.
Définition du nombre chromatique
Le nombre chromatique d'un graphe G, noté ?(G), est le
plus petit nombre de couleurs nécessaires à sa coloration. Un
sous-ensemble S de V est un
stable
s'il ne comprend que des sommets non
adjacents
deux à deux. Une coloration avec k couleurs est donc une partition de
l'ensemble des sommets en k stables.
Exemples
Si le graphe G est un cycle alors ?(G)=2 s'il est de longueur
paire et ?(G)=3 sinon.
1- Si G est stable d'ordre non nul alors ?(G)=1.
2- Si G est biparti alors ?(G)=2.
Encadrement du nombre chromatique
Majoration
?(G)  r + 1,
où r est le plus grand degré de ses sommets.
r + 1,
où r est le plus grand degré de ses sommets.
Preuve :
Soit un graphe et r le degré maximum de ses sommets.
Donnons-nous une palette de (r + 1) couleurs. Pour chaque sommet du graphe on
peut tenir le raisonnement suivant : ce sommet est adjacent à r
sommets au plus, et le nombre de couleurs déjà utilisées
pour colorer ces sommets est donc inférieur ou égal à r.
Il reste donc au moins une couleur non utilisée dans la palette, avec
laquelle nous pouvons colorer notre sommet.
Minoration
Le nombre chromatique d'un graphe est supérieur ou
égal à celui de chacun de ses sous- graphes.
Preuve :Ce résultat découle
de la définition même du nombre chromatique. L'algorithme suivant
est couramment utilisé pour obtenir une assez bonne coloration d'un
graphe, c'est-à-dire une coloration n'utilisant pas un trop grand nombre
de couleurs. Cependant il n'assure pas que le nombre de couleurs utilisé
soit égal au nombre chromatique du graphe.
Algorithme de coloration de Welsh et
Powell
Etape 1
Classer les sommets du graphe dans
l'ordre décroissant de leur degré, et attribuer à chacun
des sommets son numéro d'ordre dans la liste obtenue.
Etape
2
En parcourant la liste dans l'ordre, attribuer une couleur non
encore utilisée au premier sommet non encore coloré, et attribuer
cette même couleur à chaque sommet non encore coloré et non
adjacent à un sommet de cette couleur.
Etape
3
S'il reste des sommets non colorés dans le graphe, revenir
à l'étape 2. Sinon, la coloration est terminée.
La coloration d'un graphe est une technique efficace pour
résoudre des problèmes d'incompatibilité tels que :
deux personnes qui ne doivent pas figurer dans la même équipe,
deux matières ne doivent pas être programmées à la
même tranche de temps.
Exemple
Un formateur d'un groupe de sept étudiants A, B, C, D,
E, F et H en mastère de didactique de mathématiques se propose
constituer le minimum de groupes de travail sur des sujets de transposition
didactique.
Or, il s'avère que :
- L'étudiant A refuse de collaborer avec les
étudiants B et C.
- L'étudiant B refuse de collaborer avec les
étudiants A, C, D et E.
- L'étudiant C refuse de collaborer avec les
étudiants A, D, F et B.
- L'étudiant D refuse de collaborer avec les
étudiants C, B, F et H.
- L'étudiant E refuse de collaborer avec les
étudiants B, F et H.
- L'étudiant F refuse de collaborer avec les
étudiants D, C et H.
- L'étudiant H refuse de collaborer avec les
étudiants D, F et E.
Comment doit procéder ce formateur pour résoudre
son problème ?
D'abord, on peut représenter cette situation par le
graphe G= (V,E) où :
- V = 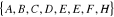
- La liste d'adjacence :
- A : B, C
- B : A, C, D, E
- C : A, D, F, B
- D : C, B, F, H
- E : B, F, H
- F : D, C, H
- H : D, F, E
E
B
D
H
A
C
F
En utilisant l'algorithme de Walsh et
Powell, on obtient le tableau suivant :
|
Sommet
|
A
|
B
|
C
|
D
|
E
|
F
|
H
|
|
Degré
|
2
|
4
|
4
|
4
|
3
|
4
|
3
|
|
Ordre
|
7
|
1
|
2
|
3
|
5
|
4
|
6
|
|
Couleur
|
C3
|
C1
|
C2
|
C3
|
C2
|
C1
|
C4
|
Si nous procédons à un
autre classement :
|
Sommet
|
A
|
B
|
C
|
D
|
E
|
F
|
H
|
|
Degré
|
2
|
4
|
4
|
4
|
3
|
4
|
3
|
|
Ordre
|
7
|
2
|
3
|
1
|
5
|
4
|
6
|
|
Couleur
|
C1
|
C2
|
C3
|
C1
|
C1
|
C2
|
C3
|
Ainsi, le nombre de couleur des
sommets de ce graphe est 3. Le nombre chromatique étant supérieur
ou égal à celui de ses sous graphes complets, on peut en
déduire que ce nombre est égal à 3. Le formateur peut, en toute quiétude annoncer
les groupes suivants :
o Groupe1 : A, D, E
o Groupe2 : B, F
o Groupe3 : C, H
Cet exemple montre que la procédure donnée
l'algorithme de Welsh et Powell dépend du classement choisis pour les
sommets de même ordre et donne parfois un nombre de couleurs
supérieur au nombre chromatique. Remarquons qu'on pouvait trouver
directement le nombre chromatique par la recherche du minimum de stables. On a
trois stables: 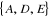 ,
, 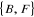 et
et 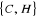 .
.
Exemple intéressant
La coloration du graphe suivant par l'algorithme de Welsh et
Powell ne donne jamais le nombre chromatique.
En effet, l'algorithme de Welsh et
Powell donne toujours 3 couleurs alors que le nombre chromatique est 2.
k) Arbres et
forêts - Algorithme de plus court chemin
Un arbre est un graphe simple connexe
et qui ne contient aucun cycle. Une forêt est un graphe simple dont les
composantes connexes sont des arbres.
Un arbre :
Une forêt :
Proposition :
· Si G=(V,E) est un arbre
alors :
· Toute arête d'un arbre
est un isthme.
· Si Card(V)=n alors
Card(E)=n-1.
· Si on ajoute une arête
à G alors on obtient un graphe G' qui ne contient qu'un seul cycle.
· Le nombre chromatique de G est
égal à 2.
· G contient au moins deux
sommets d'ordre 1 (on dit pendants).
Conséquence :
Si G=(V,E) est une forêt qui
contient p composantes connexes alors : Card(E)= Card(V)-p.
Graphe pondéré
(ou valué) :
Un graphe G= (V,E) est dit
pondéré s'il est muni d'une application :
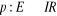
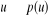 (appelé poids de l'arc
(appelé poids de l'arc 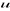 )
)
Si G' est un sous graphe de G
alors :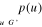 est appelé poids de G'.
est appelé poids de G'.
La longueur d'un chemin C est la
somme des poids des arêtes qui le constituent. On le note l(C).
Exemple
L'application p est définie par :
p(B-C)=2; p(D-C)=-1;
p(A-D)=4; p(H-F)=1;
p(H-K)=3; p(K-F)=5.
l(A-D-C-B)=4-1+2=5.
B A
2
C F
-1 4 1
5 H
D 3
K
On peut observer :
· Qu'il existe un chemin entre
le sommet A et chacun des sommets : B, C et D.
· Qu'il n'existe pas de chemin
entre le sommet A et les sommets : F, H et K.
· Le plus court chemin
entre :
- Les sommets F et K est : F-H-K. Il est de longueur 4
- Les sommets A et C n'existe pas.
Car, on peut suivre le chemin A-D-C qui est de longueur 3, ou bien
A-D-C-D-C qui est de longueur 1, etc.
Dans la suite, on va supposer que
tous les poids sont positifs ou nuls.
Proposition
Tout sous chemin d'un plus court
chemin est un plus court chemin.
Preuve : En effet, Supposons que :
S1-S2-.........-Sk-......Sp-......-Sm
est le plus court chemin entre les sommets S1 et
Sm. avec k<p<m.
S1
S2 S3
Sk
Sp
Sm
Alors le sous- chemin entre les
sommets Sk et Sp est le plus court ; car, sinon, on
aurait un autre chemin plus court entre S1 et Sm
utilisant un autre détour.
L'algorithme suivant permet de
déterminer le plus court chemin (s'il existe) entre un sommet s choisi
et chacun des autres sommets d'un graphe G=(V,E). Le résultat est une
arborescence.
Algorithme de Moore-
Dijkstra
Initialisation : 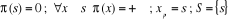
Itérations : Tant que
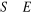 faire :
faire :
On détermine les sommets  tels que
l'arc qui relie
tels que
l'arc qui relie 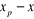 soit un élément de E. On prendra :
soit un élément de E. On prendra : 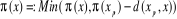 .
.
On garde l'arête 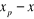 qui a permis
d'avoir ce minimum. On choisit un nouveau sommet
qui a permis
d'avoir ce minimum. On choisit un nouveau sommet 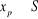 tel que
tel que 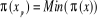 et on
posera :
et on
posera : 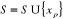 .
.
Nous allons illustrer le
mécanisme de cet algorithme à l'aide d'un exemple. Remarquons que
l'idée centrale de cet algorithme réside dans le fait que le plus
court chemin entre deux sommets est la concaténation des plus courts
chemins intermédiaires.
Exemple :
Considérons le graphe
pondéré suivant :
A 4 B
2
4
S0 1
3 7 C
4
1
5 D
F
On se propose de déterminer, à l'aide de cet
algorithme, les plus courts chemins du sommet S à tous les autres
sommets.
|
S0
|
A
|
B
|
C
|
D
|
F
|
xp
|
S
|
|
0
|
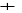
2,
S0
2, F
2
|
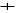
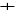
4, F
4, F
4
|
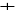
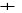
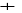
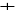
8, B
8
|
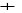
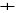
6, F
6, F
6, F
6, F
6
|
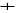
1, S0
1
|
S0
F
A
B
C
D
|
S0
S0,F
S0,F,A
S0,F,A,B
S0,F,A,B,C
S0,F,A,B,C,D
|
Ainsi, le plus court chemin de
S0 au sommet :
ü A est de longueur 2
ü B est de longueur 4
ü C est de longueur 8 ; il
s'agit du chemin : S0-F-B-C.
ü D est de longueur 6
ü F est de longueur 1
L'arborescence qui permet de suivre
ces chemins est :
A 4 B
2
4
S0
1 3 7 C
4
1
5 D
F
l) Graphes
isomorphes
Considérons le graphe G= (V,E)
défini par : V=  et
l'ensemble des arêtes E=
et
l'ensemble des arêtes E= 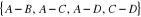 . On peut
présenter ce graphe de plusieurs manières. Par exemple :
. On peut
présenter ce graphe de plusieurs manières. Par exemple :
D
F
B
A
F
A
D
C
B
C
Ces deux graphes représentent
la même situation. On dit qu'ils sont isomorphes.
En ré
-indexant1(*) la
représentation graphique donnée à droite on obtient deux
graphes qui correspondent à une même situation (avec des noms de
sommets différents) et sont donc isomorphes.
P
S
T
R
Q
A
D
B
C
F
D'une manière
générale, on dit que deux graphes G=(V,E) et G'=(V',E') sont
isomorphes s'il existe deux bijections : 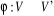 et
et 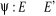 de sorte que
si
de sorte que
si 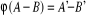 alors
alors 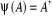 et
et 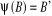 .
.
Ainsi, si deux graphes sont
isomorphes alors :
· Ils ont le même nombre
de sommets.
· Ils ont le même nombre
d'arêtes.
· Ils ont même nombre de
sommets de degré donné.
· Ils ont le même nombre
de composantes connexes.
· Ils ont le même nombre
de sous graphes complets d'ordre donné.
· Si l'un est eulérien
l'autre l'est aussi.
· Etc.
En conséquence, il est souvent
plus aisé de montrer que deux graphes ne sont pas isomorphes que de
prouver qu'ils le sont.
Exemples :
o Les deux graphes suivants ne sont
pas isomorphes car ils n'ont pas le même nombre de sommets.
o Les deux graphes suivants ont le
même nombre de sommets et le même nombre d'arêtes. Ils ne
sont pas isomorphes pour les raisons suivantes (une suffit !) :
- L'un (celui de gauche) a un sommet
de degré 3 et l'autre n'en a pas.
- L'un un sous graphe complet d'ordre
3 et l'autre n'en a pas.
- L'un est semi- eulérien non
eulérien et l'autre est eulérien.
m) Comparaison des
terminologies sur les graphes orientés et les graphes non
orientés
Les graphes orientés
présentent certaines particularités que les graphes non
orientés n'ont pas. Par exemple, si l'arc (A,B) peut relier le sommet A
au sommet B on ne peut pas affirmer autant sur le lien de B vers A comme c'est
le cas des graphes non orientés. Cette particularité doit se
traduire dans la terminologie afin de pouvoir situer le discours. On sait déjà qu'au terme arc des graphes
orientés correspond le terme arête dans les graphes non
orientés. Dans le tableau suivant on a
consigné les correspondances terminologiques entre le concept
orienté et le concept non orienté.
|
Concept non
orienté
|
Concept
orienté
|
|
Arête
|
arc
|
|
Chaîne
|
Chemin
|
|
cycle
|
Circuit
|
|
Connexité
|
Forte
connexité2(*)
|
A signaler que la plupart des
propositions présentées sur les graphes non orientés sont
applicables aux graphes orientés, notamment les deux algorithmes de
coloration et de Moore- Dijkstra.
II-3. Cadre
théorique didactique
Notre travail de recherche se situe dans le cadre de la
Théorie Anthropologique du Didactique (TAD) développée par
YVES CHEVALLARD à partir des années 1980. Nous avons puisé
la quasi- totalité de nos ressources concernant les concepts clé
de cette théorie à partir de ses articles qui figurent dans la
partie bibliographique (CHEVALLARD, 1991, 1994, 1998, 2002, 2007). Cette
théorie présente un certain nombre de postulats concernant
l'activité humaine : rapports personnels, rapports institutionnels,
les organisations praxéologiques (ponctuelles, locales et
régionales) ainsi que le destin de chaque objet et notamment l'objet du
savoir dans l'écosystème des connaissances. Nous allons
présenter, dans cette partie de notre recherche, les principaux concepts
de la Théorie Anthropologique du Didactique qui sont en rapport direct
avec les « objets » du savoir manipulés ou
même évoqués dans ce mémoire, à savoir
l'analyse praxéologique des activité du chapitre
« Initiation aux graphes » de la troisième
année économie et gestion.
II-3.1. Transposition didactique
La notion de transposition didactique a fait son entrée
dans le champ de la didactique au début des années 1980. Elle
était le premier émergent d'un programme
épistémologique qui se donne l'activité
mathématique comme principal objet de recherche. CHEVALLARD a
montré que le savoir à enseigner ne se réduit pas
à une forme dégénérée du savoir
savant. A propos de la définition de la transposition didactique,
CHEVALLARD (1991) écrit : « Tout projet social
d'enseignement et d'apprentissage se constitue didactiquement avec
l'identification et la désignation de contenus de savoirs comme contenus
à enseigner. [....] Un contenu de savoir ayant été
désigné comme savoir à enseigner subit dès lors un
ensemble de transformations adaptatives qui vont le rendre apte à
prendre place parmi les objets d'enseignement. Le
« travail » qui d'un objet de savoir à enseigner
fait un objet d'enseignement est appelé transposition
didactique. ».
Nous distinguons, dans le processus de transposition
didactique, au moins trois types de savoirs : le savoir savant, le savoir
à enseigner et le savoir enseigné.
· Le savoir savant est celui de la
communauté scientifique. Ce savoir constitue la référence
suprême du savoir à enseigner qui y trouve ses raisons
d'être et sa légitimité.
· Le savoir à enseigner est celui qu'on
trouve consigné dans le programme officiel et les documents
d'accompagnement officiels. Ce savoir est issu des décisions de la
noosphère (inspecteurs, conseillers, intervenants officiels, groupes de
pressions politiques, etc.).
· Le savoir enseigné est, comme son nom
l'indique, le savoir enseigné par les professeurs aux
élèves.
Le passage du savoir savant au savoir à enseigner suit
deux transformations. La première, qu'on qualifie de transposition
externe, concerne le passage du savoir savant au savoir à enseigner. Le
résultat de cette première transformation est
concrétisé par les programmes officiels, les manuels officiels et
les documents d'accompagnement.
La seconde transformation, appelée transposition
interne, et qui est l'oeuvre de l'enseignant, est une sorte de
scénarisation du savoir à enseigner et qui devient, par l'acte,
un savoir « effectivement » enseigné. Cette
transposition interne est conditionnée, entre autres, par :
ü La connaissance de la part de l'enseignant de l'objet
du savoir.
ü Les traditions d'enseignement.
ü Les exigences du programme officiel,
ü La vision propre de l'enseignant quant au profil de
l'élève et les manières qui vont lui permettre d'assimiler
les connaissances mais aussi de sa représentation du métier de
l'enseignant.
Savoir Savant
Savoir à enseigner
Savoir enseigné
Nous résumons par le schéma suivant :
Transposition externe
Transposition interne
La transposition didactique met en relief l'asymétrie
des rôles de l'enseignant et de l'enseigné par rapport à
l'échafaudage d'un savoir en classe. CHEVALLARD (1999) désigne
ces rôles par le terme grec topos qui signifie lieu. Cet
échafaudage, pour un savoir en construction, s'appuie sur un travail
coopératif qui prend une forme de jeu de rôles entre les
élèves et l'enseignant chacun effectuant un geste afin que toute
la construction soit accomplie.
Afin de réaliser les séquences d'enseignement-
apprentissage sur une unité d'apprentissage telle que le chapitre
« Initiation aux graphes », l'enseignant doit être en
mesure de répondre à deux questionnements :
Le premier concerne l'organisation mathématique (ou
organisation praxéologique ponctuelle) que l'on détaillera dans
le paragraphe suivant. Il s'agit, en fait, de répondre aux
questions : Quels types de graphes présenter ? Quels
théorèmes faut-il démontrer ? Quelles sont les
propriétés à admettre ? Quelles sont les techniques
à institutionnaliser ? Sous quelles formes présenter les
algorithmes ?
Le second questionnement, qui concerne l'organisation
didactique (OD), met l'accent sur la manière de réaliser ces
organisations mathématiques : Comment organiser les
séquences d'enseignement? Quels sont les topos des
élèves ? Quel est le topos de l'enseignant ? Comment
élaborer les techniques ? Comment
évaluer l'efficacité des techniques? Quels types de
situations que l'élève doit traiter pour réaliser les
objectifs du programme ?
Dans le Théorie Anthropologique du Didactique on
dénombre six types de situations appelées moments : le
premier moment correspond au moment de la première
rencontre avec le type de tâche , le deuxième moment est
celui de l'exploration de ce type de tâche et l'émergence d'une
technique permettant d'accomplir ce type de tâche , le
troisième moment est le moment de construction du bloc
technologico-théorique , le quatrième moment est celui
de l'institutionnalisation de l'organisation mathématique, le
cinquième moment concerne le travail de cette organisation
mathématique et le sixième moment est le moment de
l'évaluation.
II-3.2. Notions fondamentales
Objet, Rapports personnels
Objet :
Est considéré comme objet « toute
entité, matérielle ou immatérielle, qui existe pour au
moins un individu » (CHEVALLARD, 1999). Le terme objet en TAD
est à rapprocher au terme « élément »
dans la théorie des ensembles. Ainsi, le nombre 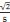
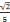 est un
objet ; mais aussi :
est un
objet ; mais aussi : 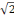
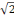 , 5 et le
signe de la fraction sont des objets. De même le nombre 2 et le signe da
racine carrée (
, 5 et le
signe de la fraction sont des objets. De même le nombre 2 et le signe da
racine carrée (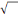
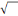 ) qui
composent le nombre
) qui
composent le nombre 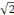
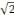 sont des
objets. La feuille sur laquelle est écrit le nombre
sont des
objets. La feuille sur laquelle est écrit le nombre 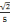
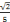 , la personne
qui l'a écrite et celle qui la lit ou la copie sont des objets.
, la personne
qui l'a écrite et celle qui la lit ou la copie sont des objets.
Rapport personnel et univers
cognitif :
Etant donnés un individu x (identifié par son
empreinte) et un objet o, on désigne par rapport personnel de x à
l'objet o « le système, noté R(x,o), de toutes les
interactions que peut avoir x avec l'objet o » (CHEVALLARD,
1999). Si une interaction entre x et o a lieu, on a R(x,o)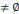
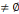 et on
considère alors que l'objet o existe pour l'individu x ou que o
appartient à l'univers cognitif de x. De nos jours, le
téléphone portable appartient à l'univers cognitif de
pratiquement tous les écoliers. En revanche, la chanson « Ne
me quittes pas » de Jacques Brel a peu de chances d'appartenir
à l'univers cognitif de ces mêmes écoliers.
et on
considère alors que l'objet o existe pour l'individu x ou que o
appartient à l'univers cognitif de x. De nos jours, le
téléphone portable appartient à l'univers cognitif de
pratiquement tous les écoliers. En revanche, la chanson « Ne
me quittes pas » de Jacques Brel a peu de chances d'appartenir
à l'univers cognitif de ces mêmes écoliers.
L'univers cognitif de x est l'ensemble : 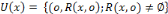
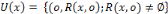 .
.
Par exemple, l'univers cognitif d'un élève
comprend : ses parents, ses amis, ses relations scolaires, les objets
qu'il utilise (brosse à dents, mp5, etc.), ses hobbies, ses idoles, ses
plaisirs, ses souffrances, etc.
Personne et individu
Une personne X est, par définition, le couple
formé par un individu et l'ensemble de ses rapports personnels aux
objets qu'il a formés à un moment donné de l'histoire de
cet individu.
L'individu est l'invariant (reconnaissable par son empreinte)
alors que ses rapports avec les objets changent d'un instant à un
autre. Le lien entre « individu » et
« personne » est comparable au lien entre un acteur (par
exemple Jacques DUFILHO) et tous les rôles qu'il a eu durant sa
carrière d'acteur.
Institution, rapports institutionnels,
assujettissements
Le rapport R(x,o) évolue selon les occasions qui
permettent à l'individu x de manipuler ou d'évoquer l'objet o. A
titre d'exemple, le rapport d'un écolier x à l'objet
géométrique « triangle » peut varier comme
suit :
· En classe préparatoire (5 ans): forme
reconnue (en fait, un triangle plein) par distinction des autres formes
(carrées, cercles, etc.).
· En sixième (12 ans): figure
géométrique qu'il peut construire et qui a : trois sommets,
trois côtés, trois angles, des médianes, des hauteurs, des
médiatrices, des bissectrices, etc.
Pour bien comprendre l'évolution de ces R(x,o) et donc
des univers cognitifs, CHEVALLARD a introduit la notion d'institution I qui est
définie comme « un dispositif social total, qui peut
n'avoir qu'une extension réduite dans l'espace social (il existe des
micro institutions ), mais qui permet - et impose- à ses sujets,
c'est-à-dire aux personnes qui viennent y occuper les différentes
positions p offertes dans I, la mise en jeu de faire et de penser
propres » (BOSCH et CHEVALLARD, 1999). Ainsi, la classe
préparatoire et la classe de sixième sont deux institutions qui
impose, chacune, à tous les individus qui occupent la position
p= « élève » sa façon propre
d'appréhender l'objet o= »triangle ». Peuvent
être des institutions : une école, une classe, un niveau, une
section, une filière, un élève, un enseignant, une
famille, etc.
Dans une institution comme l'école I, les individus
occupent des positions : élève, enseignant, parent,
conseiller d'orientation, directeur, surveillant, etc. Chacun, dans la position
p qu'il occupe a un rapport considéré par l'institution I comme
« idéal » à tel objet o; ce rapport est dit
institutionnel et est noté 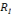
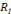 (p,o).
L'écrivain Paul GUTH rapporte dans son livre « Lettres
ouvertes aux futurs illettrés » l'histoire suivante qui
se passait en France: « Un préfet négociait la
reddition d'un gangster. Barricadé chez lui, le truand pointait son
fusil sur les forces de l'ordre. Le préfet, qui, quelques années
auparavant, avait publié un manuel de savoir vivre, crut bon, en vertu
des registres de langue, d'employer dans un mégaphone, un vocabulaire de
truand : « Ne fais pas le con ! ». Le ministre de
l'intérieur estima que ce registre de langue ne convenait pas au
représentant du président de la République. Il limogea le
grossier. ».
(p,o).
L'écrivain Paul GUTH rapporte dans son livre « Lettres
ouvertes aux futurs illettrés » l'histoire suivante qui
se passait en France: « Un préfet négociait la
reddition d'un gangster. Barricadé chez lui, le truand pointait son
fusil sur les forces de l'ordre. Le préfet, qui, quelques années
auparavant, avait publié un manuel de savoir vivre, crut bon, en vertu
des registres de langue, d'employer dans un mégaphone, un vocabulaire de
truand : « Ne fais pas le con ! ». Le ministre de
l'intérieur estima que ce registre de langue ne convenait pas au
représentant du président de la République. Il limogea le
grossier. ».
Est considéré un bon sujet dans l'institution I,
tout individu x en position p qui répond à l'exigence :
R(x,o) est conforme à 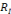
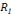 (p,o). Dans
ce cas, le sujet est considéré assujetti à l'institution
I. CHEVALLARD (1998) note que « le rapport R(x,o) n'est
jamais parfaitement conforme à un tel rapport institutionnel
(p,o). Dans
ce cas, le sujet est considéré assujetti à l'institution
I. CHEVALLARD (1998) note que « le rapport R(x,o) n'est
jamais parfaitement conforme à un tel rapport institutionnel 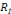
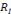 (p,o) » du fait que le rapport personnel R(x,o) est
la résultante de tous les rapports institutionnels :
(p,o) » du fait que le rapport personnel R(x,o) est
la résultante de tous les rapports institutionnels : 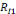
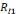 (p1,o),
(p1,o), 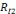
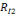 (p2,o),....,
(p2,o),....,
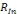
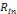 (pn,o).
(pn,o).
II-3.3. Organisation praxéologique
Parti pris épistémologique
La Théorie Anthropologique du Didactique postule que
l'activité mathématique se situe dans l'ensemble des
activités humaines, telles que : préparer une salade de
fruits de mer, tailler un arbre, préparer une leçon, casser une
noix, etc. CHEVALLARD (1998) dit en substance que « toute
activité humaine régulièrement accomplie est
subsumée à un modèle unique que résume le mot
praxéologie ».
La
notion de praxéologie ponctuelle
a) Tâche, type de tâche et genre de
tâche: Toute activité humaine peut être
décomposée en un certain nombre de tâches. Ainsi,
l'activité qui consiste à calculer le PGCD des deux entiers 180
et 240 peut être décomposée comme suit :
t1= Décomposer 18 en
éléments premiers
t2= Décomposer 24 en
éléments premiers
t3= Calcul du PGCD des deux entiers 18 et
24
t4= Déduire PGCD des deux entiers
180 et 240
![]()
Une tâche s'exprime par un verbe et suppose un objet
relativement précis. Par exemple : « Apporter le
stylo rouge qui est dans mon cartable » est une tâche t.
Celle-ci appartient au type de tâche T= « Apporter un
stylo rouge ». « Apporter » est le genre de
tâche correspondant.
b) Technique : Etant donné un type de
tâche T, la manière de réaliser ce type de tâche
s'appelle technique et se note par la lettre grecque 
 . Le bloc
[T/
. Le bloc
[T/
 ] s'appelle
bloc pratico- technique qu'on désigne habituellement par :
SAVOIR-FAIRE. Une technique peut réussir sur un certain nombre de
tâches du type T et échouer sur d'autres du même type. La
portée d'une technique relativement à un type de tâche
T est l'ensemble des tâches du type T sur lesquelles la technique
aboutit. Par exemple, considérons la technique
] s'appelle
bloc pratico- technique qu'on désigne habituellement par :
SAVOIR-FAIRE. Une technique peut réussir sur un certain nombre de
tâches du type T et échouer sur d'autres du même type. La
portée d'une technique relativement à un type de tâche
T est l'ensemble des tâches du type T sur lesquelles la technique
aboutit. Par exemple, considérons la technique 
 =
« la méthode du discriminant pour la résolution des
équations du second degré ». Cette technique
=
« la méthode du discriminant pour la résolution des
équations du second degré ». Cette technique 
 réussit lorsqu'il s'agit de résoudre l'équation de second
degré tel que : 3x²+5x-2=0 dans
réussit lorsqu'il s'agit de résoudre l'équation de second
degré tel que : 3x²+5x-2=0 dans  et
échoue lorsqu'il s'agit de la résoudre dans
et
échoue lorsqu'il s'agit de la résoudre dans 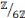
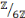 ,
étant donné que 3 est un diviseur de 0 dans
,
étant donné que 3 est un diviseur de 0 dans 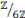
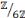 .
.
c) Technologie : C'est « un discours
rationnel (logos) sur la technique -Teckné- 
 »
(CHEVALLARD, 1998). On la note par la lettre grecque
»
(CHEVALLARD, 1998). On la note par la lettre grecque 
 . Une
technologie a trois fonctions : Justifier rationnellement une technique,
rendre celle-ci intelligible et produire des techniques. Dans le cas
où, dans une institution I, il n'existe qu'une seule technique canonique
reconnue et utilisée et donc n'appelle pas à des justifications
alors la technique en question prend le statut « auto
technologique ».
. Une
technologie a trois fonctions : Justifier rationnellement une technique,
rendre celle-ci intelligible et produire des techniques. Dans le cas
où, dans une institution I, il n'existe qu'une seule technique canonique
reconnue et utilisée et donc n'appelle pas à des justifications
alors la technique en question prend le statut « auto
technologique ».
d) Théorie : Il s'agit de la technologie de
la technologie. En d'autres termes une théorie, qu'on nomme par la
lettre grecque majuscule  , est un
discours servant à justifier la technologie
, est un
discours servant à justifier la technologie 
 . Le bloc du
savoir [
. Le bloc du
savoir [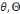
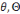 ] est appelé bloc technologico- théorique. Le bloc [T,
] est appelé bloc technologico- théorique. Le bloc [T,
 ,
,
 ,
, ] s'appelle
organisation praxéologique ponctuelle ou praxéologie
ponctuelle.
] s'appelle
organisation praxéologique ponctuelle ou praxéologie
ponctuelle.
Tâche routinière, tâche
problématique, routinisation et naturalisation
Une tâche est dite routinière si l'on dispose
d'une technique permettant de l'accomplir. Par exemple : si l'on veut
réaliser la tâche t= « Résoudre, dans  ,
l'équation 2x²-3x =0 » on dispose d'une technique
,
l'équation 2x²-3x =0 » on dispose d'une technique 
 :
:
Ø On factorise l'expression 2x²-3x.
2x²-3x= x(2x-3).
Ø On remplace l'équation donnée
par : x(2x-3)=0.
Ø On a : x=0 ou 2x-3=0.
Ø Donc : x=0 ou x= 
 .
.
Cette technique permet d'accomplir les tâches du type
T= «Résoudre une équation de la forme ax²+bx=0
avec ab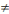 0 ». Toutes les tâches de ce type deviennent
routinières à partir du moment où la technique que nous
avons décrite est maitrisée. Le qualificatif
« routinière » se rapporte plus souvent aux types de
tâches plutôt que les tâches qui lui appartiennent comme
l'atteste l'exemple précédent. Une tâche qui n'est pas
routinière est dite problématique. Pour certaines tâches
d'un type particulier, on observe une absence de techniques, tel que le cas de
certains casse-têtes. On parle alors de situation de
pénurie praxéologique (CHEVALLARD, 1998).
Selon CHEVALLARD (1994), la routinisation d'une tâche d'un type de
tâche donné s'accomplit lorsque l'on dispose d'une technique ayant
fait ses preuves et bien maitrisée comme celle que nous avons
présentée ci-dessus. L'étape qui succède à
la routinisation est celle dans laquelle l'activité se fait
naturellement (comme respirer ou tracer une ligne à un certain niveau
scolaire) à tel point qu'elle cesse d'être
considérée comme une tâche. Au terme de cette étape,
la tâche est dite naturalisée.
0 ». Toutes les tâches de ce type deviennent
routinières à partir du moment où la technique que nous
avons décrite est maitrisée. Le qualificatif
« routinière » se rapporte plus souvent aux types de
tâches plutôt que les tâches qui lui appartiennent comme
l'atteste l'exemple précédent. Une tâche qui n'est pas
routinière est dite problématique. Pour certaines tâches
d'un type particulier, on observe une absence de techniques, tel que le cas de
certains casse-têtes. On parle alors de situation de
pénurie praxéologique (CHEVALLARD, 1998).
Selon CHEVALLARD (1994), la routinisation d'une tâche d'un type de
tâche donné s'accomplit lorsque l'on dispose d'une technique ayant
fait ses preuves et bien maitrisée comme celle que nous avons
présentée ci-dessus. L'étape qui succède à
la routinisation est celle dans laquelle l'activité se fait
naturellement (comme respirer ou tracer une ligne à un certain niveau
scolaire) à tel point qu'elle cesse d'être
considérée comme une tâche. Au terme de cette étape,
la tâche est dite naturalisée.
Praxéologie locale, praxéologie
régionale
Lorsque des praxéologies ponctuelles s'agrègent
autour d'une technologie 
 , on obtient
une organisation praxéologique locale.
, on obtient
une organisation praxéologique locale.
Praxéologie locale autour de la technologie 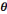
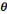 et la théorie
et la théorie 

[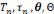
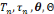 ]
]
[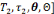
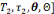
[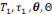
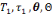 ]
]
On évoque une organisation praxéologique locale
pour mettre en avant la technologie
 . En
d'autres termes, on fait référence, dans les organisations
praxéologiques, aux mêmes définitions, aux mêmes
théorèmes et aux mêmes procédés qui
justifient les techniques utilisées. A leur tour, les
praxéologies régionales peuvent s'agréger autour d'une
théorie pour former une praxéologie régionale, et ainsi de
suite...
. En
d'autres termes, on fait référence, dans les organisations
praxéologiques, aux mêmes définitions, aux mêmes
théorèmes et aux mêmes procédés qui
justifient les techniques utilisées. A leur tour, les
praxéologies régionales peuvent s'agréger autour d'une
théorie pour former une praxéologie régionale, et ainsi de
suite...
Organisation praxéologique régionale autour de la
théorie 

Praxéologie locale autour de 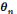
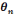 et la théorie
et la théorie 

Praxéologie locale autour de 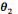
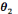 et la théorie
et la théorie 

Praxéologie locale autour de 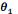
 et la théorie
et la théorie 

Nous allons étudier, dans notre travail de recherche,
et surtout dans la partie consacrée à l'analyse
praxéologique, les organisations locales autour des technologies :
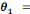
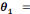 « Définition et représentation d'un graphe »,
« Définition et représentation d'un graphe »,
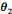
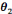 =«Lemme des
poignées de mains », .......... ,
=«Lemme des
poignées de mains », .......... ,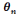
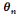 =
« Algorithme de Moore-Djikstra » de la théorie des
graphes
=
« Algorithme de Moore-Djikstra » de la théorie des
graphes 
 et qui constituent l'ensemble des technologies abordées au
chapitre « Initiation aux graphes » en troisième
année économie et gestion.
et qui constituent l'ensemble des technologies abordées au
chapitre « Initiation aux graphes » en troisième
année économie et gestion.
Ostensifs, non
ostensifs
La question de la nature d'un objet o dans une institution I
se pose dés lors que cet objet o se manifeste dans I,
c'est-à-dire est en rapport avec un individu x qui a une position p dans
l'institution I. Ainsi, la nature de l'objet mathématique o=
« Produit de deux matrices » change assez naturellement de
l'institution I1 =« Classe de troisième année
économie et gestion » à l'institution I2 =
« Deuxième année DEUG MP ». Dans la
première institution cet objet correspond à un ensemble de gestes
alors que dans la seconde institution cet objet est définie par une
formule de sommation à trois indices. C'est la raison pour laquelle
les questionnements autour de la nature des objets composant une
organisation praxéologique (Technique, Technologie et Théorie) a
été soulevée assez naturellement au cours du
développement de la Théorie Anthropologique du Didactique.
CHEVALLARD (1994) soulevaient les questions : « De quoi est
faite une technique donnée ? De quel « ingrédients
se composent-elles ? Et encore en quoi consiste « la mise en
ouvre d'une technique ? ». Ce questionnement a amené
BOCSH et CHEVALLARD (1999) à répondre par la dichotomie
fondamentale : objets ostensifs et objets non ostensifs.
a) Objets ostensifs :
« Nous parlons d'objet ostensif -du latin ostendere,
« montrer, présenter avec insistance »- pour nous
référer à tout objet ayant une nature sensible, une
certaine matérialité, et qui, de ce fait, acquiert pour le sujet
humain une réalité perceptible ». (BOSCH et
CHEVALLARD, 1999).
b) Objets non ostensifs :
« Les objets non ostensifs sont tous ces
« objets » qui, comme les idées, les intuitions ou
les concepts, existent institutionnellement- au sens où on leur attribue
une existence- sans pourtant être vus, dits, entendus, perçus ou
montrés par eux-mêmes : ils ne peuvent être
qu'évoqués ou invoqués par la manipulation adéquate
de certains objets ostensifs associés » (BOSCH et
CHEVALLARD, 1999).
c) Registres ostensifs : Dans le cadre
général de l'activité humaine, les ostensifs peuvent
être des matériaux (règle, compas, stylo), des gestes,
des mots, des graphismes ou des écritures.
BOSCH et CHEVALLARD (1999) notent que les ostensifs se
distinguent par les substances dans lesquelles ils se découpent. Selon
ces substances, ils peuvent appartenir à l'un des registres
suivants : registre de la gestualité, registre de l'oralité,
registre de la trace ou le registre de la matérialité quelconque.
Dans le tableau ci-dessous, on a consigné les principaux ostensifs qui
intéressent notre travail de recherche, leurs natures, les registres
auxquels ils appartiennent et des exemples permettant de les circonscrire.
|
Ostensif
|
Nature
|
Registre
|
Exemples
|
|
Geste
|
Ostensif gestuel
|
La gestualité
|
Gestes déictiques, gestes visuels, autres gestes : de
la tête, des bras, des épaules, etc.
|
|
Mot, discours
|
Ostensif discursif
|
L'oralité
|
« Commencer par le sommet de degré
impair »
|
|
Schéma
Dessin
Graphisme
|
Ostensif graphique
|
trace
|
Un triangle dessiné
Un tableau, le graphe d'une fonction, un dessin, etc.
|
|
Ecriture Formalisme
|
Ostensif scriptural
|
Un texte, une expression mathématique, etc.
|
|
Autres ostensifs
|
N'appartenant à aucun des registres
précédents
|
Matérialité quelconque
|
Epingler une feuille, colorier, plier un papier.
|
Tableau 1
Il est à signaler que d'autres ostensifs sont
importants mais qui ont une utilisation assez limitée dans les
institutions scolaires non spécialisées. Il s'agit des ostensifs
tactiles, olfactifs et gustatifs qui sont les
« ingrédients » principaux pour les institutions
dont les sujets sont des malvoyants et les spécialistes en arts
culinaires. Nous proposons de donner une place entière à un
nouveau registre ostensif qui englobe les trois registres ostensifs (olfactif,
tactile et gustatif) et que appellerons: registre Kinesthésique3(*).
d) Articulation entre ostensifs, dialectique entre
ostensifs et non ostensifs :
L'exemple que nous allons présenter dans la suite
(paragraphe f) illustre un certain nombre de principes concernant les natures
des éléments constitutifs d'une organisation
praxéologique.
§ La technique, la technologie et la théorie d'un
type de tâche donné mettent en route un complexe d'objets, les
uns ostensifs, les autres non ostensifs.
§ Les ostensifs se distinguent des non ostensifs par le
fait qu'ils sont manipulables alors que les non ostensifs -qui sont des
idées, des intuitions, des concepts- ne le sont pas.
§ Les ostensifs s'articulent autour des non ostensifs qui
leur donnent cohérence et consistance. Il y a une dialectique entre
ostensifs et non ostensifs: les uns ne peuvent pas s'activer sans les
autres.
e) Valence sémiotique et valence instrumentale
des ostensifs:
En théorie Anthropologique du Didactique, les objets
ostensifs ne se réduisent pas uniquement à des signes qui
évoquent des notions. Ils ont, en plus le statut d'instruments qui
permettent de réaliser des tâches. D'après BOCH et
CHEVALLARD (1999), ces deux dimensions des ostensifs peuvent être
décrites en termes de valence sémiotique et de
valence instrumentale. La valence sémiotique concerne le
potentiel d'un ostensif à évoquer des non ostensifs. Par exemple,
le signe « ln » permet d'évoquer la fonction
logarithme népérien, le PH en chimie, l'échelle
logarithmique, l'isomorphisme (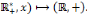
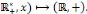 La valence
instrumentale désigne le potentiel de l'ostensif à s'engager dans
un ensemble de techniques. L'ostensif « ln » peut
être l'instrument pour réaliser une tâche du type :
trouver le plus petit entier naturel n tel que
La valence
instrumentale désigne le potentiel de l'ostensif à s'engager dans
un ensemble de techniques. L'ostensif « ln » peut
être l'instrument pour réaliser une tâche du type :
trouver le plus petit entier naturel n tel que 
 , où
(
, où
(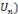
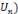 est une
suite contractante. Pour illustrer les différents concepts
rencontrés, nous allons analyser l'organisation mathématique d'un
exemple de tâche relative à type particulier d'équation du
premier degré à une inconnue.
est une
suite contractante. Pour illustrer les différents concepts
rencontrés, nous allons analyser l'organisation mathématique d'un
exemple de tâche relative à type particulier d'équation du
premier degré à une inconnue.
f) Exemple :
Nous allons nous placer dans le cadre de l'enseignement
secondaire (niveau : première année) et nous nous proposons
d'analyser en termes de dichotomie fondamentale (ostensif, non ostensifs)
de l'organisation praxéologique : [t,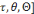
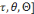 suivante :
suivante :
Ø Tâche t est :
« Résoudre, dans  ,
l'équation
,
l'équation 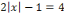
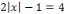 ». Cette tâche apparient au type de tâche
T=« Résoudre, dans
». Cette tâche apparient au type de tâche
T=« Résoudre, dans  ,
l'équation a
,
l'équation a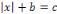
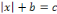 ».
».
Ø La technique 
 est :
est :
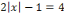
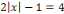
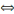
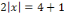
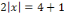
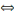
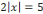
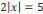
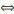
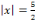
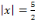
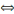
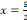
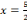 ou
ou 
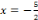
Ø La technologie 
 est :
est :
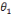
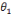 -Règle d'équivalence entre deux équations : Si
on ajoute un même réel ou on multiplie par un même
réel les deux membres d'une équation alors on obtient une
équation qui lui est équivalente (c'est-à-dire qui a les
mêmes solutions).
-Règle d'équivalence entre deux équations : Si
on ajoute un même réel ou on multiplie par un même
réel les deux membres d'une équation alors on obtient une
équation qui lui est équivalente (c'est-à-dire qui a les
mêmes solutions).
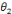
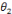 -La
propriété : Si
-La
propriété : Si 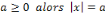
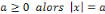
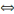
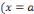
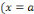 ou
ou 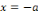
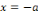 )
)
Ø La théorie  est :
est :
Calculs dans le corps  .
Algèbre des polynômes.
.
Algèbre des polynômes.
L'analyse des objets ostensifs et non ostensifs peut
être réalisée sur la technique, sur la technologie ou sur
la théorie. Nous allons nous restreindre à l'analyse de la
technique 
 , les autres éléments de l'organisation
praxéologique peuvent être analysés de la même
manière. Dans le tableau suivant, nous avons consigné, en face de
chaque étape de la technique utilisée, les ostensifs
mobilisés et les non ostensifs évoqués ainsi que les
registres de ces ostensifs. Comme on l'a déjà signalé au
début de ce paragraphe, on peut observer dans ce tableau que :
à chaque étape du développement de la technique, il y a
mobilisation d'ostensifs appartenant à des registres différents
réglés par des non ostensifs. Les deux étapes les plus
importantes articulent des ostensifs relevant de trois
registres différents: registre de la gestualité, registre de
la trace et le registre de l'oralité. Les concepts
évoqués, que ce soit dans le discursif ou du scriptural, forment
les non ostensifs autour desquels l'articulation des ostensifs a lieu.
, les autres éléments de l'organisation
praxéologique peuvent être analysés de la même
manière. Dans le tableau suivant, nous avons consigné, en face de
chaque étape de la technique utilisée, les ostensifs
mobilisés et les non ostensifs évoqués ainsi que les
registres de ces ostensifs. Comme on l'a déjà signalé au
début de ce paragraphe, on peut observer dans ce tableau que :
à chaque étape du développement de la technique, il y a
mobilisation d'ostensifs appartenant à des registres différents
réglés par des non ostensifs. Les deux étapes les plus
importantes articulent des ostensifs relevant de trois
registres différents: registre de la gestualité, registre de
la trace et le registre de l'oralité. Les concepts
évoqués, que ce soit dans le discursif ou du scriptural, forment
les non ostensifs autour desquels l'articulation des ostensifs a lieu.
|
Etapes de la technique
|
Ostensifs
|
Registre de l'ostensif
|
Non ostensifs
|
|
  , les
signes : +, = , les
signes : +, =
|
La trace
|
-Valeur absolue
-Variable, constante
-Addition dans 
-Egalité de deux expressions algébriques.
-Equation du type T
|
|
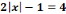
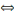
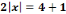 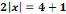
=5
|
-Déictique: montrer le mouvement de -1 vers le membre de
droite.
-Le discours accompagnant le geste.
-Scriptural : les signes d'égalité et
d'équivalence, +, écriture du membre à droite 4+1.
|
-La gestualité
-l'oralité
-La trace
|
-Règle d'équivalence entre deux
équations.
-Addition dans  . .
|
|
-Déictique: montrer le mouvement de 2 vers le
dénominateur dans le membre de droite.
-Le discours accompagnant le geste.
-Scriptural : les expressions, les signes
d'égalité et d'équivalence, écriture du membre
à droite   . .
|
-La gestualité
-L'oralité
-La trace
|
-Règle d'équivalence entre deux
équations.
-Multiplication dans  . Inverse
d'un réel. . Inverse
d'un réel.
|
|
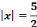
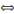
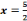 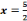 ou ou 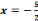 
|
-Scriptural : les expressions, les signes
d'égalité et d'équivalence, écriture des
fractions.
|
-La trace
|
Règle :
Si 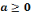 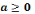
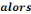
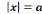 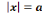 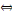 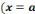 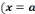 ou ou 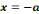 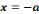 ) )
|
Tableau 2
II-4. Méthodologie
de recherche
Notre recherche est conduite selon une démarche
progressive. D'abord, le travail va porter sur les trois ingrédients
nécessaires pour la compréhension de l'analyse
praxéologique proprement dite. Il s'agit, en premier lieu, de
l'étude du lien organique entre le savoir savant et le savoir à
enseigner à ce niveau. En second lieu, de l'étude de
l'itinéraire curriculaire et du profil de l'élève de
troisième année économie et gestion ; on
découvrira si l'institution transpositive a pris acte du profil
particulier des élèves en question. Enfin, l'analyse de
l'organisation du manuel scolaire de mathématique de troisième
année EG et la description détaillée du chapitre
« Initiation aux graphes ». Ces trois
éléments d'information seront suivis de l'analyse
praxéologiques des activités du chapitre « Initiations
aux graphes » du livre scolaire de mathématique de
troisième année économie et gestion.
1- Transposition
didactique :
Dans le cas qui nous occupe, c'est-à-dire les
activités du chapitre « Initiation aux graphes »,
nous nous trouvons en présence d'une situation qui n'est pas assez
fréquente. D'abord, et comme on l'a signalé auparavant dans
l'introduction, nous ne disposons d'aucune information dans le programme
officiel qui permettrait de situer le savoir à enseigner par rapport au
savoir savant. Ensuite, il n'y a pas de document d'accompagnement qui peut
prendre en charge ce qui manque comme information dans le programme officiel.
Alors, il fallait comparer le savoir savant au savoir à enseigner selon
notre lecture des activités du chapitre « Initiation aux
graphes » du manuel scolaire. Lecture approfondie lors de notre
analyse praxéologique de toutes les tâches et qui a
corroboré notre appréhension de la dynamique transpositive.
2- Profil curriculaire de
l'élève de troisième année économie et
gestion :
L'organisation praxéologique d'une tâche t d'un
type donné T s'appuie d'abord sur un choix raisonné de la
technique permettant de réaliser la tâche, choix qui prend en
comte le profil de l'élève qui met en oeuvre (ou à qui
s'adresse) cette technique et les pré- requis en rapport avec les
composantes de cette organisation praxéologique. En d'autres termes,
l'analyse praxéologique demande un éclairage sur:
· le rapport personnel de l'individu x en position p=
« élève » à l'objet
o= « connaissances en mathématiques » dans
l'institution I=« classe de troisième année,
section : économie et gestion ».
· le rapport institutionnel RI(x,o).
· La conformité de Rp(x,o) avec
RI(x,o).
3- Organisation du manuel
scolaire :
Dans cette partie de notre recherche, nous allons
décrire le manuel scolaire officiel de mathématiques de
troisième année économie et gestion. Nous allons
focaliser notre travail essentiellement sur :
· Son organisation : les différentes
rubriques qui composent chaque chapitre.
· La description des cinq rubriques du chapitre
« Initiation aux graphes ».
· Certaines remarques concernant : la position du
chapitre dans le livre et l'énonciation ou non des compétences
à développer durant l'apprentissage des savoirs de ce
chapitre.
4- Analyse
praxéologique :
Dans cette partie, nous allons commencer par un exposé
détaillé de la praxéologie ponctuelle associée
à chaque type de tâche pour toutes les questions posées
dans les activités analysées. Nous décrivons, pour chacune
des questions posées, les éléments suivants:
· les tâches et les types de tâche
correspondants,
· la technique, notamment ses objets constitutifs de la
dichotomie fondamentale : à savoir les ostensifs mobilisés
et les non ostensifs,
· le bloc technologico- théorique.
Une synthèse des blocs pratico- techniques permettra de
circonscrire les « savoirs- faire » mobilisées tout
au long du chapitre. Nous porterons un regard assez approfondi sur les
techniques, notamment sur les registres d'ostensifs utilisés en mettant
la lumière sur les non ostensifs qui guident ces ostensifs. On
découvrira, alors, les registres d'ostensifs sur lesquels
s'étayent les techniques des organisations ponctuelles du chapitre
« Initiation aux graphes ». Par la suite, nous exposerons
une synthèse des blocs technologico- théoriques. Au terme de ce
travail de recherche, nous aurons une idée assez précise sur les
émergents spontanés d'une analyse praxéologique. Le
schéma suivant explique le cheminement suivi dans notre
recherche :
Les données objectives
Itinéraire curriculaire et profil de
l'élève
Transposition didactique
externe
Organisation du manuel scolaire et du chapitre
« Initiation aux graphes »
Analyse praxéologique
Emergents
« spontanés »
Chapitre III:
Partie analytique
Chapitre III : Partie
analytique
III-1. Analyse
transpositive
Dans cette partie, nous allons
présenter quelques éclairages à propos du passage entre
le savoir savant et le savoir à enseigner selon les activités
proposées dans le chapitre « Initiation aux
graphes » du livre scolaire de troisième année section
économie et gestion. Le nouveau programme de l'enseignement des
mathématiques4(*) met
en avant des compétences liées à la résolution des
problèmes, notamment :
- Pratiquer une démarche mathématique qui
consiste à chercher d'abord, expérimenter et formuler une
conjecture ensuite et enfin réaliser une démonstration.
- Communiquer dans un langage mathématique
- Résoudre un problème par la
modélisation d'une situation en rapport avec l'environnement de
l'apprenant puis par la mobilisation du savoir approprié.
- Utiliser les TIC.
La démarche
préconisée par ce programme consiste à émettre
des conjectures en utilisant le type de raisonnement approprié, produire
des chaînes de raisonnements déductifs afin de prouver un
résultat sinon produire un contre exemple pour montrer qu'une assertion
est fausse, élaborer une stratégie pour résoudre un
problème et, enfin, valider la solution d'un problème. Dans la page 39, le programme officiel
considère que la théorie des graphes est une partie de
l'algèbre et il n'est mentionné
que : « Théorie des graphes :
sommets, arêtes, nombre chromatique, ordre d'un graphe,
théorème d'Euler, chaînes, algorithme de
Dijkstra ». Après cela, on trouve
mentionnées quatre aptitudes dont trois concernent la théorie des
graphes. Cela pourrait donner lieu à des interprétations diverses
que ce soit de la part de ceux qui ont produit le livre scolaire ou de la part
des enseignants. Pour saisir la nature de l'objet
d'enseignement, nous allons procéder à une comparaison entre le
savoir savant présenté ci-dessus et le savoir à enseigner
tel qu'il émerge de l'analyse du contenu du chapitre «Initiation
aux graphes ». Nous estimons, en effet, que mettre le doigt sur les
différences entre le savoir savant et le savoir à enseigner, qui
nous préoccupent dans notre recherche, nous met en mesure d'avoir un
éclairage quant à la vraie intention de l'institution
transpositive sur la nature de l'objet de l'enseignement. CHEVALLARD (1998),
dans son article intitulé : Pourquoi la transposition
didactique ?, dit en substance : « Au sens
restreint, la transposition didactique désigne le passage du savoir
savant au savoir enseigné. Or, c'est la confrontation de ces deux
termes, à la distance qui les sépare, au-delà de ce qui
les rapproche et impose de les confronter, que l'on peut le mieux saisir la
spécificité didactique du savoir. ». Cette comparaison va s'étayer sur des
éléments objectifs tirés d'un côté du savoir
savant présenté et de l'autre côté par le contenu du
livre scolaire. Lequel contenu se compose essentiellement d'activités,
d'exercices, de définitions et de propriétés
énoncées (avec ou sans preuve). En plus, nous allons mettre la
lumière sur les notions utilisées et non
institutionnalisées telles que : les graphes isomorphes, les sous
graphes, etc. Nous n'avons pas analysé les
activités utilisant les TIC ni les exercices et problèmes car ils
sortent du cadre de notre étude. Comme nous
l'avons déjà signalé, le programme officiel n'est pas
très explicite ni sur le contenu de cette unité d'apprentissage
ni sur les aptitudes à développer. Nous sommes, donc, dans
l'obligation de n'étayer nos déductions que sur la base de notre
lecture du livre scolaire. L'examen des tableaux 3,
4 et 5 qui vont suivre permet de déduire l'effet de la transposition
didactique externe. Cet effet se traduit, selon
nous, par un quintuple dessein :
- Centrer les
activités sur les modélisations de situations ayant une relation
directe avec le milieu social de l'élève.
Par exemple, l'activité 1 de la page 85 traite une
situation de gestion de conflit où l'élève est dans une
situation de résolution d'un problème de maximisation du nombre
d'invités.
- Privilégier
les techniques utilisant les caractéristiques du graphe :
degrés des sommets, ordre d'un graphe, etc.
L'activité 4 est un exemple illustrant le recours
à de telles techniques. En effet, pour prouver que deux graphes
représentent la même situation, il fallait d'abord
déterminer les degrés des sommets, les ordres des sous graphes
complets, etc.
- Faire
découvrir par l'élève, au fur et à mesure,
certaines caractéristiques importantes des graphes pouvant servir comme
plateforme de résolutions de certains problèmes
intéressants, notamment concernant les circuits, le plus court chemin et
les gestions de conflits.
L'exemple donné par l'activité 3 de la page 89
permet à l'élève d'explorer les circuits et en exhiber
ceux qui sont eulériens à partir d'une caractéristique
énoncé dans le théorème d'Euler.
- Eviter de donner un
exposé classique de cette unité d'apprentissage et, surtout, ne
pas céder à la tentation des démonstrations inutiles des
théorèmes.
La démonstration du théorème d'Euler peut
être expliquée aux élèves. Cependant, et vue qu'il
s'agit d'une initiation aux graphes à des élèves de la
section économie et gestion, il n'est pas utile de céder à
la tentation de le prouver.
- Donner une
présentation fonctionnelle des algorithmes, étant donné
que les élèves n'ont pas l'habitude de traduire un algorithme
écrit sous sa forme usuelle en un discours fonctionnel.
L'algorithme de Moore-Dijkstra est le suivant :
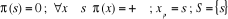
Tant que 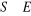 faire :
faire :
On détermine les sommets  tels que
l'arc qui relie
tels que
l'arc qui relie 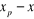 soit un
élément de E. On prendra :
soit un
élément de E. On prendra :
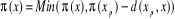 .
.
On garde l'arête 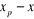 qui a
permis d'avoir ce minimum. On choisit un nouveau sommet
qui a
permis d'avoir ce minimum. On choisit un nouveau sommet 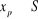 tel que
tel que
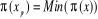 et on
posera :
et on
posera : 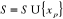 .
.
Les élèves ne peuvent pas mettre en application
cet algorithme mis sous cette forme qui utilise une forme itérative
« Tant que.... » assez complexe.
Cependant, nous avons pu remarquer
que le théorème (affirmant que dans chaque graphe d'ordre
supérieur ou égal à 2 a au moins deux sommets de
même degré) n'est pas institutionnalisé mais
présenté sous la forme d'un exercice (page 87). En outre, l'importance accordée à
l'explication de l'algorithme de Moore-Djikstra (auquel les auteurs ont
consacré six pages !) est, à notre sens,
exagérée et peut induire en erreur enseignants et
élèves quant à sa mise en application. En effet, certains
peuvent penser qu'il faut, à chaque fois, plusieurs pages pour utiliser
convenablement cet algorithme.
Dans les tableaux 3, 4 et 5 qui vont être
présentés dans les pages qui suivent, nous consignons d'un
côté les notions mathématiques telles que nous avons
présentées dans le chapitre II et, en face, les notions telles
que présentées dans le manuel scolaire. Dans la confrontation
entre le savoir savant et le savoir à enseigner, que nous allons
présenter dans les trois tableaux ci-dessous, nous allons respecter le
découpage en paragraphes adopté par les auteurs du livre
scolaire, à savoir :I-Notion de graphe, II-Coloriage d'un graphe,
III-Recherche d'une plus courte chaine, afin de mieux suivre le passage entre
le savoir savant et le savoir à enseigner selon l'interprétation
donnée par les auteurs du livre scolaire.
I-Notion de
graphe :
|
Notion mathématique
dans le savoir savant
|
Savoir à
enseigner
|
|
1- Représentation d'une
situation :
a-Définitions (d'un graphe,
de sommet, d'arête, de l'adjacence) formelles s'appuyant sur le concept
de relations dans un ensemble. On présente la définition d'un
graphe orienté, comme cas général, avant celle du graphe
non orienté comme un cas particulier.
|
1- Représentation d'une
situation :
a-Définitions (d'un graphe, de
sommet, d'arête, de l'adjacence) utilisant le langage vernaculaire et
étayées sur l'ostension d'un exemple de l'activité 1
de la page 85. On présente un exemple de graphe non orienté et on
dit « voici un graphe non orienté et voilà les
sommets et les arêtes». On observe l'amalgame entre un graphe et son
schéma (page 85).
|
|
b-Types de graphes : planaires,
bipartis, multi-graphes, complets, stables.
|
b-Types de graphes : Seuls
les graphes complets sont présentés dans le texte. La
définition est la même que dans le savoir savant.
|
|
c-Sous graphes, graphes partiels
|
c-Sous graphes, graphes
partiels : Les sous graphes sont seulement évoqués et non
institutionnalisés. On ne parle pas de graphes partiels.
|
|
d-Graphes isomorphes : La
définition utilise deux bijections, l'une entre les sommets et l'autre
entre les arêtes correspondantes.
|
d-Graphes isomorphes : Cette
appellation n'est pas indiquée dans le texte, on utilise
plutôt « graphes qui décrivent la même
situation » et on utilise, à la place des deux bijections, une
correspondance : sommet-sommet, arête- arête sans parler de
bijections.
|
|
2-Lemme des poignées de
mains : Ce lemme est donné dans un langage formel mais aussi en
langage vernaculaire.
|
2-Lemme des poignées de
mains : L'énoncé est donné en langage vernaculaire
seulement. L'activité 1 de la page 87 est destinée à
amener l'élève à conjecturer à partir de quatre
exemples. Pas de démonstration.
|
|
3-Circulation sur un
graphe :
-Définitions
de :chaîne, chaîne fermée, longueur de chaîne,
cycle, chaîne eulérienne, cycle eulérien sont
présentés soit dans un langage formel soit en langage
vernaculaire.
-Définition de la
connexité d'un graphe par une relation d'équivalence et classe
d'équivalence mais aussi en langage vernaculaire.
-Théorème d'Euler avec
démonstration.
|
3-Circulation sur un
graphe :
-Les définitions
de :chaîne, chaîne fermée, longueur de chaîne,
cycle, chaîne eulérienne, cycle eulérien sont faits
à partir d'exemples et présentés en langage
vernaculaire.
-Définition de la
connexité d'un graphe utilisant le langage vernaculaire et aussi
utilisant l'expression : « d'un seul tenant ».
-Théorème d'Euler
s'introduit d'abord à partir d'exemples simples de l'activité 3
de la page 89 puis institutionnalisé sans démonstration.
|
Tableau 3
II-Coloriage d'un
graphe :
|
Notion mathématique dans le savoir
savant
|
Savoir à
enseigner
|
|
-Définitions du coloriage d'un
graphe, du nombre chromatique.
|
-L'activité 1 de la page 91
permet de comprendre l'intérêt du coloriage d'un graphe et le
champ d'application du coloriage.
-Mêmes définitions du
coloriage d'un graphe, du nombre chromatique.
|
|
-Définitions du nombre
chromatique d'un graphe complet, d'un cycle et d'un graphe biparti.
|
-Le nombre chromatique d'un graphe
complet utilisant la même définition est étudié dans
l'activité 4 de la page 93.
-Le nombre chromatique d'un cycle est
évoqué dans l'activité 5 de la page 93.
-Le nombre chromatique d'un graphe
biparti n'est pas à enseigner.
|
|
-Comparaison du nombre chromatique
d'un graphe avec ses sous graphes.
|
-L'activité 6 de la page 93
étudie la comparaison du nombre chromatique d'un graphe avec ses sous
graphes sur un cas général.
|
|
-Encadrement du nombre
chromatique.
|
-Encadrement du nombre chromatique
à partir d'exemples, donc sans démonstration. On étaye cet
encadrement sur deux activités : l'activité 6 de la page 93
pour sa minoration et l'activité 7 de la page 93 qui présente un
cas pour sa majoration.
|
|
-Algorithme de Walsh et Powell
|
-Algorithme de Walsh et Powell :
même présentation en langage vernaculaire.
La mise en oeuvre de cet algorithme
est faite sur des exemples de l'activité 2 de la page 92.
-Le cas particulier qui montre que
cet algorithme ne donne pas toujours le nombre chromatique est donné
dans l'activité 3 page 92.
|
Tableau 4
III-Recherche d'une plus
courte chaîne:
|
Notion mathématique dans le savoir
savant
|
Savoir à
enseigner
|
|
-Définitions : d'un
arbre, d'une forêt
|
-Les définitions concernant
l'arbre, la forêt ne sont pas à enseigner.
|
|
-Définition de graphe
pondéré en langage formel où la pondération peut
être un réel positif ou négatif.
|
-La définition de graphe
pondéré n'est pas présentée dans un langage formel
mais en langage vernaculaire et le coefficient de pondération est un
réel positif.
|
|
-Les définitions du poids
d'une chaîne et d'une plus courte chaîne sont données en
langage formel.
|
-Les définitions du poids
d'une chaîne et d'une plus courte chaîne sont données en
langage vernaculaire.
|
|
-La proposition concernant les
sous chemins d'une plus courte chaîne est démontrée
|
-La proposition concernant les
sous chemins d'une plus courte chaîne est évoquée mais pas
institutionnalisée.
Cette proposition n'est pas a
démontrer.
|
|
-L'algorithme de Moore-Djikstra est
présenté dans un langage formel apprêté pour sa
traduction en langage programmable.
|
-L'algorithme de Moore-Djikstra est
expliqué en détail sur un exemple :pages 97-102 (six pages).
Le résultat final qui a une structure d'arborescence est à
signaler sans parler d'arborescence.
-Aucun texte présentant
l'algorithme n'est donnée.
|
Tableau 5
III-2. Itinéraire curriculaire et profil d'un
élève de troisième année EG
Rappelons que, dans une organisation praxéologique
d'une tâche t d'un type donné T, le choix d'une technique est
dicté, entre autres, par la connaissance du profil de celui ou celle
qui met en oeuvre cette technique. Dans le cas de notre objet de recherche, il
s'agit de l'élève de troisième année EG. Nous nous
proposons, donc, d'étudier son profil et son itinéraire
curriculaire et le situer dans l'ensemble du système scolaire tunisien.
L'enseignement scolaire tunisien est constitué
de :
· L'enseignement de base qui est réparti en deux
cycles : le cycle primaire d'une durée de six ans et le cycle
préparatoire d'une durée de trois ans.
· L'enseignement secondaire qui s'étale sur quatre
ans.
Le schéma suivant indique les itinéraires
scolaires de la première année de l'école de base
jusqu'à la terminale. On y a consigné, en gras et
souligné, l'itinéraire d'un élève de
troisième année EG à partir de la première
année de l'enseignement primaire.
Second cycle de l'enseignement de base.
Durée : 3 années
Lieu : école préparatoire
(collège)
Premier cycle de l'enseignement de base.
Durée : 6 années
Lieu : école primaire
Cycle de l'enseignement secondaire.
Durée : 4 années
Lieu : lycée
Tronc commun
ES
TI
Sciences
EG
SI
M
Sc exp
ST
L
L
4ème
3ème
2ème
1ère
EG
SI
M
Sc exp
ST
L
![]()
Itinétaire curiculaire au
lucée
Nous observons, donc, qu'un élève inscrit en
troisième année EG (qui correspond au niveau de première
dans le système français) a déjà fait six
années à l'école primaire, trois années dans un
collège pour achever le cursus de l'école de base puis entre
dans un lycée dans lequel il a passé:
- Une première année en tronc commun
- Une deuxième année en section Economie et
Services (ES)
Selon le guide d'orientation, un élève n'est
orienté vers la deuxième année ES que s'il est jugé
« assez bon en mathématiques et dans les matières
littéraires et sociales ». La réalité est toute
autre. La majorité des élèves qu'on oriente vers la
section Economie et Services sont ceux qui ne sont ni assez bon dans les
matières scientifiques et techniques pour être orientés
vers les sections scientifiques ni ayant une vocation franchement
littéraire pour être aiguillés vers la section Lettres. Ces
élèves ont, en général, une estime de soi assez
négative par rapport aux mathématiques dites classiques :
Algèbre, Géométrie, etc.
Ainsi, malgré l'innovation en matière
d'orientation (loi 2002) qui consiste à procéder par aiguillage
progressif : la filière puis la section, les conseillers
d'orientation ont noté que la section EG attire de plus en plus
d'élèves essentiellement « non orientables »
et non les élèves qui ont le profil indiqué dans la fiche
d'orientation. En termes de Théorie Anthropologique du Didactique, on
peut noter que le rapport personnel d'un élève de
troisième année EG à l'institution classe troisième
EG est différent du rapport institutionnel
« idéal ». Donc, cet élève est
considéré par les conseillers d'orientation comme un mauvais
sujet. Cette situation, bien connue d'ailleurs de tous les intervenants directs
dans le système scolaire tunisien (directeurs, inspecteurs, enseignants,
conseillers d'orientation, parents, etc.), fait l'objet de questionnements sur
les moyens d'orienter les meilleurs élèves vers la section EG.
III-3. Organisation du manuel scolaire officiel et description
du chapitre
III-3.1.Organisation du manuel
scolaire
Le manuel scolaire officiel de mathématiques de
troisième année économie et gestion est
édité par le Centre National Pédagogique (CNP) pour
être utilisé par les enseignants et les élèves comme
unique manuel officiel à partir de l'année scolaire 2006-2007. Ce
manuel est fait conformément aux choix et aux stratégies
fixés dans la nouvelle orientation du système éducatif
tunisien (la réforme 2002). Il est composé des douze chapitres
suivants :
1) Statistiques
2) Suites réelles
3) Dénombrements
4) Probabilité
5) Théorie des graphes
6) Système d'équations linéaires
7) Généralités sur les fonctions
8) Limite finie en un point et continuité
9) Extension de la notion de limite et branches infinies
10) Dérivation
11) Exemples d'études de fonctions
12) Fonctions trigonométriques
On observe que les chapitres 7 jusqu'à 12 sont
consacrés à l'analyse des fonctions et donc forment une
unité organique. Le reste des chapitres sont dédiés aux
autres activités mathématiques correspondants aux cinq
domaines suivants : dénombrement, probabilités et
statistiques, suites réelles, théorie des graphes et enfin
système d'équations linéaires. Ce manuel se
caractérise par l'organisation de chaque chapitre en cinq
rubriques identifiables par les couleurs de la bande supérieure des
pages et surtout par les intitulés:
· Pour commencer :
Cette rubrique propose des activités relatives
essentiellement aux pré-requis afin d'aborder le chapitre sans
« incidents ». Il s'agit, en fait, d'activités avec
des questions très variées allant de questions fermées du
type QCM ( chapitres 1 et 2) pour certains chapitres aux questions ouvertes
à réponses longues pour les autres chapitres à l'exception
du chapitre 4 où cette rubrique disparait. Cette rubrique est
reconnaissable par la couleur bleue de la bande supérieure des pages.
· Le cours :
Dans cette rubrique, des activités sont proposés
pour être utilisées dans les différents moments didactiques
de la leçon. Les définitions et les théorèmes sont
présentés sous une forme facilement repérable : ils
figurent dans un cadre plein colorié. Les définitions sont
placées avec leur intitulé dans un rectangle à angles
arrondis de couleur orange, les théorèmes avec leur
intitulé dans des rectangles bleus. Les remarques et les rappels sont
consignés dans des rectangles pleins de couleur jaune. Cette rubrique
est reconnaissable par la couleur rouge de la bande supérieure des
pages.
· Utilisation des TIC5(*) :
Cette rubrique, reconnaissable par la couleur orange de la
bande supérieure des pages, a pour rôle principal d'habituer
l'élève à l'utilisation de l'outil informatique pour
étudier certaines situations mais aussi pour résoudre des
exercices.
· Exercices et problèmes :
Cette rubrique propose des exercices d'application directe des
notions étudiées, des applications d'intégration,
c'est-à-dire combinant les connaissances du chapitre avec ceux relevant
d'autres domaines des mathématiques (Arithmétique, par exemple)
et des applications de transfert (tirées de contextes
différents). Certains de ces exercices et problèmes sont
liés aux situations réelles de l'activité
économique et sociale et permettent à l'élève
d'apprécier la portée et l'utilité des concepts
étudiés en classe. Cette rubrique est reconnaissable par la
couleur verte de la bande supérieure des pages.
· Math et culture :
Dans cette rubrique, on trouve des aperçus historiques
sur les notions étudiées dans le chapitre ou la biographie d'un
mathématicien de premier plan. Cette rubrique est reconnaissable par la
couleur violette de la bande supérieure des pages.
Les compétences disciplinaires à
développer en rapport avec les concepts du chapitre ne sont pas
énoncées, chose qui se faisait dans les anciens manuels. Le
chapitre annoncé au sommaire (page 3) « Théorie des
graphes » est intitulé, en fait, « Initiations aux
graphes » dans la partie du livre qui lui est consacrée (pages
82-113). Le chapitre consacré à la théorie des graphes
occupe la cinquième position sur les six chapitres qui ne sont pas
dédiés à l'analyse des fonctions et des suites
réelles. Cette avant dernière position peut suggérer aux
enseignants de traiter cette partie du programme dans les dernières
semaines de l'année scolaire mais aussi elle peut être entendue,
par les élèves, comme indice de degré d'exigence
élevé pour sa compréhension.
III-3.2.Description du
chapitre « Initiations aux graphes »
Le chapitre « Initiation aux graphes »
est, à l'instar des autres chapitres, organisé en cinq
rubriques:
-Pour
commencer.
-Cours :
v Notion de
graphe.
v
Représentation d'une situation à l'aide d'un
graphe.
v Lemme de
poignées de mains.
v circulation sur un
graphe.
v Coloriage d'un
graphe.
v Recherche d'une plus
courte chaîne.
-Utilisation
des TIC.
-Exercices et
problèmes.
-Math culture.
Nous allons décrire, une à une, toutes ces
rubriques :
o La rubrique « Pour
commencer » :
Elle est composée de cinq activités qui motivent
certes l'élève à s'intéresser aux graphes mais ne
traitent en aucun cas les connaissances antérieures indispensables
à l'élève comme annoncé par les auteurs dans la
préface à la page 2 du livre. En fait, dans cette page, les
auteurs indiquent que « dans cette rubrique sont proposées
des activités dans l'intention de faire le point sur les connaissances
antérieures indispensables à l'élève pour aborder
un nouveau chapitre ». A notre avis, les raisons de cette
absence de traitement des connaissances antérieures sont :
- La théorie des graphes est introduite pour la
première fois dans le cursus scolaire de l'élève et, en
conséquence, on ne demande pas à un élève de
mobiliser des connaissances antérieures à propos de cette
théorie.
- L'objet du chapitre est une simple initiation aux graphes
sans aucune démonstration des théorèmes et, donc, il n'y a
pas de pré-requis du même domaine pour ce chapitre.
Parmi les cinq activités proposées dans cette
rubrique nous trouvons quatre activités qui introduisent la notion de
coloration d'un graphe (ce sont les activités 1, 2, 4 et 5) et une
activité qui évoque les graphes eulériens
l'activité 3).
o La rubrique
« cours » :
La sous rubrique :« Notion de
graphe» :
Cette sous rubrique contient dix neuf activités dont
cinq intitulées « exercices ». Les auteurs
n'indiquent pas dans l'introduction les différences entre ce qu'ils
appellent « activité » et ce qu'ils désignent
par « exercice ». Cependant, nous avons noté que les
activités traitent essentiellement des situations de la vie courante
alors que les exercices (à l'exception de l'exercice du bas de la page
87), et qui ne devrait pas figurer dans cette rubrique, servent à
approfondir une notion institutionnalisée. On observe, en outre, que
l'activité 2 de la page 86 pose un problème d'existence de
boucles : un verbe est conjugué au même temps que lui
même. Or, les boucles ont une existence dans les graphes multiples, qui
ne figurent pas au programme et pas dans les graphes simples, objets du
programme de la troisième année économie et gestion.
La sous rubrique « coloration d'un
graphe » :
Dans cette rubrique, on trouve huit activités dont un
seul intitulé « exercice ». L'activité 1 de
la page 91 est la plus importante du point de vue moments didactiques car, non
seulement elle présente une situation de gestion de conflits,
principale caractéristique des problèmes faisant recours à
la modélisation et au coloriage des graphes, mais surtout elle introduit
les éléments technologiques servant à sa
résolution. En fait, si nous suivons la logique des séquences des
questions nous allons constater qu'il s'agit des étapes à suivre
pour réaliser la tâche annoncée au début par la
phrase « on se propose de résoudre le problème P
suivant : Quel est le nombre d'aquariums
nécessaires ? ». Nous sommes, ainsi, en présence
d'une activité servant au second moment didactique, c'est-à-dire
celui de l'exploration du type de tâche et de l'élaboration d'une
technique appropriée.
La sous rubrique « Recherche d'une plus courte
chaine » :
Cette rubrique est composée de cinq activités.
L'activité 3 de la page 95 est incontournable car elle explique, en
fait, comment fonctionne l'algorithme de Moore-Djikstra. L'activité 1
introduit la notion de graphe pondéré. Il s'agit de trouver le
plus court chemin entre Bizerte et Le Kef à partir du réseau
routier entre cinq villes : Le Kef, Tabarka, Jendouba, Bizerte et Tunis.
La seconde activité présente une situation où l'on cherche
à minimiser la somme dépensée en péage dans
réseau autoroutier. Dans l'activité 3, il est question
d'illustrer le mécanisme de l'algorithme de Moore-Djikstra sur un cas de
propagation d'un virus dans un réseau d'ordinateurs. L'activité 4
est une application de l'algorithme de Moore-Djikstra sur un cas d'un
réseau routier. Dans l'activité 5, nous avons un autre cas
d'application de l'algorithme de Moore-Djikstra sur la minimisation du cout de
livraison d'un commerçant.
La rubrique « Utilisation des
TIC » :
Dans cette rubrique, on trouve deux activités qui font
suite à deux travaux pratiques (pages 104-106). Ces dernières
sont une sorte de guide méthodologique de l'utilisation du logiciel en
ligne gratuit Grin40. Ce logiciel permet de créer, modifier et faire un
travail de recherche sur les caractéristiques d'un graphe orienté
ou non, soit en manipulant les informations dans la feuille des données
soit directement sur le graphe par un travail interactif sur écran. Il
permet de résoudre les problèmes liés aux grands graphes
(ayant jusqu'à 250 sommets), notamment: les cycles Eulériens et
Hamiltoniens, la coloration, les plus cours chemins et les chemins critiques.
En plus, le logiciel GRIN40 permet le passage aisé entre la matrice
d'adjacence et le graphe, ce qui permet de contrôler les donner ou de les
insérer dans un rapport. Ce logiciel gratuit est l'oeuvre de
PETCHENKINE Vitaly (E-mail :pechv@mail.ru).
o La rubrique « Exercices et
problèmes »:
Cette partie est composée de vingt sept exercices
pouvant servir au travail des techniques, donc au cinquième moment
didactique où il est question de travailler les techniques en vue de
leur routinisation.
Ces exercices ne sont réparties ni par rubrique ni par
ordre de difficulté.
o La rubrique « Math
culture » :
Dans cette rubrique, On trouve un très bref
aperçu historique de la théorie des graphes depuis Euler et
certaines applications de cette théorie dans des domaines importants de
la vie économique et sociale ainsi que dans d'autres domaines
scientifiques.
Nous avons consigné, dans le tableau suivant, la
ventilation des activités, les exercices et les travaux pratiques (TP)
du chapitre « Initiation aux graphes » par rubrique ainsi
que les éléments institutionnalisés. On peut observer
qu'il y a trente quatre activités à la disposition de
l'enseignant pour être utilisées en classe. Institutionnellement,
il peut utiliser d'autres supports pédagogiques en complément ou
à la place. Seulement, comme il est l'unique manuel officiel et que le
programme officiel n'est pas explicite, il est difficile à un enseignant
de s'en éloigner. D'où son importance.
|
Rubrique
|
Pages
|
Nombre
|
Eléments institutionnalisés
|
|
Activités
|
Exercices
|
TP
|
|
Pour commencer
|
83-84
|
5
|
-
|
-
|
-
|
|
Notion de graphe
|
85-91
|
14
|
5
|
-
|
Définitions : d'un graphe, sommet, arête,
sommets adjacents, degré d'un sommet, sommet isolé.
Lemme des poignées de mains. Chaîne, longueur
d'une chaîne, cycle, graphe connexe, chaîne eulérienne,
cycle eulérien. Théorème d'Euler.
|
|
Coloriage d'un graphe
|
91-94
|
7
|
1
|
-
|
Définitions de : coloriage d'un graphe, nombre
chromatique, nombre chromatique d'un graphe complet et d'un sous graphe.
Encadrement du nombre chromatique. Algorithme de Walsh et Powell.
|
|
Recherche d'un plus court chemin
|
95-103
|
5
|
-
|
-
|
Définition de : graphe pondéré,
poids d'une chaîne, plus courte chaîne.
Algorithme de Moore-Djikstra.
|
|
Utilisation des TIC
|
104-108
|
2
|
-
|
2
|
Utilisation d'un logiciel.
|
|
Exercices
|
109-112
|
-
|
27
|
-
|
|
|
Math culture
|
113
|
1
|
-
|
-
|
Appréciation des apports des mathématiciens.
|
|
Total
|
-
|
34
|
33
|
2
|
|
Tableau 6
III-4. Analyse
praxéologique des activités du chapitre « Initiation
aux graphes »
Dans cette partie, nous allons exposer d'abord la
praxéologie ponctuelle associée à chaque type de
tâche pour toutes les questions posées dans les activités
analysées. On présentera, pour chaque question, les tâches
et les types de tâche correspondants et, par le menu détail, la
technique ainsi que ses objets constitutifs de la dichotomie
fondamentale : à savoir les ostensifs mobilisés et les non
ostensifs et enfin le bloc technologique- théorique. Les commentaires
qui suivent l'analyse praxéologique donnent des éclairages quant
au lien entre chaque praxéologie ponctuelle exposée et :
v les éléments constitutifs du triangle
didactique, notamment le pôle « Savoir ».
v le moment didactique au cours duquel l'activité
pourrait être réalisée.
Les activités retenues pour l'analyse
sont consignées dans le tableau 7.
A la fin de ce paragraphe, nous donnerons une synthèse
des analyses praxéologiques des activités du manuel. Nous
présenterons d'abord une synthèse des blocs pratico- techniques
afin de montrer quelles sont les « Savoirs- faire »
mobilisées tout au long du chapitre. Nous mettrons en relief, quand cela
est possible, les cas de pénurie praxéologique et leur rapport
avec l'épaisseur ostensive. Ensuite, nous exposerons une synthèse
des blocs technologico- théoriques pour en tirer les
« Savoirs » mis en oeuvre qui justifient les techniques.
Le chapitre intitulé « Initiation aux
graphes » du livre scolaire de troisième année,
section : économie et gestion, compte trente activités
réparties comme suit :
· Cinq activités dans le paragraphe
« Pour commencer». Ces activités ne seront pas
analysées car, à notre avis, elles sont présentes dans le
manuel parce que cette rubrique fait partie intégrante de la structure
générale du livre telle qu'elle est conçue par ses auteurs
« dans l'intention de faire le point sur les connaissances
antérieures indispensables à l'élève pour aborder
un nouveau chapitre » alors que les activités proposées
ne répondent pas à cette intention .
· Quatre activités dans le sous paragraphe
« 1- Représentation graphique à l'aide d'un
graphe » du paragraphe « I- Notion de graphe ».
Nous avons analysé trois activités et nous n'avons pas
analysé l'activité 2 de la page 86 pour la simple raison que
cette activité pose le problème des boucles qui ne figurent pas
au programme officiel. Nous estimons que la simple présence d'une telle
activité posera des problèmes sémantiques pour les
élèves comme pour les enseignants qui vont, dans le cas
échéant, éviter d'aborder la réflexivité de
la relation proposée afin de ne pas déborder des limites du
programme.
· Cinq activités dans le sous paragraphe
« 2- Lemme de poignées de mains » du paragraphe
« I- Notion de graphe ». Nous avons analysé
l'activité 1 de la page 87 et les deux activités 4 et 5 de la
page 88. Les autres activités ne sont pas analysées car elles ne
présentent pas d'intérêt particulier. En effet,
l'activité 2 de la page 87 aborde le thème de championnat de 24
équipes, lequel thème peut être abordé de
manière spontanée en dehors du contexte des graphes ou à
la rigueur est une répétition du schéma de graphe complet.
En plus, la tâche pose un questionnement sur le type de
championnat : est-ce un championnat à aller simple ? est-ce
un championnat avec aller et retour ? L'autre activité non
abordée est l'activité 3 de la page 87 dont la technique exige
l'utilisation du raisonnement par l'absurde ou l'utilisation de la proposition
contraposée et qui, à notre sens, pourrait poser des
problèmes quant à sa compréhension.
· Cinq activités dans le sous paragraphe
« 3- Circulation sur un graphe » du paragraphe
« I- Notion de graphe ». Nous avons analysé cinq
activités (intitulées par les auteurs du manuel comme
étant quatre activités et un exercice). L'activité 5 de la
page 91 n'a pas été analysée pour la simple raison que le
texte nous semble poser un autre problème de raisonnement par
l'absurde.
· Huit activités dans le paragraphe
« II- Coloriage d'un graphe ». Nous avons analysé
sept activités et nous n'avons pas analysé l'activité 8 de
la page 94 pour la simple raison que cette activité pose le
problème représentation graphique à 24 sommets. Cette
représentation, par son encombrement, n'est évidemment pas
lisible et donc non exploitable techniquement.
· Sept activités dans le paragraphe
« III- Recherche d'une plus courte chaîne ». Nous
avons analysé les deux premières, les autres activités
sont présentées avec leurs résolutions. Il serait peut
être intéressant de les analyser mais alors cette analyse ne se
réduirait à une simple description de la technique
proposée par les auteurs et des spéculations sur les
articulations entre les registres ostensifs et surtout sur les non ostensifs du
bloc pratico- technique.
Dans le tableau 8, nous résumons de toutes les
remarques précédentes.
|
Paragraphe
|
Sous paragraphe
|
page
|
Activités
|
|
I-Notion de graphe
|
1-Représentation graphique
|
85
|
1
|
|
86
|
3 et 4
|
|
2-Lemme des poignées de mains
|
87
|
1
|
|
88
|
4 et 5
|
|
3-Circulation dans un graphe
|
88
|
1
|
|
89
|
2 ; 3 et exercice
|
|
II-Coloriage d'un graphe
|
|
91
|
1
|
|
92
|
2 et 3
|
|
93
|
4 ; 5 et 7
|
|
94
|
Exercice
|
|
III-Recherche d'une plus courte chaîne
|
|
95
|
1 et 3
|
Tableau 7
|
Paragraphe
|
Sous paragraphe
|
Activité non analysée
|
Raison
|
|
I-Notion de graphe
|
1-Représentation graphique
|
2 page 86
|
Problème de boucle.
|
|
2-Lemme des poignées de mains
|
2 et 3
page 87
|
Pas d'intérêt pour notre analyse
|
|
3-Circulation dans un graphe
|
5 page 91
|
Problème de formulation.
|
|
II-Coloriage d'un graphe
|
|
8 page 94
|
Problème de nombre de sommets
|
|
III-Recherche d'une plus courte chaîne
|
|
Les activités autres que 1 et 2
|
Sont résolues
|
Tableau 8
III-4.1.Analyse des activités par le modèle des
quatre T
Dans ce paragraphe, nous présentons, d'abord et par
activité retenue pour l'analyse, l'énoncé de
l'activité. Puis, chaque question de cette activité est traduite
en termes de tâche ou d'ensemble de tâches. Pour chaque
tâche, nous avons consigné le type de tâche, la technique
mobilisée et le bloc technologico- théorique. Nous avons
relevé, pour chaque bloc pratico technique, les ostensifs
manipulés et les non- ostensifs qui les guident. Nous avons choisi,
compte tenue de ce que nous présupposons en termes d'habitudes
gestuelles, les ostensifs déictiques mais qu'on peut remplacer, selon le
contexte, en n'importe quel ostensif gestuel jouant le même rôle.
Chaque analyse praxéologique est suivie de commentaires sur les
résultats relevés au cours de cette analyse.
Il est utile de signaler que, compte tenu de la nature des
notions abordées dans le chapitre « initiation aux
graphes », chaque type de tâche correspond à une
technique particulière, d'ailleurs ciblée par les auteurs du
manuel scolaire. Ainsi, nous ne nous trouvons pas en présence d'analyses
praxéologiques pour lesquelles un type de tâche mobilise plusieurs
organisations mathématiques et qui nous oblige à justifier le
choix de telle organisation mathématique.
Activité 1 page 85
i)Enoncé :
Une personne souhaite inviter
six amis que nous désignons par 1, 2, 3, 4, 5, 6. Malheureusement,
certains de ces six amis ont des relations difficiles ; ce sont celles
recensées dans le tableau suivant :
|
Ami
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Relations difficiles avec
|
2
|
1, 5, 6
|
5
|
5
|
2, 3 , 4, 6
|
2, 5
|
On veut résoudre le problème P
suivant : Combien de personnes au maximum peuvent être
invitées ensemble sans risque de problème ?
1) Représenter chaque ami par un point.
2) Relier deux points représentant deux personnes
ayant une relation difficile.
3) Vérifier que l'on a un des
schémas
1 3 6
1 3 2
6
2
5 1
6
2 5
4 4 5
3
6
4) Résoudre le problème P.
ii)Analyse praxéologique:
La question 1 : Représenter chaque ami par un
point.
Le travail demandé n'est pas une tâche puisqu'il
a déjà été naturalisé depuis le primaire.
La question 2 : Relier deux points
représentant deux personnes ayant une relation difficile.
Tâche et type de tâche : Pour la
tâche, il s'agit de relier deux points représentant deux personnes
ayant une relation difficile par une ligne. Cela appartient au type de
tâche T= «Relier deux points x et y d'un ensemble sur lequel on a
défini une relation R et tel que xRy ».
Il s'agit d'une tâche routinière.
Technique : On trace une ligne
d'extrémités x et y si R est symétrique et une ligne
orientée si R n'est pas symétrique.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de la trace:
traçage des lignes qui représentent les arcs (les liens de
relation difficile).
-Ostensifs discursifs relevant du registre de
l'oralité: le discours accompagnant le traçage des lignes.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants :
-On peut tracer, d'une infinité de manières,
un arc joignant deux points quelconques du plan.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Relation binaire
|
Théorie des ensembles
|
La question 3 : Vérifier que l'on a un des
schémas
Tâche et type de tâche : Pour la
tâche, il s'agit de vérifier pour chacun des graphes
proposés s'il répond aux contraintes données dans le
texte. Cette tâche appartient au type de tâche T=
«Vérification si le diagramme représente fidèlement
la relation donnée ».
La tâche semble à première vue
routinière puisqu'il s'agit de vérification de conformité.
Seulement, l'élève, ne disposant pas d'une stratégie
institutionnalisée, est obligé de proposer sa propre
stratégie afin de s'assurer du résultat.
Technique : On vérifie un à un les
liens sur le tableau à partir du diagramme. Si la ligne sur le diagramme
ne correspond pas au lien sur le tableau on élimine ce diagramme, sinon
on passe au lien suivant jusqu'à épuisement des lignes.
Les élèves découvriront que le premier
schéma ne représente pas la situation proposée alors que
les deux autres la représentent, mais au même temps ils
découvrent qu'une même situation est représentable par
plusieurs schémas.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité (plus exactement la deixis gestuelle) : On montre le
lien sur le tableau et la présence ou l'absence de ce lien sur le
schéma sélectionné. Cela se fait en pointant l'index sur
l'information existant au tableau puis sur l'information correspondante sur le
schéma.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant le gestuel.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants :
-Il vaut mieux observer les différences plutôt
que les similarités par soucis d'économie d'effort.
-Recherche d'un contre exemple.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Représentation graphique d'une relation
|
Théorie des ensembles
|
|
Preuve de la fausseté d'une proposition
|
Logique formelle
|
La question 4 : Résoudre le problème P.
Tâche et type de tâche : Pour la
tâche, il s'agit de maximiser le nombre d'invités de sorte que
chaque invité n'ait de relation difficile avec aucun autre. Cette
tâche s'inscrit dans le type de tâche T= «Maximiser le nombre
sommets xi de sorte que, xi nonR xj pour
i j
».
j
».
Cette tâche est problématique. Elle se
présente à l'élève pour la première fois et
sa résolution est loin d'être évidente et il va être
obligé de recourir à différentes stratégies pour
éliminer le minimum possible d'amis et de comparer le résultat
avec le reste des élèves.
Technique : On colorie les sommets xi
de sorte que deux sommets adjacents n'aient pas la même couleur. On
essaie de minimiser le nombre de couleurs.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs matériels relevant du registre de la
matérialité quelconque6(*): coloriage de chaque sommet.
-Ostensifs discursifs relevant du registre de
l'oralité : Les discours accompagnant le coloriage pour le choix de
la couleur, choix des sommets de même couleur, justification des choix,
etc.
-Ostensifs déictiques relevant du registre de la
gestualité : On montre que deux sommets adjacents quelconques n'ont
pas la même couleur en pointant l'index sur les sommets adjacents. .
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants :
-Il est toujours possible de faire un choix de personnes qui
n'ont pas de relations difficiles.
-la méthode connue sous l'appellation
« essai /erreur » et le travail collectif en classe,
permettent, de proche en proche, d'arriver à maximiser le nombre de ces
invités.
Bloc technologico- théorique : Lemme des
choix de Zorn, Théorie des ensembles, théorie des graphes.
|
Technologie
|
Théorie
|
|
Lemme du choix de Zorn
|
Logique formelle et théorie des ensembles
|
|
Définition du coloriage des sommets
|
Théorie des graphes
|
iii)Commentaire :
Dans cette activité, l'élève est
invité dans les deux premières questions à suivre des
consignes précises. Nous aurions préféré une
situation-problème qui ne se résout qu'en vérifiant,
d'abord, que toutes les stratégies connues par l'élève ne
permettent pas de résoudre le problème, et que la seule
stratégie qui permet de s'en sortir est celle qui utilise des points et
des courbes qui relient ces points. Les auteurs ont, peut être, sous
estimé le rôle du second moment didactique dans l'introduction du
concept « graphe » si bien que, pour un
élève, le graphe paraîtrait comme un outil artificiel non
nécessaire car imposé par le texte et non par les besoins de la
résolution d'un problème.
En principe, et vu qu'il s'agit de la première
activité proposée, elle est censée être prise comme
situation à présenter au premier moment didactique,
c'est-à-dire le moment de première rencontre avec la notion de
graphe non orienté. Cette rencontre, qui va orienter la conception de
l'élève sur ces graphes ainsi que sur leurs utilités, va
se dérouler à travers une situation pratique et qui fait
intervenir les graphes comme artefact pour sa résolution. L'analyse
praxéologique précédente montre que :
- Les deux premières tâches sont, en fait, des
tâches isolées et simples à mettre en oeuvre.
- La troisième tâche fait appel à une
technique d'identification de schémas, c'est-à-dire au concept de
« graphes isomorphes » que les élèves
n'étudieront pas mais qui sera contextualisé par
l'activité 4 de la page 86.
- La quatrième tâche, qui est en fait l'objet de
l'exercice, s'appuie sur la technique de coloriage. Mais cette technique n'est
pas encore connue des élèves. Dans ce cas, l'enseignant,
guidé par cette technique, est amené à orienter les
recherches dans la direction de la praxéologie décrite plus
haut.
En somme, on observe, durant cette activité de
première découverte, une pénurie praxéologique qui
découle de la non identification de bloc tehnologico - théorique
qui permet de justifier les réponses des élèves (tel que
la question 4). Cette pénurie praxéologique chez les
élèves est compensée par un travail empirique
s'étayant sur un ensemble d'ostensifs écrits, oraux et gestuels.
Le rapport personnel de l'élève de troisième année
économie et gestion avec la discipline va progressivement changer
à partir de cette activité.
Activité 3 page 86
i)Enoncé :
1) Dessiner un graphe d'ordre 4 tel que chaque sommet est
adjacent aux autres.
2) a/ Dessiner un graphe de sommets A, B, C, D, E et F tel
que :
-A est adjacent à C, D et E.
-B est adjacent à D.
-C est adjacent à A et E.
b/ Déterminer le nombre d'arêtes ayant
pour extrémité D.
ii)Analyse praxéologique:
La question 1 : Dessiner un graphe d'ordre 4 tel que
chaque sommet est adjacent aux autres.
Tâche et type de tâche : Pour la
tâche, il s'agit de représenter le graphe complet K4
relevant du type de tâche T= « représentation d'un
graphe complet Kn ».
Cette tâche peut être considérée
à ce stade comme routinière. En effet, l'élève sait
déjà comment représenter un graphe connaissant les listes
d'adjacence.
Technique : On place quatre sommets puis on
procède comme suit :
-On connecte le premier sommet aux trois autres.
-On connecte le second sommet au troisième et
quatrième sommet.
-On raccorde le troisième au quatrième sommet
par une arête.
On peut vérifier que tous les sommets sont
adjacents.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace: traçage des sommets et des arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant le traçage.
-Ostensifs déictiques relevant du registre de la
gestualité : On utilise l'index ou une règle ou tout autre
objet permettant l'ostentation pour accompagner la preuve que tous les sommets
sont adjacents.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant :
-Le graphe étant symétrique, on peut utiliser
le même raisonnement que pour les combinaisons 2 à 2 d'un ensemble
à 4 éléments.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Liste d'adjacence et représentation d'un graphe
|
Théorie des graphes
|
|
Définition d'un graphe complet
|
Théorie des graphes
|
La question 2)a/ Dessiner un graphe de sommets A, B, C, D,
E et F tel que :
-A est adjacent à C, D et E.
-B est adjacent à D.
-C est adjacent à A et E.
Tâche et type de tâche : Pour la
tâche, il s'agit de dessiner le graphe dont les sommets et la liste
d'adjacence sont donnés dans le texte. Cette tâche appartient au
type de tâche T= «représentation d'un graphe dont on
connaît les sommets et la liste d'adjacence ». Cette
tâche est routinière pour la même raison qu'on a
évoquée plus haut.
Technique : On place les six sommets A, B, C, D, E
et F puis on procède comme suit :
-On trace les arêtes A-C, A-D et A-E.
-On trace l'arête B-D.
-On trace l'arête C-E.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de trace:
traçage des sommets et des arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant le traçage des
arêtes.
-Ostensifs déictiques relevant du registre de la
gestualité : On utilise l'index ou une règle ou tout autre
objet permettant l'ostentation des arêtes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant :
-Le graphe est symétrique.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Représentation graphique d'un graphe
|
Théorie des graphes
|
La question 2) b/ Déterminer le nombre
d'arêtes ayant pour extrémité D.
Tâche et type de tâche : Pour la
tâche, il s'agit de déterminer le degré du sommet D
relevant du type de tâche T=«Détermination du degré
d'un sommet ».
Cette tâche est routinière.
Technique : On compte les arêtes dont le
sommet D est une extrémité.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On utilise l'index ou une règle ou tout autre
objet permettant d'accompagner le comptage des arêtes dont le sommet D
est une extrémité.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours du comptage.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant :
-On se place au sommet D sur le graphe déjà
construit pour commencer le comptage.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition du degré d'une arête dans un
graphe non orienté
|
Théorie des graphes
|
iii)Commentaire:
Cette activité correspond au cinquième moment
didactique, c'est-à-dire le moment de travail de la technique. Toutes
les tâches sont routinières et l'élève va donc
investir les savoirs acquis pour établir un rapport personnel avec
l'objet « graphe ». La première question met
l'élève en rapport avec les graphes complets qui ont un statut
spécial en théorie des graphes et qui vont lui permettre plus
tard de justifier certaines assertions (tels que le nombre chromatique). La
seconde question porte sur la représentation d'un graphe et le concept
d'adjacence. Elle va soulever la question de la diversité de
représentation d'un graphe et, en conséquence sur les conditions
pour que deux graphes représentent la même situation.
Activité 4 page 86
i)Enoncé :
Parmi les graphes ci-dessous, déterminer ceux qui
sont susceptibles de décrire une même situation.
Graphe G1 Graphe
G2 Graphe G3
Graphe G4
Graphe G5 Graphe G6
ii)Analyse praxéologique:
Tâche et type de tâche : Pour la
tâche, il s'agit de trouver les graphes isomorphes parmi les six
présentés relevant du type de tâche T= «Etant
donnés deux graphes, étudier s'ils sont isomorphes».
Cette tâche est problématique car
l'élève ne dispose pas des outils théoriques qui
permettent d'appréhender ce genre de problème.
Technique : On procède comme suit:
-On regroupe les graphes de même ordre (G1
et G3), (G2 et G5) et (G4 et
G6).
-G1 et G3 ont le même nombre
d'arêtes donc pourraient représenter la même situation.
G2 et G5 n'ont pas le même nombre d'arêtes
donc ne représentent pas la même situation. G4 et
G6 ont le même nombre d'arêtes, donc ils sont
susceptibles de représenter la même situation.
Concernant ces deux derniers graphes, il faut passer aux
degrés des sommets pour découvrir s'il y a bijection entre les
sommets et la bijection correspondante entre les arêtes. Pour cela, on
remarque que dans les deux graphes il y a deux sommets de degré 2 et
deux sommets de degré 3. Cela permet la correspondance :
1
2
3 4
Les deux graphes représentent la situation :
- Les sommets sont : 1, 2, 3 et 4.
- Les arcs sont : 1-2, 1-3, 1-4, 2-4 et 3-4.
On peut utiliser la même procédure pour prouver
que les deux graphes G1 et G3 décrivent une
même situation.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On utilise l'index ou une règle ou tout autre
objet permettant l'ostentation pour suivre le comptage des sommets et des
arêtes ainsi les correspondances entre sommets puis entre arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours de comptage et de correspondance.
-Ostensifs scripturaux relevant du registre de la
trace: Désignation des étiquettes des sommets et des
arêtes, les définitions des bijections entre sommets et entre
arêtes.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants :
-La définition de graphes isomorphes.
-Les conséquences de cette définition
(équipotence entre ensemble des sommets et aussi entre ensemble
d'arêtes correspondantes, etc.)
-Recherche de propriété manquante par ordre
croissant d'éléments d'information disponibles.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Propriétés des graphes isomorphes
|
Théorie des graphes
|
|
Analyse descendante
|
Logique formelle
|
iii)Commentaire:
En théorie des graphes, deux graphes qui
représentent la même situation sont dits isomorphes. Cette notion
d' « isomorphisme de graphes » n'est pas
institutionnalisée dans le cycle secondaire car sa définition
fait appel à une double bijection inter- reliées (bijection entre
sommets, bijection entre arêtes homologues) et qui débouche sur la
propriété fondamentale : deux graphes isomorphes ont les
mêmes propriétés. C'est cette propriété qui
va servir comme toile de fond (ou non ostensif) pour la technique
exposée ci-dessus et qui permet de répondre à cette
question. Ainsi, les élèves vont disposer, en fin de compte,
d'une technique et pas de bloc technologico - théorique qui la justifie.
La variable didactique v=(nombre de sommets, nombre d'arêtes) favorise le
travail empirique et la découverte de la technique.
Activité 1 page 87
i)Enoncé :
Pour chacun des graphes suivants donner :
1 B 1
a
b
A D 2
5
1 C
d c
e
3
g
2 E
4 f
1)a/ Le degré de chaque sommet.
b/ La somme des degrés de tous les
sommets.
c/ Le nombre d'arêtes.
2) Quelle conjecture peut-on faire ?
ii)Analyse praxéologique:
La question 1)a/ Le degré de chaque sommet.
Tâche et type de tâche : Pour la
tâche, il s'agit de donner le degré de chaque sommet. Cela
appartient au type de tâche T= «Donner le degré d'un sommet
pour un graphe donné sous la forme d'un schéma ».
Il s'agit d'une tâche routinière.
Technique : On choisit un sommet et on compte les
arêtes dont ce sommet est une extrémité. Puis, on passe au
sommet suivant et on fait le même travail jusqu'à
épuisement de tous les sommets.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On montre le sommet choisi et les arêtes dont ce
sommet est une extrémité. Cela est fait en pointant l'index sur
le sommet et les arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant les désignations sur le
tableau.
-Ostensifs scripturaux relevant du registre de la
trace: écriture des réponses sur un tableau ou toute autre forme
de rédaction.
La manipulation de ces ostensifs est guidée par le non
-ostensif suivant:
-Degré d'un sommet.
Bloc technologico- théorique
|
Technologie
|
Théorie
|
|
Définition du degré d'un sommet
|
Théorie des graphes
|
La question 1/b : La somme des degrés
de tous les sommets.
Tâche et type de tâche : Pour la
tâche, il s'agit de donner la somme des degrés de tous les
sommets. Cela appartient au type de tâche T= «Donner la somme de
nombres entiers donnés ». Il s'agit d'une tâche
routinière.
Technique7(*) : On calcule soit oralement soit en utilisant
une calculatrice les nombres trouvés.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre da
gestualité : On montre le sommet et son degré et on fait la
somme des degrés.
-Ostensifs scripturaux relevant du registre de la
trace : écriture des nombres à additionner et le
résultat de l'addition.
La manipulation de ces ostensifs est guidée par le non
-ostensif suivant:
-L'addition dans IN est commutative (on peut commencer par
n'importe quel sommet).
Bloc technologico- théorique : Addition
dans IN en Algèbre.
|
Technologie
|
Théorie
|
|
Commutativité de l'addition dans IN
|
Addition dans IN
|
La question 1)c/ : Le nombre d'arêtes.
Tâche et type de tâche : Pour la
tâche, il s'agit de donner le nombre d'arêtes. Cela appartient au
type de tâche T= «Donner le nombre d'arêtes d'un graphe
donné sous la forme d'un schéma ».
Il s'agit d'une tâche routinière.
Technique : On écrit la liste de toutes
les arêtes du graphe choisi puis on les compte8(*).
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On montre les arêtes en les pointant par
l'index
-Ostensifs scripturaux relevant du registre de la
trace: écriture des réponses.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant les gestes et le discours de
comptage.
La manipulation de ces ostensifs est guidée par le non
-ostensif suivant:
- Eléments caractéristiques d'un graphe non
orienté.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'une arête dans un graphe non
orienté
|
Théorie des graphes
|
La question 2): Quelle conjecture peut-on
faire ?
Tâche et type de tâche : Pour la
tâche, il s'agit de conjecturer sur les résultats trouvés,
c'est-à-dire sur le lien possible entre la somme des degrés de
tous les sommets et le nombre d'arêtes. Cela appartient, compte tenu des
pré-requis des élèves, au type de tâche T=
«Donner une relation linéaire liant deux variables ».
Il s'agit d'une tâche routinière surtout qu'il
s'agit de relation linéaire simple.
Technique : On dresse un tableau9(*) dans lequel sont
consignés : le graphe, la somme des degrés et le nombre
d'arêtes.
On peut alors conjecturer sur le lien entre la somme des
degrés des sommets et le nombre d'arêtes.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace: écriture des réponses trouvées dans les questions
précédentes sur le tableau.
-Ostensifs déictiques relevant du registre de la
gestualité: Les gestes accompagnant la comparaison des nombres pour
chacun des graphes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant l'établissement du
tableau, la comparaison des nombres et la rédaction.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Lien entre deux variables.
-Expression algébrique linéaire y=ax.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Degré d'un sommet
|
Théorie des graphes
|
|
Fonction linéaire
|
Algèbre linéaire et analyse
|
iii)Commentaire:
On peut observer que :
- Pour la question 1(a, b et c), la praxéologie 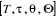 est
routinisée dès la fin du premier paragraphe
intitulé :Notion de graphe.
est
routinisée dès la fin du premier paragraphe
intitulé :Notion de graphe.
- La deuxième question présuppose que
l'élève a une connaissance bien établie sur les tableaux
de proportionnalité. A partir de cela la praxéologie 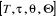 est bien
définie.
est bien
définie.
- Il y a un effet topaze déguisé car la
réponse à la question 2 figure en encadré, couleur orange,
juste en dessous de la question.
L'énoncé de la conjecture découle d'une
interprétation du tableau reliant la somme des degrés de tous les
sommets et le nombre d'arêtes. L'enseignant s'attend à ce que les
élèves énoncent la relation de linéarité qui
devrait être institutionnalisée par la suite et qu'ils admettent
la validité de cette relation dans le cas général. Pour
les élèves, c'est l'enseignant qui est garant de la
validité de cette conjecture pour tout graphe non
orienté quand il déclare : « En
théorie des graphes, on démontre que cette conjecture est valide
pour tous les graphes orientés ». L'enseignant peut, s'il
observe que les élèves ne sont pas assez convaincus, esquisser
une démonstration.
Activité 4 page 88
i)Enoncé :
On s'intéresse aux graphes dont tous les sommets
sont de degré 3.
Construire, si c'est possible, de tels graphes ayant 4, 5,
6, 7 sommets.
ii)Analyse praxéologique:
Tâche et type de tâche : Cette
question peut être divisée en deux tâches :
-La première tâche t1=
« étudier l'existence de graphes 3-réguliers d'ordre 4,
5, 6, 7 » qui appartient au type de tâche T=
«étudier l'existence d'un graphe d'ordre donné et k-
régulier»
-La seconde tâche t2= «dans le
cas où le graphe existe, construire de tels graphes » qui
appartient au type de tâche T= «Construire un graphe k-
régulier d'ordre donné ».
Il s'agit de deux tâches problématiques.
Techniques :
-Pour la tache t1, On calcule la somme des
degrés des sommets. Si la somme est impaire alors le graphe n'existe
pas. Sinon, on peut espérer que de tels graphes existent et on peut
passer à la tâche t2.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace: l'addition des degrés des sommets (qui, en fait est une
multiplication) et la conclusion.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant le raisonnement.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Le lemme des poignées de mains.
-Pour la tache t2, déjà on sait que
les graphes 3-réguliers d'ordre 5 ou 7 n'existent pas. On focalise le
travail sur ceux d'ordre 4 et 6. Pour chaque cas, on calcule le nombre
d'arêtes et on construit le graphe10(*).
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de la trace:
le marquage des sommets et le traçage des arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant le travail écrit.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Les relations entre le nombre d'arêtes et le nombre
de sommets dans le cas d'un graphe complet (premier cas).
-L'analogie avec les prismes à base triangulaires
pour le second cas.
Bloc technologico- théorique :
-Le lemme des poignées de mains en théorie des
graphes.
|
Technologie
|
Théorie
|
|
Lemme des poignées de mains
|
Théorie des graphes
|
|
Représentation d'un graphe
|
Théorie des graphes
|
iii)Commentaire:
Cette activité fait appel au théorème des
poignées de mains dans sa phase initiale et en conséquence sa
praxéologie est bien connue et routinisée. La seconde partie de
la question, c'est-à-dire la construction, pose un problème
méthodologique sur la façon de construire un graphe connaissant
le nombre de ses sommets et le nombre de ses arêtes.
L'élève et l'enseignant ne disposent pas de technique pour
résoudre ce genre de question. Nous sommes, en conséquence en
présence de pénurie praxéologique qui va être
compensée par des schémas et des figures
géométriques (quadrilatère convexe avec diagonales, prisme
à base triangulaire) qui répondent aux conditions
énoncées. Ce raisonnement par analogie ne va pas de soi chez
l'élève et c'est peut être le moment de première
rencontre entre l'élève et ce « va et vient »
entre les cadres de la théorie des graphes et la
géométrie.
Activité 5 page 88
i)Enoncé :
Sept personnes se retrouvent pour un dîner.
Certaines d'entre elles, qui se sont déjà vues dans la
journée, ne se serrent pas la main. Quatre personnes ont serré
trois mains, deux en ont serré une.
La septième personne peut elle serrer qu'une seule
main ?
ii)Analyse praxéologique:
Tâche et type de tâche : Pour la
tâche, il s'agit de répondre à la question : est-il
vrai que la septième personne ait serré une seule main ?
Cela appartient, compte tenue des hypothèses données, au type de
tâche T= «Quelle est la parité du nombre de mains que la
septième personne a serré ? ».
Il s'agit d'une tâche routinière.
Technique : On modélise d'abord la
situation (choix des sommets: S1, S2, .....,
S7 et de la relation qui indique les arêtes : se serrer
ma main). Puis, on calcule la somme des degrés des sommets11(*) afin de pouvoir conclure.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace : la désignation des sommets, l'addition des degrés
des sommets et la conclusion.
-Ostensifs discursifs relevant du registre de
l'oralité : le discours accompagnant la mise en place des ostensifs
écrits.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-La modélisation d'une situation par un graphe.
-Le lemme des poignées de mains.
-La règle: la somme de deux entiers de même
parité est paire et la somme de deux entiers de parités
différentes est impaire.
-Il n'existe pas un nombre entier à la fois pair et
impair.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Modélisation par un graphe
|
Théorie des graphes
|
|
Définition du degré d'un sommet
|
Théorie des graphes
|
|
Lemme des poignées de mains
|
Théorie des graphes
|
|
Parité de la somme de deux entiers
|
Arithmétique
|
iii)Commentaire:
Cette activité fait appel à :
- La modélisation de la situation à partir de
l'analyse sémantique du texte : choix de sommets et leurs
étiquettes, choix de la relation entre sommets qui est
représentée par les arêtes. A ce stade et avec les
données fournies, les élèves sont en mesure de
réaliser cette tâche sans difficultés. Cependant, cette
modélisation n'a pas fait l'objet de technique prouvée et,
à ce titre, elle présente une pénurie
praxéologique.
- Le lemme des poignées de mains qui est
institutionnalisé et appliqué. Donc on dispose de ce
côté d'une technique.
Nous avons, ici, un exemple de tâche dont la technique
peut se décomposer en deux sous tâches :
- pour l'une (la parité de d(S7)) on dispose
d'une technique et d'un bloc technologico - théorique.
- et pour l'autre (la modélisation) on ne dispose pas
d'une technique.
Activité 1 page 88
i)Enoncé :
A
B D
G
C F
E
Des touristes sont logés dans ville A. Ils veulent
visiter les sites B, C, D, E, F et G. Les tronçons de route sont
représentés par le graphe ci-dessous :
1) Donner un parcours qui permet d'aller de A à
E.
2) Donner un parcours qui permet d'aller de C à
F.
3) A partir de la ville A, les touristes peuvent-ils
emprunter tous les tronçons de route en passant une et une seule fois
chacun d'eux ?
4) Même question s'ils doivent obligatoirement terminer
leur circuit à la ville A.
ii)Analyse praxéologique:
La question 1) : Donner un parcours qui permet
d'aller de A à E.
Tâche et type de tâche : Pour la
tâche, il s'agit de donner trouver une chaîne
d'extrémités A et E. Cela appartient au type de tâche T=
«Donner un chemin d'extrémités deux sommets
donnés».
Il s'agit d'une tâche routinière.
Technique : On part du sommet A et on peut suivre
un itinéraire afin d'atteindre le sommet E.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On montre le sommet A puis le parcours jusqu'au sommet
E.
-Ostensifs scripturaux relevant du registre de la
trace: écriture de l'itinéraire trouvé.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant le choix de l'itinéraire.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Le graphe est d'un seul tenant, ce qui permet d'aller de
n'importe quel sommet à n'importe quel sommet.
Bloc technologico- théorique :
Définition de chaîne dans un graphe non orienté.
|
Technologie
|
Théorie
|
|
Définition d'une chaîne dans un graphe
|
Théorie des graphes
|
|
Graphes connexes
|
Théorie des graphes
|
Question 2) répond à la même analyse.
Les questions 3 et 4:
3 ) A partir de la ville A, les touristes peuvent-ils
emprunter tous les tronçons de route en passant une et une seule fois
chacun d'eux ?
4) Même question s'ils doivent obligatoirement terminer
leur circuit à la ville A.
Tâche et type de tâche : Pour la
tâche, il s'agit de trouver une chaîne eulérienne pour la
question 3 ou un cycle eulérien pour la question 4. Cela appartient au
type de tâche T= «Le graphe donné est-il semi-
eulérien? Est-il eulérien ?».
Il s'agit d'une tâche problématique.
Technique : D'abord on étudie les
degrés de tous les sommets. S'il y a zéro ou deux sommets de
degrés impairs, on conclut à l'existence d'une chaîne
eulérienne. Sinon, on conclut que le graphe n'est pas semi-
eulérien. Ensuite, on construit la chaîne en partant de n'importe
quel sommet si tous les sommets sont de degrés pairs (et on obtient
alors un cycle eulérien) ; sinon, la chaîne doit
impérativement commencer et aboutir par l'un des deux sommets de
degré impair.
On a seulement 2 sommets de degrés impairs (A et
D).
On trouve, par exemple, la chaîne
Eulérienne : A-B-C-G-A-D-F-E-C-G-D et pas de cycle Eulérien.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité: On montre le sommet de départ et l'itinéraire
choisi.
-Ostensifs scripturaux relevant du registre de la
trace: écriture des degrés des sommets sur un tableau ou toute
autre forme de rédaction.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant le choix du sommet du départ,
l'itinéraire et la vérification qu'il s'agit bien d'une
chaîne simple.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Graphe semi- eulérien.
-Le théorème d'Euler.
Bloc technologico- théorique :
Théorème d'Euler en théorie des graphes.
|
Technologie
|
Théorie
|
|
Définition d'un graphe semi-eulérien et d'un
graphe eulérien
|
Théorie des graphes
|
|
Théorème d'Euler
|
Théorie des graphes
|
iii)Commentaire:
Les questions 1 et 2 ne nécessitent pas de technique
élaborée, étant donnée la simplicité du
graphe proposé. Il suffit de commencer par le point de départ et
s'approcher du point d'arrivée en minimisant la distance qui reste
à parcourir soit visuellement soit en calculant cette distance. Les
questions 3 et 4 peuvent, par contre, poser des problèmes quant à
l'élaboration de stratégie de recherche de parcours avec la
contrainte énoncée. Il est clair que les objectifs de
l'activité sont :
- La découverte de chaînes et cycles.
- La définition de la longueur d'une chaîne.
- Un premier contact avec les graphes eulériens semi-
eulériens.
La technique pour résoudre les questions 3 et 4 et les
réponses sont connues de l'enseignant. Laquelle technique ne sera
institutionnalisée que bien plus tard. Ainsi, les élèves,
dans ce cadre d'une pénurie praxéologique, vont essayer
empiriquement de répondre à ces questions. Ils peuvent eux-
mêmes valider par ostension, au sein d'un groupe d'élèves,
leurs réponses sans l'intervention de l'enseignant.
.
Activité 2 page 89
i)Enoncé :
La figure ci-dessous représente un parcours de
santé. Dresser la liste de toutes les paires de sommets et
vérifier qu'il existe une chaîne reliant ces deux sommets.
A
B
E
F
C
D
ii)Analyse praxéologique:
Tâche et type de tâche : Il s'agit en
fait de deux tâches :
- La première t1 = « Dresser la
liste de toutes les paires de sommets du graphe donné» qui
appartient au type de tâche T1 = « Dresser la liste
des paires d'éléments d'un ensemble fini
donné ».
Il s'agit d'une tâche routinière puisqu'elle a
été traitée dans le chapitre dénombrements.
Technique : On ordonne d'abord les sommets, puis
on procède comme suit :
- on prend le premier sommet et on le couple avec les
suivants.
- On passe au second sommet et on le couple avec les sommets
suivants.
- Et ainsi de suite jusqu'à l'avant dernier sommet.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace : la liste ordonnée des sommets et les paires.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Le dénombrement des paires de sommets12(*).
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Nombre de paires des sommets
|
Dénombrements
|
- La seconde tâche t2 =
« Vérifier que pour toute paire de sommets du graphe
donné il existe une chaîne les reliant » qui appartient au
type de tâche T2 = « Vérifier que, pour toute
paire de sommets d'un graphe, il existe une chaîne les reliant».
Il s'agit d'une tâche routinière vu la
simplicité du graphe.
Technique : On dresse le tableau consignant les
paires de sommets et les chaînes les reliant.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace: traçage du tableau, la liste de toutes les paires et les
chaînes correspondantes.
-Ostensifs déictiques relevant du registre de la
gestualité : On montre les chaînes.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant les choix des
chaînes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Chaîne dans un graphe non orienté.
Bloc technologico-
théorique : Définition d'une chaîne dans un
graphe non orienté en théorie des graphes.
|
Technologie
|
Théorie
|
|
Définition d'une chaîne dans un graphe
orienté
|
Théorie des graphes
|
iii)Commentaire:
Il s'agit d'une activité qui représente le
premier moment didactique sur le concept de connexité de graphes. Dans
la première partie de la question, c'est-à-dire pour donner
toutes les paires possibles, l'élève dispose d'une technique
applicable à tous les ensembles finis. En revanche, le type de
tâche T2 se présente à l'élève
pour la première fois. Donc l'élève ne dispose pas d'une
praxéologie et va répondre empiriquement à la question qui
peut se prêter à ce genre de traitement du fait de la
simplicité du graphe proposé.
Exercice page 89
i)Enoncé :
Parmi les graphes suivants, reconnaître ceux qui
sont connexes :
G1
G2
G3
G4
G5 G6
ii)Analyse praxéologique:
Tâche et type de tâche : Pour
la tâche, il s'agit d'étudier la connexité d'un graphe
donné par son schéma. Cela appartient au type de tâche T=
«Etudier la connexité d'un graphe».
Il s'agit d'une tâche routinière puisque la
définition est déjà donnée et appliquée dans
l'activité précédente.
Technique : On commence par prouver le non
connexité du graphe sélectionné en montant qu'il y a deux
sommets qui ne peuvent pas être reliés par une chaîne.
Sinon, on utilise la technique de l'activité précédente
pour prouver la connexité.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On montre, s'ils existent, les deux sommets qui ne
peuvent pas être reliés par une chaîne. Ou bien on montre,
en faisant passer l'index sur les arêtes, que le graphe est d'un seul
tenant.
-Ostensifs scripturaux relevant du registre de la
trace: Les sommets qui ne peuvent pas être reliés par une
chaîne ou le tableau tel que l'on a indiqué dans l'activité
précédente.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les choix des sommets.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Connexité d'un graphe non orienté.
-La négation de la proposition : pour tout
couple de sommets x et y, il existe une chaîne reliant x et y.
-Le dénombrement des paires de sommets.
-Chaîne dans un graphe non orienté.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Nombre de paires dans un ensemble fini
|
Dénombrements
|
|
Négation d'un prédicat à deux variables
avec quantificateur universel
|
Logique formelle
|
|
Définition d'une chaîne dans un graphe non
orienté
|
Théorie des graphes
|
|
Définition de la connexité dans un graphe non
orienté
|
Théorie des graphes
|
iii)Commentaire:
Il s'agit d'une activité de consolidation sur la
définition de la connexité d'un graphe et qui est
institutionnalisée. La technique esquissée dans l'activité
2 de la même page est faisable pour les graphes G1 et G6. Par contre,
cette technique est très lourde concernant le graphe G3. Car elle
exigerait un travail sur 15 paires de sommets. D'autres techniques plus
économiques devraient être envisagées à partir d'une
certaine grandeur de l'ordre d'un graphe. Pour les graphes G2, G4 et G5, il
s'agit en fait de montrer qu'ils ne sont pas connexes et donc d'utiliser la
négation de la proposition : « Pour chacune des
paires de sommets, il existe une chaîne reliant ces deux
sommets ». Cette négation s'énonce :
« Il existe une paire de sommets qui ne sont pas
reliés ». Les deux graphes G2 et G5 peuvent induire en
erreur certains élèves qui pourraient penser que certaines
arêtes se croisent et déduisent que ces deux graphes sont connexes
alors qu'ils ne le sont pas. En somme, on peut observer que l'on dispose d'une
praxéologie à portée limitée par rapport au nombre
de sommets et qu'elle nécessite, dans le cas de non connexité,
à recourir à un contre-exemple. Ainsi, pour ce type de
tâche, il n'y a pas de pénurie praxéologique à
proprement parler mais nous nous trouvons en présence d'une
praxéologie à portée limitée et qui va obliger les
élèves, à partir d'un certain ordre de grandeur du nombre
de sommets, à s'investir dans d'autres techniques plus
économiques, c'est-à-dire faisables.
Activité 3 page 89
i)Enoncé :
Peut-on reproduire les graphes ci-dessous sans lever le crayon
et ne passant qu'une seule fois sur chaque arête.
G1
G2
G3
ii)Analyse praxéologique:
Tâche et type de tâche : Pour la
tâche, il s'agit de faire glisser le crayon sur la feuille afin de
reproduire le graphe proposé de sorte que chaque arête soit
tracée une seule fois. Cela appartient au type de tâche
T= «Reproduire un graphe sans passer deux fois par la même
arête».
Il s'agit d'une tâche problématique.
Technique : On procède par essai/erreur.
La simplicité du graphe permet de décider si le travail
demandé est possible ou non.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de la
trace: Le traçage des arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant le choix du sommet du départ
et le traçage des arêtes.
-Ostensifs déictiques relevant du registre de la
gestualité : On montre le sommet du départ et on simule par
le geste le mouvement entre les sommets.
-Ostensifs scripturaux relevant du registre de la
trace: On écrit le résultat qui indique soit
l'impossibilité d'une telle manoeuvre soit d'une itinéraire
solution.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Le théorème d'Euler.
Bloc technologique- théorique :
|
Technologie
|
Théorie
|
|
Théorème d'Euler
|
Théorie des graphes
|
iii)Commentaire:
Cette activité prépare le terrain pour
l'énoncé du théorème d'Euler. L'enseignant
connaît ce théorème et possède, donc, une technique
permettant de répondre à la question sur chacun des quatre cas
proposés. La forme accrocheuse de la question et la simplicité
des graphes proposés va inciter les élèves à se
prendre en charge par défi mutuel. Il en résultera une
première rencontre avec :
- La condition nécessaire et suffisante pour qu'un
graphe soit semi- eulérien.
- La condition nécessaire et suffisante pour qu'un
graphe soit eulérien.
- Une vision sémantique du théorème
d'Euler.
- Une idée précise de la façon de
procéder pour reproduire le graphe sans lever le crayon en passant
qu'une seule fois par chaque arête.
Cela étant, on remarque que sur cette activité
il y a pénurie praxéologique car il n'y a pas de technique connue
préalablement par l'élève pour réaliser cette
tâche. En fait, nous observons un cas typique de situation de
pénurie praxéologique palliée par une grande
épaisseur ostensive et qui débouche sur la mise en place d'une
praxéologie.
Activité 1 page 91
i)Enoncé :
A, B, C, D, E, F, G et H désignent huit poissons.
Dans le tableau ci-dessous, une croix signifie que les poissons ne peuvent pas
cohabiter dans un même aquarium.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
|
A
|
|
x
|
x
|
x
|
|
|
x
|
x
|
|
B
|
x
|
|
|
|
x
|
x
|
x
|
|
|
C
|
x
|
|
|
x
|
|
x
|
x
|
x
|
|
D
|
x
|
|
x
|
|
x
|
|
|
x
|
|
E
|
|
x
|
|
x
|
|
x
|
x
|
|
|
F
|
|
x
|
x
|
|
x
|
|
|
|
|
G
|
x
|
x
|
x
|
|
x
|
|
|
|
|
H
|
x
|
|
x
|
x
|
|
|
|
|
On se propose de résoudre le problème P
suivant : Quel est le nombre d'aquariums nécessaires ?
1) Représenter cette situation par un graphe. (Deux
sommets sont adjacents si les deux poissons ne cohabitent pas).
2) Expliquer pourquoi la résolution du
problème P revient à la résolution du problème
suivant : « Quel est le nombre minimal de couleurs
nécessaires pour colorier les huit sommets de ce graphe de sorte que
deux sommets adjacents ne soient pas de même
couleur ? ».
3) Les quatre sommets A, C, D et H sont deux à deux
adjacents. Déduire qu'il faut au moins quatre couleurs.
4) Vérifier que quatre couleurs suffisent.
5) Résoudre le problème P.
ii)Analyse praxéologique:
La question 1) : Représenter cette
situation par un graphe. (Deux sommets sont adjacents si les deux poissons ne
cohabitent pas).
Tâche et type de tâche : Pour la
tâche, il s'agit de représenter la situation donnée par un
graphe. Cela appartient au type de tâche T= «Représenter
la situation donnée par un graphe».
Il s'agit d'une tâche routinière, vu l'indication
du type de relation à représenter.
Technique : On représente chaque poisson
par un point et là où observe une croix (ligne x et colonne y) on
trace une arête reliant les sommets x et y.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de la trace:
les sommets et les arêtes.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les choix des sommets le
traçage des arêtes.
-Ostensifs déictiques relevant du registre de la
gestualité : On montre la correspondance entre les données
et le graphe.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Graphe non orienté.
-Représentation d'un graphe.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'un graphe orienté
|
Théorie des graphes
|
|
Représentation graphique d'un graphe
|
Théorie des graphes
|
La question 2) : Expliquer pourquoi la
résolution du problème P revient à la résolution du
problème suivant : « Quel est le nombre minimal de
couleurs nécessaires pour colorier les huit sommets de ce graphe de
sorte que deux sommets adjacents ne soient pas de même
couleur ? ».
Tâche et type de tâche : Pour la
tâche, il s'agit d'expliquer que la formulation du problème P
équivaut en termes de la théorie des graphes au texte
donné. Cela appartient au type de tâche T= «Equivalence
sémantique de deux propositions appartenant à deux registres
lexicaux différents».
Il s'agit d'une tâche problématique dans la
mesure où les élèves n'ont jamais fait auparavant, en
mathématique, ce genre de passage entre deux registres linguistiques.
Technique : On établit une correspondance
entre deux registres linguistiques, ce sont celui du langage vernaculaire et le
registre terminologique de la théorie des graphes.
Cette correspondance permet le passage (la traduction) entre
les deux registres.
|
Registre linguistique
|
|
Langage vernaculaire
|
Terminologie de la théorie des
graphes
|
|
Poisson
|
Sommet
|
|
Ne cohabitent pas
|
Adjacents, de couleurs différentes
|
|
Aquarium
|
Couleur
|
|
Nécessaire (nombre)
|
Minimal (nombre)
|
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace :
écriture des correspondances entre propositions et termes.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes de va et vient entre les
deux registres linguistiques.
-Ostensifs déictiques relevant du registre de la
gestualité : On montre la correspondance entre les deux
registres.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Définition d'un graphe non orienté.
-Analyse sémantique des propositions.
Bloc technologique- théorique :
|
Technologie
|
Théorie
|
|
Analyse sémantique des propositions
|
La sémantique
|
|
Définition d'un graphe non orienté
|
Théorie des graphes
|
La question 3) : Les quatre sommets A, C, D et H sont
deux à deux adjacents. Déduire qu'il faut au moins quatre
couleurs.
Tâche et type de tâche : Pour la
tâche, il s'agit de déduire qu'il faut au moins quatre couleurs.
Cela appartient au type de tâche T= «donner un minorant du
nombre chromatique».
Il s'agit d'une tâche routinière, vu l'indication
de l'existence d'un sous graphe complet d'ordre 4.
Technique : On remarque que le sous- graphe
engendré par les sommets A, C, D et H est complet donc son nombre
chromatique est 4, et puisque l'ordre d'un graphe est supérieur ou
égal à l'ordre de ses sous graphes. On conclut que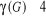 .
.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de la trace:
Le sous graphe GACDH, le nombre chromatique et les graphes complets.
-Ostensifs déictiques relevant du registre de la
gestualité: On montre les sommets à colorier.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Minoration du nombre chromatique.
Bloc technologique- théorique :
|
Technologie
|
Théorie
|
|
Définition du nombre chromatique
|
Théorie des graphes
|
|
Encadrement du nombre chromatique
|
Théorie des graphes
|
La question 4): Vérifier que quatre couleurs
suffisent.
Tâche et type de tâche : Pour la
tâche, il s'agit de vérifier que quatre couleurs suffisent. Cela
appartient au type de tâche T= «Vérifier que l'on peut
colorier le graphe donné par k couleurs, k donné».
Il s'agit d'une tâche routinière.
Technique : On commence par colorier le sous
graphe complet GACDH puis les quatre autres sommets.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs relevant du registre de la
matérialité quelconque: coloration du sous graphe complet,
coloration des autres sommets.
-Ostensifs déictiques relevant du registre de la
gestualité: On montre les sommets à colorier.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Coloration d'un graphe.
-Nombre chromatique d'un graphe complet.
Bloc technologique- théorique :
|
Technologie
|
Théorie
|
|
Propriétés du nombre chromatique
|
Théorie des graphes
|
La question 5) : Résoudre le problème
P.
Tâche et type de tâche : Pour la
tâche, il s'agit de trouver le nombre minimum d'aquariums. Cela
appartient au type de tâche T= «Calculer le nombre chromatique
du graphe donné».
Il s'agit d'une tâche routinière.
Technique : Déduire la valeur du nombre
chromatique 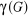 d'après les deux encadrements trouvés dans les questions
3 et 4.
d'après les deux encadrements trouvés dans les questions
3 et 4.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
les deux encadrements et la valeur de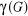 .
.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes sur les passages entre
les encadrements.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
-Déduction logique : 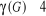 .
.
-si 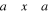 alors
alors 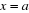
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Propriété d'antisymétrie de la relation
« inférieur ou égal » dans l'ensemble des
nombre réels
|
Comparaison des réels
|
|
Définition du nombre chromatique
|
Théorie des graphes
|
iii)Commentaire:
La première question est une tâche dont on
connaît la technique, surtout que le choix des sommets et des
arêtes a été énoncé dans le texte :
« Deux sommets sont adjacents si les deux poissons ne cohabitent
pas ». . Par contre, en ce qui a trait à la seconde
question, l'élève ne dispose pas de technique à laquelle
il peut se référer. Car il s'agit bien de traduire un texte en
langage vernaculaire en un texte utilisant une terminologie propre à la
théorie des graphes dans sa majorité. Les trois autres questions
(ou tâches) se réfèrent chacune à une
praxéologie. En somme, dans cette activité, on observe que toutes
les tâches demandées se réfèrent à une
praxéologie sauf la seconde qui présente une pénurie
praxéologique.
Activité 2 page 92
i)Enoncé :
Colorier les graphes suivants :
G1
G2
G3
G4
G5
ii)Analyse praxéologique:
Tâche et type de tâche : Pour la
tâche, il s'agit de colorier un graphe présenté par son
schéma. Cela appartient au type de tâche T= «colorier un
graphe».
Il s'agit d'une tâche routinière.
Technique : On utilise l'algorithme de Walsh et
Powell.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace :
Le tableau dans lequel sont consignés les sommets, leurs degrés,
l'ordre et la couleur.
-Ostensifs déictiques relevant du registre de la
gestualité : On désigne le sommet sélectionné,
sa couleur et les sommets suivants qui ne lui sont pas adjacents.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-L'ordre d'un sommet est déterminant pour le
déroulement de l'algorithme.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Algorithme de Walsh et Powell
|
Théorie des graphes
|
iii)Commentaire:
La tâche proposée possède une technique
du fait que l'algorithme à utiliser a été
déjà institutionnalisé. Il s'agit, en fait, d'une
application directe de l'algorithme de Walsh et Powell.
Activité 3 page 92
i)Enoncé :
On donne le graphe le graphe suivant :
C
D
A B
G H
E
F
1) a/ Colorier le graphe en utilisant l'algorithme
précédent.
b/ Quel est le nombre de couleurs
utilisées.
2) Est-il possible de colorier le graphe en utilisant
uniquement deux couleurs ?
ii)Analyse praxéologique:
La question 1) : a/ Colorier le graphe en utilisant
l'algorithme précédent.
b/ Quel est le nombre de couleurs
utilisées.
Tâche et type de tâche : Pour la
tâche, il s'agit de colorier un graphe présenté par son
schéma en utilisant l'algorithme de Wash et Powell. Cela appartient au
type de tâche T= «colorier un graphe en utilisant l'algorithme
de Walsh et Powell».
Il s'agit d'une tâche routinière.
Technique : On utilise l'algorithme de Walsh et
Powell.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace :
Le tableau dans lequel sont consignés les sommets, leurs degrés,
l'ordre et la couleur.
-Ostensifs déictiques relevant du registre de la
gestualité : On désigne le sommet sélectionné,
sa couleur et les sommets suivants qui ne lui sont pas adjacents.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-L'ordre d'un sommet est déterminant pour le
déroulement de l'algorithme.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Algorithme de Walsh et Powell
|
Théorie des graphes
|
La question 2) : Est-il possible de colorier le
graphe en utilisant uniquement deux couleurs ?
Tâche et type de tâche : Pour la
tâche, il s'agit de colorier un graphe présenté par son
schéma sans recourir à l'algorithme de Walsh et Powell. Cela
appartient au type de tâche T=«colorier un graphe».
Il s'agit d'une tâche routinière.
Technique : Il suffit de ne pas commencer par
colorier les sommets E et G.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs matériels relevant du registre de la
matérialité quelconque : Une première couleur pour
les sommets A, C, E et G ; puis le coloriage par une second couleur des
autres sommets.
-Ostensifs déictiques relevant du registre de la
gestualité : On désigne les sommets
sélectionnés A, C, E et G puis les autres sommets.
-Ostensifs discursifs relevant du registre de
l'oralité : Le discours accompagnant les choix.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Coloriage d'un graphe.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
iii)Commentaire:
La première tâche (1/a) proposée
possède une technique routinisée du fait que l'algorithme
à utiliser a été institutionnalisé. La seconde
tâche (1/b) est une simple opération de comptage. La
dernière tâche peut être réalisée en
choisissant un premier sommet différent de celui choisi par
l'algorithme de Walsh et Powell. L'enjeu didactique de cette activité
est de montrer un cas extrême : L'algorithme ne donne jamais le
nombre chromatique. Car, dans la plupart des cas, il suffit de permuter les
sommets de même degré pour obtenir le nombre chromatique. Dans ce
cas (il y en a d'autres), l'algorithme donne toujours trois couleurs alors que
l'on peut vérifier facilement que deux couleurs suffisent. En d'autres
termes, l'objet de cette activité est de modérer le rapport
personnel de l'élève à l'objet du savoir
« Algorithme de Walsh et Powell » dans la mesure où
il faut s'attendre de cet algorithme une bonne approximation du nombre
chromatique et occasionnellement le nombre lui-même.
Activité 4 page 93
i)Enoncé :
1) Quel est le nombre chromatique d'un graphe complet
d'ordre 3 ?
2) Quel est le nombre chromatique d'un graphe complet
d'ordre 5 ?
3) Quel est le nombre chromatique d'un graphe complet
d'ordre n?
ii)Analyse praxéologique:
Les questions : 1, 2 et 3.
Tâche et type de tâche : Pour la
tâche, il s'agit de déterminer le nombre chromatique d'un graphe
complet. Cela appartient au type de tâche T= «Déterminer le
nombre chromatique d'un graphe complet».
Il s'agit d'une tâche routinière dans la mesure
où la technique à utiliser a été déjà
institutionnalisée.
Technique : On remarque que tous les sommets sont
adjacents et donc tous les sommets ont des couleurs différentes.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs graphiques relevant du registre de la trace :
traçage d'un graphe complet d'ordre 2 puis un autre d'ordre 3.
-Ostensifs scripturaux relevant du registre de la trace:
Les hypothèses, analyse de la coloration.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Coloration de deux sommets adjacents.
-Généralisation des résultats
observés au cas général (question 3).
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
iii)Commentaire:
La tâche proposée possède une technique
du fait que l'algorithme à utiliser a été
institutionnalisé. Les graphes et les sous graphes complets ont un
statut particulier en théorie des graphes et en particulier dans la
recherche du nombre chromatique. Car, il suffit de commencer par colorer un
sous graphe complet d'ordre maximal et, en général les couleurs
utilisées sont suffisantes. Ainsi, l'enjeu didactique principal de cette
activité est d'établir un rapport de l'élève
à l'objet du savoir « sous graphe complet » qui
consiste à en tenir compte en premier lieu dans toute situation de
coloriage.
Activité 5 page 93
i)Enoncé :
On donne le graphe ci-contre :
1) Déterminer tous les sous graphes complets
d'ordre 4.
2) Vérifier que quatre couleurs sont suffisantes
pour colorier le graphe.
ii)Analyse praxéologique:
La question 1) : Déterminer tous les sous
graphes complets d'ordre 4.
Tâche et type de tâche : Pour la
tâche, il s'agit de déterminer les sous graphes complets d'un
graphe donné sous la forme d'un schéma. Cela appartient au type
de tâche T= «Déterminer les sous graphes complets d'un graphe
donné».
Il s'agit d'une tâche problématique.
Technique : On sélectionne un sous graphe
d'ordre 4 et on vérifie s'il est complet. On peut éliminer
visuellement la majorité des sous graphes d'ordre 4.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
Les sommets qui engendrent le sous graphe d'ordre 4
sélectionné.
-Ostensifs déictiques et visuels relevant du registre
de la gestualité : soit l'utilisation de la deixis gestuelle ou la
gestuelle visuelle pour la désignation des sous graphes d'ordre 4.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Graphe complet, sommets adjacents.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'un graphe complet
|
Théorie des graphes
|
|
Définition d'un sous graphe
|
Théorie des graphes
|
La question 2) : Vérifier que quatre
couleurs sont suffisantes pour colorier le graphe.
Tâche et type de tâche : Pour la
tâche, il s'agit de colorier le graphe ci-dessus par quatre couleurs.
Cela appartient au type de tâche T= «Colorier un graphe en utilisant
k couleurs, k donné».
Il s'agit d'une tâche routinière.
Technique : On trouve un seul sous graphe complet
d'ordre 4, il suffit de le colorier et compléter le coloriage du
graphe.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs matériels relevant du registre de la
matérialité quelconque : Les couleurs des sommets qui
engendrent le sous graphe d'ordre 4 sélectionné.
-Ostensifs déictiques et visuels relevant du registre
de la gestualité : on montre la coloration au fur et à
mesure de sa mise en place.
-Ostensifs scripturaux relevant du registre de la trace:
Le texte accompagnant la mise en place de la coloration.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Pour colorier un graphe, on commence par colorier un sous
graphe complet d'ordre maximal.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'un graphe complet
|
Théorie des graphes
|
|
Définition d'un sous graphe
|
Théorie des graphes
|
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
iii)Commentaire:
Les deux tâches de l'activité sont, par rapport
aux activités précédentes, devenues routinières.
Ils correspondent à deux praxéologies établies :
l'une qui permet de vérifier si un graphe est complet et l'autre servant
à colorier un graphe à partir de la coloration d'un sous graphe
complet d'ordre maximum.
Activité 6 page 93
i)Enoncé :
Soit G un graphe d'ordre n. Soit G' un sous graphe complet
d'ordre k.
Vérifier que 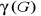 k.
k.
ii)Analyse praxéologique:
Tâche et type de tâche : Pour la
tâche, il s'agit de vérifier l'inégalité
donnée. Cela appartient au type de tâche T= «Comparer le
nombre chromatique d'un graphe et de l'un de ses sous graphes».
Il s'agit d'une tâche routinière.
Technique : On observe que le nombre de couleurs
à utiliser pour colorier un graphe est certainement supérieur ou
égal à celui de tous ses sous graphes.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
Comparaison des nombres chromatiques d'un graphe et d'un sous graphe.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Si un graphe est colorié alors il est de même
de tous ses sous graphes.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
|
Définition d'un sous graphe
|
Théorie des graphes
|
iii)Commentaire:
Cette activité peut être utilisée dans un
moment de d'exploration de l'environnement technologico- théorique. Il
s'agit, en fait, de préciser la technologie de la tâche t=
«montrer que le nombre chromatique d'un graphe est supérieur ou
égal à celui de ses sous
graphes complets» appartenant au type de tâche T=
« montrer que le nombre chromatique d'un graphe est supérieur
ou égal à celui de ses sous graphes ». Nous avons
déjà relevé l'importance de cette tâche pour la
procédure de coloration d'un graphe et la précision du nombre
chromatique. Cette activité sera suivie d'un moment
d'institutionnalisation.
Activité 7 page 93
i)Enoncé :
5
1 2
3 1
2
7
8
6 5
4 4
3
G
G'
1) Vérifier que trois couleurs suffisent pour
colorer les deux graphes G et G'.
2) Pour les deux graphes G et G', déterminer le
plus haut degré de ses sommets.
ii)Analyse praxéologique:
La question 1) : Vérifier que trois couleurs
suffisent pour colorer les deux graphes G et G'.
Tâche et type de tâche : Pour la
tâche, il s'agit de colorier le graphe ci-dessus par trois couleurs. Cela
appartient au type de tâche T= «Colorier un graphe en utilisant k
couleurs, k donné».
Il s'agit d'une tâche routinière.
Technique : On commence par colorer un sous
graphe complet d'ordre 3 puis compléter le coloriage du graphe.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs relevant du registre de la
matérialité quelconque: Les couleurs des sommets qui engendrent
le sous graphe d'ordre 3 sélectionné puis la coloration du reste
des sommets.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant la coloration des sommets.
-Ostensifs scripturaux relevant du registre de la trace :
écriture de la correspondance (sommet- couleur).
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Stratégie pour colorier un graphe : on commence
par colorier un sous graphe complet d'ordre maximal.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'un graphe complet
|
Théorie des graphes
|
|
Définition d'un sous graphe
|
Théorie des graphes
|
|
Ordre d'un sous graphe
|
Théorie des graphes
|
La question 2) : Pour les deux graphes G et G',
déterminer le plus haut degré de ses sommets.
Tâche et type de tâche : Pour la
tâche, il s'agit de déterminer le plus haut degré de ses
sommets donné par son schéma. Cela appartient au type de
tâche T= «Détermination du degré maximal d'un
graphe».
Il s'agit d'une tâche routinière.
Technique : On dresse la liste d'adjacence de
chaque sommet et on tire le degré maximal.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
Le tableau où son consignés les sommets avec leurs
degrés.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Représentation d'un graphe par sa liste d'adjacence.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'une liste d'adjacence
|
Théorie des graphes
|
|
Représentations d'un graphe
|
Théorie des graphes
|
iii)Commentaire:
Les deux tâches de cette activité
possèdent déjà des praxéologies et ne vont poser, a
priori, aucun problème à l'élève. Elles
présentent un moment de l'exploration de l'environnement technologico-
théorique pour une propriété de majoration du nombre
chromatique. Il ne s'agit pas de démontrer cette propriété
mais de l'observer sur deux exemples et de généraliser le
résultat sans démonstration même si la démonstration
n'est pas difficile à être expliquée aux
élèves par l'enseignant.
Exercice page 94
i)Enoncé :
On désire implanter 7 stations radio dans 7 villes
dont les distances mutuelles (en Km) sont données ci-dessous. Sachant
que deux stations interfèrent si elles se trouvent à moins de 100
Km l'une de l'autre.
|
B
|
C
|
D
|
E
|
F
|
G
|
|
A
|
55
|
110
|
108
|
60
|
150
|
88
|
|
B
|
|
87
|
142
|
133
|
98
|
139
|
|
C
|
|
|
77
|
91
|
85
|
93
|
|
D
|
|
|
|
75
|
114
|
82
|
|
E
|
|
|
|
|
107
|
141
|
|
F
|
|
|
|
|
|
123
|
1) Représenter cette situation à l'aide d'un
graphe G (deux sommets sont adjacents si la distance séparant les deux
villes est inférieure à 100 Km).
2) Vérifier que 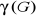 3.
3.
3) a/ Vérifier que trois couleurs suffisent pour
colorier G.
b/ Quel est alors le nombre minimum de longueurs
d'onde qu'il faut prévoir pour éviter toute
interférence ?
ii)Analyse praxéologique:
La question 1) : Représenter cette situation
à l'aide d'un graphe G (deux sommets sont adjacents si la distance
séparant les deux villes est inférieure à 100 Km).
Tâche et type de tâche : Pour la
tâche, il s'agit de représenter une situation par un graphe. Cela
appartient au type de tâche T= «représenter une situation par
un graphe».
Il s'agit d'une tâche routinière.
Technique : On réalise le schéma
de la situation en plaçant d'abord les sommets puis, deux sommets
si et sj sont reliés par une arête si le
nombre figurant dans s'intersection de la ligne i et la colonne j est
inférieur à 100.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la
trace : La matrice incomplète donnée.
-Ostensifs graphiques relevant du registre de la trace :
Les sommets et les lignes joignant les sommets.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
- La fonction distance est symétrique.
- La comparaison de la distance avec 100 indique une
présence ou l'absence de relation.
- La ligne traduit cette présence.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'une distance
|
Géométrie euclidienne
|
|
Représentation d'une situation par un graphe
|
Théorie des graphes
|
La question 2) : Vérifier que 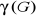 3.
3.
Tâche et type de tâche : Pour la
tâche, il s'agit de montrer que le nombre chromatique est
supérieur à 3. Cela appartient au type de tâche T=
«Minoration du nombre chromatique d'un graphe donné».
Il s'agit d'une tâche routinière.
Technique : On montre qu'il y a un sous graphe
complet d'ordre 3.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs déictiques relevant du registre de la
gestualité : On montre un sous graphe complet d'ordre 3.
-Ostensifs graphiques relevant du registre de la trace :
Les sommets et les lignes joignant les sommets du sous graphe complet d'ordre
3.
-Ostensifs discursif relevant du registre de
l'oralité : Le discours accompagnant les gestes
-Ostensifs scripturaux relevant du registre de la
trace : Le texte accompagnant le discours.
La manipulation de ces ostensifs est guidée par les
non- ostensifs suivants:
- La fonction distance est symétrique.
- La comparaison de la distance avec 100 indique une
présence ou l'absence de relation.
- La ligne traduit cette présence.
Bloc technologico- théorique
|
Technologie
|
Théorie
|
|
Minoration du nombre chromatique
|
Théorie des graphes
|
La question 3)a/ Vérifier que trois couleurs
suffisent pour colorier G.
Tâche et type de tâche : Pour la
tâche, il s'agit de colorier le graphe ci-dessus par trois couleurs. Cela
appartient au type de tâche T= «Colorier un graphe en utilisant k
couleurs, k donné».
Il s'agit d'une tâche routinière.
Technique : On commence par colorer un sous
graphe complet d'ordre 3 puis compléter le coloriage du graphe.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs matériels relevant du registre de la
matérialité quelconque : Les couleurs des sommets qui
engendrent le sous graphe d'ordre 3 sélectionné.
-Ostensifs déictiques relevant du registre de la
gestualité : par la deixis gestuelle, on montre les couleurs
à éviter ou à choisir.
-Ostensifs discursifs relevant du registre de
l'oralité : le discours accompagnant les gestes.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Stratégie pour colorier un graphe : on commence
par colorier un sous graphe complet d'ordre maximal.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition d'un graphe complet
|
Théorie des graphes
|
|
Définition d'un sous graphe
|
Théorie des graphes
|
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
La question 3)b/ : Quel est alors le nombre minimum
de longueurs d'onde qu'il faut prévoir pour éviter toute
interférence ?
Tâche et type de tâche : Pour la
tâche, il s'agit de déterminer le nombre chromatique du graphe en
utilisant les questions précédentes. Cela appartient au type de
tâche T= «Déterminer le nombre chromatique».
Il s'agit d'une tâche routinière.
Technique : On déduit des questions
précédentes que 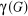 =3 et on
traduit ce résultat en langue vernaculaire.
=3 et on
traduit ce résultat en langue vernaculaire.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace :
Les deux inégalités, la traduction écrite en langage
vernaculaire.
-Ostensifs discursifs relevant du registre de
l'oralité: le discours en langage vernaculaire.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-une condition suffisante sur un minimum se traduit par une
majoration.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Définition du nombre chromatique
|
Théorie des graphes
|
|
Condition suffisante
|
Logique formelle
|
iii)Commentaire:
Les tâches de cette activité possèdent, au
moment de leur déroulement, des praxéologies. Cependant, il
convient de noter que :
o Ce qui importe dans les distances données au tableau
est leur comparaison par rapport à 100 et non les nombres
eux-mêmes. En plus, la forme de présentation par un tableau
incomplet est due au fait que la fonction distance est symétrique.
Ainsi, l'ostensif tableau donné en hypothèse est complet
contrairement aux apparences.
o Pour la question 1, l'élément crucial pour le
choix des sommets et des arêtes a été indiqué et non
laissé aux soins de l'élève.
o Pour la question 2/a, la technique a été
progressivement institutionnalisée dans les activités
précédentes et a été donc l'objet d'un débat
méta- mathématique (colorier un sous- graphe complet d'ordre 3 et
compléter le coloriage des autres sommets).
o Pour la question 2/b, il fallait déterminer le
nombre chromatique en utilisant un encadrement par le même nombre puis
traduire le résultat en langage vernaculaire.
Activité 1 page 95
i)Enoncé :
Le graphe ci-dessous représente un réseau
routier. Sur ses arêtes on a marqué les distances séparant
deux villes. Entre Bizerte et le Kef trouver le plus court chemin.
Bizerte
140
65
Tabarka
Tunis
70
166
Jendouba
175
63
Le Kef
ii)Analyse praxéologique:
Tâche et type de tâche : Pour la
tâche, il s'agit de trouver un plus court chemin entre Bizerte et Le Kef.
Cela appartient au type de tâche T= «Trouver un plus court chemin
entre deux sommets d'un graphe».
Il s'agit d'une tâche problématique.
Technique : On procède de la
manière suivante :
- On désigne les arêtes (avec leurs
étiquettes) entre le sommet Bizerte et les sommets voisins.
- Puis, on continue ainsi de voisinage en voisinage jusqu'au
sommet Le Kef et ne garder que les plus courts chemins.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace :
Les distances, les pondérations, les sommets sélectionnés
et L'ensemble S.
-Ostensifs discursifs relevant du registre de
l'oralité: Le discours accompagnant les manipulations écrites.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Toute sous chaîne d'une chaîne minimale est
minimale.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Graphe pondéré
|
Théorie des graphes
|
|
Définition de la longueur d'un sous chaîne
|
Théorie des graphes
|
|
Propriétés des chaînes minimales
|
Théorie des graphes
|
iii)Commentaire:
Les données simples de cette activité permettent
à celle-ci d'être un bon support pour une introduction à
l'algorithme de Moore- Djikstra. Car cet algorithme se base essentiellement sur
le lemme prouvant que toute sous chaîne d'une plus courte chaîne
est une plus courte chaîne et qui n'est pas connue des
élèves. Cependant, ce lemme peut être évoqué
à la suite de cet exemple pour mieux appréhender l'algorithme.
Activité 3 page 95
i)Enoncé :
On a représenté ci-dessous un réseau
d'ordinateurs qu'un virus informatique vient d'infecter par l'ordinateur A. On
a noté sur les arêtes les temps (en minutes) que met un fichier
infecté pour aller d'un ordinateur à un autre.
B
4 D
4
2 2
3 E
A
1 3
C
1) Au bout d'une minute le virus est-il arrivé en
B ? En C ?
2) a/ Reproduire le graphe ci-dessus et colorier en rouge
tous les ordinateurs atteints par le virus au bout d'une minute.
b) Indiquer, à côté du sommet C et
entre parenthèses, de quel ordinateur est venue l'attaque.
3) Quel est l'ordinateur atteint ensuite ? Au bout de
combien de temps ? Le colorier en rouge.
4) Y a-t-il un ordinateur sain qui est atteint par le
virus à la troisième minute ? À la quatrième
minute ? Le colorier en rouge et indiquer aussi de quel ordinateur est
venue l'attaque.
5) Recopier et compléter le tableau
suivant :
|
Temps (minutes)
|
Ordinateur(s) atteint(s)
pour la première fois
|
Provenance de
l'attaque
|
|
0
|
A
|
|
|
1
|
C
|
A
|
|
2
|
|
|
|
3
|
|
|
|
4
|
|
|
|
5
|
|
|
|
6
|
|
|
6) Indiquer pourquoi il n'est pas utile de continuer
après la sixième minute.
7) Indiquer le parcours du virus pour atteindre le plus
rapidement possible l'ordinateur E.
ii)Analyse praxéologique:
Les questions : 1, 2, 3 et 4 :
1) Au bout d'une minute le virus est-il arrivé en
B ? En C ?
2) a/ Reproduire le graphe ci-dessus et colorier en rouge
tous les ordinateurs atteints par le virus au bout d'une minute.
b) Indiquer, à côté du sommet C et
entre parenthèses, de quel ordinateur est venue l'attaque.
3) Quel est l'ordinateur atteint ensuite ? Au bout de
combien de temps ? Le colorier en rouge.
4) Y a-t-il un ordinateur sain qui est atteint par le
virus à la troisième minute ? À la quatrième
minute ? Le colorier en rouge et indiquer aussi de quel ordinateur est
venue l'attaque.
Tâche et type de tâche : Pour la
tâche, il s'agit d'effectuer une lecture graphique pour trouver les
ordinateurs infectés au bout de k minutes. Cela appartient au type de
tâche T= «Trouver les sommets s tels que la distance de A è S
est égale à k, k donné».
Il s'agit d'une tâche routinière, vu les
données.
Technique : On procède de la manière
suivante :
- On désigne les arêtes (avec leurs
étiquettes) entre le sommet A et les sommets s voisins tels que
d(A,s)=1.
- Puis, on continue ainsi de voisinage en voisinage jusqu'au
sommet tel que d(A,s)=k.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
Les distances et les sommets sélectionnés.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Ne pas construire un cycle.
Bloc technologico- théorique : Absence de
discours technologique.
|
Technologie
|
Théorie
|
|
Définition d'une arborescence
|
Théorie des graphes
|
La question 513(*)) Recopier et compléter le tableau
suivant :
|
Temps (minutes)
|
Ordinateur(s) atteint(s)
pour la première fois
|
Provenance de
l'attaque
|
|
0
|
A
|
|
|
1
|
C
|
A
|
|
2
|
|
|
|
3
|
|
|
|
4
|
|
|
|
5
|
|
|
|
6
|
|
|
Tâche et type de tâche : Pour la
tâche, il s'agit d'effectuer une lecture graphique pour trouver les
ordinateurs infectés au bout de k minutes et provenance de l'attaque.
Cela appartient au type de tâche T= «Trouver les sommets s tels que
la distance de A è S est égale à k, k donné et
déterminer le dernier sommet contaminé avant S».
Il s'agit d'une tâche routinière, vu les
données.
Technique : On procède de la manière
suivante :
- On marque les arêtes (avec leurs étiquettes)
entre le sommet A et les sommets s voisins tels que d(A,s)<k.
- Puis, on continue ainsi de voisinage en voisinage jusqu'au
sommet tel que d(A,s)=k.
- Garder l'étiquette de l'avant dernier sommet.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
Les distances et les sommets sélectionnés.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Tout sous chemin d'un plus court chemin est un plus court
chemin.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Chaîne de longueur k
|
Théorie des graphes
|
|
Propriétés des chaines minimales
|
Théorie des graphes
|
Les questions 6) : Indiquer pourquoi
il n'est pas utile de continuer après la sixième minute.
Tâche et type de tâche : Pour la
tâche, il s'agit de déduire des réponses
précédentes que tous les cas sont épuisés et le
plus court chemin entre les sommets A et E. Cette tâche appartient au
type de tâche T= « Montrer l'exhaustivité des cas
étudiés »
Il s'agit d'une tâche routinière, vu les
données.
Technique : On procède de la manière
suivante :
- On observe l'ensemble des ordinateurs atteints au bout de
six minutes.
- Si tous les ordinateurs sont atteints alors conclure qu'il
est inutile de continuer au-delà de six minutes. Sinon conclure le
contraire.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
L'ensemble des ordinateurs contaminés.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Raisonnement par exhaustion.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Raisonnement par exhaustion
|
Logique formelle
|
Les questions 7) : Indiquer le parcours du
virus pour atteindre le plus rapidement possible l'ordinateur E.
Tâche et type de tâche : Pour la
tâche, il s'agit de déduire, le plus court chemin entre les
sommets A et E. Cette tâche appartient au type de tâche T=
« Déterminer le plus court chemin entre deux
sommets »
Il s'agit d'une tâche routinière, puisque les
données sont visibles sur le tableau.
Technique : On procède de la manière
suivante :
- On part du sommet E et on observe sur le tableau la
provenance de l'attaque.
- On continue de proche en proche jusqu'à remonter vers
A.
Cette technique présuppose la manipulation des
ostensifs suivants :
-Ostensifs scripturaux relevant du registre de la trace:
L'ensemble des ordinateurs contaminés.
La manipulation de ces ostensifs est guidée par le non-
ostensif suivant:
-Raisonnement par exhaustion.
Bloc technologico- théorique :
|
Technologie
|
Théorie
|
|
Auto-technologique
|
|
iii)Commentaire :
Les tâches de cette activité sont facilement
réalisables et présentent dans l'ordre les étapes de
l'algorithme de Moore - Djikstra. Il s'agit, en fait d'une contextualisation de
cet algorithme qui se termine, par sa décontextualisation, à
l'énoncé en langage vernaculaire (et non en langage formel) de
l'algorithme en question.
III-4.2.Synthèse des
commentaires sur les praxéologies présentées
Synthèse des blocs pratico- techniques
Les blocs pratico- techniques présentés dans le
paragraphe précédent montrent que les techniques utilisées
sont en correspondance biunivoque avec les types de tâche. C'est la
raison pour laquelle on va, pour des raisons de commodité de
présentation des idées, on va désigner le bloc pratico-
technique par le type de tâche qui lui est sous -jacente.
a-Typologie des tâches :
Les tâches proposées dans les activités
du chapitre peuvent être répertoriés selon vingt quatre
types de tâches :
T1 = « Exécuter une tâche
naturalisée»
T2 = « Modéliser par un
graphe »
T3 = « Comparer des registres
différents de présentation d'un graphe »
T4 = « Déterminer l'ordre d'un
graphe »
T5 = « Déterminer le nombre
d'arête d'un graphe donné »
T6 = « Déterminer le degré
d'un sommet »
T7 = « Déterminer les sommets
adjacents à un sommet »
T8 = « Trouver une chaîne reliant deux
sommets»
T9 = « Montrer que le graphe est
connexe »
T10 = « Montrer que le graphe est
eulérien ou semi - eulérien »
T11 = « Trouver une chaîne
eulérienne »
T12 = « trouver un cycle
eulérien »
T13 = « Montrer que le graphe est
complet »
T14 = « Montrer que deux graphes sont
isomorphes »
T15 = « Traduire entre deux registres
linguistiques/ostensifs»
T16 = « Utiliser un algorithme
institutionnalisé »
T17 = « Colorier un graphe »
T18 = « Déterminer le nombre
chromatique »
T19 = « Encadrer le nombre
chromatique »
T20 = « Déterminer la plus courte
chaîne entre deux sommets »
T21= « Utiliser le lemme des poignées
de mains »
T22 = « Montrer l'existence d'un objet
mathématique »
T23 = « Trouver des sous graphes selon une
caractéristique donnée »
T =
Autres types de tâches.
=
Autres types de tâches.
Tableau 9
On peut observer déjà la très grande
diversité (au moins on a 24) des types de tâche
sollicitée dans un chapitre censé être une introduction
à la théorie des graphes. Cette diversité excessive
pourrait, à notre avis, s'avérer être incompatible avec le
type de rapport personnel de l'élève de troisième
économie et gestion avec la discipline (les mathématiques).
Lequel rapport se caractérisant par une certaine démotivation et
une estime de soi négative. En plus, même si l'élève
recommence à prendre goût des mathématiques du fait de la
nature particulièrement accrocheuse des activités
proposées, cette diversité peut conduire à un état
de surcharge cognitive.
b-Pénurie praxéologique et épaisseur
ostensive :
Dans le tableau 10 ci-dessous, nous avons
présenté les tâches analysées, les types de
tâches qui lui sont associés, l'information concernant si la
technique est routinière ou problématique et les registres
d'ostensifs de la technique utilisée.
|
Activité
|
Question
|
Type de tâche T
|
Technique 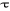
|
Ostensifs
|
|
1 page 85
|
1
|
T1
|
Naturalisée
|
Graphique
|
|
2
|
T1
|
Routinière
|
Graphique, discursif
|
|
3
|
T3
|
Problématique
|
Graphique, discursif
|
|
4
|
T16
|
Problématique
|
Matériel, discursif, déictique
|
|
3 page 86
|
1
|
T2
|
Routinière
|
Scriptural, discursif, déictique
|
|
2/a
|
T2
|
Routinière
|
Graphique, discursif, déictique
|
|
2/b
|
T5
|
Routinière
|
Déictique, discursif
|
|
4 page 86
|
|
T14
|
Problématique
|
Déictique, discursif, scriptural
|
|
1 page 87
|
1/a
|
T6
|
Routinière
|
Déictique, discursif, scriptural
|
|
1/b
|
T1
|
Routinière
|
Déictique, discursif
|
|
1/c
|
T5
|
Routinière
|
Déictique, discursif, scriptural
|
|
2
|
TX
|
Routinière
|
Déictique, discursif, scriptural
|
|
4 page 88
|
|
T19 + T18
T2
|
Routinière Problématique
|
Discursif, scriptural
Graphique, discursif
|
|
5 page 88
|
|
T19+T18
|
Routinière
|
Discursif, scriptural
|
|
1 page 88
|
1
|
T8
|
Routinière
|
Déictique, discursif, scriptural
|
|
2
|
T8
|
Routinière
|
Déictique, discursif, scriptural
|
|
3
|
T11
|
Problématique
|
Déictique, discursif, scriptural
|
|
4
|
T12
|
Problématique
|
Déictique, discursif, scriptural
|
|
2 page 89
|
|
T1
|
Routinière
|
Déictique, discursif, scriptural
|
|
Exercice p 89
|
|
T9
|
Routinière
|
Déictique, discursif, scriptural
|
|
3 page 89
|
|
T11
|
Problématique
|
Graphique, déictique, discursif, scriptural
|
|
1 page 91
|
1
|
T2
|
Routinière
|
Graphique, déictique, discursif
|
|
2
|
T15
|
Problématique
|
Déictique, discursif, scriptural
|
|
3
|
T17
|
Routinière
|
Déictique, discursif, scriptural
|
|
4
|
T17
|
Problématique
|
Matériel, déictique, discursif
|
|
5
|
Tx+T15+T3
|
Problématique
|
Discursif, scriptural
|
|
2 page 92
|
|
T17 + T16
|
Routinière
|
Déictique, discursif, scriptural
|
|
3 page 92
|
1/a
|
T17 + T16
|
Routinière
|
Déictique, discursif, scriptural
|
|
1/b
|
T1
|
Routinière
|
Déictique, discursif, scriptural
|
|
2
|
T22 + T17
|
Routinière
|
Matériel, déictique, discursif
|
|
4 page 93
|
1 et 2
|
T18
|
Routinière
|
Graphique, scriptural
|
|
3
|
T18 + TX
|
Problématique
|
Graphique, discursif, scriptural
|
|
5 page 93
|
1
|
T23 + T13
|
Routinière
|
Déictique, discursif, scriptural
|
|
2
|
T17
|
Problématique
|
Matériel, scriptural, discursif, déictique
|
|
6 page 93
|
|
T18 + T19
|
Routinière
|
Scriptural
|
|
7 page 93
|
1
|
T17
|
Routinière
|
Matériel, discursif, scriptural
|
|
2
|
T6 + T1
|
Routinière
|
Discursif, scriptural
|
|
Exercice p 94
|
1
|
T2
|
Routinière
|
Graphique, scriptural
|
|
2
|
T19
|
Routinière
|
Graphique, déictique, discursif, scriptural
|
|
3/a
|
T17
|
Routinière
|
Matériel, déictique, discursif
|
|
3/b
|
T18 + T3
|
Routinière
|
Discursif, scriptural
|
|
1 page 95
|
|
T20
|
Problématique
|
Discursif, scriptural
|
|
3 page 95
|
1
|
T1
|
Routinière
|
Scriptural
|
|
2/a
|
T1
|
Routinière
|
Scriptural
|
|
2/b
|
T1
|
Routinière
|
Scriptural
|
|
3
|
T1
|
Routinière
|
Scriptural
|
|
4
|
Tx
|
Routinière
|
Scriptural
|
|
5
|
T1
|
Routinière
|
Scriptural
|
|
6
|
Tx
|
Routinière
|
Scriptural
|
|
7
|
T19
|
Routinière
|
Scriptural
|
Tableau 10
Ce tableau appelle plusieurs remarques importantes :
1- Il y a 13 cas sur 51 de questions où il y a
pénurie praxéologique, c'est-à-dire où
l'élève ne dispose encore pas d'une technique lui permettant de
réaliser la tâche demandée.
2- On observe qu'il y a quasiment autant de tâches
routinières qui utilisent trois registres d'ostensifs (18 cas) que de
tâches routinières qui utilisent un ou deux registres d'ostensifs
(19 cas).
3- Neufs tâches sur treize de tâches
problématiques utilisent trois ou quatre registres d'ostensifs.
4- Toutes les tâches problématiques utilisent au
moins deux registres d'ostensifs.
5- On observe que pour les techniques routinières comme
pour les techniques non routinières il y a domination de trois types
d'ostensifs : les ostensifs déictiques, les ostensifs discursifs et
les ostensifs scripturaux.
Afin de rendre lisible le tableau précédent,
nous avons, à partir du tableau 10, consigné, dans le tableau 11
ci-après, le nombre de tâches selon deux paramètres :
- L'existence ou non d'une pénurie
praxéologique.
- Le nombre de registres d'ostensifs nécessaires pour
la réalisation de la tâche en classe.
|
Epaisseur ostensive
(nombre de registres)
|
Tâche
|
|
Routinière14(*)
|
Problématique
|
|
1
|
10
|
0
|
|
2
|
9
|
4
|
|
3
|
18
|
7
|
|
4
|
1
|
2
|
|
5
|
0
|
0
|
Tableau 11
c-Typologie des tâches dans la rubrique
« Exercices et problèmes » :
Dans le tableau 12 suivant, nous avons consigné, par
type de tâche, les exercices qui font appel à ces types de
tâches dans la rubrique « Exercices et
problèmes » du manuel. Il fallait connaitre les intentions des
auteurs du manuel scolaire quant aux notions, théorèmes et
techniques sur lesquels ils invitent l'utilisateur du manuel à
manifester le plus d'intérêt.
|
Type de tâche
|
Exercices
|
|
T1 = « Exécuter une tâche
naturalisée»
|
|
|
T2 = « Modéliser par un graphe »
|
2 ; 6 ; 7 ; 10 ; 11 ; 12 ;
13 ; 14 ; 16 ; 17 ; 20 ; 22 ; 23 et 27
|
|
T3 = « Comparer des registres différents
de présentation d'un graphe »
|
|
|
T4 = « Déterminer l'ordre d'un graphe
»
|
3 ; 4 ; 5 et 7
|
|
T5 = « Déterminer le nombre d'arête
d'un graphe donné »
|
2 ; 4 et 5
|
|
T6 = « Déterminer le degré d'un
sommet »
|
2 et 3
|
|
T7 = « Déterminer les sommets adjacents
à un sommet »
|
|
|
T8 = « Trouver une chaîne reliant deux
sommets»
|
|
|
T9 = « Montrer que le graphe est connexe
»
|
2 et 11
|
|
T10 = « Montrer que le graphe est eulérien
ou semi - eulérien »
|
14 ; 15 ; 18 ; 19 ; 20 ; 21 et
22
|
|
T11 = « Trouver une chaîne
eulérienne »
|
14 ; 15 et 18
|
|
T12 = « trouver un cycle eulérien
»
|
19 ; 20 ; 21 et 22
|
|
T13 = « Montrer que le graphe est complet
»
|
2 et 4
|
|
T14 = « Montrer que deux graphes sont isomorphes
»
|
1
|
|
T15 = « Traduire entre deux registres
linguistiques/ostensifs»
|
|
|
T16 = « Utiliser un algorithme
institutionnalisé »
|
24
|
|
T17 = « Colorier un graphe »
|
6 ; 8 ; 9 ; 10 ; 11 ; 12 er 13
|
|
T18 = « Déterminer le nombre chromatique
»
|
6 ; 8 ; 9 ; 10 ; 11 ; 12 er 13
|
|
T19 = « Encadrer le nombre chromatique »
|
8 et 9
|
|
T20 = « Déterminer la plus courte
chaîne entre deux sommets »
|
23 ; 25 et 26
|
|
T21= « Utiliser le lemme des poignées de
mains »
|
16 ; 17 et 27
|
|
T22 = « Montrer l'existence d'un objet
mathématique »
|
|
|
T23 = « Trouver des sous graphes selon une
caractéristique donnée »
|
|
Tableau 12
Nous observons que cette rubrique sollicite
essentiellement : la modélisation d'un graphe, les graphes
eulériens, le coloriage et la recherche de la plus courte chaine. Cette
répartition nous semble assez cohérente avec le contenu de la
rubrique « Cours » qui, justement, insiste tout
particulièrement sur ces trois thèmes de la théorie des
graphes.
Synthèse des blocs technologico-
théoriques
Dans le tableau 13 ci- dessous nous avons indiqué, pour
chaque question des activités analysées, le bloc technologico-
théorique. L'examen de ce tableau permet de relever les remarques
suivantes :
a- Au niveau de la technologie :
Pour justifier les techniques, les activités se
réfèrent :
- aux définitions (de graphe non orienté, de
graphe complet, de chaîne, de cycle, de chaîne eulérienne,
de cycle eulérien, de la connexité, du nombre chromatique,
etc.).
- aux théorèmes admis (théorème
d'Euler, propriétés concernant l'encadrement du nombre
chromatique, le lemme des poignées de mains, etc.).
- et aux algorithmes (de Walsh et Powell, de Moore et
Djikstra).
b- Au niveau de la théorie :
le chapitre « Introduction aux
graphes » :
- Fait rarement référence aux autres domaines de
mathématiques (7 questions sur les 51 analysées).
- Utilise des activités à caractère
empirique pour introduire une définition ou des activités
traitant une situation contextualisée pour admettre un
théorème par le jeu de l'altérité positive
(l'élève fait confiance à l'enseignant qui assure que le
résultat est mathématiquement correct) et des variations des
registres ostensifs.
- Fait appel assez souvent à la modélisation,
notamment la modélisation d'une situation par un graphe non
orienté et qui pose des problèmes de démarche en l'absence
d'une référence théorique. Ainsi, compte tenu de son
importance dans le traitement des questions posées, nous avons
observé que, généralement, le texte prend en charge le
choix des sommets et le choix des arêtes (Activité 1 page 85;
Activité 3 page 86; Activité 4 page 88;
Activité 5 page 88; Activité 1 page 91; Exercice page
94).
- Fait rarement référence à la
théorie des dénombrements alors que l'on sait que cette
théorie fait appel, lorsqu'on veut expliquer le raisonnement, à
des représentations par des graphes (arbres de choix ou autres). On
remarque déjà la dialectique entre les deux théories.
- Fait référence, en ce qui concerne certaines
activités, à l'algèbre : tableau de
proportionnalité (Activité 1 page 87, question 2),
encadrement du nombre chromatique (Activité 1 page 91, Question
5 ; Activité 5 page 93, Question 2 ; Exercice page
94).
- Fait appel une seule fois à l'arithmétique en
ce qui concerne la parité du degré d'un sommet à la suite
de l'utilisation du théorème des poignées de mains
(Activité 5 page 88).
- S'appuie par occasions sur la logique :
ü Négation d'une proposition avec quantificateur
universel qui exige la recherche d'un contre- exemple (tels que : la
démonstration qu'un graphe n'est pas connexe ou que deux graphes sont
isomorphes.).
ü Le nombre chromatique étant, par
définition, le nombre de couleur minimum pour la coloration d'un graphe,
il en résulte que toute coloration utilise un nombre de couleurs
supérieur ou égal au nombre chromatique. Donc, l'existence d'une
coloration à k couleurs implique une majoration du nombre
chromatique.
ü La généralisation des cas traités
en accordant une large place à l'intuition de l'élève et
au jugement de l'enseignant (Activités 1 page 87 pour
énoncer le lemme des poignées de mains ;
Activité 3 page 89 pour énoncer le théorème
d'Euler; Activités 1 et 3 page 95 pour énoncer l'algorithme
de Moore - Djikstra).
|
Activité
|
Question
|
Type de tâche T
|
Technologie
|
Théorie
|
|
1 page 85
|
1
|
T1
|
Auto- technologique
|
-
|
|
2
|
T1
|
Auto- technologique
Relation binaire dans un ensemble
|
-
Théorie des ensembles
|
|
3
|
T3
|
Représentation graphique d'une relation
Preuve de fausseté d'une proposition
|
Théorie des ensembles.
Logique formelle
|
|
4
|
T16
|
Lemme de choix
Définition du coloriage d'un graphe
|
Théorie des ensembles
Théorie des graphes
|
|
3 page 86
|
1
|
T2
|
Représentation d'un graphe - liste d'adjacence
Définition d'un graphe complet
|
Théorie des graphes
Théorie des graphes
|
|
2/a
|
T2
|
Représentation d'un graphe
|
Théorie des graphes
|
|
2/b
|
T5
|
Définition du degré d'un sommet
|
Théorie des graphes
|
|
4 page 86
|
|
T14
|
Graphes isomorphes
Analyse descendante
|
Théorie des graphes
Logique formelle
|
|
1 page 87
|
1/a
|
T6
|
Définition du degré d'un sommet
|
Théorie des graphes
|
|
1/b
|
T1
|
Auto- technologique
Propriétés de l'addition dans IN
|
-
Addition dans IN
|
|
1/c
|
T5
|
Définition d'une arête
|
Théorie des graphes
|
|
2
|
TX
|
Degré d'un sommet
Fonction linéaire
|
Théorie des graphes
Algèbre linéaire
|
|
4 page 88
|
|
T19 + T18
T2
|
Lemme des poignées de mains
Représentation graphique
|
Théorie des graphes
Théorie des graphes
|
|
5 page 88
|
|
T19+T18
|
Représentation d'une situation par un graphe Lemme des
poignées de mains,
Degré d'un sommet
Parité de la somme de deux entiers.
|
(Modélisation)15(*), théorie des graphes, Théorie des
graphes
Arithmétique
|
|
1 page 88
|
1
|
T8
|
Définition d'une chaîne, graphe connexe
|
Théorie des graphes
|
|
2
|
T8
|
Définition d'une chaîne
|
Théorie des graphes
|
|
3
|
T11
|
Définition d'une chaîne semi- eulérienne
|
Théorie des graphes
|
|
4
|
T12
|
Définition d'une chaîne eulérienne
|
Théorie des graphes
|
|
2 page 89
|
|
T1
|
Combinaisons d'ordre 2
|
Dénombrements
|
|
Exer p89
|
|
T9
|
Définition d'une chaîne
Définition de la connexité
Nombre de paires dans un ensemble fini
Négation d'un prédicat à deux variables
|
Théorie des graphes
Théorie des graphes
Dénombrements
Logique formelle
|
|
3 page 89
|
|
T11
|
Théorème d'Euler
|
Théorie des graphes
|
|
1 page 91
|
1
|
T2
|
Représentation d'une situation
Définition d'un graphe
|
(Modélisation)
Théorie des graphes.
|
|
2
|
T15
|
Analyse sémantique et traduction
Définition d'un graphe
|
(Analyse sémantique)
Théorie des graphes
|
|
3
|
T17
|
Coloration de graphes complet
|
|
|
4
|
T17
|
Définition du nombre chromatique, encadrement du nombre
chromatique.
|
Théorie des graphes
Théorie des graphes
|
|
5
|
Tx+T15+T3
|
Asymétrie de la
relation « Inférieur ou égal »
Traduction entre deux registres
Définition du nombre chromatique
|
Propriétés de IN
(Analyse sémantique)
Théorie des graphes
|
|
2 page 92
|
|
T17 + T16
|
Algorithme de Walsh et Powell
|
Théorie des graphes
|
|
3 page 92
|
1/a
|
T17 + T16
|
Algorithme de Walsh et Powell
|
Théorie des graphes
|
|
1/b
|
T1
|
Auto- technologique
|
-
|
|
2
|
T22 + T17
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
|
4 page 93
|
1 et 2
|
T18
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
|
3
|
T18 + TX
|
Définition du coloriage d'un graphe
|
Théorie des graphes
|
|
5 page 93
|
1
|
T23 + T13
|
Définition de graphe complet, d'un sous graphe
|
Théorie des graphes
|
|
2
|
T17
|
Définition de graphe complet, d'un sous graphe et du
coloriage d'un graphe
|
Théorie des graphes
|
|
6 page 93
|
|
T18 + T19
|
Définition du coloriage d'un graphe et d'un sous
graphe
|
Théorie des graphes
|
|
7 page 93
|
1
|
T17
|
Définition de graphe complet, de sous graphe et de
l'ordre d'un sous graphe
|
Théorie des graphes
|
|
2
|
T6 + T1
|
Liste d'adjacence et représentation graphique
|
Théorie des graphes
|
|
Exercice p 94
|
1
|
T2
|
Représentation d'une situation par un graphe
|
(Modélisation), théorie des graphes
|
|
2
|
T19
|
Minoration du nombre chromatique
|
Théorie des graphes
|
|
3/a
|
T17
|
Définition de graphe complet, de sous graphe et du
coloriage d'un sous graphe
|
Théorie des graphes
|
|
3/b
|
T18 + T3
|
Définition du nombre chromatique
Condition suffisante
|
Théorie des graphes
Logique formelle
|
|
1 page 95
|
|
T20
|
Définition de graphe pondéré
Définition de la longueur d'une chaîne
Propriétés des chaînes minimales
|
Théorie des graphes
Théorie des graphes
Théorie des graphes
|
|
3 page 95
|
1,2,3,4,5
|
T1
|
Arborescence
Chaîne de longueur k
Chemin de longueur minimale
|
Théorie des graphes
Théorie des graphes
Théorie des graphes
|
|
6
|
Tx
|
Raisonnement par exhaustion
|
Logique formelle
|
|
7
|
T19
|
Auto- technologique
|
-
|
Tableau
13
Chapitre IV:
Conclusions
Chapitre IV : Conclusions
Nous avons étudié l'itinéraire
curriculaire et du profil de l'élève de troisième
année économie et gestion. Puis, nous avons mis en lumière
les liens organiques entre le savoir savant et le savoir à enseigner.
Ensuite, nous avons décrit l'organisation du manuel scolaire de
mathématique de la troisième économie et gestion et nous
avons focalisé l'analyse sur le chapitre « Initiation aux
graphes ». Tout cela n'a été qu'un prélude pour
l'analyse praxéologique proprement dite. Nous avons analysé la
praxéologie ponctuelle associée à chaque type de
tâche pour toutes les questions posées dans les trente quatre
activités analysées. Nous avons présenté, pour
chaque question, les tâches et les types de tâche correspondants et
nous avons détaillé la technique ainsi que ses objets
constitutifs de la dichotomie fondamentale : à savoir les ostensifs
mobilisés et les non ostensifs et enfin le bloc technologico-
théorique. Au terme de ce travail, nous pouvons énoncer un
certain nombre de conclusions concernant :
· Les effets de la transposition didactique.
· Le profil de l'élève de troisième
année économie et gestion.
· Les blocs pratico techniques.
· Les blocs technologico-théorique
Les effets de la transposition
didactique externe:
L'analyse des liens organiques entre le savoir savant et le
savoir à enseigner selon les activités du chapitre
« Initiation aux graphes » a mis en lumière les
effets de la transposition didactique externe. Ces effets se sont traduits
par un quintuple dessein :
ü Centrer les
activités sur les modélisations de situations ayant une relation
directe avec le milieu social de l'élève.
ü Privilégier les
techniques utilisant les caractéristiques du graphe : degrés
des sommets, ordre d'un graphe, etc.
ü Faire découvrir
par l'élève, au fur et à mesure, certaines
caractéristiques importantes des graphes pouvant servir comme plateforme
de résolutions de certains problèmes intéressants,
notamment concernant les circuits, le plus court chemin et les gestions de
conflits.
ü Eviter de donner un
exposé classique de cette unité d'apprentissage et, surtout, ne
pas céder à la tentation des démonstrations inutiles des
théorèmes.
ü Donner une
présentation fonctionnelle des algorithmes, étant donné
que les élèves n'ont pas l'habitude de traduire un algorithme
écrit sous sa forme usuelle en un discours fonctionnel.
Le profil de l'élève de
troisième année économie et gestion :
Notre étude nous a donné un certain
éclairage sur le rapport personnel de l'élève de
troisième année EG à l'institution classe troisième
EG. Il en émerge, un rapport différent du rapport institutionnel
établi par les conseillers d'orientation.
Synthèse des blocs pratico-
techniques :
Nous avons relevé dans le chapitre
« Initiation aux graphes » une très grande
diversité de types de tâches (au moins 24) dans un chapitre
censé être une première initiation à la
théorie des graphes. Cette diversité excessive pourrait, à
notre avis, s'avérer être incompatible avec la place
réservée au chapitre mais aussi au rapport personnel de
l'élève de troisième économie et gestion avec la
discipline (les mathématiques). En ce qui concerne les techniques
utilisées, nous avons relevé les observations suivantes :
ü Dans pratiquement le quart des questions (13
sur 51) on a relevé une pénurie praxéologique,
c'est-à-dire où l'élève ne dispose encore pas d'une
technique lui permettant de réaliser la tâche
demandée.
ü Pour toutes les techniques (routinières
comme pour les techniques non routinières) il y a domination de trois
types d'ostensifs : les ostensifs déictiques, les ostensifs
discursifs et les ostensifs scripturaux.
Synthèse des blocs technologico-
théoriques :
L'examen des blocs technologico-théoriques nous a
permis de relever les remarques suivantes :
c- Au niveau de la technologie :
Pour justifier les techniques, les activités se
réfèrent :
Ø aux définitions (de graphe non orienté,
de graphe complet, de chaîne, de cycle, de chaîne
eulérienne, de cycle eulérien, de la connexité, du nombre
chromatique, etc.).
Ø aux théorèmes admis
(théorème d'Euler, propriétés concernant
l'encadrement du nombre chromatique, le lemme des poignées de mains,
etc.).
Ø aux algorithmes (de Walsh et Powell, de Moore et
Djikstra).
d- Au niveau de la théorie :
le chapitre « Introduction aux
graphes » :
- Fait rarement référence aux autres domaines de
mathématiques (7 questions sur les 51 analysées).
- Utilise des activités à caractère
empirique pour introduire une définition ou des activités
traitant une situation contextualisée pour admettre un
théorème par le jeu de l'altérité positive
(l'élève fait confiance à l'enseignant qui assure que le
résultat est mathématiquement correct) et des variations des
registres ostensifs.
- Fait appel assez souvent à la modélisation,
notamment la modélisation d'une situation par un graphe non
orienté et qui pose des problèmes de démarche en l'absence
d'une référence théorique.
- Fait rarement référence à la
théorie des dénombrements alors que l'on sait que cette
théorie fait appel, lorsqu'on veut expliquer le raisonnement, à
des représentations par des graphes (arbres de choix ou autres). On
remarque déjà la dialectique entre les deux théories.
- S'appuie par occasions sur la logique :
Ø Négation d'une proposition avec quantificateur
universel qui exige la recherche d'un contre- exemple.
Ø La généralisation des cas
traités en accordant une large place à l'intuition de
l'élève et au jugement de l'enseignant .
Résumons-nous:
Nous constatons, avec intérêt, la
richesse, la simplicité la et la profondeur d'une analyse
praxéologique des activités du chapitre « Initiation
aux graphes ».
En effet, notre recherche montre que l'analyse
praxéologique qui ne prend pas en compte l'information tirée du
programme officiel et des documents d'accompagnement débouche
invariablement sur l'émergence spontanée :
· des principaux objectifs ciblés par la
transposition didactique,
· de la typologie des tâches,
· des praxéologies ponctuelles et locales,
· des registres d'ostensifs sollicités et
les non ostensifs sous-jacents.
Plus important, cette analyse permet, dans le cas
usuel où l'on dispose du programme officiel et des documents
d'accompagnement:
ü de garantir une vision commune à tous
les intervenants éducatifs sur les contenus des manuels scolaires
officiels. Vision non altérée par les présuppositions du
programme officiel.
ü de porter un regard objectif sur les intentions
déclarées du programme officiel à partir des
activités et des notions institutionnalisées dans le manuel
scolaire officiel unique.
ü de mesurer le décalage entre les
intentions affichées dans le programme officiel et celles tirées
des activités du livre scolaire officiel.
ü d'aider l'enseignant à mieux caler les
activités disponibles dans le livre scolaire officiel aux
finalités, objectifs et exigences du programme officiel.
Bibliographie :
1- Théorie des graphes :
· Claude, BERGE. Théorie des graphes et ses
applications. Paris: Dunod, 1967.
· Pierre, LOPEZ. Cours de : graphes. 2007.
http://www.las.fr/Lopez/cours/GRAPHES/graphes.
html.
· Eric, SIGWARD. Introduction à la théorie
des graphes.. ac-nancy-metz.fr. 2007.
http://e.sigward@ac-nancy-metz.fr. (accès le Mars 2008).
· Claude-François, PICARD. Graphes.Tome1.
Gauthier-Villars. Paris. 1972. 145 pages.
· Germain, KREWERAS. Graphes, chaînes de Markov et
quelques applications numériques Dalloz. Paris. 1972.152 pages.
· Frank, HARARY ; Robert Z., NORMAN et
Dorwin, CARTWRIGHT. Introduction à la théorie des graphe
orientés. Dunod. Paris. 1968. 439 pages. Traduit par A. Gilbert.
2- Didactique des
mathématiques :
· Guy, BROUSSEAU. Fondements et méthodes de
la didactique des mathématiques. Recheches en
didactique des mathématique 7/2. 1986: 77-124.
· Marianna, BOSCH et Yves, CHEVALLARD. La
sensibilité des activités mathématiques aux
ostensifs. Recheches en didactique des mathématiques,
1999: 77-124.
· Yves, CHEVALLARD. La transposition didactique. Du
savoir savant au savoir eneigné. La pensée sauvage.
Grenoble. 1985.
· Yves, CHEVALLARD. Didactique, anthropologie,
mathématiques. Postface à la deuxième édition
de La transposition didactique. Du savoir savant au savoir
eneigné. La pensée sauvage. Grenoble. 1991.
· Yves, CHEVALLARD. Nouveaux objets, nouveaux
problèmes en didactique des mathématiques. In vingt ans
de didactique des mathématiques en France. Grenoble. La
pensée sauvage.1994. 313-320.
· Yves, CHEVALLARD. Le concept de rapport au
savoir : rapport personnel, rapport institutionnel, rapport officiel.
Séminaire Didatech, n°108,1998, 211-235..
· Yves, CHEVALLARD. Analyse des pratiques enseignantes
et didactique des mathématiques: L'approche anthropologique. 1998.
http://yves.chevallard.free.fr. (accès le Février 2007).
· Yves, CHEVALLARD. Approche anthropologique du rapport
au savoir et didactique des mathématiques. 2002.
http://yves.chevallard.free.fr (accès le Mai 2008).
· Yves, CHEVALLARD. Les processus de transposition
didactique et leur théorisation. 1994.
http://yves.chevallard.free.fr. (accès le Janvier 2008).
· Yves, CHEVALLARD. Organisation didactique: 1- les
cadres généraux. 1998. http://yves.chevallard.free.fr
(accès le Juin 2008).
· Yves, CHEVALLARD. Ostensifs et non ostensifs dans
l'activité mathématique. 1994.
http://yves.chevallard.free.fr. (accès le Février 2007).
· Yves, CHEVALLARD. Passé et présent de la
théorie anthropologique du didactique. 2007.
http://yves.chevallard.free.fr. (accès le Juillet 2008).
· Yves, MATHERON, et NOIRFALISE Robert. .Construire un
savoir professionnel pour le professeur de mathématique. Petit
x, 2006: 30-47.
3- Livres scolaires:
· Mathématiques.Eonomie et gestion. 3ème
année de l'enseignement secondaire. Centre national
pédagogique. 2006.
4- Programme officiel:
· Programmes de mathématiques. 3ème
et 4ème année de l'enseignement secondaire.
Ministère de l'éducation et de la formation. Direction des
programmes et du manuel scolaire. Septembre 2006.
Annexes
Annexe 1 :
Programme de mathématique de troisième
année. Section : Economie et gestion.
Annexe 2 :
Chapitre « Initiation aux graphes »
du manuel scolaire de mathématique
Section : Economie et gestion.

* 1 Ré -indexer un graphe
signifie affecter aux sommets d'autres étiquettes.
* 2 Un graphe orienté est
dit fortement connexe si pour tout couple de sommets x et y il existe un chemin
de x vers y (et donc un chemin de y vers x).
* 3 Terme emprunté
à la Programmation Neuro- Linguistique (PNL).
* 4 Livre intitulé :
Programmes de mathématiques 3ème et
4ème de l'enseignement secondaire (septembre 2006)
, pp3-6
* 5 Technologie Information
Communication.
* 6 La coloration d'un sommet
est assimilée à la fixation sur le sommet d'une punaise
coloriée.
* 7 On a :
-Pour le graphe G1 : d(1)+d(2)+d(3)=2+2+2=6.
-Pour le graphe G2 :
d(A)+d(B)+d(C)+d(D)+d(E)=2+3+2+3+2=12.
-Pour le graphe G3 :
d(1)+d(2)+d(3)+d(4)+d(5)=2+4+2+4+2=14.
-Pour le graphe G4 :
d(a)+d(b)+d(c)+d(d)+d(e)+d(f)= 3+3+4+4+2+4+2=22.
* 8 On a :
-Pour le graphe G1 : 1-2, 1-3, 2-3. Donc : 3
arêtes.
-Pour le graphe G2 : A-B, A-E, B-C, B-D, C-D, D-E.
Donc : 6 arêtes.
-Pour le graphe G1 :
1-2, 1-4, 2-3, 2-4, 2-5, 3-4, 4-5. Donc : 7
arêtes.
-Pour le graphe G1 :
a-b, a-d, a-e, b-c, b-d, c-d, d-f, c-g, c-f, g-f, e-f.
Donc : 11 arêtes.
* 9
|
Graphe
|
G1
|
G2
|
G3
|
G4
|
|
Somme des degrés
|
6
|
12
|
14
|
22
|
|
Nombre d'arêtes
|
3
|
6
|
7
|
11
|
* 10 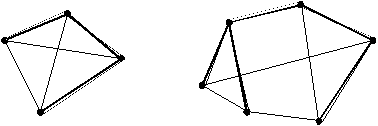
* 11
3+3+3+3+1+1+d(S7)=14+d(S7). Cette somme doit être
paire d'après le lemme des poignées de mains et donc
d(S7) doit être pair. D'où l'on tire qu'il est
impossible d'avoir d(S7)=1.
* 12 Il y a  paires.
paires.
* 13
|
Temps (minutes)
|
Ordinateur(s) atteint(s)
pour la première fois
|
Provenance de
l'attaque
|
|
0
|
A
|
|
|
1
|
C
|
A
|
|
2
|
B
|
A
|
|
3
|
-
|
-
|
|
4
|
D
|
C
|
|
5
|
-
|
-
|
|
6
|
E
|
C
|
* 14 Pouvant être
naturalisée
* 15 Les parenthèses
indiquent que l'objet en question est étranger à
l'élève.



