RESUME
Dans la transmission hertzienne, la quantité
d'information que l'on peut transporter dépend de nombreux facteurs dont
: le canal de transmission, la distance entre deux points d'une liaison, la
visibilité de la liaison, la sensibilité aux perturbations,
etc.
Le présent travail est focalisé sur
l'étude de la visibilité de la liaison de MTN Rwandacell Karongi
vers le centre ville de Kibuye, et fait le bilan des affaiblissements dus aux
obstacles pénétrant dans cette liaison ; quant à leur
impact dans la planification de ladite société des
télécommunications relative à une augmentation de la
capacité de transmission qui serait caractérisée par
l'utilisation des fréquences de plus en plus élevées.
La solution pratique d'utilisation d'un réflecteur
passif, adoptée le plus souvent dans les régions montagneuses
comme celles du cas d'étude, est proposée et consiste à
l'obtention d'une nouvelle liaison à travers laquelle les obstacles
seraient totalement dégagés, si l'on plaçait ce passif
dans l'île Nyamunini située dans le lac Kivu.
Enfin, le réflecteur est dimensionné en vue
d'optimiser la puissance de réception à la station située
au centre ville de Kibuye.
xi
ABSTRACT
In microwave link transmission, the quantity of information
which can be carried depends upon many factors such as: the distance between
two points of the link, the clearance of the link, the sensibility of
perturbations, etc.
The purpose of this project is to analyse the MTN Rwandacell
microwave link between Karongi Mount and Kibuye City-center.
MTN Rwandacell is facing problems in increasing the capacity of
transmission in such links located in the high mountains of Rwanda where it is
difficult to obtain the Line Of Site (LOS) between the two ends of the link.
This work analyses the possibilities to overcome this problem and
studies particularly the solution of using a plane reflector in order to
optimise the signal power to the receiver at the end of the link and to achieve
some performance objectives.
INTRODUCTION GENERALE
1. Choix du sujet
Depuis une décennie, le secteur des
télécommunications connaît une forte croissance de la
demande tant dans les pays développés que dans ceux en voie de
développement. Il en est de même pour notre pays qui a vu le
nombre des abonnés aux réseaux téléphoniques passer
d'une dizaine de milliers à plus d'une centaine de milliers au cours des
cinq dernières années grâce, notamment, à
l'introduction de la téléphonie mobile. Pour répondre
à cette demande en croissance considérable, il faut que la
capacité de transmission du réseau de
télécommunication soit révisée constant à la
hausse et cela avec anticipation, afin d'éviter la dégradation de
la qualité de service causée soit par le taux de blocage ou par
le délai d'attente pour la connexion.
Vu le problème que pose l'installation des liaisons
numériques de grande capacité dans un pays montagneux comme le
nôtre, il a fallu apporter notre contribution en faisant l'étude
de l'utilisation d'un réflecteur passif sur une liaison numérique
de grande capacité de KarongiKibuye.
L'emplacement du centre ville de Kibuye dans une
dépression (graben occidental), cause de difficultés
d'émettre depuis la station d'émission de Karongi, située
dans la crête Congo-Nil, vers ce centre ville puisque le signal
émis rencontre les obstacles de montagnes provoquant un faible signal de
réception, lequel signal est le résultat de la diffraction des
ondes sur ces derniers.
En effet, comme ce centre ville est à la fois le
chef-lieu de province et un lieu touristique en croissance considérable,
il va avoir bientôt besoin d'une artère de transmission de grande
capacité contrairement à l'artère de petite
capacité actuellement en service.
Tout ceci nous a conduit à la recherche d'une solution
plus ou moins adéquate à cette obstruction car aucune
société de télécommunication ne peut s'aventurer
à faire une liaison de grande capacité (par exemple une liaison
en SHF) avec un tel obstacle.
2. Problématique
Il est possible d'utiliser les ondes radio de faible
fréquence lorsqu'on transmet les signaux de faible capacité. Dans
ce cas, les ondes diffractées peuvent être utilisées
lorsqu'il n'y a pas de visibilité directe entre deux stations
adjacentes.
La question qui se pose est la nécessité
d'augmenter la capacité de cette liaison. Cela exige l'utilisation des
fréquences de plus en plus élevées qui, malheureusement,
sont bloquées par ces obstacles.
Est-il possible de surmonter ces obstacles ?
Si oui, quelle est la meilleure solution parmi celles qui sont
possibles ?
3. Objectifs de la recherche
L'objectif de cette recherche est d'étudier les
possibilités d'éviter les obstacles qui ne permettent pas de
réaliser une liaison numérique de grande capacité.
Nous nous proposons alors l'étude d'utilisation d'un
réflecteur passif qui pourrait être placé sur l'île
se trouvant dans le lac Kivu communément appelé « NYAMUNINI
».
4. Intérêt du sujet
Une fois cette étude réalisée, notre
travail aura pour intérêt l'obtention d'une liaison
numérique de grande capacité (de 32 Mbits soient 480 voies
téléphoniques à 64Kbits par voie), alors qu'avec la
diffraction de l'obstacle on pouvait arriver à 8Mbits seulement. La
réalisation de cette étude va aider les sociétés de
télécommunication à l'instar de MTN Rwandacell, TERRACOM,
d'émettre depuis la station de Karongi avec une grande
capacité.
La proposition d'utilisation d'un réflecteur passif
est l'une des meilleures solutions pratiques parmi tant d'autres possibles
telles que : L'élévation des pylônes; l'installation d'une
station relais active, etc.
5. Hypothèse de la recherche Dans notre
travail nous nous proposons l'hypothèse qui suit :
L'atténuation du signal due à la diffraction des
obstacles augmente avec l'utilisation des fréquences de plus en plus
élevées.
En effet, lorsqu'on effectue une liaison numérique "Point
to point", on doit faire un dégagement de la zone de Fresnel.
Le rayon de la zone de ce dégagement varie de
manière inversement proportionnelle à la fréquence
d'émission.
Lorsqu'il y a un obstacle sur le chemin des ondes, l'angle au
sommet du cône de diffraction diminue quand la fréquence augmente.
Ce qui fait qu'un point qui était antérieurement situé
dans la zone de pénombre se retrouve dans la zone d'ombre.
6. Délimitation du sujet
Le présent travail va se limiter à
l'étude analytique et descriptive du réflecteur passif comme une
meilleure solution comparativement à d'autres possibles pour la liaison
numérique de MTN Rwandacell Karongi-Kibuye
7. Approche méthodologique
Afin d'arriver à sa réalisation, nous
utiliserons principalement, la méthode documentaire pour le
développement du cadre théorique; un logiciel « Arcview GIS
» comme outil informatique qui nous donnera la situation
géographique de la région objet d'étude en province de
l'Ouest, du logiciel ATDI-Hertz Mapper qui nous permettra de tracer les profils
montrant le dégagement des obstacles et enfin le MATLAB 6.5.1 comme
outil de simulation de résultats.
8. Subdivision du travail
En plus de l'introduction générale, ce travail
s'articule sur les quatre chapitres suivants : CHAPITRE I :
Généralités sur les ondes
électromagnétiques
CHAPITRE II : Théories des antennes et transmissions
hertziennes
CHAPITRE III : Influence de la Terre et de l'atmosphère
sur la propagation des ondes hertziennes
CHAPITRE IV : Bilan de puissance à la réception
avec l'utilisation d'un relais passif.
Au terme de ce travail, se trouve une conclusion
générale suivie de quelques recommandations adressées aux
sociétés de télécommunication, à la
faculté des sciences appliquées et aux étudiants du
département d'électrique et électronique,
spécialement ceux de l'option d'électronique et systèmes
de télécommunication.
CHAPITRE I: GENERALITES SUR LES ONDES
ELECTROMAGNETIQUES
I.0 INTRODUCTION
Ce chapitre met en évidence la description
générale des ondes électromagnétiques au cours de
laquelle nous ferons une présentation des équations de Maxwell
ainsi que la propagation de ces ondes dans différents milieux.
I.1 Définition
Les ondes électromagnétiques sont des
éléments physiques d'une importance extrême permettant la
communication entre les systèmes grâce à leurs
propriétés de propagation dans le vide ou la matière. Une
onde électromagnétique (OEM) est constituée d'un champ
électrique

E et d'un champ magnétique H . Dans le
vide, ces deux champs sont orthogonaux et transverses (perpendiculaires
à la direction de propagation [17].
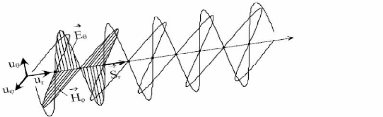
Figure I.1 : Propagation d'une onde
électromagnétique
I.2 Lois du rayonnement électromagnétique
I.2.1 Notion d'ondes sphériques
Quand une vibration se propage dans l'espace, elle le fait
sous forme d'une onde. En un point quelconque de l'espace, l'amplitude de
vibration varie sinusoïdalement si le phénomène est en
fonction du temps, et son équation est de la forme :
Y = Asin( wt+? ) (I.1)
x
vibration présente la même phase constitue une
surface équiphase de l'onde ou encore « un front d'onde
>>.
Si un ébranlement se produit en un point d'un plan, il
se propage sur ce dernier dans toutes les directions avec la même vitesse
si le milieu est isotrope. Au bout d'un temps t, la situation est la même
en tout point d'un cercle centré sur le point d'origine de
l'ébranlement. Ce cercle est donc un front d'onde. Dans le cas d'un
milieu homogène à trois dimensions, le front d'onde est une
sphère, et l'onde qui se propage est alors appelée une onde
sphérique tandis que le point d'origine de la vibration est le centre du
front d'onde.
I.2. 2 Propagation à trois dimensions: Ondes
planes progressives
Par définition, une « onde plane >> est une
onde dont le front est un plan. Dans le cas

|
d'une onde électromagnétique, il existe
simultanément un champ électrique E
|
et un champ
|
|
|
magnétique H . L'onde plane est une solution
particulière des équations de propagation et dans

ce cas, E et H sont en phase entre eux, mais
orthogonaux dans l'espace et perpendiculaires à la direction de
propagation. L'intérêt de cette notion est double :
D'une part, une onde émise par une source, peut-être
considérée localement en un point M éloigné de la
source comme ayant les propriétés d'une onde plane.
D'autres part, l'onde plane est l'instrument analytique de la
théorie des ondes. Une onde quelconque, à condition que les
propriétés du milieu soient linéaires, peut toujours
être obtenue par superposition d'ondes planes.
La théorie développée dans cette partie
s'applique à toute onde électromagnétique à quelque
domaine du spectre qu'elle appartienne.

F
y
H

z



r
Cette situation est représentée à la
figure1.2 ci-dessus, où le vecteur Ð dirigé dans le
sens de propagation est le vecteur de Poynting.
I.3 Equations de Maxwell
I.3.1 Equations fondamentales
Les équations de Maxwell, qui régissent le
comportement du champ électrique et du champ magnétique sont
groupées dans les quatre relations ci-après écrites dans
le système d'unités rationalisé. Dans tous les milieux, on
a les équations suivantes :
; Equation de Maxwell Faraday
(Phénomène d'induction) (I.2)
r
r
?B
r
rotE
t
-
?
r
; Equation de Maxwell-Ampère (I.3)
?D
+

t
r r r
rotH j
=
?
r
divD = ñ ; Equation de Maxwell-Gauss
(I.4)
r
divB = 0 ; (I.5)
L'équation (I.5) est celle du Théorème de
Gauss sous-forme différentielle pour le champ magnétique.
r r
Dans ces équations, E est le champ
électrique, D le déplacement (ou induction)
r r
électrique, B le champ (ou induction)
magnétique, H l'excitation (ou champ) magnétique;
r
ñ la densité volumique de charges
réelles et j la densité volumique de courants de
charges
réelles.
L'équation (I.4) exprime qu'il n'y a pas de distribution
en volume de masses
|
magnétiques libres; tandis que l'équation (I.3)
que
|
r
?D
?t
|
joue le même rôle qu'un vecteur
|
densité de courant. Ce terme est le vecteur densité
de courant de déplacement (Maxwell) [3]. I.3.2 Equations
complémentaires
Elles mettent en jeu la nature du milieu. Pour un milieu
homogène, isotrope, parfait au point de vue diélectrique et
magnétique, nous avons :
v r
D E
= å (I.6)
r r
B H
= u (I.7)
r
r
j E
= ó (I.8)
Oùå ,u et ó sont
respectivement la permittivité, la perméabilité et la
conductivité du milieu magnétique
I.4 Equation de propagation des ondes
électromagnétiques
La propagation des ondes est un domaine de la physique
s'intéressant aux déplacements des ondes
électromagnétiques dans les milieux. On distingue
généralement deux catégories de propagation des ondes :
- La propagation dans l'espace libre (vide, air, milieu massif
comme le verre, etc.)
- La propagation guidée (fibre optique, guide d'onde,)
I.4.1 Equation de propagation des ondes
électromagnétiques dans le vide
Les équations de Maxwell-Ampère et Maxwell-Faraday
sont des équations aux
r
dérivées partielles du premier ordre qui couplent
le champ électrique E et le champ
r
magnétique B .
L'élimination de l'un des champs conduit à obtenir
pour le second une équation du second ordre [11]:
r
? -
E o o
u å
0 ; (I.9)
2
r
?
E
=
2
t
?
r
? -
H u å
o o
; (I.10)
2
r
? H
2 0
=
?t

1
=
c
;
å u
0 0
I.4.2 Energie
électromagnétique
(I.11)
Ces équations sont celles de D'Alembert ; le champ
électromagnétique se propage dans le vide à la
célérité c avec :

2
r
r
2
E B
2 2 o
u
u = å + ;
o
(I.12)
r
:
(I.13)
Le courant d'energie est donné par le vecteur de Poynting
Ð
r r
Ð = E ×H ;
La relation de conservation locale s'écrit
= 0 ;
? u r
(I.15)
+ Ð
div
?t
La puissance qui traverse une surface est le flux du vecteur de
Poynting à travers cette
P S
surface telle que :
P = ??Ðds r r (I.15)
| 


