à‰tude des possibilités d'utilisation d'un réflecteur passif sur une liaison numérique de grande capacité : « cas de la liaison de mtn rwandacell karongi-kibuye »

I.7 Conclusion

Dans ce chapitre, nous avons vu les généralités sur les ondes électromagnétiques. La propagation de ces ondes est un domaine de la physique s'intéressant à leurs déplacements dans différents milieux. L'onde plane est l'instrument analytique de la théorie des ondes. Une onde quelconque, à condition que les propriétés du milieu soient linéaires, peut toujours être obtenue par superposition d'ondes planes.

CHAPITRE II: THEORIES DES ANTENNES ET TRANSMISSIONS HERTZIENNES II.1 THEORIES DES ANTENNES

II.1.1 Introduction

Les systèmes de communications par ondes radios sont composés d'une station d'émission, d'une station de réception et d'un certains nombre de répéteurs.

A sa sortie, un émetteur fournit un courant à haute fréquence modulé. Pour transmettre l'information à distance, le courant modulé doit être transformé en ondes électromagnétiques qui, ensuite se déplaceront dans l'atmosphère (ou dans le vide). C'est le rôle de l'antenne d'émission.

L'antenne de réception jouera un rôle de convertir l'onde électromagnétique en signal électrique susceptible d'être traité par le récepteur.

La première partie de ce chapitre traite sur les propriétés générales et les différents types d'antennes. De même, elle fait appel à des notions telles que le gain, la surface équivalente à une antenne qui nous permettront dans la suite d'établir les équations des télécommunications.

II.1.2 Caractéristiques des antennes

II.1.2.1 Directivité et diagramme de rayonnement d'une antenne

L'antenne isotrope, c'est à dire rayonnant de la même façon dans toutes les directions, est un modèle théorique irréalisable dans la pratique. En réalité, l'énergie rayonnée par une antenne est répartie inégalement dans l'espace, certaines directions étant privilégiées: Ce sont les lobes de rayonnement.

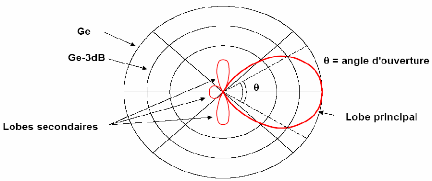
Figure II. 1 : Diagramme de rayonnement d'une antenne

On appelle l'angle d'ouverture (à 3dB) de l'antenne, l'angle autour de la direction de fort champ pour lequel la puissance est supérieure ou égale à la moitié de la puissance se propageant dans la direction du fort champ de gain G_e (fig. II.1).

Plus è3 _dB est étroit, plus il y a une grande concentration de puissance dans une

direction. On parle alors de « directivité d'antenne ». Ainsi, une antenne est directive quand elle concentre l'énergie qu'elle rayonne dans une direction de l'espace. La plupart d'antennes directives présentent un diagramme de rayonnement avec un lobe principal et des lobes secondaires. Le niveau des lobes secondaires est en général situé en dessous de celui du lobe principal (à des dizaines de dB). Le diagramme de rayonnement de l'antenne est valable aussi bien à l'émission qu'a la réception. Il permet de visualiser ces lobes dans les trois dimensions, dans le plan horizontal ou dans le plan vertical incluant le lobe le plus important [14].

La proximité et la conductibilité du sol ou des masses conductrices environnant l'antenne peuvent avoir une influence importante sur le diagramme de rayonnement. Le Diagramme de rayonnement d'une antenne détermine donc la direction de propagation de fort champ électromagnétique c- à- d de forte puissance, étant donné que la puissance par unité

P

de surface en un point est telle que :

E

2

Z_o

(r ) ² u

P

(2.1)

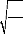
u

Avec 376,6

o

z = = ? est l'impédance caractéristique dans l'espace libre.

^o å _o

E (ur ) est le champ électrique dans la direction ur II.1.2 2. Zones de rayonnement

En fonction de la distance à l'antenne, on définit trois zones de rayonnement : la zone de Raleigh, la zone de Fresnel et la zone de Fraunhoffer comme montré sur la figure II.2

La zone de Rayleigh : c'est la zone de champ proche où il y a échange d'énergie réactive entre l'antenne et le milieu extérieur. Cette zone est dangereuse car difficile à étudier

La zone de Fresnel : il s'agit d'une zone intermédiaire dans laquelle la densité de puissance est fluctuante. C'est un phénomène électromagnétique, où la lumière ou les signaux par radio reviennent diffractés ou courbés par des objets pleins près de leur chemin.

La zone de Fraunhoffer : c'est la zone dite de champ lointain, à grande distance par rapport à la longueur d'onde où les champs sont rayonnés sous la forme d'onde quasiment plane [17].

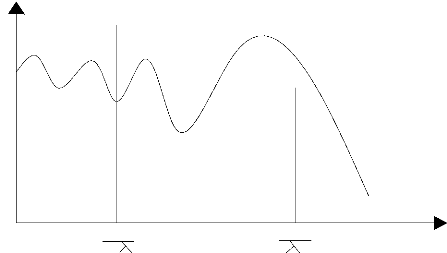
2

Champ proche

P

Champ lointain

Zone de Fresnel

Zone de Fraunhoffer

Zone de Rayleigh

o

D?²

2D^?

² r

Figure II.2 : Zones de rayonnement d'une antenne

II.1.2.3 Gain et surface équivalente d'une antenne

II.1.2.3.1 Gain d'une antenne

La puissance rayonnée par une antenne varie, en général, selon la direction considérée. On définit une antenne fictive de référence qui rayonnerait sa puissance de la même façon dans toutes les direction de l'espace : c'est la source isotrope.

Le gain G(ur ) d'une antenne dans une directionur, est le rapport entre la puissance P(ur) qu'elle rayonne par unité d'angle solide dans cette direction et la puissance que la source

isotrope rayonnerait par unité d'angle solide, avec la même puissance d'alimentation :

P_a

G u r =

( )

r

P u

4ð

P_a

( )

(2.2)

Si l'on se place à une distance de l'antenne assez grande pour qu'elle puisse être d

considérée comme une source ponctuelle, les ondes rayonnées sont sphériques et ce rapport est égal à celui des densités de puissance (puissance par unité de surface en Watts m ) :

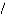
2

(2.3)

r

r p u d

( , )

G u

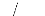
2

P ð d
a 4

( ) =

r _r

p ( u , d ) est la densité de puissance rayonnée par l'antenne selon la direction u , à la distanced.

P_a 4ðd est la densité de puissance rayonnée par la source isotrope à la distance d .

2

Le gain de l'antenne en décibels (dB) s'écrit : GdB ( u ) 10 log G ( u )

r = r (2.4)

En effet, on réserve le nom de Gain d'une antenne, sans mention de la direction considérée, à son gain dans la direction de rayonnement maximal :

P max

a

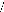
G = (2.5)
P4ð

II.1.2.3.2 Surface équivalente à une antenne

A la réception, une antenne capte une puissance égale au produit de la densité de

P

puissance p à l'endroit où elle se trouve par un coefficient ? caractéristique de l'antenne et homogène à une surface, que l'on appelle « surface équivalente à l'antenne » :

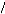
P ( W ) = p(W m² ) . ? ( m²) (2.6)

En effet, la surface équivalente ? est celle d'une ouverture plane qui, placée perpendiculairement à la direction de propagation de l'onde incidente, capterait la même puissance que l'antenne considérée. Pour les antennes à ouverture rayonnantes plane telles que les paraboloïdes ou les cornets, la surface équivalente ? est égale à la surface géométrique de

S

leur ouverture, multipliée par un coefficient f_g inférieur à 1[5] :

? = Sf_g (2.7)

Le coefficient f_g appelé aussi facteur de gain, dépend de la loi de variation de l'amplitude du champ sur l'ouverture.

II.1.2.3.3 Relation entre le gain et la surface équivalente

Une même antenne peut être utilisée à l'émission ou à la réception. Il doit donc y avoir une relation entre le gain G et la surface équivalente ? qui caractérisent respectivement son fonctionnement à l'émission et à la réception. Cette relation est donnée par l'expression :

?

G = 4 ë

ð (2.8a)

2

ë ²

G

ou ? = (2.8b)

4ð

2

Dans le cas particulier du paraboloïde de surface géométrique S = ð D , on obtient :

4

?
??

=

G

ë

2

?
??

^ðDf_g (2.9)

II.1.2.4 Résistance de rayonnement

Pour une antenne alimentée par un courant I_m rayonnant une puissance dans

P_E

l'espace libre, on définit la résistance de rayonnement par une résistance équivalente R_r telle que :

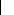
2

R I

r m

P = (2.10)

^E 2

Par ailleurs, l'impédance d'antenne est l'impédance équivalente vue par le générateur chargé par l'antenne. L'impédance d'antenne Z_a comprend en supplément de R_r :

- un terme de perte : la résistance représentant la dissipation dans les

R_d

matériaux de l'antenne

- un terme réactif : la réactance représentant l'énergie emmagasinée dans le volume constituant l'antenne.

Ainsi on a :

P t = P _E + P d (2.11)

Avec : P_t : La puissance active transmise à l'antenne

P_E : La puissance rayonnée par l'antenne dans l'espace libre. P_d : La puissance dissipée dans les matériaux de l'antenne. On écrit alors :

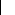
2

? Z I ? a m

P R ?? (2.12)

t = ? ??

^e 2 ?

Où R_e ( Z_a ) = R_r + R_d est la résistance d'antenne.

P d

=

?

?

? =

P E

??

? ?

R I

r m

2

2

2

2

R I

d m

Ainsi :

(2.13)

Le rendement de l'antenne est défini par la relation :
P R

ç = =

E ^r (2.14)

P R R

+

t r d

II 1.2.5 Polarisation d'une antenne

devraient avoir la même polarisation pour obtenir les meilleures performances. Cependant, comme la polarisation change avec la diffraction et les réflexions, cette règle n'est pas toujours valable. La polarisation verticale est préférée pour une couverture à longue distance car l'effet du sol atténue fortement le signal dans le cas d'une polarisation horizontale à partir d'une certaine distance [9].

II.1.2.6 Différentes sortes d'antennes

Bien qu'il existe plusieurs sortes d'antennes, dans ce paragraphe nous allons seulement parler de quelques unes d'entre elles.

II.1.2.6.1 Antenne omnidirectionnelle

L'antenne omnidirectionnelle est conçue pour offrir un diagramme de rayonnement de 360°. Elle est utilisée lorsque la zone de couverture s'étant dans toutes les directions autour d'elle.

Les antennes omnidirectionnelles sont très souvent en polarisation verticale c- à -d qu'elles reçoivent ou émettent les ondes avec un champ électrique vertical.

On peut construire une antenne omnidirectionnelle en utilisant trois antennes sectorielles dont chacune d'elles est un compromis entre les omnidirectionnelles et les directionnelles et diffuse le signal sur un angle de 120°. Les antennes de type sectoriel sont capables d'atteindre un fort gain jusqu'à 15 dB. Elles sont idéales pour couvrir une zone bien définie.

II.1.2.6.2 Antenne Yagi

L'antenne Yagi est constituée d'un dipôle replié auquel est associé un ou plusieurs éléments passifs appelés directeurs et réflecteurs, tel que représenté par la figure ci-après :

Lorsque le dipôle actif est alimenté, il émet des ondes électromagnétiques; les dipôles passifs vont être excités par des courants et ils vont rayonner à leur tour. Le champ rayonné est la somme des champs émis par tous les éléments rayonnants [4].

La présence des éléments passifs diminue la résistance de rayonnement de l'antenne, qui se situe généralement vers 75?. Le gain de l'antenne Yagi est plus élevé que celui de l'antenne dipôle.

II.1.2.6.3 Antenne parabolique

Il existe plusieurs types d'antennes paraboliques, mais la plupart d'entre elles sont constituées par un réflecteur concave R, qui renvoie le signal au foyer dans le cas de la réception, tel que représenté à la figure II.4

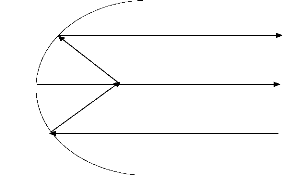
O

F

A

Emission

Reception

Reflecteur (R)

Figure II.4: Antenne parabolique

- En cas d'émission, tout rayon passant par F se réfléchit parallèlement à l'axe focal OA.

- Au cas où le diamètre du paraboloïde est supérieur à 10m on parle des antennes Cassegrain.