Sommaire
Sommaire 1
Liste des figures :
2
Introduction 3
I.Revue de littérature
4
A.Présentation des
principaux concepts étudiés 4
B.La modélisation de la
mortalité 7
II. Le modèle de Lee
Carter 9
A.Le modèle 9
B.Estimation des
paramètres 10
III.Modélisation de
l'indice 13
A.Le mouvement Brownien
13
B.Modélisation de la
dynamique de kt 14
IV.Application aux données
de la Colombie 17
A.La mortalité en Colombie
17
B.Mise en oeuvre du modèle
de Lee Carter 17
C.Modélisation
stochastique de l'indice de mortalité (kt) 20
Conclusion 25
Annexes 26
Annexe 1 : La fonction de
vraisemblance du modèle avec sauts à effets permanents
27
Annexe 2 : Estimation du
modèle de Lee Carter (codes matlab) 28
Bibliographie 31
Liste des figures :
I. Introduction
Aujourd'hui, dans les pays en voie de développement, on
vit plus longtemps comparativement aux années 1950. La chute du taux de
mortalité dans ces pays est plus brutale que dans les anciens pays
industrialisés où le développement a été
plus lent. Les retombées de la médecine moderne ont permit
d'enrayer des épidémies et d'accroître l'espérance
de vie des populations. Par ailleurs, les événements
récurrents tels que les guerres, les épidémies, les crises
socio politiques, qui sévissent dans ces pays, viennent contrer cette
baisse tendancielle du taux de mortalité. Etant à l'origine de
divers chocs sur la mortalité, ces événements peuvent
avoir des effets de court ou de long terme sur celle-ci.
Cette situation préoccupe les assureurs qui sont
exposés à un risque : la mortalité effective pourrait
s'écarter considérablement de la mortalité prévue
par les tables prospectives. L'une des bases techniques de l'assurance vie est
la table de mortalité. Elle décrit la loi de survenance des
décès, laquelle permet d'évaluer le coût moyen des
contrats souscrits par la compagnie. La détermination du montant de la
prime pure relative à un contrat d'assurance sur la vie se fait sur base
du principe d'équivalence, en vertu duquel l'espérance de la
valeur actuelle des prestations de l'assureur doit être égale
à l'espérance de la valeur actuelle des primes pures
payées par l'assuré. Si les bases techniques utilisées par
l'assureur ne reflètent pas la sinistralité réelle qu'il
s'est engagé à couvrir, l'assureur sera confronté à
des problèmes financiers. D'où l'intérêt pour
l'assureur de réduire l'incertitude sur ses prévisions de la
mortalité future.
Projeter l'évolution de la mortalité est un
exercice difficile, comme en témoignent les écarts parfois
très importants observés dans le passé entre les
projections et la réalité en ce qui concerne les pays
développés. Deux types de risques sont à prendre en compte
dans la modélisation des lois en assurance de personnes : le risque
de mortalité et le risque de longévité. D'un coté
le risque de mortalité concerne les scénarios pessimistes sur
l'évolution de la mortalité (survenance d'une pandémie).
C'est le risque d'un nombre de décès plus élevé que
prévu. Les guerres, les pandémies et les catastrophes naturelles
sont souvent à l'origine de ce risque. De l'autre coté, le risque
de longévité est le risque que les populations vivent plus
longtemps que prévue. Les progrès non anticipés de la
médecine et l'amélioration des conditions de vie sont à
l'origine de ce type de risque.
Comment modéliser la mortalité des pays en voie
de développement en prenant en compte les crises récurrentes et
la survenance d'événements extrêmes ? Quiconque se
lancerait dans l'élaboration de tables de mortalité prospectives
pour les pays en développement serait d'abord confronté à
la disponibilité de données sur de longues périodes. Du
coup il s'avère difficile de modéliser la survenance d'un
événement extrême et rare tel qu'une pandémie.
Les modèles de mortalité jusqu'ici
élaborés ont été testés sur les
données des pays développés. Peuvent-ils s'appliquer aux
données des pays en développement ? La dynamique de la
mortalité dans les PVD1(*) est différente de celle PD2(*). En effet la réduction de
la mortalité y a été brutale contrairement aux PD
où le développement a été lent et progressif. Les
PVD ont bénéficié des transferts des progrès de la
médecine émanant des PD. Par exemple, en Colombie le taux de
mortalité est passé de 14 pour 1000 en 1950 à 5 pour 1000
dans les années 1980. Soit une baisse 9 points en 30 années.
Depuis lors ce taux se stabilise autour de 5 pour 1000. Tout comme dans la
plupart des PVD, cela pourrait s'expliquer par la croissance de la
pauvreté, par de fortes incidences des maladies infectieuses,
parasitaires et diarrhéiques aux âges moins élevés
et par un environnement économique morose. Ces nombreux maux viennent
s'opposer aux effets dues au progrès de la médecine. Dans la
mesure où les sociétés des PVD et celles des PD habitent
des environnements différents, et subissent des transformations
sectorielles et culturelles différentes, leur expérience de la
morbidité et de la mortalité peut présenter de fortes
différences. Il serait donc intéressant de voire comment l'on
pourrait adapter les modèles de mortalité prospectifs,
déjà élaborés, aux réalités des
PVD.
L'objectif de ce mémoire sera de proposer une
méthode qui permette de prendre en compte tous les aspects
susmentionnés (risque de survenance de crise extrême,
environnement socio économique) de la mortalité dans
l'élaboration de tables de mortalité prospectifs pour les PVD.
Nous utiliserons comme modèle de base le célèbre
modèle de Lee Carter (1992). Vu le problème
d'indisponibilité de données (environnement socio
économique et démographique) auquel fait face les PVD, nous
modéliserons l'indice de mortalité à l'aide d'un mouvement
brownien et d'un processus de diffusion de saut. Il sera supposé que les
changements dans l'indice de mortalité proviennent d'un effet additif de
plusieurs variables indépendantes (variables macro économique,
variable démographiques).
Notre travail se subdivise en plusieurs chapitres. Le premier
chapitre fait la revue des méthodes de modélisation de la
mortalité. Dans le second nous exposerons de façon exhaustive
notre modèle de base (le modèle de Lee Carter). Le chapitre 3
présente la modélisation de l'indice de mortalité. Et nous
appliquerons dans le dernier chapitre, le modèle à un pays en
voie de développement : la Colombie.
II. Revue de
littérature
A. Présentation des principaux
concepts étudiés
Suivant la nomenclature proposée par l'Insee, une table
de mortalité se définit de la façon suivante :
«Une table de mortalité annuelle suit le cheminement d'une
génération fictive de 100 000 nouveau-nés
à qui l'on fait subir aux divers âges les conditions de
mortalité observées sur les diverses générations
réelles, durant l'année étudiée.» La
table de mortalité donne donc, pour la suite des anniversaires
x, le nombre de survivants Sx à ces
anniversaires, le nombre de décès Dx entre
deux anniversaires successifs et le quotient annuel de mortalité
(s'interprétant comme une probabilité de décès)
Qx à l'âge x. Ces tables sont alors
très utiles notamment pour les assureurs, qui les utilisent pour
déterminer leurs primes d'assurance.
Lorsqu'on construit une table de mortalité, on cherche
à obtenir des résultats sur les probabilités de survie des
individus. Une formalisation mathématique est donc nécessaire, et
la partie qui suit se propose de présenter les principaux outils
mathématiques qui sont utilisés.
A.1. Outils principaux
des modèles de durée
A.1.a) Probabilités de survie et de
décès
Considérons à une époque 0 origine des
temps, un individu d'âge x. Désignons par Tx sa
durée de vie résiduelle à partir de cet instant. Ainsi,
cet individu décèdera à l'âge de x +
Tx. La durée de vie résiduelle Tx
constitue une variable aléatoire. Nous caractérisons la loi
de probabilité de Tx par la fonction de survie
pxt = P[Tx > t] où
t est un réel positif. Inversement, on désigne par qt/
t'x la probabilité de décès entre
t et t + t' d'un individu pris en observation
à l'âge x et qxt la
probabilité de décès avant la date t d'un individu pris en
observation à l'âge x. Notons que qxt
= 1 - pxt.
La probabilité de décès s'exprime alors
en fonction de la probabilité de survie :
qt/t'x = P[t < Tx < t
+ t'] = P[t < Tx] - P[t + t'
< Tx]
A.1.b) Loi de survie
Considérons à l'intérieur d'un groupe
homogène, à un instant pris comme origine, l'ensemble des
individus d'âge x en nombre Lx. Nous allons
supposer qu'ils décèdent indépendamment les uns des
autres. Dans ce cas, on peut attacher à chaque élément du
groupe une variable aléatoire Xi(t) que nous
appellerons indicateur de survie et qui prend la valeur 1 si l'individu est
vivant et la valeur 0 s'il est mort à la date t. Les variables
Xi(t) sont alors en nombre égal à
Lx et on suppose de plus que les décès sont
indépendants. Donc :
E(Xi(t)) = 1 * pxt + 0*
qxt = pxt
V (Xi(t)) = E(Xi(t)2) - [E(Xi(t))]2
= pxt - (pxt)2 =
pxt * qxt
A l'époque t le nombre de survivants du groupe
initialement composé de Lx individus est :
Lx+t =
D'où, E(Lx+t) =
Lx * pxt
Et, comme les variables Xi(t) sont
indépendantes, on a :
V (Lx+t) = Lx *
pxt * qxt
On appelle nombre probable de vivants3(*) à l'âge x +
t et on le désigne par lx+t la quantité
:
E(Lx+t) = Lx *
pxt
Et on obtient notamment en faisant tendre t vers 0
l'égalité :
Lx = E(Lx) =
Lx
Remarquons qu'on obtient ainsi l'égalité
pxt = lx+t / lx On peut
alors à partir d'une constante de proportionnalité
Lx = lx calculer le nombre probable de
vivants pour toutes les périodes : l'ensemble des valeurs obtenues
constitue alors une loi de survie.
A.1.c) Le taux instantané de mortalité
Etant donné un individu pris en observation à
l'âge x et supposé vivant à l'époque t
(c'est-à dire à l'âge x + t), la
probabilité qu'il décède entre les dates t et
t + ?t est :
P(t < Tx < t + ?t
/ Tx>t) = P(t < Tx < t +
?t) / P(Tx > t) =
(pxt - pxt+?t) /
pxt
En supposant la fonction pxt
dérivable par rapport à t, on obtient alors,
pxt -
pxt+?t=-(pxt)' /
?t
Or, pxt = lx+t / lx
donc ( pxt )' =
lx+t' / lx et pxt -
pxt+?t = - lx+t' /
(?t / lx)
D'où /?t = -
lx+t' / lx+t
Cette limite est une fonction ux+t que
l'on appelle le taux instantané de mortalité à
l'âge x + t. Pour un âge y, on a donc
:
uy = -ly' / ly
=
Inversement, si l'on connaît la fonction
uy, on aura par intégration entre x et
x + t :
pxt =
A.1.d) L'espérance de vie
On désigne par espérance de vie à
l'âge x l'espérance mathématique de la durée de vie
résiduelle Tx. En notant ù la durée de vie
maximale, on a ainsi :
= = -
A.2. Les tables de
mortalité
Une table de mortalité suit, sur une centaine
d'année, l'évolution d'un groupe de personnes, et propose
à chaque période le nombre de vivants, le nombre probable de
vivants, le nombre de décès, et l'espérance de vie. A la
base de la construction de cette table se trouve donc la détermination
des probabilités de décès
(qxt).
A.2.a) Calcul des probabilités de
décès
Pour évaluer qxt on
met en observation Lx personnes atteignant l'âge
x dans l'année. Au bout d'un an, il reste
Lx+1 = Lx - Dx personnes
vivantes avec Dx le nombre de décès parmi le
groupe observé dans l'année écoulée. On
note alors Qx = Dx / Lx le quotient
annuel de mortalité.
On démontre alors que, pour cette variable
aléatoire Qx les relations suivantes :
E(Qx) = qx
V(Qx) =
(qx*px) / Lx
Le théorème central limite nous indique alors
que Qx suit une loi normale d'espérance
qx et de variance (qx*px) /
Lx et se met donc sous la forme :
Qx = qx + N
Où la variable aléatoire N suit une loi normale
centrée réduite.
Ainsi, la valeur exacte des variables étudiées
ne pouvant être déterminée, on doit se contenter d'une
approximation, dont on pourra déterminer un intervalle de confiance
à partir de la forme normale de Qx.
Afin de garantir l'estimation la plus précise possible,
on aura donc tout intérêt à avoir :
- Un grand nombre de variables
- Des groupes de population les plus homogènes
possibles
Dans les faits, la série des observations des
Qx est souvent très désordonnée, en
raison d'aléas statistiques. On présume que la série des
probabilités présente une certaine régularité et
notamment qu'à partir de 30 ans, les taux augmentent continûment.
On utilise parfois des méthodes de lissage des résultats et
d'ajustement.
A.2.b) L'ajustement et le lissage
La première étape, lorsqu'on recueille des
résultats, est donc de lisser la série des
Qx, c'est à dire de remplacer les valeurs
observées Qx par des valeurs qx
plus régulières, mais qui ne s'éloignent pas trop des
observations.
Sans les expliciter, signalons simplement que de nombreuses
méthodes de lissage existent : ajustement par les splines, programme de
minimisation d'écarts (Wittaker-Anderson). . . Le lissage
effectué, il est alors possible d'utiliser des méthodes
d'ajustement. En effet, les observations statistiques ne nous donnent pas
précisément qx mais plutôt un intervalle de
confiance. Cette incertitude n'est pas compatible avec la
nécessité de disposer d'une table de mortalité en vue des
calculs de primes d'assurance. Pour la réduire, on essaie donc
d'éliminer les aberrations fortuites de taux observées, en
déterminant une courbe continue
Qx = f(x) passant
à l'intérieur des intervalles de confiance.
B. La modélisation de la
mortalité
La première étape de toute projection de
mortalité consiste à réduire la dimension des
données. Il est en effet impossible de traiter simultanément
autant de séries chronologiques décrivant l'évolution au
cours du temps des taux de mortalité aux différents
âges.
B.1. La
modélisation paramétrique
Cette première approche consiste à ajuster les
observations de chaque année à l'aide d'un modèle
paramétrique. Elle est basée sur l'hypothèse selon
laquelle l'indicateur choisie pour mesurer la mortalité est une fonction
de l'âge x ,fá(x) avec
á=(á1, á2,...,
án),étant des paramètres à estimer
à l'aide des techniques de régression classiques. L'objectif
étant d'obtenir une meilleure représentation des données
avec un minimum de paramètres. Nous pouvons citer par exemple le
modèle de Makeham qui considère que le taux instantané de
mortalité `a l'âge x se décompose comme suit:
· un premier terme constant, A, qui est
indépendant de l'âge atteint x et représente la
mortalité accidentelle ainsi que celle due aux maladies pouvant survenir
indifféremment à tout âge;
· un second terme croissant en x,
âcx, qui représente la mortalité due au
vieillissement, pour laquelle on postule un comportement exponentiel.
Ceci permet de condenser l'information annuelle dans un petit
nombre de paramètres (3 dans notre exemple). Ensuite, l'évolution
au cours du temps de ces paramètres est à son tour
modélisée, afin de fournir des projections de la mortalité
dans le futur. Il ne faut néanmoins pas perdre de vue que, chaque
année, ces paramètres seront vraisemblablement fort
corrélés, ayant été estimés sur base des
mêmes données. On ne peut donc pas se contenter d'une
modélisation uni variée mais on doit recourir à un
modèle de série temporelle multi variée beaucoup plus
complexe. La pertinence de cette approche va dépendre de la bonne
spécification du modèle paramétrique. Si ce dernier
s'avère erroné, cela compromet gravement les projections qui en
découlent.
B.2. L'approche
prospective
L'objectif des analyses prospectives est d'anticiper les
évolutions futures des taux de décès aux différents
âges. On tient non seulement compte de l'âge des individus mais
aussi du temps : la loi de mortalité du groupe étudié
est caractérisée par un modèle bidimensionnel. Les
données disponibles doivent donc être plus
détaillées : il est nécessaire de connaître le
nombre de décès observés parmi les assurés pour
différents âges et différentes années (ou suivant
différentes générations). Il faut de plus que l'ajustement
des taux de mortalité passés puisse être projeté
dans le futur afin de tenir compte dans la modélisation de
l'évolution potentielle de la mortalité au cours du temps. Il
existe bon nombre de techniques pour établir une table de
mortalité prospective. Il est assez fréquent d'appliquer une
approche paramétrique. Mais les actuaires utilisent surtout la
méthode de Lee-Carter.
Dans ce modèle classique de construction de tables
prospectives, (voir notamment LEE et CARTER [1992], LEE [2000] pour une
présentation et une discussion avec les autres modèles
prospectifs), plusieurs sources d'incertitude viennent perturber la
détermination de la tendance future : choix de la période
d'observation, fluctuations stochastique des taux de mortalité,
événements exceptionnels tels que les crises
démographiques aigues (guerre, épidémies...),
etc. Cette incertitude fait peser sur les assureurs de rentes
viagères et les régimes de retraite un risque systématique
(non mutualisable) dont l'impact financier peut être très
important. Aux Etats-Unis par exemple, on estime à $4000 milliards le
déficit lié à cette situation (ACLI4(*), 2006). L'incertitude sur
l'évolution de la tendance future peut accroitre les risques sur les
fonds de pension et les provisions annuelles dans la mesure où les
primes versées aux survivants sont plus élevées que
prévues. Dans une récente étude, Cowling et Dales (2008)
ont montré que les entreprises britanniques avaient fait des
hypothèses trop optimistes sur l'évolution de la
longévité et ont estimé le déficit de ces
compagnies résultant de cette fâcheuse situation à plus de
£40 milliards. A cette mauvaise appréhension de l'évolution
de la mortalité se greffe certains risques démographiques qu'il
importe de prendre en compte. Une approche de la modélisation en
assurance vie consiste à introduire un scénario pessimiste avec
la prise en compte d'évènements démographiques
extrêmes tels que les guerres et les épidémies. Il existe
plusieurs études sur une telle modélisation du risque de
mortalité.
B.3.
Modélisation stochastique et prise en compte des sauts
A partir du modèle de référence de Lee
Carter, plusieurs auteurs (Renshaw and Haberman (2003), Li et Chan (2007)) ont
proposé des modèle stochastique de mortalité en
considérant que le taux de mortalité futur u(x,t) est
lui-même aléatoire, et que donc u(x,t) est un processus
stochastique (comme fonction de t à x fixé).
L'aléa est introduit de manière à capturer l'incertitude
sur l'estimation de la tendance future de la composante temporelle des taux de
mortalité. Cependant ces auteurs, dans leurs modèles, ne
modélisent pas explicitement les sauts qui interviennent dans
l'évolution de la mortalité. Par exemple Li et Chan (2007), dans
leurs travaux, observe les pandémies comme des interventions
exogènes non répétitives (points aberrants) et les
corrigent avant la modélisation. Ils reconnaissent toutefois que les
événements extrêmes démographiques sont très
souvent à l'origine des sauts observés. Peu d'auteurs comme Cox,
Lin et Wang (2006) se sont penché sur la modélisation des sauts,
vu leur grande importance dans l'élaboration des modèles de
mortalité. Par ailleurs Hua Chen (2007) a largement étudié
les processus de diffusions de sauts intégrés aux modèles
de mortalité. Dans sa thèse « Contingent claim pricing
with applications to financial risk management », il a introduit les
processus de diffusion de sauts dans le modèle de Lee Carter et l'a
utilisé pour prédire les taux de mortalité future.
III. Le
modèle de Lee Carter
Dans ce chapitre, nous exposerons la méthode de Lee
& Carter (1992), qui a fait ses preuves en démographie et a
été présentée aux actuaires par Lee (2000).
L'idée est de passer par une décomposition en valeurs
singulières de la matrice des taux de mortalité (doublement
indexés, par l'âge et le temps calendaire). La matrice initiale
sera ainsi approximée au rang 1 par un produit de deux vecteurs propres:
l'un d'entre eux traduira l'effet et de l'âge, et l'autre l'effet du
temps calendaire. Il suffira alors projeter dans le futur le vecteur
décrivant l'évolution temporelle pour en déduire des
tables de mortalité prospectives.
A. Le modèle
Le modèle consiste à décomposer la
mortalité en deux composantes, l'une propre à l'âge et
l'autre tendancielle, et ensuite à extrapoler celle relative au temps.
Il est bon de noter d'emblée que la méthode de Lee et Carter
possède les avantages et les inconvénients de
l'objectivité: elle n'incorpore pas d'avis d'expert sur
l'évolution présumée de la mortalité, sur les
progrès de la médecine, l'apparition de nouvelles maladies ou
encore l'évolution du style de vie. La méthode se borne donc
à extrapoler dans le futur les tendances constatées dans le
passé.
L'idée est ici de décomposer l'estimation brute
de (taux instantané de mortalité) comme suit sur
l'échelle logarithmique:
où est l'erreur qui représente la part du
phénomène qui n'est pas capté par le modèle. Ces
sont supposées centrées, indépendantes et de même
variance ó2 (hypothèse
d'homoscédasticité).
Le modèle tel que posé n'est pas identifiable
car il existe un autre jeu de paramètre qui aboutit au même
modèle. Par exemple en remplaçant par et par , le
modèle reste invariant. Des contraintes sur les paramètres
doivent donc venir compléter le modèle. Lee et Carter proposent
de fixer la valeur des sommes des et des :
L'équation , décompose le taux de
mortalité à l'âge x pour l'année t
sur l'échelle logarithmique, à un terme d'erreur près, en
la somme d'une composante spécifique à l'âge x et d'un
produit entre un paramètre temporel décrivant l'évolution
générale de la mortalité et un paramètre propre
à l'âge décrivant l'évolution du taux à
l'âge x par rapport à ceux relatifs aux autres âges. On
espère bien entendu que la variance des erreurs sera aussi petite que
possible.
Que signifie chaque paramètre du
modèle ?
est la composante du modèle liée à
l'âge. Il décrit le comportement moyen des taux instantanés
de mortalité au cours du temps. Plus précisément, exp()
est la moyenne géométrique des :
Soit :
est la sensibilité de la mortalité
instantanée par rapport à l'évolution
générale de la mortalité. Il décrit les
écarts des par rapport au comportement moyen. En effet,
En particulier, les âges x pour lesquels les
sont importants seront plus sensibles à l'évolution
générale de la mortalité.
est la composante temporelle qui décrit
l'évolution de la mortalité dans le temps.
Tout lecteur intéressé par une
présentation plus détaillé du modèle peut se
référer à Lee & Carter (1992), Bell (1997), Lee (2000)
et Lee& Miller (2000). Bien que ce modèle ait connu un grand
succès, il présente quelques limites. Le lecteur pourra se
référer à Gutterman & Vanderhoof (1999).
B. Estimation des paramètres
Les variables qui figurent à droite de
l'équation ne sont pas observables. Bien entendu, le modèle ne
peut être estimé à l'aide d'une simple régression
linéaire. L'estimation des paramètres s'effectuera donc par la
méthode des moindres carrés ordinaires, c'est-à-dire en
résolvant le programme suivant :
L'unicité de cette solution est assuré par les
contraintes et .
B.1. Etape 1 :
Estimation des
Les sont estimé par les moyennes des au cours du
temps. Nous avons :
B.2. Etape 2 :
Estimation des
Considérons une matrice de dimension
définie par . Nous chercherons à
approximer au sens des MCO, cette matrice par le produit d'une matrice colonne
et d'une matrice ligne :
avec et .
Il s'agira de minimiser :
La solution s'obtient en procédant à la
décomposition en valeur singulière de la matrice Z. Soit un
vecteur propre normé de Z'Z. Alors :
En multipliant les deux membres de la première
égalité par Z, on obtient
Ce qui montre qu'à tout vecteur propre Z'Z relatif
à une valeur propre correspond un vecteur propre de Z'Z relatif
à la même valeur propre. Ainsi, Z'Z et ZZ' ont les mêmes
valeurs propres. Soit le ième vecteur propre de ZZ'
associé à la valeur propre , on alors pour ,
Ou encore
Considérons la relation
et multiplions les deux membres de cette relation par avant
de sommer sur toutes les valeurs propres de Z'Z
Comme les sont orthogonaux et de norme 1,
avec la matrice unité de dimension, de sorte qu'on
aboutit à la décomposition :
C'est la décomposition aux valeurs singulières.
Elle assure que, sous des conditions assez générales, une matrice
rectangulaire peut être écrite de façon unique comme une
somme optimale de matrices de rang 1 (c'est-à-dire de produits d'une
matrice ligne par une matrice colonne). L'optimalité dont il est
question signifie que la première matrice de rang 1 constitue la
meilleure approximation de rang 1 de la matrice initiale (au sens des moindres
carrés), que la somme des deux premières constitue la meilleure
approximation de rang 2, etc.
Si la valeur propre surpasse nettement les autres, alors on
obtient l'approximation :
On mesure la qualité de l'approximation par le
pourcentage de variance expliquée défini par
On voit bien qu'il suffit de prendre
Avec . Il est claire que la contrainte est satisfaite par les
. De plus les vérifient aussi la contrainte car .
B.3. Etape 3 :
Réajustement des
Nous allons à présent réajuster les de
sorte que le nombre de décès prévu par le modèle
soit égal au nombre de décès observé. Les nouveaux
estimateurs sont solutions des équations
où est le nombre total de décès
observé à la date t, et est la population au sein du
groupe d'âge x.
IV. Modélisation de l'indice
Le modèle classique de Lee et Carter
présenté ci-dessus synthétise dans la série
kt toute l'information relative à l'évolution
de la mortalité dans le temps. L'objectif de ce chapitre est de
modéliser cette série temporelle pour prévoir la
mortalité future.
Nous écrirons dans toute la suite en lieu et place de
.
A. Le mouvement Brownien
Soit une variable décrivant l'évolution
temporelle d'un phénomène. Considérons la formule
Ce qui signifie que la variation de x () suit une loi
normale de moyenne et de variance. Le choix de la loi normale se justifie par
le fait que l'on suppose que la variable x est affecté
additivement par plusieurs variables aléatoires indépendantes
(théorème centrale limite).
En itérant l'on obtient une relation entre :
Et on généralise pour un intervalle de temps
T :
Cette équation est valable lorsque la variable
temporelle appartient à un ensemble discret. Mais nous pouvons
l'écrire en temps continu en choisissant un intervalle de temps
très petit. On aura alors :
L'équation différentielle stochastique
(mouvement brownien) s'écrit alors
La mortalité est un phénomène qui
résulte des effets cumulatifs de plusieurs forces qui affectent la vie
des individus. L'indice kt qui est la composante temporelle
de la mortalité dans le modèle de Lee Carter peut donc être
représenté par un mouvement brownien.
B. Modélisation de la dynamique
de kt
Nous ajusterons les k(t) à l'aide du
modèle de type (). Pour prendre en compte les éventuels sauts,
nous utiliserons une chaine de Markov discrète avec des sauts ayant des
effets transitoires ou permanents.
B.1. Processus avec
sauts à effet transitoire
Soit le nombre de chocs durant l'intervalle de temps
(0,t). Supposons qu'il y a au plus un choc (à effet
transitoire) dans chaque intervalle de temps (t-h,t), alors peut
s'écrire comme une chaine de Markov discrète avec
Soit, le nombre de choc intervenu dans la période
(t-h,t), alors suit une loi de Bernoulli de paramètre
p.
Soit, l'indice de mortalité en absence de choc.
D'après l'hypothèse faite précédemment, il peut
être représenté l'équation :
où et sont respectivement le taux d'évolution
instantané la volatilité instantané de l'indice de
mortalité en absence de choc, et est un mouvement brownien standard de
moyenne nulle et de variance t.
Si un choc intervient dans l'intervalle de temps
(t-h,h), i.e. , , on note l'ampleur du choc . On suppose que les sont
i.i.d et suivent une loi normale de moyenne et de variance , et est
indépendant du mouvement Brownien . Le choc fait que la valeur actuelle
de passe de à .
Soit
S'il n'y a pas de chocs dans l'intervalle de temps (t-h,t),
i.e., , on aura
En écrivant (4) et (5) en une seule
équation :
Par conséquent la dynamique des indices de
mortalité s'écrit comme suit :
En intégrant la première relation de t à
t+h, on obtient :
Et de la seconde équation de (7), on
déduit :
En posant, on obtient :
Si, alors est indépendant de . Si , alors est
corrolé avec du fait de la partie . Les méthodes de maximum de
vraisemblance conditionnelle permettent d'estimer les paramètres ().
B.2. Processus avec
sauts à effet permanent
Supposons maintenant que les sauts qui interviennent dans la
dynamique de ont des effets permanents contrairement au cas
précédent. Au lieu d'introduire le saut dans l'équation en
niveau de , nous l'introduirons dans l'équation différentielle.
Ainsi, nous prenons en compte les effets permanents des différents
chocs. La nouvelle équation de la dynamique de s'écrit :
Le produit représente l'impact, à l'instant dt,
des chocs à effet permanent.
Cette équation peut se résumer en une
seule :
Posons comme dans le cas précédent , alors
Les détails sur la vraisemblance de ce modèle
sont présentés en annexes.
V. Application aux données de la
Colombie
Dans ce chapitre, nous appliquerons le modèle
présenté dans les chapitres précédent aux
données de mortalité de la Colombie. La structure de la
mortalité de ce pays est relativement la même que dans les autres
PVD. Cette application permettra de révéler la qualité de
représentation du modèle présenté. Les
données que nous utiliserons dans notre travail proviennent du
Departamento Administrativo Nacional de Estadística (
www.dane.gov.co) et du
World Health Organisation Statistical Information System (
www.who.int/whosis
).
A. La mortalité en Colombie
Nous avons, à partir des données
susmentionnées, représenté l'évolution des taux
bruts de mortalité depuis 1955 jusqu'à 2005 (
Figure ).
Bien qu'ayant la même allure, les taux de
mortalité chez les hommes restent toujours supérieurs aux taux de
mortalité chez les femmes. On observe donc plus de décès
chez les hommes. Pour l'ensemble de la population, l'évolution de la
mortalité s'est faite différemment sur deux périodes. Une
première période qui part de 1955 jusqu'en 1979. On y observe une
forte amélioration de la mortalité (une baisse d'environ 70% sur
la période) avec deux chocs positifs aux dates 1970 et 1979. Ces sauts
pourraient être les conséquences d'une forte urbanisation ou d'une
action volontariste du gouvernement visant améliorer les conditions de
vie des populations. Leurs effets ne sont donc pas transitoires. Ils se
propagent dans toute la dynamique de la mortalité. Ensuite nous avons
une deuxième période (1980-2005) où la mortalité
demeure quasi constante. L'on pourrait s'interroger sur les origines du frein
à cette évolution remarquable de la mortalité durant la
première période.
En Colombie, l'assassinat en 1948 d'Eliecer Gaitan, leader
libéral qui a tenté de mobiliser les classes populaires contre
l'oligarchie, va marquer le début d'une guerre civile qui fera
300 000 morts. Face à la violence conservatrice, des guérillas
libérales et communistes font leur apparition. Tandis que les groupes
armés libéraux déposent les armes, le Parti communiste
colombien préconise une politique d'autodéfense de masses. Depuis
lors, la Colombie balance entre la guerre civile qui se tient entre les
paramilitaires (extrême droite), les FARC (Forces Armées
Révolutionnaires de Colombie, marxistes) et le pouvoir central de
Bogota. C'est les répercutions durable de cette crise (croissance de la
pauvreté, insécurité) qui viennent en partie freiner la
baisse tendancielle du taux de mortalité.
Par ailleurs, L'accès aux soins de santé est
devenu plus inéquitable aujourd'hui ; tandis que 20% de la population
à revenu le plus élevé avait une couverture d'assurance de
75% en 2000, seulement 35% du quintile le plus pauvre était couvert. Les
réformes du libre-échange et la privatisation du secteur de la
santé ont entraîné la détérioration de la
santé générale de la population. Entre 1990 et 2000, le
nombre d'enfants de moins d'un an ayant reçu la série
complète de vaccinations a chuté de 67,5% à 52%,
favorisant le retour d'épidémies telles que la rougeole, absente
depuis des années. Les couches les plus démunis (plus de 64% de
la population) ont de plus en plus du mal à bénéficier des
retombés de la médecine. Cette situation vient s'ajouter aux
effets pervers de la crise socio politique pour contrecarrer la baisse de la
mortalité et la maintenir quasi stable.
Un modèle approprié, dans le cadre de notre
travail, ne saurait omettre tous ces aspects de la mortalité en
Colombie. Nous prendrons en compte les éventuels chocs sur la
mortalité et leurs effets sur sa dynamique.
Figure : Evolution des taux bruts de mortalité
de la population colombienne
Source : Nos
calculs
B. Mise en oeuvre du modèle de
Lee Carter
Nous estimons dans cette partie les différents
paramètres du modèle de Lee Carter. Les codes source matlab qui
ont permis d'effectuer les différentes étapes sont
présenté dans annexes 2.
B.1. Etape1 :
L'estimation des ax
Les
Figure et
Figure représente cette estimation
à partir des données féminines et masculines colombienne.
S'agissant de l'allure générale de la mortalité suivant
l'âge, on y retrouve les phénomènes habituellement
observables. La courbe, relativement élevée chez les
nouveau-nés et les nourrissons, décroît rapidement avec
l'âge pour atteindre son minimum absolu vers l'âge de dix ans.
Survient alors un pic de mortalité appelé bosse-accident. Cette
bosse, qui touche les jeunes d'une vingtaine d'années, est en fait
essentiellement composée de suicides et d'accidents. Sur les
données féminines, ce pic a un niveau faible comparativement
à celui relatif aux données masculines. La jeunesse masculine est
donc beaucoup plus exposé aux risques de mortalité (accidents,
guerres, banditisme) que la jeunesse féminine .Ensuite, les logarithmes
moyens des taux instantanés de mortalité augmentent quasiment
linéairement avec l'âge.
A.1. Etape 2 :
Estimation des ßx et kt :
La décomposition en valeur singulière
(effectuée sous Matlab) nous permet de trouver un taux d'inertie
d'environ 0.7 pour les données masculines et féminines;
l'approximation semble donc être de qualité. Les figures qui
suivent représentent les estimations des paramètres
âx et kt. Les plus grandes variations temporelles
du taux de mortalité (âx) se situent chez les jeunes et
sont probablement le résultat des progrès réalisés
par la médecine pour freiner la mortalité infantile et
juvénile. Les courbes des kt sont en constante
décroissance, reflétant principalement les progrès de la
médecine induisant le rallongement de la durée de vie.
Figure : Représentation des valeurs de alpha en
fonction de l'âge (population des femmes)
Source : Nos
calculs
Figure : Représentation des valeurs de alpha en
fonction de l'âge (population des hommes)
Source : Nos
calculs
Figure :
Représentation des valeurs de beta en fonction de l'âge
(hommes)
Source : Nos
calculs
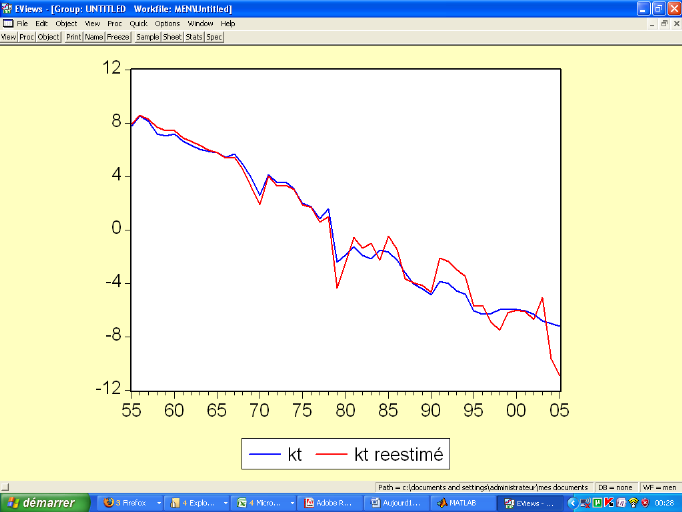
Figure : Evolution
comparée des kt et kt réestimé
(hommes)
Source : Nos
calculs
Figure :
Représentation des valeurs de beta en fonction de l'âge
(femmes)
Source : Nos
calculs
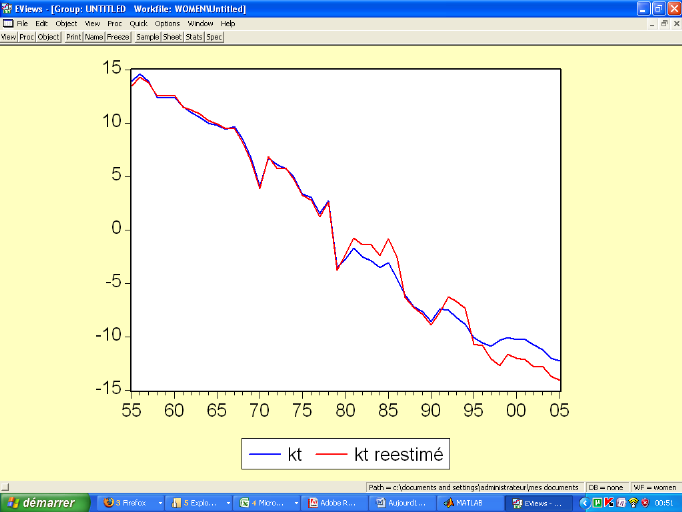
Figure : Evolution
comparée des kt et kt réestimé
(femmes)
Source : Nos
calculs
C. Modélisation stochastique de
l'indice de mortalité (kt)
En général trois approches sont utilisées
dans la modélisation stochastique de l'indice de mortalité :
l'approche sans sauts, l'approche avec sauts à effets transitoires et
l'approche avec sauts à effets permanents. Dans cette application, nous
écarterons l'approche avec sauts à effets transitoires. Les sauts
à effets transitoires sont en général des chocs pervers
sur la mortalité dont l'impact est de court terme (catastrophes
naturelles, pandémies, etc.). De 1953 à 2005, la population
colombienne n'a subi aucun choc de cette nature (
Figure ). Les principaux événements
extrêmes (guerres civiles, situation socio économique) qui ont
marqué les différentes populations ont des effets qui se
propagent durablement dans le temps.
Nous comparerons ensuite les deux modèles (sans sauts
et avec sauts à effets permanents) pour retenir celui qui s'ajuste le
mieux à nos données.
C.1. Population des
hommes
Les résultats des estimations par maximum de
vraisemblance sont présentés dans les tableaux qui suivent. La
valeur estimé de u est presque la même (-0,37) pour les deux
modèles. Ce qui signifie qu'en moyenne, l'indice de mortalité
chez les hommes baisse de -0,37 chaque année. La volatilité
instantanée de kt est plus importante dans le modèle sans sauts.
Ce modèle incorpore, en effet, les variations de sauts dans la
volatilité instantanée de kt. Le test du rapport de
vraisemblance5(*)
effectué à l'aide des log vraisemblance nous conduit à
rejeter le modèle sans saut avec un risque de 1%. Le modèle avec
sauts est donc mieux adapté à nos données et la
probabilité qu'un choc intervienne, au cours d'une année, est de
0,38. L'ampleur moyen des chocs est positif (0,18) contrairement aux PD
où l'ampleur moyen des chocs est en général
négatif. En effet, globalement, les sauts qui affectent
négativement la mortalité dominent ceux qui l'affectent
positivement. Cet état de fait est en accord avec les
réalités des PVD qui n'ont pas les moyens leur permettant de
profiter des avancées extrêmes de la médecine et qui
évoluent en permanence dans un environnement socio politique
instable.
Tableau : Estimation des
paramètres du modèle avec sauts (hommes)
|
Modèle avec sauts à effet permanents
|
|
|
|
|
|
paramètres
|
estimations
|
|
|
|
|
|
u
|
-0.376999
|
|
p
|
0.385020
|
|
m
|
0.187961
|
|
ó
|
0.443811
|
|
s
|
2.113548
|
|
|
|
|
|
Log likelihood
|
-75.87345
|
|
|
|
|
Source : Nos
calculs sur Eviews
Tableau : Estimation des
paramètres du modèle sans sauts (hommes)
|
Modèle sans sauts
|
|
|
|
|
|
paramètres
|
estimations
|
|
|
|
|
|
u
|
-0.376966
|
|
ó
|
1.387509
|
|
|
|
|
|
Log likelihood
|
-87.32367
|
|
|
|
|
Source : Nos
calculs sur Eviews
C.2. Population des
femmes
Ici également, le test du ratio de vraisemblance
rejette le modèle sans sauts. Le taux de variation moyen de kt (u) est
beaucoup plus important chez les femmes que chez les hommes. Il passe de -0,37
chez les hommes à -0,55 chez les femmes. Soit un gain de -48%. La
réduction de la mortalité dans le temps est donc beaucoup plus
rapide dans la sous population des femmes que celle des hommes. Les autres
paramètres estimés ne présentent pas d'écarts
considérables avec ceux de la population masculine.
Tableau : Estimation des
paramètres du modèle avec sauts (femmes)
|
Modèle avec sauts à effet permanents
|
|
|
|
|
|
paramètres
|
estimations
|
|
|
|
|
|
u
|
-0.551465
|
|
p
|
0.463794
|
|
m
|
0.119463
|
|
ó
|
0.462448
|
|
s
|
2.042618
|
|
|
|
|
|
Log likelihood
|
-81.88656
|
|
|
|
|
Source : Nos
calculs sur Eviews
Tableau : Estimation des
paramètres du modèle sans sauts (femmes)
|
Modèle sans sauts
|
|
|
|
|
|
paramètres
|
estimations
|
|
|
|
|
|
u
|
-0.551453
|
|
ó
|
1.467113
|
|
|
|
|
|
Log likelihood
|
-90.11268
|
|
|
|
|
Source : Nos
calculs sur Eviews
VI. Conclusion
Le but de ce travail a été de mettre en oeuvre
un modèle stochastique qui prenne en compte les caractéristiques
économiques, sociales et politiques des pays en voie de
développement dans la dynamique de la mortalité. Le modèle
devrait donc intégrer à la fois les spécificités
des sous groupes homogènes de la population et le temps. Par ailleurs,
le processus de diffusion de saut permettrait de capter les
événements extrêmes et leurs impacts.
Nous avons d'abord mis en oeuvre le modèle
logbilinéare de Lee Carter. L'objectif principal était d'extraire
la composante tendancielle relative au temps puis de la formaliser à
l'aide d'un modèle stochastique. Pour ce faire trois approches sont en
général utilisées : l'approche sans sauts qui suppose
que la probabilité de survenance d'un événement
extrême est nulle, l'approche avec sauts à effets transitoires et
l'approche avec sauts à effets permanents.
Nous retiendrons que l'approche la plus vraisemblable dans le
cadre de la modélisation stochastique de la mortalité dans les
pays en voie de développement est celle qui suppose que les
événements extrêmes qui affectent la vie des populations
ont des effets qui se propagent durablement dans le temps.
Il ressort également que l'évolution de la
mortalité observée dans les pays sous développé
diffère largement de celle observé dans les pays
développés. En effet, contrairement aux pays
développés, l'effet moyen des chocs est négatif sur la
dynamique de la mortalité. Ensuite la persistance de ceux-ci vient
s'opposer à la réduction continue des taux de
décès. Ainsi, ces taux convergent-ils vers une valeur strictement
supérieure à zéro à la différence de ceux
des pays développés qui tendent vers zéro.
Dans notre application, nous avons utilisé les
données d'un seul pays en voie de développement pour des raisons
d'indisponibilité de données. L'extrapolation des
résultats aux autres pays sous développés s'est faite sous
l'hypothèse que ces pays ont sensiblement les mêmes
caractéristiques socio politiques et économiques. Il serait donc
intéressant, dans les travaux futurs allant dans le même sens,
d'entrer en possession de données supplémentaires pour pousser
plus loin les analyses. Ce qui permettra de comprendre mieux l'évolution
de la mortalité des pays en voie de développement.
VII. Annexes
Annexe 1 : La fonction de vraisemblance du
modèle avec sauts à effets permanents 34
Annexe 2 : Estimation du modèle de Lee
Carter (codes matlab) 35
VIII. Annexe 1 : La fonction de
vraisemblance du modèle avec sauts à effets permanents
Nous avions écrit dans la partie B2 du chapitre
3 :
· Si , la variable suit une loi normale de moyenne et
de variance .
· Si , la variable suit une loi normale de moyenne et
de variance .
La fonction de densité de s'écrit :
Soit
Avec K observations et h=1, la logvraisemblnce du
modèle s'écrit :
)
IX. Annexe 2 :
Estimation du modèle de Lee Carter (codes matlab)
matrixD=input ('entrer matrice des décès D (x,t)'
);
matrixE=input ('entrer matrice des vivants E (x,t)' );
%convergence est l'erreur dans la reestimation des kt
convergence= input('entrer convergence' );
%logtauxbrut est la matrice log des taux brut de
mortalité(x=age,t=année)
% taille est une matrice 1x2 (nombre de groupe d'age,nombr
d'année)
logtauxbrut=log(matrixD./matrixE);
taille=size(logtauxbrut);
%construction de la matrice alpha (estimation des alpha)
for i=1:taille(1,1)
alpha(i)=(1/(taille(1,2))*sum(logtauxbrut(i,:)));
end;
%Z est le centrage des logtauxbrut par rapport a leur moyenne
temporelle
%construction de la matrice Z
for i=1:taille(1,1)
for j=1:taille(1,2)
Z(i,j)=logtauxbrut(i,j)-alpha(i);
end
end
%decomposition en valeure singulière de Z
[U,S,V] = svd(Z);
% le taux d'inertie mesure la qualite de l'approximation
%c'est le pourcentage de variance expliqué
tauxinertie=S(1,1)/trace(S);
%construction des vecteurs beta et k (estimation des beta et
kt)
beta=(1/sum(U(:,1))).*U(:,1);
k=S(1,1)*sum(U(:,1)).*V(:,1);
%reestimation des k(t)
for t=1:51
x=k(t);
while
abs(sum((matrixE(:,t).*(exp(alpha').*exp((x*beta))))-matrixD(:,t)))>convergence
x=x-(sum((matrixE(:,t).*(exp(alpha').*exp((x*beta))))-matrixD(:,t))/sum(matrixE(:,t).*(exp(alpha').*(beta.*exp((x*beta))))));
end
nkt(t)=x;
end
disp('le pourcentage de variance expliqué est:')
tauxinertie
disp('les matrices alpha, beta et k sont:')
alpha
beta
nkt
X. Bibliographie
Hua Chen. Contingent claim pricing with applications to
financial risk management. A Dissertation Submitted in Partial Fulfillment
of the Requirements for the Degree of Doctor of Philosophy in the Robinson
College of Business of Georgia State University, 47-81, 2008.
Arnaud At et al. Création de tables de mortalité
prospective en France. Mémoire de statistique appliquée,
ENSAE 2004.
El Horr Rawan et al. Modèle de mortalité
prospectif avec dérive contrainte. Groupe de travail, ISFA
2007.
F. Montes et R. Sala. A comparison of parametric models for
mortality graduation. Application to mortality data for the Valencia Region
(Spain). SORT 29 (2), 269-288, July-December 2005.
Siu Hang Li. Stochastic Mortality Models with Applications in
Financial Risk Management. Thesis, University of waterloo, Canada
2007.
Xiaoming Liu. Stochastic Mortality Modeling. Ph.D. Thesis,
Department of Statistics, University of Toronto, 2008.
Arnold L. Stochastic Differential Equations: Theory and
Applications. New York: John Wiley, 1974.
Edviges Coelho. The Lee - Carter Method for Forecasting
Mortality-The Portuguese experience. Instituto Nacional de
Estatística ,Portuga, 2000.
LEE R.D., CARTER L. Modelling and forecasting the time series
of US mortality. Journal of the American Statistical Association, vol.
87,659-671, 1992.
* 1 _ PVD : pays en voie
de développement
* 2 _ PD : pays
développés
* 3 _ Si la population est
suffisamment grande, alors le nombre probable de vivants à l'âge
x + t est une bonne estimation du nombre de survivants du
groupe initial à l'âge x + t
* 4 _ American Council of Life
Insurers (Association des compagnies américaines d'assurance vie).
* 5 _ La valeur critique 11.34
du chi deux à 3 degrés de libertés (alpha=0.01) est
inférieure à la statistique -2*
log(L1/L0)= -22,9



